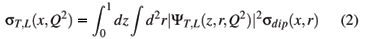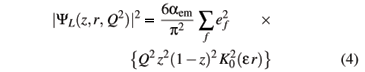Abstract
We study the predictions of CGC physics for electron-ion collisions at high energies. The nucleus at high energies acts as an amplifier of saturation effects. We have investigated some observables, using a generalization for nuclear targets of the Iancu-Itakura-Munier model, and our results indicate that the experimental analysis of these observables in the future electron-ion collider could discriminate between linear and saturation physics, as well as constrain the behavior of the saturation scale.
Electron-ion collisions; Saturation physics; Color dipole formalism
Nuclear dependence of the saturation scale and its consequences for the electron-ion collider
V. P. GonçalvesI; M. S. KugeratskiII; F. S. NavarraII
IInstituto de Física e Matemática, Universidade Federal de Pelotas Caixa Postal 354, CEP 96010-090, Pelotas, RS, Brazil
IIInstituto de Física, Universidade de São Paulo, C.P. 66318, 05315-970 São Paulo, SP, Brazil
ABSTRACT
We study the predictions of CGC physics for electron-ion collisions at high energies. The nucleus at high energies acts as an amplifier of saturation effects. We have investigated some observables, using a generalization for nuclear targets of the Iancu-Itakura-Munier model, and our results indicate that the experimental analysis of these observables in the future electron-ion collider could discriminate between linear and saturation physics, as well as constrain the behavior of the saturation scale.
Keywords: Electron-ion collisions; Saturation physics; Color dipole formalism
I. INTRODUCTION
The search for signatures of parton saturation effects has been subject of an active research in the last years (for recent reviews see, e.g. [1]). It has been observed that HERA data in the small x and low Q2 region can be successfully described with saturation models [2-4]. Moreover, the experimentally measured total cross sections [5] and charm production cross section [6] present the property of geometric scaling. The recently observed [7] supression of high pT hadron yields at forward rapidities in dAu collisions at RHIC follows the behavior anticipated on the basis of CGC ideas [8-11]. All these results provide strong evidence for saturation at HERA and RHIC. However, more definite conclusions are not possible due to the small value of the saturation scale in the kinematical range of HERA and due to the complexity of dAu collisions, where we need to consider the substructure of the projectile and the target, as well as the fragmentation of the produced partons. So far, other models (without saturation included) are able to describe the same set of data (see e.g. Refs. [12, 13]). In order to discriminate between these different models and test the CGC physics, it would be very important to consider an alternative search. To this purpose, the future electron-nucleus eRHIC collider is ideal, because it can probably determine whether parton distributions saturate or not and constrain the behavior of the nuclear gluon distribution. After the eRHIC was proposed, it became crucial to have some quantitative estimates of the impact of saturation effects on observables. Some of these estimates can be found in [14-16].
In the following section we present the color dipole formalism. In the next section we introduce the saturation scale and its possible nuclear dependences. In sequence, a comparison of the results of the model with available data on  is shown, as well as the estimate of saturation effects on the nuclear structure function. Finally, we present our conclusions.
is shown, as well as the estimate of saturation effects on the nuclear structure function. Finally, we present our conclusions.
II. DIPOLE FORMALISM
At small x, Deep Inelastic Scattering (DIS) is most conveniently computed with the dipole formalism. The virtual photon splits into a quark anti-quark dipole, which interacts with the target [17]. In this formalism the structure function of the target can be expressed as:
where
with
and
The last two expressions represent the squared photon wave function for transverse (T) and longitudinal (L) photons, respectively. The variable r defines the relative transverse separation of the pair (dipole) and z (1-z) is the longitudinal momentum fraction of the quark (antiquark). The auxiliary variable e2 = z(1-z) Q2 +  depends on the quark mass, mf. The K0,1 are the McDonald functions and the summation is performed over the quark flavors.
depends on the quark mass, mf. The K0,1 are the McDonald functions and the summation is performed over the quark flavors.
At high energy [18-20], sdip can be computed in the eikonal approximation and it is given by:
where  (x, r, b) is the forward scattering amplitude for a dipole with size r and impact parameter b. Here we assume that the impact parameter dependence of
(x, r, b) is the forward scattering amplitude for a dipole with size r and impact parameter b. Here we assume that the impact parameter dependence of  can be factorized as
can be factorized as  (x, r, b) =
(x, r, b) =  (x, r) S(b). So, sdip(x, r) = s0
(x, r) S(b). So, sdip(x, r) = s0 (x, r), with s0 = 2 p
(x, r), with s0 = 2 p (Rp is the proton radius).
(Rp is the proton radius).
In the IIM parametrization [4] the dipole-target forward scattering amplitude was assumed to have the form:
where Qs is the saturation scale discussed in the next section. The expression in the second line of Eq. (4) has the correct functional form for r » 2/Qs, as obtained either by solving the BK equation [18, 21] or from the theory of the CGC [1]. This is strictly valid only to LO accuracy, but here it is used merely as a convenient interpolation. The details of this interpolation are unimportant for the calculation of sg*p. The coefficients a and b are determined uniquely from the condition that  (r Qs,Y) and its slope be continuous at rQs = 2. The overall factor
(r Qs,Y) and its slope be continuous at rQs = 2. The overall factor  0 in the first line of Eq. (4) is ambiguous, reflecting an ambiguity in the definition of Qs. The coefficients gs and k are fixed to their LO BFKL values: gs = 0.63 and k = 9.9.
0 in the first line of Eq. (4) is ambiguous, reflecting an ambiguity in the definition of Qs. The coefficients gs and k are fixed to their LO BFKL values: gs = 0.63 and k = 9.9.
III. SATURATION SCALE
The saturation momentum, Qs (x), is the value of the transverse momentum below which saturation effects are expected to be important in the gluon distribution. It can be estimated in a simple geometrical way. Let's assume that the transverse area of one gluon in the target is approximately given by as/Q2 and that the number of gluons (per unit rapidity) ''seen'' by an external probe is x G(x,Q2). The area occupied by all these gluons is as/Q2x G(x,Q2). When this area becomes comparable to the total geometrical area of the target, p , saturation sets on. This matching of areas gives an equation, which can be solved for Q yielding the especial value Qs:
, saturation sets on. This matching of areas gives an equation, which can be solved for Q yielding the especial value Qs:
where x0 = 0.3 ×10-4 and l = 0.29. For a nuclear target we expect that, in a first approximation, x G(x,Q2) ® A x G(x,Q2), Rp® RA = Rp A1/3 and thus, from (4) we have:
Moreover, we may generalize the IIM model to nuclear collisions assuming the following basic transformation for the parameter s0:
These two transformations define what we call model IIM1. For comparison we also consider another A-dependence of the saturation momentum, which was suggested in [22]
where d = 0.79. Notice that, with this choice for d the A dependence of Qs becomes stronger. This feature arises from the inclusion of the impact parameter in all calculations, as done in [22]. The transformations (6) and (7) define the model IIM2. Further studies of the A-dependence of Qs can be found in Refs. [23, 24].
IV. RESULTS AND DISCUSSION
In this section we calculate the ratio:
where D = deuteron, with the models IIM1 and IIM2 and compare the results with the experimental data, taken by the Fermilab E665 collaboration, using inelastically scattered muons of average incident momentum 470 GeV/c []. These data, taken over a wide kinematic range, have shown that the proton and neutron structure functions are modified by a nuclear environment. The modifications depends on the parton momentum fraction: for momentum fractions x < 0.1 and 0.3 < x < 0.7, a depletion is observed in the nuclear structure functions. The low x (shadowing region) and the larger x (EMC region) are bridged by an enhancement known as antishadowing for 0.1 < x < 0.3. We refer to the entire phenomena as the nuclear shadowing effect [27]. As shown in Ref. [26] these effects can be described by the DGLAP evolution equation with a suitable set of nonperturbative initial conditions. Another possibility to describe the small-x behavior of the ratio R is to consider multiple scattering of the projectile on several target nucleons using Glauber-Gribov approach [24]. Here we are interested in the low-x region (x < 10-3), where it is believed that the behavior of R should be determined by high density QCD and parton saturation effects. In our approach we do not include higher-x corrections and rather try to understand the behavior of R in terms of parton saturation. Strictly speaking, our formalism is valid only in the very low x region, whereas the available data exist only in the intermediate x region. In order to have an idea of how well our results can reproduce the data we have to extrapolate them to intermediate x region. In doing this, we move to the region dominated by the linear regime, where saturation is not important and the dipole scattering amplitude is dominated by the first line of expression (4). In this regime, denoted color transparency regime, the scattering amplitude should behave as (rQs)2. However a careful analysis of this expression shows that the parenthesis in the exponent never becomes equal to one (!) and thus the (rQs)2 behavior is never really reached. This is a limitation of the IIM parametrization which is only valid in the saturation and extended geometric scaling regimes. In our present exercise we insist on the comparison with data, which are in general outside of these regimes. Therefore we have some freedom to play a bit with the parameters of (4). Making use of this freedom, we have multiplied the ratio R by a constant so that, at the point x = 0.1, it coincides with one, in agreement with experimental data. Since F2 is a function of Q2 this adjust has to be done for each value of Q2.
In Fig. 1, we show the ratio R computed with both models, IIM1 and IIM2, as a function of x [Fig. 1(a)] and Q2 [Fig. 1(b)] for a lead nucleus (A = 208). As expected the IIM2 model has a stronger dependence with A and therefore a larger deviation from R = 1. For comparison we also show the ratio R calculated with the EKS parametrization [26] of the ratio of nuclear structure functions. This parametrization comes from a global fit of the nuclear experimental data using DGLAP evolution. Notice that, as mentioned above, at x = 0.1 the EKS curve approaches one. Our curves IIM1 and IIM2 were constrained to pass through this point as well.
The main difference between the predictions is the behavior of the ratio R at small x. EKS predicts that the ratio is constant, and the IIM1 and IIM2 predict that the ratio still decreases in this limit (small x). We can see that for R as a function of Q2, the predictions differ significantly. This behavior arises because EKS is directly related to DGLAP evolution and the IIM1 and IIM2 models are associated to the saturation and geometric scaling regimes.
The deviation of R from one in the region 0.01 < x < 0.1 comes from the non-trivial A dependence of the dipole cross section [Eqs. (5) and (7)]. In this region our Ansatz, (5) or (7), leads to results similar to those obtained with for with the Glauber-Gribov approach [27], although they are independent from each other.
In Fig. 2 we show the ratio R as a function of x for a lead nucleus A = 208. On the top of the figure we have included the values of Q2, which are different for each x. The model IIM1 (IIM2) is represented by the dashed (dash-dotted) line. As it can be seen both models agree reasonably well with the data, especially considering that, apart from a normalization factor there was no free parameter.
In order to obtain a more precise estimate of modification in the observables F2 and FL by saturation physics, in Fig. 3 and Fig. 4 we present the ratios RF2 and  of full to linear predictions for nuclear structure function
of full to linear predictions for nuclear structure function  and
and  . We consider two typical values of the atomic number. As expected, the contribution of the saturation physics increases at larger nuclei and smaller values of x. In particular, for values of x around 10-5, we predict a reduction of about 50% in the total and longitudinal structure functions.
. We consider two typical values of the atomic number. As expected, the contribution of the saturation physics increases at larger nuclei and smaller values of x. In particular, for values of x around 10-5, we predict a reduction of about 50% in the total and longitudinal structure functions.
V. SUMMARY & CONCLUSIONS
In this work we have studied the predictions of CGC physics for electron-ion collisions at high energies, using a generalization for nuclear targets of Iancu-Itakura-Munier model. We have estimated the ratio of the nuclear to the deuteron (or proton) structure functions. We have compared our results with experimental data from the E665 collaboration and also with the EKS parametrization. Although the EKS formula does not include saturation physics and although the E665 data are taken at too low energy (for saturation effects to be dominant), the reached values of x and Q2 fall already in the saturation domain, justifying the comparison. For the sake of a preliminary estimate of saturation efects in an electron-ion collider we have computed, with the existent nuclear dependent saturation scales, the ratio of the F2 and FL structure functions, finding a strong reduction (@ 50 %) of these ratios. The impact of these results encourages us to further study the subject.
[1] E. Iancu and R. Venugopalan, hep-ph/0303204; J. Jalilian-Marian and Y. V. Kovchegov, Prog. Part. Nucl. Phys. 56, 104 (2006).
[2] K. Golec-Biernat and M. Wüsthoff, Phys. Rev. D 59, 014017 (1999), ibid. D 60, 114023 (1999).
[3] J. Bartels, K. Golec-Biernat, and H. Kowalski, Phys. Rev. D 66, 014001 (2002).
[4] E. Iancu, K. Itakura, and S. Munier, Phys. Lett. B 590, 199 (2004).
[5] A. M. Sta\'sto, K. Golec-Biernat, and J. Kwieci\'nski, Phys. Rev. Lett. 86, 596 (2001).
[6] V. P. Gonçalves and M. V. T. Machado, Phys. Rev. Lett. 91, 202002 (2003).
[7] I. Arsene et al. [BRAHMS Collaboration], ''Transverse momentum spectra in Au + Au and d + Au collisions at s(NN)**(1/2) = 200-GeV and the pseudorapidity dependence of high p(T) suppression,'' Phys. Rev. Lett. 91, 072305 (2003); Phys. Rev. Lett. 93, 242303 (2004); Phys. Rev. Lett. 94, 032301 (2005); nucl-ex/0410020.
[8] R. Baier, A. Kovner, and U. A. Wiedemann, ''Saturation and parton level Cronin effect: Enhancement vs suppression of gluon production in p A and A A collisions,'' Phys. Rev. D 68, 054009 (2003); J. Jalilian-Marian, Y. Nara and R. Venugopalan, ''The Cronin effect, quantum evolution and the color glass condensate,'' Phys. Lett. B 577, 54 (2003); D. Kharzeev, Y. V. Kovchegov, and K. Tuchin, ''Cronin effect and high-p(T) suppression in p A collisions,'' Phys. Rev. D 68, 094013 (2003); J. L. Albacete, N. Armesto, A. Kovner, C. A. Salgado, and U. A. Wiedemann, ''Energy dependence of the Cronin effect from non-linear QCD evolution,'' Phys. Rev. Lett. 92, 082001 (2004); E. Iancu, K. Itakura, and D. N. Triantafyllopoulos, ''Cronin effect and high-p(T) suppression in the nuclear gluon distribution at small x,'' Nucl. Phys. A 742, 182 (2004).
[9] A. Dumitru, A. Hayashigaki, and J. Jalilian-Marian, ''The color glass condensate and hadron production in the forward region,'' Nucl. Phys. A 765, 464 (2006); Nucl. Phys. A 770, 57 (2006).
[10] D. Kharzeev, Y.V. Kovchegov, and K. Tuchin, Phys. Lett. B 599, 23 (2004).
[11] V. P. Gonçalves, M. S. Kugeratski, M. V .T. Machado, and F. S. Navarra, Phys. Lett. B 643, 273 (2006).
[12] J. R. Forshaw, G. Kerley, and G. Shaw, ''Extracting the dipole cross-section from photo- and electro-production total cross-section data,'' Phys. Rev. D 60, 074012 (1999); J. R. Forshaw, G. R. Kerley, and G. Shaw, ''Predicting F2(D(3)) from the dipole cross-section,'' Nucl. Phys. A 675, 80C (2000).
[13] R. C. Hwa, C. B. Yang, and R. J. Fries, ''Forward production in d + Au collisions by parton recombination,'' Phys. Rev. C 71, 024902 (2005); J. w. Qiu and I. Vitev, ''Coherent QCD multiple scattering in proton nucleus collisions,'' Phys. Lett. B B=632, 507 (2006); B. Z. Kopeliovich, J. Nemchik, I. K. Potashnikova, M. B. Johnson, and I. Schmidt, Phys. Rev. C 72, 054606 (2005). ''Breakdown of QCD factorization at large Feynman x,''
[14] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 44, 577 (2005).
[15] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 46, 413 (2006).
[16] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 46, 465 (2006).
[17] V. Barone and E. Predazzi, High-Energy Particle Diffraction, Springer-Verlag, Berlin Heidelberg, (2002).
[18] I. I. Balitsky, Nucl. Phys. B 463, 99 (1996), Phys. Rev. Lett. 81, 2024 (1998), Phys. Rev. D 60, 014020 (1999), Phys. Lett. B 518, 235 (2001); I.I. Balitsky and A.V. Belitsky, Nucl. Phys. B 629, 290 (2002).
[19] E. Iancu, A. Leonidov, and L. McLerran, Nucl. Phys. A692, 583 (2001); E. Ferreiro, E. Iancu, A. Leonidov, and L. McLerran, Nucl. Phys. A 701, 489 (2002).
[20] J. Jalilian-Marian, A. Kovner, L. McLerran, and H. Weigert, Phys. Rev. D 55, 5414 (1997); J. Jalilian-Marian, A. Kovner, and H. Weigert, Phys. Rev. D 59, 014014 (1999), ibid. 59, 014015 (1999), ibid. 59 034007 (1999); A. Kovner, J. Guilherme Milhano, and H. Weigert, Phys. Rev. D 62, 114005 (2000); H. Weigert, Nucl. Phys. A 703, 823 (2002).
[21] Y.V. Kovchegov, Phys. Rev. D 60, 034008 (1999), ibid. 61 074018 (2000).
[22] N. Armesto, C.A. Salgado, and U.A. Wiedemann, Phys. Rew. Lett. B 94, (2005) 022002.
[23] A. H. Mueller, Nucl. Phys. A 724, 223 (2003).
[24] N. Armesto, Eur. Phys. J. C 26, 35 (2002).
[25] E665 Collaboration: M.R. Adams et al., Z. Phys. C 67, 403 (1995).
[26] K. J. Eskola, V. J. Kolhinen, and C. A. Salgado, Eur. Phys. J. C 9, 61 (1999).
[27] N. Armesto, J. Phys. G 32, R367 (2006).
Received on 29 September, 2006
References
- [1] E. Iancu and R. Venugopalan, hep-ph/0303204;
- J. Jalilian-Marian and Y. V. Kovchegov, Prog. Part. Nucl. Phys. 56, 104 (2006).
- [2] K. Golec-Biernat and M. Wüsthoff, Phys. Rev. D 59, 014017 (1999), ibid. D 60, 114023 (1999).
- [3] J. Bartels, K. Golec-Biernat, and H. Kowalski, Phys. Rev. D 66, 014001 (2002).
- [4] E. Iancu, K. Itakura, and S. Munier, Phys. Lett. B 590, 199 (2004).
- [5] A. M. Sta\'sto, K. Golec-Biernat, and J. Kwieci\'nski, Phys. Rev. Lett. 86, 596 (2001).
- [6] V. P. Gonçalves and M. V. T. Machado, Phys. Rev. Lett. 91, 202002 (2003).
- [7] I. Arsene et al. [BRAHMS Collaboration], ''Transverse momentum spectra in Au + Au and d + Au collisions at s(NN)**(1/2) = 200-GeV and the pseudorapidity dependence of high p(T) suppression,'' Phys. Rev. Lett. 91, 072305 (2003);
- Phys. Rev. Lett. 93, 242303 (2004);
- Phys. Rev. Lett. 94, 032301 (2005);
- nucl-ex/0410020.
- [8] R. Baier, A. Kovner, and U. A. Wiedemann, ''Saturation and parton level Cronin effect: Enhancement vs suppression of gluon production in p A and A A collisions,'' Phys. Rev. D 68, 054009 (2003);
- J. Jalilian-Marian, Y. Nara and R. Venugopalan, ''The Cronin effect, quantum evolution and the color glass condensate,'' Phys. Lett. B 577, 54 (2003);
- D. Kharzeev, Y. V. Kovchegov, and K. Tuchin, ''Cronin effect and high-p(T) suppression in p A collisions,'' Phys. Rev. D 68, 094013 (2003);
- J. L. Albacete, N. Armesto, A. Kovner, C. A. Salgado, and U. A. Wiedemann, ''Energy dependence of the Cronin effect from non-linear QCD evolution,'' Phys. Rev. Lett. 92, 082001 (2004);
- E. Iancu, K. Itakura, and D. N. Triantafyllopoulos, ''Cronin effect and high-p(T) suppression in the nuclear gluon distribution at small x,'' Nucl. Phys. A 742, 182 (2004).
- [9] A. Dumitru, A. Hayashigaki, and J. Jalilian-Marian, ''The color glass condensate and hadron production in the forward region,'' Nucl. Phys. A 765, 464 (2006);
- Nucl. Phys. A 770, 57 (2006).
- [10] D. Kharzeev, Y.V. Kovchegov, and K. Tuchin, Phys. Lett. B 599, 23 (2004).
- [11] V. P. Gonçalves, M. S. Kugeratski, M. V .T. Machado, and F. S. Navarra, Phys. Lett. B 643, 273 (2006).
- [12] J. R. Forshaw, G. Kerley, and G. Shaw, ''Extracting the dipole cross-section from photo- and electro-production total cross-section data,'' Phys. Rev. D 60, 074012 (1999);
- J. R. Forshaw, G. R. Kerley, and G. Shaw, ''Predicting F2(D(3)) from the dipole cross-section,'' Nucl. Phys. A 675, 80C (2000).
- [13] R. C. Hwa, C. B. Yang, and R. J. Fries, ''Forward production in d + Au collisions by parton recombination,'' Phys. Rev. C 71, 024902 (2005);
- J. w. Qiu and I. Vitev, ''Coherent QCD multiple scattering in proton nucleus collisions,'' Phys. Lett. B B=632, 507 (2006);
- B. Z. Kopeliovich, J. Nemchik, I. K. Potashnikova, M. B. Johnson, and I. Schmidt, Phys. Rev. C 72, 054606 (2005). ''Breakdown of QCD factorization at large Feynman x,''
- [14] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 44, 577 (2005).
- [15] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 46, 413 (2006).
- [16] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 46, 465 (2006).
- [17] V. Barone and E. Predazzi, High-Energy Particle Diffraction, Springer-Verlag, Berlin Heidelberg, (2002).
- [18] I. I. Balitsky, Nucl. Phys. B 463, 99 (1996),
- Phys. Rev. Lett. 81, 2024 (1998),
- Phys. Rev. D 60, 014020 (1999),
- Phys. Lett. B 518, 235 (2001);
- I.I. Balitsky and A.V. Belitsky, Nucl. Phys. B 629, 290 (2002).
- [19] E. Iancu, A. Leonidov, and L. McLerran, Nucl. Phys. A692, 583 (2001);
- E. Ferreiro, E. Iancu, A. Leonidov, and L. McLerran, Nucl. Phys. A 701, 489 (2002).
- [20] J. Jalilian-Marian, A. Kovner, L. McLerran, and H. Weigert, Phys. Rev. D 55, 5414 (1997);
- J. Jalilian-Marian, A. Kovner, and H. Weigert, Phys. Rev. D 59, 014014 (1999), ibid. 59, 014015 (1999), ibid. 59 034007 (1999);
- A. Kovner, J. Guilherme Milhano, and H. Weigert, Phys. Rev. D 62, 114005 (2000);
- H. Weigert, Nucl. Phys. A 703, 823 (2002).
- [21] Y.V. Kovchegov, Phys. Rev. D 60, 034008 (1999), ibid. 61 074018 (2000).
- [22] N. Armesto, C.A. Salgado, and U.A. Wiedemann, Phys. Rew. Lett. B 94, (2005) 022002.
- [23] A. H. Mueller, Nucl. Phys. A 724, 223 (2003).
- [24] N. Armesto, Eur. Phys. J. C 26, 35 (2002).
- [25] E665 Collaboration: M.R. Adams et al., Z. Phys. C 67, 403 (1995).
- [26] K. J. Eskola, V. J. Kolhinen, and C. A. Salgado, Eur. Phys. J. C 9, 61 (1999).
- [27] N. Armesto, J. Phys. G 32, R367 (2006).
Publication Dates
-
Publication in this collection
24 Apr 2007 -
Date of issue
Mar 2007
History
-
Received
29 Sept 2006

 Nuclear dependence of the saturation scale and its consequences for the electron-ion collider
Nuclear dependence of the saturation scale and its consequences for the electron-ion collider