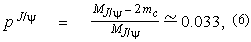Abstract
Recent DESY-HERA data on J/<FONT FACE="Symbol">Y</font> elasticity distribution show that it emerges mostly as a fast particle. Interpreting photoproduction as a collision between a pre-formed charmed hadron and the proton, the outcoming J/<FONT FACE="Symbol">Y</font> is a leading particle of the collision. We analyse these data using a model formulated to describe energy flow in hadron-hadron reactions. The measured J/<FONT FACE="Symbol">Y</font> spectrum can be successfully described in terms of this model. We conclude that the observed transparency of the charmed hadron-proton collisions arises because of the particularly small gluonic content of the initial c - <img src="http:/img/fbpe/bjp/v28n4/image200.gif" alt="Image200.gif (847 bytes)" align="absbottom"> state.
Leading particle effect in the J/y elasticity distribution
F.O. Durães1,2* * e-mail: fduraes@if.usp.br e-mail: navarra@if.usp.br e-mail: Grzegorz.Wilk@fuw.edu.pl 1 By gluonic clouds we understand a sort of "effective gluons'' which include also their fluctuations seen as sea pairs. , F.S. Navarra2,3 * e-mail: fduraes@if.usp.br e-mail: navarra@if.usp.br e-mail: Grzegorz.Wilk@fuw.edu.pl 1 By gluonic clouds we understand a sort of "effective gluons'' which include also their fluctuations seen as sea pairs. and G. Wilk3 * e-mail: fduraes@if.usp.br e-mail: navarra@if.usp.br e-mail: Grzegorz.Wilk@fuw.edu.pl 1 By gluonic clouds we understand a sort of "effective gluons'' which include also their fluctuations seen as sea pairs.
1Instituto Superior Técnico, Universidade Técnica de Lisboa
Av. Rovisco Pais 1, 1-1096 Lisboa Codex, Portugal
2Instituto de Física, Universidade de São Paulo
C.P. 66318, 05389-970 São Paulo, SP, Brazil
3Soltan Institute for Nuclear Studies, Nuclear Theory Department
ul.  69, 00-681 Warsaw, Poland
69, 00-681 Warsaw, Poland
Recent DESY-HERA data on J/Y elasticity distribution show that it emerges mostly as a fast particle. Interpreting photoproduction as a collision between a pre-formed charmed hadron and the proton, the outcoming J/Y is a leading particle of the collision. We analyse these data using a model formulated to describe energy flow in hadron-hadron reactions. The measured J/Y spectrum can be successfully described in terms of this model. We conclude that the observed transparency of the charmed hadron-proton collisions arises because of the particularly small gluonic content of the initial c -
state.
PACS number(s): 13.85.Qk, 11.55.Jy
The leading particle effect is one of the most interesting features of multiparticle production in hadron-hadron collisions [1]. In these reactions the valence quarks of the projectile emerge from the collision carrying the initial state quantum numbers. All produced particles come essentially from the gluons and quark-anti-quark pairs already pre-existing in the projectile and target, or radiated during the collision. This qualitative picture takes different implementations in the many existing multiparticle production models. In one of them, the Interacting Gluon Model (IGM) [2, 3, 4, 5], the produced particles (and consequently the energy released in the secondaries and lost by the projectiles) come almost entirely from the pre-existing gluons in the incoming hadrons. This conjecture may be directly tested using a high energy, nearly gluonless hadronic projectile. In this case, according to the IGM, inspite of the high energy involved, the production of secondaries would be suppressed (in comparison to the production observed in ordinary hadron induced reactions) and the energy would be mostly carried away by the projectile leading particle (LP) which would then be observed with a hard xF spectrum. This type of gluonless projectile is available in J/Y photoproduction, where the photon can be understood as a virtual c -  pair which reacts with the proton and turns into the finally observed J/Y. There are low energy data taken by the FTPS Collaboration [6] and very recently high energy data became available at HERA [7].
pair which reacts with the proton and turns into the finally observed J/Y. There are low energy data taken by the FTPS Collaboration [6] and very recently high energy data became available at HERA [7].
It has been shown by a number of authors that the simple vector meson dominance mechanism (VDM), in which the photon is converted directly to a J/Y before the interaction with the proton, does not describe many aspects of data. However, as it was shown in ref. [8], the charm anti-charm pair can be understood as a supperposition of many hadronic states: J/Y, Y¢, ... . Whereas relevant for the calculation of the cross sections, the inclusion of all the other charmonium states does not change the fact that the projectile, whatever it may be, is a hadron with low gluonic content. For the study of the outgoing J/Y momentum spectrum, this is the most important information, which allows us to test the picture proposed by the IGM.
At lower energies we can compare the momentum spectrum of the J/Y measured in gp ® J/Y X collisions [6] with the leading meson (p and K) momentum spectra measured [1] in p p ® p X and K p ® K X reactions at the same c.m.s. energy. One observes that the charmed leading particles are much harder. This comparison is however not completely meaningful because the J/Y data contain a diffractive component which was subtracted in the hadronic data.
At HERA a J/Y z (z = EJ/Y/Eg) spectrum presumably free from the diffractive component was presented. Although the energy is different a comparison with the leading particle spectra measured in hadronic reactions is still meaningful because the LP spectra have a relatively weak energy dependence. The J/Y momentum spectrum is clearly harder, according to what we expect in the IGM. The ¡ z spectra, which will be eventually measured at HERA in a near future, will be even harder.
In J/Y photoproduction, because of the large charm mass, perturbative QCD (PQCD) is expected to be valid. Indeed, all the main features of both J/Y hadro and photoproduction are well described by PQCD. However, in hadroproduction perturbative calculations fail at large xF [9], where non-perturbative effects become stronger. In the eighties charmonium production was studied with the color singlet model [10]. In the nineties this model was seen to fail badly when applied to Tevatron data. At the same time was developed the non-relativistic effective field theory of QCD, called just non-relativistic QCD (NRQCD) [11]. The main new feature of NRQCD is the introduction of the color octet components of the quarkonium wave function. In the HERA experiments, the z distributions have been studied using pT ³ 1 GeV. The surprising features of the comparisons [12] of the NRQCD results with data is that the color-singlet model prediction is in agreement with data while including the color-octet component leads to violent disagreement with the data at large z. In ref. [13] the failure of NRQCD was discussed and attributed to the pT kinematic cuts. At such small values of pT (and also for z very close to unity) there could be significant non-perturbative soft physics effects. The way, chosen in ref. [13], to parametrize these effects is to include the transverse momentum smearing of the partons inside the proton. In this way one introduces the effect of the "hadron walls''. The resulting z distributions become then flatter, in better agreement with data. The highest z data points, however, are still not accounted for. This situation justifies, in our opinion, the more phenomenological examination of these spectra given by the IGM.
We present now our quantitative calculations, which illustrate the qualitative discussion made above. The IGM is a model which has been developed primarily to analyse energy-momentum spectra of leading particles [2, 3, 4, 5]. This work continues therefore the application of the IGM to photon initiated reactions presented in [5] putting them on an equal footing with the hadronic processes studied before [2, 3] (including diffractive dissociation ones [4]).
In Fig. 1 we show schematically the IGM picture of a photon-proton collision. According to it, during the interaction the photon is converted into a hadronic state which interacts with the incoming proton. This hadronic state contains the c -  and some gluons and we call it simply "hadron''. The hadron-proton interaction follows then the usual IGM picture, namely: the valence quarks fly through essentially undisturbed whereas the gluonic clouds of both projectiles interact strongly with each other1
*
e-mail:
fduraes@if.usp.br
e-mail:
navarra@if.usp.br
e-mail:
Grzegorz.Wilk@fuw.edu.pl
1
By gluonic clouds we understand a sort of "effective gluons'' which include also their fluctuations seen as
sea pairs.
. In the course of interaction the hadronic state looses fraction x of its original momentum and gets excited forming what we call a leading jet (LJ) which carries fraction z = 1 - x of the initial momentum. The proton looses fraction y of its momentum forming another leading jet. In the IGM we consider two possible types of g+ p interactions: non-diffractive and diffractive. In each of these reactions the J/Y can come either from the fragmentation of the mesonic leading jet or from the hadronization of the central gluonic fireball. In this work we shall concentrate only on the data taken at HERA [7] for
and some gluons and we call it simply "hadron''. The hadron-proton interaction follows then the usual IGM picture, namely: the valence quarks fly through essentially undisturbed whereas the gluonic clouds of both projectiles interact strongly with each other1
*
e-mail:
fduraes@if.usp.br
e-mail:
navarra@if.usp.br
e-mail:
Grzegorz.Wilk@fuw.edu.pl
1
By gluonic clouds we understand a sort of "effective gluons'' which include also their fluctuations seen as
sea pairs.
. In the course of interaction the hadronic state looses fraction x of its original momentum and gets excited forming what we call a leading jet (LJ) which carries fraction z = 1 - x of the initial momentum. The proton looses fraction y of its momentum forming another leading jet. In the IGM we consider two possible types of g+ p interactions: non-diffractive and diffractive. In each of these reactions the J/Y can come either from the fragmentation of the mesonic leading jet or from the hadronization of the central gluonic fireball. In this work we shall concentrate only on the data taken at HERA [7] for  GeV2 and 0.5 £ z £ 0.9. In this case, it is enough to consider the single non-diffractively J/Y produced from the fragmentation of the photonic leading jet, cf. Fig. 1. All other contributions can be safely neglected here.
GeV2 and 0.5 £ z £ 0.9. In this case, it is enough to consider the single non-diffractively J/Y produced from the fragmentation of the photonic leading jet, cf. Fig. 1. All other contributions can be safely neglected here.
Figure 1. IGM description of a photon-proton scattering with J/y production.
In order to calculate this spectrum we start (cf., [4, 5] for details) with the function c(x, y), which describes the probability to form a central gluonic fireball (CF) carrying momentum fractions x and y of the two colliding projectiles:
where
Here c0 denotes the normalization factor provided by the requirement that  being the minimal inelasticity defined by the mass m0 of the lightest possible central fireball CF (represented by the blob in Fig. 1). The dynamical input of the IGM is contained in the, so called, spectral function w(x, y) given by
being the minimal inelasticity defined by the mass m0 of the lightest possible central fireball CF (represented by the blob in Fig. 1). The dynamical input of the IGM is contained in the, so called, spectral function w(x, y) given by
where G(x) and G(y) denote the effective number of gluons in the charmed hadron and in the proton, respectively. They are approximated by the respective gluonic structure functions. W is the photon-proton c.m. energy. sgg is the gluon-gluon cross section, which is computed over a wide range of scales given by xyW2. Whenever the scale is larger than 2.3 GeV lowest order perturbative QCD formulas are used. Otherwise a parametrization which represents non-perturbative physics is employed [2]. At the energies W considered here the bulk of the interaction happens in the non-perturbative domain. s is the relevant meson-proton cross section.
The final momentum spectrum of the produced J/Y is then given in terms of c(x, y) as follows:
where
and  is the J/Y energy fraction (which in the IGM, where all masses have been consistently neglected coincides with the momentum fraction). Because we are dealing here with the leading particle spectra, we have to introduce the additional kinematical constraint,
is the J/Y energy fraction (which in the IGM, where all masses have been consistently neglected coincides with the momentum fraction). Because we are dealing here with the leading particle spectra, we have to introduce the additional kinematical constraint,  , which ensures that the mass MX ( MX
, which ensures that the mass MX ( MX
 GeV2, to account for the minumum transverse momentum present at our data points).
GeV2, to account for the minumum transverse momentum present at our data points).
Whenever possible we keep all parameters the same as in the previous applications of the IGM [2]-[5]. However, the inelastic (c- ) - p scattering cross section and the number of gluons in the charmonium state are different from the corresponding quantities encountered so far.
) - p scattering cross section and the number of gluons in the charmonium state are different from the corresponding quantities encountered so far.
The charmonium-hadron cross section, which we shall approximate by  , has been subject of intensive research in the context of nuclear physics and signatures of quark gluon plasma. Calculations seem to converge to
, has been subject of intensive research in the context of nuclear physics and signatures of quark gluon plasma. Calculations seem to converge to  @ 6-9 mb [14]. As for the distribution G(x), which we may call GJ/y(x), we shall assume that it has the same shape as in other mesons, i.e., GJ/y(x) = Gr0(x) = Gp(x) and use, for the latter, the SMRS parametrization [15]. The specific shape chosen for these distributions does not affect much the results. Their normalization ph = ò01dx x Gh(x), i.e., the amount of momentum allocated to the gluonic component, plays, however, a crucial role here and we should try to estimate it somehow. It is known that in a nucleon or in a light meson ph
@ 6-9 mb [14]. As for the distribution G(x), which we may call GJ/y(x), we shall assume that it has the same shape as in other mesons, i.e., GJ/y(x) = Gr0(x) = Gp(x) and use, for the latter, the SMRS parametrization [15]. The specific shape chosen for these distributions does not affect much the results. Their normalization ph = ò01dx x Gh(x), i.e., the amount of momentum allocated to the gluonic component, plays, however, a crucial role here and we should try to estimate it somehow. It is known that in a nucleon or in a light meson ph  0.5 , i.e., gluons carry half of the momentum of the hadron. The charmonium, however, is a non-relativistic system and almost all its mass comes from the quark masses. The gluonic field, responsible for a weak binding, carries only a small fraction of the energy (and momentum) of the bound state. We expect therefore the normalization factor pJ/y of GJ/y(x) to be of the order of the energy stored in the field divided by the mass of the state. In the case of a J/y we have:
0.5 , i.e., gluons carry half of the momentum of the hadron. The charmonium, however, is a non-relativistic system and almost all its mass comes from the quark masses. The gluonic field, responsible for a weak binding, carries only a small fraction of the energy (and momentum) of the bound state. We expect therefore the normalization factor pJ/y of GJ/y(x) to be of the order of the energy stored in the field divided by the mass of the state. In the case of a J/y we have:
where mc has been taken 1.5 GeV and MJ/y = 3.1 GeV. In the IGM those two parameters are in fact entering only as a combination pJ/Y/ . Because out of those two quantities relevant here only the pJ/Y is so far completely unknown, we shall, in what follows, take for definiteness
. Because out of those two quantities relevant here only the pJ/Y is so far completely unknown, we shall, in what follows, take for definiteness  = 9 mb and leave pJ/Y to be a free parameter.
= 9 mb and leave pJ/Y to be a free parameter.
In Fig. 2 we compare our results (F(z)) with the experimental data. As it can be seen the agreement is very good and it was obtained with essentially only one new (but heavily constrained) parameter equal to the ratio of the amount of momentum carried by gluons in the c  state and its inelastic cross section with the proton. The observed flatteness comes (once
state and its inelastic cross section with the proton. The observed flatteness comes (once  is fixed) entirely from the small value of the pJ/Y parameter, what can be seen if we compare our best result (pJ/Y = 0.033) shown in the full line, with results for other values of pJ/Y. The dashed line represents the choice pJ/Y = 0.066 and the dotted line corresponds to pJ/Y = 0.016. Notice the high sensitivity of the results to the changes of the parameter pJ/Y.
is fixed) entirely from the small value of the pJ/Y parameter, what can be seen if we compare our best result (pJ/Y = 0.033) shown in the full line, with results for other values of pJ/Y. The dashed line represents the choice pJ/Y = 0.066 and the dotted line corresponds to pJ/Y = 0.016. Notice the high sensitivity of the results to the changes of the parameter pJ/Y.
Comparison of the IGM distribution F(z) with data of ref. [7] with restricted acceptance pT2³ 1 (GeV/c)2 and 0.5 £ z £ 0.9 for fixed value of
To summarize: assuming that the photon may be represented by a hadronic state containing a charm anti-charm pair, we have successfully described the leading spectra of photoproduced J/Y's in terms of the IGM. At the same time we have demonstrated that (again: within the IGM scheme) they depend crucially on the amount of momentum carried by gluons in the charmed hadron, pJ/Y (provided its cross section  with the nucleon is known from somewhere else, otherwise they depend of the ratio of these two parameters). It means that the knowledge of the leading spectra and the inelastic cross section should allow us to estimate the amount of the gluonic momenta in the projectile. For high energies (as those encountered here) this result is universal and insensitive to the mass of the projectile under consideration.
with the nucleon is known from somewhere else, otherwise they depend of the ratio of these two parameters). It means that the knowledge of the leading spectra and the inelastic cross section should allow us to estimate the amount of the gluonic momenta in the projectile. For high energies (as those encountered here) this result is universal and insensitive to the mass of the projectile under consideration.
Acknowledgements: This work has been supported by CNPq, CAPES and FAPESP under contract number 93/2463-2.
References
-
[1]
- EHS/NA22 Collab., N.H. Agababyan et al., Z. Phys. C75, 229 (1996). [2]
- F.O.Durães, F.S.Navarra and G.Wilk, Phys. Rev. D47, 3049 (1993) and references therein. [3]
- F.O.Durães, F.S.Navarra, C.A.A. Nunes and G.Wilk, Phys. Rev. D53, 6136 (1996). [4]
- F.O.Durães, F.S.Navarra and G.Wilk, Phys. Rev. D55 (1997) 2708. [5]
- F.O.Durães, F.S.Navarra and G.Wilk, Phys. Rev. D56, R2499 (1997). [6]
- B.H. Denby et al. Phys. Rev. Lett. 52, 795 (1984) . [7]
- S.Aid et al., (H1 Collab.), Nucl. Phys., B472, 3 (1996) ; M.Derrick et al. (ZEUS Collab.), Phys. Lett. B350, 120 (1995) ; J.Breitweg et al. (ZEUS Collab.), Z. Phys. C76, 599 (1997). [8]
- J.Hüfner and B.Z.Kopeliovich, J/YN and Y¢N total cross sections from photoproduction data: failure of vector dominance, hep-ph/9712297. [9]
- see for example P.E. Karchin, Hadroproduction of Charm and Beauty, hep-ph/9703331 - to appear in the Proc. of the XVI Int. Conf. on Physics in Collisions, Mexico City, 1996. [10]
- R. Baier and R. Ruckl, Z. Phys. C19, 251 (1983)1; E.L. Berger and D. Jones, Phys.Rev. D23, 2349 (1992) . [11]
- G.T. Bodwin, E. Braaten and G.P. Lepage, Phys.Rev. D51, 1125 (1995) . [12]
- Cf., for example, P.Hoyer, Nucl. Phys. A622, 284c (1997) and Charmonium production at ELFE energies, hep-ph/9702385, and references therein; M. Kramer, Nucl. Phys. B459, 3 (1996) ; M. Cacciari and M. Kramer, Phys. Rev. Lett. 76, 4128 (1996). [13]
- K. Sridhar, A.D. Martin, W.J. Stirling, J/Y production at the Tevatron and HERA: the effects of kT smearing, hep-ph/9806253. [14]
- D. Kharzeev and H. Satz, Phys. Lett. B366, 316 (1996) ; B356, 365 (1995) ; B334, 155 (1994). [15]
- P.J. Sutton, A.D. Martin, R.G. Roberts and W.J. Stirling, Phys.Rev. D45, 2349 (1992) .
- [7] S.Aid et al., (H1 Collab.), Nucl. Phys., B472, 3 (1996) ; M.Derrick et al. (ZEUS Collab.), Phys. Lett. B350, 120 (1995) ;
- [10] R. Baier and R. Ruckl, Z. Phys. C19, 251 (1983)1; E.L. Berger and D. Jones, Phys.Rev. D23, 2349 (1992) .
- [12] Cf., for example, P.Hoyer, Nucl. Phys. A622, 284c (1997) and Charmonium production at ELFE energies, hep-ph/9702385, and references therein;
- M. Kramer, Nucl. Phys. B459, 3 (1996) ; M. Cacciari and M. Kramer, Phys. Rev. Lett. 76, 4128 (1996).
 sea pairs.
sea pairs. Publication Dates
-
Publication in this collection
26 Aug 1999 -
Date of issue
Dec 1998