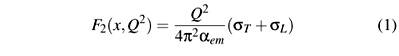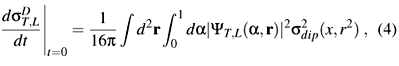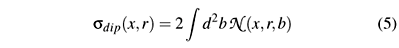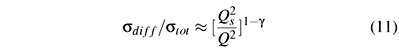Abstract
In this paper we investigate the saturation physics in diffractive deep inelastic electron-ion scattering. We estimate the energy and nuclear dependence of the ratio sigmadiff/sigmatot. We show that saturation physics predicts that up to 37 % of the events observed at eRHIC should be diffractive. We have also studied how our results depend on the prescription to extend the saturation scale to the nuclear case.
Nuclear diffraction; Dipole formalism; Saturation physics
SMALL-x PHYSICS AND DIFFRACTION
Saturation and the Ratio sdiff/stot in an electron-ion collider
V. P. GonçalvesI; M. S. KugeratskiII; F. S. NavarraII
IInstituto de Física e Matemática, Universidade Federal de Pelotas. Caixa Postal 354, CEP 96010-900, Pelotas, RS, Brazil
IIInstituto de Física, Universidade de São Paulo, C.P. 66318, 05315-970 São Paulo, SP, Brazil
ABSTRACT
In this paper we investigate the saturation physics in diffractive deep inelastic electron-ion scattering. We estimate the energy and nuclear dependence of the ratio sdiff/stot. We show that saturation physics predicts that up to 37 % of the events observed at eRHIC should be diffractive. We have also studied how our results depend on the prescription to extend the saturation scale to the nuclear case.
Keywords: Nuclear diffraction; Dipole formalism; Saturation physics
I. INTRODUCTION
Significant progress in understanding diffraction has been made at the ep collider HERA (See, e.g. Refs. [1]). Currently, there exist many attempts to describe the diffractive part of the deep inelastic cross section within pQCD (See, e.g. Refs. [2-4]). One of the most successful approaches is the saturation one [2] based on the dipole picture of DIS [5, 6]. It naturally incorporates the description of both inclusive and diffractive events in a common theoretical framework, as the same dipole scattering amplitude enters in the formulation of the inclusive and diffractive cross sections. As shown in Ref. [3], current data are not yet precise enough, nor do they extend to sufficiently small values of  , to discriminate between different theoretical approaches.
, to discriminate between different theoretical approaches.
Recently, in Refs. [7, 8], we have considered a set of inclusive observables which could be analyzed in a future electron-ion collider [9]. Our results have demonstrated that the saturation physics cannot be disregarded in the kinematical range of eRHIC. Our goal in this work is to understand to what extent the saturation regime of QCD manifests itself in diffractive deep inelastic eA scattering. In particular, we will study the energy and nuclear dependence of the ratio between diffractive and total cross sections (sdiff/stot).
Diffractive processes in eA collisions were studied in Refs. [10-14]. Here we extend these studies to a large number of observables, considering the dipole approach and a generalization for nuclear targets of the CGC dipole cross section proposed in Ref. [15]. As this model successfully describes the HERA data, we believe that it is possible to obtain realistic predictions for the kinematical range of the electron-ion collider eRHIC.
II. DIPOLE FORMALISM OF DIFFRACTIVE DIS
At small x, Deep Inelastic Scattering (DIS) is most conveniently computed with the dipole formalism. The virtual photon splits into a quark anti-quark dipole (represented by the quantity |YT,L (a, r, Q2)|2 ), which interacts with the target [1] (sdip(x, r) describes this interaction). In this formalism the structure function of the target can be expressed as:
where
Similarly, the total diffractive cross sections take on the following form (See e.g. Refs. [1, 2, 5])
where
and we have assumed a factorizable dependence on t with the diffractive slope BD.
At high energies [16, 17], sdip can be computed in the eikonal approximation and it is given by:
where  (x, r, b) is the forward scattering amplitude for a dipole with size r and impact parameter b. Here we assume that the impact parameter dependence of
(x, r, b) is the forward scattering amplitude for a dipole with size r and impact parameter b. Here we assume that the impact parameter dependence of  can be factorized as
can be factorized as  (x, r, b) =
(x, r, b) =  (x, r) S(b). So, sdip(x, r) = s0
(x, r) S(b). So, sdip(x, r) = s0 (x, r).
(x, r).
In the IIM parametrization [15] the dipole-target forward scattering amplitude was assumed to have the form:
where  = 0.7 and we will call the exponent in first line of Eq. (6) as geff. The expression in the second line of Eq. (6) has the correct functional form for r
= 0.7 and we will call the exponent in first line of Eq. (6) as geff. The expression in the second line of Eq. (6) has the correct functional form for r  2/Qs, as obtained either by solving the BK equation [16, 18] or from the theory of the CGC [19]. This is strictly valid only to LO accuracy, but here it is used merely as a convenient interpolation. The details of this interpolation are unimportant for the calculation of sg* p. The coefficients a and b are determined uniquely from the condition that
2/Qs, as obtained either by solving the BK equation [16, 18] or from the theory of the CGC [19]. This is strictly valid only to LO accuracy, but here it is used merely as a convenient interpolation. The details of this interpolation are unimportant for the calculation of sg* p. The coefficients a and b are determined uniquely from the condition that  (r Qs,Y) and its slope be continuous at rQs= 2. The overall factor
(r Qs,Y) and its slope be continuous at rQs= 2. The overall factor  in the first line of Eq. (6) is ambiguous, reflecting an ambiguity in the definition of Qs, which is given by:
in the first line of Eq. (6) is ambiguous, reflecting an ambiguity in the definition of Qs, which is given by:
where x = Q2/(W2 + Q2), W is the photon-proton (or photon-nucleus) center of mass energy,  = 1.0 GeV2 and the coefficients gs and k are fixed to their LO BFKL values: gs = 0.63 and k = 9.9. The only free parameters are s0, x0 and l, which were fixed by fitting the structure function F2, given by (1), to HERA data. This fit was performed in [15]. Since the dipole cross section is universal, i.e., the same for gp and pp scatterings, a better procedure would be to fit simultaneously HERA and RHIC data. The determination of a dipole cross section compatible with both sets of data was discussed in [20, 21].
= 1.0 GeV2 and the coefficients gs and k are fixed to their LO BFKL values: gs = 0.63 and k = 9.9. The only free parameters are s0, x0 and l, which were fixed by fitting the structure function F2, given by (1), to HERA data. This fit was performed in [15]. Since the dipole cross section is universal, i.e., the same for gp and pp scatterings, a better procedure would be to fit simultaneously HERA and RHIC data. The determination of a dipole cross section compatible with both sets of data was discussed in [20, 21].
In [7, 8] we have generalized the IIM model for nuclear collisions assuming the following basic transformations:
Another A dependence of the saturation scale was proposed in [22]:
where d = 0.79 and Rp = 0.641fm. When extending (3) to the nuclear case we need to change the slope BD to the nuclear slope parameter, BA. In the absence of more reliable information concerning BA we will assume that it may be approximated by BA =  , where RA is given by RA = 1.2 A1/3 fm [23].
, where RA is given by RA = 1.2 A1/3 fm [23].
III. RESULTS AND DISCUSSION
In order to obtain an approximate expression for the ratio sdiff/stot we will disregard the r-dependence of the effective anomalous dimension, i.e. geff = g = constant. In this case, we obtain:
Assuming g = 0.84, as in Ref. [15], we predict that the ratio decreases with the photon virtuality and presents a weak energy dependence. However, analyzing the A-dependence, we expect a growth of approximately 30 % when we increase A from 2 to 208.
In the ratio (11) both cross sections grow with the atomic number A, but the diffractive one, in the numerator, grows faster. This behavior comes from the dipole cross section and, more precisely, from the non-trivial A dependence of the saturation scale. The geometrical A dependence of the pre-factors s0 and BA cancels out. The approximate analytical behavior of (11) with A is discussed in more detail in [8].
In the kinematical range where Q2 <  the ratio of cross sections presents a similar behavior. The main difference is that in the asymptotic regime of very large energies the cross section for diffraction reaches the black disk limit of 50 % of the total cross section.
the ratio of cross sections presents a similar behavior. The main difference is that in the asymptotic regime of very large energies the cross section for diffraction reaches the black disk limit of 50 % of the total cross section.
In Fig. 1 we show the ratio sdiff/stot, as a function of W and x for different values of A. We have used (9) as the nuclear saturation scale. The black disk limit, sdiff/stot = 1/2, is also presented in the figure. We can see that the ratio depends weakly on W and on x but is strongly suppressed for increasing Q2. This suggests that in the deep perturbative region, diffraction is more suppressed. This same behavior was observed in diffractive ep data [24]. Moreover, the energy dependence of the ratio is remarkably flat, increasing with A, becoming up to 30 % larger for lead in comparison to deuteron. This behavior agrees qualitatively with the previous calculation of [12] and with our previous estimate. Similar results have been obtained in Ref. [10] in a different context. The appearance of a large rapidity gap in 37 % of all eA scattering events would be a striking confirmation of the saturation picture.
In order to check how sensitive the results of Fig. 1 are to the A dependence of the saturation scale, we calculate the same ratio using (10) instead of (9) and show the result in Fig. 2. As it can be seen in the figure, the two possible nuclear extentions of Qs, called IIM1 (with(9)) and IIM2 (with (10)), lead to similar results.
The two upper dot-dashed lines in the figure define a band which is a measure of the uncertainty associated with our poor knowledge of the A dependence of the saturation scale. There are several other uncertainties in our calculations: i) in expression (3) it is assumed that sD depends on t only through the multiplicative exponential factor exp (Bt); ii) equation (5) implies the eikonal approximation; iii) the factorization of the dipole amplitude  (x, r, b) =
(x, r, b) =  (x, r) S(b) is also an approximation; iv) eq. (6) is an assumption. Although the constants a, b, gs and k are fixed by requirements like continuity, analiticity and compatibility with HERA data, the mathematical form of (3) is not unique and we should test other forms. There is a systematic error to be estimated; v) the same can be said about the form assumed for the saturation scale, eq. (7); vi) the expression BA =
(x, r) S(b) is also an approximation; iv) eq. (6) is an assumption. Although the constants a, b, gs and k are fixed by requirements like continuity, analiticity and compatibility with HERA data, the mathematical form of (3) is not unique and we should test other forms. There is a systematic error to be estimated; v) the same can be said about the form assumed for the saturation scale, eq. (7); vi) the expression BA =  is also an assumption and contains some uncertainty. For the moment we are more interested in the central values of the predictions. In the future a refinement of these predictions will certainly include a complete estimate of the theoretical errors.
is also an assumption and contains some uncertainty. For the moment we are more interested in the central values of the predictions. In the future a refinement of these predictions will certainly include a complete estimate of the theoretical errors.
IV. SUMMARY & CONCLUSIONS
In this work we address nuclear diffractive DIS and the ratio sdiff/stot in the dipole picture. In particular, we have investigated the potential of eA collisions as a tool for revealing the details of the saturation regime. Since sdiff is proportional to  , diffractive processes are expected to be particularly sensitive to saturation effects. Moreover, due to the highly non-trivial A dependence of sdip, diffraction off nuclear targets is even more sensitive to non-linear effects. Without adjusting any parameter, we have found that the ratio sdiff/stot is a very flat function of the center-of-mass energy W, in good agreement with existing HERA data. Extending the calculation to nuclear targets, we have shown that this ratio remains flat and increases with the atomic number. At larger nuclei we predict that approximately 37 % of the events observed at eRHIC should be diffractive.
, diffractive processes are expected to be particularly sensitive to saturation effects. Moreover, due to the highly non-trivial A dependence of sdip, diffraction off nuclear targets is even more sensitive to non-linear effects. Without adjusting any parameter, we have found that the ratio sdiff/stot is a very flat function of the center-of-mass energy W, in good agreement with existing HERA data. Extending the calculation to nuclear targets, we have shown that this ratio remains flat and increases with the atomic number. At larger nuclei we predict that approximately 37 % of the events observed at eRHIC should be diffractive.
Acknowledgements
This work was partially financed by the Brazilian funding agencies CNPq, FAPESP and FAPERGS.
[1] V. Barone and E. Predazzi, High-Energy Particle Diffraction, Springer-Verlag, Berlin Heidelberg, (2002).
[2] K. Golec-Biernat and M. Wüsthoff, Phys. Rev. D 59, 014017 (1999); ibid. D 60, 114023 (1999).
[3] J. R. Forshaw, R. Sandapen, and G. Shaw, Phys. Lett. B 594, 283 (2004).
[4] A. D. Martin, M. G. Ryskin, and G. Watt, Eur. Phys. J. C 44, 69 (2005).
[5] N. N. Nikolaev and B. G. Zakharov, Z. Phys. C 49, (1991) 607; Z. Phys. C 53, 331 (1992).
[6] A. H. Mueller, Nucl. Phys. B 415, 373 (1994); A. H. Mueller and B. Patel, Nucl. Phys. B 425, 471 (1994).
[7] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 46, 465 (2006).
[8] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 46, 413 (2006).
[9] A. Deshpande, R. Milner, R. Venugopalan, and W. Vogelsang, Ann. Rev. Nucl. Part. Sci. 55, 165 (2005). Physics at HERA'', DESY, September 1995, arXiv:hep-ph/9610423.
[10] N. N. Nikolaev, B. G. Zakharov, and V. R. Zoller, Z. Phys. A 351, 435 (1995).
[11] Y. V. Kovchegov and L. D. McLerran, Phys. Rev. D 60, 054025 (1999); Erratum-ibid. D 62, 019901 (2000).
[12] E. Levin and M. Lublinsky, Nucl. Phys. A 712, 95 (2002).
[13] V. P. Gonçalves and M. V. T. Machado, Eur. Phys. J. C 30, 387 (2003).
[14] L. Frankfurt, V. Guzey, and M. Strikman, Phys. Lett. B 586, 41 (2004).
[15] E. Iancu, K. Itakura, and S. Munier, Phys. Lett. B 590, 199 (2004).
[16] I. I. Balitsky, Nucl. Phys. B 463, 99 (1996); Phys. Rev. Lett. 81, 2024 (1998); Phys. Rev. D 60, 014020 (1999).
[17] E. Iancu, A. Leonidov, and L. McLerran, Nucl.Phys. A 692, 583 (2001); E. Ferreiro, E. Iancu, A. Leonidov, and L. McLerran, Nucl. Phys. A 701, 489 (2002).
[18] Y.V. Kovchegov, Phys. Rev. D 60, 034008 (1999); ibid. 61 074018 (2000).
[19] E. Iancu and R. Venugopalan, QGP3, Eds. R.C. Hwa and X.N.Wang, World Scientific; hep-ph/0303204.
[20] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 44, 577 (2005).
[21] V. P. Gonçalves, M. S. Kugeratski, M. V. T. Machado, and F. S. Navarra, Phys. Lett. B 643, 273 (2006).
[22] N. Armesto, C. A. Salgado, and U. A. Wiedemann, Phys. Rev. Lett. 94, 022002 (2005).
[23] H. Abramowicz, L. Frankfurt, and M. Strikman, Surveys High Energ. Phys. 11, 51 (1997).
[24] S. Chekanov et al. [ZEUS Collaboration], Eur. Phys. J. C 38 (2004) and references therein.
Received on 31 October, 2006; revised version received on 26 February, 2007
- [1] V. Barone and E. Predazzi, High-Energy Particle Diffraction, Springer-Verlag, Berlin Heidelberg, (2002).
- [2] K. Golec-Biernat and M. Wüsthoff, Phys. Rev. D 59, 014017 (1999); ibid. D 60, 114023 (1999).
- [3] J. R. Forshaw, R. Sandapen, and G. Shaw, Phys. Lett. B 594, 283 (2004).
- [4] A. D. Martin, M. G. Ryskin, and G. Watt, Eur. Phys. J. C 44, 69 (2005).
- [5] N. N. Nikolaev and B. G. Zakharov, Z. Phys. C 49, (1991) 607;
- Z. Phys. C 53, 331 (1992).
- [6] A. H. Mueller, Nucl. Phys. B 415, 373 (1994);
- A. H. Mueller and B. Patel, Nucl. Phys. B 425, 471 (1994).
- [7] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 46, 465 (2006).
- [8] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 46, 413 (2006).
- [9] A. Deshpande, R. Milner, R. Venugopalan, and W. Vogelsang, Ann. Rev. Nucl. Part. Sci. 55, 165 (2005).
- Physics at HERA'', DESY, September 1995, arXiv:hep-ph/9610423.
- [10] N. N. Nikolaev, B. G. Zakharov, and V. R. Zoller, Z. Phys. A 351, 435 (1995).
- [11] Y. V. Kovchegov and L. D. McLerran, Phys. Rev. D 60, 054025 (1999); Erratum-ibid. D 62, 019901 (2000).
- [12] E. Levin and M. Lublinsky, Nucl. Phys. A 712, 95 (2002).
- [13] V. P. Gonçalves and M. V. T. Machado, Eur. Phys. J. C 30, 387 (2003).
- [14] L. Frankfurt, V. Guzey, and M. Strikman, Phys. Lett. B 586, 41 (2004).
- [15] E. Iancu, K. Itakura, and S. Munier, Phys. Lett. B 590, 199 (2004).
- [16] I. I. Balitsky, Nucl. Phys. B 463, 99 (1996);
- Phys. Rev. Lett. 81, 2024 (1998);
- Phys. Rev. D 60, 014020 (1999).
- [17] E. Iancu, A. Leonidov, and L. McLerran, Nucl.Phys. A 692, 583 (2001);
- E. Ferreiro, E. Iancu, A. Leonidov, and L. McLerran, Nucl. Phys. A 701, 489 (2002).
- [18] Y.V. Kovchegov, Phys. Rev. D 60, 034008 (1999); ibid. 61 074018 (2000).
- [19] E. Iancu and R. Venugopalan, QGP3, Eds. R.C. Hwa and X.N.Wang, World Scientific; hep-ph/0303204.
- [20] M. S. Kugeratski, V. P. Gonçalves, and F. S. Navarra, Eur. Phys. J. C 44, 577 (2005).
- [21] V. P. Gonçalves, M. S. Kugeratski, M. V. T. Machado, and F. S. Navarra, Phys. Lett. B 643, 273 (2006).
- [22] N. Armesto, C. A. Salgado, and U. A. Wiedemann, Phys. Rev. Lett. 94, 022002 (2005).
- [23] H. Abramowicz, L. Frankfurt, and M. Strikman, Surveys High Energ. Phys. 11, 51 (1997).
- [24] S. Chekanov et al. [ZEUS Collaboration], Eur. Phys. J. C 38 (2004) and references therein.
Publication Dates
-
Publication in this collection
10 Aug 2007 -
Date of issue
June 2007
History
-
Reviewed
26 Feb 2007 -
Received
31 Oct 2006