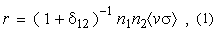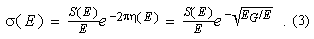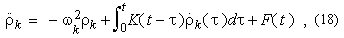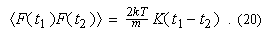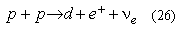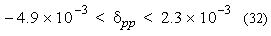Abstract
The physics of nuclear reactions in stellar plasma is reviewed with special emphasis on the importance of the velocity distribution of ions. Then the properties (density and temperature) of the weak-coupled solar plasma are analysed, showing that the ion velocities should deviate from the Maxwellian distribution and could be better described by a weakly-nonextensive (|q-1| < 0.02) Tsallis' distribution. We discuss concrete physical frameworks for calculating this deviation: the introduction of higher-order corrections to the diffusion and friction coefficients in the Fokker-Planck equation, the influence of the electric-microfield stochastic distribution on the particle dynamics, a velocity correlation function with long-time memory arising from the coupling of the collective and individual degrees of freedom. Finally, we study the effects of such deviations on stellar nuclear rates, on the solar neutrino fluxes, and on the pp neutrino energy spectrum, and analyse the consequences for the solar neutrino problem.
Thermal distributions in stellar plasmas, nuclear reactions and solar neutrinos
M. Coraddu1,2,* * Electronic address: massimo.coraddu@ca.infn.it Electronic address: kaniadakis@polito.it Electronic address: lavagno@polito.it § Electronic address: marcello.lissia@ca.infn.it ¶ Electronic address: giuseppe.mezzorani@ca.infn.it || Electronic address: quarati@polito.itemail1 1 We consider situations where quantum effects are negligible, e.g., in the solar plasma small quantum corrections to the statistics exist for electrons but not for ions. More generally, one could also analyse plasma corrections to the standard Fermi or Bose distributions. , G. Kaniadakis3, * Electronic address: massimo.coraddu@ca.infn.it Electronic address: kaniadakis@polito.it Electronic address: lavagno@polito.it § Electronic address: marcello.lissia@ca.infn.it ¶ Electronic address: giuseppe.mezzorani@ca.infn.it || Electronic address: quarati@polito.itemail1 1 We consider situations where quantum effects are negligible, e.g., in the solar plasma small quantum corrections to the statistics exist for electrons but not for ions. More generally, one could also analyse plasma corrections to the standard Fermi or Bose distributions. , A. Lavagno3,4, * Electronic address: massimo.coraddu@ca.infn.it Electronic address: kaniadakis@polito.it Electronic address: lavagno@polito.it § Electronic address: marcello.lissia@ca.infn.it ¶ Electronic address: giuseppe.mezzorani@ca.infn.it || Electronic address: quarati@polito.itemail1 1 We consider situations where quantum effects are negligible, e.g., in the solar plasma small quantum corrections to the statistics exist for electrons but not for ions. More generally, one could also analyse plasma corrections to the standard Fermi or Bose distributions. , M. Lissia2,1,§ * Electronic address: massimo.coraddu@ca.infn.it Electronic address: kaniadakis@polito.it Electronic address: lavagno@polito.it § Electronic address: marcello.lissia@ca.infn.it ¶ Electronic address: giuseppe.mezzorani@ca.infn.it || Electronic address: quarati@polito.itemail1 1 We consider situations where quantum effects are negligible, e.g., in the solar plasma small quantum corrections to the statistics exist for electrons but not for ions. More generally, one could also analyse plasma corrections to the standard Fermi or Bose distributions. , G. Mezzorani1,2,¶ * Electronic address: massimo.coraddu@ca.infn.it Electronic address: kaniadakis@polito.it Electronic address: lavagno@polito.it § Electronic address: marcello.lissia@ca.infn.it ¶ Electronic address: giuseppe.mezzorani@ca.infn.it || Electronic address: quarati@polito.itemail1 1 We consider situations where quantum effects are negligible, e.g., in the solar plasma small quantum corrections to the statistics exist for electrons but not for ions. More generally, one could also analyse plasma corrections to the standard Fermi or Bose distributions. , and P. Quarati3,2,|| * Electronic address: massimo.coraddu@ca.infn.it Electronic address: kaniadakis@polito.it Electronic address: lavagno@polito.it § Electronic address: marcello.lissia@ca.infn.it ¶ Electronic address: giuseppe.mezzorani@ca.infn.it || Electronic address: quarati@polito.itemail1 1 We consider situations where quantum effects are negligible, e.g., in the solar plasma small quantum corrections to the statistics exist for electrons but not for ions. More generally, one could also analyse plasma corrections to the standard Fermi or Bose distributions. ,
1Dipartimento di Fisica, Università di Cagliari, I-09042 Monserrato, Italy
2Istituto Nazionale di Fisica Nucleare, Sezione di Cagliari, I-09042 Monserrato, Italy
3Dipartimento di Fisica and INFM, Politecnico di Torino, I-10129 Torino, Italy
4Istituto Nazionale di Fisica Nucleare, Sezione di Torino, I-10125 Torino, Italy
Received 23 November, 1998
The physics of nuclear reactions in stellar plasma is reviewed with special emphasis on the importance of the velocity distribution of ions. Then the properties (density and temperature) of the weak-coupled solar plasma are analysed, showing that the ion velocities should deviate from the Maxwellian distribution and could be better described by a weakly-nonextensive (|q-1| < 0.02) Tsallis' distribution. We discuss concrete physical frameworks for calculating this deviation: the introduction of higher-order corrections to the diffusion and friction coefficients in the Fokker-Planck equation, the influence of the electric-microfield stochastic distribution on the particle dynamics, a velocity correlation function with long-time memory arising from the coupling of the collective and individual degrees of freedom. Finally, we study the effects of such deviations on stellar nuclear rates, on the solar neutrino fluxes, and on the pp neutrino energy spectrum, and analyse the consequences for the solar neutrino problem.
I Introduction
Thermonuclear reactions are of enormous importance for the physics of stars and of our Sun. The general formalism that describes these reactions exists since a long time and there is a wide consensus about our good understanding of the relevant physics [1, 2, 3].
However, quantitative calculations of specific reaction rates need experimental inputs and theoretical assumptions. Cross sections must be known. In the best cases, they can be directly measured at the relevant energies; other cross sections can be only measured at higher energies and need to be extrapolated; in some situations only theoretical predictions exist (for a recent review of the cross sections relevant to the Sun see Ref. [4]). In addition, rates depend on weighted thermal averages of the cross sections; therefore, knowledge about the thermal distribution is also needed.
Because many nuclear reactions in the stellar burning core proceed by way of quantum penetration of a high Coulomb barrier, their cross sections grow exponentially with energy. Therefore, thermal averages do not probe the average energy of the distribution (kT), but its high-energy tail. Consequently, rates are sensitive to a relatively small part of the distribution.
The ion velocity distribution in stellar calculations is always assumed Maxwellian1 * Electronic address: massimo.coraddu@ca.infn.it Electronic address: kaniadakis@polito.it Electronic address: lavagno@polito.it § Electronic address: marcello.lissia@ca.infn.it ¶ Electronic address: giuseppe.mezzorani@ca.infn.it || Electronic address: quarati@polito.itemail1 1 We consider situations where quantum effects are negligible, e.g., in the solar plasma small quantum corrections to the statistics exist for electrons but not for ions. More generally, one could also analyse plasma corrections to the standard Fermi or Bose distributions. . In fact, it is almost universally accepted as a fact that physical conditions in the solar interior (density and temperature) lead to an equilibrium velocity distribution that is Maxwellian. In this article we review the assumptions underlying this general statement, discuss why they are only approximately true, and argue that the consequent small corrections to the distribution have significant effects on the rates.
The dynamics of the solar plasma is not trivial, since at such densities and temperatures there is no clear scale separation between collective and individual degrees of freedom [5]. The presence of more than just one energy scale (kT) in the relevant range of energies results in deviations from the pure exponential behavior, exp(-E/kT), which is determined only by kT. We have tried several new approaches to this strongly interacting many-body system for which a realistic microscopic calculation does not exist yet.
In one approach [6, 7] we exploit the knowledge that the distribution in the solar interior cannot be too much different from the Maxwellian one and add small corrections (higher-order terms in a derivative expansion) to the coefficients of the standard Fokker-Planck equation. Tsallis' [9, 10] and Druyvenstein-like distributions are immediately generated.
A second approach [8] focuses on the electric microfields that have been shown to exists in plasmas and tries to link their distribution and the connected effective cross sections with deviations from the Maxwellian distribution. Different classes of microfields distributions and effective cross sections yield several non-Maxwellian distributions among which we again find Tsallis and Druyvenstein-like distributions.
The third approach has been just started and aims to connect the distribution of collective variables [11] to memory effects and long-time correlations between velocities. There should exist solutions compatible with the Tsallis' distribution and/or other non-Maxwellian distributions.
These three approaches are not exhaustive and not necessary alternative. Nevertheless, it is suggestive that all of them point in the same direction: the Maxwell-Boltzmann distribution of velocity should have small but nonnegligible corrections in the solar plasma and the Tsallis' distribution could provide a better description.
Nowadays solar modeling seems to have reached a satisfactory stage [1, 3, 12]. The inclusion in the latest models of higher-order effects, such as the diffusion of heavy elements, brings the theoretical predictions in good agreement even with the detailed helioseismological data [13, 14]. However, there still exist a discrepancy between the solar neutrino experiments and the predicted neutrino fluxes [15]. In this context, there has been a considerable amount of work devoted to answering questions such as: how large are the uncertainties of the solar model input parameters? Has something been left out of standard solar models? How does this affects predictions for the fluxes and the status of solar neutrino problem (SNP) [16, 17, 18, 19, 20, 21]?
Therefore, we find extremely important to assess the consequences of the possible small deviations from the standard statistics on the solar model and, in particular, on the neutrino fluxes. At least two effects should be considered: changes of the total rates caused by the different thermal average and modifications of the shape of the energy spectra. The effect on the rates was already considered by Clayton [22, 23] two decades ago. New experimental data, better solar models and a considerable better understanding of nonstandard distributions and of how they can arise in solar plasmas convinced us of the necessity of reconsider this earlier suggestion. Even if experimental detection of small modifications of the neutrino spectra might appear still far from being possible, it is useful to have a clear assessment of what the signal would be.
Our paper is organized as follows. In Sec. II we review the physics of subbarrier thermonuclear reactions and how the velocity distribution influences reaction rates. Section III, which is dedicated to the solar plasma, contains the central part of our work: three approaches to velocity distribution calculation and the resulting nonstandard distributions. In Sec.IV we calculate the reaction rates with the modified distributions, while we obtain the neutrino spectrum from the pp reaction in the presence of Tsallis' statistics and compare it to the standard one in Sec. V. The solar neutrino problem is analysed in the light of our results on nonstandard velocity distributions in Sec.VI, and Sec. VII is reserved to our conclusions.
II Thermonuclear reaction rates
Reliable calculations of nuclear reaction rates in stellar interiors is fundamental for a quantitative understanding of the structure and evolution of stars. In fact, while the overall stellar structure is rather robust, changes of some of the rates by few percent can produce detectable discrepancies, when precise measurements are possible, e.g., in the case of the solar photon and neutrino luminosity, and mechanical eigenfrequencies [24].
In this Section, we review the basic physics underlying thermonuclear reactions and the main ingredients of their calculation [1].
A. Introduction
Let us consider a gas with n1 particles of type 1 and n2 particles of type 2 per cubic centimeter and relative velocity v; the reaction rates r (the number of reactions per unit volume and unit time) is given by
where s = s(v) is the nuclear cross section of the reaction. The reaction rate per particle pair is defined as
where the particles distribution function f(v) is a local function of the temperature.
Therefore, the reaction rate per particle pair ávsñ is determined by the specific cross section and by the velocity distribution function of the incoming particles. In general, cross sections do not have very strong dependence on the energy, when no energy barrier is present and away from resonances. Therefore, most of the contribution to ávsñ comes from particles with energy of the order of kT, and the dependence on the specific form of f(v) is weak. We shall see that the situation is very different in the presence of the Coulomb barrier.
B. Subbarrier reactions
Most of the nuclear reactions that power the stars are between charged particles. These particle must penetrate a Coulomb barrier that is very large in units of kT. The penetration probability is proportional to the Gamow factor exp[-2ph(E)], where  is the Sommerfeld parameter, a is the fine structure constant and m is the reduced mass; this factor can be also written as exp[
is the Sommerfeld parameter, a is the fine structure constant and m is the reduced mass; this factor can be also written as exp[ ], defining the Gamow energy EG = 2mc2 (Z1Z2ap)2 . This exponentially small probability makes the cross section grow extremely fast with the energy; therefore, one usually defines the astrophysical S factor, whose energy dependence is weaker
], defining the Gamow energy EG = 2mc2 (Z1Z2ap)2 . This exponentially small probability makes the cross section grow extremely fast with the energy; therefore, one usually defines the astrophysical S factor, whose energy dependence is weaker
This reaction mechanism has at least two main consequences for the study of stellar structure.
(1) Since the bulk of particles in the stellar plasma have thermal energies of the order of kT, which is far below the Coulomb barrier, only a small number of particles in the high-energy tail of the distribution has a chance of reacting: this high-energy tail plays a crucial rôle for the reaction rates, which becomes very sensitive to small changes of the distribution.
(2) The cross sections of some of the reactions, e.g., weak reactions with Coulomb barrier such as p+p® d + e+ +n, are extremely small at the low energies relevant to stellar physics (of the order of tens of keV for reactions in the Sun). Therefore, some of them have only been calculated theoretically, others have only been measured at higher energies and then extrapolated to the lower thermal energies of the stellar interiors.
Both these two facts lead to considerable uncertainties in the reaction rates. The second point has been extensively discussed, and it is common opinion that the present standard theory of stars, and in particular of the Sun [21, 4], has already taken properly into account the uncertainties in the cross sections. On the contrary, the first point, the possibility that small changes of the particle energy distribution could strongly affect reaction rates, has received little attention [22, 25, 26, 5], or dismissed on the ground that the energy distribution in stars is allegedly well-know [3]. In this paper, we shall discuss mainly this point, the energy distribution in stellar plasmas and its implication for nuclear rates.
C. Maxwell distribution and the Gamow peak
Normal stellar matter, such as the one in the Sun, is nondegenerate, i.e., quantum effects are small (in fact, they are small for electrons and completely negligible for ions), it is nonrelativistic, and it is in good thermodynamical equilibrium. On this ground, the particle velocity distribution is almost universally taken to be a Maxwell-Boltzmann distribution, without much questioning.
However, derivations of the ubiquitous Maxwell-Boltzmann distribution are based on several assumptions [5]. In a kinetical approach, one assumes (1) that the collision time be much smaller than the mean time between collisions, (2) that the interaction be sufficiently local, (3) that the velocities of two particles at the same point are not correlated (Boltzmann's Stosszahlansatz), and (4) that energy is locally conserved when using only the degrees of freedom of the colliding particles (no significant amount of energy is transferred to collective variables and fields). In the equilibrium statistical mechanics approach, one uses the assumption that the velocity probabilities of different particles are independent, corresponding to (3), and that the total energy of the system could be expressed as the sum of a term quadratic in the momentum of the particle and independent of the other variables, and a term independent of momentum, but if (1) and (2) are not valid the resulting effective two-body interaction is not local and depends on the momentum and energy of the particles. Finally, even when the one-particle distribution is Maxwellian, additional assumptions about correlations between particles are necessary to deduce that the relative-velocity distribution, which is the relevant quantity for rate calculations, is also Maxwellian.
At least in one limit the MB distribution can be rigorously derived: systems that are dilute in the appropriate variables, whose residual interaction is small compared to the one-body energies. In spite of the fact that the effects of the residual interaction cannot be neglected, as a good first approximation the solar interior can be studied in this dilute limit; therefore, it is reasonable to suppose that the velocity distribution in the Sun is not too far from the Maxwellian one. This fact is consistent with the many successes of the standard treatment and suggests that we start discussing the standard results and improve them later.
In the ordinary treatment, the single particle energy distribution for protons and other ions is taken as
When this distribution and a cross section of the form of Eq. (3) are inserted in Eq. (2), the resulting integrand goes to zero both at large energies, because of the exponentially small number of particles, see Eq. (4), and also at small energies, because of the exponentially small probability of barrier penetration, see Eq. (3). In fact, the integrand has a maximum at the temperature-dependent energy
which it is called the most effective energy [1], since most of the particles that react have energies close to E0; we have defined the adimensional parameter t = E0/kT = [EG/(4 kT)]1/3.
Fig. 1 gives a pictorial demonstration of how the Gamow peak originates. The exponentially decreasing function (solid curve labeled "Maxwell'') is the Maxwellian factor exp(-E/kT) multiplied times 400 to emphasize the tail of the distribution. The rapidly growing function (dotted curve labeled "Penetration factor'') is the factor exp  with the choice of EG = 4000 kT, which corresponds to a most effective energy E0 = (EG (kT)2 / 4)1/3 = 10 kT; it has been arbitrarily normalized such that it is equal to 400 at E = 20kT. The product of the two functions yields the Gamow peak (solid curve labeled Gamow), which has been normalized to one at its maximum (E = E0 = 10 kT). It is important to notice that the area under the Maxwellian curve for energies larger than about 6 kT (where one finds most of the contribution to the peak) is less then 0.3% of the total area.
with the choice of EG = 4000 kT, which corresponds to a most effective energy E0 = (EG (kT)2 / 4)1/3 = 10 kT; it has been arbitrarily normalized such that it is equal to 400 at E = 20kT. The product of the two functions yields the Gamow peak (solid curve labeled Gamow), which has been normalized to one at its maximum (E = E0 = 10 kT). It is important to notice that the area under the Maxwellian curve for energies larger than about 6 kT (where one finds most of the contribution to the peak) is less then 0.3% of the total area.
The Gamow peak for the Maxwellian and the Tsallis' distribution. The exponentially decreasing solid (dashed) curve labeled Maxwell (Tsallis) shows the Maxwellian (Tsallis with q = 0.98) energy distribution. Both the energy distributions have been normalized to a huge 400 at E/kT = 0, to emphasize their tiny difference (the part of the distributions shown contains only about 0.3% of the total area). The rapidly increasing dotted curve shows the behavior of the penetration factor exp-
In this framework, one performs the integral in Eq. (2) using the saddle-point asymptotic expansion around the maximum E0 of the Gamow peak and finds that the reaction rate per particle pair is, apart for small calculable corrections,
Table 1 reports the values of E0 in units of kT (t) for several reactions. We notice that E0 can be much larger than kT and, therefore, only a very small number of particles in the far tail of the distribution contributes to the rate, e.g., for the 3He + 3He reaction the most effective energy is about 17 kT: there are less than about 40 particles out of a million that have energies so large or larger. It is not sufficient anymore to know that the Maxwellian distribution is good approximation, we must be sure that there are no corrections to a very high accuracy.
Most effective energies for thermonuclear reactions and exponents g that characterize the change of the thermal average ávsñ to the leading order in d, when the energy distribution changes by a factor exp{ -d(E/kT)2 }: áv sñd = áv sñ0 exp{ -dg}.
III Velocity distributions in nonideal plasmas
As discussed in Sec. II, several subtle points must be assumed in the derivation of the often-taken-for-granted Maxwellian velocity distribution. Likewise, one often assumes that the solar core could be treated as an ideal (Debye) plasma. However, there are physical conditions and/or specific applications that needs higher accuracy for which becomes necessary to take into account modifications of the standard plasma theory.
In this Section we discuss how the physics of nonideal plasmas, and in particular of the solar interior, can result in equilibrium velocity distributions that deviate from the "standard'' one. In addition, we present specific physical frameworks where non-Maxwellian distributions arise and microscopic mechanisms that allow a reliable estimation of the size of deviations.
A. Ideal and nonideal plasma
In literature, a plasma is characterized by the value of the plasma parameter G
where a = n-1/3 is of the order of the interparticle average distance (n is the average density). The plasma parameter is a measure of the ratio of the mean (Coulomb) potential energy and the mean kinetic (thermal) energy.
Depending on the value of the plasma parameter, we can distinguish three regimes that are characterized by different effective interactions and require different theoretical approaches.
-
G << 1. The plasma is described by the Debye-Hückel mean-field theory as a dilute weakly interacting gas. The screening Debye length
is much greater than the average interparticle distance a, hence there is a large number of particles in the Debye sphere (ND º (4p/3)RD3). Collective degrees of freedom are present (plasma waves), but they are weakly coupled to the individual degrees of freedom (ions and electrons) and, therefore, do not affect their distribution. Binary collisions through screened forces produce the standard velocity distribution.
-
G » 0.1. The mean Coulomb energy potential is not much smaller of the thermal kinetic energy and the screening length
RD »
a. It is not possible to clearly separate individual and collective degrees of freedom. The presence of at least two different scales of energies of the same rough size produces deviations from the standard statistics which describes the system in terms of a single scale,
kT.
-
G > 1. This is a high-density/low-temperature plasma where the Coulomb interaction and quantum effects start to dominate and determine the structure of the system.
B. The solar interior
In the solar interior the plasma parameter is G » 0.1; therefore, the solar core is a weakly nonideal plasma where the Debye-Hückel conditions are only approximately verified. Similar behaviors are expected in other astrophysical systems characterized by plasma parameters in the range 0.1 £ G £ 1; examples are brown dwarfs, the Jupiter core and stellar atmospheres.
» 0.1; therefore, the solar core is a weakly nonideal plasma where the Debye-Hückel conditions are only approximately verified. Similar behaviors are expected in other astrophysical systems characterized by plasma parameters in the range 0.1 £ G £ 1; examples are brown dwarfs, the Jupiter core and stellar atmospheres.
Studies of systems with this intermediate values of G are the most difficult; it is possible to use/combine several different approaches none of which, however, is completely justified.
The reaction time necessary to build up screening after a hard collision can be estimated from the inverse solar plasma frequency  , and it is comparable to the collision time tcoll = ásvn ñ-1» 10-17 sec. Therefore, several collisions are likely necessary before the particle looses memory of the initial state and the scattering process can not be considered Markovian. In addition, screening starts to become dynamical: the time necessary to build up again the screening after hard collisions is not negligible any more.
, and it is comparable to the collision time tcoll = ásvn ñ-1» 10-17 sec. Therefore, several collisions are likely necessary before the particle looses memory of the initial state and the scattering process can not be considered Markovian. In addition, screening starts to become dynamical: the time necessary to build up again the screening after hard collisions is not negligible any more.
C. Three roads towards nonstandard distributions
For concreteness we consider three possible approaches to weakly-noninteracting plasmas that yield nonstandard distributions. These approaches are not alternative, but they could perhaps be seen as different and partial descriptions of the same complicated physical problem. The main purpose of their presentation is to give concrete examples of how nonstandard statistics arises. However, they are not by any mean the last word on the topic: we must still develop their full potentiality and alternative approaches must also be pursued.
1. Fokker-Planck
In the Fokker-Planck context it is possible to introduce corrections (i) to the lowest order friction coefficient J(v), and (ii) to the lowest order diffusion coefficient D(v) [6, 7, 5]. Similar corrections have already been shown to exist in hydrodynamic systems.
We assume that the system is not too far from the standard regime that leads to the MB distribution, so that an expansion starting from the usual formalism makes sense. The Fokker-Planck equation, given in the Landau form, is
where f(t, v) is the distribution probability of particles with velocity v at time t and J(v) and D(v) are the dynamical friction and diffusion coefficients. The stationary distributions are the asymptotic solutions of the above equation. To lowest order J(v) = v/t and D(v) =  /t, where the constant t > 0 has dimension of time (m / t is the friction constant) and
/t, where the constant t > 0 has dimension of time (m / t is the friction constant) and  has dimension of a velocity (
has dimension of a velocity ( = kT/m for Brownian motion). At equilibrium one obtains the well-known Maxwellian distribution
= kT/m for Brownian motion). At equilibrium one obtains the well-known Maxwellian distribution
We can generalize the standard Brownian kinetics considering the expressions of the quantities J(v) and D(v) to the next order in the velocity variable: J(v) = v/t (1+b1v2/ ) and D(v) =
) and D(v) =  /t (1 + g1v2/
/t (1 + g1v2/ ); these higher derivative terms can be interpreted as signals of nonlocality in the Fokker-Planck equation.
); these higher derivative terms can be interpreted as signals of nonlocality in the Fokker-Planck equation.
If b1 = 0 and g1¹ 0 we find the Tsallis' distribution
where q-1 = 2g1/(2g1+1), Q is the Heaviside step-function, and kT/m º  (2-q). When the characteristic parameter q is smaller than 1 (-1/2 < g1 < 0), this distribution has a upper cut-off: mv2/2 £ kT/(1-q) (the tail is depleted). The distribution correctly reduces to the exponential Maxwell-Boltzmann distribution in the limit q® 1 (g1® 0). When the parameter q is greater than 1 (g1 > 0), there is no cut-off and the (power-law) decay is slower than exponential (the tail is enhanced).
(2-q). When the characteristic parameter q is smaller than 1 (-1/2 < g1 < 0), this distribution has a upper cut-off: mv2/2 £ kT/(1-q) (the tail is depleted). The distribution correctly reduces to the exponential Maxwell-Boltzmann distribution in the limit q® 1 (g1® 0). When the parameter q is greater than 1 (g1 > 0), there is no cut-off and the (power-law) decay is slower than exponential (the tail is enhanced).
If b1¹ 0 and g1 = 0, we find a Druyvenstein-like distribution:
which has also the functional form suggested by Clayton [23] to parameterize a small deviation (depletion) from the Maxwellian statistics.
2. Random fields
Each particle is affected by the total electric field distribution due to the other charges in the plasma. If external fields and large scale internal fields due to collective modes are subtracted from the total electric field, the single particle see the remaining field as a relative small random component. The density of these random electric microfields has been studied [27, 28] and it is often expressed in terms of the dimensionless parameter F as áE2ñ = (F e/a2)2, where 4pa3/3 = 1/n; the distribution of F in plasmas depends on the value of G [28]. These microfields have in general long time correlations, and can generate anomalous diffusion.
The total (micro)field can be decomposed into three main components.
(i) A slow-varying (relative to the collision time) component due to collective plasma oscillations, which the particle sees as an almost constant external mean field E over several collisions.
(ii) A fast random component due to particles within a few Debye radii, whose effect can be described by an elastic diffusive cross section s1 ~ v-1. When only this cross section is present, the distribution remains Maxwellian even in presence of the slow mean field E.
(iii) A short-range two-body strong Coulomb effective interaction, that can be described by the ion sphere model [29]. The strict enforcement of this model as implemented by Ichimaru [29] yields the elastic cross section s0 = 2pa2a2, where a is the interparticle distance, a an adimensional parameter whose order of magnitude can be inferred from the parameter F that characterizes the microfields, F » a-2. Since F2~ 3/G » 40, for G = 0.07, one can estimate 0.4 < a < 1. In the present model, it is this component of the electric field that turns out to be mainly responsible of the correction factor exp .
.
In this framework, the stationary solution of the kinetic equation valid for small deviations from the MB distribution can be shown to be the Druyvenstein distribution:
where
k = 2 mamb/(ma+mb)2 is the elastic energy-transfer coefficient between two particles a and b, and d is proportional to the square of the ratio of the energy densities of the electric field and of the thermal motion.
In the small correction limit, relevant to the solar interior,  and the
and the  parameter is:
parameter is:
From Eq. (13), we see that the presence of electric microfields implies a deviation from the Maxwell-Boltzmann distribution and that the entity of this deviation depends on the value of the plasma parameter. As already mentioned, in the solar core G » 0.1, hence, the order of magnitude of the deviation parameter
» 0.1, hence, the order of magnitude of the deviation parameter  is about 0.01 and in this intermediate region long-range and memory effects take place.
is about 0.01 and in this intermediate region long-range and memory effects take place.
3. Memory effects and collective variables
As already discussed, in the solar core collective effects have time scales comparable to the average time between collisions (e.g., compare the inverse plasma frequency with the average collision time  ) and it is not possible a description that separates the collective and the individual degrees of freedom.
) and it is not possible a description that separates the collective and the individual degrees of freedom.
A rigorous microscopic approach would imply the resolution of the dynamical equations of motion with a Hamiltonian that explicitly contains collective and individual degrees of freedom and their mutual interactions. Our scope is more modest: we want to give a concrete example where memory effects (long-time correlations) are important.
The authors of Ref. [30, 11] introduce the collective variables
and describe these collective variables as harmonic oscillator variables weakly coupled to the individual degrees of freedom, which, therefore, act as a thermostat for the collective variables.
Generalizing this approach, we write down a generalized Langevin equation for the collective variables
where K(t-t) is the memory friction kernel, which takes into account the long-time tail of the correlations in the solar interior, and F(t) is the stochastic fluctuating thermal force due to the interactions with the individual degrees of freedom. In weakly nonideal plasmas, the longitudinal waves have the following dispersion law
The two functions K(t-t) and F(t) are not independent but related by the second fluctuation-dissipation theorem
In the limit of negligible memory effects, the memory kernel becomes a d-function, that is, K(t) = g d(t), where g is the effective friction coefficient, which can be written in terms of the Landau (gL) and collisional (gc) damping [11].
The explicit form of the memory kernel depends on the specific system and, in principle, should be deduced from a microscopic calculation. At the moment, we have been able to verify that, in the framework of Tsallis nonextensive statistics, the memory kernel can be written, for q » 1, as
The above expression is consistent with the prescription of the nonextensive statistics and implies anomalous subdiffusion for q < 1 and superdiffusion for q > 1. A more complete analysis of this possibility is still under way; it is also important to study the effects of such a memory kernel for the collective modes on the individual degrees of freedom.
At the moment, we can speculate that such correlations among the collective modes could lead to a long-time asymptotical behavior of the velocity-correlation of the ions of the kind áv(0)v(t)ñ ~ t-(1+g). If g ³ 1, i.e., the correlation decays sufficiently fast, the diffusion process is no qualitative different from the delta-function case: áx2(t)ñ ~ t. In this case, one can show [31, 32] that if 0 < g < 1 and 0 < òáv(0)v(t)ñ < ¥, the standard distribution of velocity is still valid. However, if 0 < g < 1 and òáv(0)v(t)ñ = 0 (or very small), or if -1 < g £ 0, the diffusion is anomalous áx2(t)ñ ~ t1+g ( ~ tlogt, if g = 0). Indeed, Tsallis [33] shows that the generalized entropy quite naturally generate both anomalous diffusion (áx2(t)ñ ~ t1+g) and the non-Maxwellian probability distribution for the velocities of Eq. (11).
D. Summary
In this Section we have presented theoretical arguments that the velocity distribution in the solar core should deviate from the standard one and, in particular, that it could follow Tsallis' distribution [9, 10] shown in Eq. (11). We have also estimated the deviation from the standard statistics from the known microfield distribution. If we use the parameterization suggested by Clayton [22, 23] (Druyvenstein distribution)
 should be of the order of 0.01. Since in the limit q® 1 the Tsallis distribution can be asymptotically described as a Druyvenstein with
should be of the order of 0.01. Since in the limit q® 1 the Tsallis distribution can be asymptotically described as a Druyvenstein with  , we have also estimated that q should be a few percent different from 1.
, we have also estimated that q should be a few percent different from 1.
In the next section, we shall demonstrate how even such small deviations from the Maxwell-Boltzmann distribution can be very important for solar physics.
IV Reaction rates and modified thermal distribution
Both from general considerations about the successes of the standard approach and from the estimates and calculations that we have shown, it should be clear that the deviations from the Maxwellian distribution in the Sun are small. Therefore, it is completely general to make an asymptotic expansion of the following kind:
where we have disregarded terms with powers higher than (E/kT)2 in the exponent and all other power corrections outside the exponential, apart the ones (not shown) needed to correctly normalize the distribution. This result becomes the more accurate the more d is small. Note that the exponential can not be expanded.
This same kind of parameterization was already considered by Clayton [23]. One can easily convince oneself that the distributions previously discussed can be put in this form in the limit of small deviations. We have seen that the the Tsallis' distribution plays a special rôle: it can be also approximated to first order in (1-q) by Clayton's form with d = (1-q)/2 and a renormalized temperature T ¢ = T + T(1-q). In Sec. II we performed a saddle point expansion of the integral over the velocity distribution with the introduction of the most effective energy, E0, and approximating the integrand around the maximum E0 with a Gaussian function (Gamow peak). The same kind of asymptotic expansion can be repeated for this modified distribution yielding the following analytical expression for the change of the rate:
where E0 is the most effective energy of Eq. (5)
which depends on the reaction i, through the charges Z and weights A of the ions, and on the relevant average temperature T (Tc = 1.36 keV is the temperature at the center of the Sun), and where ávsiñ0 is the expression in Eq. (6).
We shall use the expression in Eq. (24) to discuss the effects of modified statistics on the solar thermonuclear rates: it has a sufficient numerical accuracy for this situation and it is physically more transparent. However, we perform the integral over the distribution numerically in physical situations where stronger deviations from the Maxwellian distribution are expected, and when we want to check whether the asymptotic expansion is sufficiently accurate.
The dramatic effect of small deviations from the Maxwellian distribution on the rate can be appreciated by looking at Fig.1. The steep decreasing dashed curve shows the high-energy tail of the Tsallis' distribution [1 + (q - 1)E/kT]1/(1 - q) with q = 0.98 compared with the corresponding Maxwellian distribution (solid curve). The tails of the two distributions shown in Fig.1 contain about 0.30% (Maxwell) and 0.26% (Tsallis) of their total area and have been multiplied times a factor 400 to make their small difference more visible. The product of each of these two very similar distributions times the same penetration factor (dotted curve) yields two very different Gamow peaks. The peak corresponding to the Tsallis distribution (dashed curve) is not only shifted at lower energy by more than one unit of kT compared to the Maxwellian peak (solid curve), but it is also much lower: a tiny change of the distribution tail (4×10-4 less probability in the tail) makes the probability in the peak smaller by a factor of about 0.3!
V Thermal effects on the neutrino energy spectrum
Because of their small interaction cross section, neutrinos that reach the earth have not interacted with the solar matter and carry direct information from the solar core. One might hope that their energy spectrum could tell us something about the particle velocity distribution in the Sun.
The neutrino energy spectrum for a given reaction depends on the total energy available in the center of mass to the final products, total energy that is the sum of the thermal energy of the incoming particles and of the energy released by the reaction, and on the velocity of the center of mass that produces Doppler broadening. As a specific example, we shall use the pp fusion reaction, since its neutrino spectrum is easily calculable from phase space and since it releases a relatively low excess energy leaving more space for thermal effects.
The reaction
releases an excess energy of Q = 2mp - md - me = 2×938.272- 1875.613 - 0.511 = 0.420 MeV, which is shared among the kinetic energies of the outgoing particles. Note the the total energy released by the reaction is 1.442 MeV, since the positron annihilation gives additional 1.022 MeV; this energy, however, does not contribute to the kinetic energy of the neutrino (this should be contrasted to the more rare reaction p + p + e ® d + ne).
Since there are three particles in the final state, the neutrino energy in the center of mass has a known probability distribution. For simplicity, we report only the result that disregards the recoil energy (a relative correction of the order of 2×10-4)
The neutrino energy goes from zero to to the maximal energy
where K is the relative kinetic energy of the incoming protons, the approximate equality disregards the recoil energy consistently with Eq. (27), and where F is the Fermi function
which takes into account the Coulomb repulsion of positron and deuteron in the final state.
The neutrino energy spectrum is obtained by convoluting this result with the distribution for K: S(En) ~ òdKPK(En) f(K). In Fig.2, we show the energy distribution of the neutrinos from the pp reaction for three cases: (1) T = 0 (dotted curve), (2) T = 1.36 keV with a Maxwellian distribution (solid curve) and (3) T = 1.36 keV with a q = 1.2 Tsallis' distribution (dashed curve).
Figure 2. The spectrum of solar neutrinos produced by the pp reaction. The solid line shows the spectrum at kT = 1.36 keV (about the solar central temperature) with the Maxwellian distribution for the proton relative energy, the dashed line the spectrum with the Tsallis' distribution at the same temperature. For comparison the dotted line shows the spectrum with a Maxwellian distribution at T = 0.
Note that relative large value of |q-1| » 0.1 are necessary in order that the effect on the spectrum of having a different distribution be of the same order of magnitude of the standard thermal effect.
In principle, precise measurements of the neutrino spectrum give information on the thermal distribution of the proton kinetic energies f(K). Let us estimate the necessary accuracy. The central temperature of the Sun is about kTc = 1.36 keV and the most effective energy E0 (maximum of the Gamow peak) is about five times as big for the pp reaction (see t in Table 1); therefore, thermal effects give a relative change of the maximal energy about 5 ·1.36 / 420 » 0.02 and, in general, modify the shape of the spectrum by a few percent. The center of mass motion gives also contributions of order kT. Spectral measurements with accuracy better than 1% start to be sensitive to the particle thermal motion and can measure the solar internal temperature. However, measurements that are two orders of magnitude more accurate are necessary to measure the temperature with a few percent error and/or discriminate between the Maxwellian distribution and those slightly distorted distributions (|q-1| » 0.01 or less) that we shall consider in the next paragraph. Such kind of experiments are not expected to be feasible in the near future.
VI Solar neutrino experiments and the solar neutrino problem
A. The solar neutrino problem
The solar neutrino problem is one of the most interesting long standing puzzle of the modern physics. The combined results from the solar neutrino experiments (Homestake, GALLEX, SAGE, Kamiokande and SuperKamiokande) cannot be reconciled with the predictions of the standard solar models (SSM). Since SSMs have been very successful in predicting the stellar structure and have given excellent descriptions of measurements as detailed and accurate as the helioseismic ones, the neutrino experiments have suggested that the minimal standard electroweak model should be extended and include small neutrino masses and lepton flavor nonconservation [15, 21]. Neutrino oscillation theory would have far-reaching consequences for both particle physics and cosmology: therefore, it is of great importance to ask whether the solar neutrino problem can be solved, or at least alleviated, in the framework of the conventional physics [34].
The problem can be more precisely appreciated with the help of Fig. 3 and Table 3. Fig. 3 shows the energy spectrum of the main neutrino fluxes coming out of the Sun. The same figure shows also the part of the spectrum that contributes to each of the three present neutrino measures. The energy dependence of each single flux depends practically only on nuclear physics and it is independent of the SSM (see the discussion about the pp spectrum in the Sec. V). However, the integrated fluxes, which are reported in the first column of Table 3, and, therefore, the relative weight of the different components of the spectrum, depend on the SSM.
The solar neutrino spectrum. For continuous sources, the differential flux is in cm-2s-1 MeV-1. For the lines, the total flux is in cm-2s-1. There are also indicated the thresholds of the three kinds of present experiments. The radiochemical experiment at Homestake [37, 48] that uses the reaction ne + 37Cl ® 37Ar (Chlorine) has the threshold 0.814 MeV. The radiochemical experiments Gallex [38, 46] and SAGE [39, 47] that use the reaction ne + 71Ga ® 71Ge (Gallium) have the threshold 0.2332 MeV. The thresholds of the Kamiokande and Superkamiokande experiments [35, 44, 45], which detect the Cherencov light emitted by the scattered electrons in water (Water Cherenkov) are chosen between 5.5 and 8 MeV.
One should compare these predictions with the experimental data (last column of Table 3).
Only one experiment, the one performed by Kamiokande and SuperKamiokande, (detection of the Cherencov light emitted in water by electrons that are elastically scattered by solar neutrinos, for the latest updated results see Ref. [35]) measures neutrinos from a single solar reaction (8B ® 2a+ e+ + ne, the so-called boron neutrinos), since its threshold (see Fig. 3) is too high to see any of the other lower energy neutrinos. Therefore, its determination of the boron flux is solar-model independent; its present result corresponds to less than one half of the predicted flux. This experiment has measured also the energy spectrum of the boron neutrinos confirming the expected shape apart for same discrepancy for energies greater than about 14 MeV, discrepancy that could be interpreted as evidence for oscillations [36].
The other two kinds of (radiochemical) experiments [37, 38, 39] have lower thresholds and, since they do not have energy information, measure a combination of several neutrino fluxes. Their interpretation in terms of individual fluxes partially depends on the relative weight of the fluxes in the solar model. However, they also show lower signals than predicted. For a review on the SNP see Refs. [15, 21].
B. Standard attempts of astrophysical solutions
The SSM flux predictions have ranges of variability, whose magnitudes mostly depend on their importance in the energy production mechanism. The pp flux is almost independent of the SSM (a few percent uncertainty), the 7Be is fairly stable (about 10% uncertainty), while the boron flux, which is produced in a marginal chain of the energy production, has a larger (more than 30%) uncertainty. The ranges of predictions of the SSM fluxes come mainly from the experimental/theoretical uncertainties in the input parameters (nuclear cross sections, photon opacities and initial contents).
The have been numerous attempts of reconciling solar models and neutrinos experiments by allowing all theoretical inputs to vary within and also considerably outside their uncertainties. Others have assumed arbitrary changes of the internal structure of the models (scaling of the temperature profile, fast element mixing, etc.). This approach to the SNP is called the "astrophysical solution'' (references could be found in Ref. [21]).
The most radical astrophysical solution consists in leaving the neutrino fluxes as free parameters (no solar model) with the only constraint that the produced energy should match the solar luminosity. Nevertheless, there remains a discrepancy at about the 3-4 s level (the central predictions of the SSM are more than 10s's from the experimental results) [18, 40, 41, 21, 42].
C. Nonstandard velocity distributions
A different velocity distribution yields a different ávsñ, as discussed in Sec. IV, and, therefore, a different solar model and different neutrino fluxes.
In principle, the same variation of ávsñ that is obtained by a different velocity distribution can also be obtained by an appropriate change of the cross section, for instance by means of the astrophysical factor S in Eq. (3). Therefore, allowing a modified velocity distribution does not span a different set of neutrino fluxes than the arbitrary variation of all the astrophysical factors. In particular, one cannot hope to achieve a better agreement with the data than the one achieved by leaving the fluxes themselves as free parameters.
In practice, however, arbitrary large variations of the astrophysical factors contrast with our theoretical understanding of the nuclear reactions and often with experimental measurements. Allowing generous, but not arbitrary, ranges for the input parameters, implies a much more restricted values of the possible neutrino fluxes.
On the contrary, small changes of the velocity distribution can give huge changes of ávsñ. Therefore, changing the velocity distribution has several motivations. (1) When one is able to calculated the velocity distribution from the microscopic physics, it gives a predictions for ávsñ. (2) Even when one can only estimate the size of the deviation, it gives a physical mechanism to justify large and correlated changes of ávsñ. (3) In any case, a given uncertainty in the form of the distribution yields calculable greater ranges of solar model predictions compared to the ones of the SSM, which assumes the distribution function known to high accuracy.
Changing ávsñ for the ith reaction will affect the whole solar model and, in general, all fluxes will change. We use Eq. (24) as a general parameterization of the rate change for small deviations from the standard distribution. The effects of modifying the rates on the fluxes can be estimated by using the power-law dependences
for the fluxes j = 7Be, 8B, 13N and 15O, and using the solar luminosity constraint [21] to determine the pp flux, Rpp = 1+0.087×(1-RBe) +0.010×(1-RN) +0.009×(1-RO), and keeping fixed the ratio x º Fpep/Fpp = 2.36×10-3. The exponents aij = ¶lnFj / ¶lnávsiñ (see Table 2) have been taken from Ref. [21], where it is also discussed why solar models depend only on the combination  and why it is a good approximation to keep the ratio x constant.
and why it is a good approximation to keep the ratio x constant.
The first four rows show aij = ¶lnFj/¶lnáv sñi, the logarithmic partial derivative of neutrino fluxes with respect to the parameter shown at the left of the row. These numbers are discussed in Ref. [21]. The last three rows show bj, bjBe and bjHe, the logarithmic partial derivative of the fluxes with respect to the parameters d's; as discussed in the text, they are linear combinations of the a's weighted by the factors g of Table 1.
The first three columns show the predicted fluxes, and the predicted gallium and chlorine signals in the SSM [12] and in the two models with nonstandard distribution described in the text. The last column shows the present experimental results. For the three models is also given the c2 resulting by the comparison with the experimental data.
A direct microscopic calculation would determine d that could be different for every reaction (d® di). The energy distribution can be influenced by the specific properties of the ion (charge and mass) and by the different conditions of the environment in those parts of the Sun where each of the reactions mostly takes place. However, such a direct calculation is not simple and it does not exist for the solar interior. Therefore, for the purpose of estimating the effect of nonstandard distributions, we consider two simple models and consider d('s) as free parameter(s). The first model assumes the same deviation d for all distributions, the second model assumes that only the p+7Be and 3He + 4He relative energy distributions are nonstandard and introduces d(17) and d(34) to parameterize their deviations.
In the first case, one finds by substituting Eq. (24) into Eq. (30) that
where bj = åi ajigi are reported in Table 2. This dependence of the fluxes on d is in good agreement with Clayton's numerical calculation [23]. Using the model of Ref. [12] as reference model and the experimental results up to the end of 1997 (see Table 3), we obtain the best fit for d = 0.005 with a c2 = 35.
In the second case, we proceed similarly, but we use d(17) for the reaction p+ 7Be and d(34) for the reaction 3He + 4He: the corresponding  and
and  are also reported in Table 2. As shown in Table 3 the best fit is obtained for d(17) = -0.018 (negative d corresponds to an enhanced tail, q > 1 in Tsallis' distribution) and d(34) = 0.030 with a c2 = 20.
are also reported in Table 2. As shown in Table 3 the best fit is obtained for d(17) = -0.018 (negative d corresponds to an enhanced tail, q > 1 in Tsallis' distribution) and d(34) = 0.030 with a c2 = 20.
As expected from the discussion in the first parts of this Section, this result is not a solution to the SNP, in the sense of providing a model to fit the experimental results within one (a few) sigma. However, we have shown that deviations from standard statistics corresponding to values of d of about 1% can change the neutrino fluxes of factors comparable to those that constitute the SNP. Perhaps, the actual values of the neutrino fluxes coming out of the Sun could result from the interplay of several mechanisms that are disregarded in the standard picture [34].
Moreover, it is clear that the uncertainties of the neutrino fluxes are considerably underestimated by not considering the possibility of nonextensive distributions.
D. Helioseismic constraints
Helioseismology provides very detailed and precise information on the solar structure. The extremely precise measurements of a tremendous number of frequencies give the possibility of extracting values of the sound speed even near the solar core where the energy is generated. In addition, several properties of the convective envelope are accurately determined.
It is important to verify that nonstandard distributions do not contrast with such data. This study has been done for the velocity distribution of protons [43] if d is within with following limits
there is no incompatibility between helioseismic data and nonstandard statistics.
As we have seen, even such small values of d have very important consequences for the neutrino fluxes; in addition, this limit does not automatically apply to the distribution of other ions.
VII Conclusion
The solar core, where its energy is produced, is a weakly nonideal plasma.
Many approaches are possible to such systems. The standard Debye-Hückel theory is very successful, but it is not sufficient to give an accurate description when one needs to calculate the energy (velocity) distribution function to a high accuracy.
We have tried several new approaches to this complex problem. In particular, we have considered corrections to the Fokker-Planck equations, the known stochastic distribution of electric microfields, and memory effects arising from the interaction of individual and collective variables.
All our attempts indicate that the velocity distribution of ions in the plasma could be different from the Maxwellian one, and should be well described by a Tsallis' distribution slightly nonextensive (|q-1| ~ 0.01).
Such small deviations from the standard statistics produce effects on the energy dependence of the neutrino spectra or on the helioseismic observables that are not in contrast with present data.
However, even such small deviations of the energy distribution produce dramatic effects on those nuclear rates whose main contributions come from the high-energy tail of the distribution, as it is best exemplified by Fig. 1.
This theoretical possibility enlarges the range of predictions for the solar neutrino fluxes and, while it is not sufficient to solve the solar neutrino problem, can make it somewhat less dramatic.
References
-
[1]
- D. D. Clayton, Principles of stellar evolutions and nucleosynthesis (The University of Chicago Press, 1968). [2]
- C. E. Rolfs and W. S. Rodney, Couldrons in the Cosmos (The University of Chicago Press, 1988). [3]
- J. N. Bahcall, Neutrino Astrophysics (Cambridge University Press, 1989). [4]
- E. G. Adelberger et al., Rev. Mod. Phys. 70, 1265 (1998). [5]
- G. Kaniadakis, A. Lavagno, M. Lissia and P. Quarati, preprint astro-ph/9710173, Physica A 261, 359 (1998). [6]
- G. Kaniadakis and P. Quarati, Physica A 192, 677 (1993). [7]
- G. Kaniadakis and P. Quarati, Physica A 237, 299 (1997). [8]
- G. Gervino, et al., preprint physics/9809001, to appear in the Proceedings of Nuclei in the Cosmos V. [9]
- C. Tsallis, J. Stat. Phys. 52, 479 (1988). [10]
- E. M. F. Curado and C. Tsallis, J. Phys. A 24, L69 (1991); ibid. 24, 3187(E) (1991); ibid. 25, 1019(E) (1992). [11]
- A. Valuev, A. Kaklyugin, G. Norman, Journ. of Exp. Theor. Phys. 86, 480 (1998). [12]
- J. N. Bahcall and M. H. Pinsonneault, Rev. Mod. Phys. 67, 781 (1995). [13]
- J N. Bahcall, M. H. Pinsonneault, S. Basu and J. Christensen-Dalsgaard, Phys. Rev. Lett. 78, 171 (1997). [14]
- B. Ricci, V. Berezinsky, S. Degl'Innocenti, W. A. Dziembowski, G. Fiorentini, Phys. Lett. B 407, 155 (1997). [15]
- J. N. Bahcall, R. Davis, Jr., P. Parker, A. Smirnov and R. K Ulrich (editors), Solar Neutrino: The First Thirty Years (Addison Wesley, 1995). [16]
- L. M. Krauss, E. Gates, and M. White, Phys. Lett. B 299, 94 (1993). [17]
- G. L. Fogli and E. Lisi, Astropart. Phys. 2, 91 (1994). [18]
- N. Hata and P. Langacker, Phys. Rev. D 50, 632 (1994). [19]
- G. L. Fogli and E. Lisi, Astropart. Phys. 3, 185 (1995). [20]
- J. N. Bahcall and P. I. Krastev, Phys. Rev. D 53, 4211 (1996). [21]
- V. Castellani et al., Phys. Rep. 281, 309 (1997). [22]
- D. D. Clayton, Nature 249, 131 (1974). [23]
- D. D. Clayton, E. Eliahu, M. J. Newman, and R. J. Talbot, Jr., Astrophys. J. 199, 494 (1975). [24]
- S. Degl'Innocenti, G. Fiorentini, and B. Ricci, Phys. Lett. B 416, 365 (1998). [25]
- H. Haubold and A. M. Mathai, Astrophys. Space Sci. 228, 77 (1995); ibid. 228, 113 (1995). [26]
- G. Kaniadakis, A. Lavagno, and P. Quarati, Phys. Lett. B 369, 308 (1996). [27]
- C. Iglesias, J. Lebowitz, D. Mac Gowan, Phys. Rev. A 28, 1667 (1983). [28]
- M. Romanovsky and W. Ebeling, Physica A 252, 488 (1998). [29]
- X.-Z. Yan, S. Ichimaru, Phys. Rev. A 34, 2167 (1986). [30]
- D. Bohm, General Theory of Collective Variables, Moscow, Mir, 1964. [31]
- R. Muralidhar, D. Ramkrishna, H. Nakanishi, and D. Jacobs, Physica A 167, 539 (1990). [32]
- K. G. Wang, Phys. Rev. A 45, 833 (1992). [33]
- C. Tsallis, et al., Phys. Rev. Lett. 75, 3589 (1995); ibid. 77, 5442(E) (1996). [34]
- A. Dar and G. Shaviv, Ap. J. 468, 933 (1996); A. Dar, astro-ph/9707015. [35]
- Y. Suzuki (SuperKamiokande Coll.), in : Neutrino 98, Proceedings of the XVIII International Conference on Neutrino Physics and Astrophysics, Takayama, Japan, 4-9 June 1998, Y. Suzuki and Y. Totsuka eds. To be published in Nucl. Phys. B (Proc. Suppl.). [36]
- V. Berezinsky, G. Fiorentini, and M. Lissia, hep-ph/9811352 (1998). [37]
- K. Lande, in : Neutrino 98, Proceedings of the XVIII International Conference on Neutrino Physics and Astrophysics, Takayama, Japan, 4-9 June 1998, Y. Suzuki and Y. Totsuka eds. To be published in Nucl. Phys. B (Proc. Suppl.). [38]
- T. Kirsten, in : Neutrino 98, Proceedings of the XVIII International Conference on Neutrino Physics and Astrophysics, Takayama, Japan, 4-9 June 1998, Y. Suzuki and Y. Totsuka eds. To be published in Nucl. Phys. B (Proc. Suppl.). [39]
- V. N. Gavrin (SAGE Coll.), in : Neutrino 98, Proceedings of the XVIII International Conference on Neutrino Physics and Astrophysics, Takayama, Japan, 4-9 June 1998, Y. Suzuki and Y. Totsuka eds. To be published in Nucl. Phys. B (Proc. Suppl.). [40]
- K. M. Heeger and R. G. H. Robertson, Phys. Rev. Lett. 77, 3720 (1996). [41]
- V. Berezinsky, G. Fiorentini, and M. Lissia, Phys. Lett. B 365, 185 (1996). [42]
- J. N. Bahcall, P. I. Krastev, and A. Yu. Smirnov, preprint hep-ph/9807216 4211 (1998). [43]
- S. Degl'Innocenti, G. Fiorentini, M. Lissia, P. Quarati, and B. Ricci, preprint astro-ph/980707, Phys. Lett. B 441, 291 (1998). [44]
- Y. Fukuda et al. (Kamiokande Collaboration), Phys. Rev. Lett. 77, 1683 (1996). [45]
- K. Inoue (Super-Kamiokande Collaboration), preliminary result presented at Int. Workshop TAUP97, Sept. 7-11, 1997, Laboratori Nazionali del Gran Sasso, Assergi (Italy). [46]
- Preliminary result presented at TAUP97, Sept. 7-11, 1997, Laboratori Nazionali del Gran Sasso, Assergi (Italy). [47]
- V. Gavrin et al. (SAGE Collaboration), in Neutrino 96, Proceedings of the 17th International Conference on Neutrino Physics and Astrophysics, Helsinki, Finland, 13-19 June 1996, edited by K. Huitu, K/ Enqvist, and J. Maalampi (World Scientific, Singapore, in press). [48]
- K. Lande, in Proc. of Neutrino 96, edited by K. Enqvist, K. Huitu, and J. Maalampi (World Scientific, Singapore, 1996), p. 25.
- [18] N. Hata and P. Langacker, Phys. Rev. D 50, 632 (1994).
- [30] D. Bohm, General Theory of Collective Variables, Moscow, Mir, 1964.
- [35] Y. Suzuki (SuperKamiokande Coll.), in : Neutrino 98, Proceedings of the XVIII International Conference on Neutrino Physics and Astrophysics, Takayama, Japan, 4-9 June 1998, Y. Suzuki and Y. Totsuka eds. To be published in Nucl. Phys. B (Proc. Suppl.).
- [44] Y. Fukuda et al. (Kamiokande Collaboration), Phys. Rev. Lett. 77, 1683 (1996).
- [46] Preliminary result presented at TAUP97, Sept. 7-11, 1997, Laboratori Nazionali del Gran Sasso, Assergi (Italy).
- [47] V. Gavrin et al. (SAGE Collaboration), in Neutrino 96, Proceedings of the 17th International Conference on Neutrino Physics and Astrophysics, Helsinki, Finland, 13-19 June 1996, edited by K. Huitu, K/ Enqvist, and J. Maalampi (World Scientific, Singapore, in press).
Publication Dates
-
Publication in this collection
17 Sept 1999 -
Date of issue
Mar 1999
History
-
Received
23 Nov 1998