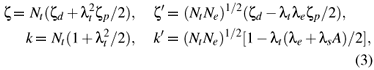Abstract
The electron paramagnetic resonance(EPR) parameters g-factors g i(i = x,y,z) and the hyperfine structure constants Ai for the substitutional Mo5+ in rutile are theoretically studied from the perturbation formulas of these parameters for a d¹ ion in a rhombically compressed octahedron. On the basis of the studies, The oxygen octahedron around Mo5+ is found to transform from the original elongation on the host Ti4+ site to compression in the impurity center due to the Jahn-Teller effect. The calculated EPR parameters based on the above local structure in this work are in good agreement with the experimental data.
Electron paramagnetic resonance (EPR); Crystal- fields and spin hamiltonians; Mo5+; Rutile(TiO2)
Theoretical studies of the local structure and the EPR parameters for substitutional Mo5+ in TiO2
Ji-Zi Lin* * Electronic address: linjizi13@126.com
Department of physics, Jiangsu University of Science and Technology, Zhangjiagang 215600, P.R. China
ABSTRACT
The electron paramagnetic resonance(EPR) parameters g-factors gi(i = x,y,z) and the hyperfine structure constants Ai for the substitutional Mo5+ in rutile are theoretically studied from the perturbation formulas of these parameters for a d1 ion in a rhombically compressed octahedron. On the basis of the studies, The oxygen octahedron around Mo5+ is found to transform from the original elongation on the host Ti4+ site to compression in the impurity center due to the Jahn-Teller effect. The calculated EPR parameters based on the above local structure in this work are in good agreement with the experimental data.
Keywords: Electron paramagnetic resonance (EPR); Crystal-fields and spin hamiltonians; Mo5+; Rutile(TiO2).
1. INTRODUCTION
Rutile (TiO2) doped with transition-metal ions has attracted interest extensively because of its unique phase transition [1] and magnetic [2-4], optical [5,6] and catalytic [7-9] properties. In general, these properties are sensitively dependent upon the local structures around the impurity ions in the host, It is well known that electron paramagnetic resonance (EPR) is a useful technique to study the electronic and local structure properties of paramagnetic impurities in crystals. For example, EPR investigations were performed decades ago, and one rhombic center was observed for the substitutional Mo5+ in rutile by means of EPR technique, and the EPR parameters anisotropic g factors gi(i = x,y,z) and the hyperfine structure constants Ai were also measured at 77ºK [10].
Till date, however, the above experimental results have not been satisfactorily interpreted. In the treatments of the g factors based on angular overlap model and the simple perturbation formulas in Refs [11]. , the contributions from the ligand orbitals and spin-orbit coupling interactions were ignored. In fact, the covalency effect and hence the admixtures between the orbitals of the metal and the ligand ions may become significant, due to the high valence state of the impurity Mo5+. Meanwhile, the energy denominators in the formulas of g factors were not correlated with the local structure around the impurity center. Actually, the local structure properties around Jahn-Teller ions(such as Ni3+, Ti3+,V4+) in crystals may be dissimilar to those of the hosts due to the local modification of bond-lengths and angles arising from the Jahn-Teller effect [12-14], In view that the studies on the Jahn-Teller behaviours of Mo5+ in rutile would be useful to understand the properties of this material with dopants. In addition, the hyperfine structure constants were not interpreted.
In order to make further investigations on the EPR parameters for the substitutional Mo5+ center in rutile, the EPR parameters are quantitatively analyzed from the second-order perturbation formulas of these parameters for a d1 ion in rhombic symmetry, by considering reasonable local lattice (angular) distortion around the impurity ion. In these formulas, the contributions from the rhombic distortion as well as the spin-orbit coupling and the orbitals of the ligands are taken into account based on the cluster approach.
2. CALCULATIONS
In rutile, there are one substitutional and one interstitial octahedral site which can be occupied by the doping transition-metal ions. The oxygen octahedra in both sites exhit significant low symmetrical distortions. For the substitutional site, the ligand octahedron is slightly elongated with two longer bond-lengths R||( ≈ 1.99 Å) parallel with the [110] axis and four coplanar shorter bond-lengths R⊥( ≈ 1.94 Å) perpendicular to the axis, with the planar bonding angle q of about 81º [15] .The above low symmetrical distortions can be characterized by the axial distortion angle Δα = α α0, with α ≈ tan1(R⊥/R//) and α0≈ 45º of the cubic symmetry. Thus, we have Δα ≈ 0.73º for the host substitutional site [15]. Additionally, the ligand octahedron for this site also suffers large perpendicular (or rhombic) distortion characterized by the deviation Δθ of the plannar bonding angle θ related to the cubic value θ0 ( = 90º), i.e., Δθ = θ θ0 = 9º [15]. Thus, the ligand octahedron has large rhombic distortion for the host substitutional site . When Mo5+ is doped into the lattice of TiO2, it may occupy the substitutional site [10]. and the local structure around the ion Mo5+ may exhibit deformation because of the Jahn-Teller effect, the impurity-ligand bonding lengths and angles may be unlike those in the host and lead to local lattice (angular) distortion.
For a d1(Mo5+) ion in rhombically-distorted octahedra, its higher orbital doublet 2Eg of the original cubic case would split into two orbital singlets 2A1g ( |z2 > ) and 2A'1g( |xy > ), while the original lower orbital triplet 2T2g would be separated into three orbital singlets 2B2g ( |xz > ), 2B3g |yz > ) and 2B1g ( |x2-y2 > ), with the latter lying lowest [11]. Note that in the above notations xy > and |x2-y2 > are interchanged due to a rotation of the frame of axes in the XY plane.
According to Refs. [11], the perturbation formulas of the g factors for a d1 ion in rhombic symmetry were established based on the conventional crystal-field theory. The experimental g factors were investigated from the above formulas by adjusting various parameters (i.e.,the energy separations between the ground and the excited states). Nevertheless, the contributions from the ligand orbitals and spin-orbit coupling interactions were ignored in these treatments. By including the above contributions and the similar perturbation procedure in Refs. [16], the perturbation formulas of the g factors and the hyperfine structure constants for the d1 ion in rhombically-distorted octahedra can be obtained on the basis of the cluster approach:
where gs ( = 2.0023) is the spin-only value. P0 is the dipolar hyperfine structure parameter of the free d1 ion. κ is the isotropic core polarization constant. N is the average covalency factor, characteristic of the covalency effect of the studied system. The energy denominators E1, E2 and E3 stand for the energy separations between the excited 2B2g, 2B3g and 2A'1g and the ground 2B1g states and can be obtained from the strong cubic field approach:
Here Dq is the cubic field parameter, and Ds, Dt, Dξ and Dη the rhombic ones.
Based on the cluster approach, the spin-orbit coupling coefficients ζ, ζ' and the orbital reduction factors k, k' in equation (1) may be written as
where ζd and ζp are the spin-orbit coupling coefficients of the d1 and the ligand ions in free states, respectively. A denotes the integral  , where R is the impurity-ligand distance in the studied system. Nγ and λγ (or λs) are, respectively, the normalization factors and the orbital mixing coefficients for the cubic (Oh) irreducible representations γ( = eg and t2g). They are usually determined from the normalization conditions
, where R is the impurity-ligand distance in the studied system. Nγ and λγ (or λs) are, respectively, the normalization factors and the orbital mixing coefficients for the cubic (Oh) irreducible representations γ( = eg and t2g). They are usually determined from the normalization conditions
and the approximate relationships
Here N is the average covalency factor. Sdpγ (and Sds) are the group overlap integrals. In general, the mixing coefficients increase with increasing the group overlap integrals, and one can approximately adopt the proportional relationship between the mixing coefficients and the related group overlap integrals, i.e., λe/Sdpe ≈ λs/Ss within the same irreducible representation eg.
From the superposition model [17] and the geometrical relationship of the studied impurity center, and rhombic field parameters can be determined as follows:
Here θ'(=θ0 + Δθ') denotes the planar bonding angle for the substitutional site in rutile, .  2 (R0) and
2 (R0) and  4(R0) are the intrinsic parameters (with the reference bonding length R0), while t2 ( ≈ 3) and t4( ≈ 5) are the power-law exponents [18]. The relationships
4(R0) are the intrinsic parameters (with the reference bonding length R0), while t2 ( ≈ 3) and t4( ≈ 5) are the power-law exponents [18]. The relationships  4(R0) =
4(R0) =  Dq and
Dq and  2(R0 ) = 9 ~ 12
2(R0 ) = 9 ~ 12 4 (R0 ) can be obtained from Refs. [18] and we take
4 (R0 ) can be obtained from Refs. [18] and we take  2(R0) = 12
2(R0) = 12 4 (R0 ) here. The reference bonding length R0 can be reasonably estimated from the empirical relationship R0≈
4 (R0 ) here. The reference bonding length R0 can be reasonably estimated from the empirical relationship R0≈  + (ri rh)/2,
+ (ri rh)/2,  = (R// + 2R⊥)/3 ≈ 1.957 Å (the average metal-ligand bonding length), ri ( ≈ 0.66 Å )and rh ( ≈ 0.68 Å) denote the ionic radius for the impurity Mo5+ and the host Ti4+ [19]. From the distance R0 ( ≈ 1.947 Å) and the Slater-type SCF functions [20,21] the integrals Sdpt ≈ 0.047, Sdpe ≈ 0.1168, Sds ≈ 0.0935 and A ≈ 1.2673 are obtained. As mentioned before, because of the Jahn -Teller effect, the impurity-ligand bonding lengths R'// and R'⊥, and hence the angle α' ≈ tan-1(R'⊥/R'//) may be different from those (R//, R⊥ and α) in the host. The impurity-ligand bonding lengths can be written in terms of the local distortion angle >Δα'( = α' α0), the average distance
= (R// + 2R⊥)/3 ≈ 1.957 Å (the average metal-ligand bonding length), ri ( ≈ 0.66 Å )and rh ( ≈ 0.68 Å) denote the ionic radius for the impurity Mo5+ and the host Ti4+ [19]. From the distance R0 ( ≈ 1.947 Å) and the Slater-type SCF functions [20,21] the integrals Sdpt ≈ 0.047, Sdpe ≈ 0.1168, Sds ≈ 0.0935 and A ≈ 1.2673 are obtained. As mentioned before, because of the Jahn -Teller effect, the impurity-ligand bonding lengths R'// and R'⊥, and hence the angle α' ≈ tan-1(R'⊥/R'//) may be different from those (R//, R⊥ and α) in the host. The impurity-ligand bonding lengths can be written in terms of the local distortion angle >Δα'( = α' α0), the average distance  as:
as:
For TiO2:Mo5+, to our knowledge, no optical spectra data were reported. However, the value Dq ≈ 2500cm1 was obtained for the [MoO4] 3 cluster in CaWO4:Mo5+ [22] .thus, the value Dq ≈ 3750cm1 can be approximately estimated for the studied octahedral [MoO6] 7 cluster here.
Thus, by using the formulas of the g factors (Eq. (1)), and fitting the calculated g factors to the experimental data, we have
The values Nt ≈ 0.7550, Ne ≈ 0.8124, λt≈ 0.6187, λe≈ 0.5098 and λs≈ 0.4081 are calculated from equations (4) and (5). Then the parameters ζ ≈ 799cm1, ζ' ≈ 788cm1, k ≈ 0.899 and k' ≈ 0.534 can be determined from equation (3) and the free-ion values ζd≈ 1030cm-1 for Mo5+ [22] and ζ ≈ 151cm1 for O2 [23].
In the formulas of the hyperfine structure constants, the free-ion value P0 is about 68.2 × 104 cm1 for Mo5+ [24]. By fitting the calculated hyperfine structure constants to the observed values, the core polarization constant is determined: κ ≈ 0.42.
The corresponding EPR parameters are shown in table 1. For comparisons, the calculated results based on the formulas of the g factors within the scheme of the conventional crystal-field theory and various fitted parameters in Refs. [11] are also collected in Table 1.
3. DISCUSSION
From table 1, one can find that the calculated EPR parameters based on the perturbation formulas in Eq. (1) by considering the local lattice deformation as well as the ligand orbital and spin-orbit coupling contributions show better agreement with the experimental data than those in the absence of the above contributions. This means that the formulas and the related parameters adopted in this work can be regarded as suitable.
The local axial and rhombic distortion angles Δα' and Δθ' for the impurity center are different from those in the host sites. The ligand octahedron in the substitutional center is found to be slightly (Δα' ≈ 0.995º) compressed while elongated (Δα ≈ 0.73º) in the host Ti4+ site, and the perpendicular distortion (Δθ' ≈ 0.305º) are much smaller than that (Δθ ≈ 9.0º) in the replaced cation site. The above distortions can be described as the contraction (by about 0.08Å) and relaxation (by about 0.04Å) of the parallel and perpendicular bond lengths, and the angle θ' is much closer to that ( ≈ 90º) of cubic case. As a result, the ligand octahedron is slightly compressed. The reason may be due to the Jahn-Teller effect which may lend to compress the ligand octahedron, as Ni3+ on the octahedral Al3+ site in LaSrAlO4 [12]. Interestingly, similar local lattice modifications around impurity ions in crystals are also found for substitutional V4+ centres in rutile-type crystals [13]. Thus, the local structure properties around Mo5+ ion in rutile obtained in this work can be regarded as reasonable and the anisotropy of the experimental g factors can be understood, by considering the local axial and rhombic distortion angles Δα' and Δθ'.
Seen from Table 1 one can find that the agreement between the theoretical g factors and the experimental data in present work is better than that in Refs. [11]. Based on the formulas of the g factors within the scheme of the conventional crystal-field theory in Refs. [11], the observed g factors were explained by various fitted parameters and the energy separations were not determined from the local structure of the impurity center. In addition, the contributions from the SO coupling coefficient and the orbitals of the ligands were not taken into account. In view of the high valence state of Mo5+, the distinct covalency and hence, significant admixture of the metal and ligand orbitals can be expected. This point may be illustrated by the small covalency factor N ( ≈ 0.733 < 1) in equation (5) and the obvious mixing coefficients (λt≈ 0.6187, λe≈ 0.5098 and λs≈ 0.4081) obtained in this work. Based on the studies, inclusion of the contributions from the SO coupling coefficient and the orbitals of the ligands leads to the variations of about 0.04, 0.05 and 0.016 for the calculated gx, gy and gz, respectively. Obviously, for the impurity ion Mo5+ with high valence state in the octahedral cluster, the above contributions could not to be ignored.
There may be some errors in the above calculations. First, the approximation of the perturbation formulas and the cluster approach adopted here can induce some errors. Second, the cubic field parameter Dq extrapolated from the [MoO4] 3 cluster in CaWO4 would lead to some errors. Finally, the impurity-ligand distance is obtained from the empeirical relationship related to the difference between the ionic radius for imputity and host ions, which may bring forward some errors in the average distance  for present system. It means that the actual average distance can be slightly different from
for present system. It means that the actual average distance can be slightly different from  . This would bring small errors to the group overlap integrals in the calculations. In fact, the errors in the final g factors and distortion angles in Eqs. (1) and (7) due to the above variation in the average distance
. This would bring small errors to the group overlap integrals in the calculations. In fact, the errors in the final g factors and distortion angles in Eqs. (1) and (7) due to the above variation in the average distance  turn out to be no more than 0.4%, since
turn out to be no more than 0.4%, since  is mainly related to the magnitude of the g factors.
is mainly related to the magnitude of the g factors.
4. CONCLUSIONS
The electron paramagnetic resonance (EPR) parameters g-factors gi(i=x,y,z) and the hyperfine structure constants Ai for the substitutional Mo5+ in rutile are theoretically investigated in this work. Based on the studies, The oxygen octahedron around Mo5+ is found to transform from the original elongation on the host Ti4+ site to compression in the impurity center due to the Jahn-Teller effect. The theoretical EPR parameters based on the above local structure in this work are in good agreement with the experimental data.
(Received on 17 April, 2010)
- [1] H.L. Ma, J.Y. Yang, Y. Dai, Y.B. Zhang, B. Lu, G. H. Ma. Appl. Surf. Sci., 253, 7497 (2007).
- [2] G.Y. Gao, K.L. Yao, Z.L. Liu. Phys. Lett. A, 359, 523 (2006).
- [3] N. Akdogan, B.Z. Rameev, R.I.K. haibullin, A. Westphalen, L.R. Tagirov, B. Aktas, H. Zabel. J. Magn. Mater., 300, e4 (2006).
- [4] G.Y. Gao, K.L. Yao, Z.L. Liu, Y.L. Li, J.L. Jiang, Y.C. Li. Physica B, 382,14 (2006).
- [5] T.N. Ishikawa, T. Nakajima ,Y. Shinohara. J. Mol. Struct-Theochem., l545, 67 (2001).
- [6] F. Gravier , B. Boulanger. Opt. Mater. 30, 33 (2007).
- [7] J. Wang, Y.H. Lv, L.Q. Zhang, B. Liu, R.Z. Jiang, G.X. Han, R. Xu, X.D. Zhang. Ultrason Sonochem, 17, 642 (2010).
- [8] X.W. Zhang, L.C. Lei. J. Haza. Mater.,153, 827 (2008).
- [9] Y. Dongsun, K. Iigon, K. Sangsoo, H. H. Chang, L. Changyu, C. Seongjin. Appl. Surf. Sci., 253, 3888 (2007).
- [10] R. T. Kyi. Phys. Rev., 128, 151 (1962).
- [11] P. DE Montgolfier, Y. Boudeville. Chem. Phys. Lett., 37 (1), 97 (1976).
- [12] Y.V. Yablokov, T.A. Ivanova. Coord .Chem. Rev., 190-192, 1255 (1999).
- [13] S.Y. Wu, L.H. Wei, Z.H. Zhang, X.F. Wang, J.Z. Lin. Z. Naturforsch. 63a, 523 (2008).
- [14] S. Lenjer, O. F. Schirmer, H. Hesse, Th. W. Kool. Phys. Rev B, 66, 165106 (2002).
- [15] H. Hikita, K. Takeda, Y. Kimura. Phys. Rev. B, l46 (22), 14381 (1992).
- [16] D. Gourier, L. Colle, A.M. Lejus, D. Vivien, R. Moncorge. J. Appl. Phys., l63, 1144 (1988).
- [17] D.J. Newman, B. Ng. Rep. Prog. Phys., 52, 699 (1989).
- [18] W. L. Yu, X. M. Zhang, L. X. Yang, B. Q. Zen. Phys. Rev. B, 50, 6756 (1994).
- [19] K. Chandrasekharan, V.S. Murty, F.J. Kumar, P. Ramaswamy, P.S. Rao. J. Mater. Sci., 35, 1561 (2000).
- [20] E. Clementi, D.L. Raimondi. J. Chem. Phys., 38 (11), 2686 (1963).
- [21] E. Clementi, D.L. Raimondi, W.P. Reinhardt. J. Chem. Phys., 47 (4), 1300 (1967).
- [22] A.S. Chakravarty. Introuduction to the Magnetic Properties of Solids. New York: Wiley -Interscience Publication.1980.
- [23] E.K. Hodgson, I. Fridovich. Biochem. Biophys. Res. Commun., 54, 270 (1973).
- [24] B.R. McGarvey. J. Phys. Chem., 71 (1), 51 (1967).
Publication Dates
-
Publication in this collection
27 Sept 2010 -
Date of issue
Sept 2010
History
-
Received
17 Apr 2010