Abstract
Self-induced decoherence formalism and the corresponding classical limit are extended from quantum integrable systems to non-integrable ones.
Classical limit of non-integrable systems
Mario Castagnino
Institutos de Física de Rosario y de Astronomía y Física del Espacio, Casilla de Correos 67, Sucursal 28, 1628 Buenos Aires, Argentina
ABSTRACT
Self-induced decoherence formalism and the corresponding classical limit are extended from quantum integrable systems to non-integrable ones.
1 Introduction
Decoherence was initially considered to be produced by destructive interference [1]. Later the strategy changed and decoherence was explained as caused by the interaction with an environment [2], but this approach is not conclusive because:
i.- The environment cannot always be defined, e. g. in closed system like the universe.
ii.-There is not a clear definition of the ''cut'' between the proper system and its environment.
iii.- The definition of the pointer basis is not simple.
So we need a new and complete theory: The self-induced approach , based in a new version of destructive interference, which will be explained in this talk in its version for non-integrable systems. The essential idea is that this interference is embodied in Riemann-Lebesgue theorem where it is proved that if f(n)Î 1 then
1 then
If we use this formula in the case when n = w - w', where w,w' are the indices of the density operator  , in such a way that n = 0 corresponds to the diagonal, we obtain a catastrophe, since all diagonal and not diagonal terms would disappear. But, if f(n) = Ad(n)+f1(n), where now f1(n)Î
, in such a way that n = 0 corresponds to the diagonal, we obtain a catastrophe, since all diagonal and not diagonal terms would disappear. But, if f(n) = Ad(n)+f1(n), where now f1(n)Î 1, we have
1, we have
and the diagonal terms n = 0 remain while the off-diagonal ones vanish. This is the trick we will use below.
2 Weyl-Wigner-Moyal mapping
Let  be the phase space. The functions over
be the phase space. The functions over 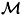 will be called f(f), where f symbolizes the coordinates of
will be called f(f), where f symbolizes the coordinates of 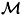
Then the Wigner transform reads
where  Î
Î and
and  (f)Î
(f)Î where
where  is the quantum algebra and the classical one is
is the quantum algebra and the classical one is  . We can also introduce the star product
. We can also introduce the star product
and the Moyal bracket, which is the symbol corresponding to the commutator
so we have
To obtain the inverse symb-1 we will use the symmetrical or Weyl ordering prescription, namely
Then we have an isomorphism between the quantum algebra  and the classical one
and the classical one 
The mapping so defined is the Weyl-Wigner-Moyal symbol.
For the state we have
and it turns out that
Namely the definition  Î
Î , as afunctional on
, as afunctional on  , is equal to the definition symbrÎ
, is equal to the definition symbrÎ , as afunctional on
, as afunctional on  .
.
3 Decoherence in non integrable systems
3.1 Local CSCO.
a.- When our quantum system is endowed with a CSCO of N+1 observables, containing 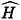 the underlying classical system is integrable. In fact, let N+1-CSCO be {
the underlying classical system is integrable. In fact, let N+1-CSCO be {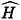
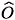 1,...,
1,...,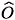 N} the Moyal brackets of these quantities are
N} the Moyal brackets of these quantities are
where I, J,... = 0,1,...,N and 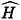 =
= 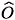 0. Then when
0. Then when  ® 0 from Eq.(1) we know that
® 0 from Eq.(1) we know that
then as H(f) = O0(f) the set {OI(f)} is a complete set of N+1 constants of the motion in involution, globally defined over all 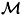 , and therefore the system is integrable. q. e. d.
, and therefore the system is integrable. q. e. d.
b.- If this is not the case N+1 constants of the motion in involution {H,O1,...,O N} always exist locally, as can be shown integrating the system of equations (3). Then, if fiÎ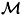 there is maximal domain of integration
there is maximal domain of integration 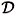 fñaround fiÎ
fñaround fiÎ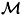 where these constants are defined. In this case the system in non-integrable. Moreover we can repeat the procedure with the system
where these constants are defined. In this case the system in non-integrable. Moreover we can repeat the procedure with the system
Then we can extend the definition of the constant {H,O1,...,O N}, defined in each 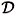 fñ, outside
fñ, outside 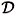 fñ as null functions. Their Weyl transforms {
fñ as null functions. Their Weyl transforms {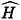
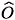 N} can be considered as a local N+1-CSCOs related each one with a domain
N} can be considered as a local N+1-CSCOs related each one with a domain 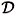 fñ that we will call {
fñ that we will call {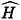 ,
, 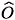 1fi,...,
1fi,...,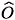 Nfi} (we consider that
Nfi} (we consider that 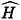 is always globally defined).
is always globally defined).
c.-We also can define an ad hoc positive partition of the identity
where Ifi(f) is the characteristic function or index function, i.e.:
where the domains DfiÌ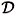 fñDfiÇ Dfj = Æ. Then åiIfi(f) = 1. Then we can define Afi(f) = A(f)Ifi(f) and
fñDfiÇ Dfj = Æ. Then åiIfi(f) = 1. Then we can define Afi(f) = A(f)Ifi(f) and
and using symb-1
We can further decompose
where the |jñfi are the corresponding eigenvectors of the local N+1-CSCO of DfiÌ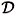 fñ where a local N+1-CSCO is defined.. So
fñ where a local N+1-CSCO is defined.. So
all over 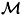 . It can be proved that for i ¹ k it is
. It can be proved that for i ¹ k it is
so the last decomposition is orthonormal, thus decomposition (5) generalizes the usual eigen-decomposition of integrable system to the non-integrable case. We will use this decomposition below.
3.2 Decoherence in the energy.
a.- Let us define in each Dfi a local N+1-CSCO {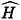 ,
,  } (as we have said we consider that
} (as we have said we consider that 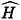 is always globally defined) as
is always globally defined) as
where we have used decomposition (5). The energy spectrum is 0 < w < ¥ and mIfi = {m1fi,...,mNfi},mIfiÎ . Therefore
. Therefore
where, from the orthonormality of the eigenvector and Eq.(5), we have
áw,m| fi |w',m 'ñfj =d(w - w') dmm'dij
b.- A generic observable, in the orthonormal basis just defined, reads:
where Õ(w,w')fimm' is a generic kernel or distribution in w, w'. As explained in the introduction, the simplest choice to solve our problem is the van Hove choice [4].
where we have a singular and a regular term, so called because the first one contains a Dirac delta and in the second one the O(w,w')fimm' are ordinary functions of the real variables w and w'. As we will see these two parts appear in every formulae below. So our operators belong to an algebra  and they read
and they read
The observables are the self adjoint O= O operators. These observables belong to a space  Ì
Ì  . This space has the basis {|w,m,m')fi, |w,w',m,m')fi} defined as:
. This space has the basis {|w,m,m')fi, |w,w',m,m')fi} defined as:
|w, m, m')fi |w, mñ fiáw, m'|fi ,
|w, mñ fiáw, m'|fi ,
|w, w', m, m')fi |w, mñ fiáw', m'|fi
|w, mñ fiáw', m'|fi
c.- Let us define the quantum states 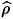 Î
Î 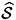 Ì
Ì  , where img is a convex set. The basis of
, where img is a convex set. The basis of  is {(w,mm'|fi, (ww',mm'|fi} and its vectors are defined as functionals by the equations:
is {(w,mm'|fi, (ww',mm'|fi} and its vectors are defined as functionals by the equations:
(w, m, m'| fi |h, n, n')fi = d(w - h)dmn dm'n'dij,
(w, w', m, m'| fi | h, h', n, n')fj =
d(w - h) d(w' - h') dmn dm'n'dij,
and all others (.|.) are zero. Then, a generic quantum state reads:
We require that:
where
dwåim|w,mñ fiáw,m|fi is the identity operator. Then, in fact,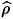 Î
Î 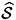 , where
, where 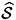 is a convex set, and we have
is a convex set, and we have
If we now take the limit t ® ¥ and use the Riemann-Lebesgue theorem, being O(w,w') and  fimm' regular (namely '
fimm' regular (namely ' fimm'O(w,w')Î
fimm'O(w,w')Î in the variable n = w - w'), we arrive to
in the variable n = w - w'), we arrive to
or to the weak limit
where only the diagonal-singular terms remain showing that the system has decohered in the energy.
Remarks
i.- It looks like that decoherence takes place without a coarse-graining, or an environment. It is not so, the van Hove choice (6) and the mean value (8) are a restriction of the information as effective as the coarse-graining is to produce decoherence.
ii.-Theoretically decoherence takes place at t ® ¥. Nevertheless, for atomic interactions, the characteristic decoherence time is tD = 10-15s [5]. For macroscopic systems this time is even smaller (e.g., 10-38s). Models with two characteristic times (decoherence and relaxation) can also be considered [6].
3.3 Decoherence in the other variables.
By a change of basis we can diagonalize the  in m and m':
in m and m':
r(w)fimm'® r(w)fipp' = rfi (w)p dpp' .
in a new basis orthonormal {|w,pñfi}. Therefore rfi(w)pdpp'.is now diagonal in all its coordinates in a final local pointer basis in each Dfi, which, in the case of the observables is { |w,p,p')fi, |w,w',p,p')fi} (i. e. essentially {|w',p'ñfi}), so in this pointer basis we have obtained a boolean quantum mechanics with no interference terms and we have the weak limit:
or in the case of  with continuous spectra:
with continuous spectra:
the only case that we will consider below.
4 The classical statistical limit
a.- Let us now take into account the Wigner transforms. There is no problem for regular operators which are considered in the standard theory. Moreover these operators are irrelevant since they disappear after decoherence.
b.- So we must only consider the singular ones as
where now the  have continuous spectra. So
have continuous spectra. So
But 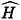 ,
,  commute thus
commute thus
and if Ofi(w,p) = d(w-w')d(p-p') we have
symb|w', p'ñfi áw', p'|fi = d(H(f) - w') ( Pfi (f) - p)
(really up to 0( 2), but for the sake of simplicity we will eliminate these symbols from now on).
2), but for the sake of simplicity we will eliminate these symbols from now on).
Let us now consider the singular dual, the symb
S as the functional on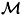 that must satisfy Eq.(2) that now reads
that must satisfy Eq.(2) that now reads
Then we define a density function rS(f) = symb
S = åirfiS(f) such that
 , is constant of the motion, so rfi(f) = f(H(f),Pfi(f)). Then we locally define at Dfi the local action-angle variables (q0,q1,...,qN,
, is constant of the motion, so rfi(f) = f(H(f),Pfi(f)). Then we locally define at Dfi the local action-angle variables (q0,q1,...,qN,  ), where
), where  would just be H,Pfi1,...,PfiN and we make the canonical transformation fa®
would just be H,Pfi1,...,PfiN and we make the canonical transformation fa®  , H,Pfi1,...,PfiN so that
, H,Pfi1,...,PfiN so that
Now we will integrate of the functions f(H,Pfi) = f(H,Pfi,...,Pfi) using the new variables.
where we have integrated the angular variables  , obtaining the configuration volume Cfi(H,Pfi) of the portion of the hypersurface defined by (H = const.,Pfi = const.) and contained in Dfi. So Eq.(10) reads
, obtaining the configuration volume Cfi(H,Pfi) of the portion of the hypersurface defined by (H = const.,Pfi = const.) and contained in Dfi. So Eq.(10) reads
for any Ofi(w,p) so rSfi(H,P) =  rfi(H,P) for fÎ
rfi(H,P) for fÎ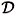 fñ and
fñ and
Putting rfi(w,p) = d(w-w')dN(p-p') for some i and all other rfj(w,p) = 0 for j ¹ i, we have
c.- Moreover the symb of Eq.(9) reads
So we have obtained a decomposition of r*(f) = rS(f) in classical hypersurfaces (H = w, Pfi(f) = pfi), containing chaotic trajectories (since the system is not integrable), summed with different weight coefficients rfi( w,p) /Cfi(H,Pfi).
d.- Finally only after decoherence the positive definite diagonal-singular part remains and from Eqs.(7) and (11) we see that
rfi (w, p) > 0 Þ r*(f) > 0
so the classical statistical limit is obtained.
5 The classical limit
The classical limit can be decomposed into the following processes
Quantum Mechanics - (decohence) ®
Boolean Quantum Mechanics - (symb and  ® 0 ) ®
® 0 ) ®
Classical Statistical Mechanics - (choice of a trajectory)
® Classical Mechanics
where the first two have been explained. It only remains the last one: For t(f) =  (f) and at any fixed t we have
(f) and at any fixed t we have
then we can include this 1 in decomposition (11) and we obtain
namely a sum of classical chaotic trajectories satisfying:
H(f) = w, t (f) = t0 + wt) ,
Pfi = pfi, qfi (f) = qfi0 + pfit
weighted by  ,where we can choose any one of them. In this way the classical limit is completed, in fact we have found the classical limit of a quantum system since we have obtained the classical trajectories, so the correspondence principle is also obtained as a theorem.
,where we can choose any one of them. In this way the classical limit is completed, in fact we have found the classical limit of a quantum system since we have obtained the classical trajectories, so the correspondence principle is also obtained as a theorem.
6 Conclusion
i.- We have defined the classical limit in the non-integrable case.
ii.- Essentially, we have presented a minimal formalism for quantum chaos [7].
iii.- We have deduced the correspondence principle.
References
[1] N.G. van Kampen, Physica XX, 603 (1954). A. Daneri, A. Loinger, and G.M. Prosperi, Nucl. Phys. 33, 297 (1962).
[2] J.P. Paz and W. Zurek, "Environment-induced decoherence and the transition from classical to quantum'', arXiv: quant-ph/0010011 (2000).
[3] M. Castagnino and R. Laura, Phys. Rev., A62, 022107 (2000). M. Castagnino, Physica A 335, 511 (2004). M. Castagnino and O. Lombardi, Stud. Phil. and Hist. Mod. Phys. 35, 73 (2004). M. Castagnino and O. Lombardi, "Self-Induced decoherence and the classical limit of quantum mechanics'', Phil. of Sci., in press (2004).
[4] L. van Hove, Physica 21, 517 (1955); 23, 441 (1957); 25, 268 (1959).
[5] M. Castagnino, M. Gadella, R. Liotta, and R. Id Betan, Journ. Phys. A34, 10067 (2001). M. Castagnino, R. Laura, R. Liotta, and R. Id Betan, Journ. Phys. A35, 6055 (2002).
[6] M. Castagnino, "The master and Fokker-Plank equations of the self-induced approach'', in preparation (2004).
[7] M. Castagnino, "Quantum chaos according to the self-induced approach'', in preparation (2004).
Received on 6 January, 2005
- [1] N.G. van Kampen, Physica XX, 603 (1954).
- A. Daneri, A. Loinger, and G.M. Prosperi, Nucl. Phys. 33, 297 (1962).
- [3] M. Castagnino and R. Laura, Phys. Rev., A62, 022107 (2000).
- M. Castagnino, Physica A 335, 511 (2004).
- M. Castagnino and O. Lombardi, Stud. Phil. and Hist. Mod. Phys. 35, 73 (2004).
- M. Castagnino and O. Lombardi, "Self-Induced decoherence and the classical limit of quantum mechanics'', Phil. of Sci., in press (2004).
- [4] L. van Hove, Physica 21, 517 (1955);
- [5] M. Castagnino, M. Gadella, R. Liotta, and R. Id Betan, Journ. Phys. A34, 10067 (2001).
- M. Castagnino, R. Laura, R. Liotta, and R. Id Betan, Journ. Phys. A35, 6055 (2002).
Publication Dates
-
Publication in this collection
06 Sept 2005 -
Date of issue
June 2005
History
-
Received
06 Jan 2005

















































