Soliton dynamics of magnetization driven by a magnetic field in uniaxial anisotropic ferromagnet

REGULAR ARTICLES

Soliton dynamics of magnetization driven by a magnetic field in uniaxial anisotropic ferromagnet

Zhong-Xi Zheng^I; Qiu-Yan Li^II; Zai-Dong Li^II; Ting-Dun Wen^I

^IDepartment of Physics, North University of China, Taiyuan 030051, China

^IIDepartment of Applied Physics, Hebei University of Technology, Tianjin 300130, China

ABSTRACT

We study the nonlinear magnetic excitation in an anisotropic ferromagnet with a magnetic field. In the long wave approximation, the Landau-Lifschitz equation with easy axis anisotropy is transformed into the nonlinear Schrödinger type. By means of a straightforward Darboux transformation we obtain the one- and two-soliton solutions of uniaxial anisotropic ferromagnet. From a careful analysis for the asymptotic behavior of two-soliton solution we find that the collision between two magnetic solitons is elastic. This will be very helpful to understand the significant nature of the interactions between solitons in the future.

Keywords: Soliton; Darboux transformation; Soliton interactions

The Heisenberg model of spin-spin interactions can be considered as the starting point for understanding the complex magnetic structures in solid physics. In particular, it explains the existence of ferromagnetism and antiferromagnetism at temperature below the Curie temperature. This model has attracted considerable attentions in nonlinear science and condensed-matter physics [1]. The concept of soliton in spin chain which exhibits both coherent and chaotic structures depending on the nature of the magnetic interactions [1-3] has been studied for decades. In the present time soliton in quasi one-dimensional magnetic systems is no longer a theoretical concept but can be probed by neutron inelastic scattering [4], nuclear magnetic resonance [5], and electron spin resonance [6]. The magnetic soliton [7], which describes localized magnetization, is an important excitation in the classical Heisenberg spin chain. In particular, the continuum limit for the nonlinear dynamics of magnetization in the classical ferromagnet is governed by the Landau-Lifschitz (L-L) equation [8]. This equation governs a classical nonlinear dynamically system with novel properties. In a one-dimensional case, some types of L-L equation is complete integrable. The isotropic case has been studied in various aspects [9, 10], and the construction of soliton solutions of L-L equation with an easy axis is also discussed [11]. It is worth to noted that the inverse scattering transformation [10, 12] is a useful method to solve the L-L equation. On the other hand great efforts [13] are also devoted to construct the soliton solution by means of the Darboux transformation [14-17].

In the recent years, considerable attentions have been devoted to the study of soliton interactions in nonlinear science. However, the soliton collisions in spin chain is not fully explored. In this paper, we investigate soliton interactions of uniaxial anisotropic ferromagnet with an external magnetic field. By transforming the L-L equation with an easy-axis into an equation of the nonlinear Schrödinger (NLS) type we obtain the one- and two-soliton solutions by using the Darboux transformation.

In the classical limit, the dynamics of spin chain is governed by the magnetization vector M = (M_x,M_y,M_z). The energy function including the exchange energy, anisotropic energy and the Zeeman energy can be written as [7]

where a is the exchange constant and b is the uniaxial anisotropic constant, b > 0 corresponds to easy-axis anisotropy while b < 0 corresponds to easy-plane type. The dynamics of the magnetization vector M(x,t) is determined by the following equation

where µ₀ is Bohr magneton. Substituting Eq. (1) into Eq. (2), we can get the L-L equation

where e₃ is the unit vector along the z-axis, and B = (0,0,B(t)). Taking into account the integral of motion M² º = constant, and introducing a single function Y, instead of two independent components of M,

where m º (m_x,m_y,m_z) = M/M₀,M₀ is the equilibrium magnetization. Thus Eq. (3) becomes

In ground state, vector M directs along the anisotropy axis e₃. Now we consider the low excitation, namely, the small deviations of M from e₃ which correspond to the values |Y| 1, then m_z » 1-1/2|Y|². In the long-wavelength approximation and the case b > 0, Eq. (5) may be simplified by keeping only the nonlinear terms of the order of the magnitude of |y| ²y. As a result, we have the following dimensionless Schrödinger equation:

For the convenience we have rescaled the space x and the time t by the 2l₀ and 1/w₀, where l₀ = is the characteristic magnetic length and w₀ = bm₀M₀/ is the homogeneous ferromagnetic resonance frequency.

In the following, we use the Darboux transformation to get exact soliton solutions of Eq. (6). By employing Ablowitz-Kaup-Newell-Segur technique one can construct the lax representation for Eq. (6) as follows

where y = (y₁ y₂)^T, the superscript "T" denotes the matrix transpose. The lax pairs L and M are given in the forms

with

where the overbar denotes the complex conjugate. Thus the Eq. (6) can be recovered from the compatibility condition

L -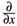 M + [L,M] = 0. Based on the Lax pair (7), we can obtain the general one- and two-soliton solution by using a straightforward Darboux transformation [18,19].

Consider the following transformation

where K satisfies

Letting

where L₁ = lJ + P₁, P₁ = , and with the help of Eqs. (7), (8) and (9), we obtain the Darboux transformation for Eq. (6) from Eq. (10) in the form

It is easy to verify that, if y = (y₁ y₂)^T is a eigenfunction of Eq. (7) corresponding to the eigenvalue l = l₁, then ( –₂

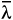₁)^T is also the eigenfunction, while with the eigenvalue -₁. Hence if taking the following notations

which ensures that Eq. (9) is held, we can obtain

where y^T = |y₁|² + |y₂|², and Eq. (11) becomes

where y is the eigenfunction of Eq. (7) corresponding to the eigenvalue l₁ for the solution Y. Thus by solving the Eq. (7) which is a first-order linear differential equation, we can generate a new solution Y₁ of the Eq. (6) from a known solution Y which is usually called "seed" solution.

To obtain exact N-order solution of Eq. (6), we firstly rewrite the Darboux transformation in Eq. (14) as in the form

where y[1,l] = (y₁[1,l], y₂[1,l])^T denotes the eigenfunction of Eq. (7) corresponding to eigenvalue l. Then repeating above the procedure for N times, we can obtain the exact N-order solution

where

here y[j',l] is the eigenfunction corresponding to l_j' for Y_j'-1 with Y₀º Y and s,l = 1,2, j' = 1,2,...,n-1, n = 2,3,...,N. Thus if choosing a "seed" as the basic initial solution, by solving linear characteristic equation system (7), one can construct a set of new solutions for Eq. (6) by employing the formula (16).

Taking the spectral parameter l₁ = µ₁+in₁ we get the one-soliton solution from Eqs. (16) and (4)

where

The parameters x'₀/µ₁ and x''₀/n₁ represent the initial center position and initial phase. To show the physical significance of our solutions, it is useful to give the parameter dependence of polar angle of the magnetization vector such that m = (sin q cos j,sin q sin j,cos q), namely the z-axis is the polar axis in a spherical coordinate. From Eq. (17) we have that

The expression (18) describes a magnetization precession characterized by four real parameters: velocity 2n₁, frequency [(-) - 1 - B(t) / (bM₀)] , initial center position /µ₁ and initial phase /n₁. Therefore, we can see that the external magnetic field contribute to precession frequency only.

The magnetic soliton collision is an interesting phenomenon in spin dynamics. To this purpose we should obtain the two-soliton solution of Eq. (6). Taking the spectral parameter l_j = µ_j + in_j, j = 1,2, from the expressions (16) and (4) we obtain the two-soliton solution of magnet as

where

where g = |l₂+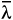₁|,f₀ = arg (l₂+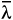₁), and the parameters Q_j and F_j, j = 1,2, are defined as

The solution (19) describes a general scattering process of two solitary waves with different center velocities 2n₁ and 2n₂, different phases F₁ and F₂. Before collision, they move towards each other, one with velocity 2n₁ and shape variation frequency W₁ = [(-) - 1 - B(t)/(bM₀)] and the other with 2n₂ and W₂ = [(-) - 1 - B(t)/(bM₀)]. In order to understand the nature of two-soliton interaction, we analyze the asymptotic behavior of two-soliton solution (19). Asymptotically, the two-soliton waves (19) can be written as a combination of two one-soliton waves (17) with different amplitudes and phases. The asymptotic form of two-soliton solution in limits t® ¥ and t® ¥ is similar to that of the one-soliton solution (17). In order to analyze the asymptotic behavior of two-soliton solutions (19) we consider the following asymptotic discussion for Q₁ ~ 0, Q₂ ~ ±¥, as t® ± ¥; and (ii) Q₂ ~ 0, Q₁ ~ ¥, as t ® ± ¥. This leads to the following asymptotic forms for the two-soliton solution.

(i) Before collision-namely, the case of limit t ® -¥.

(a) Soliton 1 (Q₁ ~ 0, Q₂® -¥).

(b) Soliton 2 (Q₂ ~ 0, Q₁® +¥).

(ii)After collision-namely, the case of limit t ® +¥.

(a) Soliton 1 (Q₁ ~ 0, Q₂ ~ +¥)

(b) Soliton 2 (Q₂ ~ 0, Q₁ ~ -¥)

where the parameters c₀ and f_j, j = 1,2 in equations (20) to (23) are defined by

From equations (20), (21), (22), and (23) we can see that there is no amplitude exchange among three components m_x, m_y and m_z for magnetization vector soliton 1 and soliton 2 during collision. However, from Eq. (20) to (23) one can see that there is a phase change 2f₂(2f₁) for the components m_x and m_y of the soliton 1(2), and the center position change -2c₀(+2c₀) for the components m_z for soliton 1(2) during collision. This interaction between two magnetic solitons is called elastic collision. The magnetic soliton solutions in Eqs. (17) and (19), which describes localized magnetization, is an important excitation in the Heisenberg spin chain. The significant importance of the study for the soliton is that it can travel over long distances with neither attenuation nor change of shape, since the dispersion is compensated by nonlinear effects. This type of the elastic soliton collision shows that the information held in each soliton will almost not be disturbed by each other in soliton propagation. These properties may have potential application in future quantum communication.

In conclusion, by transforming the L-L equation with an easy-axis into an equation of the nonlinear Schrödinger type we investigate the nonlinear magnetic excitations in an anisotropic ferromagnet with a magnetic field. From a straightforward Darboux transformation the one- and two-soliton solutions of uniaxial anisotropic ferromagnet with an external magnetic field are reported. Moreover, by analyzing carefully the asymptotic behavior of two-soliton solution we find that the collision between two magnetic solitons is elastic. This is very helpful to understand significant nature of the interactions between solitons in the future.

This work was supported the Natural Science Foundation of China No. 10647122 and 60476063, the Doctoral Foundation of Education Bureau of Hebei Province No. 2006110, the key subject construction project of Heibei Provincical University, and the Natural Science Foundation of Shanxi Province No. 20041011.

[1] Y. S. Kivshar and B. A. Malomed, Rev. Mod. Phys. 61 763, (1989).

[2] S. E. Trullinger, V. E. Zakharov and V. L. Pokrovsky, Solitons (Elsevier, New York), (1986).

[3] M. J. Ablowitz and P. A. Clarkson Solitons, Nonliear Evoluation Equations and Inverse Scattering (Cambrige University Press, Cambrige), (1991).

[4] J. P. Boucher, R. Pynn, M. Remoissenet, L. P. Regnault, Y. Endoh, and J. P. Renard, Phys. Rev. Lett. 64 1557, (1990).

[5] J. P. Boucher and J. P. Renard, Phys. Rev. Lett. 45 486, (1980).

[6] T. Asano, H. Nojiri, Y. Inagaki, J. P. Boucher, T. Sakon, Y. Ajiro, and M. Motokawa, Phys. Rev. Lett. 84 5880, (2000).

[7] A. M. Kosevich, B. A. Ivanoy and A. S. Kovalev, Phys. Rep. 194 117, (1990).

[8] L. D. Landau and E. M. Lifschitz, Phys. Z. Sowjetunion 8 153, (1935).

[9] M. Laksmanan, Phys. Lett. A 61 53, (1977); J. Tjon and J. Wright, Phys. Rev. B 15 3470, (1977); T, Shimizu, J. Phys. Society of Japan 53 507, (1984).

[10] L. A. Takhtajan, Phys. Lett. A 64 235, (1977).

[11] A. E. Bolovik, Sov. Phys.-JETP Lett. 28 629, (1978); G. R. W. Quispel and H. W. Capel, Physica A 117 76, (1983).

[12] H. C. Fogedby, J. Phys. A 13 1467, (1980); Z. Y. Chen, N. N. Huang and Z. Z. Liu, J. Phys. Condens. Matter 7 4533, (1995); Z. D. Li, Lu Li, W. M. Liu, J. Q. Liang and T. Ziman Phys. Rev. E 68 036102, (2003); Z. D. Li, J. Q. Liang, Lu Li, and W. M. Liu, Phys. Rev. E 69 066611, (2004).

[13] H. J. Mikeska, Physica C 11 L29, (1978); K. A. Long and A. R. Bishop, J. Phys. A 12 1325, (1979).

[14] N. N. Huang, Z. Y. Chen, and Z. Z. Liu, Phys. Rev. Lett. 75 1395, (1995).

[15] W. M. Liu, Shu-Li Yang, Fu-Cho Pu, and Nian-Ning Huang, Z. Phys. B 103 105, (1997); W. M. Liu, Wu-Shou Zhang and Fu-Cho Pu, Phys. Rev. B 60 12893, (1999); W. M. Liu, B. Wu, X. Zhou, D. K. Campbell, S. T. Chui and Q. Niu, Phys. Rev. B 65 172416, (2002).

[16] Q. Y. Li, Z. W. Xie, L. Li, Z. D. Li, and J. Q. Liang, Annals of Physics 312, 128, (2004); Z. D. Li, Lu Li and J. Q. Liang, Chin. Phys. Lett. 20 39, (2003); Z. D. Li, Lu Li and J. Q. Liang, Chin. Phys. Lett. 21 443, (2004).

[17] X. J. Chen, L. J. Hou, and Wa Kun Lam, Chin. Phys. Lett. 22 830, (2005).

[18] V. B. Matveev and M. A. Salli, Darboux Transformations and Solitons, (Springer Series in Nonlinear Dynamics, Springer, Berlin), (1991).

[19] C. H. Gu, H. S. Hu, Z. X. Zhou, Darboux Transformation in Soliton Theory and its Geometric Applications (Shanghai Scientific and Technical Publishers, in Chinese), (1999).

Received on 9 October, 2006

Publication Dates

• Publication in this collection
  21 June 2007
• Date of issue
  Dec 2006

History

• Received
  09 Oct 2006