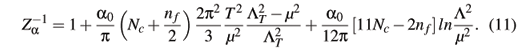Abstract
We study the running of the QCD coupling with the momentum squared (Q²) and the temperature scales in the high temperature limit (T > Tc), using a mass dependent renormalization scheme to build the Renormalization Group Equations. The approach used guaranty gauge invariance, through the use of the Hard Thermal Loop approximation, and independence of the vertex chosen to renormalize the coupling. In general, the dependence of the coupling with the temperature is not logarithmical, although in the region Q² ~ T² the logarithm approximation is reasonable. Finally, as known from Debye screening, color charge is screened in the coupling. The number of flavors, however, is anti-screened.
Finite temperature QCD; Running coupling
REGULAR ARTICLES
The temperature dependence of the QCD running coupling
F. M. Steffens
NFC - FCBEE - Universidade Presbiteriana Mackenzie, Rua da Consolação 930, 01302-907, São Paulo, SP, Brazil
IFT - UNESP, Rua Pamplona 145, 01405-900, São Paulo, SP, Brazil
ABSTRACT
We study the running of the QCD coupling with the momentum squared (Q2) and the temperature scales in the high temperature limit (T > Tc), using a mass dependent renormalization scheme to build the Renormalization Group Equations. The approach used guaranty gauge invariance, through the use of the Hard Thermal Loop approximation, and independence of the vertex chosen to renormalize the coupling. In general, the dependence of the coupling with the temperature is not logarithmical, although in the region Q2 ~ T2 the logarithm approximation is reasonable. Finally, as known from Debye screening, color charge is screened in the coupling. The number of flavors, however, is anti-screened.
Keywords: Finite temperature QCD; Running coupling
One of the important questions in perturbative QCD at finite temperature T is what is the temperature dependence of the strong coupling constant, as(T). According to an early study by Collins and Perry [1], where arguments from the Renormalization Group Equations (RGE) were used, temperature replaces the momentum as the running scale, implying that as(T) decreases as a logarithm as T increases. This conclusion is based on general considerations, where no specific calculations of the vertices and self-energies were done. Later, more rigorous treatments based on the RGE were developed [2, 3], with applications to perturbative QCD [2, 4]. However, it was soon realized that the resulting coupling was strongly dependent on both the gauge [5-7] and vertex chosen to renormalize it [4, 8, 9]. In any case, some of the calculations did not result in the logarithmical dependence of the coupling in the temperature. Recently, in the context of a semiclassical background field method, it has also been calculated [10] that as has an inverse logarithmical dependence in the temperature, where reference to the earlier calculations based on the RGE was said to substantiate the result. Moreover, applications to the perturbative calculations of energy density, pressure, etc, using the logarithmical dependence are frequently used in the literature [11-13].
In the early 1990's the problem of gauge invariance of two, three and four points Green functions was solved with the introduction of the Hard Thermal Loops (HTL) [14]. In particular, it was shown that the dominant, gauge invariant, contributions to the N-point functions have a T2 dependence, and that they satisfy abelian type Ward identities [14, 15]. From the gluon self-energy in the HTL, it is possible to build an effective coupling at finite temperature, which goes with the inverse of the Debye mass and thus does not have a logarithmic dependence on the temperature [16]. However, there has been no extensive calculation of the RGE for the ultra-violet regime of the running coupling using the dominant, gauge invariant, results from the HTL. Rigorously, there is no extra ultra-violet divergence induced by thermal effects, meaning that the renormalization of QCD at T = 0 is sufficient to make QCD at T ¹ 0 finite. Still, we can redefine the theory by a finite renormalization, relating parameters like mass and coupling constants at different temperatures with the aid of temperature dependent renormalization constants, with appropriate renormalization conditions [3]. The purpose of this letter is to calculate the running of the QCD coupling with the momentum scale and with the temperature using the vertices and self-energies calculated from the HTL. Although it is an immediate application, we think that given the discrepancies found in the literature, this is an useful exercise with an impact in all the perturbative QCD calculations at finite temperature.
We will treat the mass scale introduced in the system by the temperature in the same way quark masses are handled in the T = 0 theory [17], in a mass dependent renormalization scheme1 1 In fact, in the Quasi-Particle picture [16] the terms proportional to the square of the temperature are identified with thermal masses. Hence, the analogy with QCD at T=0 but massive quarks is complete, only that masses in the present case have an origin in the temperature . In this case, the general form for the renormalized n-points Green function will be:
where µ is the renormalization scale, k is the external momentum and g the renormalized coupling at the scale µ. Using the standard approach of the RGE, i.e., taking the derivative of the unrenormalized Green function with respect to µ, one gets:
where gn(g2, ) is the anomalous dimension of the n fields appearing in Gn and
) is the anomalous dimension of the n fields appearing in Gn and
the beta function and the temperature anomalous dimension, respectively. The temperature dependence in the beta function and anomalous dimensions indicates that we are working in a mass dependent renormalization scheme. The relation between the bare and renormalized coupling is given by:
where Za is the renormalization constant of the coupling, a0 =  /4p is the bare coupling, and as = g2/4p is the coupling at the subtraction point µ and temperature T.
/4p is the bare coupling, and as = g2/4p is the coupling at the subtraction point µ and temperature T.
If we want a meaningful result for the running coupling, any vertex should be equally good to renormalize it. If we use the triple gluon vertex, then
where Z3 renormalizes the gluon field while Z1 renormalizes the triple gluon vertex. We start with the renormalization of the gluon field. To include temperature in the renormalization constants and simultaneously preserve the Slavnov-Taylor identities, we will work in the framework of the HTL resummation program, where the dominant terms are known to be gauge invariant. A direct computation of the transverse part of the gluon self-energy at one loop gives [18, 19]:
where k is the four momentum of the external gluon. Only the dominant term in the high temperature expansion was written because of its gauge invariance. One can see that Eq. (6) vanishes for k0 << | |, and that it is reduced to
|, and that it is reduced to
for k0 >> | |, and LT is a mass scale (
|, and LT is a mass scale ( º |
º | |k0).
|k0).
We will be working in a Momentum Subtraction Scheme (MOM), which is suitable for a mass dependent renormalization scheme as in the present case, with the temperature replacing the mass. Although a MOM scheme usually breaks the Slavnov-Taylor identities, the deviation among the couplings defined through different vertices is vanishingly small [20]. As a renormalization condition, we impose that the thermal part of the renormalized gluon self-energy, calculated at the subtraction point µ2, be given by:
Including the T = 0 part, we then calculate the renormalization constant Z3:
where a is the gauge parameter. We now need the one loop correction to the triple gluon vertex, which is a known quantity [16]: it has the same functional form of Eq. (7). Imposing again that the temperature dependent part of the renormalized vertex be equal to the bare one, with the replacement of LT ® m, we calculate the triple gluon vertex renormalization constant to be:
Using Eqs. (9) and (10) in (5), we get:
Notice that the temperature dependence, unlike the momentum scale, is not logarithmical. Before we proceed to calculate the running of the coupling, we make a few remarks on the calculation of  using other vertices. For instance, if we use the ghost-gluon vertex, then:
using other vertices. For instance, if we use the ghost-gluon vertex, then:
where
3 is the ghost field renormalization constant and 1 is the gluon-ghost vertex renormalization constant. It happens that in the HTL approximation the external momenta in the numerators of the loop integrals are disregarded, as the main contribution comes from the internal momenta of order T, with T taken to be large. Compared to the gluon self-energy, the ghost self-energy does not have enough powers of internal momenta in the numerator to produce the leading, T2, behavior in the temperature. The same happens to the ghost vertex, something that can be immediately inferred from the abelian Ward identities relating the ghost vertex to its self-energy. Hence, the thermal parts of
1 is the gluon-ghost vertex renormalization constant. It happens that in the HTL approximation the external momenta in the numerators of the loop integrals are disregarded, as the main contribution comes from the internal momenta of order T, with T taken to be large. Compared to the gluon self-energy, the ghost self-energy does not have enough powers of internal momenta in the numerator to produce the leading, T2, behavior in the temperature. The same happens to the ghost vertex, something that can be immediately inferred from the abelian Ward identities relating the ghost vertex to its self-energy. Hence, the thermal parts of  3 and
3 and  1 will be sub-leading to Z3 in the temperature. In such case, the thermal part of Za will be dominated by Z3 and we recover Eq. (11). Finally, we could have used the quark-gluon vertex to calculate Za:
1 will be sub-leading to Z3 in the temperature. In such case, the thermal part of Za will be dominated by Z3 and we recover Eq. (11). Finally, we could have used the quark-gluon vertex to calculate Za:
where Z2 is the fermion field renormalization constant while Z1F is the quark-gluon vertex renormalization constant. The HTL calculation for the dominant part of the quark self-energy and the quark-gluon vertex at one loop are known [16]. Their T2 dependence are the same. Imposing renormalization conditions of the type of Eq. (8) for the calculation of Z2 and Z1F, it follows that their T2 dependence are the same, cancelling in the ratio of Eq. (13). As before, Z3 will dominate the temperature dependence of Za, and we once again recover Eq. (11).
The calculation of the b function (including the T = 0 and the T ¹ 0 parts), for a fixed temperature but an arbitrary renormalization point is now straightforward. Using Eqs. (3), (4), and (11), we have:
to order  . This is the only RGE for as because there is only one renormalization scale for both the T = 0 and T ¹ 0 parts. The solution of Eq. (14) is:
. This is the only RGE for as because there is only one renormalization scale for both the T = 0 and T ¹ 0 parts. The solution of Eq. (14) is:
It is helpful to rewrite Eq. (15) in the same format of the T = 0 theory. To this end, we define effective, scale dependent, numbers of colors and flavors:


With the help of Eqs. (16) and (17), the expression for the running coupling is written as:
Equations (16) and (17) tell us that for fixed  and T2, with Q2® 0, the effective number of color decreases,
and T2, with Q2® 0, the effective number of color decreases,  < Nc, while the effective number of flavors increases: color charge is screened, and the number of flavors are anti-screened. The same argument applies when keeping Q2 and
< Nc, while the effective number of flavors increases: color charge is screened, and the number of flavors are anti-screened. The same argument applies when keeping Q2 and  fixed, while taking T2 going to infinity. To quantify these assertions, we show in Fig. 1 the Q2 dependence of
fixed, while taking T2 going to infinity. To quantify these assertions, we show in Fig. 1 the Q2 dependence of  and
and  for T2 = 1 GeV2,
for T2 = 1 GeV2,  =
=  , and Nc = nf = 3. As expected,
, and Nc = nf = 3. As expected,  decreases while
decreases while  increases as Q2 decreases from
increases as Q2 decreases from  to T2.
to T2.
In Fig. 2 we show the behavior of as for 3 values of the temperature. For as( , T2), we use the experimental value measured at mZ » 91 GeV and at zero temperature [22]. That is, we assume that at such high values of the virtuality of the probe, temperatures of the order of 1 GeV are not relevant. This seems to be the case as, in this region,
, T2), we use the experimental value measured at mZ » 91 GeV and at zero temperature [22]. That is, we assume that at such high values of the virtuality of the probe, temperatures of the order of 1 GeV are not relevant. This seems to be the case as, in this region,  ® Nc and
® Nc and  ® nf. At T = 0 GeV we have, as usual, the coupling growing rapidly for Q2 < 10 GeV2. However, at T = 0.5 and 1 GeV, as(Q2,T2) starts to change its behavior in the region around Q2 = 20 GeV2. Instead of the rapid growth observed at the T = 0 case, for finite T there is first an almost Q2 independence of the coupling, and then it decreases with Q2, showing the color screening, and flavor anti-screening, in action. In fact, we observe that as changes its qualitative behavior (from a divergence to finite values), for small values of Q2, in the region around T ~ 0.2 GeV, although any conclusion based on a perturbative RGE analysis for such low values of T and Q2 should be taken with extreme caution. In any case, in general the running coupling does not have a logarithm dependence on the temperature. But if we consider the particular region where Q2 ~ T2, taking
® nf. At T = 0 GeV we have, as usual, the coupling growing rapidly for Q2 < 10 GeV2. However, at T = 0.5 and 1 GeV, as(Q2,T2) starts to change its behavior in the region around Q2 = 20 GeV2. Instead of the rapid growth observed at the T = 0 case, for finite T there is first an almost Q2 independence of the coupling, and then it decreases with Q2, showing the color screening, and flavor anti-screening, in action. In fact, we observe that as changes its qualitative behavior (from a divergence to finite values), for small values of Q2, in the region around T ~ 0.2 GeV, although any conclusion based on a perturbative RGE analysis for such low values of T and Q2 should be taken with extreme caution. In any case, in general the running coupling does not have a logarithm dependence on the temperature. But if we consider the particular region where Q2 ~ T2, taking  >> T2, we get from Eq. (16-18) that:
>> T2, we get from Eq. (16-18) that:
In summary, we have presented a RGE calculation of the running coupling at finite temperature QCD, introducing the temperature scale as the mass scale is introduced in the T = 0 theory, in a mass dependent renormalization scheme. We restricted the calculation to the dominant, gauge invariant, HTL terms. As a result, the coupling is shown to be independent of the vertex used to renormalize it. As is well known from Debye screening, the number of colors are screened by the temperature. The number of flavors, however, is anti-screened. Also, although in general the temperature dependence of the coupling is not logarithmic, in some especial cases, where Q2 ~ T2, the logarithmic dependence can be a good approximation.
Acknowledgments
I would like to thank F. T. Brandt for helpful discussions on thermal field theory, and the support of the Special Research Centre for the Subatomic Structure of Matter at the University of Adelaide during the initial stages of this work. This work was supported by FAPESP (03/10754-0), CNPq (308932/2003-0) and MackPesquisa .
[1] J. C. Collins and M. J. Perry, Phys. Rev. Lett. 34, 1353 (1975).
[2] J. I. Kapusta, Phys. Rev. D 20, 989 (1979).
[3] H. Matsumoto, Y. Nakano, and Y. Umezawa, Phys. Rev. D 29, 1116 (1984).
[4] H. Nakkagawa and A. Niégawa, Phys. Lett. B 193, 263 (1987); H. Nakkagawa, A. Niégawa, and H. Yokota, Phys. Rev. D 38, 2566 (1988).
[5] P. Elmfors and R. Kobes, Phys. Rev. D 51, 774 (1995).
[6] M. Chaichian and M. Hayashi, Acta. Phys. Polon 27, 1703 (1996).
[7] K. Sasaki, Nucl. Phys. B 490, 472 (1997).
[8] Y. Fujimoto and H. Yamada, Phys. Lett. B 200, 167 (1988).
[9] R. Baier, B. Pire, and D. Schiff, Phys. Lett. B 238, 367 (1990).
[10] R. A. Schneider, Phys. Rev. D 67, 057901 (2003); Phys. Rev. D 66, 036003 (2002).
[11] A. Peshier et al., Phys. Rev. D 54, 2399 (1996).
[12] R. A. Schneider and W. Weise, Phys. Rev. C 64, 055201 (2001).
[13] P. N. Meisinger, M. C. Ogilvie, and T. R. Miller, Phys. Lett. B 585, 149 (2004).
[14] E. Braaten and R. D. Pisarski, Phys. Rev. Lett. 64, 1338 (1990); Nucl. Phys. B 337, 569 (1990); 339, 310 (1990).
[15] J. Frenkel and J. C. Taylor, Nucl. Phys. B 334, 199 (1990).
[16] Michel Le Bellac, in Thermal Field Theory, edited by P. V. Landshoff, D. R. Nelson, D. W. Sciana and S. Weiberg (Cambridge University Press, Cambridge, 1996)
[17] H. Georgi and H. D. Politzer, Phys. Rev. D 14, 1829 (1976).
[18] E. Braaten and R. D. Pisarski, Phys. Rev. D 42, 2156 (1990).
[19] F. T. Brandt and J. Frenkel, Phys. Rev. D 56, 2453 (1997); F. T. Brandt, J. Frenkel and F. R. Machado, Phys. Rev. D 61, 125014 (2000).
[20] Andrei Smilga, Lectures on Quantum Chromodynamics, World Scientific 2001.
[21] P. Pascual and R. Tarrach, in QCD: Renormalization for the Practitioner, edited by H. Araki et al. (Springer Verlag, Berlin - Heidelberg, 1984).
[22] Particle Data Group, Phys. Rev. D 54, 1 (1996).
Received on 6 February, 2006
- [1] J. C. Collins and M. J. Perry, Phys. Rev. Lett. 34, 1353 (1975).
- [2] J. I. Kapusta, Phys. Rev. D 20, 989 (1979).
- [3] H. Matsumoto, Y. Nakano, and Y. Umezawa, Phys. Rev. D 29, 1116 (1984).
- [4] H. Nakkagawa and A. Niégawa, Phys. Lett. B 193, 263 (1987);
- H. Nakkagawa, A. Niégawa, and H. Yokota, Phys. Rev. D 38, 2566 (1988).
- [5] P. Elmfors and R. Kobes, Phys. Rev. D 51, 774 (1995).
- [6] M. Chaichian and M. Hayashi, Acta. Phys. Polon 27, 1703 (1996).
- [7] K. Sasaki, Nucl. Phys. B 490, 472 (1997).
- [8] Y. Fujimoto and H. Yamada, Phys. Lett. B 200, 167 (1988).
- [9] R. Baier, B. Pire, and D. Schiff, Phys. Lett. B 238, 367 (1990).
- [10] R. A. Schneider, Phys. Rev. D 67, 057901 (2003); Phys. Rev. D 66, 036003 (2002).
- [11] A. Peshier et al., Phys. Rev. D 54, 2399 (1996).
- [12] R. A. Schneider and W. Weise, Phys. Rev. C 64, 055201 (2001).
- [13] P. N. Meisinger, M. C. Ogilvie, and T. R. Miller, Phys. Lett. B 585, 149 (2004).
- [14] E. Braaten and R. D. Pisarski, Phys. Rev. Lett. 64, 1338 (1990); Nucl. Phys. B 337, 569 (1990); 339, 310 (1990).
- [15] J. Frenkel and J. C. Taylor, Nucl. Phys. B 334, 199 (1990).
- [16] Michel Le Bellac, in Thermal Field Theory, edited by P. V. Landshoff, D. R. Nelson, D. W. Sciana and S. Weiberg (Cambridge University Press, Cambridge, 1996)
- [17] H. Georgi and H. D. Politzer, Phys. Rev. D 14, 1829 (1976).
- [18] E. Braaten and R. D. Pisarski, Phys. Rev. D 42, 2156 (1990).
- [19] F. T. Brandt and J. Frenkel, Phys. Rev. D 56, 2453 (1997);
- F. T. Brandt, J. Frenkel and F. R. Machado, Phys. Rev. D 61, 125014 (2000).
- [20] Andrei Smilga, Lectures on Quantum Chromodynamics, World Scientific 2001.
- [21] P. Pascual and R. Tarrach, in QCD: Renormalization for the Practitioner, edited by H. Araki et al. (Springer Verlag, Berlin - Heidelberg, 1984).
- [22] Particle Data Group, Phys. Rev. D 54, 1 (1996).
Publication Dates
-
Publication in this collection
31 July 2006 -
Date of issue
June 2006