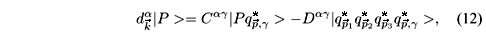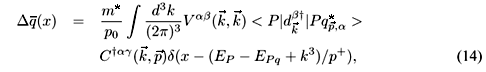The flavor asymmetry in the polarized proton sea

Abstract

We perform a careful study on the effect of the Pauli blocking to the light polarized antiquark structure of the proton sea. We develop the formal expressions for the polarized antiquark distributions, highlighting the role played by quark statistics and the vacuum structure. The ratio involving the polarized antiquarks is calculated. In particular, it is found that D<img id="_x0000_i1026" src="../../../../img/revistas/bjp/v34n1a/a17img01.gif" align=absbottom>(x)/D<img id="_x0000_i1027" src="../../../../img/revistas/bjp/v34n1a/a17img02.gif" align=absbottom>(x) should be negative and x independent.

The flavor asymmetry in the polarized proton sea

F. M. Steffens

Mackenzie University - FCBEE, Rua da Consolacao 930, 01302-907, São Paulo, SP, Brazil

Instituto de Física Teórica, UNESP, Rua Pamplona 145, 01405-900, São Paulo, SP, Brazil

ABSTRACT

We perform a careful study on the effect of the Pauli blocking to the light polarized antiquark structure of the proton sea. We develop the formal expressions for the polarized antiquark distributions, highlighting the role played by quark statistics and the vacuum structure. The ratio involving the polarized antiquarks is calculated. In particular, it is found that D(x)/D(x) should be negative and x independent.

Spin physics has atracted a lot of attention in the last 15 years, both experimentally and theoretically. Since the first precise results on the proton longitudinal polarized structure function was released, in the late 1980's, we have learned a great deal about how the quarks and gluons combine to produce the observed spin of the proton [1]. However, we are still uncertain abou the correct size of the gluon distribution as well as the decomposition of the quark contribution to the total spin in terms of its quark and antiquark parts. COMPASS at CERN is starting to measure the polarized gluon distribution directly using a polarized muon beam. On the quark side, the semi-inclusive program of HERMES has released some recent results for the quark polarizations of u, , d, , and s + [2]. There is a good agreement between their data and parametrizations for the valence distributions in NLO QCD. However, the antiquark distributions are still plagued with sizeable statistical uncertainties. In particular, it is not possible to determine weather the light antiquarks are flavor asymmetric, as observed in unpolarized scattering, in the case of polarized distributions.

There are, on the other hand, a strong theoretical motivation for the asymmetry to be present also in the polarized sector, and this work is devoted to advocate what should be the most compelling mechanism: the fundamental role played by the quark statistics in both the polarized and unpolarized antiquark distributions. This work is a more detailed version of some previously published results [3] on this problem.

In order to isolate the Pauli blocking effects to the sea structure of the proton, we work out the formal definition of the antiquark distributions to a point where some actual predictions can be made without the introduction of a number of model parameters. From this point, we are able to study to what extent Pauli Blocking is a correction or is the main phenomenon behind the sea asymmetry of the light quarks.

We start with the formal definition of the polarized antiquark distribution [4]:

with x > 0. To calculate Eq. (1), we remember that:

with the field operators expanded in terms of free plane waves:

Using Eqs. (2) and (3) in Eq. (1), we get:

where = = , and the time dependence of the creation and annihilation operators is calculated from:

where is the time independent operator that destroys a quark with spin up (down) and momentum .

Quarks in the proton are not free and that can be translated into a complicated vacuum structure where the confined quarks live [5,6,7,8,9]. In this environment, the free space vacuum is certainly not a good approximation for the ground state of the confined quark operators. Instead, one has to build a new vacuum structure based on bound quark operators. Following this direction, we extend the work of Tsushima, Thomas and Dunne [6], to derive general forms for the polarized antiquark distributions which incorporate the effects from the modified vacuum. The bound state operators (denoted by a ''*'') and the vacuum of the bound states are defined such that:

The bound quark operators can be related to the free quark operators in the following way:

where the A^ba(k,p), B^ba(k,p), C^ab(k,p) and D^ab(k,p) factors are the overlaps between the bound and free quark states. The calculation of the anticomutator between the free and bound operators gives:

and similar for the other operators. Finally, the proton state is written in terms of the bound quark operators as:

where is a function of the effective quark operators, with the individual momentum of the three valence quarks. Although only the valence quarks appear explicitly in the functional, it is understood that it may be populated by quark - antiquark pairs. In this way, the notation only shows the net, or unpaired, number of quarks and antiquarks.

Thus the action of the free antiquark annihilation operator in the proton state results in:

and similar for the quark operator. The state | > represents a quark that was created in the original proton state, while the state | > means that one antiquark, of the original infinite number of pairs present in the proton state, was destroyed in the proton state, leaving 4 unpaired quarks in total. When using Eqs. (11) and (12) in the polarized quark distribution, Eq. (4), we see that conservation of energy momentum impose that the part involving the quark operators vanish, and we have left only the terms involving the antiquark operators.

In order to reach any conclusion regarding the sea quark structure of the proton, we should specify what is the state |P > in Eq. (4). The proton state, as a bound state of quarks, has to be built from bound state quark operators acting on the modified vacuum, as described by Eqs. (6) and (7). The simplest form one can use for such state is that given by the SU(6) wave function:

For this simple wave function, where no anti-quarks are present, we must have no contribution from the term proportional to D^ag in Eq. (12). In this way, the polarized antiquark distribution is written as:

where E_Pq in the eigenstate of the Hamiltonian operator acting on the | > state.

Notice that the polarized antiquark distribution comes from the expectation values involving the bound quark states. In the case of a proton state built from free quarks there is no antiquark distributions, as in that case |C|² ® 0. We can, of course, generate the sea quarks through perturbation theory once we know the quark - gluon vertex from QCD, a procedure which has actually been implemented before [10,11]. In this case, it happens that the quark-antiquark pairs generated from perturbative gluons produce an excess of antiquarks over antiquarks - in clear contradiction to the naive expectation from the Pauli principle. The solution to this dilemma is straightforward and will be presented in a forthcoming work.

To proceed, we need the calculation of the expectation value between the bound quark states. A direct calculation, using the SU(6) wave function, gives 4/3 for the polarized anti-quarks, and –1/3 for the polarized anti-quarks. As all the remaining terms are the same for both distributions, we naturally have that:

As the polarized distributions are not affected by pionic corrections, this result should stand exact for the SU(6) wave function. Of course, more complicated wave functions would produce different numerical factors, but it would not introduce an extra x dependence. In this case, the experimental value for D(x)/ D(x) should be very close to a straight line. Finally, there has been previous estimates of nonperturbative effects from the vacuum structure to the polarized distributions. In particular, the Chiral Soliton Model has been used [8] to predict the shape of the polarized antiquark distribution, and calculations by the Adelaide group [9] also reproduce the results encapsulated in Eq. (15).

We have seen that developing the formal expression for the polarized antiquark distribution, Eq. (1), as far as possible in terms of the quark operators, allows us to derive some general conclusions about the physics responsible for the polarized antiquark asymmetry in the proton sea. We see that the vacuum structure inside the proton, as expressed by Eq. (12), is decisive in reaching this conclusion. However, it is not the final story, as Eq. (12) would exist even if quarks were bosons. The fact that quarks are fermions is fundamental, and probably the only sizeable effect, for a future asymmetry observation in the polarized sea of the proton. Of course, to extract numbers we need to model the proton wave function. Using the SU(6) quark wave function, we see that the x dependence cancels when ratios are taken. Thus, apart from quark mass effects in the large x region, Eq. (15) should hold. In this way, the polarized ratio is expected to be x independent.

I would like to thank A. W. Thomas and Kazuo Tsushima for helpful discussions. This work was done under contract number PV-IFT/005.

References

[1] M. Anselmino, A. Efremov, and E. Leader, Phys. Rep. 261, 1 (1995); X. Ji, Int. J. Mod. Phys. A18, 1303 (2003).

[2] D. Ryckbosch, on behalf of the HERMES Collaboration, hep-ex/0311021.

[3] F. M. Steffens, Phys. Lett. B541, 346 (2002).

[4] R. L. Jaffe, Nucl. Phys. B229, 205 (1983).

[5] A. Szczurek, A. J. Buchmann, and A. Fassler, J. Phys. G 22, 1741 (1996).

[6] K. Tsushima, A. W. Thomas, and Gerald V. Dunne, ADP-01-27-T461, Presented at Workshop on Lepton Scattering, Hadrons and QCD, Adelaide, Australia, 26 Mar - 6 Apr. 2001, hep-ph/0107042.

[7] D. Diakonov et al., Nucl. Phys. B480, 341 (1996).

[8] D. Diakonov et al., Phys. Rev. D56, 4069 (1997); K. Goeke et al., Nucl. Phys. A680, 307 (2000).

[9] A. W. Schreiber, A. I Signal, and A. W. Thomas, Phys. Rev. D44, 2653 (1991).

[10] J. F. Donough and E. Golowich, Phys. Rev. D15, 3421 (1977).

[11] F. M. Steffens and A. W. Thomas, Phys. Rev. C55, 900 (1997).

Received on 15 August, 2003.

Publication Dates

• Publication in this collection
  11 May 2004
• Date of issue
  Mar 2004

History

• Accepted
  15 Aug 2003
• Received
  15 Aug 2003