Applications of quantum field theory in condensed matter

ROUND TABLE: WHAT IS UP IN FIELD THEORY?

Applications of quantum field theory in condensed matter

E. C. Marino

Instituto de Física, Universidade Federal do Rio de Janeiro, Cx.P. 68528, Rio de Janeiro RJ 21941-972, Brazil

ABSTRACT

We present a brief review of some applications of quantum field theory in condensed matter systems. These include isotropic and anisotropic antiferromagnetic chains, strongly correlated organic conductors, such as the Bechgaard salts, carbon nanotubes and high-Tc superconductors. The review is by no means exhaustive and points to a vast range of new interesting possible applications.

1 Introduction

Quantum field theory, since its birth, has been the basic framework for describing the physics of elementary particles and their interactions. Firstly, its success in quantum electrodynamics has been enormous, leading to the best theoretical predictions of the whole physics. Later on, use of quantum field theory in the description of the weak and strong interactions, was also extremely successful, converging for the standard model, which has a vast and impressive body of experimental support. It was in the 80's, however, that the efforts to produce a quantum field theory based grand unified model for the weak, strong and electromagnetic interactions, failed. This was the starting point for the attempts to use new methods such as string theory in high-energy physics.

Coincidentally, three paradigms of condensed matter physics fell in the 80's, namely, the independent electron approximation, the Landau theory of the Fermi liquid and the BCS theory of superconductivity. The first one is the basis upon which the so called solid state physics has been built and allows a thorough understanding of metals, insulators and semiconductors. The second one is a systematic procedure for introducing interactions among the electrons and describes quite well a large variety of systems in condensed matter. Both of them failed to provide an adequate description of new complex materials presenting strong electronic correlations, found in the 80's and 90's. BCS theory, on the other hand, for 30 years was the fundamental framework for understanding the phenomenon of superconductivity. Nevertheless, it was unable to provide an explanation for the mechanism underlying the new high-temperature superconducting cuprates discovered in the mid 80's.

Quantum field theory, being the natural framework for the quantum description of interacting many-particle systems, found a fertile field of applications, precisely in the description of those condensed matter systems, which could not be described by traditional methods. A new and active area of applications of quantum field theory in condensed matter has thus been opened and is the object of this brief review. We are going to concentrate basically in low-dimensional quantum magnetic systems, strongly correlated low-dimensional conductors, carbon nanotubes and high-Tc superconductors.

2 Quantum magnetic chains

2.1 Isotropic Heisenberg antiferromagnet

Let us consider the one-dimensional AF Heisenberg hamiltonian (XXZ)

The isotropic case corresponds to d = 1. We can map this into a fermionic system through the Jordan-Wigner transformation [1]

Taking the continuum limit, we can use bosonization to map the original spins into a bosonic system [2], namely

and

where f and q are dual bosonic fields satisfying

where K = b²/4p,

and v = is the characteristic velocity (spin-wave velocity). Observe that the isotropic case (d = 0) corresponds to b² = 2p. After bosonization, the original hamiltonian (1) becomes

A similar expression can be obtained in terms of q by using (5).

Usually, the most relevant quantity in a magnetic system is the magnetic susceptibilty, which is given by

in the static homogeneous case. This can be evaluated by using (3) and (7). In order to obtain finite temperature corrections conformal perturbation theory must be used to correct the conformal invariant hamiltonian (7). The result is [3]

where T₀~ 7.7 J. This expression for the susceptibility is in excellent agreement with the experiment for Sr₂CuO₃, which is the best experimental realization of the antiferromagnetic quantum Heisenberg chain [4], provided we choose the exchange coupling as J = 2200K.

2.2 Heisenberg antiferromagnet in an anisotropic field - copper benzoate

Copper benzoate Cu(C₆H₅COO)₂ · 3 H₂O is a quite peculiar quantum magnetic chain, because if we apply to it an external magnetic field H in the z-direction, a transverse staggered magnetic field proportional to H is generated. Indeed, the hamiltonian is

where h << H.

Specific heat measurements clearly show [5] that a field induced gap is generated the spectrum, namely D(H) µ H^0.65±0.03. The quantum field theory treatment of this system provides a beautiful explanation for this effect. Indeed, using the bosonization technique described in the previous subsection, we can write the hamiltonian above as the one of the sine-Gordon theory [6]

where q is one of the two dual bosonic fields introduced before. Using scaling arguments one can show that the above hamiltonian possesses a gap [6]

In the isotropic case b² = 2p (weak field), we see that D µ h^2/3 [6], which is in excellent agreement with the experimental results for the specific heat [5].

The sine-Gordon description of copper benzoate is also very successful in describing the specific heat curves of this material at low temperature. By means of thermal Bethe ansaatz, one can obtain the free energy, namely [7]

where

with

is the first breather mass. The specific heat, given by c = T¶²f/¶T², thereby obtained is in excellent agreement with the experiment [7].

Another successful application of sine-Gordon theory in copper benzoate concerns its spectrum of excitations. From (14) we can obtain the ratio of the breather M₁ and soliton D masses. This may be compared with neutron scattering experiments made with an applied magnetic field of 7 T. For this value of magnetic field, Bethe ansatz calculations indicate a value of b²/2p = 0.82 [7]. Introducing this value in (14), we get

The neutron scattering cross sections at 7 T [5] present a breather peak at 0.17 meV and a soliton peak at 0.22 meV whose ratio is precisely ~ 0.78!

3 Strongly correlated organic conductors

There is a class of quasi one-dimensional systems with very rich physical propetries. These are the organic conductors known as Bechgaarad salts, namely (TMTSF)₂X, where X = PF₆ , ClO₄, AsF₄. These highly anisotropic materials consist in stacks of the planar TMTSF-molecules. At high temperatures, the conductivity along the stack axis is two orders of magnitude higher than along the transverse ones. The electron dynamics along this direction is described by the Hubbard hamiltonian

where is the creation operator for an electron with spin s at the site i and n_i,s = c_is. The first term in (17) is a tight binding hamiltonian (independent electrons), which corresponds to an electron energy E(k) = - 2t cos ka, where a is the lattice spacing. Filling the valence band and expanding about the Fermi points (±p/a in the case of half filling), we arrive at a continuum fermionic system. This can be bosonized as

where

and

with v_F being the Fermi velocity (v_F = 2ta at half-filling). The last term in (18) corresponds to the so called umklapp term, describing the interaction of electrons in the vicinity of one Fermi point with the ones around the opposite Fermi point, for a filling factor of . The bosonic field is related to the original fermionic field as follows. Calling y₁ and y₂, respectively, the continuum fields associated to the electrons around k = +k_F and k = -k_F (right and left movers), we have

A relevant quantity in the electronic system is the dynamic conductivity, given by

where P(w,q) is the Fourier transform of the retarded current-curent correlator, namely,

The conductivity (22) can be evaluated by using (18) and (21). For frequencies much higher than the sine-Gordon gap (w >> D), one obtains [8]

This can be comparaed with the experimental results for (TMTSF)₂X and adjusted to the value 4n²K -5 = - 1.3 [8]. For half-filling (n = 1), we would have K » 0.93, indicating that the system would be almost free in this case (K = 1 is the free case). In the quarter filled case, which corresponds to the real situation in the Bechgaard salts, conversely, we have K » 0.23. This is very far from 1 (0 < K < 1) and implies these materials are quite strongly correlated.

4 Carbon nanotubes

Carbon nanotubes are extremely interesting highly anisotropic systems consisting in graphite sheets folded in cylindrical tubes with a diameter of approximately 1.5nm. The electrons corresponding to the p-orbitals of graphite can move along the tube and may be modeled by the continuum hamiltonian [9]

In this expression, the right and left moving fields (R and L) are obtained by expanding the tight-binding dispersion relation about the two Fermi points at +k_F and -k_F, respectively. The sum in a = 1,2 runs over the two bands obtained by folding the graphite sheet and expanding around the Fermi points [9]. s = , ¯ are the two spin orientations. The effective Coulomb potential along the cylinder axis is such that its Fourier transform is given by [9]

where R is the cylinder radius, L, its length and k » 1.4 is the (experimentally determined) dieletric constant.

Applying the standard bosonization method [2] to the y-fields, we get

where

and

Using the experimental value for the Fermi velocity, namely, v_F ~ 8×10⁵m/s and the typical dimensions of a carbon nanotube, R » 0.75nm and L » 1mm, we get K » 0.28. We see, therefore that carbon nanotubes, like the organic conductors considered in the previous section, are strongly correlated electronic systems.

A very interesting experimental set up, consists in applying a voltage difference V to the carbon nanotube and measuring the current through it. For a density of states, given as a function of the energy as r(e) = e^a, at a temperature T, the differential conductance is given by [10]

This has been obtained by using tunneling theory [10]. From (30), we can infer that

The parameter a associated to the electronic density of states in the nanotube may be determined from bosonization theory and (27), giving [11]

for tunneling into the bulk of the nanotube and

for tunneling into the edge. Eq. (30) with a given by (32) and (33) is in excellent agreement with the experiments [12]

5 High Tc superconductors

High-temperature superconductors are among the most interesting and challenging materials ever investigated. Discovered in 1986, the mechanism of superconductivity they present, resists up to now its comprehension, despite the many theories that have been proposed for their description. Here we present a field theory based model, which has been quite successful in describing part of the phase diagram of the two best studied superconducting cuprates, namely LSCO (La_2-dSr_dCuO₄) and YBCO (Y Ba₂Cu₃O_6+d).

A common feature in all superconducting cuprates is the presence of CuO₂ planes, with Cu⁺⁺ ions on the sites and O^-- ions on the links of a square lattice. The Cu⁺⁺ ions possess a localized electron per site. Upon doping (d ¹ 0) holes are introduced in the oxygen ions. These can move and interact among themselves and with the Cu⁺⁺ spin background, eventually forming the superconducting Cooper pairs beyond a certain critical doping and below a critical temperature T_c(x).

The model we propose is defined by the partition function [13]

where

In this description, the localized spins of the Cu⁺⁺ ions are given by = , where z_i ( = 1) are CP¹ fields (Schwinger bosons) describing the fluctuations of the spin background, _m is a Hubbard-Stratonovich field, g₀ is a coupling constant related to the original Heisenberg exchange for these spins. The creation operators for holes in the O^-- ions are given by , (a = ,¯) with creating a chargeless spin (spinon) and creating a spinless charge (chargon). The Dirac field y_a,l that appears in (35) is built out of the f fields (l = Fermi surface branch ) [13] and q is the spinon-Schwinger boson coupling. The chargon operator is identified with the quantum skyrmion (topological excitations) creation operator whose quantum properties have been described in [14].

The quantum skyrmion correlation function is a powerful tool for evaluating the antiferromagnetic order parameter for the Cu⁺⁺ spin lattice. Indeed, this is given by [14,13]

where M(d,T) is the staggered (sublattice) magnetization of the Cu⁺⁺ spin lattice, as a function of temperature and doping. Evaluation of (36) gives [15]

for YBCO and

for YBCO. The constants A, B and C have been computed in detail from first principles in [15]. Expressions (37) and (38), which have no adjustable parameters, are in excellent agreement with the experimental results [15]. By studying M²(d,T = 0 ), we can obtain an expression for the Néel temperature T_N(d) as a function of doping, which is also in excellent agreemet with the experiments for both compounds [15].

We can also describe in our theory the superconducting transition. Since skyrmions are the charge carriers, we must investigate the skyrmion-skyrmion interacting potential predicted by the theory described by (35). For two static charges of the same sign at positions

₁ and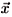 ₂, we get [13]

where S(, 0) º P_B() + P_F() is related to the vacuum polarization tensor corresponding to (35) as

Notice that the bosonic and fermionic contributions to the potential (39) correspond, respectively, to the spin fluctuations associated to the localized Cu⁺⁺ spins (Schwinger bosons) and to the spin part of the O^-- holes (spinons).

We can evalute the potential (39) as a function of T and d. In order to find the superconducting temperature, we study the condition for this potential to have a minimum. This leads to the critical temperature T_c(d). Our expression for T_c(d) is in good agreement with the experimental data for LSCO and YBCO below optimal doping [13]. Our results are actually not valid beyond optimal doping because in this region we are outside the pseudogap phase where the continuum limit leading to (35) was taken.

6 Concluding remarks

The few cases described in this review allow us to conclude that Quantum Field Theory is an extremely powerful and efficient method for describing Condensed Matter systems. It is specially useful for the case of low-dimensional and strongly correlated systems where the traditional methods of Condensed Matter fail. Our review has not been, by no means, exhaustive and many interesting applications of Quantum Field Theory in the description of Condensed Matter systems have not been covered. These include the Chern-Simons-Landau-Ginzburg theory for Quantum Hall systems, conjugated polymers like polyacethilene, ferromagnetic chains like the XY-model, Josephson junction arrays, superfluid helium, heavy fermions and manganites among many others. We conclude by pointing out that a vast field of applications of Quantum Field Theory in Condensed Matter is open. This includes some fundamental problems like the one of high-Tc superconductivity.

Acknowledgments

This work has been supported in part by CNPq, FAPERJ and PRONEX-66.2002/1998-9.

References

[1] P. Jordan and E. Wigner, Z. Phys. 47, 631 (1928)

[2] I. Affleck, in Fields, Strings and Critical Phenomena, Les Houches Summer School Proccedings, Vol. 49, Eds. E.Brézin and J.Zinn-Justin (North Holland, Amsterdam (1990); S. Sachdev, Quantum Phase Transitions, Cambridge University Press, Cambridge (1999)

[3] S. Eggert, I. Affleck, and Takahashi, Phys. Rev. Lett. 73, 332 (1994)

[4] N. Motoyama et al., Phys. Rev. Lett. 76, 3212 (1996)

[5] D.C. Dender et al., Phys. Rev. Lett. 79, 1750 (1997)

[6] I. Affleck and M. Oshikawa, Phys. Rev. B60, 1038 (1999)

[7] F. Essler, Phys. Rev. B59, 14376 (1999)

[8] A. Schwartz et al. Phys. Rev. BB58, 1261 (1998)

[9] R. Egger and A.O. Gogolin, Phys. Rev. Lett. 79, 5082 (1997); C. Kane, L. Balents, and M.P.A. Fisher, Phys. Rev. Lett. 79, 5086 (1997)

[10] H.W.C. Postma et al. Phys. Rev. B62, R10653 (2000)

[11] S. Eggert, Phys. Rev. Lett. 84, 4413 (2000)

[12] M. Bockrath et al., Nature 397, 598 (1999)

[13] E.C. Marino and M.B. Silva Neto, Phys. Rev. B66, 224512 (2002)

[14] E.C. Marino, Phys. Rev. B61, 1588 (2000)

[15] E.C. Marino, Phys. Lett. A263, 446 (1999); E.C. Marino and M.B. Silva Neto, Phys. Rev. B64, 092511 (2001).

Publication Dates

• Publication in this collection
  28 Jan 2005
• Date of issue
  Dec 2004

History

• Received
  18 Dec 2003