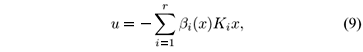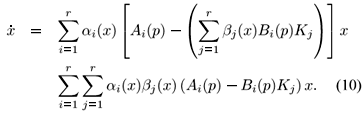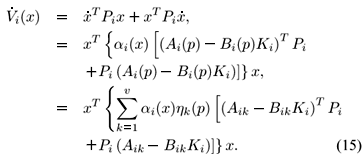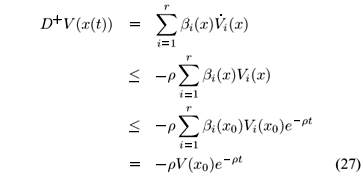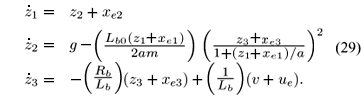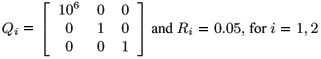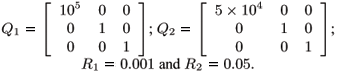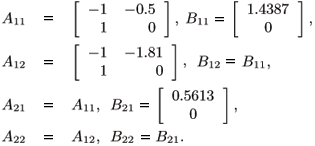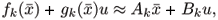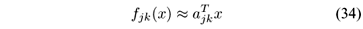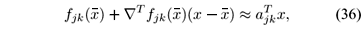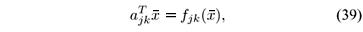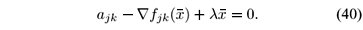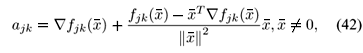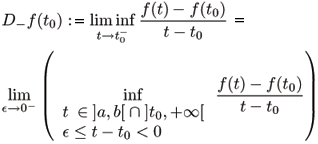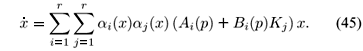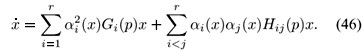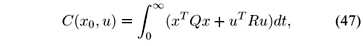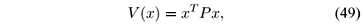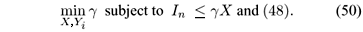Abstracts
A new stability analysis and design of a fuzzy switching control based on uncertain Takagi-Sugeno fuzzy systems are proposed. The fuzzy system adopted is composed by a family of local linear uncertain systems with aggregation. The control design proposed uses local state feedback gains obtained from an optimization problem with guaranteed cost performance formulated in the context of linear matrix inequalities and a fuzzy switching scheme built from local Lyapunov functions. The global stability is guaranteed by considering a class of piecewise quadratic Lyapunov functions. Examples are given to illustrate the applicability of the proposed approach.
Switching fuzzy control; Guaranteed cost fuzzy control; Uncertain Takagi-Sugeno fuzzy systems; Piecewise quadratic Lyapunov functions
Neste trabalho, uma nova análise de estabilidade e projeto de controle fuzzy chaveado baseado em sistemas fuzzy Takagi-Sugeno com incertezas são propostos. O sistema fuzzy adotado é composto por uma família de sistemas lineares incertos locais com agregação fuzzy. O projeto de controle proposto utiliza ganhos de realimentação de estado locais obtidos da solução de um problema de otimização com desempenho de custo garantido formulado em termos de desigualdades matriciais lineares e um esquema de chaveamento fuzzy baseado em funções de Lyapunov, que são usadas quando a trajetória do estado do sistema está na fronteira de subespaços definidos do espaço de estado. A estabilidade global é garantida considerando uma classe de funções de Lyapunov quadráticas por partes. Exemplos ilustram a aplicação da abordagem proposta.
Controle fuzzy chaveado; Controle fuzzy de custo garantido; Sistemas fuzzy Takagi-Sugeno com incertezas; Funções de Lyapunov quadráticas por partes
SISTEMAS INTELIGENTES
Synthesis of an LMI-based fuzzy control system with guaranteed cost performance: a piecewise Lyapunov approach
Natache S. D. ArrifanoI; Vilma A. OliveiraI; Lúcia V. CossiII
IDepartamento de Engenharia Elétrica, Universidade de São Paulo Av. Trabalhador São Carlense, 400 CEP 13566-590, São Carlos, SP, BRASIL; natachea@sel.eesc.usp.br; vilmao@sel.eesc.usp.br
IIDepartamento de Matemática, Universidade Federal da Paraíba Cx. Postal 5080 CEP 58051-970, João Pessoa, PB, BRASIL; cossi@ufpb.br
ABSTRACT
A new stability analysis and design of a fuzzy switching control based on uncertain Takagi-Sugeno fuzzy systems are proposed. The fuzzy system adopted is composed by a family of local linear uncertain systems with aggregation. The control design proposed uses local state feedback gains obtained from an optimization problem with guaranteed cost performance formulated in the context of linear matrix inequalities and a fuzzy switching scheme built from local Lyapunov functions. The global stability is guaranteed by considering a class of piecewise quadratic Lyapunov functions. Examples are given to illustrate the applicability of the proposed approach.
Keywords: Switching fuzzy control, Guaranteed cost fuzzy control, Uncertain Takagi-Sugeno fuzzy systems, Piecewise quadratic Lyapunov functions.
RESUMO
Neste trabalho, uma nova análise de estabilidade e projeto de controle fuzzy chaveado baseado em sistemas fuzzy Takagi-Sugeno com incertezas são propostos. O sistema fuzzy adotado é composto por uma família de sistemas lineares incertos locais com agregação fuzzy. O projeto de controle proposto utiliza ganhos de realimentação de estado locais obtidos da solução de um problema de otimização com desempenho de custo garantido formulado em termos de desigualdades matriciais lineares e um esquema de chaveamento fuzzy baseado em funções de Lyapunov, que são usadas quando a trajetória do estado do sistema está na fronteira de subespaços definidos do espaço de estado. A estabilidade global é garantida considerando uma classe de funções de Lyapunov quadráticas por partes. Exemplos ilustram a aplicação da abordagem proposta.
Palavras-chave: Controle fuzzy chaveado, Controle fuzzy de custo garantido, Sistemas fuzzy Takagi-Sugeno com incertezas, Funções de Lyapunov quadr´aticas por partes.
1 INTRODUCTION
Takagi-Sugeno (TS) fuzzy-model-based control has been successful used to control nonlinear systems in several applications (Tanaka et al., 1999; Feng et al., 1997; Wang et al., 1996). Most of the techniques of robust control have been used in the TS fuzzy-model-based control due to the fact that the TS fuzzy systems can be interpreted as differential inclusions (Jadbabaie et al., 1998a; Cao et al., 1997; Tanaka et al., 1996). However, when treating uncertain nonlinear systems, we need to distinguish nonlinearity from uncertainty, otherwise, the results obtained are in general conservatives. Several approaches have appeared to the robust stabilization of uncertain nonlinear systems (Lee et al., 2001; Cao et al., 2001; Teixeira and  ak, 1999; Tanaka et al., 1996). In the framework of TS fuzzy systems, parametric uncertainty can be represented by norm-bounded or polytopic uncertain sets. Different robust control solutions for the TS fuzzy system with norm-bounded and polytopic uncertainty representations can be found in Tanaka et al. (1996) and Lee et al. (2001), and Cao et al. (2001), respectively.
ak, 1999; Tanaka et al., 1996). In the framework of TS fuzzy systems, parametric uncertainty can be represented by norm-bounded or polytopic uncertain sets. Different robust control solutions for the TS fuzzy system with norm-bounded and polytopic uncertainty representations can be found in Tanaka et al. (1996) and Lee et al. (2001), and Cao et al. (2001), respectively.
Stability is one of the most important issues when analyzing control systems. Most of the methods of fuzzy-model-based control yields stability analysis and design procedures by means of the parallel distributed compensation (PDC) using a common quadratic Lyapunov function (Teixeira et al., 2000; Tanaka et al., 1998; Tanaka et al., 1997). This approach requires a common positive definite matrix that is a solution of all the Lyapunov inequalities built from the local linear systems of the global feedback TS fuzzy system, which are usually formulated in terms of linear matrix inequalities (LMI's) in both the state feedback gain and Lyapunov matrix. However, when applied to uncertain nonlinear systems, this approach may not provide feasible results because it is not possible to find a common positive definite Lyapunov matrix as a solution of several Lyapunov inequalities. To remove this deficiency, recently, attractive stability results for the TS fuzzy-model-based control using piecewise quadratic Lyapunov functions appeared (Zhang et al., 2001; Johansson et al., 1998). These results explore the gain-scheduled nature of the fuzzy controllers and have found application in the stability analysis of systems whose dynamics depends on the subspace of the state space their trajectory is.
This paper presents a fuzzy switching controller for uncertain nonlinear systems which are represented by a class of TS fuzzy systems with uncertainties. The controller proposed uses local guaranteed cost control laws and a switching scheme based on local quadratic Lyapunov functions when the state is on the boundary of defined subspaces of the state space. A sufficient condition for the stability of the uncertain nonlinear system with state feedback is given in terms of a piecewise quadratic Lyapunov function. This approach produces less conservative results than those obtained with the fuzzy blending controller for TS fuzzy systems with uncertainties. In addition, this approach may be applied to control highly nonlinear systems, where available robust control techniques are not successful.
The remainder of the paper is organized as follows. In Section 2, the fuzzy system modeling for a class of uncertain nonlinear systems, the fuzzy switching control and the guaranteed cost control design are presented. The stability analysis of the feedback fuzzy system is the subject of the Section 3. In Section 4, simulation results are presented to illustrate the effectiveness of the proposed approach. Finally, the paper concludes with brief remarks in Section 5.
2 FUZZY SYSTEM MODELING AND CONTROL
We consider a class of uncertain nonlinear dynamic systems which are described by the differential inclusion
where x is the system state vector, u is the input vector, Co denotes the convex hull, fk(·), gk(·) are smooth nonlinear functions which define the called vertex systems, fk(0) = 0, gk(0) = 0, and v is the number of vertexes, k = 1,2,...,v, with fk: n ® and
n ® and  n gk :
n gk : n® F(
n® F( m,
m,  n) for F(
n) for F( m,
m,  n) = {h:D(h) ®
n) = {h:D(h) ®  n: D(h) Í
n: D(h) Í  m.
m.
Considering an uncertain parameter vector p Î  s, a polytopic representation of (1) has the form
s, a polytopic representation of (1) has the form
where hk:  s ®
s ®  with hk(p) > 0, k = 1,2,...,v,
with hk(p) > 0, k = 1,2,...,v,  hk(p) = 1.
hk(p) = 1.
2.1 Fuzzy system modeling
The TS fuzzy system is described by fuzzy IF-THEN rules representing local input-output relations of the nonlinear system (Takagi and Sugeno, 1985). The basic idea of this approach is decompose the input space into many subspaces, approximating the nonlinear system by a blending of the local linear systems associated to each subspace. In fact, it is proved that the TS fuzzy systems are universal approximators (Tanaka and Wang, 2001). In order to consider uncertainties in the TS fuzzy system, we use a fuzzy system built from local uncertain linear systems whose the ith inference rule is given by
Rule i:
where  , j = 1,2,...,n are fuzzy sets, r is the number of inference rules, and matrices Ai(p) Î M(
, j = 1,2,...,n are fuzzy sets, r is the number of inference rules, and matrices Ai(p) Î M( n,
n,  n) and Bi(p)) Î M(
n) and Bi(p)) Î M( n,
n,  m) have a polytopic representation, that is, Ai(p) =
m) have a polytopic representation, that is, Ai(p) =  hk(p)Aik and Bi(p) =
hk(p)Aik and Bi(p) =  hk(p)Bik, for hk(p) > 0, k = 1,2,...,v,
hk(p)Bik, for hk(p) > 0, k = 1,2,...,v,  hk(p) = 1. Matrices Ai(p) and Bi(p), i = 1,2,...,r can be obtained from (2) using the linearization formula proposed by Teixeira and
hk(p) = 1. Matrices Ai(p) and Bi(p), i = 1,2,...,r can be obtained from (2) using the linearization formula proposed by Teixeira and  ak (1999), which yields a good linear approximation of nonlinear systems in the vicinity of an operating point even if it is not an equilibrium point. The Teixeira &
ak (1999), which yields a good linear approximation of nonlinear systems in the vicinity of an operating point even if it is not an equilibrium point. The Teixeira &  ak linearization formula used in this paper is presented in Appendix AAppendix A denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices we have Consider the uncertain nonlinear systems in its polytopic description as defined in (2). Following, we present the linearization formula used to obtain the uncertain linear approximations of the nonlinear functions which are the vertexes of the polytope. For this purpose, let denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices Ak and Bk such that in the vicinity of we have .
ak linearization formula used in this paper is presented in Appendix AAppendix A denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices we have Consider the uncertain nonlinear systems in its polytopic description as defined in (2). Following, we present the linearization formula used to obtain the uncertain linear approximations of the nonlinear functions which are the vertexes of the polytope. For this purpose, let denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices Ak and Bk such that in the vicinity of we have .
Given the pair (x,u), the overall fuzzy system with uncertainties is inferred as a weighted average of all local uncertain linear approximations (Ai(p),Bi(p)), i = 1,2,...,r of (3), which is given by
where
denotes the normalized membership function, with  (xj) Î [0,1] the grade of membership of xj, j = 1,2,...,n, in the fuzzy set
(xj) Î [0,1] the grade of membership of xj, j = 1,2,...,n, in the fuzzy set  . Considering the fact that in (5)
. Considering the fact that in (5)  (xj) > 0, i = 1,2,...,r and j = 1,2,...,n, we have ai(x) > 0 and
(xj) > 0, i = 1,2,...,r and j = 1,2,...,n, we have ai(x) > 0 and  ai(x) = 1, "t > 0.
ai(x) = 1, "t > 0.
2.2 Fuzzy switching control
In this section we propose a switching scheme so that local controllers are switched according to the subspace that the state vector x enters. For this purpose,  let denote the ith subspace in the state space
let denote the ith subspace in the state space
where the superscript º in Si denotes an open subspace, let ¶Sil denote the transition subspace in the state space
and let Si =  È ¶Sil. Using (6) and (7), we define the switching scheme for each rule i
È ¶Sil. Using (6) and (7), we define the switching scheme for each rule i
Rule i:
where Vi(x) = xTPix is a local quadratic Lyapunov function, with Pi =  , Pi > 0 and bi(x) Î {0,1} a crisp function which changes as x leaves subspace
, Pi > 0 and bi(x) Î {0,1} a crisp function which changes as x leaves subspace  following the membership function changes. Thus, bi(x) = 1 only when x Î Si =
following the membership function changes. Thus, bi(x) = 1 only when x Î Si =  È ¶Sil and bi(x) = 0, otherwise. Additionally,
È ¶Sil and bi(x) = 0, otherwise. Additionally,  bi(x) = 1, "t > 0.
bi(x) = 1, "t > 0.
Adopting (8) and following the idea of the PDC scheme, we propose the fuzzy switching control as
where Ki Î M( m,
m,  n), i = 1,2,...,r are the state feedback gains to be designed for rule i. In order to obtain the state feedback fuzzy system, we substitute (9) in (4), which gives
n), i = 1,2,...,r are the state feedback gains to be designed for rule i. In order to obtain the state feedback fuzzy system, we substitute (9) in (4), which gives
Recalling that from (8) bi(x) = 1 only when x Î Si, we can write (10) as
The state feedback fuzzy system (11) is recognized as an aggregation of r local feedback uncertain systems described in a polytopic form.
2.2.1 Guaranteed cost control design
In this section, we propose a robust control design in terms of the optimal quadratic guaranteed cost problem as in Costa and Oliveira (2002). This approach is based on the local stability of each feedback fuzzy system of (11) in the subspace of the state space. In order to obtain a systematic control design, we formulate the problem in the context of the convex analysis using LMI's.
Definition 1 The ith feedback uncertain linear system of (11) is said to be asymptotically stable, if there exists a stabilizing control u = -Kix, i = 1,2,...,r, such that an upper bound on the quadratic performance index
along the system trajectory is minimized, with Qi Î  nxn, Ri Î
nxn, Ri Î  mxm, Qi > 0, and Ri > 0 weighting symmetric matrices which are chosen to yield the desired performance.
mxm, Qi > 0, and Ri > 0 weighting symmetric matrices which are chosen to yield the desired performance.
Definition 2 If there exist a stabilizing control law u = -Kix, i = 1,2,...,r and a positive scalar  i, such that, Ci(x0,u) <
i, such that, Ci(x0,u) <  i along the system trajectory, then
i along the system trajectory, then  i is a guaranteed cost and u is a guaranteed control law.
i is a guaranteed cost and u is a guaranteed control law.
Proposition 1 Consider the ith uncertain linear system of (4), control law u = -Kix, i = 1,2,...,r and cost performance (12). If there exist symmetric positive definite matrices Xi and matrices Yi, i = 1,2,...,r of appropriate dimensions satisfying the LMI's
where
then u = -Kix, with Ki = Yi , i = 1,2,...,r is a guaranteed control law and the cost given by
, i = 1,2,...,r is a guaranteed control law and the cost given by  i =
i = 
Proof: Consider a local quadratic Lyapunov function candidate as
which is a continuous-time function along the trajectory of (11) in the subspace  . Taking its derivatives, it results
. Taking its derivatives, it results
Now assume that there exist symmetric positive definite matrices Pi =  and matrices Ki = Yi
and matrices Ki = Yi satisfying LMI's in (13). Then, using the Schur complement (Boyd et al., 1994) after performing some algebraic manipulations, (13) can be reduced to
satisfying LMI's in (13). Then, using the Schur complement (Boyd et al., 1994) after performing some algebraic manipulations, (13) can be reduced to
Using  hk(p) = 1, after some algebraic manipulations, (16) can be written as
hk(p) = 1, after some algebraic manipulations, (16) can be written as
Using (17) in (15), as ai(x) > 0, we have  i(x) < 0, "x ¹ 0, x Î
i(x) < 0, "x ¹ 0, x Î  . Now, substituting (9) in (12) and using the fact that bi(x)bj(x) = 0, i ¹ j, i, j = 1,2,...,r and bi(x)bi(x) = 1, for x Î
. Now, substituting (9) in (12) and using the fact that bi(x)bj(x) = 0, i ¹ j, i, j = 1,2,...,r and bi(x)bi(x) = 1, for x Î  it results
it results
The results then follows by Definitions 2.2.1 and 2.2.1.
The optimal quadratic guaranteed cost control problem involves the minimization of the cost bounds given by  i =
i =  Pix0, i = 1,2,...,r which depends on the initial condition x0Î
Pix0, i = 1,2,...,r which depends on the initial condition x0Î  . To remove this dependence on x0 one may assume it is a zero mean random variable satisfying E[
. To remove this dependence on x0 one may assume it is a zero mean random variable satisfying E[ x0] = 1 and consider the minimization of Tr(Pi) as E[Ci] < E[
x0] = 1 and consider the minimization of Tr(Pi) as E[Ci] < E[ x0] = Tr(Pi), with E[·] the expectancy operator and Tr(·) is the trace (Jadbabaie et al., 1998b; Petersen and Macfarlane, 1994). Instead, we construct an optimization problem for the guaranteed cost control by minimizing an upper bound on the guaranteed cost
x0] = Tr(Pi), with E[·] the expectancy operator and Tr(·) is the trace (Jadbabaie et al., 1998b; Petersen and Macfarlane, 1994). Instead, we construct an optimization problem for the guaranteed cost control by minimizing an upper bound on the guaranteed cost  i.
i.
Lemma 1If iis a guaranteed cost for the ith state feedback uncertain linear system of (11) under performance index (12) then for x0Î
iis a guaranteed cost for the ith state feedback uncertain linear system of (11) under performance index (12) then for x0Î 
i = 1,2,...,r, is a guaranteed cost for the ith state feedback uncertain linear system of (11) and an upper bound for (12), with lmax[·] the maximum eigenvalue and ||·|| the Euclidean vector norm.
Proof: Using singular value decompositions the result follows straightforward.
Using both Proposition 2.2.1 and Lemma 2.2.1, we can construct the generalized eigenvalue problem (GEVP) (Boyd et al., 1994) for the guaranteed cost control design as
If (20) is feasible, we have gi > lmax[ ] and Ki = Yi
] and Ki = Yi , i = 1,2,...,r.
, i = 1,2,...,r.
3 STABILITY ANALYSIS
In Section 2 an approach to obtain the feedback gains and the quadratic Lyapunov functions associated is presented. Now, we establish a condition for the global stability of the feedback fuzzy system (11) by considering a class of piecewise quadratic Lyapunov functions and the fuzzy switching control proposed.
Theorem 2The equilibrium x = 0 of the global feedback TS fuzzy system with uncertainties (11) is asymptotically stable in the large if each uncertain linear system of (4) is locally stabilizable by the fuzzy switching controller (9) with bi(·) as defined in (8) and Ki resulting from (20), which is time continuous in the open subspace  .
.
Proof: Let
be a piecewise quadratic Lyapunov function candidate with Vi(x) as in (14) and Pi =  , Xi resulting from (20) for each subspace
, Xi resulting from (20) for each subspace  of the state space. In order to evaluate the derivative of (21) along the system trajectory, we replace
of the state space. In order to evaluate the derivative of (21) along the system trajectory, we replace  (·) by the Dini derivative D*V(·), where the superscript * in DV(·) represents any of the four Dini derivatives (Rouche et al., 1977). At any point where
(·) by the Dini derivative D*V(·), where the superscript * in DV(·) represents any of the four Dini derivatives (Rouche et al., 1977). At any point where  (·) exists, all four Dini derivatives have a common value equal to the derivative
(·) exists, all four Dini derivatives have a common value equal to the derivative  (·) at that point. See Apendix B for more details on the Dini derivatives. Let us consider the stability at the switching time. In the sequence, we use x(t) to emphasize the analysis.
(·) at that point. See Apendix B for more details on the Dini derivatives. Let us consider the stability at the switching time. In the sequence, we use x(t) to emphasize the analysis.
Suppose that for some particular time t, x(t) Î  which yields bi(x(t)) = 1 using (8). Also, suppose that the system equilibrium x(t) = 0 does not exclusively belong to
which yields bi(x(t)) = 1 using (8). Also, suppose that the system equilibrium x(t) = 0 does not exclusively belong to  , otherwise there might be no switching of controllers. After a period of time, a switching occurs, say at t = t1, and x(t) leaves the subspace
, otherwise there might be no switching of controllers. After a period of time, a switching occurs, say at t = t1, and x(t) leaves the subspace  and enters the lth subspace
and enters the lth subspace  . We can thus write
. We can thus write  bi(x(t)) = bi(x(t1)) = 1 and
bi(x(t)) = bi(x(t1)) = 1 and  bl(x(t)) = bl(x(t1)) = 1. The corresponding upper and lower Dini derivatives of (21) in the transition region ¶Sil are thus as
bl(x(t)) = bl(x(t1)) = 1. The corresponding upper and lower Dini derivatives of (21) in the transition region ¶Sil are thus as
To have V(·) decreasing along the system trajectory any of the four Dini derivatives must be negative definite on the open subspace  (see Corollary 7 in Appendix BAppendix B and consider a function and a point Definition 3 Let ]a,b[ Ì and consider a function f: ]a,b[ ® and a point t0Î ]a,b[. ). By the switching scheme (8), D+V(·) in (22) is equal to
(see Corollary 7 in Appendix BAppendix B and consider a function and a point Definition 3 Let ]a,b[ Ì and consider a function f: ]a,b[ ® and a point t0Î ]a,b[. ). By the switching scheme (8), D+V(·) in (22) is equal to  l(·) which is negative definite as x Î
l(·) which is negative definite as x Î  . Then, as bi(·) is a crisp function associated to each subspace
. Then, as bi(·) is a crisp function associated to each subspace  , i = 1,2,...,r, we can write
, i = 1,2,...,r, we can write
Now, using (11) we can write (24) as
with Ki = Yi , Xi and Yi, i = 1,2,...,r resulting from (20). Using the proof of Proposition 1, for bi(·) given by (8) we have D+V(x) < 0, "x, x ¹ 0, which assures that system (11) is stable.
, Xi and Yi, i = 1,2,...,r resulting from (20). Using the proof of Proposition 1, for bi(·) given by (8) we have D+V(x) < 0, "x, x ¹ 0, which assures that system (11) is stable.
We proceed with the proof showing the stability in the large. Let us define
where Nik =  , Nik > 0. For x Î
, Nik > 0. For x Î  , x ¹ 0, i = 1,2,...,r, we have
, x ¹ 0, i = 1,2,...,r, we have  i(x) < -rVi(x) where r is a positive number defined by r: =
i(x) < -rVi(x) where r is a positive number defined by r: =  {lmin[Nik]/lmax[Pi]}, lmin[·] and lmax[·] denote the minimum and maximum eigenvalues, respectively. By the well-known Gronwall-Bellman lemma (Khalil, 1996) we can show that for x0Î
{lmin[Nik]/lmax[Pi]}, lmin[·] and lmax[·] denote the minimum and maximum eigenvalues, respectively. By the well-known Gronwall-Bellman lemma (Khalil, 1996) we can show that for x0Î  , Vi(x) £ Vi(x0) e-rt. Thus, from (24), it follows that
, Vi(x) £ Vi(x0) e-rt. Thus, from (24), it follows that
as bi(·) is a crisp function associated to each subspace  , i = 1,2,...,r, which completes the proof.
, i = 1,2,...,r, which completes the proof.
Remark 1 In order to compare the results given, we include in Appendix CAppendix C, a fuzzy blending control approach which is also formulated as an optimal quadratic guaranteed cost control problem but adopting a common quadratic Lyapunov function (Arrifano and Oliveira, 2002).
Remark 2 To consider the stability of an uncertain nonlinear system for the case the origin x = 0 is not the equilibrium, one should perform a change of coordinates to make it the equilibrium, before designing the fuzzy switching control (9) with bi(·) as defined in (8). This change of coordinates is important because real systems, in general, have equilibrium different from the origin and the control design proposed considers asymptotic stability around the equilibrium x = 0.
4 SIMULATION RESULTS
In this section, the usefulness of the switching fuzzy control is illustrated. We consider the stabilization of a magnetic suspension system and a mass-spring-damper system using the optimal quadratic guaranteed cost control. A feasible solution for the latter system can be obtained with the blending fuzzy control by means of a common Lyapunov function (see Appendix CAppendix C) but no feasible solution is found for the former system.
Example 3 Nonlinear magnetic suspension system. We consider the same example as in Costa and Oliveira (1999), a nonlinear magnetic suspension system depicted by
where xr1 is the ball vertical position [m], xr2 is the ball vertical speed [m/s], xr3 is the coil current [A], ur is the coil applied voltage [V], g is the acceleration due to gravity [m/\texts2], m is the ball mass [Kg], Lb is the coil inductance [H], Rb is the coil resistance [W], a is a constant [m], and Lb0 expresses the relationship between the inductance and the ball vertical position [H]. Table 1 shows the numerical values of physical parameters. Note that the equilibrium of (28) (xe,ue) is not the origin. As mentioned in Remark 2, it is necessary to perform a change of coordinates to bring the equilibrium of the system to the origin. For this purpose, we adopt z = xr-xe and v = u-ue, with xe = [0.010 0 0.8775] and ue = 17.4621 the equilibrium of (28). Using these new coordinates, we may write (28) as
The uncertain linear systems are obtained using the linearization formula given in Appendix AAppendix A denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices we have Consider the uncertain nonlinear systems in its polytopic description as defined in (2). Following, we present the linearization formula used to obtain the uncertain linear approximations of the nonlinear functions which are the vertexes of the polytope. For this purpose, let denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices Ak and Bk such that in the vicinity of we have considering Lb0 as the uncertain parameter with deviations of about ±80% from its nominal value. Adopting r = 2 as the number of linearization points chosen and 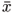 (r = 1) = [0.005 0 0.6045] and
(r = 1) = [0.005 0 0.6045] and  (r = 2) = [0.015 0 1.1505] as the linearization points, we found the matrices representing the extreme linearized systems of each vertex system as
(r = 2) = [0.015 0 1.1505] as the linearization points, we found the matrices representing the extreme linearized systems of each vertex system as
Figure 1 shows the membership functions adopted for xr1Î [ 0, 0.020 ] and xr3Î [0, 1.5 ]. Following, we present simulation results which are organized in two cases: (Case 1) Lb0(xr1) = Lb0 as in Costa and Oliveira (1999) and (Case 2) Lb0(xr1) = Lb0(0.85+0.5/(1+xr1/a)), with Lb0 = 0.0245 H, the nominal value for Lb0(·). The proposed approach is systematically accomplished by using the Matlab LMI solver as well as the ordinary differential equation (ODE) solver. We adopt the initial condition as x0 = [0.005 0 0.6045].
In Case 1 we adopt the weighting matrices
as in Costa and Oliveira (1999). In Case 2 we adopt the weighting matrices
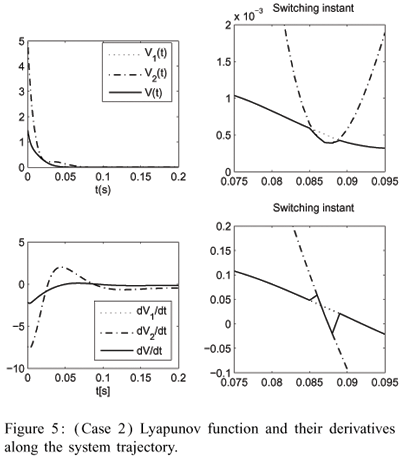
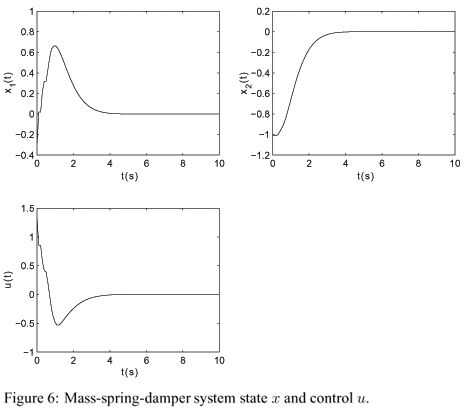
The numerical results are summarized in Table 2 and 3 for Cases 1 and 2, respectively. Figures 2 and 3 show the responses of system (28) for Case 1 and Figures 4 and 5 present the responses for Case 2. Using the fuzzy switching control approach, the switching in the control law can be flattered by adjusting the width and the type of the membership functions adopted as well as the matrices Qi and Ri, i = 1,2,...,r. Therefore, the proposed solution can yield smother solutions than the one given in Costa and Oliveira (1999) using attraction domains for the switching control scheme. Other characteristic of this approach is that the switching is related to the smaller value of the associated Lyapunov function when the state is on the boundary of the defined subspaces, but the system solution always returns to the subspace that better represents the dynamics of the nonlinear system. After the state vector enters the subspace where the equilibrium point xe is, the switching occurs if the resulting Lyapunov functions have not reached the origin or if the system are subjected to perturbations.
Example 4 Nonlinear mass-spring-damper system. We consider now the same example as in Tanaka et al. (1996), a nonlinear mass-spring-damper system with an uncertain parameter, which is described as
where M is the mass [Kg], u is the force [N], y is the vertical position [m],  is the speed [m/s], g(y,
is the speed [m/s], g(y, ) = c1y + c2
) = c1y + c2 , f(y) = c, and f(
, f(y) = c, and f( ) = 1+c5
) = 1+c5
 ]T, we can write (30) in the state space representation
]T, we can write (30) in the state space representation
As system (31) presents one uncertain parameter, we have two vertexes in the polytopic description. We adopt r = 2 and again we obtain the uncertain linear systems using the linearization formula for the following linearization points 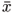 :
: 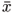 (r = 1) = [1.9740 0]T and
(r = 1) = [1.9740 0]T and 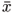 (r = 2) = [-1.9740 0]T, which gives
(r = 2) = [-1.9740 0]T, which gives
The performance of the proposed approach can be verified adopting a1(x) = 0.5+  /6.75, a2(x) = 0.5-
/6.75, a2(x) = 0.5- /6.75 and c = 1.155+0.655 cos
/6.75 and c = 1.155+0.655 cos for x1Î [-1.5, 1.5] and x2Î [-1.5, 1.5]. The control design is systematically developed by solving the optimization problem (50). We choose Q = I2 and R = 0.07 for both rules and adopt initial condition x0 = [-0.5 -1.0]T. Using the Matlab LMI solver, we obtain the main results summarized in Table 4. Figure 6 shows the feedback uncertain nonlinear system responses. The proposed approach is comparable to the one given in Tanaka et al. (1996). Its advantage is that it follows a systematic procedure and minimizes an upper bound on the quadratic performance cost.
for x1Î [-1.5, 1.5] and x2Î [-1.5, 1.5]. The control design is systematically developed by solving the optimization problem (50). We choose Q = I2 and R = 0.07 for both rules and adopt initial condition x0 = [-0.5 -1.0]T. Using the Matlab LMI solver, we obtain the main results summarized in Table 4. Figure 6 shows the feedback uncertain nonlinear system responses. The proposed approach is comparable to the one given in Tanaka et al. (1996). Its advantage is that it follows a systematic procedure and minimizes an upper bound on the quadratic performance cost.
5 CONCLUSION
In this paper we propose a fuzzy switching control design to stabilize a class of uncertain nonlinear systems represented by uncertain TS fuzzy systems. A sufficient condition for the stability of the state feedback fuzzy system is given in terms of a piecewise quadratic Lyapunov function. The control design is formulated in the context of the guaranteed cost control problem with the minimization of an upper bound on the guaranteed cost. The fuzzy switching control produces less conservative results than the fuzzy blending control approach which uses a common quadratic Lyapunov function. In addition, the approach given may be applied to highly nonlinear systems, where available robust control techniques are not successful. The proposed approach yields a computationally tractable solution to the control design in the context of LMI's. Further, different control techniques to design the local controllers can also be explored using the framework presented.
ACKNOWLEDGEMENTS
The authors thank the anonymous referees by the useful comments and suggestions. This work was supported by the Fundação do Amparo à Pesquisa do Estado de São Paulo (FAPESP) under grant 00/05060-1 and by the Conselho de Desenvolvimento Científico e Tecnológico (CNPq) under grant 301982/03-1.
Artigo submetido em 28/11/2002
1a. Revisão em 26/06/2003
2a. Revisão em 18/03/2004
3a. Revisão em 29/05/2006
Aceito sob recomendação do Editor Associado Prof. Cairo Lucio Nascimento Jr
and
with fk(·), gk(·), x and u as defined before. Since u is arbitrary, we have gk(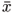 ) = Bk. Thus, the procedure reduces to finding matrices Ak such that, in the vicinity of
) = Bk. Thus, the procedure reduces to finding matrices Ak such that, in the vicinity of 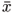 , we have
, we have
and
Following (Teixeira and  ak, 1999), let
ak, 1999), let  denote the jth row of matrix Ak. Then, conditions (32) and (33) can be written as
denote the jth row of matrix Ak. Then, conditions (32) and (33) can be written as
and
respectively, where fjk(·):  n ®
n ®  is the jth component of fk(·) for j = 1,2,...,n. Expanding the left hand side of (34) over
is the jth component of fk(·) for j = 1,2,...,n. Expanding the left hand side of (34) over 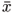 and neglecting the second and higher order terms we obtain
and neglecting the second and higher order terms we obtain
where Ñfjk(·):  n ®
n ®  n is the gradient, a column vector of fjk(·) computed with respect to x. Now, using (35) and (36), we have
n is the gradient, a column vector of fjk(·) computed with respect to x. Now, using (35) and (36), we have
where x is arbitrary but "close'' to 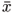 . Finally, we obtain a constant vector ajk as close as possible to Ñfjk(
. Finally, we obtain a constant vector ajk as close as possible to Ñfjk(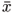 ) satisfying
) satisfying 
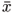 = fjk(
= fjk(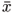 ) solving the constrained optimization problem
) solving the constrained optimization problem
According to Teixeira and  ak (1999), the first order conditions to solve this optimization problem are
ak (1999), the first order conditions to solve this optimization problem are
and
where l in (38) is the Lagrange multiplier and the subscript ajk in Ñajk indicates that the gradient Ñ is computed with respect to ajk. Performing the required differentiation in (38), it yields
Pre-multiplying (40) by
T and using (39), we obtain
Now, substituting (41) in (40), we obtain
which are the columns of the vertex matrix Ak. This formula produces linear approximations instead of affine approximations, which are in general obtained by the Taylor linearization formula given by
and the approximation of fk(x) around 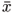 is
is
Note that for fk(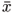 ) ¹ 0, this approach produces affine systems instead of linear ones, as mentioned before. Using (42), several linear approximations of the uncertain linear system (2) can be obtained for different linearization points, even if these points are not equilibrium points.
) ¹ 0, this approach produces affine systems instead of linear ones, as mentioned before. Using (42), several linear approximations of the uncertain linear system (2) can be obtained for different linearization points, even if these points are not equilibrium points.
The Dini derivatives are a generalization of the classical derivative and inherit some important properties from it. Because the Dini derivatives are point-wise defined, they are more suited than some more modern approaches to generalize the concept of a derivative like Sobolev Space or Distributions. The Dini derivatives are defined as follows (Rouche et al., 1977).
(i) Let t0 be a limit point of ]a,b[ Ç ]t0,+¥[. Then the right-hand upper Dini derivate D+ of f at t0 is given by
and the right-hand lower Dini derivate D+ of f at t0 is given by
where t ®  means simply that one considers, in the limiting processes, only the values of t > t1. A similar meaning is attached to t ®
means simply that one considers, in the limiting processes, only the values of t > t1. A similar meaning is attached to t ®  .
.
(ii) Let t0 be a limit point of ]a,b[ Ç ]-¥,t0[. Then the left-hand upper Dini derivate D- of f at t0 is given by
and the left-hand lower Dini derivate D- of f at t0 is given by
In the framework of the elementary calculus, if f:]a,b[ ®  is a function from a non-empty open subset ]a,b[ Ì
is a function from a non-empty open subset ]a,b[ Ì  into
into  and t0Î ]a,b[, then all four Dini derivatives D+f(t0), D+f(t0), D-f(t0), and D-f(t0) of f at the point t0 exist. This means that if ]a,b[ is a non-empty open interval, then the functions D+f, D+f, D-f and D-f: ]a,b[ ®
and t0Î ]a,b[, then all four Dini derivatives D+f(t0), D+f(t0), D-f(t0), and D-f(t0) of f at the point t0 exist. This means that if ]a,b[ is a non-empty open interval, then the functions D+f, D+f, D-f and D-f: ]a,b[ ®  , where
, where  : =
: =  È {-¥} È {+¥}, are all defined in the canonical form. In this case, the classical derivative df/dt: ]a,b[ ®
È {-¥} È {+¥}, are all defined in the canonical form. In this case, the classical derivative df/dt: ]a,b[ ®  exists, if and only if the Dini derivatives are all real valued and D+f = D+f = D-f = D-f.
exists, if and only if the Dini derivatives are all real valued and D+f = D+f = D-f = D-f.
Remark 3 We have the inequality for limsup
in which a derivative defined in this form is not a linear operation at all; notwithstanding, if the right-hand limit of the function g exists, then
These results also hold for liminf.
The latter equality leads to the following lemma.
Lemma 5Let f and g be real valued functions, the domains of which are subsets of and let D*Î { D+f, D+f, D-f, D-f } be a Dini derivative. Let t0Î
and let D*Î { D+f, D+f, D-f, D-f } be a Dini derivative. Let t0Î  be such that the Dini derivative D*f(t0) is properly defined; that is D*f(t0) Î
be such that the Dini derivative D*f(t0) is properly defined; that is D*f(t0) Î  and g is differentiable at t0 in the classical sense. Then
and g is differentiable at t0 in the classical sense. Then
Theorem 6Let I be a non-empty interval in , C be a countable subset of I and f:I ®
, C be a countable subset of I and f:I ®  be a continuous function. Let D*Î { D+f, D+f, D-f, D-f } be a Dini derivative and let J be an interval such that D*f(t) Î J for all t Î I/C. Then
be a continuous function. Let D*Î { D+f, D+f, D-f, D-f } be a Dini derivative and let J be an interval such that D*f(t) Î J for all t Î I/C. Then
for all t1,t2Î I, t1¹ t2.
Corollary 7Let I be a non-empty interval in , C be a countable subset of I, f:I ®
, C be a countable subset of I, f:I ®  be a continuous function, and D*Î { D+f, D+f, D-f, D-f } be a Dini derivative. Then
be a continuous function, and D*Î { D+f, D+f, D-f, D-f } be a Dini derivative. Then
D*f(t) > 0 for all t Î I/C implies that f is increasing on I,
D*f(t) > 0 for all t Î I/C implies that f is strictly increasing on I,
D*f(t) < 0 for all t Î I/C implies that f is decreasing on I,
D*f(t) < 0 for all t Î I/C implies that f is strictly decreasing on I.
For the purpose of comparison, we present a fuzzy blending control which is also used to stabilize (4). This stabilizing control approach is given in terms of the PDC scheme and a common quadratic Lyapunov function using the guaranteed cost control optimization problem in the context of the convex analysis using LMI's (Arrifano and Oliveira, 2002).
According to the PDC scheme, a fuzzy blending control shares the same structure of (3) in its premise part. As in (4), this fuzzy control is also inferred as a weighted average of all feedback gains Ki, i = 1; 2, ..., r which is given by
with ai(·) as in (5). In order to obtain the state feedback fuzzy system, we substitute (44) in (4), which gives
Defining Gi(p) := Ai(p) - Bi(p) Ki and Hij(p) := Ai(p) - Bi(p) Kj + Aj(p) - Bj(p) Ki, i, j = 1, 2, ..., r, after some algebraic manipulations using  ai(x) = 1,we can write (45) as
ai(x) = 1,we can write (45) as
In (46),  means, for instance for r = 3,
means, for instance for r = 3,  aij Û a12 + a13 + a23.
aij Û a12 + a13 + a23.
C.1 Guaranteed cost control design via LMI's
In this section we summarize the optimal quadratic guaranteed cost control problem for the fuzzy blending control design.
Definition 4 The fuzzy system (4) is said to be stable if there exists a stabilizing control law as in (44) such that an upper bound on the quadratic performance index
along the feedback fuzzy system trajectory is minimized with Q Î  nxn,
nxn,  Î
Î  mxm, Q > 0, and R > 0 weighting symmetric matrices which are chosen to yield the desired performance.
mxm, Q > 0, and R > 0 weighting symmetric matrices which are chosen to yield the desired performance.
Definition 5 If there exist a stabilizing control law as in (44) and a positive scalar  such that C(x0,u) <
such that C(x0,u) <  along the feedback fuzzy system trajectory then
along the feedback fuzzy system trajectory then  is a guaranteed cost and (44) is a guaranteed control law.
is a guaranteed cost and (44) is a guaranteed control law.
Proposition 2 Consider the fuzzy system (4), the fuzzy blending control (44) and the performance index (47). If there exist a common symmetric positive definite matrix X and matrices Yi, i = 1,2,...,r of appropriate dimensions satisfying the LMI's
where
then (44) with Ki = YiX-1, i = 1,2,...,r is a guaranteed control law and the cost given by  =
=  X-1x0 is a guaranteed cost.
X-1x0 is a guaranteed cost.
Proof: The proof can be obtained following the proof of Proposition 1, considering a common quadratic Lyapunov function candidate as
along the feedback fuzzy system trajectory.
As in Section 2.2.1, using both Proposition 2 and Lemma 1, we can construct the following GEVP for the guaranteed cost control design to the feedback fuzzy system (46):
If (50) is feasible, we have g > lmax[X-1] and Ki = YiX-1 for i = 1,2,...,r.
- Arrifano, N. S. D. and Oliveira, V. A. (2002). Guaranteed cost fuzzy controllers for a class of uncertain nonlinear dynamic systems, XIV Congresso Brasileiro de Automática, pp. 18731877.
- Boyd, S., Ghaoui, L. E., Feron, E. and Balakrishnan, V. (1994). Linear Matrix Inequalities in System and Control Theory, SIAM, Philadelphia, PA.
- Cao, S. G., Rees, N. W. and Feng, G. (1997). Further results about quadratic stability of continuous-time fuzzy control systems, International Journal of Systems Science 4(28): 397404.
- Cao, S. G., Rees, N. W. and Feng, G. (2001). H¥ control of uncertain fuzzy continuous-time systems, Fuzzy Sets and Systems 115(2): 171190.
- Costa, E. F. and Oliveira, V. A. (1999). Gain scheduled controllers for dynamic systems with sector nonlinearities, 14th IFACWorld Congress, Vol. E, Beiging, China, pp. 357362.
- Costa, E. F. and Oliveira, V. A. (2002). On the design of guaranteed cost controllers for a class of uncertain linear systems, Systems & Control Letters 46(1): 1729.
- Feng, G., Cao, S. G., Rees, N. W. and Chack, C. K. (1997). Design of fuzzy control systems with guaranteed stability, Fuzzy Sets and Systems 85(1): 110.
- Jadbabaie, A., Abdallah, C. T., Farmularo, D. and Dorato, P. (1998b). Robust, non-fragile and optimal controller design via linear matrix inequalities, American Control Conference, Philadelphia, PA, pp. 28422846.
- Jadbabaie, A., Jamshidi, M. and Titli, A. (1998a). Guaranteed cost design of continuous-time takagi-sugeno fuzzy controllers via linear matrix inequalities, IEEE International Conference on Fuzzy Systems, Vol. 1, Anchorage, AK, pp. 268273.
- Johansson, M., Rantzer, A. and Arzén, K. (1998). Piecewise quadratic stability of fuzzy systems, IEEE Transactions on Fuzzy Systems 7(6): 713722.
- Khalil, H. (1996). Nonlinear Systems, Prentice-Hall, Upper Saddle River, NJ.
- Lee, K. R., Jeung, E. T. and Park, H. B. (2001). Robust fuzzy H¥ control for uncertain nonlinear systems via state feedback: an LMI approach, Fuzzy Sets and Systems 120(1): 123134.
- Petersen, I. R. and Macfarlane, D. C. (1994). Optimal guaranteed cost control and filtering for uncertain linear systems, IEEE Transactions on Automatic Control 39(9): 19711977.
- Rouche, N., habets, P. and Laloy, M. (1977). Stability Theory by Lyapunov's Direct Method, Springer-Verlag, New York, NY.
- Takagi, T. and Sugeno, M. (1985). Fuzzy identification of systems and its application to modeling and control, IEEE Transactions on Systems, Man and Cybernetic 15(1): 116132.
- Tanaka, K., Hori, T., Yamafugi, K. and Wang, O. H. (1999). An integrated fuzzy control system design for nonlinear systems, 38th IEEE Conference on Decision and Control, Vol. 5, Phoenix, Arizona, pp. 43494354.
- Tanaka, K., Ikeda, T., andWang, H. O. (1997). Fuzzy control system design via LMI, American Control Conference, Vol. 5, Albuquerque, NM, pp. 28732877.
- Tanaka, K., Ikeda, T. and Wang, H. O. (1996). Robust stabilization of a class of uncertain nonlinear systems via fuzzy control: quadratic stabilizability, H¥ control theory and linear matrix inequalities, IEEE Transactions on Fuzzy Systems 4(1): 113.
- Tanaka, K., Ikeda, T. and Wang, H. O. (1998). Fuzzy regulators and fuzzy observers: relaxed stability conditions and LMI-based designs, IEEE Transactions on Fuzzy Systems 8(2): 250265.
- Tanaka, K. and Wang, H. O. (2001). Fuzzy Control Systems Design and Analysis: a Linear Matrix Inequality Approach, John Wiley and Sons, New York, NY.
- Teixeira, M. C. M., Pietrobom, H. C. and Assunção, E. (2000). Novos resultados sobre a estabilidade e controle de sistemas não-lineares utilzando modelos fuzzy e LMI, Controle & Automação: Revista da Sociedade Brasileira de Automática 11(1): 3748.
- Teixeira, M. C. M. and Zak, S. H. (1999). Stabilizing controller design for uncertain nonlinear systems using fuzzy models, IEEE Transactions on Fuzzy Systems 15(1): 116132.
- Wang, H. O., Tanaka, K. and Griffin, M. F. (1996). An approach to fuzzy control of nonlinear: stability and design issues, IEEE Transactions on Fuzzy Systems 4(1): 1423.
- Zhang, J. M., Li, R. H. and Zhang, P. A. (2001). Stability analysis and systematic design of fuzzy control systems, Fuzzy Sets and Systems 120(1): 6572.
Appendix A
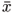 denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices
denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices 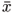 we have
we have Consider the uncertain nonlinear systems in its polytopic description as defined in (2). Following, we present the linearization formula used to obtain the uncertain linear approximations of the nonlinear functions which are the vertexes of the polytope. For this purpose, let 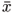 denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices Ak and Bk such that in the vicinity of
denote a linearization point, which is not necessarily an equilibrium point. The objective is to obtain matrices Ak and Bk such that in the vicinity of 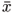 we have
we have
Appendix B
 and consider a function
and consider a function  and a point
and a point Definition 3 Let ]a,b[ Ì  and consider a function f: ]a,b[ ®
and consider a function f: ]a,b[ ®  and a point t0Î ]a,b[.
and a point t0Î ]a,b[.
Appendix C
Publication Dates
-
Publication in this collection
07 Mar 2007 -
Date of issue
June 2006
History
-
Received
28 Nov 2002 -
Reviewed
29 May 2006