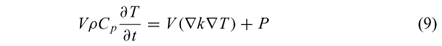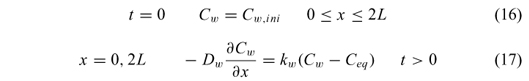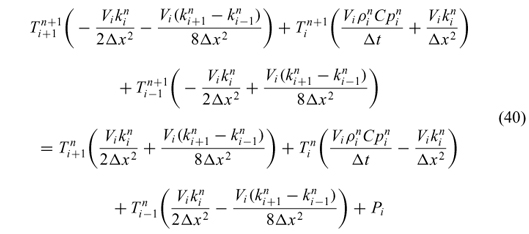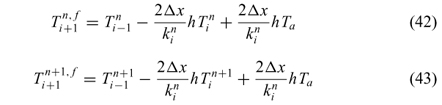Numerical solution of coupled mass and energy balances during osmotic microwave dehydration

Numerical solution of coupled mass and energy balances during osmotic microwave dehydration

Javier R. Arballo^I,II,*; Laura A. Campañone^I,II; Rodolfo H. Mascheroni^I,II

^ICIDCA (Centro de Investigación y Desarrollo en Criotecnología de Alimentos). (CONICET La Plata - UNLP), Calle 47 y 116, La Plata (1900), Argentina

^IIMODIAL - Facultad de Ingeniería, Universidad Nacional de la Plata (UNLP). E-mails: [e-mail] / [e-mail] / [e-mail]

ABSTRACT

The mass and energy transfer during osmotic microwave drying (OD-MWD) process was studied theoretically by modeling and numerical simulation. With the aim to describe the transport phenomena that occurs during the combined dehydration process, the mass and energy microscopic balances were solved. An osmotic-diffusional model was used for osmotic dehydration (OD). On the other hand, the microwave drying (MWD) was modeled solving the mass and heat balances, using properties as function of temperature, moisture and soluble solids content. The obtained balances form highly coupled non-linear differential equations that were solved applying numerical methods. For osmotic dehydration, the mass balances formed coupled ordinary differential equations that were solved using the Fourth-order Runge Kutta method. In the case of microwave drying, the balances constituted partial differential equations, which were solved through Crank-Nicolson implicit finite differences method. The numerical methods were coded in Matlab 7.2 (Mathworks, Natick, MA). The developed mathematical model allows predict the temperature and moisture evolution through the combined dehydration process.

Mathematical subject classification: Primary: 06B10; Secondary: 06D05.

Key words: mathematical modeling, osmotic-microwave, combined dehydration.

1 Introduction

Osmotic dehydration (OD) has the ability to protect the food for further drying treatments, as it generates a defense from losses in volatile compounds and lowers the risks of chemical and physical changes. It consists in food immersion in a hypertonic solution that produces a partial water removal. To complete the drying process and reach a stable product it is necessary another procedure like microwave drying (MWD). Microwaves have the ability to penetrate and heat within products, due to the interaction of the electric field with water molecules. When using microwave as a final drying stage, the removing of inner water is enhanced because foods heat uniformly increasing water vapor pressure which forces vapor toward the surface [1].

There exist mathematical models to describe the mass transfer process during osmotic dehydration that cover a wide range of approaches and forms. According to Spiazzi and Mascheroni [2] the OD models could be divided into two main groups: the phenomenological and microscopic-structural ones. In the present work osmotic diffusional model developed by Spiazzi and Mascheroni [3], based on the research works of Toupin et al. [4] and Marcotte et al. [5], was used to model osmotic dehydration process, which is based on the mass transfer through cellular membranes and multicomponent diffusion between intercellular spaces.

Besides, the electromagnetic-food interaction has to be considered in the model formulation. The behavior of the electromagnetic field inside the microwave oven is very complex; then it can be used an approximation that considers an exponential decay inside the food, the Lambert's law [6, 7].

To model the combined process of osmotic dehydration followed by microwave drying it is necessary to solve the microscopic mass and energy balances. The obtained balances constitute a system of nonlinear differential equations highly coupled. For osmotic dehydration process, the mass balances constitute ordinary coupled differential equations; in the case of microwave drying the balances constitute partial differential equations. For the characteristics of the equation system, it should be solved applying numerical methods.

According of the previous considerations the objectives of this work were:

— To obtain an adequate numerical model that predicts process variables during osmotic-microwave dehydration (OD-MWD), solving the microscopic mass and energy balances.

— To solve the non-linear mathematical model considering that the thermal, electromagnetic and transport properties are temperature and composition dependent.

— To apply the developed model to simulate the mass and temperature profiles under different operating conditions.

2 Mathematical Modeling

In the development of the mathematical model two fundamentals steps have been considered: osmotic dehydration process and the application of microwave as a final drying step.

2.1 Osmotic dehydration (Step 1)

In this step Spiazzi and Mascheroni [3] model was used, that considers the mass transfer through cellular membranes and the multicomponent diffusion between intercellular spaces. In order to obtain the concentration profiles, the whole volume was divided into N concentric and equal volume shells. In each element two phases may be distinguished: the plasmatic content and the intercellular spaces. Each volume of intercellular space is subjected to a diffusive-convective flux between adjacent volumes and a transmembrane diffusive flux from the cellular plasma [3]. The mass balances for each volume V_ξ (ξ = 1, N) are presented as follows:

where M, n and c are the mass, flux and concentration of the j specie, respectively. The subscripts c and o indicate cellular and extracellular space; D and kw are the apparent diffusion coefficient of the j species and the mass transfer coefficient, respectively; A_c and A_o are the cellular and extracellular transfer areas and z represents the distance between each volume element V_ξ. Δ(c_j,c) indicates the concentration difference between intra and extra cellular spaces of the component j and ∇(c_j,o) is the concentration gradient between adjacent volume elements.

The model considers the shrinkage rate u, which can be calculated from the following relation:

The cellular and extracellular transfer areas can be calculated as follows:

where N_cell and C_g are constants which depend on the cell shape, the number of cells per unit volume and the shape of the product piece; V_c and V_o are the cellular and extracellular volume; e represents the fraction of the geometric area which belongs to the extracellular spaces.

The concentration values in the hypertonic solution are deduced from thetotal mass balances:

where corresponds to the mass of component j inside the osmotic solution and subscript sol indicates osmotic solution.

2.2 Microwave dehydration (Step 2)

In the final drying step two stages must be considered: stage 2.1 - Heating with weak evaporation and stage 2.2 - Intensive evaporation. Besides, the following assumptions were made when developing the microwave mathematical model [8]:

— Uniform initial temperature and water content within the product,

— Temperature – and moisture content-dependent dielectric properties,

— Volume changes are not considered,

— Convective boundary conditions,

— Regular one-dimensional geometry (1D),

— Uniform electric field distribution around the sample, and a dominant polarization of the electric field normal to the surface.

2.2.1 Microwave heating

The stage 2.1 involves the heating of the food up to the moment when the whole product reaches the equilibrium temperature Teq. To describe heat transfer, an energy balance must be developed that considers a source term of internal heat generation due to the energy supplied by MW [9]. The resulting microscopic energy balance can be expressed in terms of power as [10]:

where V is product volume, ρ is density, Cp specific heat capacity, T temperature, t time, k thermal conductivity and P is the power generated bythe absorption of microwaves. Fresh food physical properties are used inequation 9.

To complete the model, the following initial and boundary conditions areconsidered:

where L is the half thickness, T_ini is initial temperature, h is the heat transfercoefficient, T_a is the environment temperature, L_vap is the water heat vaporization, k_m is the mass transfer coefficients, C_w and C_eq are the moisture and equilibrium concentrations. Equation 11 includes vaporization at the food surface. This assumption is valid only for the heating step because the exposure time is short and the product temperature over this period is below Teq. In this step, it could be assumed that weak evaporation occurs and equation 11 can be applied. Other authors also used this boundary condition in microwave heating processes, when modeling the initial heating step [6, 11, 12]. A valueof 5 (W m^-2 C^-1) was employed for natural convection around the product slab [13]. The model considers the analogy between heat and mass transfer to evaluate km. The Chilton and Colburn's J factors for heat and mass transfer J_H = J_D allowed to estimate k_m from h values [13]. The power absorbed during microwave irradiation on both sides is represented by the term P. Heat generation is a function of the temperature in each point of the material. In this work, Lambert's Law is deemed as valid.

where is the incident power at the surface (W), Ri and Le indicate right and left sides, λ is the wavelength of radiation and α is the attenuation factor, which is a function of the dielectric constant ∈^' and of the loss factor ∈^".

To predict the humidity profile during the heating stage, a microscopic balance of mass is needed that considers the water diffusion in the inner part of the food. This balance is:

The following initial and boundary conditions are considered:

2.2.2 Microwave intensive vaporization

The stage 2.2 of microwave drying takes place when the whole product reaches T_eq and intensive evaporation begins. T_eq is the temperature achieved when the power absorbed is equilibrated with the energy used in water vaporization [8]. This step finishes at the end of the constant temperature period, unless there is a requirement to heat the material after it is dried. In the energy transfer step, the temperature is supposed to be at the equilibrium value in whole the food T_eq.

Then Lambert's law was applied to evaluate the distribution of electromagnetic energy inside the food. The following equation was applied:

where α_d is the attenuation factor calculated using dielectric properties of the dehydrated material.

The model takes into account the continuous or intermittent application of MW power considering null the incident microwave power when the magnetron is turned off in the cycling operation mode.

During this final stage, water vaporization is considered to take place volumetrically within the product. The generation of water vapor is calculatedsupposing that all the power generated by MW is used for removal of water:

where m_v is the rate of water vaporization (kg s^-1).

3 Results

3.1 Numerical solution

3.1.1 Osmotic dehydration model (step 1)

In this step the model solves 2N equations for water (j = w) and N equations for soluble solids content (j = s), in order to calculate water and soluble solids content inside the food. The obtained ordinary differential equation system can be solved through Fourth Order Runge-Kutta method coded in Matlab 7.2 (Mathworks, Natick, MA). The domain was divided into 10 volume elements and the equations - were solved for each volume and time increment (Δt):

Cell volume

Intercellular volume

where Δt is the time increment (0.1s for all the runs), f(t, c_j,c) and g(t, c_{j o}) correspond to mass variation of the j component with respect to time, inside the cell (subscript c) and between adjacent intercellular spaces (subscript o); and are the new values of mass of water or solids at time t + Δt, in the cellular and extracellular volume, respectively; k_RK and m_RK are the coefficients of Runge Kutta method [14, 15].

3.1.2 Microwave drying model (steps 2)

The mass and energy balances in the stage 2.1 with their boundary conditionsare coupled and form a system of nonlinear partial differential equations. Therefore, Crank-Nicolson finite difference method, characterized by being unconditionally stable and convergent, was used for solving the final equation system. A finite difference algorithm, previously developed by Campañone et al. [16], was implemented to solve the unidirectional energy transfer. A time increment of 0.1s was used and the domain was divided into 15 space increments. Thefollowing equations were obtained for the inner points to calculate the temperature profiles.

This equation is valid for 0 < i < b being b the number of nodes in the discretized domain. Vi is the volume of an element located between the nodes (i + 1 / 2) and (i – 1 /2), and P_i is the power calculated in the same nodes:

At the food surface (i = b), equation 40 presents two fictitious points (i+1, n) and (i+1, n+1). Using boundary condition equation 11, the following equations were obtained:

By replacing equation 42 and 43 in the general expression equation 40, the temperature prediction equation was:

Equations 40 and 42 for both boundaries, form a system of linear equations. The solution allows calculate the inner and surface temperatures. The same procedure was implemented to solve the microscopic mass balance equations 15-17. In stage 2.2, moisture content for each time step was calculated using equation 20.

The equation system solution to obtain temperatures and moisture profiles were coded in Matlab 7.2 (Mathworks, Natick, MA).

3.2 Process simulation

The mathematical model can be used for a wide variety of food materials. Firstly, the model was employed to predict the water loss and solid gain during OD process (Step 1) applied to pumpkin in sucrose solution.

Table 1 summarizes the physical properties and adjustment parameters needed to run the simulation.

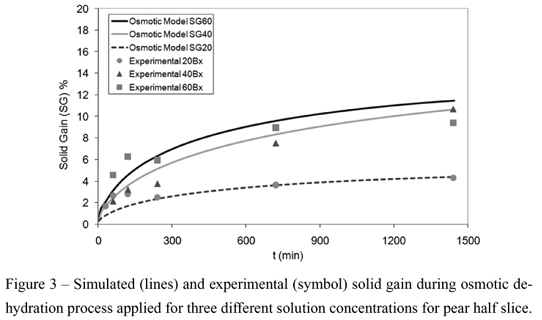
In this Table the subscript 60 indicates the concentration of osmotic solution (Brix units). In Figures 1a and ^b it can be seen the experimental and simulated values of water loss and solid gain. The model follows the experimental behavior; a rapid increase in the first 300 minutes, and from then a trend to equilibrium.

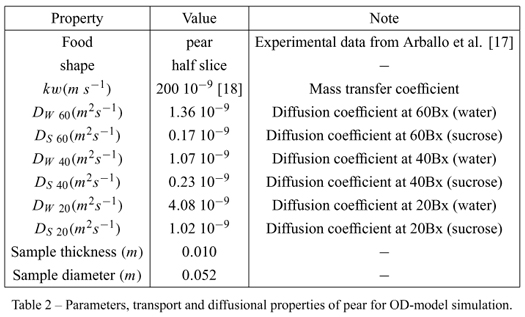
Then, the model was run with several process conditions as parameters, in particular the effective mass diffusion coefficient. Table 2 shows the properties and the parameters used in the simulation of the OD process of pears in sucrose solutions.

Figures 2 and 3 show the predicted water loss and solid gain as function oftime during the osmotic dehydration process; it can be seen that the model predicts the rapid water mass loss in the beginning of the process; then, an asymptotic trend is developed due to the descent in driving force (chemical potential difference for water between the food and the solution). The dehydration behavior of pears presents a behavior similar to that of pumpkin, but pumpkin underwent more water content reduction and gained more solids than pears; it corresponds to the different values of the Dw and Ds parameters for the two foods, and is based mainly in differences in structure.

Besides, the mathematical model also considered the variation of OD solution concentration, shape and size of the product.

With respect to OD solution concentration, the experimental values for pear fruit ranged between 20 to 60 Brix. The model is sensible to the change of solution composition as can be seen in Figures 2 and 3, showing a good accuracy in the predicted curves as compared to experimental data.

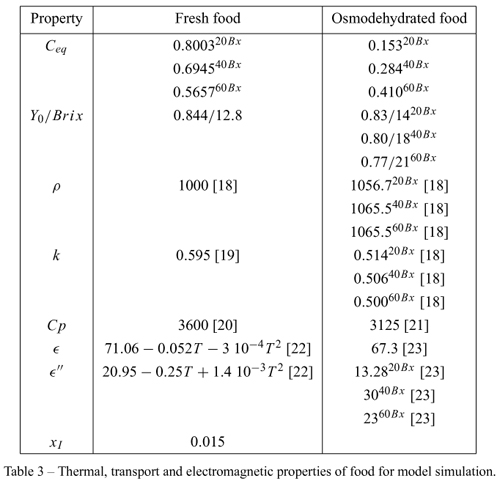
For Step 2 (MWD), Table 3 shows the thermal, transport and electromagnetic properties used as inputs in the runs of the numerical model.

The model allows predict the evolution of temperature and moisture content during step 2 (Figs. 4 and 5). OD process applied to pears in sucrose solution during two hours was considered as initial condition for this stage. Different OD pre treatments affect the initial water and solute content. The model takes into account this fact varying moisture and solid content of the food (Fig. 4).

The mathematical model shows a good sensibility to the changes of physical properties, due to OD pretreatment. The uptake of solids during OD step, provokes a change of composition of the food material affecting its dielectric properties (∈^', ∈^"), and its ability to interact with radiation (Fig. 5).

The microwave oven operates in continuous or intermittent modes, according to power used. The dehydration process of fruits and vegetables can be enhanced applying on-off cycles (Campañone et al. [24]). The model was able to followthe intermittency of microwave power application (on-off operation), being stable and showing no perturbations in the predicted temperature and moisture profiles (Fig. 5).

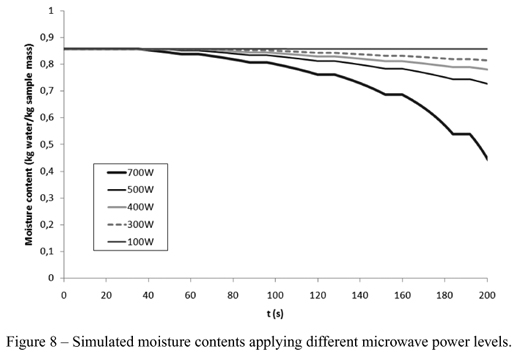
In addition, the numerical simulation permits to evaluate the effect of the microwave power on the profiles. It was ranged between 300 to 500 W and the predicted temperature (surface and centre of the slice) and moisture profiles are shown in Figures 6, 7 and 8. The mathematical model can differentiate the effect of diverse power levels. The use of high power values provokes a rapid increase on temperature (Figs. 6 and 7), as is expected, and a maximum water loss at the same time (Fig. 8).

Finally, the effect of the sample thickness was evaluated in the present work (Figs. 9a and ^b). The power absorption depends on water content, and then large samples with high water content absorb more microwave power, increasing their dehydration rate. This functionality was incorporated in the simulation codes as a Matlab function.

4 Conclusions

A complete and relatively simple and easy to use mathematical model has been developed for simultaneous prediction of temperature and moisture profiles during the combined process of osmotic-microwave dehydration. Its main originality is that it can consider the initial process of osmotic dehydration and couple the predicted water and solute concentration profiles to the simultaneous mass and energy transfer in the microwave heating step including, also, the inner heat generation, the on-off control effect of the microwave oven and different power levels. The model considers two numerical techniques to solve differential equations: Runge Kutta (fourth order) for Step 1 and Finite Differences for Step 2. The numerical solution of the balances was implemented in Matlab environment and it permits to interpret and simulate a technological and industrial process.

From the experimental data and numerical simulations, the effect of the variety of food materials, concentration of osmotic solutions, shape and size of the product was analyzed during OD process. These food characteristics and operating conditions affect directly to microwave dehydration during the second step, mainly changing the physical properties of the food. Besides microwave power level and the size of the product was included in the analysis for this step.

Finally, we obtained an integrated model that can be used for the prediction of weight loss in a wide range of operating conditions.

Received: 22/IX/12.

Accepted: 28/IX/12.

#CAM-700/12.

References

• [1] A.K. Datta and J. Zhang, Porous media approach to heat and mass transfer insolid foods Department of Agriculture And Biology Engineering, Cornell University (1999).
• [2] E.A. Spiazzi and R.H. Mascheroni, Modelo de deshidratación osmótica dealimentos vegetales MAT Serie A, 4 (2001), 23-32.
• [3] E.A. Spiazzi and R.H. Mascheroni, Mass transfer model for osmotic dehydration of fruits and vegetables. I. Development of the simulation model Journal of Food Engineering, 34 (1997), 387-410.
• [4] C.J. Toupin, M. Marcotte and M. Le Maguer, Osmotically induced mass transfer in plant storage tissues: a mathematical model - Part I Journal of Food Engineering, 10 (1989), 13-38.
• [5] M. Marcotte, C.J. Toupin and M. Le Maguer, Mass transfer in cellular tissues. Part I: The mathematical model Journal of Food Engineering, 13 (1991), 199-220.
• [6] C.H. Tong and D.B. Lund, Microwave heating of baked dough products with simultaneous heat and moisture transfer Journal of Food Engineering, 19 (1993), 319-339.
• [7] H. Ni and A.K. Datta, Moisture as related to heating uniformity in microwave processing of solids foods Journal of Food Process Engineering, 22 (2002), 367-382.
• [8] J.R. Arballo, L.A. Campañone and R.H. Mascheroni, Modelling of microwave drying of fruits Drying Technology, 28 (2010), 1178-1184.
• [9] Y.E. Lin, R.C. Anantheswaran and V.M. Puri, Finite element analysis of microwave heating of solid foods Journal of Food Engineering, 25 (1995), 85-112.
• [10] L.A. Campañone and N.E. Zaritzky, Mathematical analysis of microwave heating process Journal of Food Engineering, 69 (2005), 359-368.
• [11] L. Zhou, V.M. Puri, R.C. Anantheswaran and G. Yeh, Finite element modelling of heat and mass transfer in food materials during microwave heating-model, development and validation Journal of Food Engineering, 25 (1995), 509-529.
• [12] M. Pauli, T. Kayser, G. Adamiuk and W. Wiesbeck, Modeling of mutual coupling between electromagnetic and thermal fields in microwave heating IEEE, 2007 (2007), 1983-1986.
• [13] R.B. Bird, W.E. Stewart and E.N. Lightfoot, Transport phenomena John Wiley and Sons, New York (1976).
• [14] A. Constantinides and N. Mostoufi, Numerical Methods for Chemical Engineers with Matlab Applications Prentice-Hall (1999).
• [15] S.C. Chapra and P.P. Canale, Métodos Numéricos para Ingenieros Fifth Edition. México, Mc Graw-Hill (2007).
• [16] L.A. Campañone, V.O. Salvadori and R.H. Mascheroni, Weight loss during freezing and storage of unpackaged foods Journal of Food Engineering, 47 (2001), 69-79.
• [17] J.A. Arballo, R.R. Bambicha, L.A. Campańone, M.E. Agnelli and R.H. Mascheroni, Mass transfer kinetics and regressional-desirability optimization duringosmotic dehydration of pumpkin, kiwi and pear International Journal of Food Science and Technology, 47 (2012), 306-314.
• [18] M.E. Agnelli, C.M. Marani and R.H. Mascheroni, Modelling of heat and mass transfer during (osmo) dehydrofreezing of fruits Journal of Food Engineering, 69 (2005), 415-424.
• [19] V.E. Sweat, Experimental values of thermal conductivity of selected fruits and vegetables Journal of Food Science, 39 (1974), 1080-1083.
• [20] S.L. Polley, O.P. Snyder and P. Kotnour, A compilation for thermal properties of foods Food Technology, 34 (1980), 76-94.
• [21] A.M. Tocci and R.H. Mascheroni, Determinación por calorimetría diferencial de barrido de la capacidad calorífica y entalpía de frutas parcialmente deshidratadas en soluciones acuosas concentradas de azúcar In: I Congreso Ibero-Americano de Ingeniería de Alimentos, I (1996), 411-420.
• [22] O. Sipahioglu and S.A. Barringer, Dielectric properties of vegetables and fruits as a function of temperature, ash and moisture content Journal of Food Science, 68 (2003), 234-239.
• [23] A.K. Datta and R.C. Anantheswaran, Handbook of Microwave Technology for Food Applications Marcel Dekker, USA (2001).
• [24] L.A. Campańone, Carlos A. Paola and R.H. Mascheroni, Modeling and simulation of microwave heating of foods under different process schedules Food and Bioprocess Technology, 5 (2012), 738-749.

*

The first author is supported by Universidad Nacional de La Plata

Publication Dates

• Publication in this collection
  28 Nov 2012
• Date of issue
  2012

History

• Received
  22 Sept 2012
• Accepted
  28 Sept 2012