ABSTRACT
In this study, Max and Burkhart (1976)’s segmented taper model was used to describe stem profile and predict stem volume of oriental spruce in Turkey. Thirty procedures were evaluated, which include five fitting methods and six adjustment strategies. The fitting methods resulted in parameters that were optimized for (1) taper, (2) cumulative volume, (3) taper and cumulative volume, (4) taper and total volume, and (5) taper, cumulative volume, and total volume. The adjustment strategies are (1) unadjusted, and adjusted to match (2) DBH, (3) predicted total volume, (4) DBH and predicted total volume, (5) a combined estimator, and (6) DBH and a combined estimator. Results showed that, without adjustment, the model with parameters optimized for taper gave good prediction for both taper and cumulative volume. Mixed results were obtained when various adjustment strategies were used on different fitting techniques. The overall best-ranked procedure for predicting both taper and volume was the model optimized for taper and cumulative volume and then adjusted to fit the combined estimator.
Keywords:
Volume; Adjustment; Optimization; Segmented models; Diameter; Height
INTRODUCTION
Prediction of tree volume in a stand, either total volume or merchantable volume, are essential for forest management and planning. Predicting tree merchantable volume for any utilization standard can be done by use of volume ratios (Honer 1964HONER, T.G. The use of height and squared diameter ratios for the estimation of merchantable cubic foot volume. The Forestry Chronicle , 40:324-331, 1964., Burkhart 1977BURKHART, H.E. Cubic-foot volume of loblolly pine to any merchantable top limit. Southern Journal of Applied Forestry 1, p. 7-9, 1977., Cao and Burkhart 1980CAO, Q.V.; BURKHART, H.E. Cubic-foot volume of loblolly pine to any height limit. Southern Journal of Applied Forestry 4, p. 166-168, 1980.; Teshome 2005TESHOME, T. A ratio method for predicting stem merchantable volume and associate taper equations for Cupressus lusitanica, Ethiopia. Forest Ecology and Management , 204, p. 171-179, 2005.) or by integrating stem profile models. Numerous taper equations, from simple to complex, have been used to describe stem profile of various tree species (Kozak 2004; Jordan et al. 2005JORDAN, L.; BERENHAUT, K.; SOUTER, R.; DANIELS, R.F. Parsimonious and completely compatible taper, total, and merchantable volume models. Forest Science , 51, p. 578-584, 2005.; Diéguez-Aranda et al. 2006DIÉGUEZ-ARANDA, U.; CASTEDO-DORADO, F.; ÁLVAREZ-GONZÁLEZ, J.G.; ROJO, A. Compatible taper function for Scots pine plantations in northwestern Spain. Canadian Journal of Forest Research, 36, p. 1190-1205, 2006.; Li and Weiskittel 2010LI, R.; WEISKITTEL, A.R. Comparison of model forms for estimating stem taper and volume in the primary conifer species of the north American Acadian. Annals of Forest Science , 67, p. 302-302, 2010.; Schröder et al. 2015; Özçelik and Crecente-Campo 2016ÖZÇELIK, R.; CRECENTE-CAMPO, F. Stem taper equations for estimating merchantable volume of Lebanon cedar trees in the Taurus mountains, southern Turkey. Forest Science 62, p. 78-91, 2016.). Flexible equations such as variable-exponent taper models (Kozak 1988KOZAK, A. A variable-exponent taper equation. Canadian Journal of Forest Research , 18, p. 1363-1368, 1988.; Bi 2000; Kozak 2004; Newnham 1992NEWNHAM, R. Variable-form taper functions for four Alberta tree species. Canadian Journal of Forest Research , 22, p. 210-223, 1992.; Sharma and Zhang 2004SHARMA, M.; ZHANG, S. Variable-exponent taper equations for jack pine, black spruce, and balsam fir in eastern Canada. Forest Ecology and Management , 198, p. 39-53, 2004.) cannot be analytically integrated, and therefore need to be numerically integrated for volume computation. On the other hand, volume by integration exists in closed form for segmented taper equations (Max and Burkhart 1976MAX, T.A.; BURKHART, H.E. Segmented polynomial regression applied to taper equations. Forest Science , 22, p. 283-289, 1976.; Cao et al. 1980CAO, Q.V.; BURKHART, H.E.; MAX, T.A. Evaluation of two methods for cubic-volume prediction of loblolly pine to any merchantable limit. Forest Science 26, p. 71-80, 1980.; Clark et al. 1991CLARK, A.; SOUTER, R.; SCHLAEGEL, B. Stem profile equations for southern tree species (Research Paper SE-282). USDA Forest Service:113, 1991.; Fang and Bailey 2000), which can also be directly solved to produce an estimate of merchantable height for a given top diameter (Kozak and Smith 1993KOZAK, A.; SMITH, J. Standards for evaluating taper estimating systems. The Forestry Chronicle , 69, p. 438-444, 1993.).
Demaerschalk (1972DEMAERSCHALK, J. Converting volume equations to compatible taper equations. Forest Science , 18, p. 241-245, 1972.) introduced the concept of a compatible taper and volume system, in which integration of the taper model produces volume that equals the volume predicted by a volume equation. This is because taper and volume are mathematically and biologically related (Munro and Demaerschalk 1974MUNRO, D.D.; DEMAERSCHALK, J.P. Taper-based versus volume-based compatible estimating systems. The Forestry Chronicle , 50, p. 197-199, 1974.). A compatible taper equation can be obtained either by deriving from a total or merchantable volume equation (Demaerschalk 1972, Clutter 1980CLUTTER, J.L. Development of taper functions from variable-top merchantable volume equations. Forest Science , 26, p. 117-120, 1980.), or by applying constraints to ensure that its integration produces specified stem volume (Goulding and Murray 1976GOULDING, C.; MURRAY, J. Polynomial taper equations that are compatible with tree volume equations. NZJ For. Sci, 5, p. 312-325, 1976.; Cao et al. 1980CAO, Q.V.; BURKHART, H.E. Cubic-foot volume of loblolly pine to any height limit. Southern Journal of Applied Forestry 4, p. 166-168, 1980.; Van Deusen et al. 1982VAN DEUSEN, P.C.; MATNEY, T.G.; SULLIVAN, A.D. A compatible system for predicting the volume and diameter of sweetgum trees to any height. Southern Journal of Applied Forestry , 6, p. 159-163, 1982., 1988; Reed and Green 1984REED, D.D.; GREEN, E.J. COmpatible stem taper and volume ratio equations. Forest Science , 30, p. 977-990, 1984.; Lenhart et al. 1987LENHART, J.D.; HACKETT, T.L.; LAMAN, C.J.; WISWELL, T.J.; BLACKARD, J.A. Tree content and taper functions for loblolly and slash pine trees planted on non-old-fields in east Texas. Southern Journal of Applied Forestry , 11, p. 147-151, 1987.; Fang and Bailey 1999FANG, Z.; BAILEY, R.L. Compatible volume and taper models with coefficients for tropical species on Hainan Island in Southern China. Forest Science , 45, p. 85-100, 1999.; Diéguez-Aranda et al. 2006).
A method to simultaneously fit equations in the taper and volume system substantially reduced the total estimation error (Reed 1982REED, D. Simultaneous estimation of tree taper and merchantable volume in loblolly pine. VA J. Science 33, p. 85, 1982., Reed and Green 1984). This simultaneous estimation problem was reformulated by Van Deusen (1988)VAN DEUSEN, P.C. Simultaneous estimation with a squared error loss function. Canadian Journal of Forest Research , 18, p. 1093-1096, 1988. as a seemingly unrelated regressions (SUR) problem, which can be easily solved using standard statistical software packages.
Oriental spruce (Picea orientalis L.) is an important tree species in northeastern of Turkey and it occupies an area of 328.000 ha, with the standing volume about 71.4 million m3 (GDF 2018GDF. Forest Resources. The General Directorate of Forests, Ankara, 2018.). This species is utilized for pulpwood and cellulose. However, because of ever-changing market conditions, existing equations and local volume tables that are based on fixed merchantability limits no longer suffice. In addition, environmental benefits from oriental spruce forests in northeastern Turkey include conservation of biological diversity, climate change mitigation and adaptation, and protection of soil and water resources. Therefore, forest managers need detailed information supplied by growth and yield prediction models, such as volume classified by merchantable products, for sustainable management of these forests.
Some taper models have been tested to describing stem profile and predict volume for some tree species in Turkey (Brooks et al. 2008BROOKS, J.R.; JIANG, L.; ÖZÇELIK, R. Compatible stem volume and taper equations for Brutian pine, Cedar of Lebanon, and Cilicica fir in Turkey. Forest Ecology and Management 256, p. 147-151, 2008.; Sakici et al. 2008SAKICI, O.E.; MISIR, N.; YAVUZ, H.; MISIR, M. Stem taper functions for Abies nordmanniana subsp bornmulleriana in Turkey. Scandinavian Journal of Forest Research, 23, p. 522-533, 2008.; Özçelik et al. 2014ÖZÇELIK, R.; DIAMANTOPOULOU, M.; BROOKS, J.R. The use of tree crown variables in over-bark diameter and volume prediction models. İForest, 7, p. 132-139, 2014.; Özçelik and Crecente-Campo 2016 and Özçelik and Cao 2017; Sakici and Ozdemir, 2018SAKICI, O.E.; OZDEMIR, G. Stem taper estimations with artificial neural networks for mixed Oriental beech and Kazdaği fir stands in Karabük region, Turkey. CERNE, 24, P. 439-451, 2018.). Taper equations generally are specific to each species, meaning that a separate set of parameters is needed for each species to identify its unique bole shape (Sharma and Parton 2004SHARMA, M.; ZHANG, S. Variable-exponent taper equations for jack pine, black spruce, and balsam fir in eastern Canada. Forest Ecology and Management , 198, p. 39-53, 2004.).
The Max and Burkhart’s (1976MAX, T.A.; BURKHART, H.E. Segmented polynomial regression applied to taper equations. Forest Science , 22, p. 283-289, 1976.) taper equation was used in this study because it is straightforward to predict height at a given stem diameter. This model included three quadratic functions, which are joined together. The result is a continuous and smooth stem profile. For a flexible model, it was relatively simple, and therefore has been frequently used to describe stem profile of many tree species (Byrne and Reed 1986BYRNE, J.C.; REED, D.D. Complex compatible taper and volume estimation systems for red and loblolly pine. Forest science 32, p. 423-443, 1986.; Muhairwe 1999MUHAIRWE, C.K. 1999. Taper equations for Eucalyptus pilularis and Eucalyptus grandis for the north coast in New South Wales, Australia. Forest Ecology and Management , 113(2):251-269.; Jiang et al. 2005JIANG, L.; BROOKS, J.R.; WANG, J. Compatible taper and volume equations for yellow-poplar in West Virginia. Forest Ecology and Management , 213, p. 399-409, 2005.; Diéguez-Aranda et al. 2006; Schröder et al. 2014SCHRÖDER, T.; COSTA, E.A.; VALERIO, A.F.; Dos SANTOS LISBOA, G. Taper equations for Pinus elliottii Engelm. in southern Parana, Brazil. Forest Science , 61, p. 311-319, 2014.; Scolforo et al. 2018;). Constraints have been applied to ensure that the taper curve go through diameter at breast height (DBH) (Cao 2009CAO, Q.V. Calibrating a segmented taper equation with two diameter measurements. Southern Journal of Applied Forestry 33, p. 58-61, 2009.) and/or an upper-stem diameter ( Czaplewski and McClure 1988CZAPLEWSKI, R.L.; MCCLURE, J.P. Conditioning a segmented stem profile model for two diameter measurements. Forest Science , 34, p. 512-522, 1988.; Cao 2009; Cao and Wang 2011CAO, Q.V.; WANG, J. Calibrating fixed-and mixed-effects taper equations. Forest Ecology and Management 262, p. 671-673, 2011.; Sabatia and Burkhart 2015SABATIA, C.O.; BURKHART, H.E. On the use of upper stem diameters to localize a segmented taper equation to new trees. Forest Science , 61, p. 411-423, 2015.). Working with black pine in Turkey, Özçelik and Cao (2017ÖZÇELIK, R.; CAO, Q.V. Evaluation of fitting and adjustment methods for taper and volume prediction of black pine in Turkey. Forest Science , 63, p. 349-355, 2017. ) found that various fitting and adjustment strategies for taper and volume predictions did not improve performance of the taper model. However, they did not consider the possibility of adjustment based on a combined estimator, which is a weighted average of predicted stem volumes from the taper and volume models.
The objective of this study was to evaluate various combinations of methods for estimating parameters and calibrating a modified form of Max and Burkhart’s (1976MAX, T.A.; BURKHART, H.E. Segmented polynomial regression applied to taper equations. Forest Science , 22, p. 283-289, 1976.)’s segmented taper equation for oriental spruce.
MATERIAL AND METHODS
Data
Data used in this study consist of 5859 outside-bark diameter observations from measurements of 642 destructively sampled oriental spruce trees. The data was collected from natural stands located throughout the area of distribution of oriental spruce in northeastern Turkey. Sample trees were selected to represent diameter and height distibutions, based on information from a previous inventory. Diameter at breast height (at 1.3 m above ground level, dbh) and total bole length were measured to the nearest 0.1 cm and 0.01 m for each tree, respectively. Stump height averaged 0.30 m. The all data ranged from 5.2 to 74.3 cm for dbh and 4.1 to 37.7 m for total height. The felled trees were sectioned at 2 m intervals starting from the stump to the tree tip. Two measures of diameter outside bark (dob) perpendicular to each other were collected and averaged to obtain dob measurement up the stem. Smalian’s formula was used to calculate the volume of sections in cubic meters. The volume of the last portion (from the last measurement to the tree tip) was treated as a cone. Total tree volume (above stump) was then obtained by summing up volumes of all sections. Table 1 summarizes the relevant variables (dbh, total height and total volume) for the trees used in this study.
Methods
Total volume equation
A myriad of equations have been developed to predict stem volume of a tree. Schumacher and Hall’s (1933SCHUMACHER, F.X.; HALL, F.D.S. Logarithmic expression of timber-tree volume. J. Agric. Res., 47, p. 719-734, 1933.) model, which has been widely used for many tree species, was applied in this study to estimate total stem volume, whereV i = total stem volume of tree i in m3, D i = diameter at breast height (dbh) of tree i in cm, H i = total height of tree i in m, a, b, and c = regression coefficients, and = error.
Taper equation
The segmented taper model by Max and Burkhart (1976MAX, T.A.; BURKHART, H.E. Segmented polynomial regression applied to taper equations. Forest Science , 22, p. 283-289, 1976.) is preferred because volume can be easily integrated and height prediction from diameter can be directly obtained. A modified form of this taper equation (Cao 2009CAO, Q.V. Calibrating a segmented taper equation with two diameter measurements. Southern Journal of Applied Forestry 33, p. 58-61, 2009.) was used in this study, where: predicted value of y, d ij: outside-bark diameter in cm at height h ij of location j on tree i, h ij: height from the ground in m, = relative height from the tree tip, , k = 1, 2, and a h and b h: regression coefficients.
Performance was improved when d ij was used as a dependent variable rather than equation 3. The regression model is: where = error; Volume (vi) from height h i1 to height h i2 is obtained by integrating the taper equation as follows. whereK = 0.00007854, a constant to convert diameter in cm to area in m2.
In this paper, total volume is defined as volume from the stump to the tree tip, and cumulative volume is volume from the stump to where diameter is measured.
Five different methods were employed to estimate parameters (b 1-b 4 and a 1-a 2) of the stem profile model.
Fitting method 1 - Optimized for taper
The least squares approach used in this method is commonly employed in fitting taper equations. The parameters were selected to minimize , where n i is number of diameter measurements for tree i, N is number of trees, and j is predicted bole diameter at location j on tree i.
Fitting method 2 - Optimized for cumulative volume
The goal was to produce good prediction for cumulative volume by integrating the taper model. This was done by minimizing , where v ij and are observed and predicted cumulative volume of tree i from the stump to the j th diameter measurement, respectively.
Fitting method 3 - Optimized for both taper and cumulative volume
Both and were simultaneously minimized in this approach by use of seemingly unrelated regression (SAS proc MODEL, option SUR). This method endures that predictions for both diameter and cumulative volume are reliable.
Fitting method 4 - Optimized for both taper and total volume
Similar to the previous approach, the objective was to simultaneously minimize and , where are predicted total volume of tree i, obtained by integrating the taper equation (3). Seemingly unrelated regression (SUR) was also used for optimizing both diameter and total volume.
Fitting method 5 - Optimized for taper, cumulative volume, and total volume
In this approach, the objective was to simultaneously minimize , and SUR was again used for this approach.
In each of the five fitting methods, parameters were adjusted so that predictions from the resulting taper model that match various attributes.
Adjustment strategy 1 - Unadjusted
No adjustment was made; estimates of parameters remained unchanged.
Adjustment strategy 2 - Adjusted to match DBH
When the Max and Burkhart (1976MAX, T.A.; BURKHART, H.E. Segmented polynomial regression applied to taper equations. Forest Science , 22, p. 283-289, 1976.) taper equation is applied to breast height (h= 1.30 m), predicted diameter at this point does not necessarily equal to dbh. This adjustment procedure, proposed by Cao (2009CAO, Q.V. Calibrating a segmented taper equation with two diameter measurements. Southern Journal of Applied Forestry 33, p. 58-61, 2009.), replaced parameter b 1 with such that predicted diameter at breast height is D i:
Adjustment strategy 3 - Adjusted to match total volume
In this strategy, replaced b 1 such that the resulting total volume matches , which is predicted from the total volume equation (1), where K = 0.00007854, a constant to convert diameter in cm to area in m2,h iS = stump height for tree i.
Adjustment strategy 4 - Adjusted to match both DBH and total volume
In this adjustment strategy, parameters b 1 and b 2 were replaced with and , respectively, so that predicted diameter at breast height matches D i and the resulting total volume matches :
Adjustment strategy 5 - Adjusted to match combined estimator for total volume
The combined estimator for total volume () is the weighted average of predicted volumes from the taper equation () and the volume model (), where w is obtained by minimizing .
This is adjustment strategy 3, with the combined estimator () replacing the total stem volume estimated from the total volume equation ().
Adjustment strategy 6 - Adjusted to match DBH and combined estimator for total volume
This strategy is identical to adjustment strategy 4, with the exception that replacing to predict total volume.
Model Evaluation
In this study, a total of 30 procedures (five fitting methods × six adjustment strategy) were evaluated. The two-fold evaluation approach was applied. For this purpose, the data were randomly divided into two groups; each containing 321 trees. The coefficients obtained by fitting data from one group were used to predict for the other group. The predicted values from both groups were then pooled to calculate evaluation statistics for both diameters and total volumes. The evaluation statistics included mean bias (MB) between measured and predicted values, mean of absolute bias (MAB), and fit index (FI). MB measures the average bias of the prediction, MAB measures the magnitude of the bias, and FI is analogous to R 2 in linear regression. These statistics are computed as follows, where x ij = either diameter (d ij ) or volume (v ij ), and are predicted and average values of x ij , respectively.
For each procedure and for each evaluation statistic, a relative rank (Poudel and Cao 2013POUDEL, K.P.; CAO, Q.V. Evaluation of methods to predict Weibull parameters for characterizing diameter distributions. Forest Science , 59, p. 243-252, 2013.) was computed. The best and the worst procedures in this ranking system have relative ranks of 1 and k, respectively, where k is number of procedures being evaluated. The remaining procedures have ranks as real numbers between 1 and k. Because this scheme considers both magnitude and order of the evaluation statistic, the relative ranking system should offer more information than the traditional ordinal ranks. The sum of the relative ranks from the three evaluation statistics for each procedure was calculated and then ranked again to give an overall rank for each procedure.
RESULTS AND DISCUSSION
Total volume prediction
Table 2 shows that, based on all three statistics, total volume prediction was better from the total volume model (relative rank of 1.26) than from integrating the various taper models (relative ranks between 7.00 to 11.00). The five fitting methods attained good results in predicting total volume, explaining between 97.91% to 98.01% of the variation, but still slightly worse than 98.92% when predicted from the total volume model. Surprisingly, the inclusion of total volume in the optimization methods (fitting methods 4 and 5) did not improve total volume prediction, as compared to fitting method 1 that optimized only taper. The total volume model produced similar evaluation statistics to those obtained from the combined estimators (relative ranks between 1.00 to 1.30), which is a weighted average of total volume estimates from the total volume model and from integrating the taper equations.
Evaluation statistics for total volume. Bold, italic numbers denote the best method for each criterion, whereas underlined numbers denote the worst method.
Diameter prediction
Table 3 shows that the modified form of Max and Burkhart (1976MAX, T.A.; BURKHART, H.E. Segmented polynomial regression applied to taper equations. Forest Science , 22, p. 283-289, 1976.) model was adequate in estimating tree taper for this data set, regardless of optimization techniques or adjustment strategies. The resulting taper equations produced a mean absolute difference ranging from 1.17 cm to 1.42 cm, and explained between 97.59% and 98.45% of the variation in diameter.
Evaluation statistics for taper. Bold, italic numbers denote the best method for each criterion, whereas underlined numbers denote the worst method.
Without adjustment, the taper equation with parameters optimized only for cumulative volume (fitting method 2) gave the worst prediction for taper (Table 3). On the other hand, the taper optimization (fitting method 1) fared better than the other fitting methods, as expected.
The DBH adjustment constrained the taper curve to go through DBH and therefore resulted in better taper prediction than did the unadjusted taper equations (Table 3). In fact, the DBH adjustment for fitting method 5 (optimized for taper, cumulative volume, and total volume) was the best in predicting taper. The other adjustment strategies, with some exceptions, also improve taper prediction, compared to the unadjusted strategy.
Cumulative volume prediction
All of the taper equations resulting from various fitting and adjustment strategies yielded acceptable results in predicting cumulative volume, from 94.66% to 98.74% in fit index, and from 0.04 m3 to 0.12 m3 in mean absolute deviation (Table 4).
Evaluation statistics for cumulative volume. Bold, italic numbers denote the best method for each criterion, whereas underlined numbers denote the worst method.
Table 4 also shows that, without adjustment, the taper optimization method (fitting method 1) attained the higher relative rank (1.51) than did the rest of the fitting methods (ranging from 2.48 to 3.07 in ranks).
The DBH adjustment did not help to predict cumulative volume, resulting in the worst relative ranks (23.70 to 30.00) among all methods (Table 4). Conversely, adjustment for total volume (adjustment strategies 4 and 5), by use of either prediction from a total volume model or a combine estimator, did improve the cumulative volume prediction. The improvement was enhanced when this adjustment was coupled with the DBH adjustment (adjustment strategies 4 and 6).
Diameter and cumulative volume prediction
Results from Tables 3 and 4 shows that most fitting/adjustment procedures tended to favor either cumulative volume or taper prediction, but not both. In order to evaluate each procedure based on its ability to predict both taper and volume, we summed the relative ranks for taper and cumulative volume. The sum of the relative ranks for taper and cumulative volume for each procedure was then ranked to yield an overall rank (Table 5).
Overall comparisons of optimization and adjustment methods. Bold, italic numbers denote the best method for each criterion, whereas underlined numbers denote the worst method
Cao et al. (1980CAO, Q.V.; BURKHART, H.E. Cubic-foot volume of loblolly pine to any height limit. Southern Journal of Applied Forestry 4, p. 166-168, 1980.) found that a taper equation (that was optimized for taper), while being excellent in predicting predicted taper, did not predict cumulative volume as well as a volume ratio model. Results from this study tell a different story. The taper model in this study with parameters optimized for cumulative volume (fitting method 2) can be considered somewhat similar to a volume ratio model, yet ranked lower in volume prediction (3.07) than the model optimized for taper (1.51). Indeed, the taper optimization method produced the best prediction of both taper and cumulative volume.
Reed and Green (1984REED, D.D.; GREEN, E.J. COmpatible stem taper and volume ratio equations. Forest Science , 30, p. 977-990, 1984.) found that simultaneous optimizing for both taper and cumulative volume produced smaller total system squared error, but did not show how the system behaved separately for taper and volume. In this study, the method of optimizing for both taper and cumulative volume (fitting method 3) did not improve but rather worsened predictions for taper and volume, as compared to optimizing for taper only.
Compared to the unadjusted strategy, the DBH adjustment (adjustment strategy 2) resulted in better evaluation statistics for taper prediction, but worse statistics for prediction of cumulative volume. Adjustment for predicted total volume (from either a total volume model or a combined estimator), in many cases, bettered prediction of both taper and cumulative volume. Adding DBH to the above adjustment actually lowered the overall ranks (Table 5).
The worst overall procedure (rank of 30.00), which is the cumulative volume optimization coupled with DBH adjustment, gave poor prediction for both taper and volume. The best overall rank came from a taper equation optimized for taper and cumulative volume (fitting method 3) which was then adjusted for the combined estimator (adjustment strategy 5). This procedure achieved relative ranks of 2.07 and 1.03 for predicting taper and cumulative volume, respectively.
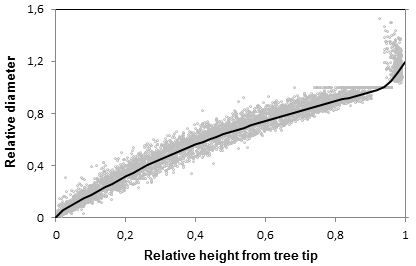
Finally, the proposed taper and stem volume models for optimization alternatives were refit to the entire data set using all five fitting methods (Table 6). Figure 1 shows the observed data, overlaid with predictions from the taper model of fitting method 5.
Estimates of parameters (and standard errors) for taper and volume equations of different fitting methods based on all sample data.
Graph of observed data and predictions from the taper model optimized for taper, cumulative volume, and total volume
CONCLUSIONS
In this study, a simpler form of the Max and Burkhart’s (1976MAX, T.A.; BURKHART, H.E. Segmented polynomial regression applied to taper equations. Forest Science , 22, p. 283-289, 1976.) taper model was used to predict taper and stem volume of oriental spruce. A total of thirty procedures was evaluated, including five fitting methods (optimized for taper, cumulative volume, taper and cumulative volume, taper and total volume, and taper and both cumulative and total volumes) and six adjustment strategies (unadjusted, and adjusted to match DBH, predicted total volume predicted from either a total volume model or a combined estimator, and DBH and predicted total volume). Results of this study indicated that, without adjustment, the model with parameters optimized for taper gave good prediction for both taper and cumulative volume. Mixed results were obtained when various adjustment strategies were used on different fitting techniques. The overall best-ranked procedure for estimating both taper and stem volume was the model optimized for taper and cumulative volume and then adjusted to fit the combined estimator.
ACKNOWLEDGEMENTS
We give special thanks to The General Directorate of Forestry for its contribution to field work. Partial support for data analysis was received from the National Institute of Food and Agriculture, US Department of Agriculture, Mclntire-Stennis project LAB94379.
REFERENCES
- ALEMDAG, I.S. A ratio method for calculating stem volume to variable merchantable limits, and associated taper equations. The Forestry Chronicle 64: 18-28, 1988.
- BROOKS, J.R.; JIANG, L.; ÖZÇELIK, R. Compatible stem volume and taper equations for Brutian pine, Cedar of Lebanon, and Cilicica fir in Turkey. Forest Ecology and Management 256, p. 147-151, 2008.
- BURKHART, H.E. Cubic-foot volume of loblolly pine to any merchantable top limit. Southern Journal of Applied Forestry 1, p. 7-9, 1977.
- BURKHART, H.E.; TOMÉ, M. Modeling forest trees and stands. Springer Netherlands. XIV, 458p, 2012.
- BYRNE, J.C.; REED, D.D. Complex compatible taper and volume estimation systems for red and loblolly pine. Forest science 32, p. 423-443, 1986.
- CAO, Q.V. Calibrating a segmented taper equation with two diameter measurements. Southern Journal of Applied Forestry 33, p. 58-61, 2009.
- CAO, Q.V.; BURKHART, H.E.; MAX, T.A. Evaluation of two methods for cubic-volume prediction of loblolly pine to any merchantable limit. Forest Science 26, p. 71-80, 1980.
- CAO, Q.V.; BURKHART, H.E. Cubic-foot volume of loblolly pine to any height limit. Southern Journal of Applied Forestry 4, p. 166-168, 1980.
- CAO, Q.V.; WANG, J. Calibrating fixed-and mixed-effects taper equations. Forest Ecology and Management 262, p. 671-673, 2011.
- CLARK, A.; SOUTER, R.; SCHLAEGEL, B. Stem profile equations for southern tree species (Research Paper SE-282). USDA Forest Service:113, 1991.
- CLUTTER, J.L. Development of taper functions from variable-top merchantable volume equations. Forest Science , 26, p. 117-120, 1980.
- CZAPLEWSKI, R.L.; MCCLURE, J.P. Conditioning a segmented stem profile model for two diameter measurements. Forest Science , 34, p. 512-522, 1988.
- DEMAERSCHALK, J. Converting volume equations to compatible taper equations. Forest Science , 18, p. 241-245, 1972.
- DIÉGUEZ-ARANDA, U.; CASTEDO-DORADO, F.; ÁLVAREZ-GONZÁLEZ, J.G.; ROJO, A. Compatible taper function for Scots pine plantations in northwestern Spain. Canadian Journal of Forest Research, 36, p. 1190-1205, 2006.
- FANG, Z.; BAILEY, R.L. Compatible volume and taper models with coefficients for tropical species on Hainan Island in Southern China. Forest Science , 45, p. 85-100, 1999.
- GDF. Forest Resources. The General Directorate of Forests, Ankara, 2018.
- GOULDING, C.; MURRAY, J. Polynomial taper equations that are compatible with tree volume equations. NZJ For. Sci, 5, p. 312-325, 1976.
- HONER, T.G. The use of height and squared diameter ratios for the estimation of merchantable cubic foot volume. The Forestry Chronicle , 40:324-331, 1964.
- JIANG, L.; BROOKS, J.R.; WANG, J. Compatible taper and volume equations for yellow-poplar in West Virginia. Forest Ecology and Management , 213, p. 399-409, 2005.
- JORDAN, L.; BERENHAUT, K.; SOUTER, R.; DANIELS, R.F. Parsimonious and completely compatible taper, total, and merchantable volume models. Forest Science , 51, p. 578-584, 2005.
- KOZAK, A. A variable-exponent taper equation. Canadian Journal of Forest Research , 18, p. 1363-1368, 1988.
- KOZAK, A.; SMITH, J. Standards for evaluating taper estimating systems. The Forestry Chronicle , 69, p. 438-444, 1993.
- LENHART, J.D.; HACKETT, T.L.; LAMAN, C.J.; WISWELL, T.J.; BLACKARD, J.A. Tree content and taper functions for loblolly and slash pine trees planted on non-old-fields in east Texas. Southern Journal of Applied Forestry , 11, p. 147-151, 1987.
- LI, R.; WEISKITTEL, A.R. Comparison of model forms for estimating stem taper and volume in the primary conifer species of the north American Acadian. Annals of Forest Science , 67, p. 302-302, 2010.
- MAX, T.A.; BURKHART, H.E. Segmented polynomial regression applied to taper equations. Forest Science , 22, p. 283-289, 1976.
- MUHAIRWE, C.K. 1999. Taper equations for Eucalyptus pilularis and Eucalyptus grandis for the north coast in New South Wales, Australia. Forest Ecology and Management , 113(2):251-269.
- MUNRO, D.D.; DEMAERSCHALK, J.P. Taper-based versus volume-based compatible estimating systems. The Forestry Chronicle , 50, p. 197-199, 1974.
- NEWNHAM, R. Variable-form taper functions for four Alberta tree species. Canadian Journal of Forest Research , 22, p. 210-223, 1992.
- ÖZÇELIK, R.; DIAMANTOPOULOU, M.; BROOKS, J.R. The use of tree crown variables in over-bark diameter and volume prediction models. İForest, 7, p. 132-139, 2014.
- ÖZÇELIK, R.; CRECENTE-CAMPO, F. Stem taper equations for estimating merchantable volume of Lebanon cedar trees in the Taurus mountains, southern Turkey. Forest Science 62, p. 78-91, 2016.
- ÖZÇELIK, R.; CAO, Q.V. Evaluation of fitting and adjustment methods for taper and volume prediction of black pine in Turkey. Forest Science , 63, p. 349-355, 2017.
- POUDEL, K.P.; CAO, Q.V. Evaluation of methods to predict Weibull parameters for characterizing diameter distributions. Forest Science , 59, p. 243-252, 2013.
- REED, D. Simultaneous estimation of tree taper and merchantable volume in loblolly pine. VA J. Science 33, p. 85, 1982.
- REED, D.D.; GREEN, E.J. COmpatible stem taper and volume ratio equations. Forest Science , 30, p. 977-990, 1984.
- SABATIA, C.O.; BURKHART, H.E. On the use of upper stem diameters to localize a segmented taper equation to new trees. Forest Science , 61, p. 411-423, 2015.
- SAKICI, O.E.; MISIR, N.; YAVUZ, H.; MISIR, M. Stem taper functions for Abies nordmanniana subsp bornmulleriana in Turkey. Scandinavian Journal of Forest Research, 23, p. 522-533, 2008.
- SAKICI, O.E.; OZDEMIR, G. Stem taper estimations with artificial neural networks for mixed Oriental beech and Kazdaği fir stands in Karabük region, Turkey. CERNE, 24, P. 439-451, 2018.
- SCHRÖDER, T.; COSTA, E.A.; VALERIO, A.F.; Dos SANTOS LISBOA, G. Taper equations for Pinus elliottii Engelm. in southern Parana, Brazil. Forest Science , 61, p. 311-319, 2014.
- SCHUMACHER, F.X.; HALL, F.D.S. Logarithmic expression of timber-tree volume. J. Agric. Res., 47, p. 719-734, 1933.
- SHARMA, M.; ZHANG, S. Variable-exponent taper equations for jack pine, black spruce, and balsam fir in eastern Canada. Forest Ecology and Management , 198, p. 39-53, 2004.
- TESHOME, T. A ratio method for predicting stem merchantable volume and associate taper equations for Cupressus lusitanica, Ethiopia. Forest Ecology and Management , 204, p. 171-179, 2005.
- VAN DEUSEN, P.C. Simultaneous estimation with a squared error loss function. Canadian Journal of Forest Research , 18, p. 1093-1096, 1988.
- VAN DEUSEN, P.C.; MATNEY, T.G.; SULLIVAN, A.D. A compatible system for predicting the volume and diameter of sweetgum trees to any height. Southern Journal of Applied Forestry , 6, p. 159-163, 1982.
HIGHLIGHTS
-
1
A modified form of Max and Burkhart’s (1976) taper model was used in this study.
-
2
We tested all combinations of five fitting methods and six adjustment strategies.
-
3
Mixed results were obtained when various fitting/adjustment procedures were used.
-
4
The model optimized for taper and cumulative volume and then adjusted to fit the combined estimator was the most appropriate.
Publication Dates
-
Publication in this collection
30 Mar 2020 -
Date of issue
Oct-Dec 2019
History
-
Received
18 Oct 2019 -
Accepted
04 Dec 2019