ABSTRACT
The goal of this study was to use the spatial bootstrap method to model the spatial dependence structure of soybean yield and soil chemical attributes in an agricultural area. The study involved developing confidence intervals in probability plots to determine the probability distributions assumed by the data; determine the empirical distributions of the semivariances and model parameters, allowing to obtain statistics and confidence intervals; and to construct maps for the variables. The quantile-quantile plots indicated that the data follows a normal distribution. The confidence intervals for the semivariances helped to model the spatial dependence structure, and the descriptive statistics of the bootstrap replicates of the model parameters allowed to test the consistency of the estimates. The soil chemical attributes (calcium, potassium, and organic matter) were at levels suitable for soybean cultivation. However, the pH was below the ideal range in most of the study area, and water stress during cultivation decreased the mean yield. Therefore, according to the results, a recommendation to the farmer is to correct the soil pH to increase the yield.
KEYWORDS
confidence intervals; quantile-quantile plot; resampling; spatial dependence
INTRODUCTION
One of the main goals in Geostatistics is to estimate parameters to understand the spatial variability and to predict values (Chipeta et al., 2016Chipeta M, Terlouw D, Phiri K, Diggle P (2016) Inhibitory geoestatistical designs for spatial prediction taking account of uncertain covariance structure. Environmetrics 28:e2425. DOI: https://doi.org/10.1002/env.2425
https://doi.org/10.1002/env.2425...
). Therefore, geostatistics methods are essential in precision agriculture by allowing determining spatial variations in soil attributes and crops (Ramzan & Wani, 2018Ramzan S, Wani MA (2018) Geographic information system and geostatistical techniques to characterize spatial variability of soil micronutrients including toxic metals in an agricultural farm. Communications in Soil Science and Plant Analysis 49(4):463-477. DOI: https://doi.org/10.1080/00103624.2018.1431264
https://doi.org/10.1080/00103624.2018.14...
; Sawant et al., 2018Sawant SS, Nagaraju MSS, Srivastava R, Prasad J, Nasre RA, Mohekar DS (2018) Mapping of spatial variability in soil properties for site-specific nutrient management of Nagpur Mandarin in Central India. Indian Journal of Horticulture 75(2):209-217. DOI: http://dx.doi.org/10.5958/0974-0112.2018.00038.5
http://dx.doi.org/10.5958/0974-0112.2018...
). Given that little geostatistical data are available, there is uncertainty about the obtained values and, consequently, the shape of the semivariogram is debatable (Olea & Pardo-Iguzquiza, 2011Olea RA, Pardo-Igúzquiza E (2011) Generalized bootstrap method for assessment of uncertainty in semivariogram inference. Mathematical Geosciences 43(2):203-228. DOI: https://doi.org/10.1007/s11004-010-9269-6
https://doi.org/10.1007/s11004-010-9269-...
). This topic has been gaining prominence because of the need to obtain realistic results during geostatistical modeling (Sari et al., 2015Sari KN, Pasaribu US, Neswan O, Permadi, AK (2015) Estimation of the parameters of isotropic semivariogram model through bootstrap. Applied Mathematical Sciences 9(103):5123-5137. DOI: http://dx.doi.org/10.12988/ams.2015.54293
http://dx.doi.org/10.12988/ams.2015.5429...
; Dalposso et al., 2018Dalposso GH, Uribe-Opazo MA, Johann JA, Galea M, De Bastiani F (2018) Gaussian spatial linear model of soybean yield using bootstrap methods. Engenharia Agrícola 38(1): 110-116. DOI: http://dx.doi.org/10.1590/1809-4430-eng.agric.v38n1p110-116/2018
http://dx.doi.org/10.1590/1809-4430-eng....
).
An alternative to traditional methods is the spatial bootstrap method (Solow, 1985Solow A (1985) Bootstrapping correlated data. Mathematical Geology 17(7):769-775.), an adaptation of the bootstrap method (Efron, 1979Efron B (1979) Bootstrap methods: Another look at the jackknife. Annals of Statistics 7(1):1-26.) for spatial data. Bootstrap has been used in soil studies to predict soil carbon levels (Luo et al., 2016Luo Z, Wang E, Shao Q, Conyers MK, Liu Dl (2016) Confidence in soil carbon predictions undermined by the uncertainties in observations and model parameterization. Environmental Modelling & Software 80:26-32. DOI: https://doi.org/10.1016/j.envsoft.2016.02.013
https://doi.org/10.1016/j.envsoft.2016.0...
), to obtain sample sizes to control error estimates in measuring soil density (Han et al., 2016Han Y, Zhang J, Mattson KG, Zhang W, Weber T (2016) Sample sizes to control error estimates in determining soil bulk density in California forest soils. Soil Science Society of America Journal 80: 756-764. DOI: http://dx.doi.org/10.2136/sssaj2015.12.0422
http://dx.doi.org/10.2136/sssaj2015.12.0...
), and to model soybean yield as a function of soil physical and chemical attributes (Dalposso et al., 2016Dalposso GH, Uribe-Opazo MA, Johann JA (2016) Soybean yield modeling using bootstrap methods for small samples. Spanish Journal of Agricultural Research 14(3):e0207. DOI: http://dx.doi.org/10.5424/sjar/2016143-8635
http://dx.doi.org/10.5424/sjar/2016143-8...
).
However, few studies to date used the bootstrap method to analyze spatial data. This method was also used to monitor arsenic pollution in Portugal (García-Soidán et al., 2014García-Soidán P, Menezes R, Rubiños Ó (2014) Bootstrap approaches for spatial data. Stochastic Environmental Research & Risk Assessment 28(5):1207-1219.), to obtain robust empirical estimators of variance for spatial autocorrelation (Villoria & Liu, 2018Villoria NB, Liu J (2018) Using spatially explicit data to improve our understanding of land supply responses: An application to the cropland effects of global sustainable irrigation in the Americas. Land Use Policy 75:411-419. DOI: https://doi.org/10.1016/j.landusepol.2018.04.010
https://doi.org/10.1016/j.landusepol.201...
), and to model the spatial dependence of soybean yield using soil chemical attributes as covariates (Dalposso et al., 2018Dalposso GH, Uribe-Opazo MA, Johann JA, Galea M, De Bastiani F (2018) Gaussian spatial linear model of soybean yield using bootstrap methods. Engenharia Agrícola 38(1): 110-116. DOI: http://dx.doi.org/10.1590/1809-4430-eng.agric.v38n1p110-116/2018
http://dx.doi.org/10.1590/1809-4430-eng....
).
The objective of this study is to use spatial bootstrap in the geostatistical modeling of soybean yield and soil chemical attributes to test the assumption of normality using confidence intervals in probability plots, determine empirical distributions of semivariances and model parameters, and construct maps.
MATERIAL AND METHODS
Study area and data
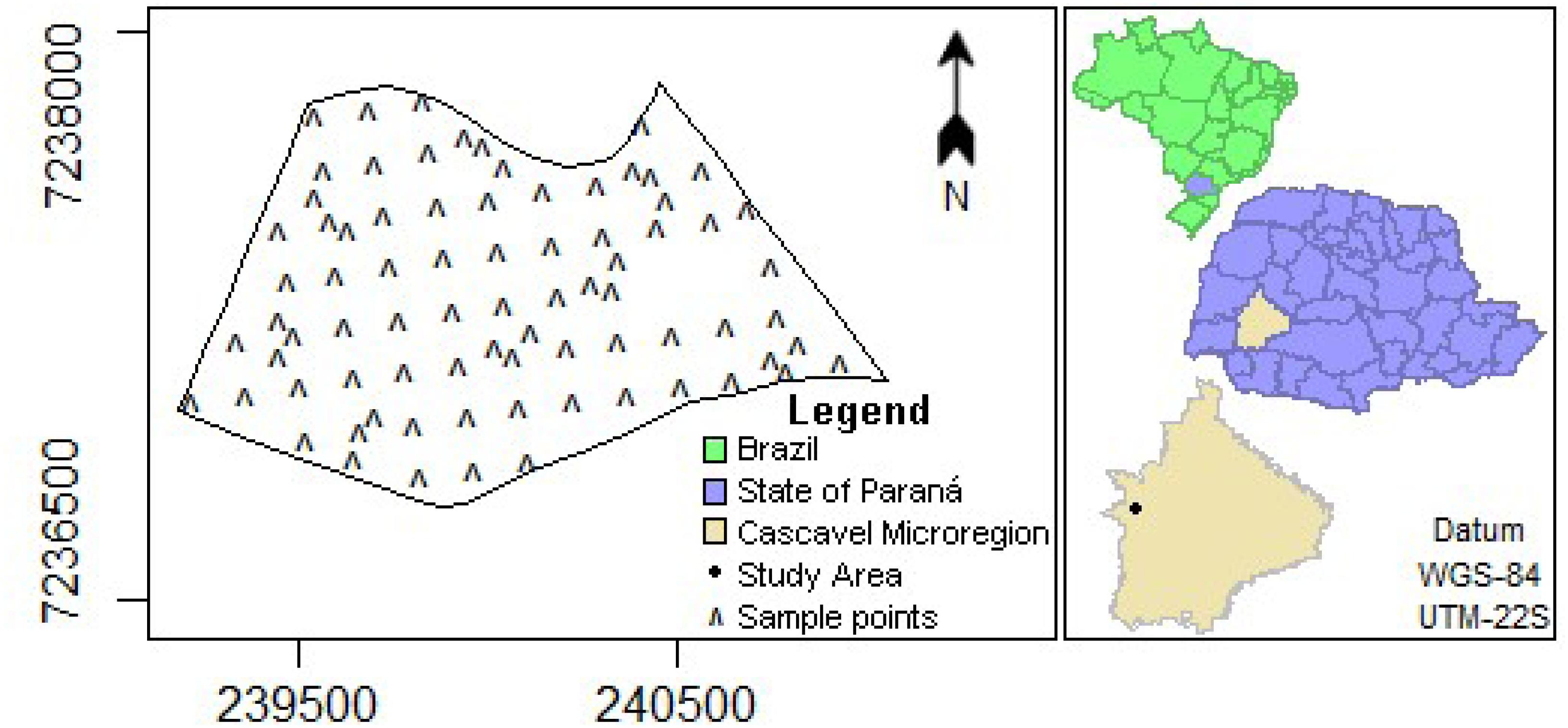
The dataset was collected in 2014/2015 crop year, from a farming area of 127.16 hectares sited in the Cascavel microregion in the western region of Paraná, Brazil (latitude, 24°57′25″S, longitude 53°34′29″W, and mean altitude, 714 m) (Figure 1).
According to the classification of Köppen, the climate of the region is type Cfa (Aparecido et al., 2016Aparecido LE, Rolim GS, Richetti J, Souza PS, Johann JA (2016) Köppen, Thornthwaite and Camargo climate classifications for climatic zoning in the State of Paraná, Brazil. Ciência e Agrotecnologia 40(4):405-417. DOI: http://dx.doi.org/10.1590/1413-7054201640400391
http://dx.doi.org/10.1590/1413-705420164...
) and the soil was classified as Oxisol. Systematic sampling with lattice plus close pairs, composed of 78 sample elements georeferenced with a GEOEXPLORE 3 GPS receiver, was performed. At each sampling point, the soybean yield (SY, t ha–1) of cultivar AMS TIBAGI was measured, and the following soil chemical attributes were determined: calcium (Ca, cmolc dm–3), potassium (K, cmolc dm–3), organic matter (OM, g dm–3), and pH. These variables were chosen because they presented spatial variability in the area and because they help in decision-making about fertilization and liming activities. The variables Ca and K affect soil pH (Malavolta, 1980Malavolta E (1980) Elementos de Nutrição Mineral de Plantas. São Paulo, Ceres, 251p.) and crop yield. The variable OM affects soil temperature and clay content, which controls the release of organic nutrients to the plants.
Geostatistical analysis
To model the spatial dependence structure of a regionalized variable, we considered a second-order stochastic process Z = {Z(s),s ∊ S} in which s = (x,y)T is the vector that represents a certain site in the study area , and is the two-dimensional Euclidean space. It is assumed that the data of this isotropic process Z = (Z(s1), …,Z(sn))T are recorded in known sites (s1, …,sn) and were generated by the model Z = μ1 + ε, where μ represents an unknown parameter to be estimated, 1 is a vector of n × 1, and ε = (ε(s1), …,ε(sn))T represents a vector of random errors n × 1, with an n-variate normal distribution, with E(ε) = 0 and covariance matrix Var(ε) = Σ. In the parametric form (Uribe-Opazo et al., 2012Uribe-Opazo MA, Borssoi JA, Galea M (2012) Influence diagnostics in gaussian spatial linear models. Journal of Applied Statistics 3(39):615-630. DOI: https://doi.org/10.1080/02664763.2011.607802
https://doi.org/10.1080/02664763.2011.60...
; De Bastiani et al., 2015De Bastiani F, Cysneiros AHMA, Uribe-Opazo MA, Galea M (2015) Influence diagnostics in elliptical spatial linear models. Test 24(2):322-340. DOI: http://dx.doi.org/10.1007/s11749-014-0409-z
http://dx.doi.org/10.1007/s11749-014-040...
), the covariance matrix 2 can be defined as , where In is an identity matrix n × n, φ1 ≥ 0 is the nugget effect, φ2 ≥ 0 is the sill, φ3 ≥ 0 is the parameter that defines the range (a) of the model, and R(φ3) = [(rij)] is a definite positive symmetrical matrix n × n. The elements rij, i,j = 1,…, n, represent the association between the points st and Sj, where rij = 1 if i = j and hij = 0, rij = 0 if i ≠ j and φ2=0, and if i ≠ j and ; C(hij) = C(Z(si),Z(sj)) is the theoretical covariance function, and hy = ||si — sj|| is the Euclidean distance between si and Sj.
Omnidirectional experimental semivariograms were constructed using the Matheron estimator to identify the spatial dependence structure of the study variables, and Matern family models with form parameters k = {0.5; 1; 1.5; 2} and k → ∞ were used to model spatial dependence structures. When k = 0.5 represents the exponential model, and k → ∞ represents the Gaussian model (Jin & Kelly, 2017Jin R, Kelly G (2017) A comparison of sampling grids, cut-off distance and type of residuals in parametric variogram estimation. Communications in Statistics - Simulation and Computation 46(3):1781-1795. DOI: https://doi.org/10.1080/03610918.2015.1011785
https://doi.org/10.1080/03610918.2015.10...
). The model parameters were estimated using the maximum likelihood (ML) method. The best fits were chosen by cross-validation (Faraco et al., 2008Faraco MA, Uribe-Opazo MA, Silva EAA, Johann JA, Borssoi JA (2008) Seleção de modelos de variabilidade espacial para elaboração de mapas temáticos de atributos físicos do solo e produtividade da soja. Revista Brasileira de Ciências do Solo 32:463-476. DOI: http://dx.doi.org/10.1590/S0100-06832008000200001
http://dx.doi.org/10.1590/S0100-06832008...
), and the predictions were performed using ordinary kriging.
Spatial bootstrap
The spatial bootstrap method (Solow, 1985Solow A (1985) Bootstrapping correlated data. Mathematical Geology 17(7):769-775.) is presented in Algorithm 1.
Algorithm 1. Spatial bootstrap.
a) Considering the spatial dataset {z(s1),…, z(sn)}, determine the vector of the residuals , where is the estimator of μ, and is the ML estimator of the covariance matrix Σ; b) Considering , use the Cholesky decomposition method to obtain ; c) Using the inverse matrix , determine , which is the vector of uncorrelated residuals; d) Considering the elements of vector , perform n resampling with substitution to form the bootstrap vector ; e) The obtained spatial bootstrap sample is represented by .
Quantification of uncertainties in the geostatistical analysis
The estimators of μ and Σ of each regionalized variable and Algorithm 1 were used to determine B = 1000 bootstrap samples from the dataset (Efron & Tibshirani, 1986Efron B, Tibshirani R (1986) Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statistical Science 1(1):54-75.). For each sample, an experimental semivariogram was constructed and a model was fitted, allowing obtaining the empirical distribution of the semivariances, model parameters and, therefore, determine 68% confidence intervals (Olea & Pardo-Iguzquiza, 2011Olea RA, Pardo-Igúzquiza E (2011) Generalized bootstrap method for assessment of uncertainty in semivariogram inference. Mathematical Geosciences 43(2):203-228. DOI: https://doi.org/10.1007/s11004-010-9269-6
https://doi.org/10.1007/s11004-010-9269-...
) using the percentile bootstrap method (Efron, 2014Efron B (2014) Estimation and accuracy after model selection. Journal of the American Statistical Association 109(507):991-1007. DOI: doi:10.1080/01621459.2013.823775
https://doi.org/10.1080/01621459.2013.82...
). This confidence level was chosen to eliminate replicates obtained from poorly fitted models, which happens because some bootstrap samples have atypical spatial structures and the fits are automatic. To assess the normality assumption, the uncorrelated residuals and i = 1,…,n, were ordered, and the graphical position points p — valuei = (i — 0.5)/n and i = 1,…,n were calculated. Considering Qx(p) as the quantile of order p — value (0 <p < 1) of the observations, , i = 1, …,n.. After determining the experimental quantiles, the theoretical quantiles Qt(p — valued = F–1(p – valuei), t = 1, …,n and i = 1,…,n were calculated, where F–1 represents the inverse cumulative distribution function of the standardized normal distribution. The ordered pairs (Qt (p – valued, Qx(p – value) were arranged in a Cartesian plane, and the residuals were normally distributed if the points formed a line. Since sample data are usually not perfectly consistent with a normal distribution, ordered pairs tend to deviate from the reference line. To visualize this variation, a parametric bootstrap method (Algorithm 2) can be used to establish a confidence interval in the QQ plot (Zieffler et al., 2011Zieffler AS, Harring JR, Long JD (2011) Comparing groups: Randomization and bootstrap methods using R. Hoboken, John Wiley & Sons, 320p.).
Algorithm 2. A 95% confidence interval for the QQ plot using parametric bootstrap.
a) Construct a dataset with n elements (sample size) obtained from resampling with the substitution of a standardized normal distribution and organize them in ascending order ; b) Repeat the previous process B = 1000 times, forming the sets ; c) Organize the elements of the vector for i = 1,…,n in ascending order, and determine the lower limits (LLi) and higher limits (HLi) using the percentile method (Efron, 2014Efron B (2014) Estimation and accuracy after model selection. Journal of the American Statistical Association 109(507):991-1007. DOI: doi:10.1080/01621459.2013.823775
https://doi.org/10.1080/01621459.2013.82...
); and d) Construct straight lines by connecting the points (Qt (p – valuei),LLi) and (Qt(p – valuei), HLi).
Computational resources
The analyses were developed using R software. Geostatistical modeling was performed using the geoR package (Ribeiro Junior & Diggle, 2001Ribeiro Junior PJ, Diggle, PJ (2001) geoR: A package for geostatistical analysis. R-News 1(2): 15-18.). The spatial bootstrap algorithm and the QQ plots routines were developed by the authors.
RESULTS AND DISCUSSION
The cross-validation method indicated that the Gaussian model (Minf) with a range of approximately 296 m is the best fit for the spatial dependence structure of soybean yield (Table 1). This model indicated that the mean soybean yield in the area was 2.37 t ha–1. This value is considered low because it was lower than the state mean (3.29 t ha–1) and national mean (3.00 t ha–1) in the same crop year (Conab, 2017Conab - Companhia Nacional de Abastecimento (2017) Soja - Brasil: Série histórica de produtividade. Available: http://www.conab.gov.br. Accessed Dec 22, 2017.
http://www.conab.gov.br...
).
The spatial dependence structures of Ca and pH were fitted according to an exponential model (M0.5) and presented the lowest values when compared with the other attributes (Table 1). The highest values were obtained for K and OM using the structures fitted with the Matern model with form parameter k = 2.0 (M2.0) (Table 1).
It should be noted that some parameters presented a high standard deviation (Table 1), demonstrating instability. Therefore, it is necessary to investigate data distribution, the fitted models, and the empirical distribution of their respective parameters.
The analysis of the QQ plots (Figure 2) indicates that the points are inside the confidence intervals, evidencing that the data follow a normal distribution.
Quantile-quantile (q-q) plots and 95% confidence intervals for the variables: (a) soybean yield (SY, t ha–1), (b) calcium (Ca, cmolc dm–3), (c) potassium (K, cmolc dm–3), (d) organic matter (OM, g dm–3), and (e) soil pH. In each plot, the straight line that passes through the ordered pairs formed with quantiles of order 0.25 and 0.75 is highlighted.
Given that the actual values of semivariances are unknown, 68% bootstrap confidence intervals of the experimental semivariances (Figure 3) were used for a more detailed investigation of the fit of the theoretical models. The analysis of the semivariograms of SY, Ca, and OM (Figures 3a, b, and d, respectively), indicates that, although there were variations in accuracy, evidenced by the different amplitudes of the confidence intervals, the theoretical models are correctly fitted, with an increase in the initial distances, and the intervals are concentrated in the bootstrap confidence intervals.
The 68% boostrap confidence intervals for the experimental semivariances (): (a) soybean yield (SY, t ha–1), (b) calcium (Ca, cmolc dm–3), (c) potassium (K, cmolc dm–3), (d) organic matter (OM, g dm–3), and (e) soil pH. The fitted models are shown in red.
It is important to note that the bootstrap confidence intervals for K and pH (Figures 3c and e, respectively) seemed to be constant. In this respect, the uncertainty associated with the parameters of the spatial models of these variables should be quantified because, in this situation, several models can be fitted, including models with an almost pure nugget effect and models with a range close to the minimum distance between points.
The estimated values of the parameters of the model for SY (Table 2) indicate that the standard deviations of the nugget effect and sill were similar to the respective values obtained by the asymptotic theory (Table 1). The parameter that defines the range remained high, although its standard deviation decreased from 336.70 (value obtained by asymptotic theory) to 101.6 (value obtained by bootstrap). This result can be explained by the characteristic of the empirical distribution of bootstrap replicates of the range parameter, which presented a positive asymmetry of 2.08, indicating the low frequency of high values.
Descriptive statistics of the geostatistical model for calcium (Table 2) indicated that 50% of the bootstrap replicates had no nugget effect. However, the value obtained from the original sample (0.35) is more coherent because the calcium levels for distances shorter than the minimum distance between samples (49.07 m) are unknown. The descriptive statistics of the estimated sill () of the geostatistical model of calcium (Table 2) indicated that the standard deviation of the bootstrap replicates (0.60) was lower than the asymptotic standard deviation (1.69) (Table 1). This result demonstrates that the asymptotic standard deviation may be overestimated, i.e., the dispersion of the sill is less than 1.69.
The analysis of the statistics of the bootstrap replicates of the range parameter of the geostatistical model of calcium (Table 2) indicates that the empirical distribution formed by the bootstrap replicates has a positive asymmetry. This result is evidenced by the lower frequency of high values. However, the value obtained from the original sample (62.91) is not considered atypical because it is close to the mean and median and is within the confidence interval.
Therefore, the nugget effect of the geostatistical model of potassium (Table 2) is a non-zero value because, in addition to the value obtained from the original sample (0.02) being non-zero, 75% of the bootstrap replicates of this parameter are also non-zero values.
The range parameter of the geostatistical model of potassium is considered high, because it was higher than the third quartile of the distribution of the bootstrap replicates and was located outside the confidence interval.
The results of descriptive statistics of the estimated values of OM (Table 2) did not invalidate the values obtained from the original sample, indicating that the model was well fitted. In relation to descriptive statistics of the pH, it should be noted that the parameters obtained from the original sample are consistent, demonstrating the nullity of the nugget effect in 75% of the bootstrap replicates, as well the positive asymmetry of the empirical distribution of the range parameter (Table 2).
Maps of SY and soil attributes (Ca, K, OM, and pH) were constructed after selecting the geostatistical model and estimating its parameters (Figure 4). The SY map shows that the area is heterogeneous (Figure 4a). The southwestern and northern regions of the area stand out because they had the highest yield whereas the central region, which extends to the southeast and part of the northwest region of the area, had the lowest yield. The difference in the mean yield between the class with the lowest yield (2.20 − 2.28 t ha–1) and highest yield (2.53 − 2.61 t ha–1) in an agricultural area of 127.16 ha was 14.7%, demonstrating the importance of monitoring the whole area by the farmer using precision agriculture to increase yield.
Maps: (a) soybean yield (SY, t ha–1); (b) calcium (Ca, cmolc dm–3); (c) potassium (K, cmolc dm–3); (d) organic matter (OM, g dm–3); and (e) soil pH.
The map of calcium (Figure 4b) shows that most of the monitored area presents values higher than 3.1 cmolc dm–3, which are considered high (Junio et al., 2013Junio GRZ, Sampaio RA, Nascimento AL, Santos GB, Santos LDT, Fernandes LA (2013) Produtividade de milho adubado com composto de lodo de esgoto e fosfato natural de Gafsa. Revista Brasileira de Engenharia Agrícola e Ambiental 17(7):706-712.). Therefore, it is of note that the soil does not present insufficient levels of calcium, which could be harmful because yield could be lower (White & Broadley, 2003White PJ, Broadley MR (2003) Calcium in plants. Annals of Botany 92(4):487-511. DOI: https://doi.org/10.1093/aob/mcg164
https://doi.org/10.1093/aob/mcg164...
). In this respect, there was no spatial relationship between the yield map and the calcium map.
Although the map of potassium (Figure 4c) shows that the lowest values are concentrated in the western region, there is no evidence of a decrease in SY because the potassium levels were classified as high and very high (Borkert et al., 1997Borkert CM, Farias JRB, Sfredo GJ, Tutida F, Spoladori CL (1997) Resposta da soja à adubação e disponibilidade de potássio em Latossolo Roxo álico. Pesquisa Agropecuária Brasileira 32(11):1119-1129.), which guarantees high yields. The OM values (Figure 4d) can be classified as high because they are higher than the means (25 – 40 g dm–3) usually found in soils in southern Brazil (Spera et al., 2008Spera ST, Denardin JE, Escosteguy PAV, Santos HP, Figueroa EA (2008) Dispersão de argila em microagregados de solo incubado com calcário. Revista Brasileira de Ciência do Solo 32:2613-2620.), evidencing that the study area is suitable for grain production.
The pH in most of the monitored area (Figure 4e) was between 4 and 5, indicating the presence of exchangeable aluminum, which can inhibit root growth and decrease the availability of other nutrients (Sobral et al., 2015Sobral LF, Barretto MCV, Silva AJ, Anjos JL (2015) Guia prático para interpretação de resultados de análises de solo. Aracajú, Embrapa Tabuleiros Costeiros, 15p. (Documentos 206). Available: http://www.infoteca.cnptia.embrapa.br/infoteca/handle/doc/1042994. Accessed: Jan 08, 2018.
http://www.infoteca.cnptia.embrapa.br/in...
). The higher availability of nutrients to soybean crop, which limits the toxic effect of some nutrients, occurs at a soil pH of 5.4 − 5.9 (Sfredo, 2008Sfredo GJ (2008) Calagem e adubação da soja. Londrina, Embrapa Soja, 12p. (Circular Técnica 61). Available: https://www.infoteca.cnptia.embrapa.br/infoteca/handle/doc/470943. Accessed: Jan 17, 2018.
https://www.infoteca.cnptia.embrapa.br/i...
). Therefore, the pH of most of the studied area is lower than the above recommendation, which may be related to the low mean yield (2.37 t ha–1) in this crop year (Figure 4e).
In the pH map (Figure 4e), circular areas centered on sample points (bull eyes effect) occur when the model has a spatial dependence radius smaller than the distance between sample points (Menezes et al., 2016Menezes MD, Silva SHG, Mello CR, Owens PR, Curi, N (2016) Spatial prediction of soil properties in two contrasting physiographic regions in Brazil. Scientia Agricola 73(3):274-285. DOI: http://dx.doi.org/10.1590/0103-9016-2015-0071
http://dx.doi.org/10.1590/0103-9016-2015...
). The analysis of the distances between the pairs of sample points in the study area (Figure 1) demonstrated that, of the 3003 existing pairs, only 168 presented a distance smaller than the radius of spatial dependence (174.8 m). This characteristic justifies the weak spatial dependence, and consequently, the fact that most of the monitored area is classified as having pH values close to the mean value of 4.8.
Several factors may have contributed to the pH being lower than the ideal range, including soil chemical attributes and the amount of rainfall in the region. It is important to highlight that the sown AMS TIBAGI soybean cultivar has a super-early cycle within the maturation group 5.0. Therefore, the climatic conditions strongly affect yield. This cultivar requires regular rainfall, especially during the period of flowering, pod formation, and grain filling. The crop was sown on October 14, 2014, and the data of the meteorological station of SIMEPAR in Cascavel indicated that there was a period of 14 days of low rainfall (total of 14 mm from October 17 to November 3, 2014). In addition, pod formation, grain filling, and water stress (rainfall of only 21.4 mm from November 23 to December 18, 2015) occurred during the flowering period. These periods of water stress strongly undermined yield.
CONCLUSIONS
The spatial bootstrap method allows quantifying the uncertainties associated with the spatial dependence model of SY and soil chemical attributes in the monitored agricultural area. The elaboration of the confidence intervals in the quantile-quantile plot allowed testing the normality assumption of the data.
Therefore, the use of confidence intervals for semivariances helps model the spatial dependence structure of the data. With respect to the uncertainty associated with spatial model parameters, it is important to note that the descriptive statistics of the bootstrap replicates of the nugget effect are fundamental to assess the consistency of the estimated values, because there is no information on distances smaller than the minimum distance.
The maps enabled determining the spatial variability of SY and soil chemical attributes in non-sampled areas, which is fundamental for activities related to precision agriculture, including the local application of neutralizing agents.
The chemical attributes (Ca, K, and MO) were at levels suitable for soybean cultivation. However, the pH was below the ideal range (5.4 − 5.9) in most of the study area, which may have been caused by other chemical attributes and water stress. These factors contributed to the low mean yield (2.372 t ha–1) in this crop year, and pH correction is recommended to increase crop yield in the next crop year.
ACKNOWLEDGMENTS
The authors are grateful for the partial financial support from UTFPR, UNIOESTE/PGEAGRI, Support for Scientific and Technological Development of Paraná - Brazil (Araucaria Foundation), Coordination for the Improvement of Higher Level Personnel - Brazil (CAPES) - Finance Code 001, National Technological and Scientific Development (CNPq) and FONDECYT Chile (Project No. 1150325).
REFERENCES
- Aparecido LE, Rolim GS, Richetti J, Souza PS, Johann JA (2016) Köppen, Thornthwaite and Camargo climate classifications for climatic zoning in the State of Paraná, Brazil. Ciência e Agrotecnologia 40(4):405-417. DOI: http://dx.doi.org/10.1590/1413-7054201640400391
» http://dx.doi.org/10.1590/1413-7054201640400391 - Borkert CM, Farias JRB, Sfredo GJ, Tutida F, Spoladori CL (1997) Resposta da soja à adubação e disponibilidade de potássio em Latossolo Roxo álico. Pesquisa Agropecuária Brasileira 32(11):1119-1129.
- Chipeta M, Terlouw D, Phiri K, Diggle P (2016) Inhibitory geoestatistical designs for spatial prediction taking account of uncertain covariance structure. Environmetrics 28:e2425. DOI: https://doi.org/10.1002/env.2425
» https://doi.org/10.1002/env.2425 - Conab - Companhia Nacional de Abastecimento (2017) Soja - Brasil: Série histórica de produtividade. Available: http://www.conab.gov.br Accessed Dec 22, 2017.
» http://www.conab.gov.br - Dalposso GH, Uribe-Opazo MA, Johann JA (2016) Soybean yield modeling using bootstrap methods for small samples. Spanish Journal of Agricultural Research 14(3):e0207. DOI: http://dx.doi.org/10.5424/sjar/2016143-8635
» http://dx.doi.org/10.5424/sjar/2016143-8635 - Dalposso GH, Uribe-Opazo MA, Johann JA, Galea M, De Bastiani F (2018) Gaussian spatial linear model of soybean yield using bootstrap methods. Engenharia Agrícola 38(1): 110-116. DOI: http://dx.doi.org/10.1590/1809-4430-eng.agric.v38n1p110-116/2018
» http://dx.doi.org/10.1590/1809-4430-eng.agric.v38n1p110-116/2018 - De Bastiani F, Cysneiros AHMA, Uribe-Opazo MA, Galea M (2015) Influence diagnostics in elliptical spatial linear models. Test 24(2):322-340. DOI: http://dx.doi.org/10.1007/s11749-014-0409-z
» http://dx.doi.org/10.1007/s11749-014-0409-z - Efron B (1979) Bootstrap methods: Another look at the jackknife. Annals of Statistics 7(1):1-26.
- Efron B (2014) Estimation and accuracy after model selection. Journal of the American Statistical Association 109(507):991-1007. DOI: doi:10.1080/01621459.2013.823775
» https://doi.org/10.1080/01621459.2013.823775 - Efron B, Tibshirani R (1986) Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statistical Science 1(1):54-75.
- Faraco MA, Uribe-Opazo MA, Silva EAA, Johann JA, Borssoi JA (2008) Seleção de modelos de variabilidade espacial para elaboração de mapas temáticos de atributos físicos do solo e produtividade da soja. Revista Brasileira de Ciências do Solo 32:463-476. DOI: http://dx.doi.org/10.1590/S0100-06832008000200001
» http://dx.doi.org/10.1590/S0100-06832008000200001 - García-Soidán P, Menezes R, Rubiños Ó (2014) Bootstrap approaches for spatial data. Stochastic Environmental Research & Risk Assessment 28(5):1207-1219.
- Han Y, Zhang J, Mattson KG, Zhang W, Weber T (2016) Sample sizes to control error estimates in determining soil bulk density in California forest soils. Soil Science Society of America Journal 80: 756-764. DOI: http://dx.doi.org/10.2136/sssaj2015.12.0422
» http://dx.doi.org/10.2136/sssaj2015.12.0422 - Jin R, Kelly G (2017) A comparison of sampling grids, cut-off distance and type of residuals in parametric variogram estimation. Communications in Statistics - Simulation and Computation 46(3):1781-1795. DOI: https://doi.org/10.1080/03610918.2015.1011785
» https://doi.org/10.1080/03610918.2015.1011785 - Junio GRZ, Sampaio RA, Nascimento AL, Santos GB, Santos LDT, Fernandes LA (2013) Produtividade de milho adubado com composto de lodo de esgoto e fosfato natural de Gafsa. Revista Brasileira de Engenharia Agrícola e Ambiental 17(7):706-712.
- Luo Z, Wang E, Shao Q, Conyers MK, Liu Dl (2016) Confidence in soil carbon predictions undermined by the uncertainties in observations and model parameterization. Environmental Modelling & Software 80:26-32. DOI: https://doi.org/10.1016/j.envsoft.2016.02.013
» https://doi.org/10.1016/j.envsoft.2016.02.013 - Malavolta E (1980) Elementos de Nutrição Mineral de Plantas. São Paulo, Ceres, 251p.
- Menezes MD, Silva SHG, Mello CR, Owens PR, Curi, N (2016) Spatial prediction of soil properties in two contrasting physiographic regions in Brazil. Scientia Agricola 73(3):274-285. DOI: http://dx.doi.org/10.1590/0103-9016-2015-0071
» http://dx.doi.org/10.1590/0103-9016-2015-0071 - Olea RA, Pardo-Igúzquiza E (2011) Generalized bootstrap method for assessment of uncertainty in semivariogram inference. Mathematical Geosciences 43(2):203-228. DOI: https://doi.org/10.1007/s11004-010-9269-6
» https://doi.org/10.1007/s11004-010-9269-6 - Ramzan S, Wani MA (2018) Geographic information system and geostatistical techniques to characterize spatial variability of soil micronutrients including toxic metals in an agricultural farm. Communications in Soil Science and Plant Analysis 49(4):463-477. DOI: https://doi.org/10.1080/00103624.2018.1431264
» https://doi.org/10.1080/00103624.2018.1431264 - Ribeiro Junior PJ, Diggle, PJ (2001) geoR: A package for geostatistical analysis. R-News 1(2): 15-18.
- Sari KN, Pasaribu US, Neswan O, Permadi, AK (2015) Estimation of the parameters of isotropic semivariogram model through bootstrap. Applied Mathematical Sciences 9(103):5123-5137. DOI: http://dx.doi.org/10.12988/ams.2015.54293
» http://dx.doi.org/10.12988/ams.2015.54293 - Sawant SS, Nagaraju MSS, Srivastava R, Prasad J, Nasre RA, Mohekar DS (2018) Mapping of spatial variability in soil properties for site-specific nutrient management of Nagpur Mandarin in Central India. Indian Journal of Horticulture 75(2):209-217. DOI: http://dx.doi.org/10.5958/0974-0112.2018.00038.5
» http://dx.doi.org/10.5958/0974-0112.2018.00038.5 - Sfredo GJ (2008) Calagem e adubação da soja. Londrina, Embrapa Soja, 12p. (Circular Técnica 61). Available: https://www.infoteca.cnptia.embrapa.br/infoteca/handle/doc/470943 Accessed: Jan 17, 2018.
» https://www.infoteca.cnptia.embrapa.br/infoteca/handle/doc/470943 - Sobral LF, Barretto MCV, Silva AJ, Anjos JL (2015) Guia prático para interpretação de resultados de análises de solo. Aracajú, Embrapa Tabuleiros Costeiros, 15p. (Documentos 206). Available: http://www.infoteca.cnptia.embrapa.br/infoteca/handle/doc/1042994 Accessed: Jan 08, 2018.
» http://www.infoteca.cnptia.embrapa.br/infoteca/handle/doc/1042994 - Solow A (1985) Bootstrapping correlated data. Mathematical Geology 17(7):769-775.
- Spera ST, Denardin JE, Escosteguy PAV, Santos HP, Figueroa EA (2008) Dispersão de argila em microagregados de solo incubado com calcário. Revista Brasileira de Ciência do Solo 32:2613-2620.
- Uribe-Opazo MA, Borssoi JA, Galea M (2012) Influence diagnostics in gaussian spatial linear models. Journal of Applied Statistics 3(39):615-630. DOI: https://doi.org/10.1080/02664763.2011.607802
» https://doi.org/10.1080/02664763.2011.607802 - Villoria NB, Liu J (2018) Using spatially explicit data to improve our understanding of land supply responses: An application to the cropland effects of global sustainable irrigation in the Americas. Land Use Policy 75:411-419. DOI: https://doi.org/10.1016/j.landusepol.2018.04.010
» https://doi.org/10.1016/j.landusepol.2018.04.010 - White PJ, Broadley MR (2003) Calcium in plants. Annals of Botany 92(4):487-511. DOI: https://doi.org/10.1093/aob/mcg164
» https://doi.org/10.1093/aob/mcg164 - Zieffler AS, Harring JR, Long JD (2011) Comparing groups: Randomization and bootstrap methods using R. Hoboken, John Wiley & Sons, 320p.
Publication Dates
-
Publication in this collection
19 June 2019 -
Date of issue
May-Jun 2019
History
-
Received
10 Sept 2018 -
Accepted
08 Mar 2019