Use of signal thresholds to determine significant changes in microarray data analyses

HUMAN AND MEDICAL GENETICS

RESEARCH ARTICLE

Use of signal thresholds to determine significant changes in microarray data analyses

Xinmin Li^I; Jaejung Kim^I; Jian Zhou^I; Weikuan Gu^III; Richard Quigg^{I, II}

^IThe University of Chicago, Functional Genomics Facility, Chicago, IL, USA

^IIThe University of Chicago, Division of Biological Sciences, Section of Nephrology, Chicago, IL, USA

^IIIUniversity of Tennessee Health Science Center, Department of Orthopedic Surgery, Center of Genomics and Bioinformatics & Center of Diseases of Connective Tissues, Memphis, TN, USA

^{Correspondence}

ABSTRACT

The use of a constant fold-change to determine significant changes in gene expression has been widely accepted for its intuition and ease of use in microarray data analysis, but this concept has been increasingly criticized because it does not reflect signal intensity and can result in a substantial number of false positives and false negatives. To resolve this dilemma, we have analyzed 65 replicate Affymetrix chip-chip comparisons and determined a series of user adjustable signal-dependent thresholds which do not require replicates and offer a 95% confidence interval. Quantitative RT-PCR shows that such thresholds significantly improve the power to discriminate biological changes in mRNA from noise and reduce false calls compared to the traditional two-fold threshold. The user-friendly nature of this approach means that it can be easily applied by any user of microarray analysis, even those without any specialized knowledge of computational techniques or statistics. Noise is a function of signal intensity not only for Affymetrix data but also for cDNA array data, analysis of which may also be benefited by our methodology.

Key words: microarray, signal threshold, affymetrix, data analysis.

Introduction

Affymetrix oligonucleotide arrays (Lockhart et al., 1996) are widely used for measuring global changes in gene expression (Landis et al., 2004; Zamurovic et al., 2004; Baechler et al., 2004; Hunter et al., 2002). While the power of this technology has been recognized, how thresholds for significant changes should be determined remains an open question.

To date, fold-change thresholds have been the most commonly used method for filtering false positives and declaring significant changes (Bassett et al., 1999; Der et al., 1998; Fambrough et al., 1999; Wang et al., 1999). Because this is an arbitrary decision and has no statistical basis, different thresholds have been used in the literature, varying from 2- to 6-fold (Amundson et al., 1999; Coller et al., 2000; Schena et al., 1996; Tamayo et al., 1999). Although this approach is intuitively appealing, it does not take into account absolute signal intensities and ignores the fact that the confidence levels of fold-change appear to be signal-dependent. Such constant thresholds tend to produce false positives when signal intensities are low and false negatives when signal intensities are high.

Several statistical treatments of microarray data analysis have been explored to overcome these weaknesses, (Chen et al., 1997; Kerr et al., 2000; Newton et al., 2001; Tusher et al., 2001; Li and Wong, 2001, Long et al., 2001, Goryachev et al., 2001; Strand et al., 2002). Locally weighted linear regression (Lowess) (Cleveland and Devlin 1988) has been proposed as a normalization method for microarray data analysis (Yang et al., 2002; Dudoit et al., 2002) to remove intensity-dependent dye-specific effects. Hughes et al (2000) proposed a mathematical model to estimate intensity-dependent differential expression, which can identify biologically meaningful differential regulation at levels lower than twofold in a compendium of 300 different yeast mutants and chemical treatments. Use of a smoothed estimate of the SD as a function of the fluorescence intensity has also been discussed (Baggerly et al., 2001). These treatments are responsive to signal intensity and provide a better discrimination of true change from noise but suffer from a common drawback in that they require that the researcher who uses them has both statistical and computational training. To address this problem, a relatively simpler approach has been proposed to identify differentially expressed genes using the intensity-dependent calculation of a standard Z-score (Yang et al., 2003).

Because traditional fold-change thresholds (traditional thresholds) are popular but have limitations we theorized that signal-dependent fold-change thresholds (signal thresholds) could be used because signal thresholds take into account the fact that fold-change variability is a function of signal intensity. In this paper we report the use of multiple replicate comparisons to establish and validate user-adjustable signal thresholds which have improved power to discriminate true change from noise without the drawbacks of traditional thresholds.

Materials and Methods

Sources of data

All data were generated by the Functional Genomics Facility (FGF), University of Chicago, Illinois, USA. Sixty-five duplicate chip-chip comparison data sets were derived from 14 experiments, performed over a period of 11 months, using Human Genome U133A and U95A, Rat Genome U34A and Murine Genome U74Av2 arrays. Thirty-three comparisons were biological replicates in which RNA was extracted from different samples that were genetically identical and exposed to the same manipulation; 16 were technical replicates in which the same RNA source was used for replicate experiments; and 16 were cell line replicates in which RNA was extracted from different batches of daughter cells.

RNA quality assurance

All RNA samples submitted to the FGF for hybridization had a 260nm/280 nm optical density ratio (OD_260/280) > 1.8 and a total RNA concentration > 1 mg/mL and the quality of the RNA was validated using an Agilent 2100 Bioanalyzer (Agilent Technologies, Palo Alto, CA, USA).

Target preparation

The target preparation protocol followed the Affymetrix GeneChip® Expression Analysis Manual (Affymetrix, Inc. Santa Clara, CA) with minor modifications. Briefly, 10 mg of total RNA was used to synthesize double-stranded cDNA using the Superscript Choice System (Life Technologies). First strand cDNA synthesis was primed with a T7-(dT₂₄) oligonucleotide. From 3 mg of log-phase Gel-purified cDNA, biotin-labeled antisense cRNA was synthesized using the BioArray High Yield RNA Transcript Labeling Kit (Enzo Diagnostics, Farmingdale, NY, USA). After precipitation with 4 M Lithium Chloride, 20 mg of cRNA was fragmented in fragmentation buffer (40 mM Tris-Acetate, pH 8.1, 100 mM KOAc, 30 mM MgOAc) for 35 minutes at 94 °C and then hybridized to Affymetrix Arrays for 16 hours at 45 °C and 60 rpm in an Affymetrix Hybridization Oven 640. The arrays were washed and stained with streptavidin phycoerythrin in Affymetrix Fluidics Station 400 using the Affymetrix GeneChip protocol and then scanned using the Affymetrix Agilent GeneArray Scanner.

Data analysis and definitions

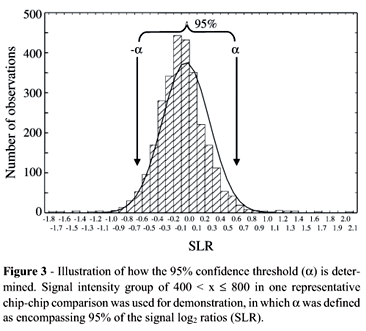
Hybridization signals were analyzed using Affymetrix Microarray Suite version 5.0 (MAS 5.0) with the default analytic parameters (Alpha 1: 0.04; Alpha 2: 0.06; Tau: 0.015; global scaling target signal: 500). The qualitative output of MAS 5.0 includes detection calls and change calls, the confidence of each call being reflected by a p value which is a new feature of MAS 5. Quantitative output includes signal intensities from absolute analyses and signal log₂ ratios (SLRs) from comparison analyses. Data analysis in this study involved three stages: visual examination of the scatter plot using MAS 5.0 software, two-step data filtration (see results section for details) and empirically determining signal thresholds. For each replicate comparison (after data filtration), genes were divided into six groups based on the average signal intensity of two replicates (see results for grouping criteria) and then a 95% confidence threshold (a) was determined based on all SLRs within each group, 95% of SLRs of a given signal intensity group being encompassed within ½a½. The signal threshold was the average value of a derived from 65 replicate comparisons. This study established six signal thresholds, one for each signal intensity group. There were six a values for each replicate comparison, i.e. one for each signal intensity group. The interarray variability (b) is a measure of signal intensity variation between the two replicate samples being compared, where b = S[½A_i-B_i½/(A_i+B_i)]/n where A_i is the signal intensity of the i^th gene in replicate A, B_i is the signal intensity of the i^th gene in replicate B and n is the total number of genes on the GeneChip® array. Experimental variation between replicate experiments was defined as the interarray variability (b), which was used to predict the weighted average threshold (d), the weighted average value of all six a values from a replicate comparison. This study used 65 replicate comparisons and therefore 65 d were derived. As an alternative approach for data visualization (Dudoit et al., 2002), a standard M vs. A plot was derived, in which M_g = log₂(Y_g/X_g) and A_g = log₂ (X_gY_g)^1/2 for expressions X_g and Y_g from the two arrays being compared for all genes g = 1, 2, 3, ..., G.

Results

Visualization of signal intensity scatter plot

We started the data analysis by plotting two replicate experiments on a log scale, it being known that all data points in the plot should theoretically be located on the line of identity (y = x) and that deviation from this line represents noise. Visually examination of these plots provided important information for developing the subsequent data analysis strategy. Firstly, the scatter plot clearly showed (Figure 1A) that the degree of signal variation was a function of the signal intensity, with the variation increasing as the signal intensities decreased. This fundamental relationship was also seen in 3-D plots where the third dimension was the SLR (Figure 1B) and also in MvA plots (Figure 1C). These observations illustrate the practical difficulty in using a constant fold-change threshold for all genes under study and suggests that thresholds for significant change should vary in accordance with the signal intensity, the premise which formed the basis for the current study.

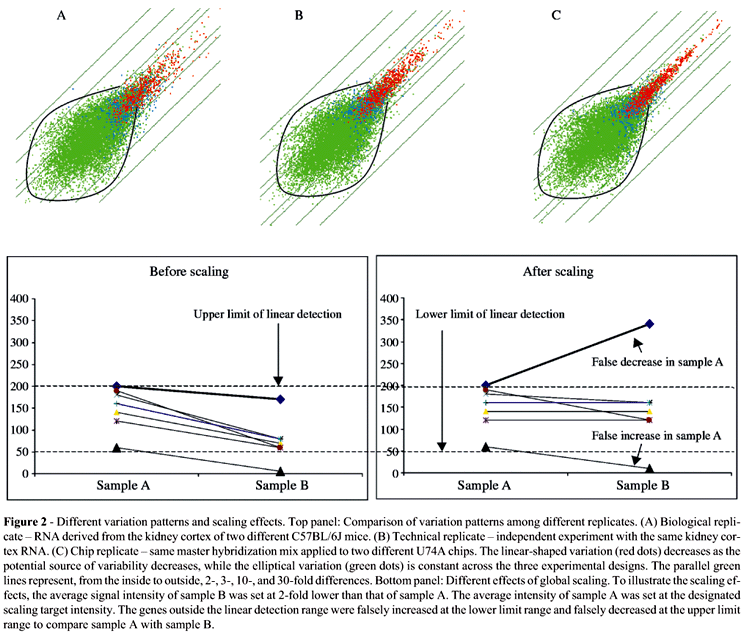
Secondly, genes with low signal intensities and absent calls (green dots in the plot) had an elliptical variation pattern which did not obey the linear functional relationship described above. Figure 2 shows plots of two replicate experiments using three potential sources of variation: the RNA derived from different mice (A); using the same RNA sample but with separate enzymatic reactions (B); and using the same hybridization master mix (C). It is clear that the degree of variation increases as the number of potential sources of variation increase (A > B > C) for genes with present calls but the variation seems constant for genes with absent calls (elliptical variation, i.e. elliptical noise). About 50% of genes have absent calls and account for most of the false positives. This observation highlights the need to filter out this constant noise before performing data analysis.

Thirdly, scatter plots provides a convenient way to evaluate the non-random noise contributed by scaling itself. The relationship between the level of gene expression and signal intensity reported by a scanner is linear only within a certain range of intensities, being limited by detection sensitivity below and subject to saturation above that range. When the overall signal intensity in sample A is significantly higher than that in sample B (i.e. the scaling factor is higher in sample B than in sample A), scaling itself could introduce false increases in the low non-linear range and false decreases in the high non-linear range in a comparison of A vs. B (Figure 2). We plotted all chip-chip comparisons and scatter plots with a characteristic sigmoidal shape (about 2% of the plots examined) were eliminated from the analysis.

Data filtration

After visualization of scatter plots, it was clear that raw data needed to be filtered to avoid excessive noise at the low signal intensity range. We used a two-step filtration strategy to balance the removal of noise with the retention of the true biological information. The first filtration step was to filter genes with a signal intensity in both replicate experiments of < 100 intensity units, a rather conservative but effective strategy which resulted in the vast majority of elliptical noise being eliminated at this cut-off intensity (Figure 1A). The second filtration step was to remove the genes with a signal intensity < 200 and also having an absent call in both replicate experiments. About 50% of genes were eliminated by this two-step filtration strategy. The remaining genes were used to determine signal thresholds.

Signal thresholds with 95% confidence

After data filtration, average signal intensities were calculated for each gene in each pair of comparisons and sorted in ascending order. The genes were then divided into the following six groups based on average signal intensities: c < 200, 200 < c <400, 400 < c < 800, 800 < c < 1600, 1600 < c <3200, and c > 3200. A 95% confidence threshold (a) for each of the 6 groups was determined for each replicate comparison as illustrated in Figure 3. The average value of all a values from 65 replicate comparisons in a particular intensity group represents the signal threshold for that group (Table 1). For example, when signal intensity is < 200 the magnitude of change should be a > SLR of 1.72 (3.3-fold) in order to declare that it represents a significant change with 95% confidence, while a significant change can be declared at a SLR of > 0.41 (1.3-fold) when the signal intensity is > 3600. Table 1 also shows a considerable degree of variability in the 95% confidence threshold over 65 replicate comparisons as indicated by the difference between the maximum and minimum threshold values as well as by the standard deviation. This variation motivated us to explore how these signal thresholds could be adjusted using specific experimental variation.

Signal thresholds are user-adjustable

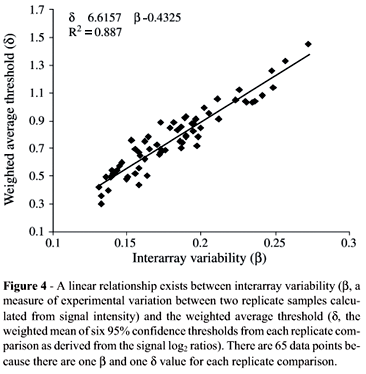
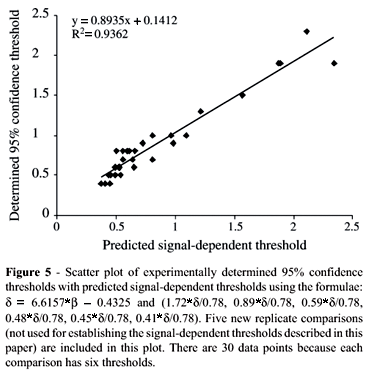
We used the interarray variability, b, to measure signal intensity variation between two replicate samples and weighted average threshold, d, to reflect variability at the SLR level. As shown in Figure 4, b was linearly correlated with d, the correlation being so good that d can be predicted for a particular comparison from the formula d = 6.6157b – 0.4325, where b can be determined from the signal intensity of two replicate samples (hence, experimental variation is directly related to the 95% confidence thresholds). The ratio of predicted d values from a particular replicate comparison versus the mean weighted average threshold (0.78, calculated from 65 weighted average thresholds) can be used to convert the signal thresholds established in this study (1.72, 0.89, 0.59, 0.48, 0.45, 0.41) to a new set of signal-dependent thresholds (1.72*d/0.78, 0.89*d/0.78, 0.59*d/0.78, 0.48*d/0.78, 0.45*d/0.78, 0.41*d/0.78), where d is derived from the formula above. These converted signal-dependent thresholds reflect the experimental variation of that particular comparison. We validated this conversion strategy using 5 new replicate comparisons with different experimental variability. There was no significant difference between the predicted and practically determined thresholds for each of five comparisons. A plot of determined against predicted thresholds for all 5 comparisons showed a correlation coefficient of 0.94 (Figure 5).

The interarray variability in this study was derived from replicate experiments and thus represents only experimental noise, while in a typical experiment comparing control and experimental treatments interarray variability includes both experimental noise and expected biological variation. There is a potential complication when the signal thresholds derived from replicate experiments are used to predict the expected signal thresholds for a biological comparison. We evaluated this potential complication by analyzing a set of real experimental data which included 7 biological samples each with two replicates. We compared interarray variability derived from replicate samples with those derived between biological samples and our results showed that the biological sample-derived interarray variability is on average 2.7% greater than the replicate sample-derived interarray variability. This suggests that the interarray variability mainly consists of experimental noise and that a small number of genes with biological changes in a typical experiment have only a limited effect (about 2.7% increase) on the magnitude of the interarray variability. This small effect could slightly increase the confidence interval of adjusted signal thresholds ( 95%) and further reduce false discovery rates.

Validation of signal thresholds in predicting changes using real-time PCR

To test the validity of the signal thresholds, we designed two independent RT-PCR experiments. The first experiment was to assess whether or not the signal thresholds can identify small biological changes at the high signal intensity range that traditional thresholds fail to detect. Eleven genes were selected that were known to have changed significantly in respect to their signal threshold but not by the traditional 2-fold change. The RT-PCR method showed that 10 out of the 11 genes were up-regulated 50% or more relative to the controls (Table 2). The second experiment involved 15 genes randomly selected from an Affymetrix microarray experiment that were independently evaluated by RT-PCR. Use of our signal threshold produced a false positive rate of 9% and a false negative rate of 7%, while the use of a 2-fold change threshold would have produced a false positive rate of 27% and a false negative rate of 20% (Table 3). The RNA samples used in both RT-PCR experiments were the same as those used for the compared microarray experiments.

Discussion

Traditional fold-change thresholds are currently in common use in microarray data analysis for at least four reasons: 1) researchers are used to the concept that fold-change defines change; 2) the traditional thresholds are intuitive and easy to use; 3) many of the statistical approaches available require substantial statistical knowledge and computational ability; and 4) the majority of microarray experiments have no replicates, which is a practical limitation to the use of replicate-based statistical strategies (Long et al., 2001; Tusher et al., 2001).The use of traditional thresholds to determine significant changes in transcriptional quantities has three limitations: 1) the decisions made are arbitrary and without a statistical basis; 2) traditional thresholds do not reflect signal intensity, which carries important information about signal variability; and 3) traditional thresholds are particularly vulnerable to artifacts produced by global scaling. These factors led us to develop a novel threshold strategy which, like traditional thresholds, could easily be applied by the microarray community but has a significantly improved predictive power combined with a certain level of statistical assurance incorporating more sophisticated data treatment approaches. The signal-dependent fold-change thresholds reported in this paper offer such features since they are responsive to signal intensity, adjustable to specific experimental variation, carry 95% confidence levels and are user-friendly in that they do not require advanced statistical knowledge or extensive computational ability.

Our strategy to establish these empirical thresholds involved three steps: visual examination of scatter plots, data filtration and the determination of 95% confidence intervals for each of the signal intensity groups. We consider visualization of scatter plots as a critical starting point for any microarray data analysis, and our visual analysis showed three important observations: 1) variation as a function of signal intensity is a general phenomenon regardless of the type of chips, tissue type, or species used, this universal linear functional relationship providing the rationale for establishing signal thresholds; 2) genes with low signal intensity and absent calls have a constant variation pattern across different experimental designs, suggesting that this unusual eliptical variation is governed by a specific factor independent of biological, technical and chip-to-chip variability. This invariable variation seems beyond experimental control and is most likely caused by the perfect match- mismatch probe pair subtraction procedure (this variation pattern was not seen when either perfect match intensity or mismatch intensity was used for data analysis). Identification of this constant noise provided a foundation for developing a data filtration strategy; 3) global scaling can introduce false positives when two samples have substantially different signal intensities. This important source of variation was largely ignored until Mills and Gordon (2001) demonstrated it hypothetically. Scaling-induced false positives at the high non-linear range are particularly problematic because experimental variation between experiments at the high intensity range is significantly smaller. A small deviation from the identity line could be treated as a significant change when using signal thresholds, which is why the comparisons with obvious scaling-induced sigmoidal curves were eliminated from this study. When users apply the empirical thresholds reported in this paper it is important to make sure of the absence of a sigmoidal curve in the chip-chip comparisons. Otherwise, interpretation of changes at the two extreme intensity ranges must be made with caution.

We adopted a two-step data filtration strategy, which was designed to maximize the capacity of eliminating noise and minimize the possibility of excluding biological information. The rationale for choosing 100 as the first-step cutoff intensity was based on our observation that the final concentration of spike control BioB in the hybridization mix is 1.5 pM, which is equivalent to 1-3 RNA molecules per cell, but the signal intensity of BioB is normally above 100 when the global scaling target signal is set as 500 (Affymetrix Microarray Suit default setting). Thus, the signal intensity of BioB can be used as a guideline to determine the lower limit of intensity which still carries biological information. Furthermore, over 99% of the genes with a signal intensity of < 100 are called absent by MAS 5. The second filtration step considered both signal intensities of between 100 and 200 and an absent detection call. Since the MAS 5 has independent algorithms to calculate signal intensities and absent detection calls their use as filters enhance the power of MAS 5 to distinguish noise from real biological variation. We believe that the direct use of a relatively high cutoff signal intensity (Grundschober et al., 2002; Sreekumar et al., 2002) to filter data may sacrifice biological information. By surveying 11 independent experiments involving different human, mouse and rat tissue, we found that 10-35% of the genes with a signal intensity of 100-200 were called present or marginal by the Affymetrix software, many of these genes being transcription factors. For example, ER81, an important transcription factor responsive to many signals via mitogen-activated protein kinases (Wu and Janknecht, 2002), was expressed in mouse kidney at a signal intensity of 146 (present call) but in the vitamin D receptor knock-out mouse its expression was reduced to 20 (absent call), an extremely important observation in this particular study because this gene would be detected by the double filtration strategy but not if a signal intensity of 200 was used as the only cutoff threshold.

The 65 chip-chip comparisons for determining signal thresholds involved 14 experiments, 4 different types of chips and 9 different tissues, and included biological, technical and cell line replicates. The thresholds we established using such a wide range of replicate experiments should be representative and robust enough to guide GeneChip data analysis while also being as easy to use as traditional threshold. Unlike traditional thresholds, signal thresholds vary according to signal intensity and thus overcome the weakness of the traditional 2-fold threshold which is normally too low for genes within the low signal intensity range but too high for genes in the high signal intensity range. Signal thresholds also have the advantage that the threshold for a particular gene can be determined with 95% confidence simply by examining the signal intensity of the gene.

Though convenient, the use of a constant set of signal thresholds for different experiments can be criticized because some experiments are more variable than others and one set of thresholds may not be ideal for all type of experiments. We addressed this potential problem by identifying a linear relationship between the interarray variability b which is a measure of experimental variation between two replicate samples and the weighted average threshold d which is the weighted mean of six 95% confidence thresholds from each replicate comparison, the linear relationship making it possible to adjust the thresholds based on the extent of experimental variation in a particular experiment. We validated the feasibility of this adjustment by directly comparing the predicted thresholds with experimentally determined thresholds and found no significant difference between the two. User-adjustable signal thresholds are applicable to all types of experiments with different degrees of variation but are particularly useful for those experiments without replicates, these types of experiments accounting for the majority of published microarray experiments. Signal thresholds can either be used directly as a guideline for microarray data analysis or three simple steps can be followed to convert the signal thresholds into a new set of thresholds to suit a specific experiment, these steps being: 1) calculating the interarray variability b as b = S[|A_i-B_i|/(A_i+B_i)]/n, where A_i is the signal intensity of the i^th gene in experiment A and B_i is the signal intensity of the i^th gene in the control (easily achieved using Excel®); 2) predicting the weighted average threshold d using d = 6.6157*b – 0.4325; and 3) converting the established signal thresholds into a new set of thresholds (1.72*d/0.78, 0.89*d/0.78, 0.59*d/0.78, 0.48*d/0.78, 0.45*d/0.78, 0.41*d/0.78). The whole conversion procedures requires less than 10 min using the Excel^® spreadsheet and a hand calculator.

Mills and Gordon (2001) have also developed an empirical approach for eliminating noise from Affymetrix mouse GeneChip^® data sets in order to overcome the weakness of traditional thresholds. In this case, Mills and Gordon used three-dimensional plots to characterize noise in the context of biological variation and summarized the noise in the form of tables of look-up scores which they used to evaluate the reliability of the 'increase' or 'decrease' in the calls produced by the Affymetrix software. This approach is useful for initial screening and has proven to be more effective than the traditional thresholds but has the following drawbacks: the look-up tables were derived from only 18 chip-chip comparisons of the same mouse chips; the score system (particularly for a partner chip) has no rules to follow and is difficult to remember; the use of the score is still an arbitrary decision with no statistical basis. In contrast, the signal thresholds described in our present paper were derived from 65 replicate comparisons involving different samples and chips; the signal intensity bins were grouped in increments of c_i-1 (c_i = 2*c_i-1); and the thresholds carry 95% confidence levels and offer significantly enhanced power in predicting change compared to traditional thresholds. Quantitative RT-PCR showed that the use of signal-dependent thresholds produced three times less false change calls than the use of the traditional two-fold thresholds.

In summary, we have established user-adjustable, signal thresholds for declaring significant changes in Affymetrix GeneChip^® data analyses. These thresholds combine the user-friendly feature of traditional fold-change thresholds with the confidence intervals of other statistical treatments, offering a strategy to bridge the gap between a widely-accepted but somewhat primitive methodology and the sophisticated statistical approaches that can be difficult to apply. Given the fundamental fact that variation is a function of signal intensity for all types of microarray data, the experimental approach to filtering data and defining signal-dependent thresholds may be applicable to cDNA arrays as well.

Acknowledgments

We thank Kay Macleod, Anning Lin, Eric Svensson, Chyung-Ru Wang, Michelle LeBeau, Erich Jaeger, Tina Harr, Audrey Esclatine, Yanchun Li, Mitchel Villereal and Brunella Taddeo for giving us permission to use their replicate comparisons in this study. This work was in part supported by the Division of Biological Sciences, the Cancer Research Center and the NIDDK Biotechnology Center at the University of Chicago (U24D55370).

Received: June 26, 2003; Accepted: October 14, 2004.

Associate Editor:Emmanuel Dias Neto

• Amundson SA, Bittner M, Chen Y, Trent J, Meltzer P and Fornace Jr AJ (1999) Fluorescent cDNA microarray hybridization reveals complexity and heterogeneity of cellular genotoxic stress responses. Oncogene 18:3666-3672.
• Baechler EC, Batliwalla FM, Karypis G, Gaffney PM, Moser K, Ortmann WA, Espe KJ, Balasubramanian S, Hughes KM, Chan JP, Begovich A, Chang SY, Gregersen PK and Behrens TW (2004) Expression levels for many genes in human peripheral blood cells are highly sensitive to ex vivo incubation. Genes Immun 5:347-353.
• Baggerly KA, Coombes KR, Hess KR, Stivers DN, Abruzzo LV and Zhang W (2001) Identifying differentially expressed genes in cDNA microarray experiments. J Comput Biol 8:639-659.
• Bassett Jr DE, Eisen MB and Boguski MS (1999) Gene expression informatics It is all in your mine. Nature Genet 21:51-55.
• Chen Y, Dougherty ER and Bittner M (1997) Ratio-based decisions and the quantitative analysis of cDNA microarray images. J Biomed Opt 2:364-374.
• Cleveland W and Devlin S (1988) Locally weighted linear regression: An approach to regression analysis by local fitting. J Am Stat Assoc 83:596-609.
• Coller HA, Grandori C, Tamayo P, Colbert T, Lander ES, Eisenman RN and Golub TR (2000) Expression analysis with oligonucleotide microarrays reveals that MYC regulates genes involved in growth, cell cycle, signaling, and adhesion. Proc Natl Acad Sci USA 97:3260-3265.
• Der SD, Zhou A, Williams BR and Silverman RH (1998) Identification of genes differentially regulated by interferon alpha, beta, or gamma using oligonucleotide arrays. Proc Natl Acad Sci USA 95:15623-15628.
• Dudoit S, Yang YH, Callow M and Speed T (2002) Statistical methods for identifying differentially expressed genes in replicated cDNA microarray experiments. Statistica Sinica 12:111-139.
• Fambrough D, McClure K, Kazlauskas A and Lander ES (1999) Diverse signaling pathways activated by growth factor receptors induce broadly overlapping, rather than independent, sets of genes. Cell 97:727-741.
• Goryachev AB, Macgregor PF and Edwards AM (2001) Unfolding of microarray data. J Comp Biol 8:443-461.
• Grundschober C, Malosio ML, Astolfi L, Giordano T, Nef P and Meldolesi J (2002) Neurosecretion competence: A comprehensive gene expression program identified in PC12 cells. J Biol Chem 277:36715-36724.
• Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coffey E, Dai H, He YD, Kidd MJ, King AM, Meyer MR, Slade D, Lum PY, Stepaniants SB, Shoemaker DD, Gachotte D, Chakraburtty K, Simon J, Bard M and Friend SH (2000) Functional discovery via a compendium of expression profiles. Cell 102:109-126.
• Hunter BG, Beatty MK, Singletary GW, Hamaker BR, Dilkes BP, Larkins BA and Jung R (2002) Maize opaque endosperm mutations create extensive changes in patterns of gene expression. Plant Cell 14:2591-612.
• Kerr MK, Martin M and Churchill GA (2000) Analysis of variance for gene expression microarray data. J Comp Biol 7:819-837.
• Landis GN, Abdueva D, Skvortsov D, Yang J, Rabin BE, Carrick J, Tavare S and Tower J (2004) Similar gene expression patterns characterize aging and oxidative stress in Drosophila melanogaster Proc Natl Acad Sci USA 101:7663-8.
• Li C and Wong WH (2001) Model-based analysis of oligonucleotide arrays: Expression index computation and outlier detection. Proc Natl Acad Sci USA 98:31-36.
• Lockhart DJ, Dong H, Byrne MC, Follettie MT, Gallo MV, Chee MS, Mittmann M, Wang C, Kobayashi M, Horton H and Brown EL (1996) Expression monitoring by hybridization to high-density oligonucleotide arrays. Nat Biotechnol 14:1675-80.
• Long AD, Mangalam HJ, Chan BYP, Toller L, Hatfield GW and Baldi P (2001) Improved statistical inference from DNA microarray data using analysis of variance and a Bayesian statistical framework. J Biol Chem 276:19937-19944.
• Mills JC and Gordon JI (2001) A new approach for filtering noise from high-density oligonucleotide microarray datasets. Nucleic Acids Res 29:E72-2.
• Newton MA, Kendziorski CM, Richmond CS, Blattner FR and Tsui KW (2001) On differential variability of expression ratios: Improving statistical inference about gene expression changes from microarray data. J Comp Biol 8:37-52.
• Schena M, Shalon D, Heller R, Chai A, Brown PO and Davis RW (1996) Parallel human genome analysis: Microarray-based expression monitoring of 1000 genes. Proc Natl Acad Sci USA 93:10614-10619.
• Sreekumar R, Halvatsiotis P, Schimke JC and Nair KS (2002) Gene expression profile in skeletal muscle of type 2 diabetes and the effect of insulin treatment. Diabetes 51:1913-1920.
• Strand AD, Olson JM and Kooperberg C (2002) Estimating the statistical significance of gene expression changes observed with oligonucleotide arrays. Hum Mol Genet 11:2207-2221.
• Tamayo P, Slonim D, Mesirov J, Zhu Q, Kitareewan S, Dmitrovsky E, Lander ES and Golub TR (1999) Interpreting patterns of gene expression with self-organizing maps: Methods and application to hematopoietic differentiation. Proc Natl Acad Sci USA 96:2907-2912.
• Tusher VG, Tibshirani R and Chu G (2001) Significance analysis of microarrays applied to the ionizing radiation response. Proc Natl Acad Sci USA 98:5116-5121.
• Wang Y, Rea T, Bian J, Gray S and Sun Y (1999) Identification of the genes responsive to etoposide-induced apoptosis: Application of DNA chip technology. FEBS Lett 445:269-273.
• Wu J and Janknecht R (2002) Regulation of the ETS transcription factor ER81 by th e 90 kDa ribosomal S6 kinase 1 and protein kinase A. J Biol Chem 277:42669-42679.
• Yang IV, Chen E, Hasseman JP, Liang W, Frank BC, Wang S, Sharov V, Saeed AI, White J, Li J, Lee NH, Yeatman TJ and Quackenbush J (2003) Within the fold: Assessing differential expression measures and reproducibility in microarray assays. Genome Biol 3(11):research0062.
• Yang YH, Dudoit S, Luu P, Lin DM, Peng V, Ngai J and Speed TP (2002) Normalization for cDNA microarray data: A robust composite method addressing single and multiple slide systematic variation. Nucleic Acids Res 30:e15.
• Zamurovic N, Cappellen D, Rohner D and Susa M (2004) Coordinated activation of Notch, Wnt and TGF-beta signaling pathways in BMP-2 induced osteogenesis: Notch target gene Hey1 inhibits mineralization and Runx2 transcriptional activity. J Biol Chem 279:37704-37715.

Publication Dates

• Publication in this collection
  11 July 2005
• Date of issue
  2005

History

• Accepted
  14 Oct 2004
• Received
  26 June 2003