Abstract
The Goal Programming (GP) is a multi-criteria approach of Operational Research that has been used for solving complex decision problems. This paper proposes a new Fuzzy Goal Programming (FGP) model to handle the process of capital budget of companies in an economic environment under uncertainty. For performance comparison purposes, the FGP and another recently published model developed for the same purposes were applied to data from a company that was the object of the study. The modeling and optimization were made with the GAMS software - 23.6.5 and using the CPLEX solver. The results obtained from the FGP model provided higher improvements than those obtained with the alternative model, as for example: increased profitability index, reduced payback and better application of the capital available in the budget. Furthermore, the FGP model has flexibility features that allow the manager to simulate, quickly and easily obtaining results about scenarios under uncertainty.
Keywords:
Fuzzy Goal Programming; Capital budget; Economic environment under uncertainty
Resumo
A Programação por Metas (Goal Programming - GP) é uma abordagem multicritério da Pesquisa Operacional que vem sendo empregada na solução de complexos problemas de decisão. Este trabalho propõe um novo modelo de Programação por Metas Fuzzy (Fuzzy Goal Programming - FGP) para tratar o processo de orçamento de capital de empresas em um ambiente econômico sob incerteza. Para fins de comparação de desempenho, o modelo FGP e outro modelo desenvolvido com os mesmos fins, recentemente publicado, foram aplicados considerando-se os dados de uma empresa que foi o objeto do estudo. A modelagem e otimização foram feitas com o software GAMS - 23.6.5 e utilizando-se o solver CPLEX. Os resultados do modelo FGP proporcionaram melhorias com relação aos obtidos com o modelo alternativo citado, por exemplo: aumento do índice de lucratividade, redução do payback e melhor aplicação do capital disponível no orçamento. Além disto, o modelo FGP tem características de flexibilidade que permitem ao gestor simular, obter resultados rapidamente e com facilidade, acerca de cenários sob incerteza de seu interesse.
Palavras-chave:
Programação por Metas Fuzzy; Orçamento de capital; Ambiente econômico sob incerteza
1 Introduction
In complex industrial problems, the decision taking involves inaccurate or incomplete information, multiple decision agents and, in general, multiple objectives that can be conflicting with each other (Deb, 2001Deb, K. (2001). Multi-objective optimization using evolutionary algorithms. England: John Wiley & Sons.). This is the case of investment project selection problems, or capital budget problems, (Santos & Barros, 2011Santos, J. O., & Barros, C. A. S. (2011). O que determina a tomada de decisão financeira: razão ou emoção? RBGN: Revista Brasileira de Gestão de Negócios, 13(38), 7-20. http://dx.doi.org/10.7819/rbgn.v13i38.785.
http://dx.doi.org/10.7819/rbgn.v13i38.78...
), according to Brigham et al. (2001)Brigham, E. F., Gapenski, L. C., & Ehrhardt, M. C. (2001). Administração financeira: teoria e prática. São Paulo: Atlas., there are many ways to select the best set of investment projects, and the traditional investment assessment methods are (Abensur, 2012Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
):
-
Net Present Value Method (NPV) – it allows comparing initial investments with future returns, in which, when the NPV is positive, it means that the capital invested will be recovered;
-
Internal Rate of Return Method (IRR) – it considers the discount rate that equates the inflows and outflows of an investment, in which, for the project to be viable, the value of the IRR must be greater than or equal to the Minimum Attractive Rate of Return (MARR) adopted by the company;
-
Payback Method – it analyzes the recovery period of the invested capital, that is, the period necessary to a certain investment can be paid;
-
Profitability Index Method (PI) – it considers the ratio between the NPV of net cash inflows of the project and the initial investment value.
In this type of problem, the budget constraint plays important role with respect to limit the decisions that can be taken in the selection of the investment projects, and it is recommended the use of optimization techniques aiming at the optimal allocation of available financial resources (Abensur, 2012Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
).
In this sense, an alternative is to apply to this type of complex and critical situation for companies, the models and techniques of the Goal Programming (GP). In fact, the GP is a method of Operational Research (OR), which allows the modelling and solution of multiobjective problems, including under the occurrence of uncertainties, as is typical in economic scenarios associated with decisions in investment portfolios (Silva & Marins, 2014Silva, A. F., & Marins, F. A. S. (2014). A Fuzzy Goal Programming model for solving aggregate production-planning problems under uncertainty: a case study in a Brazilian sugar mill. Energy Economics, 45, 196-204. http://dx.doi.org/10.1016/j.eneco.2014.07.005.
http://dx.doi.org/10.1016/j.eneco.2014.0...
). Some researchers developed interesting related works:
-
Bradi et al. (2000)Bradi, M. A., Davis, D., & Davis, D. (2000). A comprehensive 0-1 goal programming model for project selection. International Journal of Project Management, 19, 243-252. applied a binary GP model to the problem of project selection, without considering the occurrence of uncertainty;
-
Lee & Kim (2000)Lee, J. W., & Kim, S. H. (2000). Using analytic network process and goal programming for interdependent information system project selection. Computers & Operations Research, 27(4), 367-382. http://dx.doi.org/10.1016/S0305-0548(99)00057-X.
http://dx.doi.org/10.1016/S0305-0548(99)... combined the ANP (Analytic Network Process) (Saaty, 2006Saaty, T. L. (2006). Decision making with the analytic network process. International Series in Operations Research & Management Science, 95, 1-26. http://dx.doi.org/10.1007/0-387-33987-6_1.
http://dx.doi.org/10.1007/0-387-33987-6_... ) with the GP to select information system projects; -
Santos et al. (2012)Santos, A., Lavarda, C. E. F., & Marcello, I. E. (2012). The relationship between cost management knowledge and budgetary participation with managers’ performance. Revista Brasileira de Gestão de Negócios, 16, 124-142. investigated the performance of business managers based on the knowledge about cost management and budget participation;
-
Ghahtarani & Najafi (2013)Ghahtarani, A., & Najafi, A. A. (2013). Robust goal programming for multi-objective portfolio selection problem. Economic Modelling, 33, 588-592. http://dx.doi.org/10.1016/j.econmod.2013.05.006.
http://dx.doi.org/10.1016/j.econmod.2013... combined the robust stochastic optimization (Mulvey et al., 1995Mulvey, J. M., Vanderbei, R. J., & Zenios, S. A. (1995). Robust optimization of large-scale systems. Operations Research, 43(2), 264-281. http://dx.doi.org/10.1287/opre.43.2.264.
http://dx.doi.org/10.1287/opre.43.2.264... ) with the GP, developing the Robust Goal Programming (RGP) model, which was applied in selecting investment portfolios in the stock market; -
Bakirli et al. (2013)Bakirli, B. B., Gencer, C., & Aydogăn, E. K. (2013). A combined approach for fuzzy multi-objective multiple knapsack problems for defence project selection. The Journal of the Operational Research Society, 65(7), 1001-1016. http://dx.doi.org/10.1057/jors.2013.36.
http://dx.doi.org/10.1057/jors.2013.36... combined the AHP method (Saaty, 1977Saaty, T. L. (1977). A scaling method for priorities in hierarchical structures. Journal of Mathematical Psychology, 15(3), 234-281. http://dx.doi.org/10.1016/0022-2496(77)90033-5.
http://dx.doi.org/10.1016/0022-2496(77)9... ) and a Fuzzy Goal Programming (FGP) model with the QFD (Quality Function Deployment) matrix (Lam & Lai, 2015Lam, J. S. L., & Lai, H.-H. (2015). Developing environmental sustainability by ANP-QFD approach: the case of shipping operations. Journal of Cleaner Production, 105, 275-284. http://dx.doi.org/10.1016/j.jclepro.2014.09.070.
http://dx.doi.org/10.1016/j.jclepro.2014... ), to select projects that offer the maximum benefits when performed within various budgets; -
Abensur (2013)Abensur, E. O. (2013). Orçamento de capital: um caso especial de sequenciação de projetos. Gestão & Produção, 20(4), 979-991. http://dx.doi.org/10.1590/S0104-530X2013000400016.
http://dx.doi.org/10.1590/S0104-530X2013... evaluated the capital budget in a context in which the managers can establish the completion sequence of projects previously selected, which minimizes the need for investment; -
Khalili-Damghani et al. (2013)Khalili-Damghani, K., Sadi-Nezhad, S., & Tavana, M. (2013). Solving multi-period project selection problems with fuzzy goal programming based on TOPSIS and a fuzzy preference relation. Information Sciences, 252, 42-61. http://dx.doi.org/10.1016/j.ins.2013.05.005.
http://dx.doi.org/10.1016/j.ins.2013.05.... applied the FGP model combined with the TOPSIS - Technique for Order Preference by Similarity to Ideal Solution multicriteria method (Joshi & Kumar, 2016Joshi, D., & Kumar, S. (2016). Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. European Journal of Operational Research, 248(1), 183-191. http://dx.doi.org/10.1016/j.ejor.2015.06.047.
http://dx.doi.org/10.1016/j.ejor.2015.06... ) to select multi-period projects in a context under uncertainty; -
Li & Wan (2014)Li, D.-F., & Wan, S.-P. (2014). A fuzzy inhomogenous multiattribute group decision making approach to solve outsourcing provider selection problems. Knowledge-Based Systems, 67, 71-89. http://dx.doi.org/10.1016/j.knosys.2014.06.006.
http://dx.doi.org/10.1016/j.knosys.2014.... developed a Fuzzy Linear Programming model for the selection of supply chain projects.
Although there are many studies linked to the selection of investment projects, the use of Fuzzy Goal Programming (FGP) models in this type of problem is recent, corroborating therefore the importance of this research. So, this study aimed to develop and apply a FGP model to solve the capital budget problem. In addition, it was performed a comparison of its results with those obtained by Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
, who proposed, recently, an alternative model to the same class of investment problems.
Considering the classification proposed by Bertrand & Fransoo (2002)Bertrand, J. W. M., & Fransoo, J. C. (2002). Operations management research methodologies using quantitative modeling. International Journal of Operations & Production Management, 22(2), 241-264. http://dx.doi.org/10.1108/01443570210414338.
http://dx.doi.org/10.1108/01443570210414...
, this research can be classified as an applied research, because it provides contributions for the current literature, possessing normative empirical objective, since the model aims to understand policies and strategies that allow actions to better understand a current situation. Besides, with respect to the form of approach of the problem, the research is quantitative type and the research method adopted is the modeling.
This article is organized in 5 sections. Section 2 briefly describes the theoretical foundations of the GP and, in particular, addresses the FGP model. Section 3 addresses the problem description; Section 4 presents the problem modeling and the results obtained; finally, Section 5 brings the conclusion and the recommendations for future researches, followed by the bibliography.
2 Goal programming
According to Charnes & Cooper (1961)Charnes, A., & Cooper, W. W. (1961). Management model and industrial application of linear programming. New York: Wiley., Romero (2001Romero, C. (2001). Extended lexicographic goal programming: a unifying approach. Omega, 29(1), 63-71. http://dx.doi.org/10.1016/S0305-0483(00)00026-8.
http://dx.doi.org/10.1016/S0305-0483(00)...
, 2004Romero, C. (2004). A general structure of achievement function for a goal programming model. European Journal of Operational Research, 153(3), 675-686. http://dx.doi.org/10.1016/S0377-2217(02)00793-2.
http://dx.doi.org/10.1016/S0377-2217(02)...
), Silva & Marins (2014Silva, A. F., & Marins, F. A. S. (2014). A Fuzzy Goal Programming model for solving aggregate production-planning problems under uncertainty: a case study in a Brazilian sugar mill. Energy Economics, 45, 196-204. http://dx.doi.org/10.1016/j.eneco.2014.07.005.
http://dx.doi.org/10.1016/j.eneco.2014.0...
, 2015Silva, A. F., & Marins, F. A. S. (2015). Revisão da literatura sobre modelos de programação por metas determinística e sob incerteza. Production Journal, 25(1), 92-112. http://dx.doi.org/10.1590/S0103-65132014005000003.
http://dx.doi.org/10.1590/S0103-65132014...
), Chang (2007Chang, C.-T. (2007). Multi-choice goal programming. Omega: International Journal of Management Sciences, 35(4), 389-396. http://dx.doi.org/10.1016/j.omega.2005.07.009.
http://dx.doi.org/10.1016/j.omega.2005.0...
, 2008Chang, C.-T. (2008). Revised multi-choice goal programming. Applied Mathematical Modelling, 32(12), 2587-2595. http://dx.doi.org/10.1016/j.apm.2007.09.008.
http://dx.doi.org/10.1016/j.apm.2007.09....
), Jamalnia & Soukhakian (2009)Jamalnia, A., & Soukhakian, M. A. (2009). A hybrid fuzzy goal programming approach with different goal priorities to aggregate production planning. Computers & Industrial Engineering, 56(4), 1474-1486. http://dx.doi.org/10.1016/j.cie.2008.09.010.
http://dx.doi.org/10.1016/j.cie.2008.09....
and Yaghoobi & Tamiz (2007)Yaghoobi, M. A., & Tamiz, M. (2007). A method for solving fuzzy goal programming problems based on MINMAX approach. European Journal of Operational Research, 177(3), 1580-1590. http://dx.doi.org/10.1016/j.ejor.2005.10.022.
http://dx.doi.org/10.1016/j.ejor.2005.10...
, the three most used types of deterministic models of the GP, are:
-
Weighted Goal Programming (WGP) – weights are attributed to the (positive and negative) deviation variables with regard to the goals chosen for the objectives. This was the first model of GP developed and, due to this; it will be briefly described below;
-
Lexicographic Goal Programming (LGP) or Preemptive Goal Programming – objective functions are ordered according to their importance established from a prioritization made by the managers;
-
Minmax Goal Programming (Minmax GP) – objective functions, which consider the sum of the deviation variables, are included in the model.
2.1 Weighted Goal Programming
In the WGP models, the deviation variables present equivalent hierarchies, being the weighting what will distinguish the most important objectives. The decision-makers need to estimate the weights in such a way that a large part of the objectives is satisfied, which generates problems with the subjectivism in the estimation of these weights. To try minimizing the subjectivism, a method that has been very adopted in the prioritization of objectives is the Analytic Hierarchy Process – AHP (Saaty, 1977Saaty, T. L. (1977). A scaling method for priorities in hierarchical structures. Journal of Mathematical Psychology, 15(3), 234-281. http://dx.doi.org/10.1016/0022-2496(77)90033-5.
http://dx.doi.org/10.1016/0022-2496(77)9...
).
According to Martel & Aouni (1998)Martel, J. M., & Aouni, B. (1998). Diverse imprecise goal programming model formulations. Journal of Global Optimization, 12(2), 127-138. http://dx.doi.org/10.1023/A:1008206226608.
http://dx.doi.org/10.1023/A:100820622660...
, the original WGP model can be expressed by:
Equation 1 are weights attributed, respectively, to
Subject to:
Constraint 2 where x is the vector of the decision variables of the model xi; fi (x) is an objective function I, gi is a goal value chosen to fi, are, respectively, the auxiliary (positive and negative) deviation variables related to the goal gi
Constraint 3A and c are, respectively, a matrix of the LHS (Left Hand-Side) coefficients and a RHS (Right Hand-Side) vector for hard restrictions in the original multi-criteria model, and F is Feasible set.
Constraint 4 It is observed that, by only one of the deviation variable associated with each goal can have value different from zero.
There are other deterministic GP models; however, they are not presented in this work, for more details it is recommended to consult a GP review by Silva & Marins (2015)Silva, A. F., & Marins, F. A. S. (2015). Revisão da literatura sobre modelos de programação por metas determinística e sob incerteza. Production Journal, 25(1), 92-112. http://dx.doi.org/10.1590/S0103-65132014005000003.
http://dx.doi.org/10.1590/S0103-65132014...
.
2.2 Fuzzy Goal Programming (FGP) Model
It should be noted that management decision problems have as natural characteristics the occurrence of uncertainty in their parameters, such as, for example, problems related to aggregate production planning and budgetary problems (Wang & Liang, 2004Wang, R. C., & Liang, T. F. (2004). Projects management decisions with multiple fuzzy goals. Construction Management and Economics, 22(10), 1047-1056. http://dx.doi.org/10.1080/0144619042000241453.
http://dx.doi.org/10.1080/01446190420002...
). The main GP models under uncertainty are (Silva & Marins, 2015Silva, A. F., & Marins, F. A. S. (2015). Revisão da literatura sobre modelos de programação por metas determinística e sob incerteza. Production Journal, 25(1), 92-112. http://dx.doi.org/10.1590/S0103-65132014005000003.
http://dx.doi.org/10.1590/S0103-65132014...
):
-
Multi-Choice Goal Programming (Chang, 2007Chang, C.-T. (2007). Multi-choice goal programming. Omega: International Journal of Management Sciences, 35(4), 389-396. http://dx.doi.org/10.1016/j.omega.2005.07.009.
http://dx.doi.org/10.1016/j.omega.2005.0... ); -
Revised Multi-Choice Goal Programming (Chang, 2008Chang, C.-T. (2008). Revised multi-choice goal programming. Applied Mathematical Modelling, 32(12), 2587-2595. http://dx.doi.org/10.1016/j.apm.2007.09.008.
http://dx.doi.org/10.1016/j.apm.2007.09.... ); -
Integer Multi-Choice Goal Programming (Silva et al., 2013aSilva, A. F., Marins, F. A. S., & Montevechi, J. A. B. (2013a). Multi-choice mixed integer goal programming optimization for real problems in a sugar and ethanol milling company. Applied Mathematical Modelling, 37(9), 6146-6162. http://dx.doi.org/10.1016/j.apm.2012.12.022.
http://dx.doi.org/10.1016/j.apm.2012.12.... ); -
Fuzzy Multi-Choice Goal Programming (Bankian-Tabrizi et al., 2012Bankian-Tabrizi, B., Shahanaghi, K., & Saeed Jabalameli, M. (2012). Fuzzy multi-choice goal programming. Applied Mathematical Modelling, 35(4), 1415-1420. http://dx.doi.org/10.1016/j.apm.2011.08.040.
http://dx.doi.org/10.1016/j.apm.2011.08.... ); -
Multi-Segment Goal Programming (Liao, 2009Liao, C. N. (2009). Formulating the multi-segment goal programming. Computers & Industrial Engineering, 56(1), 138-141. http://dx.doi.org/10.1016/j.cie.2008.04.007.
http://dx.doi.org/10.1016/j.cie.2008.04.... ); -
Revised Multi-Segment Goal Programming - RMSGP (Chang et al., 2012aChang, C.-T., Chen, H.-M., & Zhuang, Z.-Y. (2012a). Revised multi-segment goal programming: percentage goal programming. Computers & Industrial Engineering, 63(4), 1235-1242. http://dx.doi.org/10.1016/j.cie.2012.08.005.
http://dx.doi.org/10.1016/j.cie.2012.08.... ); -
Multi-Coefficients Goal Programming - MCGP (Chang et al., 2012bChang, C.-T., Chen, H.-M., & Zhuang, Z.-Y. (2012b). Multi-coefficients goal programming. Computers & Industrial Engineering, 62(2), 616-623. http://dx.doi.org/10.1016/j.cie.2011.11.027.
http://dx.doi.org/10.1016/j.cie.2011.11.... ); -
Revised multi-choice Goal Programming - LHS (Silva et al., 2015Silva, A. F., Marins, F. A. S., & Dias, E. X. (2015). Addressing uncertainty in sugarcane harvest planning through a revised multi-choice goal programming model. Applied Mathematical Modelling, 39(18), 5540-5558. http://dx.doi.org/10.1016/j.apm.2015.01.007.
http://dx.doi.org/10.1016/j.apm.2015.01.... ); -
Fuzzy Goal Programming - FGP (Silva & Marins, 2014Silva, A. F., & Marins, F. A. S. (2014). A Fuzzy Goal Programming model for solving aggregate production-planning problems under uncertainty: a case study in a Brazilian sugar mill. Energy Economics, 45, 196-204. http://dx.doi.org/10.1016/j.eneco.2014.07.005.
http://dx.doi.org/10.1016/j.eneco.2014.0... ; Jamalnia & Soukhakian, 2009Jamalnia, A., & Soukhakian, M. A. (2009). A hybrid fuzzy goal programming approach with different goal priorities to aggregate production planning. Computers & Industrial Engineering, 56(4), 1474-1486. http://dx.doi.org/10.1016/j.cie.2008.09.010.
http://dx.doi.org/10.1016/j.cie.2008.09.... ; Yaghoobi & Tamiz, 2007Yaghoobi, M. A., & Tamiz, M. (2007). A method for solving fuzzy goal programming problems based on MINMAX approach. European Journal of Operational Research, 177(3), 1580-1590. http://dx.doi.org/10.1016/j.ejor.2005.10.022.
http://dx.doi.org/10.1016/j.ejor.2005.10... ; Liang & Wang, 1993Liang, G.-S., & Wang, M. J. (1993). Evaluating human reliability using Fuzzy relation. Microelectronics and Reliability, 33(1), 63-80. http://dx.doi.org/10.1016/0026-2714(93)90046-2.
http://dx.doi.org/10.1016/0026-2714(93)9... ; Zimmermann, 1978Zimmermann, H. J. (1978). Fuzzy programming and linear programming with several objective function. Fuzzy Sets and Systems, 1(1), 45-55. http://dx.doi.org/10.1016/0165-0114(78)90031-3.
http://dx.doi.org/10.1016/0165-0114(78)9... ); -
Robust stochastic optimization (Mulvey et al., 1995Mulvey, J. M., Vanderbei, R. J., & Zenios, S. A. (1995). Robust optimization of large-scale systems. Operations Research, 43(2), 264-281. http://dx.doi.org/10.1287/opre.43.2.264.
http://dx.doi.org/10.1287/opre.43.2.264... ).
In this research, it was applied the FGP model, because it is the oldest GP model under uncertainty, having a wide range of real applications (Silva & Marins, 2014Silva, A. F., & Marins, F. A. S. (2014). A Fuzzy Goal Programming model for solving aggregate production-planning problems under uncertainty: a case study in a Brazilian sugar mill. Energy Economics, 45, 196-204. http://dx.doi.org/10.1016/j.eneco.2014.07.005.
http://dx.doi.org/10.1016/j.eneco.2014.0...
, 2015Silva, A. F., & Marins, F. A. S. (2015). Revisão da literatura sobre modelos de programação por metas determinística e sob incerteza. Production Journal, 25(1), 92-112. http://dx.doi.org/10.1590/S0103-65132014005000003.
http://dx.doi.org/10.1590/S0103-65132014...
). Concepts and results relating to the inclusion of uncertainty occurrence in the problem data, the contribution of the GP, and the basic theory of Fuzzy sets to handle these situations are presented (Chang, 2007Chang, C.-T. (2007). Multi-choice goal programming. Omega: International Journal of Management Sciences, 35(4), 389-396. http://dx.doi.org/10.1016/j.omega.2005.07.009.
http://dx.doi.org/10.1016/j.omega.2005.0...
).
Zimmermann (1978)Zimmermann, H. J. (1978). Fuzzy programming and linear programming with several objective function. Fuzzy Sets and Systems, 1(1), 45-55. http://dx.doi.org/10.1016/0165-0114(78)90031-3.
http://dx.doi.org/10.1016/0165-0114(78)9...
used the triangular fuzzy number to characterize linguistic values and Liang & Wang (1993)Liang, G.-S., & Wang, M. J. (1993). Evaluating human reliability using Fuzzy relation. Microelectronics and Reliability, 33(1), 63-80. http://dx.doi.org/10.1016/0026-2714(93)90046-2.
http://dx.doi.org/10.1016/0026-2714(93)9...
justified the use of triangular fuzzy functions, because they properly characterize the human trials, and also allow simulating uncertainty occurrence in the data and parameters involved. This was the option adopted in this work that is going to be detailed subsequently.
In this line, according to Jamalnia & Soukhakian (2009)Jamalnia, A., & Soukhakian, M. A. (2009). A hybrid fuzzy goal programming approach with different goal priorities to aggregate production planning. Computers & Industrial Engineering, 56(4), 1474-1486. http://dx.doi.org/10.1016/j.cie.2008.09.010.
http://dx.doi.org/10.1016/j.cie.2008.09....
, and Yaghoobi & Tamiz (2007)Yaghoobi, M. A., & Tamiz, M. (2007). A method for solving fuzzy goal programming problems based on MINMAX approach. European Journal of Operational Research, 177(3), 1580-1590. http://dx.doi.org/10.1016/j.ejor.2005.10.022.
http://dx.doi.org/10.1016/j.ejor.2005.10...
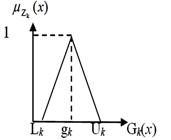
, there are three most common types of pertinence functions, denoted by for a given objective function Gk, when we are working with triangular fuzzy numbers, as show the expressions (5)-(7) and illustrate the Figures 1, 2, 3. It was adopted the notation [~] to represent a fuzzy goal value (desired and imprecise) gk chosen to a fuzzy objective function Gk:
Equation 5 there is a fuzzy objective function of the type “the lower its value in relation to gk, the better it is”;
Equation 6 there is a fuzzy objective function of the type “the higher its value in relation to gk, the better it is”
Equation 7 there is a objective function that is wanted to be achieved exactly at the value gk chosen.
The fuzzy goals can be identified as fuzzy sets defined on the feasible set of solutions associated with a pertinence function. The linear pertinence functions are the functions most adopted both in the theoretical and practical works (Jamalnia & Soukhakian, 2009Jamalnia, A., & Soukhakian, M. A. (2009). A hybrid fuzzy goal programming approach with different goal priorities to aggregate production planning. Computers & Industrial Engineering, 56(4), 1474-1486. http://dx.doi.org/10.1016/j.cie.2008.09.010.
http://dx.doi.org/10.1016/j.cie.2008.09....
). For the fuzzy constraints (5) and (6), by adopting the triangular fuzzy numbers, in which Lk and Uk, respectively, are the minimum and maximum values chosen by the decision-maker to be attributed to the fuzzy goal gk, the linear pertinence functions can be expressed by (8)-(10):
Other form to visualize this pertinence functions is in Figures 1, 2, 3:
It is observed that, usually, the limits Lk and Uk are subjectively chosen by the decision-makers, or are associated with the tolerances existing in a technical process. The choice of these tolerance limits is very important, once they directly influence the model optimization (Silva & Marins, 2014Silva, A. F., & Marins, F. A. S. (2014). A Fuzzy Goal Programming model for solving aggregate production-planning problems under uncertainty: a case study in a Brazilian sugar mill. Energy Economics, 45, 196-204. http://dx.doi.org/10.1016/j.eneco.2014.07.005.
http://dx.doi.org/10.1016/j.eneco.2014.0...
).
The model of the Fuzzy Goal Programming (FGP), proposed by Yaghoobi & Tamiz (2007)Yaghoobi, M. A., & Tamiz, M. (2007). A method for solving fuzzy goal programming problems based on MINMAX approach. European Journal of Operational Research, 177(3), 1580-1590. http://dx.doi.org/10.1016/j.ejor.2005.10.022.
http://dx.doi.org/10.1016/j.ejor.2005.10...
, using the triangular pertinence functions, can be expressed by:
Equation 11 objective function aims to maximize the total degree of fuzzy achievement and, when λ =1, it means that all fuzzy goals were fully satisfied or met.
Subject to:
Constraint 12 represents a situation for which it is desired to penalize the positive deviation.
Constraint 13 represents a situation for which it is desired to penalize the negative deviation.
Constraint 14 represents a situation for which it is desired to penalize both positive and negative deviations.
Constraints 15 to 17 are related to the limitations imposed to the degree of achievement of the scenarios associated to constraints (5)-(7).
Constraints 18 to 19 indicate the domains of variables.
where λ = is the degree of achievement of the fuzzy goals, gi is the level of aspiration (or desired value) for the objective function Gi, are, respectively, the difference between the minimum value (L) and the maximum value (U) with respect to the goal gi.
It can be observed that and, when the value of =1, it means that the fuzzy, goal gi was fully achieved. In this
In the sequence, it is presented the capital budget problem and the steps followed for its resolution.
3 Problem description and research steps
In this article, the FGP model was applied to the capital budget problem, considering the economic environment in which there is occurrence of uncertainties in the data and parameters involved in the decision taking. The research steps were:
-
Problem identification – It was chosen the capital budget problem proposed and studied by Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012... , in which it is desired to select, among a set of 45 investment projects, which projects should be executed; -
Data collection – The data used were those available in Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012... and they are in Table 1; -
Modeling, model solution and comparison of results – The FGP model was developed and implemented using the GAMS software - version 23.6.5, and was solved using the CPLEX Solver, as described in Section 4 (GAMS, 2014General Algebraic Modeling System – GAMS. (2014). Recuperado em 28 de agosto de 2014, de http://Gams.Com/Dd/Docs/Solvers/Cplex.Pdf
http://Gams.Com/Dd/Docs/Solvers/Cplex.Pd... ).
For the comparison between the results of the FGP model and the model of Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
, three objective functions were considered, related to:
-
The Profitability Index (PI) – given by the ratio between the NPV and the initial payout value;
-
The Total Discounted Payback (TDP) – associated with the time taken to recover the capital invested;
-
The Degree of Total Financial Leverage (DTFL) – is a risk measure to evaluate investment projects.
The constraints considered in the model by Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
are relating to:
-
Mutually exclusive relationships and relationships of dependence of projects;
-
Investment limits foreseen for the projects;
-
Additional relationships that ensure that the projects of the optimal solution have Modified Internal Rate of Return (MIRR) above the Minimum Acceptable Rate of Return (MARR), PI above 1 and TDP lower or equal to the useful life (economic life or their duration) of projects.
The model by Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
also has as premises that:
-
All projects begin their activities on the same initial date;
-
The project groups are independent of each other;
-
There are groups with mutually exclusive projects;
-
There are independent projects;
-
There are projects with relationship of dependence;
-
The capital budget constraint occurs only once on the initial date of analysis of the projects;
-
It is attributed, in the second stage of the model, the same weight to all components of the objective function.
Besides, to consider the situation of economic environment under uncertainty, the values of the upper (U) and lower (L) limits, desired for the fuzzy goals to PI, TDP and DTFL (see Table 2), were chosen by the researchers involved with this work, seeking to provide a better use of the budget, that is, seeking the reduction of the gap that occurred in the solution proposed by Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
.
-
Analysis of Results and Conclusions – These issues are developed in Sections 4 and 5.
In the next section, the FGP model is customized for solving the investment problem studied by Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
.
4 Problem modeling
Initially, the indices, sets, parameters and variables considered in the FGP model proposed are presented:
Indices and Sets:
j Projects j ∈ J, J = {1, 2,…, 45}.
i Objective functions, i ϵ I, I = {1, 2, 3}.
Parameters:
: Initial payout of the project j;
: Minimum Acceptable Rate of Return of the project j;
: Profitability Index of the project j;
: Modified Internal Rate of Return of the project j;
: Discounted Payback of the project j;
: Degree of Leverage of the project j;
: Useful life of the project j.
Decision variables:
xj: Binary variable associated with the selection of the project j.
Auxiliary variables:
: Positive deviation variable for the ith goal
: Negative deviation variable for the ith goal
: Degree achievement fuzzy function with 0 ≤ λi ≤ 1.
Fuzzy goal objective functions
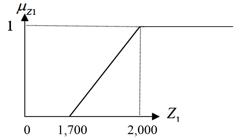
The expressions (20)-(22) are related to the maximization of the liquidity index (function Z1) under uncertainty, being adopted the values of the upper and lower limits given in Table 2:
Figure 4 illustrates the behavior of the fuzzy goal 1 (liquidity index accumulated), being considered a linear function of triangular pertinence:
Function of triangular pertinence for the fuzzy goal associated to the accumulated liquidity index.
The expressions (23)-(25) are bound to the minimization of the payback (function Z2) under the situation with uncertainty, being adopted the values of the upper and lower limits given in Table 2:
Figure 5 describes the behavior of the fuzzy goal 2 (total payback), as a linear triangular pertinence function:
Triangular Pertinence Function for the fuzzy goal associated to the minimization of the total payback.
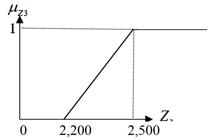
The expressions (26)-(28) are related to the maximization of the DTFL (function Z3) under uncertainty, being adopted the values of the upper and lower limits given in Table 2:
Figure 6 shows the behavior of the fuzzy goal 3 (DTFL), as a linear triangular pertinence function:
Finally, considering the data in Table 1, the FGP model can be formulated for the situation proposed by Abensur (2012)Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
:
FGP Model
Equation 29 is the objective function, which aims the maximization of the degree of achievement of the fuzzy goals associated to each objective.
Subject to:
Hard constraints (Abensur, 2012Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007.
http://dx.doi.org/10.1590/S0104-530X2012...
)
Constraint 30 is the constraint that concerned to the budget use.
Constraints 31 to 32 are constraints to the mutually exclusive projects.
Constraint 33 is the constraint that establishes that the total modified internal rate of return must be higher or equal to the total minimum acceptable rate of return.
Fuzzy constraints (new)
Constraints 34 to 35 are fuzzy constraints that associate the maximization of liquidity to the goal value R$1,700.00.
Constraints 36 to 37 are fuzzy constraints that associate the minimization of the total discounted payback to the goal value established in 4 years.
Constraints 38 to 39 are fuzzy constraints that associate the maximization of the degree of total financial leverage to the goal value R$2,200.00.
Constraints 40 is the constraint associated to the domain of the variables.
Tables 3 and 4 summarize the results obtained with both models (FGP Model and Abensur Model), being highlighted that the Abensur model does not contemplate the occurrence of uncertainty and that the resolution times of the FGP model, for any scenarios, were on average 4 seconds that facilitate the generation of alternative scenarios of interest for the problem manager.
Analysis with respect to degree of achievement fuzzy functions and deviation variables values.
It can be observed in Tables 3 and 4 that:
-
There was an increase of 380% in the number of projects selected by FGP Model (24 projects) in comparison to Abensur Model (only 05 projects). This represents that FGP Model offers a higher flexibility to the manager;
-
It was generated a higher value of PI (= R$1,660.50) by FGP Model than by Abensur Model (PI = R$854.17), corresponding to an increase of 94.4%. This means that the FGP model provided a better remuneration of invested capital;
-
It was generated a higher value of DTFL (= R$2,181.38) by FGP Model than by Abensur Model (DTFL = R$1,031.72), corresponding to an increase of 111.4%. This means that the FGP model allows a better financial turnover;
-
Using FGP Model, the value of TDP (=0.02 year) was substantially lower (99.5%) than by Abensur Model (TDP = 4.4 years), despite the occurrence of uncertainty in the data. This means that FGP Model allows shorter time to investment recovery;
-
There was a better use of the budget available (R$452,000.00) by FGP Model (investing R$446,450.00, almost 98.77% of the total resources available for investment) than by Abensur Model (investing R$149,705.00, only 33,12% of the total resources available for investment);
-
The degree of achievement for TDP was equal to 1.0. This means that, with the FGP model, it was obtained a value of TDP below the chosen fuzzy goal (4 years);
-
•
The degree of achievement for PI was equal to 0.87. This means that, with the FGP Model, the value of PI was only 13% below the chosen fuzzy goal (R$1,700.00), which is fully acceptable due to the uncertainties were incorporated to the data;
-
•
The degree of achievement for DTFL was equal to 0.91. This means that, with the FGP Model, the value of DTFL was only 9% below the chosen fuzzy goal (R$ 2,200.00), which is fully acceptable due to the uncertainties were incorporated to the data.
As an additional exercise to verify the sensitivity of the FGP model, two scenarios were generated with respect to the requirements for PI and DTFL values. In the first scenery it was considered a decrease in those values – it means a less strict project selection, and in the second scenery it was considered an increase in the values - it means a stricter project selection, as explained below, and the new solution results are in Tables 5 and 6:
New degree of achievement fuzzy function and deviation variables values (Sensibility Analysis).
-
First scenery – the fuzzy goal for PI was decreased from R$1,700.00 to R$1,600.00 and the fuzzy goal for DTFL was decreased from R$2,200.00 to R$2,100.00;
-
Second scenery – the fuzzy goal for PI was increased from R$1,700.00 to R$1,800.00 and the fuzzy goal for DTFL was increased from R$2,200.00 para R$2,300.00.
As can be observed in Tables 5, for both new scenarios with uncertainty, the number of projects selected was the same previously obtained by FGP Model, i.e. 24 projects, but note that projects 6, 11 and 43 were selected only for the first scenery. As justification for this different selection, it is verified that for the second scenery are selected projects with the highest goals values, which is not the case of these three projects mentioned.
In Table 5, it can be observed, also, that, although for the first scenery has presented lower values of PI and DTFL, it presents the higher value of payback and provides the best allocation of the available resources.
Observing Table 6, for the first scenery (with uncertainty), all fuzzy goals were fully achieved (= 1), and it presents the best allocation (almost 99% were invested) of the available resources, while the Abensur Model proposed to invest only 33% for a situation without uncertainty.
For the second scenery, the values of PI, TDP and DTFL were the same previously got by FGP Model, but the degree of achievement of the fuzzy goals associated to PI and DTFL objectives were substantially lower, respectively, 0.54 and 0.41, than those previously got by FGP Model, respectively, 0.87 and 0.91.
The sensitivity analysis shows the existence of trade-offs between objectives, enabling managers assess the impact on the solution caused by changing goals of an objective function. It also allows the decision maker identifies which are the most important objective functions for certain projects, for example, for the shareholder would be desirable to maximize profitability, and, for other hand, the company would can be interested in to obtain the return on investment in the project in a shortest possible time.
5 Conclusions
The project selection of different nature is a very difficult task, because usually there are many criteria (objectives) to be optimized, the traditional investment analysis method are restricted to a mono-objective function, and they do not consider the occurrence of uncertainty. This was the main motivation to this work that used multi-objective GP models under uncertainty.
As conclusions of this paper, it can be affirmed that the application of the FGP model was viable and relevant to solve the capital budget problem, presenting advantages in relation to the adoption of classical optimization methods (deterministic). In the case described here, the improvements found were, mainly, with regard to the increase in the number of projects included in the selected portfolio, in PI and DTFL values, in the reduction of the payback and in a better resources allocation.
In fact, the FGP model had a better performance than Abensur Model, offering better PI, TDP and DTFL values in all optimizations carried out, allowing more flexibility to the managers with regard to the use of the resources, allowing testing variations in the goals.
Finally, it should also be highlighted that the FGP model allows aggregating the occurrence of uncertainty in the problem of capital budget, as it is much verified in the practice, not occasioning higher mathematical and computational complexity both in the modeling phase and model solution, presenting low solution times.
As proposals for future researches, it is suggested to apply to the capital budget problems:
-
Data Envelopment Analysis - DEA Models (Silva et al., 2013bSilva, A. F., Marins, F. A. S., & Santos, M. V. B. (2013b). Programação por metas e análise por envoltória de dados na avaliação da eficiência de plantas mundiais de manufatura. PODes, 5(2), 172-184.);
-
The Revised Multi-Choice Goal Programming - RCMGP- LHS (Silva et al., 2015Silva, A. F., Marins, F. A. S., & Dias, E. X. (2015). Addressing uncertainty in sugarcane harvest planning through a revised multi-choice goal programming model. Applied Mathematical Modelling, 39(18), 5540-5558. http://dx.doi.org/10.1016/j.apm.2015.01.007.
http://dx.doi.org/10.1016/j.apm.2015.01.... ); -
Monte Carlo simulation combined with GP models under uncertainty (Silva et al., 2014Silva, A. F., Marins, F. A. S., & Silva, M. F. (2014). Otimização estocástica com múltiplos objetivos e simulação de Monte Carlo no desenvolvimento de estratégia de vendas. PODes, 6(1), 35-53.);
-
Models proposed by Ekel et al. (2008)Ekel, P. Y. A., Martini, J. S. C., & Palhares, R. M. (2008). Multicriteria analysis in decision making under information uncertainty. Applied Mathematics and Computation, 200(2), 501-516. http://dx.doi.org/10.1016/j.amc.2007.11.024.
http://dx.doi.org/10.1016/j.amc.2007.11.... and Pereira et al. (2015)Pereira, J. G., Jr., Ekel, P. Y. A., Palhares, R. M., & Parreiras, R. O. (2015). On multicriteria decision making under conditions of uncertainty. Information Sciences, 324, 44-59. http://dx.doi.org/10.1016/j.ins.2015.06.013.
http://dx.doi.org/10.1016/j.ins.2015.06.... combined with GP models under uncertainty.
Acknowledgements
This research was partially supported by The National Council for Scientific and Technological Development (CNPq - 306214/2015-6, CNPq - 431758/2016-6), São Paulo Research Foundation (FAPESP - 2015/12711-4; FAPESP- 2015/24560-0), and FAPEMIG (APQ-01188-16). We thank the contributions and suggestions from reviewers.
-
Financial support: This research was partially supported by The National Council for Scientific and Technological Development (CNPq - 306214/2015-6, CNPq - 431758/2016-6), São Paulo Research Foundation (FAPESP - 2015/12711-4; FAPESP - 2015/24560-0), and FAPEMIG (APQ-01188-16).
Referências
- Abensur, E. O. (2012). Um modelo multiobjetivo de otimização aplicado ao processo de orçamento de capital. Gestão & Produção, 19(4), 747-758. http://dx.doi.org/10.1590/S0104-530X2012000400007
» http://dx.doi.org/10.1590/S0104-530X2012000400007 - Abensur, E. O. (2013). Orçamento de capital: um caso especial de sequenciação de projetos. Gestão & Produção, 20(4), 979-991. http://dx.doi.org/10.1590/S0104-530X2013000400016
» http://dx.doi.org/10.1590/S0104-530X2013000400016 - Bakirli, B. B., Gencer, C., & Aydogăn, E. K. (2013). A combined approach for fuzzy multi-objective multiple knapsack problems for defence project selection. The Journal of the Operational Research Society, 65(7), 1001-1016. http://dx.doi.org/10.1057/jors.2013.36
» http://dx.doi.org/10.1057/jors.2013.36 - Bankian-Tabrizi, B., Shahanaghi, K., & Saeed Jabalameli, M. (2012). Fuzzy multi-choice goal programming. Applied Mathematical Modelling, 35(4), 1415-1420. http://dx.doi.org/10.1016/j.apm.2011.08.040
» http://dx.doi.org/10.1016/j.apm.2011.08.040 - Bertrand, J. W. M., & Fransoo, J. C. (2002). Operations management research methodologies using quantitative modeling. International Journal of Operations & Production Management, 22(2), 241-264. http://dx.doi.org/10.1108/01443570210414338
» http://dx.doi.org/10.1108/01443570210414338 - Bradi, M. A., Davis, D., & Davis, D. (2000). A comprehensive 0-1 goal programming model for project selection. International Journal of Project Management, 19, 243-252.
- Brigham, E. F., Gapenski, L. C., & Ehrhardt, M. C. (2001). Administração financeira: teoria e prática São Paulo: Atlas.
- Chang, C.-T. (2007). Multi-choice goal programming. Omega: International Journal of Management Sciences, 35(4), 389-396. http://dx.doi.org/10.1016/j.omega.2005.07.009
» http://dx.doi.org/10.1016/j.omega.2005.07.009 - Chang, C.-T. (2008). Revised multi-choice goal programming. Applied Mathematical Modelling, 32(12), 2587-2595. http://dx.doi.org/10.1016/j.apm.2007.09.008
» http://dx.doi.org/10.1016/j.apm.2007.09.008 - Chang, C.-T., Chen, H.-M., & Zhuang, Z.-Y. (2012a). Revised multi-segment goal programming: percentage goal programming. Computers & Industrial Engineering, 63(4), 1235-1242. http://dx.doi.org/10.1016/j.cie.2012.08.005
» http://dx.doi.org/10.1016/j.cie.2012.08.005 - Chang, C.-T., Chen, H.-M., & Zhuang, Z.-Y. (2012b). Multi-coefficients goal programming. Computers & Industrial Engineering, 62(2), 616-623. http://dx.doi.org/10.1016/j.cie.2011.11.027
» http://dx.doi.org/10.1016/j.cie.2011.11.027 - Charnes, A., & Cooper, W. W. (1961). Management model and industrial application of linear programming New York: Wiley.
- Deb, K. (2001). Multi-objective optimization using evolutionary algorithms England: John Wiley & Sons.
- Ekel, P. Y. A., Martini, J. S. C., & Palhares, R. M. (2008). Multicriteria analysis in decision making under information uncertainty. Applied Mathematics and Computation, 200(2), 501-516. http://dx.doi.org/10.1016/j.amc.2007.11.024
» http://dx.doi.org/10.1016/j.amc.2007.11.024 - General Algebraic Modeling System – GAMS. (2014). Recuperado em 28 de agosto de 2014, de http://Gams.Com/Dd/Docs/Solvers/Cplex.Pdf
» http://Gams.Com/Dd/Docs/Solvers/Cplex.Pdf - Ghahtarani, A., & Najafi, A. A. (2013). Robust goal programming for multi-objective portfolio selection problem. Economic Modelling, 33, 588-592. http://dx.doi.org/10.1016/j.econmod.2013.05.006
» http://dx.doi.org/10.1016/j.econmod.2013.05.006 - Jamalnia, A., & Soukhakian, M. A. (2009). A hybrid fuzzy goal programming approach with different goal priorities to aggregate production planning. Computers & Industrial Engineering, 56(4), 1474-1486. http://dx.doi.org/10.1016/j.cie.2008.09.010
» http://dx.doi.org/10.1016/j.cie.2008.09.010 - Joshi, D., & Kumar, S. (2016). Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. European Journal of Operational Research, 248(1), 183-191. http://dx.doi.org/10.1016/j.ejor.2015.06.047
» http://dx.doi.org/10.1016/j.ejor.2015.06.047 - Khalili-Damghani, K., Sadi-Nezhad, S., & Tavana, M. (2013). Solving multi-period project selection problems with fuzzy goal programming based on TOPSIS and a fuzzy preference relation. Information Sciences, 252, 42-61. http://dx.doi.org/10.1016/j.ins.2013.05.005
» http://dx.doi.org/10.1016/j.ins.2013.05.005 - Lam, J. S. L., & Lai, H.-H. (2015). Developing environmental sustainability by ANP-QFD approach: the case of shipping operations. Journal of Cleaner Production, 105, 275-284. http://dx.doi.org/10.1016/j.jclepro.2014.09.070
» http://dx.doi.org/10.1016/j.jclepro.2014.09.070 - Lee, J. W., & Kim, S. H. (2000). Using analytic network process and goal programming for interdependent information system project selection. Computers & Operations Research, 27(4), 367-382. http://dx.doi.org/10.1016/S0305-0548(99)00057-X
» http://dx.doi.org/10.1016/S0305-0548(99)00057-X - Li, D.-F., & Wan, S.-P. (2014). A fuzzy inhomogenous multiattribute group decision making approach to solve outsourcing provider selection problems. Knowledge-Based Systems, 67, 71-89. http://dx.doi.org/10.1016/j.knosys.2014.06.006
» http://dx.doi.org/10.1016/j.knosys.2014.06.006 - Liang, G.-S., & Wang, M. J. (1993). Evaluating human reliability using Fuzzy relation. Microelectronics and Reliability, 33(1), 63-80. http://dx.doi.org/10.1016/0026-2714(93)90046-2
» http://dx.doi.org/10.1016/0026-2714(93)90046-2 - Liao, C. N. (2009). Formulating the multi-segment goal programming. Computers & Industrial Engineering, 56(1), 138-141. http://dx.doi.org/10.1016/j.cie.2008.04.007
» http://dx.doi.org/10.1016/j.cie.2008.04.007 - Martel, J. M., & Aouni, B. (1998). Diverse imprecise goal programming model formulations. Journal of Global Optimization, 12(2), 127-138. http://dx.doi.org/10.1023/A:1008206226608
» http://dx.doi.org/10.1023/A:1008206226608 - Mulvey, J. M., Vanderbei, R. J., & Zenios, S. A. (1995). Robust optimization of large-scale systems. Operations Research, 43(2), 264-281. http://dx.doi.org/10.1287/opre.43.2.264
» http://dx.doi.org/10.1287/opre.43.2.264 - Pereira, J. G., Jr., Ekel, P. Y. A., Palhares, R. M., & Parreiras, R. O. (2015). On multicriteria decision making under conditions of uncertainty. Information Sciences, 324, 44-59. http://dx.doi.org/10.1016/j.ins.2015.06.013
» http://dx.doi.org/10.1016/j.ins.2015.06.013 - Romero, C. (2001). Extended lexicographic goal programming: a unifying approach. Omega, 29(1), 63-71. http://dx.doi.org/10.1016/S0305-0483(00)00026-8
» http://dx.doi.org/10.1016/S0305-0483(00)00026-8 - Romero, C. (2004). A general structure of achievement function for a goal programming model. European Journal of Operational Research, 153(3), 675-686. http://dx.doi.org/10.1016/S0377-2217(02)00793-2
» http://dx.doi.org/10.1016/S0377-2217(02)00793-2 - Saaty, T. L. (1977). A scaling method for priorities in hierarchical structures. Journal of Mathematical Psychology, 15(3), 234-281. http://dx.doi.org/10.1016/0022-2496(77)90033-5
» http://dx.doi.org/10.1016/0022-2496(77)90033-5 - Saaty, T. L. (2006). Decision making with the analytic network process. International Series in Operations Research & Management Science, 95, 1-26. http://dx.doi.org/10.1007/0-387-33987-6_1
» http://dx.doi.org/10.1007/0-387-33987-6_1 - Santos, A., Lavarda, C. E. F., & Marcello, I. E. (2012). The relationship between cost management knowledge and budgetary participation with managers’ performance. Revista Brasileira de Gestão de Negócios, 16, 124-142.
- Santos, J. O., & Barros, C. A. S. (2011). O que determina a tomada de decisão financeira: razão ou emoção? RBGN: Revista Brasileira de Gestão de Negócios, 13(38), 7-20. http://dx.doi.org/10.7819/rbgn.v13i38.785
» http://dx.doi.org/10.7819/rbgn.v13i38.785 - Silva, A. F., & Marins, F. A. S. (2014). A Fuzzy Goal Programming model for solving aggregate production-planning problems under uncertainty: a case study in a Brazilian sugar mill. Energy Economics, 45, 196-204. http://dx.doi.org/10.1016/j.eneco.2014.07.005
» http://dx.doi.org/10.1016/j.eneco.2014.07.005 - Silva, A. F., & Marins, F. A. S. (2015). Revisão da literatura sobre modelos de programação por metas determinística e sob incerteza. Production Journal, 25(1), 92-112. http://dx.doi.org/10.1590/S0103-65132014005000003
» http://dx.doi.org/10.1590/S0103-65132014005000003 - Silva, A. F., Marins, F. A. S., & Dias, E. X. (2015). Addressing uncertainty in sugarcane harvest planning through a revised multi-choice goal programming model. Applied Mathematical Modelling, 39(18), 5540-5558. http://dx.doi.org/10.1016/j.apm.2015.01.007
» http://dx.doi.org/10.1016/j.apm.2015.01.007 - Silva, A. F., Marins, F. A. S., & Montevechi, J. A. B. (2013a). Multi-choice mixed integer goal programming optimization for real problems in a sugar and ethanol milling company. Applied Mathematical Modelling, 37(9), 6146-6162. http://dx.doi.org/10.1016/j.apm.2012.12.022
» http://dx.doi.org/10.1016/j.apm.2012.12.022 - Silva, A. F., Marins, F. A. S., & Santos, M. V. B. (2013b). Programação por metas e análise por envoltória de dados na avaliação da eficiência de plantas mundiais de manufatura. PODes, 5(2), 172-184.
- Silva, A. F., Marins, F. A. S., & Silva, M. F. (2014). Otimização estocástica com múltiplos objetivos e simulação de Monte Carlo no desenvolvimento de estratégia de vendas. PODes, 6(1), 35-53.
- Wang, R. C., & Liang, T. F. (2004). Projects management decisions with multiple fuzzy goals. Construction Management and Economics, 22(10), 1047-1056. http://dx.doi.org/10.1080/0144619042000241453
» http://dx.doi.org/10.1080/0144619042000241453 - Yaghoobi, M. A., & Tamiz, M. (2007). A method for solving fuzzy goal programming problems based on MINMAX approach. European Journal of Operational Research, 177(3), 1580-1590. http://dx.doi.org/10.1016/j.ejor.2005.10.022
» http://dx.doi.org/10.1016/j.ejor.2005.10.022 - Zimmermann, H. J. (1978). Fuzzy programming and linear programming with several objective function. Fuzzy Sets and Systems, 1(1), 45-55. http://dx.doi.org/10.1016/0165-0114(78)90031-3
» http://dx.doi.org/10.1016/0165-0114(78)90031-3
Publication Dates
-
Publication in this collection
17 Aug 2017 -
Date of issue
Jan-Mar 2018
History
-
Received
01 June 2015 -
Accepted
26 Oct 2015