Abstracts
In this paper we briefly review the basic requirements that must be satisfied by any wave function representing many-electron systems. Following that, we examine the conditions under which the classical concepts of molecular structure, chemical structure and chemical bond can be translated into a quantum-mechanical language. Essential to this aim is the utilization of an independent particle model (IPM) for a many-electron system. In spite of the great popularity of the Hartree-Fock (HF) model only Valence-Bond (VB) type wave functions with optimized, singly occupied and non necessarily orthogonal atomic-like orbitals, can provide a quantum-mechanical translation of the classical concepts of chemical structure and chemical bond, although the HF model can still be useful for translating the concept of molecular structure. Finally, a quantum-dynamical-type of analysis allows us to conclude that, from the quantum mechanical point of view, the chemical bond is a consequence of interference effects. From the energetic point of view, the interference effect responsible for the bond formation manifests itself as a reduction of the kinetic energy of the electrons as the bond is formed.
chemical bond; generalized valence bond; quantum interference; permutation symmetry; many-electrons wave function
As condições básicas que devem ser satisfeitas por qualquer função de onda representando um sistema polieletrônico são apresentadas e discutidas. Em seguida, examinamos como construir funções de onda para sistemas polieletrônicos que satisfaçam àquelas condições e analisamos as condições sob as quais os conceitos clássicos de estrutura molecular, estrutura química e de ligação química podem ser traduzidos para a mecânica quântica. Uma vez estabelecido que essa tradução requer o uso de modelos de partículas independentes, os modelos mais usuais são analisados quanto à capacidade de gerarem funções de onda que satisfaçam as condições básicas anteriormente estabelecidas. Desta análise resulta que somente funções de onda do tipo Generalized Valence Bond (GVB) e Spin-Coupled VB (SCVB) apresentam as propriedades necessárias para representar um sistema polieletrônico, átomo ou molécula. Além disso, somente funções do tipo GVB, com orbitais do tipo atômico, otimizados, mono-ocupados e não necessariamente ortogonais, permitem uma tradução quanto-mecânica dos conceitos clássicos de estrutura molecular, estrutura química e de ligação química. Funções de onda construídas com base no modelo de orbitais moleculares (MO), não são aceitáveis para representar sistemas polieletrônicos e não se prestam à tradução dos conceitos clássicos de estrutura química e de ligação química, podendo, quando muito, ser usadas para definir estrutura molecular. Finalmente, uma análise quanto-eletrodinâmica permite concluir que, do ponto de vista da mecânica quântica, a formação de uma ligação química é conseqüência de efeitos de interferência. Do ponto de vista do balanço energético do processo de formação de uma ligação química, os efeitos de interferência, responsáveis pela formação da ligação, manifestam-se como uma redução da energia cinética dos elétrons, à medida que a ligação é formada.
REVIEW
The nature of the chemical bond
Marco Antonio Chaer Nascimento*
Instituto de Química, Universidade Federal do Rio de Janeiro, Cidade Universitária, CT Bloco A sala 412, 21941-909 Rio de Janeiro-RJ, Brazil
ABSTRACT
In this paper we briefly review the basic requirements that must be satisfied by any wave function representing many-electron systems. Following that, we examine the conditions under which the classical concepts of molecular structure, chemical structure and chemical bond can be translated into a quantum-mechanical language. Essential to this aim is the utilization of an independent particle model (IPM) for a many-electron system. In spite of the great popularity of the Hartree-Fock (HF) model only Valence-Bond (VB) type wave functions with optimized, singly occupied and non necessarily orthogonal atomic-like orbitals, can provide a quantum-mechanical translation of the classical concepts of chemical structure and chemical bond, although the HF model can still be useful for translating the concept of molecular structure. Finally, a quantum-dynamical-type of analysis allows us to conclude that, from the quantum mechanical point of view, the chemical bond is a consequence of interference effects. From the energetic point of view, the interference effect responsible for the bond formation manifests itself as a reduction of the kinetic energy of the electrons as the bond is formed.
Keywords: chemical bond, generalized valence bond, quantum interference, permutation symmetry, many-electrons wave function
RESUMO
As condições básicas que devem ser satisfeitas por qualquer função de onda representando um sistema polieletrônico são apresentadas e discutidas. Em seguida, examinamos como construir funções de onda para sistemas polieletrônicos que satisfaçam àquelas condições e analisamos as condições sob as quais os conceitos clássicos de estrutura molecular, estrutura química e de ligação química podem ser traduzidos para a mecânica quântica. Uma vez estabelecido que essa tradução requer o uso de modelos de partículas independentes, os modelos mais usuais são analisados quanto à capacidade de gerarem funções de onda que satisfaçam as condições básicas anteriormente estabelecidas. Desta análise resulta que somente funções de onda do tipo Generalized Valence Bond (GVB) e Spin-Coupled VB (SCVB) apresentam as propriedades necessárias para representar um sistema polieletrônico, átomo ou molécula. Além disso, somente funções do tipo GVB, com orbitais do tipo atômico, otimizados, mono-ocupados e não necessariamente ortogonais, permitem uma tradução quanto-mecânica dos conceitos clássicos de estrutura molecular, estrutura química e de ligação química. Funções de onda construídas com base no modelo de orbitais moleculares (MO), não são aceitáveis para representar sistemas polieletrônicos e não se prestam à tradução dos conceitos clássicos de estrutura química e de ligação química, podendo, quando muito, ser usadas para definir estrutura molecular. Finalmente, uma análise quanto-eletrodinâmica permite concluir que, do ponto de vista da mecânica quântica, a formação de uma ligação química é conseqüência de efeitos de interferência. Do ponto de vista do balanço energético do processo de formação de uma ligação química, os efeitos de interferência, responsáveis pela formação da ligação, manifestam-se como uma redução da energia cinética dos elétrons, à medida que a ligação é formada.
1. Introduction1
Prior to the advent of quantum mechanics, chemistry was essentially an empirical science. In spite of all the efforts by Boyle and others to revive the atomistic theory and of Daltons proposition of his atomic theory, the lack of a model for the atom, which could be used as the building block for a structural chemistry, contributed to maintain chemistry as an empirical science. In fact, until the end of the 19th century most chemists did not believe in the existence of the atom. It is hard to evaluate how much of this disbelief could be attributed to the lack of an atomic model or to the strong influence of some prominent chemists, such as Lavoisier, who considered of pure metaphysical nature any discussion regarding the atomic constitution of matter.
Until the end of the 19th century most of the effort was directed towards the development of a general classificatory theory for the known chemical substances. Due mainly to the efforts of Lavoisier, Dumas, Berzelius, Wohler and Leibig, the elemental composition of several different substances was determined. The concept of chemical formula or chemical composition was then introduced to represent the relative quantities of each element present in a given substance.
The idea that each chemical substance could be represented by a unique chemical formula suffered its first drawback when Leibig and Wohler, in 1823, showed that silver cyanide and fulminate, two very different substances, presented identical chemical compositions. This result led Gay-Lussac and Chevreul to argue that chemists should seriously take into consideration that chemical substances might differ in their "internal" arrangement. In 1830, Berzelius observed that it was impossible to detect any differences in the chemical compositions of the tartaric acids and their racemic mixture. He coined the term isomerism to express the fact that different substances may have identical chemical formulas. At this point it became clear that the concept of chemical formula alone could not be used to univocally identify a chemical substance and therefore could not be used as a single piece of a classificatory system.
Many other classificatory schemes were proposed but none of them could rationalize all the data about the properties of the known chemical substances. Among the proposed schemes, the classification by types played a very important role in the development of the concept of molecular structure. Briefly, the classification by types assumed the existence of some reference substances from which all the others could be derived by substituting of one or more of their atoms by other atoms or groups of atoms, called radicals. An important point to be noticed is that this sort of representation somehow suggests that a certain atom links or coordinates to other atoms or groups of atoms of the substance. However, it is also important to notice that at that time the word atom was used with two different meanings: the chemical atom, which formed the conceptual basis for assigning relative elementary weights and the chemical formula in any classificatory system; and the atom, as conceived by the Greeks and by Dalton, as the ultimate natural building blocks of all substances. While most chemists would very comfortably use the word atom in the context of a classificatory system, at the same time they would deny any physical reality to it.
Little by little, the search for a general classificatory scheme led chemists to conclude that the "internal" arrangement of the atoms of a substance should indeed be taken into account. The concept of chemical formula was then superseded by the idea of structural formula, which can be viewed as the precursor to the concept of molecular structure. The search for a structural formula for a substance which would be consistent with its observed properties led to the concept of valence and to the idea that atoms could be linked together. The works by Kekulé, Couper, Butlerov, Brown and Erlenmeyer not only reinforced the importance of the concept of structural formula but also the idea that the internal arrangement of the atoms would define the chemical properties of a substance, as emphatically defended by Laurent many years before.
Until 1874 the structural formulas of substances were represented by planar figures showing the relative positions of the atoms and how they were linked. However, the idea that these formulas would indeed represent the "real" arrangement of the atoms (and therefore determine all the properties of a substance) was challenged by the phenomenon of stereoisomerism, discovered by Biot in 1815. For instance, it was impossible to distinguish the two stereoisomers of tartaric acid, identified by Pasteur, using planar representations. The problem of representing stereoisomers by structural formulas was solved by vant Hoff, in 1874, by adopting three-dimensional structures and assuming that each carbon atoms would be at the center of a tetrahedral and that the atoms to which it was linked would occupy the positions defined by the vertices of the tetrahedron. The work by vant Hoff determined the turning point from the attempts at building classificatory schemes to that of establishing a structural chemistry, where structural formulas would indeed define the properties of a substance.
Therefore, to the extent that the structural formula indeed represents the real internal arrangement of the atoms of the substance, it is reasonable to adopt the term molecular structure to designate this internal arrangement. Thus, at the end of the 19th century chemists would picture a molecule as a three-dimensional arrangement of atoms, held together by chemical bonds. The relative positions of the atoms would define a molecular structure and each particular way of connecting the atoms would define a different chemical structure. However, the nature of the forces keeping the atoms together, i. e., the bond, was totally unknown.
The discovery of the electron by Thomson opened the possibility for developing atomic models and electronic theories of the chemical bond. Among the models proposed to describe the formation of a chemical bond, Lewis2 idea of atoms sharing pairs of electrons was the most successful in explaining how single and multiple bonds could be formed between atoms and why some atoms may present different "valences". Also, with his ideas Lewis was able to extend the concepts of acid and base as substances capable of accepting or donating a pair of electrons.
The advent of quantum mechanics forced a complete revision of that picture and as soon as it was realized that Schroedingers equation could be only exactly solved for very simple systems, the need for approximate methodologies for obtaining the wave functions became evident. At this point it would be instructive to ask: is it possible to translate to quantum mechanics the concepts of molecular structure and chemical structure? Else, could quantum mechanics provide an explanation for the origin of the chemical bond?
Before one attempts at answering to these questions, it is important to realize that there are certain basic conditions which must be satisfied by any wave function representing a many-electrons system, either atoms or molecules. After reviewing these conditions we will show that only wave functions satisfying them can be used to translate to quantum mechanics the concepts of chemical structure and chemical bond. Moreover, this translation will allow us to considerably enlarge the classical concept of chemical bond as resulting from the pairing of electrons by adjacent atoms of the molecule.
2. Molecular Hamiltonian and its Symmetries3
The Schroedinger equation (SE), even for the simplest molecule (H2+), can only be solved analytically under the Born-Oppenheimer approximation.4 Within this approximation, one solves for the electronic motion in the field of the fixed nuclei, using the electronic Hamiltonian (Hel) and after for the motion of the nuclei in the average field provided by the electrons, making use of the nuclear Hamiltonian (Hnuc).
For certain molecules, it is possible to find operators, Ô, which exchange the position of two or more nuclei keeping Hel and consequently the electronic energy invariants. These operators commute with Hel, [ Hel , Ô] = 0. The existence of such operators implies that the Hamiltonian exhibits point group symmetry. On the other hand, the energy invariance imposes some conditions to the electronic wave functions. Thus:
since Hel commutes with Ô and Eel is constant. From equation (1) it is clear that if |yel> represents a non-degenerate state of the molecule, the energy invariance requires that:
If the state is degenerate, the action of Ô over |yel> can generate either another component of the state defined by Eel or a linear combination of the various degenerate components. In either case the energy invariance is observed.
Although very useful in the study of molecules, point group symmetry is restricted to less than 10% of the known molecules. On the other hand, the Hamiltonian of any many-electrons system, atom or molecule, exhibits another type of symmetry: the permutation symmetry.5,6 Consider the set of all operators Pij which exchange the position coordinates of any two electrons of the system. Since the electrons are indistinguishable, the Hamiltonian and the energy will be invariant to the action of any such operators:
and, in order to keep the energy invariant:
In conclusion, the presence of symmetries in the molecular Hamiltonian imposes some condition on any wave function, exact or approximate, representing the many-electrons system. In addition of being well behaved, wave functions describing quantum systems of identical particles must transform like one of the irreducible representations of the Hamiltonian point group (if point group symmetry is present) and must be totally symmetric or anti-symmetric with respect to the exchange of the position coordinates of any two identical particles of the system. In another words, the wave function must transform like the totally symmetric or anti-symmetric representation of the permutation (or symmetric) group SN, where N stands for the number of identical particles of the system. There remains the question of which wave function should be used to describe a many-electrons system: the totally symmetric or the totally anti-symmetric.
3. Electronic Spin and the Correct Form of a Many-electrons Wave Function
In order to fully express the correct symmetries of the wave function and answer the question above, the spin must be included in our description. However, since the non-relativistic Hamiltonian does not contain spin coordinates, the spin must be included through an ad-hoc procedure, by introducing the two spin functions, a and b, which are simultaneous eigenfunctions of the S2 and Sz operators:
In a non-relativistic formulation the spin, as we will see, is only an indicator.7 It does not play any direct dynamical role in the electronic Hamiltonian, but its inclusion as an electronic coordinate is essential to properly account for the symmetry requirements of the total electronic wave function. However, since the non-relativistic Hamiltonian does not contain any terms involving the spin coordinates, one cannot obtain any information about the spin of the system by solving Schroedingers equation H |y> = E |y>. That is, the solutions of Schroedingers equation only depend on the spatial coordinates of electrons and nuclei:
where x stands for the set of nuclear coordinates. Notice that the same must be true for any approximate wave function obtained through the variational principle.3 However, one may include information about the spin state of the system by multiplying the spatial part of the wave function by a spin wave function, c. The resulting wave function Y, though not a solution of the Schroedingers equation, does satisfy this equation because H does not operate on c:
This is not an approximation. In fact, this is the exact form of the total wave function for any non-relativistic many-particle system. Note that, so far, we do not know anything about the spin wave function c, but since all the electrons have the same spin, Pij |c (s1, s2, .. sN )> = ± |c (s1, s2, .. sN )>, that is, the spin wave functions must also be symmetric or anti-symmetric relative to the permutation of the spin coordinates of any two electrons.
According to the anti-symmetry principle, for any system of identical particles with semi-integer spin, the total wave function must be anti-symmetric. Electrons have spin (1/2) and therefore any acceptable wave function describing a many-electrons system must be anti-symmetric relative to the exchange of the spatial and spin coordinates of any two electrons. However, since the total wave function must be a product of spatial and spin parts, there are two ways of obtaining a total anti-symmetric wave function:
In order to obtain solutions, exact or approximate, to the SE for a many-electrons system one must define a priori the spin state of the system. This is so because the SE does not contain any information about the spin of the system. Once the spin of the system is defined one immediately knows if |c (s1, s2, .. sN) > is symmetric (S) or anti-symmetric (A). And once the symmetry of the spin part is known the symmetry of the spatial part is automatically defined. Therefore, in a non-relativistic formulation of quantum mechanics the spin is just an indicator7 of which symmetry the spatial part of the total wave function must exhibit so that the total wave function conforms to the anti-symmetry principle.
In summary, in order to take into account the anti-symmetry principle and the fact that electrons are indistinguishable, any acceptable wave function for a non-relativistic many-electrons system must satisfy the following conditions: a) the total wave function must be a product of a spatial and a spin part; b) both the spatial and spin parts must independently exhibit permutation symmetry, i.e., must transform like the irreducible representations of the symmetric (SN) group; c) the total wave function must be anti-symmetric.
4. Translating to Quantum Mechanics the Concepts of Molecular Structure, Chemical Structure and Chemical Bond
Having established the conditions that must be satisfied by any wave function, exact or approximate, describing a many-electrons system, we are ready to examine the problem of how to translate to quantum mechanics the classical concepts of molecular structure, chemical structure and chemical bond.
4.1. Molecular structure
Classically, the molecular structure is defined by the relative positions of the atoms of the molecule. However, the SE for any molecule contains terms corresponding to the kinetic energy of all the nuclei. Since all the nuclei are in constant motion, there is no guarantee that the atoms of the molecule will keep their relative positions as time evolves.
If the Born-Oppenheimer approximation is imposed, one can solve SE for the electronic motion at several different nuclear configurations {xi}. This set of solutions allows us to construct a potential energy hyper-surface representing how the electronic energy depends on the nuclear coordinates. The nuclear problem can then be solved by inserting the electronic potential energy into the nuclear Hamiltonian and solving the corresponding Schroedinger equation. If the potential energy hyper-surface exhibits a minimum, (Eel)min, which added to the minimum value of the nuclear energy, also called zero-point vibration energy, EZPE, furnishes a total energy less than the sum of the energies of the isolated atoms of the molecule, one says that the molecule is bound. In this case, the nuclear configuration corresponding to (Eel)min in the hyper-surface can be used to define the molecular structure. However, contrary to the classical belief, the relative positions of the nuclei are not fixed, but the atoms vibrate around their equilibrium positions at the configuration of minimum energy.
In conclusion, the concept of molecular structure can be translated to quantum mechanics, but it relies on the validity of the Born-Oppenheimer approximation.
4.2. Chemical structure
Given a molecular structure, in order to define chemical structure one must specify which atoms of the molecule are connected and their degree of connectivity. Each distinct way of connecting the atoms will define a different chemical structure. The problem of translating the concept of chemical structure to quantum mechanics is therefore more complex than that of translating molecular structure. This is so because the number of bonds, in the Lewis sense,2 between two atoms is almost always much smaller than the number of electrons of each atom. Therefore, only a small fraction of the electrons (the valence electrons) take part in the bonding process. Thus, unless the one-electron states (orbitals) of an atom can be univocally determined, it would be impossible to separate the valence from the non-valence states and to predict how many and what kind of bonds can be formed. On the other hand, since each particular way of binding the atoms of a molecule defines a different structure, the translation to quantum mechanics of the concept of chemical structure also depends on the knowledge of the individual one-electron states. In conclusion, any attempt at translating to quantum mechanics the classical concept of chemical structure has to be made within the framework of an Independent Particle Model (IPM).
In spite of the fact that IPMs are approximations to the electronic Schroedingers equation, they should provide solutions which conform to the conditions previously established for any acceptable wave function representing a non-relativistic many-electrons system, namely they must be a product of a spatial part and a spin part, both being basis for the symmetric group and such that this product is anti-symmetric. Besides that, in order to define chemical structure, the one-electron states, or orbitals, must be univocally determined.
Molecular quantum mechanics has been developed along two distinct IPMs, namely the valence-bond (VB)8-15 and the molecular orbital (MO)16-19 model. The capability of these two models was greatly improved with the incorporation of the Hartree's average field approximation and the self-consistent procedure to obtain the one-electron states. The modern versions of these models are known by the acronyms GVB (Generalized Valence Bond)20 or SCVB (Spin Coupled VB)21 and HF-MO (Hartree-Fock MO).22
In spite of the great popularity of the HF model only the GVB and the SCVB models provide wave-functions which conform to all the requirements mentioned above.3,23 Therefore, the translation to quantum mechanics of the concept of chemical structure requires the use of either the GVB or the SCVB model. Nevertheless, the HF-MO model can still be useful for determining molecular structure. In fact, according to Mulliken, the MO model was idealized to exactly avoid the idea of chemical structure and chemic bond and to highlight the concept of molecular structure. In his own words:24 "The fact that valence electrons almost always occur in pairs in saturated molecules appear to have after all no fundamental connection with the existence of chemical bonding A clearer understanding of molecular structure can be often obtained by dropping all together the idea of atoms and ions held together by valence forces, and adopting the molecular point of view, which regards each molecule as a distinct individual built up of nuclei and electrons".
The GVB wave function, in its most general form, can be written as:
where  = (1/N!) SPdP P is the anti-symmetrizer operator and {ji} are atomic-like, singly occupied and not necessarily orthogonal orbitals. The orbitals {ji} and the spin function c are simultaneously optimized by requiring the functional EGVB = <YGVB|Hel|YGVB> to be stationary. No restrictions are imposed to the spin function other than being a basis for SN and an eigenfunction of
= (1/N!) SPdP P is the anti-symmetrizer operator and {ji} are atomic-like, singly occupied and not necessarily orthogonal orbitals. The orbitals {ji} and the spin function c are simultaneously optimized by requiring the functional EGVB = <YGVB|Hel|YGVB> to be stationary. No restrictions are imposed to the spin function other than being a basis for SN and an eigenfunction of  2 and
2 and  z. Notice that, by definition, |YGVB> has the form required for a wave function representing a non-relativistic many-electrons system (equation 6).
z. Notice that, by definition, |YGVB> has the form required for a wave function representing a non-relativistic many-electrons system (equation 6).
There is a vast literature showing the use of this wave function and other simplified forms of it (Strong Orthogonal GVB, SOGVB and the Perfect-Pairing GVB, GVB/PP) to determine chemical structures of molecules in their ground and electronic excited states.3,25,26 Therefore, I will not pursue this point any further but the interested reader may consult the literature to see that this wave function indeed allows a perfect translation of the classical concept of chemical bond.
4.3. Nature of the chemical bond
It still remains to see if quantum mechanics can provide an explanation for the origin of the chemical bond. The work by Heitler and London8 (HL) showing that quantum mechanics could predict that H2 is stable relative to the isolated atoms is considered by many as the birth of quantum chemistry. Making use of the Born-Oppenheimer approximation and of VB-type wave functions, those authors showed that the potential energy surface for the H2 system exhibits a minimum for a value of energy much lower than the sum of the energies of the isolated atoms plus the zero-point vibration energy. Many improvements to the HL treatment of the H2 have been proposed27-29 but regardless of the type of wave function used (VB, MO or other variation wave functions), any analysis of the chemical bond based on the decomposition of the total electronic energy (Eel) into the kinetic (T) and potential (V) contributions (Figure 1)29 led to the same conclusion: that the chemical bond results from a decrease in the total potential energy of the H2 system as the molecule is formed.
However, this conclusion does not make any sense at all! As the nuclei approach each other, the nuclear repulsion increases and in order to balance it, electrons must be brought from regions near the nuclei to the bonding region. But, in order to do that, work must be performed to overcome the coulombic attraction and the electron-nucleus potential energy also increases! Thus, the conclusion that the chemical bond is formed due to a decrease in the potential energy of the system is obviously wrong! Unfortunately this interpretation prevails in most of the chemical literature and certainly in most chemistry classrooms.
Only a few people realized that the partitioning of the total energy into kinetic and potential contributions was not appropriate for examining the origin of the chemical bond. In particular, the papers by Ruedenberg,30 Wilson and Goddard,31 and Kutzelnigg32 present a very detailed analysis of the problem and in spite of the fact that quite different approaches have been used, the same conclusions have been reached about the energetic of the chemical bond formation. The common objective of those authors was to find ways of partitioning the total energy in a way that it would make sense for analyzing the formation of a chemical bond. Quite interesting, after being able of performing some sort of partitioning of the energy they were also able to identify the quantum effect responsible for the bond formation. However, the problem of which type of IPM model would be the appropriate one for this type of analysis was not discussed. The papers cited are not easy to follow, mainly the one by Ruedenberg,30 and I believe that this is the reason why their conclusions remain ignored by most chemists.
In what follows I would like to show that those same conclusions can be reached, in a much simpler way, if instead of searching for schemes of energy partition one tries first to identify the quantum phenomenon responsible for the chemical bond. Once this objective is attained, everything else, i.e, how to partition the energy and the proper wave function (VB or MO) to be used, will follow naturally. In fact, this type of analysis provides a much deeper insight into the nature of the chemical bond and allows us to extend this concept beyond its classical limits.
Before starting our analysis, let us recall the famous double-slit experiment shown in Figure 2.
This simple experiment reveals one of the most fundamental and intriguing laws governing the quantum world but very often forgotten. If photons or electrons are sent through slit 1 (with slit 2 closed), the distribution of intensity for electrons arriving at different points of the backstop is represented by curve P1. Similarly, curve P2 represents the same when the quantum particles are sent through slit 2 with slit 1 closed. Classically, if the experiment is repeated with both slits opened, the total intensity would be just the sum P1 + P2. However, this is not what is experimentally observed, as shown on the right of Figure 2. Nevertheless, the observed distribution P12 can be obtained from curves P1 and P2 just by adding the amplitudes (f1 and f2) for each separate event, and expressing the result as:

The first two terms represent the classical result while the third term is a quantum effect. It is important to emphasize that the closer the frequencies (energies) of the photons or the energy of the electrons, the stronger is the interference effect. Thus, the fundamental law revealed by this experiment is the following: "When an event can occur in several alternative and indistinguishable ways, the amplitude for observing the event is the sum of the amplitudes for each way considered separately".
To proceed with the analysis of the chemical bond, I will make use of simple Feynman (space-time) diagrams.33,34 Remember that within the Born-Oppenheimer approximation, the nuclei are fixed in space. And since the chemical bond concept can only be formulated within the framework of an IPM, only the zero-order Feynman diagrams (those not showing interaction lines between the electrons) need to be used.
Figure 3 shows the diagram corresponding to electron 1 moving from point 1 to point 2 interacting with proton 1, while electron 2 moves from point 3 to 4, interacting with proton 2.
The amplitude for observing this event is just the product of the amplitudes for the motion of electron from point 1 to point 2 and for the motion of electron 2 from point 3 to 4, since their motions are independent:
A1 = Ae1 (1 ® 2) Ae2 (3 ® 4)
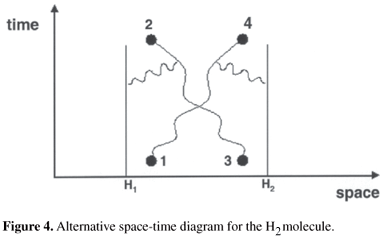
But the event can also take place as shown in Figure 4, since electrons are indistinguishable:
whose amplitude is:
A2 = Ae1 (1 ® 4) Ae2 (3 ® 2)
According to the fundamental law, the probability of observing such a system constituted by two electrons moving independently of each other, under the influence of the two nuclei, will be:

At this point it is important to mention that considering the electrons to move independently of each other does not rule out the possibility that they interact through an average field as usually assumed in IPMs. This condition can be simply incorporated in the model used to compute the amplitudes A1 and A2.
Let us denote by ja and jb the amplitudes for observing the electrons at points 2 and 4, after the system has propagated for a time t. If the time evolution of the system is given by the diagram in Figure 3, the amplitude for finding e1 at point 2 and simultaneously e2 at point 4, at the time t, will be:
where E = Ea +Eb.
On the other hand, this event is indistinguishable from the one depicted in Figure 4 whose amplitude is:
Therefore, the total amplitude, i.e., the wave functions representing the system, hydrogen molecule, is given by:
Notice that we did not specify any IPM for calculating the amplitudes ja and jb. In spite of that, because electrons are indistinguishable, the application of the fundamental law leads us directly to the wave function Y(1, 2) which has the form of a VB-type wave function!
The probability density of observing electrons arriving simultaneously at points 2 and 4 is given by:
It is clear from equation (12) that first two terms correspond to the classical probability and therefore everything else is due to the quantum interference effect. Also, if one asks for the probability of observing the two electrons around points 2 and 4, the quantum part will be proportional to the overlap of the amplitudes ja and jb. Thus the interference effect is directly related to the amplitudes overlap.
The next point to be examined is how this interference effect contributes to the stabilization of the system (H2 molecule). In order to answer this question one needs to compute the energy associated to the wave function (11), at different values of the internuclear distance (RH1H2). But, in order to proceed further we must know the amplitudes ja and jb or, using a terminology more familiar to chemists, one needs to specify the orbitals. It is common practice to choose orbitals centered on the atoms. Thus, let us assume that ja and jb are atomic-like orbitals centered on protons H1 and H2, respectively. These orbitals could be taken to be identical to the hydrogen orbitals for all values of RH1H2 or else could be optimized, in a self-consistent way, for each value of RH1H2 . The first choice corresponds to the old VB model and the second choice to the GVB model. The conclusions will not depend on the model chosen, but the GVB model is quantitatively much more accurate.
The energy of the wave function (12) is given by:
where H is the exact non-relativistic Born-Oppenheimer Hamiltonian for the H2 molecule, and E1 + E2 is the total energy of the isolated atoms. According to equation (13), the molecule will be formed only if:
 or if Q + A < 0 ,
or if Q + A < 0 ,
where:
and S =< ja (1)jb(1) > = < ja (2)jb(2) >
The first two terms in the expression for Q represent the attraction of the electron density ja ja* to the nucleus H2 and of the electron density jb jb* to the nucleus H1 respectively, also known as penetration terms. The third term corresponds to the repulsion energy between the electron densities ja ja* and jb jb* and the last term is the nuclear repulsion energy. Q is therefore simply the equivalent to the classical electrostatic energy between two hydrogen atoms. However, it is well known that the stability of the molecule cannot be explained as resulting from the classical superposition of the electronic densities of the isolated atoms. On the other hand, Q, the quantum mechanical counterpart, is also positive except for values of RH1H2 smaller than the equilibrium internuclear distance, when it becomes slightly negative but still much smaller than the zero point vibration energy, which is always positive. Thus, the molecule will be formed only if A < 0 and |A| > Q. As shown above, the term A, also known as the exchange integral in the VB theory, is made up of four contributions, the first two proportional to S, the third exactly equal to the exchange integral as defined in the HF model and the last one proportional to S2:
In equation (14) K > 0, C1 and C2 > 0 and  > 0
> 0
Therefore if S = 0, i.e., in the absence of interference, no chemical bond is formed.
Thus, we arrive to the first important conclusion about the origin of the chemical bond: from the quantum-mechanical point of view, the chemical bond is a consequence of interference effect. Having identified the quantum origin of the chemical bond we are now in a much better position to analyze its energetic. Since the chemical bond is a manifestation of interference effects, the proper way of partitioning the total energy for analyzing the formation of the chemical is to write it as the sum of two terms, one of them containing the contributions equivalent to the classical energy, the other being related to the stabilization brought about by the interference effect:
Using wave functions with the form given by equation (11) it is indeed possible to write the total energy as a sum of Eclassical and Einterference contributions, where Eclassical is just the energy associate to the product jajb (see equation 12):
and
In equation (16) Ec, Vee, Vnn, Ven are respectively the kinetic energy of electrons, their coulombic repulsion, the nuclei repulsion, and the electron-nuclei attraction terms. From the expression for A given above, it is clear that A = A(S) is such that  A(S) = 0, and from equation (17) it is also clear that in the absence of interference (S = 0), Einterference= 0 and Equantum = Eclassical, that is, no molecule can be formed. Thus, the energetic of the bond formation is completely defined by Einterference.
A(S) = 0, and from equation (17) it is also clear that in the absence of interference (S = 0), Einterference= 0 and Equantum = Eclassical, that is, no molecule can be formed. Thus, the energetic of the bond formation is completely defined by Einterference.
One can proceed even further to decompose Einterference into kinetic and potential contributions:
where Tab =< ja |- Ñ2 | jb > and Jaband Kabare the standard Coulomb and exchange integrals. Figure 5 shows how these two contributions vary with the internuclear distance for the H2 molecule, at the GVB/6-31G* level of calculation. Form the figure it is clear that the stabilization of the molecule is due to a reduction of the kinetic energy of the electrons. This is exactly the conclusion reached by previous works.30-32
Ñ2 | jb > and Jaband Kabare the standard Coulomb and exchange integrals. Figure 5 shows how these two contributions vary with the internuclear distance for the H2 molecule, at the GVB/6-31G* level of calculation. Form the figure it is clear that the stabilization of the molecule is due to a reduction of the kinetic energy of the electrons. This is exactly the conclusion reached by previous works.30-32
In conclusion, from the quantum mechanical point of view, the formation of a chemical bond is a consequence of interference effects. From the energetic point of view, the interference responsible for the bond formation manifests itself as reduction of the kinetic energy of the electrons as the bond is formed.
5. One-electron Bonds
We are now in the position to show that the classical idea (Lewis) that chemical bond involves the pairing of electron is highly inadequate. The most simple example is the H2+ molecule which is quite stable (Do = 2.651 eV) but very reactive. From the diagrams of Figure 6 it is clear that interference is the factor determining the bond formation.
The total amplitude will be A = A1 + A2. Using the same notation as before:
Y = ja(1) + jb(1)
and
Thus, in spite of the fact that the molecule has only one electron, the interference term between the 1-e states ja and jb will respond for the formation of the bond. Notice that in this case the wave function takes the form of a combination of atomic orbitals, which is the most popular way of building molecular orbitals. In fact, in the early days of quantum mechanics, this molecule was used by Mulliken18 to illustrate the limitations of the VB theory and the superiority of the MO model. However, the attentive reader will not see this fact as a limitation of the VB model. Much on the contrary, this example exposes the limitations of the MO model. The only reason why Y takes the form of an MO is because, for 1-e system, there is no need to take into account the permutation symmetry of the electrons. And, for this same reason, there is no need for a VB-type wave function.
There is another interesting result concerning this molecule. While the interference energy for H2 depends on S2 (equation 17), for the H2+ molecule a similar analysis shows that it varies with the first power of S. Thus, for smaller values of the overlap it might just happen that the one-electron bond becomes stronger than the two-electron one. In fact, for RH-H > 2.5 bohr, the interference energy for H2+ becomes larger than that for H2.
Let us examine the situation in Li2 and Li2+. In these cases, the bonding electrons occupy 2s-type orbitals. They are quite diffuse and in spite of the fact that electrons in these orbitals have a non-negligible probability of penetrating the core region, they are more probable to be found outside that region. Thus, much less work will be needed to bring the 2s electrons to the bonding region. However, since the orbitals are diffuse, they will start to overlap at much larger values of the internuclear distance when compared to either H2 or H2+. Besides that, one should expect an overlap much smaller between these diffuse orbitals than for the compact 1s orbitals of H2 and H2+. But, according to our previous analysis, these conditions should favor the one-electron bond relative the traditional two-electrons bond. In another words, according to our previous analysis one should expect the Li2+ molecule to be more bound than the neutral one. This is exactly what is observed experimentally [Do (Li2) = 1.04 eV; Do (Li2+) = 1.44 eV].35 This is also true for all the other homonuclear diatomics of this family and also for the halogen family. By the way, according to the MO description, one should expect just the opposite because to form the cation of all those molecules one has to remove one electron from a bonding orbital.
6. Enlarging the Concept of Chemical Bond
From the above discussion, it is clear that the formation of a chemical bond is not determined by the number of electrons involved but by the interference of one-electron states. In the examples examined in the preceding sections, we saw that while bonds can be formed with either one or two electrons, the interference of at least two one-electron states is required. This requirement poses the following question: are there situation where more than two one-electron states may be involved in forming chemical bonds?
The benzene molecule is the prototype of a class of molecules known to be quite stable relative to their cyclic polyenes counterparts. This extra stability is normally attributed to resonance (VB) or to delocalization of the p electrons (MO), depending on the IPM used to analyze the problem. However, it has been recently shown that the HF-MO wave functions for many of these molecules are not stable, i.e., they do not correspond to global minima in the respective hypersurfaces.36 On the other hand, attempts at converging GVB-like wave functions for the Kékule structures also led to unstable solutions.37 Also,38 it does not seem possible to decompose the D6h point group (the point group of the Hamiltonian for benzene) into a direct product containing either the D3h group (Kékule hybrids) or the D2h group (Dewar hybrids). However, either a CAS-GVB or a SCVB calculation, both of which take into account the permutation symmetry, shows that the p space consists of six atomic-like orbitals each localized at one of the carbon atoms, as shown in Figure 7.
For the ground singlet state of the molecule the spin part of the wave function is such that electrons in adjacent carbon atoms have opposite spins and therefore we expect a considerable overlap, that is, interference among them. Preliminary calculations show that this is exactly the case.39 Of course, all six electrons will take part in the process and the stabilization results from this strong interference effect. Thus, one could extend the classical concept of chemical bond by saying that the stabilization of benzene is brought about by a six-electron bond.
As the size of the molecule and/or the number of electrons increases, the energy decomposition analysis becomes more complex. However, once a general expression for the interference energy is developed, it will be possible to generalize this kind of analysis and to considerably enlarge the concept of chemical bond. Work in this direction is in progress.40
7. Conclusions
The basic requirements that must be satisfied by any wave function representing a non-relativistic many-electron system have been presented. It has been shown that in order to properly represent a many-electron non-relativistic system, the total wave function must be a product of a spatial and a spin part; both the spatial and spin parts must independently exhibit permutation symmetry, i.e., must transform like the irreducible representations of the symmetric (SN) group and the total wave function must be anti-symmetric.
Two independent particle models, namely the HF(MO) and the VB models, have been analyzed for these symmetry requirements. From these two models, VB-type wave functions are the only ones to satisfy the required symmetries. As a consequence, strictly speaking, only VB-type wave functions with optimized, singly occupied and non necessarily orthogonal (except when symmetry imposes) localized atomic-like orbitals are acceptable wave functions to describe many-electron systems at the IPM level. Also, only VB type wave functions can provide a quantum-mechanical translation of the classical concepts of molecular structure, chemical structure and chemical bond. The HF model can at most be used to define molecular structure.
Finally, a quantum electro-dynamical analysis of the chemical bond is presented. This type of analysis clearly reveals that the chemical bond is formed as a result of quantum interference effects. It also reveals that only VB-type wave functions are consistent with quantum-electrodynamics and that the benzene (and other non-resonant "conjugated systems") stability can be understood in terms of the interference of many one-electron states, thus allowing us extend the concept of chemical bond as resulting not from pairing of electrons but from the interference of degenerate or near-degenerate one-electron states.
Acknowledgments
The author thanks CNPq and FAPERJ for financial support. He also thanks the organizers for the invitation to contribute to this special issue. It is a real pleasure and an honor to participate from this celebration to Prof. Ricardo Ferreira.

Marco Antonio Chaer Nascimento
Industrial Chemist, National School of Chemistry, University of Brazil (1968). Ph.D., Chemical Physics, California Institute of Technology, EUA (1977). Full Professor of Physical Chemistry, IQ/UFRJ. Member of the Brazilian National Academy of Sciences (2000). Commendatary of the National Order of the Scientific Merit, granted by the President of Brazil (2005), "Simão Mathias" Brazilian Chemical Society Award (2005). "Augusto Araújo Lopes Zamith" Award IQ/UFRJ (2004). Distinguished Scientist Award, State of Rio de Janeiro Secretary for Science and Technology (1999). Director of the Center for Research (PRONEX) in "Hydrocarbon Functionalization" (1999- ). Chairman of the Chemistry Committee CNPq (1993-1995). Chairman of the division of Surface Phenomena and Catalysis, State of Rio de Janeiro Virtual Institute for Nanoscience and Nantoecnology. Member of the editorial board of Progress in Theoretical Chemistry and Physics".
Areas of research: a) structure and spectroscopy of nanoclusters; b) molecular modeling (heterogeneous catalysis: mechanism and design of catalysts, mechanism of protein folding, design of protein inhibitors and of non-linear optical materials, development of specific force fields, materials for hydrogen storage); c) new computational methodologies and d) theory of the chemical bond.
Received: September 10, 2007
Published on the web: February 22, 2008
References
- 1. Partigton, J. R.; A Short History of Chemistry, Dover: New York, 1989.
- 2. Lewis, G. N.; J. Am. Chem. Soc 1916, 38, 762.
- 3. Nascimento, M. A. C. In Métodos de Química Teórica e Modelagem Molecular, Morgon, N. H.; Coutinho, K., eds.; Editora Livraria da Física: São Paulo, 2007, pp. 209.
- 4. Born, M.; Oppenheimer, J. R.; Ann. Physik 1927, 84, 457.
- 5. Heisenberg, W.; Z. Phys 1926, 38, 411; ibid. 1926, 39, 501.
- 6. Wigner, E.; Z. Phys 1926, 40, 883.
- 7. van Vleck, J. H.; Sherman, A.; Rev. Mod. Phys 1935, 7, 167.
- 8. Heitler, W.; London, F.; Z. Phys 1927, 44, 445.
- 9. Rumer, G.; Göttingen Nach. 1932, 337.
- 10. Pauling, L.; Proc. Natl. Acad. Sci. USA 1932, 18, 293.
- 11. Pauling, L.; Wheland, G. W.; J. Chem. Phys 1933, 1, 362.
- 12. Pauling, L.; Sherman, J.; J. Chem. Phys 1933, 1, 606.
- 13. Eyring, H.; J. Am. Chem. Soc. 1932, 54, 3191.
- 14. Slater, J. C.; Phys. Rev. 1931, 37, 481; ibid. 1931, 38, 1109.
- 15. Pauling, L.; J. Am. Chem. Soc 1931, 53, 1367; ibid. 1931, 53, 3225.
- 16. Hund, F.; Z. Phys. 1928, 51, 759.
- 17. Hund, F.; Angew. Chem. Intl. Ed. 1977, 16, 87.
- 18. Mulliken, R. S.; Phys. Rev 1928, 32, 761.
- 19. Hückel, E.; Z. Phys. 1931, 60, 204; ibid. 1932, 72, 310; ibid 1932, 76, 628.
- 20. Goddard III, W. A.; Phys. Rev. 1967, 157, 73; ibid. 157, 81.
- 21. Gerratt, J.; Lipscomb, W. N.; Proc. Nat. Acad. Sci. 1968, 59, 332.
- 22. Fock, V.; Z. Phys. 1930, 15, 126.
- 23. Nascimento, M. A. C.; Barbosa, A. G. H. In Fundamental World of Quantum Chemsitry, Brandas, E. J; Kryachko, E. S., eds.; Kluwer: Dordrecht, 2003, vol. 1, pp. 371.
- 24. Mulliken, R. S.; Phys. Rev 1929, 33, 730.
- 25. Goddard III, W. A.; Dunning, T. H.; Hunt, J. W.; Hay, J. P.; Acc. Chem. Res 1973, 6, 368.
- 26. Goddard III, W. A.; Harding, L. B.; Ann. Rev. Phys. Chem 1978, 29, 363.
- 27. Coulson, C. A.; Trans.Faraday Soc 1937, 33, 1479.
- 28. Weinbaum, S.; J. Chem. Phys 1933, 1, 593.
- 29. Kolos, W.; Wolniewicz, L.; J. Chem. Phys 1965, 43, 2429.
- 30. Ruedenderg, K.; Rev. Mod. Phys 1962, 34, 326.
- 31. Goddard III, W. A.; Wilson Jr., C. W.; Theor. Chim. Acta 1972, 26, 211.
- 32. Kutzelnigg, W.; Theor. Chim. Acta 1976, 43, 1.
- 33. Feynman, R. P.; Quantum Electrodynamics, Westview Press: Boudder, 1973.
- 34. Mattuck, R. D.; A Guide to Feynman Diagrams in the Many-Body Problem, McGraw-Hill: New York, 1967.
- 35. Huber, K. P.; Herzberg, G.; Constants of Diatomic Molecules, Van Nostrand: New York, 1979.
- 36. Dehareng, D.; Dive, G.; J. Comp. Chem 2000, 21, 483.
- 37. Barbosa, A. G. H.; personal communication.
- 38. Nascimento, M. A. C.; Barbosa, A. G. H; Prog. Theor. Phys. Chem 2003, 12, 247.
- 39. Barbosa, A. G. H; PhD Thesis, Instituto de Química da Universidade Federal do Rio de Janeiro, Brazil, 2002.
- 40. Cardozo, T. M; Nascimento, M. A. C.; work in progress.
Publication Dates
-
Publication in this collection
08 Apr 2008 -
Date of issue
2008
History
-
Accepted
22 Feb 2008 -
Received
10 July 2007

 The nature of the chemical bond
The nature of the chemical bond