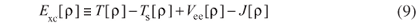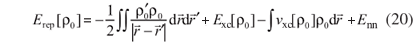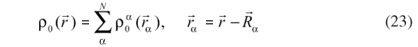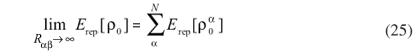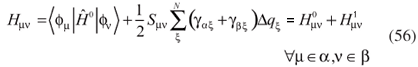Abstracts
The DFTB method, as well as its self-consistent charge corrected variant SCC-DFTB, has widened the range of applications of fundamentally well established theoretical tools. As an approximate density-functional method, DFTB holds nearly the same accuracy, but at much lower computational costs, allowing investigation of the electronic structure of large systems which can not be exploited with conventional ab initio methods. In the present paper the fundaments of DFTB and SCC-DFTB and inclusion of London dispersion forces are reviewed. In order to show an example of the DFTB applicability, the zwitterionic equilibrium of glycine in aqueous solution is investigated by molecular-dynamics simulation using a dispersion-corrected SCC-DFTB Hamiltonian and a periodic box containing 129 water molecules, in a purely quantum-mechanical approach.
DFT; DFTB; SCC; glycine; zwitterion
O método DFTB, bem como a sua extensão com carga corrigida auto-consistente SCC-DFTB, tem ampliado a faixa de aplicações das ferramentas teóricas com fundamentos bem estabelecidos. Como uma aproximação do método do funcional de densidade, o método DFTB mantém aproximadamente a mesma precisão, mas com custo computacional menor, permitindo a investigação da estrutura eletrônica de sistemas grandes que não podem ser explorados com métodos ab initio convencionais. No presente artigo, os fundamentos dos métodos DFTB, SCC-DFTB e da inclusão das forças de dispersão de London são revisados. Para mostrar um exemplo da aplicabilidade do método DFTB, o equilíbrio zwitteriônico de glicina em solução aquosa é investigado. Foram realizadas simulações de dinâmica molecular usando o hamiltoniano SCC-DFTB corrigido para incluir a dispersão e uma caixa periódica contendo 129 moléculas de água, a partir de uma abordagem puramente mecânico-quântica.
REVIEW
Density-functional based tight-binding: an approximate DFT method
Augusto F. Oliveira * e-mail: augusto.oliveira@chemie.tu-dresden.de; duarteh@ufmg.br I, II, * * e-mail: augusto.oliveira@chemie.tu-dresden.de; duarteh@ufmg.br ; Gotthard SeifertII; Thomas HeineIII; Hélio A. Duarte * e-mail: augusto.oliveira@chemie.tu-dresden.de; duarteh@ufmg.br I, * * e-mail: augusto.oliveira@chemie.tu-dresden.de; duarteh@ufmg.br
IDepartamento de Química, Instituto de Ciências Exatas, Universidade Federal de Minas Gerais, Av. Antonio Carlos, 6627, 31270901 Belo Horizonte-MG, Brazil
IIPhysikalische Chemie, Technische Universität Dresden, Mommsenstr, 13, D01062 Dresden, Germany
IIISchool of Engineering and Sciences, Jacobs University, P.O. Box 750 561, 28725 Bremen, Germany
ABSTRACT
The DFTB method, as well as its self-consistent charge corrected variant SCCDFTB, has widened the range of applications of fundamentally well established theoretical tools. As an approximate density-functional method, DFTB holds nearly the same accuracy, but at much lower computational costs, allowing investigation of the electronic structure of large systems which can not be exploited with conventional ab initio methods. In the present paper the fundaments of DFTB and SCCDFTB and inclusion of London dispersion forces are reviewed. In order to show an example of the DFTB applicability, the zwitterionic equilibrium of glycine in aqueous solution is investigated by molecular-dynamics simulation using a dispersion-corrected SCCDFTB Hamiltonian and a periodic box containing 129 water molecules, in a purely quantum-mechanical approach.
Keywords: DFT, DFTB, SCC, glycine, zwitterion
RESUMO
O método DFTB, bem como a sua extensão com carga corrigida auto-consistente SCC-DFTB, tem ampliado a faixa de aplicações das ferramentas teóricas com fundamentos bem estabelecidos. Como uma aproximação do método do funcional de densidade, o método DFTB mantém aproximadamente a mesma precisão, mas com custo computacional menor, permitindo a investigação da estrutura eletrônica de sistemas grandes que não podem ser explorados com métodos ab initio convencionais. No presente artigo, os fundamentos dos métodos DFTB, SCC-DFTB e da inclusão das forças de dispersão de London são revisados. Para mostrar um exemplo da aplicabilidade do método DFTB, o equilíbrio zwitteriônico de glicina em solução aquosa é investigado. Foram realizadas simulações de dinâmica molecular usando o hamiltoniano SCC-DFTB corrigido para incluir a dispersão e uma caixa periódica contendo 129 moléculas de água, a partir de uma abordagem puramente mecânico-quântica.
1. Introduction
Density functional theory (DFT) methods are the standard and the most used theoretical techniques for electronic structure calculations.1-5 The advent of the generalized gradient approximation (GGA) for the exchange-correlation functional enhanced the DFT accuracy6 and the predicted molecular structures, relative energies and frequencies are nearly comparable to the second order Møller-Plesset perturbation theory (MP2) method, with remarkable success to treat transition metal complexes.7 Efficient algorithms to solve the Kohn-Sham equations have been implemented, scaling to N3 with respect to the size of the basis sets and, hence, being much more efficient than the N5 of the MP2 methods. DFT is the method chosen for a huge range of applications. The formalism of the DFT and its extension to the reactivity indexes are subject of intensive research and many empirical concepts such as electronegativity, chemical potential and hardness are now formally defined within the DFT framework.3,5,8-10 With respect to the methodology, developments concerning improved exchange-correlation functionals and hybrid quantum-mechanics/molecular-mechanics (QM/MM) methods are still the main subjects of research of many theoreticians.11 Chemical property estimates based on DFT are now well established, and even optical properties are accessible through the generalization to time-dependent DFT,7,12,13 a method which is nowadays implemented in many different computer codes.
Notwithstanding the marvelous ability of the DFT to treat systems of increasing complexity, many systems are still intractable at the actual stage of computer technology development. Biosystems, adsorption processes, nanostructures, molecular dynamics, clusters and aggregates with thousands of atoms, self-assembling systems, nanoreactors and supramolecular chemistry are some of the fields in which ab initio methods cannot be used with adequate chemical models. For this range of systems, semi-empirical methods seem to have their applicability. Semi-empirical methods such as AM1,14 PM315-17 and, more recently, RM118 have many empirical parameters that are fitted to a set of molecular properties, estimated either theoretically or experimentally. Therefore, the applicability of such methods is restricted.
Density-functional tight-binding (DFTB) is an approximate method based on the density functional framework which does not require large amounts of empirical parameters. The virtues and weaknesses of the DFTB are a heritage from DFT. In fact the parameters are consistently obtained from DFT calculations of a few molecules per pair of atom types. On the other side, DFTB is closely connected to the tight-binding methods. In fact, it can be seen as a non-orthogonal tight-binding method parameterized from DFT. The self-consistent charge extension of DFTB (SCC-DFTB) improves very much the accuracy of the method. For improvement of physical approximations, all DFT extensions, such as treatment of relativistic effects and London dispersion, can be easily used in the DFTB method. Large number of applications has been reported showing its usefulness in the calculations of hyperfine coupling constants, magnetic properties, vibrational spectra of solids and molecules, nuclear magnetic shielding tensors, geometries, dynamic properties and many others.19-24 Calculation of optical properties is also possible due to the time-dependent DFTB,25-27 which is not covered in the present paper.
The goal of the present review is to call the attention of the chemistry community to the DFTB method, which can be a good complement of the set of semi-empirical methods available. Its advantages and weaknesses are highlighted. As an example of application, the zwitterionic and neutral forms of glycine in aqueous solution are discussed in terms of fully quantum mechanical molecular dynamics of this molecule in water.
2. Background Fundaments
Density functional theory has been extensively reviewed.7,28 In this section a very brief review of DFT is done in order to highlight its crucial aspects to the formulation of the DFTB method.
The Hohenberg-Kohn (HK) theorems29 have rigorously made the electronic density acceptable as basic variable to electronic-structure calculations. However, development of practical DFT methods only became relevant after W. Kohn and L. J. Sham published their famous set of equations: the so-called Kohn-Sham (KS) equations.30
The use of the electronic density within the KS scheme allows a significant reduction of the computational demand involved in quantum calculations. Furthermore, the KS method paved the way for studying systems that could not be investigated by conventional ab initio methods (which use the wave function as basic variable).
Even though DFT methods have been successfully applied for systems of increasing complexity, methods which can include approximations to reduce even more the computational demand, without compromising the reliability of results, are still required.
The application of tight-binding (TB) to the calculation of electronic structures starts with the paper by J. Slater and G. Koster.31 The main idea behind this method is to describe the Hamiltonian eigenstates with an atomic-like basis set and replace the Hamiltonian with a parameterized Hamiltonian matrix whose elements depend only on the internuclear distances (this requires the integrals of more than two centers to be neglected) and orbital symmetries.
Although the SlaterKoster method was conceived for the calculation of band structures in periodic systems, it was later generalized to an atomistic model, capable of treating finite systems as well. The transition to atomistic has three main requirements, as discussed by Goringe et al.32
First, the elements of the Hamiltonian matrix must have a functional dependence on the interatomic distance. In the case of band structures one just has to know the matrix elements for discrete values of distance. This requirement was solved by Froyen and Harrison,33 who proposed that the interatomic distance was related to the Hamiltonian elements by 1/r2.
The second requirement is to obtain an expression for the total energy and not only for the band energy. In 1979 Chadi34 proposed that the total energy could be described as a sum of two contributions,
where Ebnd is the sum over the energies of all occupied orbitals obtained by diagonalization of the parameterized Hamiltonian matrix, and Erep is the repulsive contribution, obtained by the sum of the atomic-pair terms,
in which N is the number of atoms in the system.
The third and last requirement is the possibility to derive the atomic forces from the total energy. This is especially important for geometry optimization and molecular dynamics. By assuming differentiability of Uαβ in equation 2, the only problem is to derive Ebnd, which depends on the parameterization method chosen for the Hamiltonian matrix.
The DFTB method attends these three requirements with the additional advantage of completely avoiding any empirical parameterization, since the Hamiltonian and overlap matrices are calculated using atom-like valence-orbitals which are derived from DFT. Therefore, the DFTB method can be considered as a simplification of the KohnSham method.
3. The KohnSham Method
Although the Hohenberg and Kohn theorems29 have proven that the electronic energy of a system can be totally determined from its electronic density through the variational principle, they did not propose any procedure to perform this calculation. This was done about one year later, by Kohn and Sham,30 with the publication of their equations known as Kohn-Sham equations.
The solution of Kohn and Sham starts from the idea of using monoelectronic orbitals to calculate the kinetic energy in a simple, yet reasonably precise, way leaving a residual correction that could be calculated apart. Thus, one starts with a reference system of M non-interacting electrons subjected to the external potential nS, with Hamiltonian
Where
in which there are no electronelectron repulsion terms and for which the electronic density is exactly the same as in the corresponding system of interacting electrons. By introducing the single particle orbitals ψi all electronic densities physically acceptable for the system of non-interacting electrons can be written in the form
Therefore, the HK functional can be written as
where TS represents the kinetic-energy functional for the reference system of M non-interacting electrons, given by
J represents the classic Coulomb interaction functional
and the remaining interactions are grouped in Exc, the exchange-correlation functional, which contains the difference between the exact kinetic energy T and TS, besides the non-classic part of the electron-electron interactions Vee, i.e.
After combining equations 6, 7 and 8 within the second HK theorem, the chemical potential can be written as
with the KS effective potential
where νext is the external potential, normally due to the atomic nuclei, and the exchange-correlation potential νxc is defined as
Equation 10, restricted by ∫ρ( )d
)d = M, is exactly the same equation that would be obtained for a system of M non-interacting electrons submitted to the external potential νS = νKS. Thus, for a given νKS a suitable value of ρ can be calculated for equation 10 by solving the M monoelectronic equations
= M, is exactly the same equation that would be obtained for a system of M non-interacting electrons submitted to the external potential νS = νKS. Thus, for a given νKS a suitable value of ρ can be calculated for equation 10 by solving the M monoelectronic equations
and by using the calculated ψi in equation 5.
Equations 5 and 11-13 are the so-called Kohn-Sham equations. Since νKS depends on ρ through νxc the KS equations must be solved iteratively using a self-consistent procedure similar to the one depicted in Figure 1. An electronic density modelρ0 is normally chosen to start the iterative procedure. In principle, any positive function normalized for the number of electrons would be applicable, but a good initial estimate of ρ can significantly accelerate convergence.
At the end of the iterative procedure, the total energy can be calculated, which is given in the KS method by the following expression:
The most difficult part of the KS scheme is to calculate νxc in equation 12. The existence of an exact density functional is assured by the first HK theorem, but the exact form of the Exc functional remains unknown. However, many approximations of this functional have been described in the scientific literature over the last 30 years. In practice, the approximation chosen for Exc and the way by which the KS orbitals are represented define the different DFT methods.
4. DFT as Basis for a TightBinding Method
Following Foulkes and Haydock35 the electronic density is written as a reference densityρ0 plus a small fluctuation δρ,
This electronic density is then inserted in equation 14:
where  = ρ0(
= ρ0( ') and δρ' = δρ(
') and δρ' = δρ( ') are defined as short-hand notations. The second term in equation 16 corrects the double counting in the Coulomb term; the third term corrects the new exchange-correlation contribution; and the fourth term results from splitting the Coulomb energy into one part related to ρ0 and another related to δρ. Enn is the nuclear repulsion.
') are defined as short-hand notations. The second term in equation 16 corrects the double counting in the Coulomb term; the third term corrects the new exchange-correlation contribution; and the fourth term results from splitting the Coulomb energy into one part related to ρ0 and another related to δρ. Enn is the nuclear repulsion.
Afterwards, Exc [ρ0 + δρ] is expanded in a Taylor series up to the second-order term:
Substitution of equation 17 into 16 and use of the definition (δ Exc/δρ)ρ0 = νxc[ρ0] results in
From equation 18 it is possible to define four important terms. The first is a reference Hamiltonian
0 depending only upon ρ0
The sum in the first line of equation 18 is analogue to Ebnd in equation 1. The terms in the second line of equation 18 define the repulsive contribution,
Finally, the last term in equation 18 includes the corrections related to the fluctuations in the electronic density. This term is defined as
Therefore, equation 18 can be rewritten as
In order to obtain a good estimate of the reference electronic density, ρ0 is written as a superposition of atom-like densities centered on the nuclei α,
With this approximation it is assured that Erep does not depend on the electronic-density fluctuations. Furthermore, due to the neutrality of  the Coulomb contributions become negligible for long distances. Therefore, Erep can be expanded as
the Coulomb contributions become negligible for long distances. Therefore, Erep can be expanded as
The contributions of 3 and more centers are rather small and can be neglected. These approximations can also be justified by Coulomb screening, i.e., since  is the electronic density of a neutral atom, the electron-electron interaction terms with more than two centers are canceled by the nucleus-nucleus interactions.
is the electronic density of a neutral atom, the electron-electron interaction terms with more than two centers are canceled by the nucleus-nucleus interactions.
Due to the screening of terms of more than two centers, one can assume the two-center contributions to be short ranged. However, the repulsion energy does not decay to zero for long interatomic distances. Instead, it decays to a constant value given by the atomic contributions:
Thus,  is assumed in order to make Erep dependent only on two-center contributions:
is assumed in order to make Erep dependent only on two-center contributions:
Although it would be possible to calculate Erep for known values of  , it is more convenient to adjust Erep to ab initio results. Thus, Erep is fitted to the difference between the DFT energy and Ebnd as a function of the interatomic distance Rαβ using a suitable reference structure, i.e.
, it is more convenient to adjust Erep to ab initio results. Thus, Erep is fitted to the difference between the DFT energy and Ebnd as a function of the interatomic distance Rαβ using a suitable reference structure, i.e.
The value of Ebnd can be obtained by diagonalization of the Hamiltonian matrix, which leads to
The value of Erep is usually fitted to a polynomial function or to a series of splines. Typical plots of EDFT, Ebnd and Erep for a reference structure are shown in Figure 2.
Based on the considerations discussed so far, the DFTB model can be derived.
5. The Standard DFTB Model without Self-Consistency
In the standard DFTB scheme, the second-order correction term, E2nd of equation 22, is neglected. Therefore, the calculation of the total energy does not depend on the electronic-density fluctuations δρ and, accordingly, it does not have to be solved iteratively.
In DFTB the KS orbitals are represented with a linear combination of atomic orbitals (LCAO) centered on the nuclei. Denoting the basis functions by øν and the expansion coefficients by Ciν one can write the KS orbitals in the form
From this LCAO model, one obtains the secular problem
where the elements  of the Hamiltonian matrix and Sµν of the overlap matrix are defined as follows:
of the Hamiltonian matrix and Sµν of the overlap matrix are defined as follows:
The second term of equation 22 can be transformed, with equations 29 and 11, into
in which the elements of the density matrix P are defined as follows
In order to restrict the LCAO to valence orbitals only, it is necessary to assure the orthogonality of the basis functions with respect to the core basis-functions of the remaining atoms (by using atomic orbitals as basis functions the orthogonality between the core and valence functions within the same atoms is already assured).
Denoting |ø) as a non-orthogonalized basis-function and  as the core basis-functions of atom β, the corresponding orthogonalized basis-function of |ø) is obtained by:
as the core basis-functions of atom β, the corresponding orthogonalized basis-function of |ø) is obtained by:
By using this orthogonalization procedure, equation 32 is transformed into
where  denotes the eigenvalue of the state c in atom β. The effective potential νKS and the core correction in equation 35 can be interpreted as a pseudo-potential (Vpp). Writing νKS as the sum of potentials Vα centered on the atoms,
denotes the eigenvalue of the state c in atom β. The effective potential νKS and the core correction in equation 35 can be interpreted as a pseudo-potential (Vpp). Writing νKS as the sum of potentials Vα centered on the atoms,
and using this definition in equation 35, the effective potential is transformed into a pseudo-potential for all atoms in the system, except for atoms to which øµ and øν belong. Therefore, the pseudo-potential appears in the three-center terms and in the two-center terms whose valence orbitals belong to the same atom (so called crystal field terms). The pseudo-potential contributions are considerably smaller than the contributions of the full potentials and are neglected. Thus, the Hamiltonian matrix elements are defined as
where δαβ is the Kronecker's delta. This approach, the potential superposition, has been used since the 1980's for the calculation of DFTB parameters. In 1998, Elstner et al.36 presented an alternative approach to derive the DFTB equations through a second order expansion of the DFT total energy with respect to the electron density. As result the Hamiltonian matrix elements are calculated as density superpositions, which is identical to equation 37 except for the contribution of the exchange correlation potential. Indeed, due to the non-linear nature of νxc, the effective potential cannot be described as a simple sum of reference potentials within this approach, instead one obtains
Both approaches are physically motivated and their results are similar, which is not surprising if the potential difference between equations 37 and 38 is explicitly calculated. Both approaches have been used extensively in the past, the potential superposition being more popular for standard DFTB calculations, and the density superposition more widely used for SCC-DFTB.
The øν basis functions and the reference atom-like densities  are obtained by solving the Schrödinger equation
are obtained by solving the Schrödinger equation
for the free atom within a self-consistent DFT method, as shown in Figure 1. The contraction potential (r/r0)2 in equation 39 constrains the wave functions, resulting in better basis sets for the study of condensed-phase systems and free molecules as well. The value for the parameter r0 is normally chosen between 1.85rcov and 2rcov, with rcov being the atomic covalent radius.37
In practice, the Hamiltonian matrix elements are calculated as follows: For the diagonal elements the energy level of the free atom is chosen, which ensures correct dissociation limits. Due to the orthogonality of the basis functions the off-diagonal elements of the intra-atomic blocks are exactly zero. The interatomic blocks are computed as given in equation 37 or 38, depending on the choice of potential generation. Within the density superposition approach the Hamiltonian matrix elements unfold as follows:
It should be noted that the Hamiltonian elements  depend only on atoms α and β and, therefore, only the two-center matrix elements are explicitly calculated, as well as two-center elements of the overlap matrix. According to equation 40 the free atom eigenvalues form the diagonal of the Hamiltonian matrix, which assures the correct limit for free atoms.
depend only on atoms α and β and, therefore, only the two-center matrix elements are explicitly calculated, as well as two-center elements of the overlap matrix. According to equation 40 the free atom eigenvalues form the diagonal of the Hamiltonian matrix, which assures the correct limit for free atoms.
By using øν and  the Hamiltonian and overlap matrix elements can be calculated and tabulated as a function of the distance between atomic pairs. Thus, it is not necessary to recalculate any integrals during, e.g., a geometry optimization or molecular dynamics simulation.
the Hamiltonian and overlap matrix elements can be calculated and tabulated as a function of the distance between atomic pairs. Thus, it is not necessary to recalculate any integrals during, e.g., a geometry optimization or molecular dynamics simulation.
At last, an analytic expression for atomic forces can be derived from the total energy with respect to the atomic space-coordinates,
By this approach, the DFTB method covers all three requirements for an atomistic tight-binding approach.
6. The SelfConsistent Charge Correction: SCC-DFTB
The non-self-consistent DFT scheme described so far is very suitable to study systems in which the polyatomic electronic density can be well represented by a sum of atom-like densities, i.e. homonuclear covalent systems or highly ionic systems. However, the uncertainties in the standard DFTB increase when the chemical bonds in the system are controlled by a more delicate charge balance between atoms, especially in the case of heteronuclear molecules and polar semiconductors. In order to have a better description of electronic systems and better transferability of DFTB in the cases where long-range Coulomb interactions are significant, the method has been improved, giving rise to the self-consistent charge correction DFTB (SCC-DFTB).36 In this new scheme, the electronic density is corrected through inclusion of the second-order contributions E2nd in equation 22, which are neglected in standard DFTB.
In order to include the density fluctuations in a simple yet efficient way according to a tight-binding approach, δρ is written as the superposition of atom-like contributions δρα, which fast decay along the distance from the corresponding atomic center,
where the atom-like contributions can be simplified with the monopole approximation:
Here Δqα is the Mulliken charge, difference between the atomic Mulliken population qα38 and the number of valence electrons of the neutral free atom  denotes the normalized radial dependence of the density fluctuation in atom a approximated to spherical by the angular function Y00. In other words, the effects of charge transfer are included, but changes in the shape of the electronic density are neglected. Equation 21 then becomes
denotes the normalized radial dependence of the density fluctuation in atom a approximated to spherical by the angular function Y00. In other words, the effects of charge transfer are included, but changes in the shape of the electronic density are neglected. Equation 21 then becomes
in which the notation γαβ was introduced merely for convenience.
In order to solve equation 44, γαβ must be analyzed. In the limit case where the interatomic separation is very large (| α -
α -  β|=|
β|=| -
-  '| → ∞) one finds, by GGA-DFT, that the exchange-correlation term goes to zero and γαβ describes the interaction of two normalized spherical electronic densities, basically reducing to 1/|
'| → ∞) one finds, by GGA-DFT, that the exchange-correlation term goes to zero and γαβ describes the interaction of two normalized spherical electronic densities, basically reducing to 1/| α -
α -  β |, thus,
β |, thus,
In the opposite case, for which the interatomic distance tends to zero (|
α - β |=|
β |=| -
-  '| → 0), γαβ describes the electron-electron interaction within the atom α and can be related with the chemical hardness ηα,39 or Hubbard parameter γαα = 2ηα = Ua. Typically, the atomic hardness can be calculated using the difference between ionization potential Iα and electron affinity Aα of atom α: 2hα = Iα -Aα. Due to practical problems, in particular related to the non-existence of various anions and accordingly missing experimental validation of the electron affinity of the corresponding elements, it is more convenient to exploit DFT to obtain these parameters. Application of Janak's theorem40 relates the atomic hardness to the derivative of the HOMO energy with respect to the occupation number of the HOMO
'| → 0), γαβ describes the electron-electron interaction within the atom α and can be related with the chemical hardness ηα,39 or Hubbard parameter γαα = 2ηα = Ua. Typically, the atomic hardness can be calculated using the difference between ionization potential Iα and electron affinity Aα of atom α: 2hα = Iα -Aα. Due to practical problems, in particular related to the non-existence of various anions and accordingly missing experimental validation of the electron affinity of the corresponding elements, it is more convenient to exploit DFT to obtain these parameters. Application of Janak's theorem40 relates the atomic hardness to the derivative of the HOMO energy with respect to the occupation number of the HOMO  and hence the energy change with respect to electron change within the HOMO. This approach offers the possibility to treat the charge contribution shell- or even orbital-wise, which is important for the calculation of certain elements with sp and d bonding contributions, in particular for transition metals. Orbital hardness values
and hence the energy change with respect to electron change within the HOMO. This approach offers the possibility to treat the charge contribution shell- or even orbital-wise, which is important for the calculation of certain elements with sp and d bonding contributions, in particular for transition metals. Orbital hardness values  have been reported in the literature for elements from H to Xe.41 In the following, we concentrate on the atomic SCC procedure, which implies that all sums over charges run over the atomic index α. For orbital-dependent SCC the summation index for the charge would run over the shell index ξ. Within the monopole approximation, Uα can be calculated, using a DFT procedure, as the second derivative of the total atomic energy of atom α with respect to its atomic charge:
have been reported in the literature for elements from H to Xe.41 In the following, we concentrate on the atomic SCC procedure, which implies that all sums over charges run over the atomic index α. For orbital-dependent SCC the summation index for the charge would run over the shell index ξ. Within the monopole approximation, Uα can be calculated, using a DFT procedure, as the second derivative of the total atomic energy of atom α with respect to its atomic charge:
In order to obtain a well-defined and useful expression for systems in all scales, and still keep consistence with the afore approximations, an analytical expression was developed36 to approximate the density fluctuations with spherical electronic densities. In accordance with Slater-type orbitals (Gaussian-type orbitals can also be employed) used to solve the KS equations,42,43 it is assumed an exponential decay of the normalized spherical electronic density:
Omitting the second-order contributions of Exc in equation 44 one obtains:
Integration over  ' gives:
' gives:
Setting R = | α -
α -  β|, after some coordinate transformations one gets
β|, after some coordinate transformations one gets
where s is a short-range function with exponential decay, so that
Once it was assumed that the second-order contribution can be approximated by the Hubbard parameter when R = 0, according to equation 46, the exponents of equation 51 are obtained:
This result can be interpreted by noting that harder elements tend to have localized wave functions. The chemical hardness of a spin-depolarized atom is calculated by the energy derivative of the highest occupied atomic orbital with respect to its occupation number, equation 46, using a fully self-consistent ab initio method. Therefore, the influence of second-order contributions of the exchange-correlation energy is included in γαβ for short distances, where it is important. The fact that, within GGA, the exchange-correlation energy vanishes for large interatomic distances is taken into account. In the case of periodic systems, the long-range part can be calculated using the standard Ewald summation, whereas the short-range part s decays exponentially and can be summed over a small number of unit cells. Thus, equation 50 is a well-defined expression for extended and periodic systems.
Finally, the total energy within SCCDFTB is written as
with γαβ = γαβ(Uα,Uβ,|  α -
α -  β|). Here the contribution due to the Hamiltonian
β|). Here the contribution due to the Hamiltonian  0 is exactly the same as in the standard DFTB scheme. Note that the first term in equation 53 does only simplify to the sum of MO energies, the convenient notation for DFTB, if all charges are zero. Like in the non-self-consistent method, the wave functions yi are expanded in a LCAO model, equation 29, and equation 53 gives:
0 is exactly the same as in the standard DFTB scheme. Note that the first term in equation 53 does only simplify to the sum of MO energies, the convenient notation for DFTB, if all charges are zero. Like in the non-self-consistent method, the wave functions yi are expanded in a LCAO model, equation 29, and equation 53 gives:
The charge fluctuations are calculated by Mulliken population analysis:38
and secular equations similar to those in equation 30 can be obtained, with modified elements in the Hamiltonian matrix:
The matrix elements  and Sµν are identical to those defined in the standard DFTB method, in equation 31. Since the atomic charges depend on the monoatomic wave functions ψi it is necessary to use a self-consistent procedure. Once the elements Sµν extend to some neighboring atoms, multi-particle interactions are introduced. The second-order correction is achieved by introducing the elements
and Sµν are identical to those defined in the standard DFTB method, in equation 31. Since the atomic charges depend on the monoatomic wave functions ψi it is necessary to use a self-consistent procedure. Once the elements Sµν extend to some neighboring atoms, multi-particle interactions are introduced. The second-order correction is achieved by introducing the elements  , which depend on the Mulliken charges.
, which depend on the Mulliken charges.
Identically to the standard DFTB, the repulsive potential is fitted according to equation 27 using a suitable reference system.
As the self-consistent charge correction allows for the explicit treatment of charge-transfer effects, the transferability of Erep is considerably better, in comparison with the non-self-consistent scheme.
As in the standard DFTB, a simple analytic expression for the atomic forces can be derived accordingly:
DFTB schemes have been successfully used in a wide range of applications, from molecular compounds22,44 to systems in solid state.19,45-47 Indeed, a symposium dedicated to the DFTB methods was held during the 232nd National Meeting of the American Chemical Society, from 10th to 14th of September, in 2006. A special section with contributions presented in this symposium was published in the Journal of Physical Chemistry A, issue 26 of 2007,48 presenting the actual development state of DFTB with respect to its formalism, implementation and applications.
7. Weak Forces: Dispersion-Corrected (SCC-)DFTB
London interactions, also called dispersion forces, are defined as attractive forces between nonpolar molecules, due to their mutual polarizability.49 London dispersion forces are several orders of magnitude weaker than typical covalent or ionic interactions and also about 10 times weaker than hydrogen bridge interactions. Therefore, dispersion forces have negligible effect in short-range interactions and can be understood as the long-range component of van der Waals forces.
Despite their weak nature, London interactions affect many fundamental processes in chemistry, physics, and biology. They influence the formation of molecular crystals, the structure of biological molecules such as proteins and DNA, adsorption processes, ππ stacking interactions, among others.
However, as explained above, both the standard and self-consistent DFTB methods treat only short-range atomic potentials and terms with more than two centers are neglected. Therefore, the Hamiltonian matrix elements fall off quickly and become negligible at interatomic distances typically found in the region of the van der Waals minimum. Hence, DFTB completely disregards van der Waals interactions, especially dispersion forces.
Two treatments meant to include dispersion interactions a posteriori have been proposed.50,51 In both cases the dispersion energy Edisp is calculated separately using empirical potentials and then added to the DFTB total energy expression. Since van der Waals forces are totally absent in DFTB, the addition of Edisp does not introduce any double-counting errors to the energy.
Since both treatments are somewhat similar, we describe that used in the present work.51 This correction was implemented in an experimental version of the deMon code52 and makes use of the UFF force field,53 already available in deMon. The dispersion interaction Uαβ between atoms α and β at a distance R is given in Lennard-Jones-type form, which includes two parameters: van der Waals distance (Rαβ) and well depth (dαβ):
The Rαβ and dαβ parameters are reported in the original paper53 and are available from H to Lw in the periodic table of elements. In UFF the van der Waals term is set to zero according to an adjacency criteria; however, this imposes an inflexible topology of the system, which is not desirable in a quantum-mechanical method. To overcome this problem, equation 58 is used only when Uαβ is attractive (London interactions are never repulsive), i.e. R < 2-1/6Rαβ. In addition, a short-range potential is derived using the polynomial
where U0, U1, and U2 are calculated to make the interaction energy and its first and second derivatives match equation 58 at R = 2-1/6Rαβ. The best value suggested for n is 5, which gives the following U0, U1, and U2 parameters:51
Therefore, the dispersion potential for the DFTB method can be written as
and the dispersion energy is given by
This term is then added to the total DFTB energy calculated either using standard DFTB (section 5) or the SCC scheme (section 6).
8. Glycine in Aqueous Solution
Glycine (aminoethanoic acid) is the simplest among the essential aminoacids. In solution an intramolecular proton transfer from the carboxylic group to the amino group takes place, establishing the zwitterionic equilibrium shown in Figure 3. The charge separation in the zwitterionic form is stabilized by the solvent, which must have large dielectric constant, as it is the case in water. Thus, the neutral species is favored in nonpolar solvents.
In this work, Born-Oppenheimer molecular dynamics was carried out using the DCSCCDFTB method, as implemented in the deMon package.52 The glycine molecule was placed within a 16 Å periodic box containing 129 water molecules.
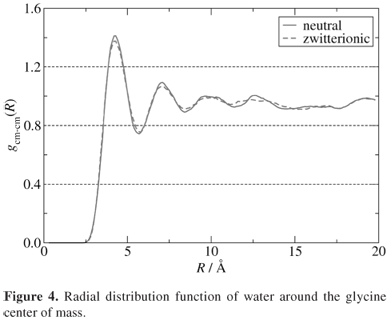
The data were collected during a 100 ps simulation time with a 0.5 fs time step. The simulation was carried out after a thermalization time of 50 ps. It is important to emphasize that both glycine and water molecules were calculated within a full quantum-mechanical approach. The radial distribution function (RDF) of water with respect to the glycine center of mass is shown in Figure 4. The first solvation shell integrates to 22 water molecules.
Table 1 shows the calculated geometrical properties of glycine in solution. The optimized geometric parameters are shown at the PBE/TZVP and DCSCCDFTB levels of theory. The estimated angles are in good agreement with the previously published results.54 The OC=O angle presents the largest discrepancy for the zwitterionic form. The PBE/TZVP estimated OC=O angle is 13 degrees larger than the value estimated with DCSCCDFTB. Furthermore, the OC=O angle is expected to increase from the neutral to the zwitterionic form due to the deprotonation of the carboxyl group. However, DCSCCDFTB seems to be insensitive to the large charge on the deprotonated carboxyl and the angle remains similar to that in the neutral form. The mean values of the angles and dihedrals from MD (last column in Table 1) are close to the optimized values with a standard deviation of about 4 degrees, except for the OCCN dihedral. This dihedral involves rotation around a single CC bond, therefore, large standard deviation is indeed expected, explaining the apparent disagreement with the gas phase PBE/TZVP results.
Wada et al.55 estimated the Gibbs free energy variation between the two glycine forms in aqueous solution to be about 7.0 kcal mol-1 (ΔH = 10.3 kcal mol-1). The change of the expected value between the two forms from the NVE molecular dynamics (ΔENVE) was estimated to be about 25.5 kcal mol-1. We have also used the continuum model to estimate the ΔG of this reaction at the PBE/TZVP/PCM level of theory and a value of 23.4 kcal mol-1 was obtained.
9. Final Remarks
DFTB is an approximate density-functional method which, in principle, does not employ any empirical parameter, in the sense that all quantities are calculated within DFT (Slater-Koster integrals) or they are calculated from reference structures by DFT calculations (Erep). It has been implemented in many different codes.56
Density Functional methods have along the time become a standard method for electronic structure calculations and substantially helped to unify organic chemistry, inorganic chemistry, surface chemistry, materials science and, more recently, biochemistry.4 With the advent of DFTB, the approximate DFT method, a plethora of challenging systems are now accessible for electronic structure calculations, enlarging the frontiers of the applicability of fundamentally well established theoretical tools. Nanostructured, self-assembled and nanoreactor systems are some of those for which DFTB can provide substantial help in the investigative work.
Acknowledgments
The financial support of the Brazilian agencies CNPq and FAPEMIG are gratefully acknowledged. We also thank the joint PROBRAL action of CAPES (Brazil) and DAAD (Germany) for financial support.
IMG11
Hélio A. Duarte graduated in Chemical Engineering (1990) and received his MSc in Inorganic Chemistry (1993) from the Federal University of Minas Gerais-UFMG. He finished his PhD at the University of Montreal in 1997 under the supervision of Prof. Dennis R. Salahub, working with adsorption on metal surfaces using density functional methods-DFT. Currently, he is associate professor at the Department of Chemistry-UFMG. His research activities are centered on the development and applications of DFT (and approximate DFT) methods to investigate chemical speciation, inclusion compounds, sulphide minerals, nanostructured clay minerals and solid/liquid interface phenomena. (http:www.qui.ufmg.br/~duarteh).
IMG12
Thomas Heine (PhD TU Dresden 1999). After pre- and postdoctoral stages at the Universities of Montreal, Exeter, Bologna and Geneva, he became Assistant Professor at TU Dresden in 2002, where he received his venia legendi in Physical Chemistry in 2006. He was appointed as Associate Professor for Theoretical Physics/Computational Materials Science at Jacobs University Bremen in 2008. His main research interests are the development of new quantum-mechanical methods and their implementation and application. He currently works on actual topics as storage of molecular hydrogen, design of new materials and nanoelectromechanics. Prof. Heine has more than 100 publications in peer-reviewed international journals, among them one Nature and two PNAS, and more than 1000 citations, leading to an h index of 25. (http://physics.jacobs-university.de/theine/index.html)
IMG13
Gotthard Seifert studied Chemistry at the TU Dresden where he received his diploma in 1975 and also graduated as Dr. rer. nat. (PhD) in 1979. He worked as a research assistant at the Institute of Theoretical Physics at TU Dresden from 1979 to 1992. He received his habilitation in theoretical physics in 1988. In 1989 and 1990, he worked as a visiting scientist and visiting professor at the International School for Advanced Studies (SISSA) in Trieste and at the EPFL. In 1991, he was a visiting scientist at the Forschungszentrum in Jülich. From 1992 to 1998, he was again at the Institute of Theoretical Physics at the TU Dresden as a lecturer/professor. He moved to the Universität Paderborn in 1998 and became a professor of Physical Chemistry at TU Dresden in 2001. His research interests are in the areas of quantum chemistry, cluster physics and chemistry and computational materials research.
IMG14
Augusto Faria Oliveira graduated in Chemistry at Federal University of Minas Gerais-UFMG (2001) and received his MSc in 2004. He completed his PhD in Quantum Chemistry (2008) under the supervision of Prof. Hélio A. Duarte at UFMG. During his PhD he spent one year in the group of Prof. Seifert at TU-Dresden. Currently he is a post-doctoral fellow at TU-Dresden in the same group, working with inorganic nanotubes. His current interests are the development and application of DFT and DFTB methods to investigate inorganic nanotubes and ion adsorption on minerals.
Received: August 6, 2008
Web Release Date: May 29, 2009
- 1. Argaman, N.; Makov, G.; Am. J. Phys. 2000, 68, 69.
- 2. Chermette, H.; Coord. Chem. Rev. 1998, 180, 699.
- 3. Chermette, H.; J. Comput. Chem. 1999, 20, 129.
- 4. Kohn, W.; Becke, A. D.; Parr, R. G.; J. Phys. Chem. 1996, 100, 12974.
- 5. Ladeira, A. C. Q.; Ciminelli, V. S. T.; Duarte, H. A.; Alves, M. C. M.; Ramos, A. Y.; Geochim. Cosmochim. Acta 2001, 65, 1211.
- 6. Sousa, S. F.; Fernandes, P. A.; Ramos, M. J.; J. Phys. Chem. A 2007, 111, 10439.
- 7. Koch, W.; Holthausen, M. C.; A Chemist's Guide to Density Functional Theory; Wiley-VCH: New York, 2001.
- 8. De Proft, F.; Geerlings, P.; Chem. Rev. 2001, 101, 1451.
- 9. Geerlings, P.; De Proft, F.; Langenaeker, W.; Chem. Rev. 2003, 103, 1793.
- 10. Duarte, H. A.; Quim. Nova 2001, 24, 501.
- 11. Shao, Y.; Molnar, L. F.; Jung, Y.; Kussmann, J.; Ochsenfeld, C.; Brown, S. T.; Gilbert, A. T. B.; Slipchenko, L. V.; Levchenko, S. V.; O'Neill, D. P.; DiStasio, R. A.; Lochan, R. C.; Wang, T.; Beran, G. J. O.; Besley, N. A.; Herbert, J. M.; Lin, C. Y.; Van Voorhis, T.; Chien, S. H.; Sodt, A.; Steele, R. P.; Rassolov, V. A.; Maslen, P. E.; Korambath, P. P.; Adamson, R. D.; Austin, B.; Baker, J.; Byrd, E. F. C.; Dachsel, H.; Doerksen, R. J.; Dreuw, A.; Dunietz, B. D.; Dutoi, A. D.; Furlani, T. R.; Gwaltney, S. R.; Heyden, A.; Hirata, S.; Hsu, C. P.; Kedziora, G.; Khalliulin, R. Z.; Klunzinger, P.; Lee, A. M.; Lee, M. S.; Liang, W.; Lotan, I.; Nair, N.; Peters, B.; Proynov, E. I.; Pieniazek, P. A.; Rhee, Y. M.; Ritchie, J.; Rosta, E.; Sherrill, C. D.; Simmonett, A. C.; Subotnik, J. E.; Woodcock, H. L.; Zhang, W.; Bell, A. T.; Chakraborty, A. K.; Chipman, D. M.; Keil, F. J.; Warshel, A.; Hehre, W. J.; Schaefer, H. F.; Kong, J.; Krylov, A. I.; Gill, P. M. W.; Head-Gordon, M.; Phys. Chem. Chem. Phys. 2006, 8, 3172.
- 12. Burke, K.; Werschnik, J.; Gross, E. K. U.; J. Chem. Phys. 2005, 123, 062206.
- 13. Kaupp, M.; Bühl, M.; Malkin, V. G.; Calculation of NMR and EPR Parameters, Wiley-VCH Verlag GmbH & Co. KGaA, 2004.
- 14. Dewar, M. J. S.; Zoebisch, E. G.; Healy, E. F.; Stewart, J. J. P.; J. Am. Chem. Soc. 1993, 115, 5348.
- 15. Stewart, J. J. P.; J. Comput. Chem. 1989, 10, 209.
- 16. Stewart, J. J. P.; J. Comput.-Aided Mol. Des. 1990, 4, 1.
- 17. Stewart, J. J. P.; J. Comput. Chem. 1990, 11, 543.
- 18. Rocha, G. B.; Freire, R. O.; Simas, A. M.; Stewart, J. J. P.; J. Comput. Chem. 2006, 27, 1101.
- 19. Frenzel, J.; Oliveira, A. F.; Duarte, H. A.; Heine, T.; Seifert, G.; Z. Anorg. Allg. Chem. 2005, 631, 1267.
- 20. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrzewski, V. G.; Montgomery, J. A.; Stratmann, R. E.; Burant, J. C.; Dapprich, S.; Millan, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G. A.; Ayala, P. Y.; Cui, Q.; Morokuma, K.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, J. V.; Baboul, A. G.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Pikorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Gonzales, C.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Andreas, J. L.; Head-Gordon, M.; Reploge, E. S.; Pople, J. A.; Gaussian, Inc.: Pittsburg, PA, 1998.
- 21. Hazebroucq, S.; Picard, G. S.; Adamo, C.; Heine, T.; Gemming, S.; Seifert, G.; J. Chem. Phys. 2005, 123, 134510.
- 22. Heine, T.; dos Santos, H. F.; Patchkovskii, S.; Duarte, H. A.; J. Phys. Chem. A 2007, 111, 5648.
- 23. Heine, T.; Seifert, G.; Fowler, P. W.; Zerbetto, F.; J. Phys. Chem. A 1999, 103, 8738.
- 24. Ivanovskaya, V. V.; Heine, T.; Gemming, S.; Seifert, G.; Phys. Status Solidi B 2006, 243, 1757.
- 25. Frauenheim, T.; Seifert, G.; Elstner, M.; Niehaus, T.; Kohler, C.; Amkreutz, M.; Sternberg, M.; Hajnal, Z.; Di Carlo, A.; Suhai, S.; J. Phys.: Condens. Matter 2002, 14, 3015.
- 26. Heringer, D.; Niehaus, T. A.; Wanko, M.; Frauenheim, T.; J. Comput. Chem. 2007, 28, 2589.
- 27. Niehaus, T. A.; Suhai, S.; Della Sala, F.; Lugli, P.; Elstner, M.; Seifert, G.; Frauenheim, T.; Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 63, 085108.
- 28. Parr, R. G.; Yang, W.; Density-Functional Theory of Atoms and Molecules; Oxford University Press, 1989.
- 29. Hohenberg, P.; Kohn, W.; Phys. Rev. B: Condens. Matter Mater. Phys. 1964, 136, B864.
- 30. Kohn, W.; Sham, L. J.; Phys. Rev. 1965, 140, 1133.
- 31. Slater, J. C.; Koster, G. F.; Phys. Rev. 1954, 94, 1498.
- 32. Goringe, C. M.; Bowler, D. R.; Hernandez, E.; Rep. Prog. Phys. 1997, 60, 1447.
- 33. Froyen, S.; Harrison, W. A.; Phys. Rev. B: Condens. Matter Mater. Phys. 1979, 20, 2420.
- 34. Chadi, D. J.; Phys. Rev. Lett. 1979, 43, 43.
- 35. Foulkes, W. M. C.; Haydock, R.; Phys. Rev. B: Condens. Matter Mater. Phys. 1989, 39, 12520.
- 36. Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G.; Phys. Rev. B: Condens. Matter Mater. Phys. 1998, 58, 7260.
- 37. Frauenheim, T.; Seifert, G.; Elstner, M.; Hajnal, Z.; Jungnickel, G.; Porezag, D.; Suhai, S.; Scholz, R.; Phys. Status Solidi B 2000, 217, 41.
- 38. Mulliken, R. S.; J. Chem. Phys. 1955, 23, 1833.
- 39. Parr, R. G.; Pearson, R. G.; J. Am. Chem. Soc. 1983, 105, 7512.
- 40. Janak, J. F.; Phys. Rev. B: Condens. Matter Mater. Phys. 1978, 18, 7165.
- 41. Mineva, T.; Heine, T.; Int. J. Quantum Chem. 2006, 106, 1396.
- 42. Porezag, D.; Frauenheim, T.; Kohler, T.; Seifert, G.; Kaschner, R.; Phys. Rev. B: Condens. Matter Mater. Phys. 1995, 51, 12947.
- 43. Seifert, G.; Porezag, D.; Frauenheim, T.; Int. J. Quantum Chem. 1996, 58, 185.
- 44. Hu, H.; Lu, Z.; Elstner, M.; Hermans, J.; Yang, W.; J. Phys. Chem. A 2007, 111, 5685.
- 45. Frenzel, J.; Joswig, J. O.; Seifert, G.; J. Phys. Chem. C 2007, 111, 10761.
- 46. Kuc, A.; Enyashin, A.; Seifert, G.; J. Phys. Chem. B 2007, 111, 8179.
- 47. Luschtinetz, R.; Oliveira, A. F.; Frenzel, J.; Joswig, J. O.; Seifert, G.; Duarte, H. A.; Surf. Sci. 2008, 602, 1347.
- 48. Elstner, M.; Frauenheim, T.; McKelvey, J.; Seifert, G.; J. Phys. Chem. A 2007, 111, 5607.
- 49. Muller, P.; Pure Appl. Chem. 1994, 66, 1077.
- 50. Elstner, M.; Hobza, P.; Frauenheim, T.; Suhai, S.; Kaxiras, E.; J. Chem. Phys. 2001, 114, 5149.
- 51. Zhechkov, L.; Heine, T.; Patchkovskii, S.; Seifert, G.; Duarte, H. A.; J. Chem. Theory Comput. 2005, 1, 841.
- 52. Koester, A. M.; Flores, R.; Geudtner, G.; Goursot, A.; Heine, T.; Patchkovskii, S.; Reveles, J. U.; Vela, A.; Salahub, D. R.; deMon VS. 1.1; NRC: Ottawa, Canada, 2004.
- 53. Rappe, A. K.; Casewit, C. J.; Colwell, K. S.; Goddard, W. A.; Skiff, W. M.; J. Am. Chem. Soc. 1992, 114, 10024.
- 54. Tortonda, F. R.; Pascual-Ahuir, J. L.; Silla, E.; Tunon, I.; Ramirez, F. J.; J. Chem. Phys. 1998, 109, 592.
- 55. Wada, G.; Tamura, E.; Okina, M.; Nakamura, M.; Bull. Chem. Soc. Jpn. 1982, 55, 3064.
-
56http://www.dftb.org, accessed in May 22, 2009.
» link
Publication Dates
-
Publication in this collection
28 Aug 2009 -
Date of issue
2009
History
-
Received
06 Aug 2008 -
Accepted
29 May 2009