Abstract
The Jiles-Atherton scalar hysteresis model presents five parameters used to represent the material tested and used to calculate the magnetic losses. This article presents a comparative analysis of the performance of two methods of identifying these parameters. In the first method, the equations of Jiles-Atherton were assembled into a single non-linear ordinary differential equation as a function of the variables of interest. An algebraic system of five equations with five unknowns is obtained by evaluating the non-linear ordinary differential equation in five points belonging to the branch of the experimental hysteresis loop. The parameters are obtained by solving this system of equations using the method of Non-Linear Least Squares (NLLS). In the second method, the inverse model of Jiles-Atherton is used to calculate the magnetic field H from the experimental values of magnetic induction B. Using the method of genetic algorithms (MGA), the objective function given by the sum of the relative error of calculated magnetic field and experimental magnetic field along the hysteresis loop is minimized. To validate methods the experimental curves were compared with calculated ones. When applying the methods, it was verified that NLLS besides providing more accurate results, it is faster when compared to MGA. In the MGA the convergence of the calculated magnitudes to the experimental magnitudes improves when one of the chromosomes of the initial population is the solution obtained applying NLLS.
Index Terms
Magnetic hysteresis; magnetic materials; method of genetic algorithms; non-linear least squares method
I. INTRODUCTION
Ferromagnetic materials are used in electrical engineering applications to provide a robust structure to electrical machines, to conduct magnetic flux and mainly to amplify the magnetic inductions up to a limit value imposed by the saturation of the material. The inability to traverse the same paths of flux in the material, the need for energy to reorient the magnetic domains of the material, the delay considering the magnetic induction B and the magnetic field H and the pinning points that hinder the movement of the domain walls originate the phenomenon of hysteresis in ferromagnetic materials.
The model for the magnetic hysteresis phenomenon presented by Jiles-Atherton is widely used [11 [1] D. C. Jiles, J. B. Thoelke, and M. K. Devine, “Numerical determination of hysteresis parameters the modeling of magnetic properties using the theory of ferromagnetic hysteresis,” IEEE Trans. Magn., vol. 28, no. 1, pp. 27-35, Jan. 1992.]-[1212 [12] F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “Insertion of a sixth parameter in Jiles-Atherton hysteresis scalar model and the method for parameters identification,” 17th Biennial IEEE Conference on Electromagnetic Field Computation CEFC2016 proceedings, Miami, FL/USA.] and is based on the flexion and translation movement of magnetic domain wall. Consequently, the total magnetization M is composed of two plots: the reversible magnetization Mrev (due to the bending of the walls), and the irreversible magnetization Mirr (due to the displacement of the walls). The anhysteretic magnetization Man is the ideal state of configuration of the domains: condition that requires less energy. A domain wall located in the region between two domains, whose moments are aligned in parallel and antiparallel to the direction of magnetic field applied to the material, flexes in one way when M > Man, and otherwise when M < Man. When M = Man the wall is planar (without bending). The amount of bending of the domain wall is linearly dependent on the difference between Man and M. The coefficient of proportionality is represented by the parameter c in the Jiles-Atherton model. Man is modeled by the modified Langevin equation, in which the parameter a represents the shape of the anhysteretic magnetization and the ms parameter represents the saturation magnetization. The difficulty of moving the domain walls, due to the non-idealities of the material, is represented by the parameter k. An inter-domain coupling that affects the effective magnetic field is represented by the parameter α.
In the original Jiles-Atherton model, magnetic field is the independent variable and magnetic induction is the dependent variable. A modification of the Jiles-Atherton model is presented in [99 [9] N. Sadowski, N. J. Batistela, J. P. A. Bastos, and M. Lajoie-Mazenc, “An inverse Jiles-Atherton model to take into account hysteresis in time stepping finite element calculations,” IEEE Trans. Magn., vol. 38, no. 2, pp. 797-800, Mar. 2002.]: in the inverse model, magnetic induction becomes the independent variable. Through this modification, the model is naturally adapted to the calculation of fields by Finite Element Method with formulation in potential magnetic vector.
To identify the parameters of the model, the methods found in the literature are based on non-linear least squares [33 [3] P. Kis and A. Iványi, “Parameter identification of Jiles–Atherton model with nonlinear least-square method,” Physica B, 343, pp. 59–64, 2004.], [1010 [10] F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “An improved method for acquisition of the parameters of Jiles-Atherton hysteresis scalar model using integral calculus,” Journal of Microwaves Optoelectronics and Electromagnetic Applications, vol. 16, no.1, pp. 165-179, March 2017.], genetic algorithms [44 [4] J. V. Leite, S. L. Avila, N. J. Batistela, W. P. Carpes Jr., N. Sadowski, P. Kuo-Peng, and J. P. A. Bastos, “Real coded genetic algorithm for Jiles–Atherton model parameters identification,” IEEE Trans. Magn., vol. 40, no. 2, pp. 888-891, Mar. 2004.], [55 [5] K. Chwastek and J. Szczyglowski, “Identification of a hysteresis model parameters with genetic algorithms,” Mathematics and Computers in Simulation, vol. 71, pp. 206–211, 2006.], differential evolution [66 [6] M. Toman, G. Stumberger, and D. Dolinar, “Parameter identification of the Jiles–Atherton hysteresis model using differential evolution,” IEEE Trans. Magn., vol. 44, no. 6, pp. 1098-1101, Jun. 2008.], particle swarm optimization [77 [7] R. Marion, R. Scorretti, N. Siauve, M. Raulet, and L. Krähenbühl, “Identification of Jiles–Atherton model parameters using particle swarm optimization,” IEEE Trans. Magn., vol. 44, no. 46, pp. 894-897, Jun. 2008.] and branch and bound optimization method [88 [8] K. Chwastek and J. Szczygowski, “An alternative method to estimate the parameters of Jiles–Atherton model,” Journal of Magnetism and Magnetic Materials, vol. 314, pp. 47–51, 2007.]. This work proposes a comparative analysis of the performance of two methods of identifying the parameters of the hysteresis scalar model of Jiles-Atherton. The possibility of improving the precision of the parameter set using combination of techniques is also verified. The method of NLLS is applied to calculate the parameters of the model solving two systems of nonlinear algebraic equations. Each system represents a branch of the hysteresis loop and presents five equations with five unknowns. The unknowns are the five parameters of the Jiles-Atherton hysteresis model. The equations of the system resulted from the evolution of an ordinary differential equation in five main points strategically positioned in the branch of the hysteresis loop. The MGA is used to calculate model parameters that minimize the relative error of calculated magnetic field and experimental magnetic field along the hysteresis loop. The two methods were applied to calculate the parameters of the Jiles-Atherton hysteresis model of several samples. The results calculated by each of the methods will be compared with experimental results. Regarding the importance of this research, a set of parameters that adequately represent the material enables an optimized design and a more reliable analysis of the machine. The set of parameters also influences the convergence of numerical systems, for example, in the calculation of fields by finite element considering magnetic hysteresis. The original technique proposed allows to obtain an accurate set of parameters. The experimental data used in this study were obtained through an Epstein frame, a data acquisition system and material samples.
In the algorithm of the inverse model, magnetic field is calculated from the experimental values of magnetic induction and magnetization as follows:
In which: M is the magnetization; H is the magnetic field; B is the magnetic induction; and μ0 is the magnetic permeability of the vacuum.
II. NON-LINEAR LEAST SQUARES METHOD
The problem of material characterization consists of: for a given sample of steel, low-frequency B-H curves are obtained, which guarantees that the dynamic losses can be disregarded. For this set of experimental data, a set of five parameters must be found so that the hysteresis model can represent the behavior of this sample.
To solve the above problem, the equations of the Jiles-Atherton hysteresis scalar model are used. These equations involve variables other than those whose values are known, and beyond those whose values are intended. Consequently, there is a need to manipulate the equations of the model to obtain a unique equation, involving only the variables of interest H, B, and the model parameters. This manipulation, in addition to better organizing the data, also assists in identifying the problem behind the determination of the parameters. Thus, the equations of the model were manipulated, and a nonlinear ordinary differential equation was obtained. This non-linear ordinary differential equation is the problem behind the determination of the parameters and is represented compactly by dB/dH = f(H,B). The proposed methodology to determine the parameters of the model consists in transforming the non-linear ordinary differential equation obtained in an algebraic equation as a function of B and H. In this regard, it is necessary to choose five points of the experimental hysteresis loop; and numerically calculate the derivatives at these points. The non-linear ordinary differential equation is evaluated at the first chosen point, resulting in an algebraic equation. When the non-linear ordinary differential equation is evaluated at all points chosen from the experimental data, five algebraic equations are obtained, and a system is constructed. To calculate the parameters, it is sufficient to solve this system of equations. Given an algebraic system of five nonlinear equations.
In which x = [ms α a k c] are the five unknowns. The goal is to find a vector x such that Fl(x) = 0 for 1≤ l ≤5. To solve this system of equations the sum of squares is minimized. If the sum of squares is zero, then the system of equations is solved. The method NLLS was used to solve the system.
We intend to calculate the parameters (of the model) of the curve that best fits the experimental data (B and H) for a given material. These parameters which adjust (through the least squares method) the nonlinear function F(x) to the set of experimental points (B and H), can be identified, for example, by applying trust region techniques. Deterministic methods (NLLS) usually perform well when the starting point is clearly defined. As the parameters the model assume positive values a starting set would be ms ≈ Bs/μ0; 10−6< α <10−4; a ≈ coercive field; 0< c <1. In order to obtain the result shown in Fig. 4, it was used the starting set x0 = [1.72x106 2x10−4 1 72 1 00 0.5].
Fig. 1 shows the main steps of numerical procedure to calculate the parameters by non-linear least squares method.
III. QUALITATIVE COMPARISON BETWEEN NLLS AND MGA
The MGA is used to calculate the five parameters of the Jiles-Atherton hysteresis model that minimize the sum of the relative error of calculated H and experimental H along the hysteresis loop ((3) is minimized).
Subject to: 10−6 ≤ ms ≤ 108, 10−6 ≤ α ≤ 10−4, 10−6 ≤ a ≤ 103, 10−6 ≤ k ≤ 104, 10−6 ≤ c ≤ 0.999.
In which n is the number of points of the experimental hysteresis loop, Hcalculated is obtained using (1).
In NLLS these parameters were identified differently by solving a system of equations written using dB/dH = f(H,B).
The minimum of the objective function is calculated within the allowed range for each parameter. In the zero iteration a random population (values of a uniform distribution) of chromosomes is generated. The chromosome is a vector whose components are the five parameters of the model. Random values are mapped within the allowed range. This population presents 100 initial values for the set of parameters x0 = [ms0 α0 a0 k0 c0], …, x99 = [ms99 α99 k99 k99 c99]. The MGA processes the population of chromosomes that represents a possible solution of the problem, whereas in NLLS the process starts with a single initial value for the set of parameters x0.
In the MGA, for a given x0 and experimental Bi are calculated Hi using (1) and gi(x0) using (3), with i = 1, …, n. For the complete hysteresis loop . This procedure is repeated for all initial sets of parameters x0, …, x99, obtaining g(x0), … , g(x99). The values g(xj), j = 0, …, 99, are organized and for g(xj) of the smallest error is assigned a maximum fitness two, and for g(xj) of the greatest error is assigned a null fitness. At the intermediate values of g(xj) are attributed aptitudes with N=100 chromosomes x in the population. It completes the initial population analysis. A population of 100 chromosomes was used because in this way a sufficiently large matrix of 100x13 is constructed in which for each of the 100 chromosomes x the five random values of the parameters are specified, these five values mapped in the allowed range, the value of the objective function g(xj), the aptitudes and the accumulated aptitudes. So we have 13 columns.
In the first iteration is built the first generation from the initial generation. This is done by selecting the most apt x chromosomes in the initial generation: two chromosomes are randomly selected and the one with the greatest aptitude is called parent1=[msj αj aj kj cj]. The process is repeated to select parent2 ≠ parent1. The crossover operator BLX-0.5 is applied to generate child , β a uniform distribution random number in the interval [−0.5, 1.5]. The child c1 presents five genes c1(1)=ms, …, c1(5)=c. Initially, β is used to calculate all c1 genes. Check if c1 is a doable child. If c1 is an infeasible child then the λ-th gene of c1 is outside the allowed range for the gene, λ =1,…,5. A new λ-th gene must be generated using new β. This is repeated until the λ-th gene is within the allowed range. In this way we obtain a feasible child c1 with all its genes within the respective allowed intervals.
The mutation operator is applied to one parent to generate a single mutated child. parent = parent1 or parent2 is randomly chosen to undergo mutation. One of the five parent genes are randomly selected to mutate. Let the λ-th gene be selected to undergo mutation. A random number rm of uniform distribution is generated in the interval [0, 1]. If rm <0.5 the λ-th gene is replaced by the minimum limit of its allowed range; otherwise the λ-th gene is replaced by the maximum limit of its allowed range. Thus, the child c2 is obtained.
The two children calculated c1 and c2 replace the two worst-fit chromosomes of initial generation, if these children are not yet in initial generation (zero generation). In this way the first generation of 100 chromosomes is obtained. For each of the chromosomes the information mentioned in initial generation is stored in a matrix 100x13.
For MGA from the initial generation was built the next generation. The initial generation is constructed randomly, its population is evaluated, and each chromosome receives an aptitude score that reflects the quality of the solution that the chromosome represents. The fittest chromosomes are selected and modified through the crossover and mutation operators generating offspring for the next generation. The process is repeated until a satisfactory solution is found.
In NLLS method, for each initial value x0 reported by the user a sequence of values x1, x2, … is constructed which is expected to converge to x* a local minimum for the function to be adjusted. In each iteration there is a direction of descent and a step is given in that direction. A merit function can be used to decide whether x in the next iteration is better or worse than x in the current iteration.
In the MGA, the selection of the most fit chromosomes can be made through the roulette wheel process or tournament selection. The fitness can be equal to the objective function or it can be defined by the ordering of the chromosome in the population. The search mechanism is crossover and mutation, and the latter improves the diversity of chromosomes in the population. The best chromosome can be transferred from one generation to the next without undergoing changes. In the MGA with real representation can be used medium crossover, geometric mean crossover, BLX-alpha crossover, linear crossover, uniform mutation, gaussian mutation, creep mutation and limit mutation. Solutions found by other methods can be inserted in the initial population. Some caution is needed: combating premature convergence by limiting the number of children by chromosomes, maintaining the diversity of chromosomes in the population, avoiding identical chromosomes in the initial population, keeping the population with all chromosomes distinct from each other. All population is replaced in every generation or only 2 children are raised per generation to replace the 2 worst chromosomes of the population. The MGA is slow when compared to NLLS.
In NLLS, the system of equations can be solved using one of the three algorithms: reflexive trust region; dogleg trust region; and Levenberg-Marquardt.
The MGA converges when 95% of the chromosomes represent the same value of g(x). For the MGA, the process is repeated until it reaches the stopping criterion (maximum number of iterations or convergence). The parameters found are inserted in the inverse model to compare experimental and calculated data as it occurs in NLLS.
Fig. 2 shows the main steps of numerical procedure to calculate the parameters by genetic algorithms method.
IV. CHARACTERIZATION RESULTS
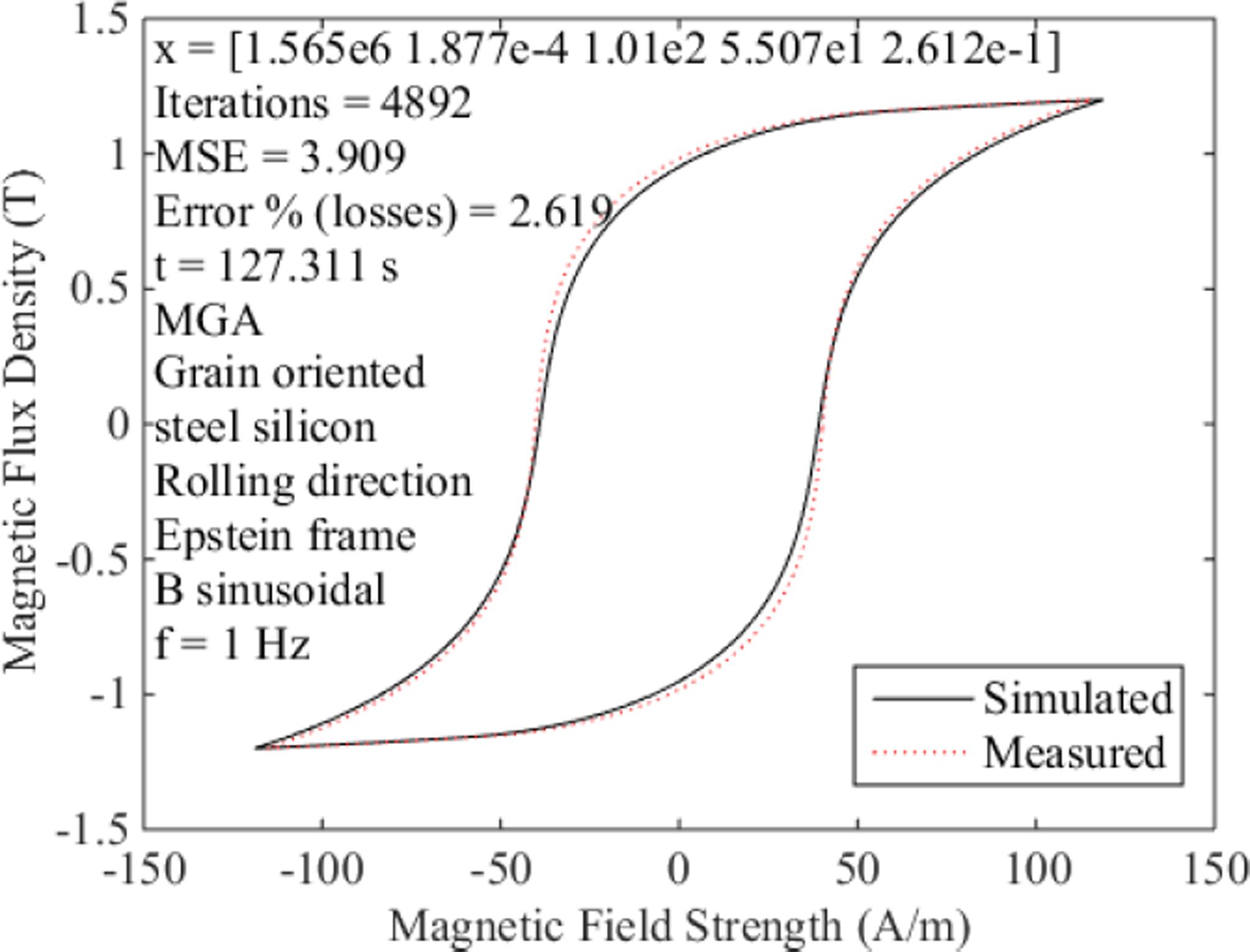
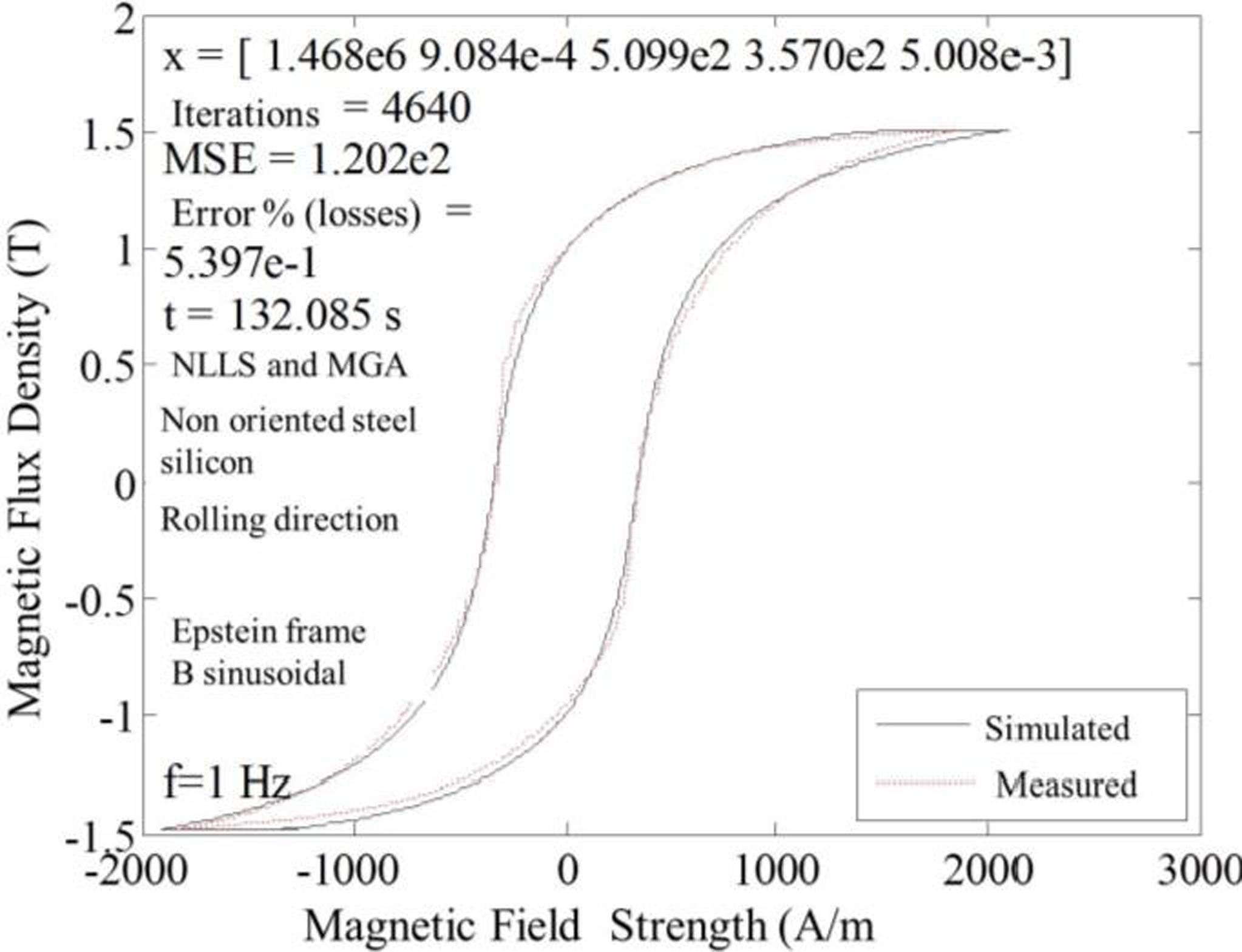
In this section, it is presented characterization results obtained using NLLS and the MGA. The calculated parameters x, the number of iterations required for the algorithm to converge, the mean squared error (MSE), the percentage error considering the measured magnetic loss and the calculated magnetic loss, the simulation time t, the type and the cutting direction of the sample, the test instrument used, the test conditions, the simulated hysteresis loop and the experimental hysteresis loop can be seen in Fig. 3-11.
To allow a quantitative discussion of the results, NLLS and the MGA were submitted to the same conditions: test material, hardware used and experimental data. Thus, an appropriate quantitative comparison between NLLS and the MGA may be made by looking at Fig. 3 and Fig. 4. NLLS led to a more accurate result when compared to the result that the MGA provided. The MSENLLS = 1.709 is lower than the MSEMGA = 3.909. NLLS converged in only 4 iterations while the MGA converged in 4892 iterations. NLLS is faster taking only 21 s to provide the parameters of the material while the MGA took 127 s. As can be seen in Fig. 4, for NLLS the calculated loop is very close to the measured loop (the loops overlap), and consequently, the calculated parameters describe very well the experimental behavior of the material. NLLS is faster and more accurate then MGA and has a better convergence than MGA.
To improve the results provided by the MGA, the solution found by NLLS was included in the initial population. The result of this alliance can be observed in Fig. 5. Observing Fig. 3 and Fig. 5 it is possible to note that the MSE improved from 3.909 to 1.606 and the simulated and measured hysteresis loops overlap. Observing Fig. 4 and Fig. 5 it is possible to verify that the alliance between NLLS and the MGA improved the accuracy of the set of parameters found since the MSE was reduced from 1.709 to 1.606.
Also, in Fig. 6-11 it is possible to observe the results of the characterization of several types of samples, cut in several directions, using the MGA with previous information from NLLS. Also, for these cases the agreement between experimental and calculated data satisfies expectations. These results enable more efficient designs of electric machines, reducing energy consumption and environmental impacts. This study is limited in the modeling of hysteresis loops at magnetic induction levels from 1 to 1.5 T. The model used is restricted to a smooth sigmoid hysteresis loop.
V. WORKBENCH USED TO ACQUIRE EXPERIMENTAL DATA
The experimental data used in this work was obtained with a workbench [1313 [13] N. J. Batistela, Caracterização e Modelagem Eletromagnética de Lâminas de Aço ao Silício, Ph.D. dissertation, Universidade Federal de Santa Catarina, Florianópolis, SC, 2001.] containing a standardized Epstein frame. This workbench can be observed in Fig. 12.
The Epstein frame contains a primary and secondary winding. The test samples form the ferromagnetic core of the transformer. The Epstein frame also has a winding to compensate the dispersed magnetic flux. The input voltage is applied on the secondary winding, in order to ensure a sinusoidal induction waveform, and the primary current is left to free circulation.
The Epstein frame power is supplied by a sine wave inverter that is variable in amplitude and frequency, also it is possible to operate with a harmonic content or with pulsed waveforms. Voltage and current are measured simultaneously and acquired for numerical treatment. The magnetic field and the magnetic induction are obtained by numerical calculations using the current and voltage measured according to the Brazilian standard NBR 5161:
Where: Bm is the magnetic flux density in the sample (T), Ū2 is the secondary voltage (V), f is the frequency (Hz), N2 is the number of secondary turns of the Epstein frame, S is the cross section of the sample (m2), Hm is the magnetic field strength (A/m), N1 is the number of primary turns of the Epstein frame, I1 is the rms value of the primary current (A), lm is the length of the effective magnetic path (m).
Several non-oriented and grain-oriented materials were tested in the Epstein framework. The Epstein test allows several samples to be tested on the same apparatus, without windings needed to be made for each sample. The Epstein test presents high reproducibility and, being one of the most used tests, the results are well accepted by consumers of silicon steel as reference.
On the other hand, the magnetic circuit of Epstein's frame is not homogeneous. The magnetization of the material is not uniform because in addition to the small gaps that increase the reluctance, there is an amount of additional mass coming from the superposition of the samples in the corners of the frame. To minimize the air gap, local pressure (as recommended by standards NBR 5161, ASTM A 343, JISC 2550, IEC 404-2) is applied, resulting in a mechanical stress that can alter the magnetic properties of the material. The disadvantages of the test are also related to the time spent in sample preparation (number of sheets); waste of material; assembly and disassembly of the test sample; to the need for sample annealing to relieve shear stresses due to sample size.
For the Epstein test, the samples used have no curvature (plan deviation) originated by the material storage coils. If they show curvature, the samples are forced when inserted into the frame resulting in elastic deformations. These deformations increase the magnetic loss. During the test the sheets may vibrate causing indentations in the hysteresis curve. In samples for the Epstein test, magnetic flux density and magnetic field strength are measured at sample length. This sample may be stamped in the longitudinal, transverse direction or any other direction of the rolling direction of the material.
VI. CONCLUSION
In this article, an appropriate qualitative and quantitative comparison between NLLS and the MGA was presented. The equations of the Jiles-Atherton model were assembled into a single equation, which was applied to model the hysteresis loop of the material in two steps. One technique, which uses experimental points to generate the global system, was developed. The algorithm, which is based on NLLS, was robust, fast and provided a more precise set of parameters when compared to the MGA. For the MGA to find more precise parameters it was necessary to include in the initial population information previously obtained by the prior method. In this study, the efficacy of the combination of the two techniques was investigated, using smooth hysteresis loop, noisy content loop, samples cut in different directions, grain oriented and non-oriented samples. Considering the results obtained, the resulting combined technique was validated by comparing the experimental hysteresis loop with the calculated hysteresis loop. This approach was used for the first time in this type of electromagnetic problem, thus constituting the main contribution of this work. As this paper dealt with an important industrial problem for continuity of this research, the methodologies presented will be compared with other methods presented in the literature.
APPENDIX
The equations of the Jiles-Atherton model are as follows:
Where: M is the magnetization; Mirr is irreversible magnetization; Mrev is reversible magnetization; Man is anhysteretic magnetization; ms, α, a, k, and c are the parameters of the material; He is the effective magnetic field; δ assumes the values ±1; H is the magnetic field; B is the magnetic induction and μ0 is the magnetic permeability of the vacuum.
Equations (4)-(9) allow to obtain an ODE, ordinary differential equation, nonlinear as a function of H, and of B: where the five parameters of model, ms; α; a; k; and c, also appear. The methodology is shown below. Isolating the total magnetization of the other variables in (9) immediately follows: . Taking this expression to (8), the effective magnetic field can be written as follows: . Placing the magnetic field in evidence, follows:
To conduct mathematical modeling, Fig. 13 shows a B-H curve of a ferromagnetic material. There is interest in modeling this loop according to the Jiles-Atherton approach, and mathematically the loop could be represented by two functions: the first function to model the ascending branch, belonging to the first, third, and fourth quadrants; and the last function to model the descending branch, belonging to the first, second, and third quadrants.
Considering (7), for δ = 1 we have the ascending branch, and for δ = −1 we have the descending branch. After this, the analysis is organized in two stages: observing in the first moment the ascending branch of the B-H curve.
For the ascending branch we have δ = 1.
It is observed that equation (7) establishes the rate of change of the irreversible magnetization with the effective magnetic field , and this allows to formalize the first affirmation: irreversible magnetization is dependent on the effective magnetic field, that is, Mirr = Mirr(He). On the other hand, observing (10) it is possible to formalize the second affirmation: the effective magnetic field is dependent on the magnetic field and the magnetic induction, otherwise, He = He(H,B). Taking these two statements into consideration, it follows clearly: Mirr = Mirr(He(H,B)), consequently, one can derive (chain rule) irreversible magnetization and consider the first portion as follows:
Considering the term dHe/dH of (11), and based on (10) it is possible to determine the expression of the derivative of the effective magnetic field with respect to the magnetic field, as follows:
In turn, equation (9) allows to write: . Isolating the total magnetization of the other variables in this last equation we have:
As M = M(H,B), and since total magnetization is the sum of its reversible and irreversible components, then: Mirr = Mirr(H,B) and Mrev = Mrev(H,B).
Substituting (5) into (4) we have: , that is, , meaning, . Isolanting the irreversible component of magnetization, from the other variables in the latter equation, it is also true that:
Substituting (14) into (15) yields:
Equation (16) allows the expression of the derivative of the irreversible magnetization with respect to the magnetic field to be obtained as follows:
On the other hand, replacing (7) in (11), and considering δ =1 we have: that with equation (13) generate: , that is, with equation (16) we can write:
The equation above can be written as:
Putting Man in evidence it is also true that:
and consequently,
Equation (17) can be altered without impairing equality, and written in a new way as:
Substituting (13) in this new form of (17) we have:
Equations (18) and (19) show the expression of the derivative of irreversible magnetization in relation to the magnetic field, and consequently, (18) is equal to (19), and follows:
However, substituting (10) into (6) gives the following result:
The equation (6) allows the derivation of the derivative of the anhysteretic magnetization in relation to the effective magnetic field, as follows:
Being .
It implies in .
As , it follows:
On the other hand, and consequently,
Finally, replacing equations (21), (22), and (10) in equation (20), we have:
Equation (23) is written in terms of H, B, dB/dH, and the five parameters sought: ms, α, a, k, and c. The term dB/dH can be isolated from the other variables in (23), as follows:
Where:
The preceding equation has special importance: (24) is the main equation used to identify the parameters of the model. This non-linear ODE can be represented, in a simplified way, by:
ACKNOWLEDGMENT
Laura Carvalho de Barros many thanks for your assistance.
REFERENCES
-
1[1] D. C. Jiles, J. B. Thoelke, and M. K. Devine, “Numerical determination of hysteresis parameters the modeling of magnetic properties using the theory of ferromagnetic hysteresis,” IEEE Trans. Magn, vol. 28, no. 1, pp. 27-35, Jan. 1992.
-
2[2] J. V. Leite, N. Sadowski, P. Kuo-Peng, N. J. Batistela, and J. P. A. Bastos, “The inverse Jiles–Atherton model parameters identification,” IEEE Trans. Magn, vol. 39, no. 3, pp. 1397-1400, May 2003.
-
3[3] P. Kis and A. Iványi, “Parameter identification of Jiles–Atherton model with nonlinear least-square method,” Physica B, 343, pp. 59–64, 2004.
-
4[4] J. V. Leite, S. L. Avila, N. J. Batistela, W. P. Carpes Jr., N. Sadowski, P. Kuo-Peng, and J. P. A. Bastos, “Real coded genetic algorithm for Jiles–Atherton model parameters identification,” IEEE Trans. Magn, vol. 40, no. 2, pp. 888-891, Mar. 2004.
-
5[5] K. Chwastek and J. Szczyglowski, “Identification of a hysteresis model parameters with genetic algorithms,” Mathematics and Computers in Simulation, vol. 71, pp. 206–211, 2006.
-
6[6] M. Toman, G. Stumberger, and D. Dolinar, “Parameter identification of the Jiles–Atherton hysteresis model using differential evolution,” IEEE Trans. Magn, vol. 44, no. 6, pp. 1098-1101, Jun. 2008.
-
7[7] R. Marion, R. Scorretti, N. Siauve, M. Raulet, and L. Krähenbühl, “Identification of Jiles–Atherton model parameters using particle swarm optimization,” IEEE Trans. Magn, vol. 44, no. 46, pp. 894-897, Jun. 2008.
-
8[8] K. Chwastek and J. Szczygowski, “An alternative method to estimate the parameters of Jiles–Atherton model,” Journal of Magnetism and Magnetic Materials, vol. 314, pp. 47–51, 2007.
-
9[9] N. Sadowski, N. J. Batistela, J. P. A. Bastos, and M. Lajoie-Mazenc, “An inverse Jiles-Atherton model to take into account hysteresis in time stepping finite element calculations,” IEEE Trans. Magn, vol. 38, no. 2, pp. 797-800, Mar. 2002.
-
10[10] F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “An improved method for acquisition of the parameters of Jiles-Atherton hysteresis scalar model using integral calculus,” Journal of Microwaves Optoelectronics and Electromagnetic Applications, vol. 16, no.1, pp. 165-179, March 2017.
-
11[11] K. Hoffmann, J. P. A. Bastos, J. V. Leite, N. Sadowski, and F. B. R. Mendes, “A vector Jiles-Atherton model for improving the FEM convergence,” IEEE Transactions on Magnetics, vol. 53, no. 6, June 2017.
-
12[12] F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “Insertion of a sixth parameter in Jiles-Atherton hysteresis scalar model and the method for parameters identification,” 17th Biennial IEEE Conference on Electromagnetic Field Computation CEFC2016 proceedings, Miami, FL/USA.
-
13[13] N. J. Batistela, Caracterização e Modelagem Eletromagnética de Lâminas de Aço ao Silício, Ph.D. dissertation, Universidade Federal de Santa Catarina, Florianópolis, SC, 2001.
Publication Dates
-
Publication in this collection
12 Sept 2019 -
Date of issue
Sept 2019
History
-
Received
31 Oct 2018 -
Reviewed
01 Nov 2018 -
Accepted
15 Aug 2019