Abstract
Free vibration of a bimaterial circular nano-tube is investigated. The tube is formed by bonding together a Si3N4/SUS304 functionally graded upper semi tube and a ZrO2/Ti-6Al-4V functionally graded lower semi tube. The material properties of the tube are assumed to vary along the radius according to power law with the power index of upper semi tube differing from that of lower semi tube. Based on non-local elasticity theory and Hamilton’s principle, a refined beam model considering the effect of transverse shear deformation is used to derive the governing equations, then analytical solution is obtained by using a two-steps perturbation method. Our results were compared with the existing ones. The effects on tube’s linear and non-linear frequency are analyzed of the factors, including small scale parameter, temperature, the double volume fraction indexes, slenderness ratio and different types of beam model. A new approach is suggested in this article to change the natural frequency of the tubes by adjusting constituent materials. In contrast to conventional approach, the new one can result in more accurate frequency control in the same dimensionless size of tubes.
Key words:
Functionally graded material; Non-local; Vibration; Bi-semi-tubes; Perturbation method;
1. Introduction
Non-homogeneous composite materials composed of functionally graded material (FGM) in which the effective material properties can be changed in a certain direction have captured extensive attention in a multitude of industries (Jha et al., 2013; Koizumi, 1997). Owing to superior performance, such material could satisfy the majority of design requirements of each component. In order to analyze its mechanical properties, classical formulas were modified and new theories were proposed (Huang and Li, 2010b; Shafiei et al., 2016a; Shafiei et al., 2016b; Zhang, 2013; Hosseini et al., 2016; Thinh et al., 2016). However, with emerging new demands in manufacturing and engineering, most of the previous studies related to FGMs whose effective material properties only vary in the direction of thickness or length can’t meet those needs and challenges very well (Nemat-Alla, 2003; Fan et al., 2013; Lü et al., 2009; Wang et al., 2016; Lei et al., 2016; Gupta et al., 2015; Thang and Nguyen-Thoi, 2016). Consequently, in recent years, more and more researchers have been studying structural components made of two or three-directional functionally graded materials and subjected to different types of functionally graded distribution (Şimşek, 2015; Hao and Wei, 2016; Lü et al., 2008; Nguyen et al., 2017; Pydah and Sabale, 2017; Nejad and Hadi, 2016a; Nejad and Hadi, 2016b; Nejad et al., 2016).
In practical uses, FGMs may be fabricated into different structural components, e.g. plates, rods and tubes. Among these components, tube is one of the most important and frequently used structural components in many industries. Fig.1 shows some potential fields for functionally graded materials as well as tubes application(Hosseini et al., 2017; Jha et al., 2013; Zhang et al., 2014; Kiani and Eslami, 2013; Kakar, 2013; Djamaluddin et al. 2015; Huang et al. 2016; Adeli et al. 2017; Hadi et al. 2018; Shishesaz et al. 2017). For efficient use of such components, it is necessary to study its mechanical behaviors like vibration, buckling and bending. Thereinto, the investigation on the vibration of FGM tubes and cylindrical shells was, is and remains to be a hot research subject. Yang et al. (2014) studied the effect of outer diameter, Poisson’s ratio and flow velocity on the vibration frequency. Zhong et al. (2016) utilized a two-steps perturbation method to analyze the influence of different dimension parameters on linear frequency and nonlinear frequency.
As can be shown in the open literature, most of the researchers change natural frequency of tubes through altering dimensions. However, they could not change the frequency of tubes to satisfy demands very well since dimension of tubes cannot be changed arbitrarily (Dohmann and Hartl, 1997). To overcome this deficiency, we design double functionally graded distributions to change and control frequencies of tubes through adjusting respective material compositions. The design has an advantage to break the limits of dimensions.
It is a practicable technique to bond two materials together (Qiao and Chen, 2008; Suhir, 2016). The strengthening method can provide effective stress transfer from one to the other and secure the durability of components. Owing to good performance, bimaterial structures have been widely used in engineering practice, such as scarf joints (Le, 2011), pumping membrane (Hsu et al., 2000), thermal sensor (Lim et al., 2005). Noël et al. (2016) undertook an analytical sensitivity analysis for shape optimization of bimaterial structure. Huang et al. (2009) studied deflection of two kinds of thermal bimaterial structure in which two materials present excellent interlaminar bonding ability. Zheng (2012) developed another analytical model to study torsional bimaterial cantilever, which can predict some performance.
Various methods have been developed to solve equations of nonlinear vibration, such as high dimensional harmonic balance method(Hall et al., 2002; Liu et al., 2007), harmonic balance method(Dai et al., 2014), perturbation methods(Mook and Nayfeh,1979). Perturbation methods are frequently used. Nazemnezhad and Hosseini-Hashemi (2014) studied non-linear free vibration of FG beams under different boundary conditions with the aid of the multiple-scale perturbation method. Ghadiri et al. (2017) used Euler-Bernoulli beam model to analyze forced vibration of beams subjected to moving concentrated load. To obtain analytical solution from non-linear differential equations, they used the perturbation technique. Shen and Wang (2014) used a two-steps perturbation technique, to investigate vibration of beams exposed to different types of thermal environment.
In analysis of vibration problems involving nano-structures(Hosseini et al. 2018), the non-local elasticity theory proposed by Eringen (1983) is extensively used to study the small-scale effec ts. To analyze post-buckling of porous nano-tubes, She et al. (2017a) put forward a non-classical model based on non-local elasticity theory. Rahmani and Pedram (2014) analyzed the size-dependent effect on the vibration of FGM nano-beams by utilizing non-local elasticity theory and obtained a closed form solution. Zenkour et al. (2015) used this theory to describe the small-scale effect on the behavior of respective field variables. Salehipour et al. (2015). modified the non-local elasticity theory in analysis of FGM at nanoscale. The influence of non-local parameter was analyzed in detail based on an improved non-local elasticity theory. Hosseini and Rahmani (2016) investigated thermal buckling as well as non-linear vibration of a curved FG beam based on Eringen’s different formulation. Narendar (2017) studied thermodynamic of a rod subjected to a moving heat source based on the Eringen’s non-local model. Differing from above references adopted Eringen’s equivalent differential formulation, Tuna and Kirca (2016) analyzed buckling and vibration of beams by using the original integral constitutive equation. To obtain the exact solution of the original integral model, the Laplace transform method was adopted.
To date, there is no free vibration analysis of nano-tubes consisted of functionally graded bi-semi-tubes.From the perspective of bimaterial structure, we design a tube that is formed by bonding together a Si3N4/SUS304 functionally graded upper semi tube and a ZrO2/Ti-6Al-4V functionally graded lower semi tube and used a two-steps perturbation method to obtain corresponding analytical solutions. Through adjusting respective material compositions, linear frequencies and nonlinear frequencies is studied in detail. The purpose of this work is to put forward alternative approach to change and control frequencies of tubes whose results can provide a route toward designing tubes and undertaking nan-analysis of materials.
2. Basic theoretical formulation
2.1 Functionally graded bi-semi-tubes
Proposed in this section, the basic equations of bi-functionally graded materials can serve as benchmark theoretical formulation for exactly analytical solutions of the equilibrium equations in later chapters.
An FGM tube with outer radius R 0, inner radius R i, as well as length L shown in Fig. 2 is formed by bonding together a Si3N4/SUS304 functionally graded upper semi-tube with a ZrO2/Ti-6Al-4V functionally graded lower semi-tube. The behavior of the FGM tube made of two types of functionally graded semi-tube must comply with general mechanics theorem; besides, both Si3N4/SUS304 functionally graded semi-tube material properties and ZrO2/Ti-6Al-4V functionally graded semi-tube material properties should continuously vary along the radius directions, respectively. Thus, the effective material properties P f including Young’s modulus, thermal expansion, Poisson’s ratio, as well as mass density, can be assumed to vary according to power-law and thus can be expressed as:
where p 1, p 2, p 3, p 4 stand for the material constituents of SUS304, Si3N4, Ti-6Al-4V and ZrO2 respectively. The symbol of N 1 aligned with N 2 represent the volume fraction index in their respective angle intervals. The temperature factor is assumed to be a nonlinear function of temperature, which can be described as (Ghiasian et al., 2014)
Here P 0, P -1, P 1, P 2, and P 3 denote the coefficients of Kelvin’s temperature-dependence which are tabulated in Table 1.
The temperature can be separated into two parts: T=T 0+ΔT, where ΔT is the thermal increment from certain reference temperature T 0=300K at which a tube has no thermal strains. Notice from the expression of the effective material properties P f that inner surface (r=R i) of FGM tube is made of SUS304 and Ti-6Al-4V, whereas outer surface (r=R 0) of FGM tube is made of Si3N4 and ZrO2. Obviously, this differs from the conventional functionally graded tube or cylinder. When N 1 and N 2 are both equal to zero, the composite tube of the effective material properties P f degenerates to the bi-material tube consisted of two different materials.
2.2 non-local elasticity theory
When dealing with nano-structures, the effect of long-range inter-atomic forces can’t be ignored in the process of analysis. Eringen (1983) took the effect of long-range inter-atomic into account and put forward the non-local elasticity theory based on the experiment of phonon dispersion as well as atomic theory of the lattice dynamics. According to his theory, the stress at any point x in a body varies along with not only the strain at that point but also those at all other points x’ of the body. Therefore, the whole stress field σ ij(x) can be arrived at
where the factor α (|x-x’|, μ), small scale, is the non-local attenuation function, which incorporates into the constitutive equations the influences at the reference point x generated by the local strain at the source point x’, where |x-x’| represents the Euclidean distance. The factor α can be expressed as α=e 0 a/L where e 0 is a material constant determined by experiments or by reliable theoretical models. The parameters a and L are the internal (e.g. lattice parameter) and external characteristic lengths (e.g. crack length and wavelength) of the nano-solids, respectively.
However, it is difficult to obtain analytical results by applying the above expressions, therefore Eringen (1983) turned the integral constitutive relations to an equivalent differential form as
It is obviously observed that the non-local constitutive relation can degenerate to the classical elasticity theory when the result of μ is taken as zero.
2.3 Equilibrium equations
As shown in Fig. 2, the functionally graded nano-tube of length L¸ inner radius R i and outer radius R 0, is consisted of upper semi-tube made of functionally graded materials (Si3N4/SUS304) and lower semi-tube made of functionally graded materials (ZrO2/Ti-6Al-4V). Besides, the nano-tube is subjected to a uniform temperature field as well as a uniform transverse load.
Suppose that its middle-axis coincides with the Ox-axis of a Cartesian coordinate system O-xyz and the positive Z-axis is perpendicular to the X-axis and directed upwards. The origin of a Cartesian coordinate system O-xyz is set at the middle surface of the tube
For circular tube, three displacement functions (u 1, u 2, u 3) can be listed as follows (Zhang and Fu, 2013)
where u(x, t) and w(x, t) stand for the X-dire and lateral displacements respectively, and θ(x, t) stands for the rotation of the normal relative to the Y axis. To easily deduce the relationship of the strain and displacement based on the von karman non-linearity theory, the displacement function Eq. (4) can be rewritten in a simplification form
in which
The nonlinear strain-displacement expressions in line with the von karman non-linearity theory can be induced as:
According to the Hooke’s law, for the case of a uniform thermal environment, the stresses associated with strain components from Eq. (6) can be determined as
in which
It should be mentioned that the Poisson’s ratio v of four materials in this tube are all set to be 0.3, the same value (She et al., 2017b). This assumption is made by referring the fact that, Cao and Evans (1989) in their experiment found the upper and lower beams possess similar Poisson’s ratio when the thickness ratio is equivalent to 0.1 and Other researchers (Yang et al., 2014) also demonstrated different Poisson’s ratio for FGM to have no obvious effect on the results.
The necessary boundary conditions for the stress of the tube at the places (r=R 0, R i) must satisfy Eq. (8).
The virtual strain energy of the tube is assumed to be
in which Ω stands for the volume of the tube. By substituting Eq. (6) into Eq. (9), the virtual strain energy is reappraised as
Besides, the work performed by the external force is illustrated as
where
The kinetic energy of the studied tube is elevated as
So, Eq. (12) can be deduced to
In terms of the Hamilton principle, the corresponding governing equations can be induced as
Substituting Eq. (10), (11), and (13) into Eq. (14) and set these coefficients of δu, δθ, δw into zero, we obtain the nonlinear equilibrium equations can be expressed as
where N in Eq. (15) is a constant and can be written in the form.
Moreover, certain general forces and moments of inertia involved with Eq. (15) are presented as
Combined with the non-local constitutive relations, general forces of the tube are defined as
where Δ is the Laplace operator. Other coefficients in Eq. (18) and (19) are given by
Eq. (15) can be reformulated as
For simply supported ends, necessary boundary conditions of the tube are given by
For the calculation convenience, we introduce the non-dimensional parameters.
where
General governing equations described in Eq. (20) can be rewritten in terms of dimensionless variables as
Meanwhile, the dimensionless boundary conditions can be described as
3. Solution of the model
In this section, we obtain corresponding analytical solutions of Eq. (22) and (23) by using a two-steps perturbation procedure. To begin with, to get a set of vibration equations, we suppose that the expanded form of dimensionless displacement, dimensionless rotation angle and dimensionless transverse load can be expressed as:
Where the small perturbation parameter(ε) has no physical meaning, which is introduced into Eq. (22) and (23). Then, we collect terms of the same order(ε) to arrive at
To solve the differential perturbation equations, asymptotic solutions of dimensionless displacement as well as dimensionless rotation angle, satisfying simply supported ends, are given by
Substituting Eq. (30) into Eq. (26), we could have
By substituting Eq. (30) and (31) into Eq. (27), we obtain the equation to determine.
Later, the substitution of Eq. (30) and Eq. (31) into Eq. (28) yields:
is determined by substituting Eq. (30), (31) and (33) into Eq. (29)
Eventually, the analytical solution of non-dimension transverse load can be expressed as
Because the value of λ q is equivalent to zero when solving free vibration problems, we apply the method of Galerkin in Eq. (35) to obtain the Duffing equation.
where
So, the analytical solution of Eq. (36) can be written as
where the symbol of () is dimensionless amplitude of the vibration of the tube. ω L and ω NL stand for dimensionless linear frequency and dimensionless nonlinear frequency, respectively.
So far, most of the theories were established based on three classical models. They are Euler beam model, Timoshenko beam model as well as Reddy beam model. They could be taken to be the specific of our model.
When f=-z, the displacement function Eq. (5) can be converted to that of Euler-Bernoulli model. Corresponding coefficients are
When f=0, the displacement function of Eq. (5) can be converted to that of Timoshenko model. The corresponding coefficients are
where the shear factor k s is copied from Zhang and Fu (2013) and is given by
in whichand the Poisson’s ratio v is assumed to be the average value of the four materials.
When,the displacement function Eq. (5) can be converted to that of Reddy model. Corresponding coefficients are the same as ones of the present model. More detail information can be found in Eq. (36).
4. Results and discussions
In this part, we fully utilize above analytical solution to discuss the vibration behavior of the nanotubes consisted of functionally graded bi-semi-tubes. As is shown by the results, some novel behaviors of the bi-semi-tubes are rather different from those of the conventional FGM nanotubes.
4.1 validation research
Owing to no existing data for the functionally graded bi-material tube in the published literature, both dimensionless free vibration frequencies of functionally graded tube and non-dimension frequencies of isotropic tube are calculated by present mathematical model. The results obtained in such a way can be conveniently used to verify the present deduced results directly. In Table. 2, the dimensionless frequency of a functionally graded nanotube with (R i=0.5R 0, L=20R 0, R 0=1nm, T=300K, N=1) is used to verify the current solution. That this table demonstrates a small difference between the results reported by Fuh-Gwo Yuan and the ones in this study clearly indicates that present solution is reliable and reasonable. To further validate the present model, the dimensionless natural frequency for an isotropic cylindrical shell with (R i=0.998R 0, L=20R 0, v=0.3, T=300K) under simply supported ends are tabulated in Table 3. As is seen in Table 3, present results show a good agreement with published ones. Therefore, the two examples convince us the validation of the present model.
Comparisons of non-dimension natural frequencies ()for a simply supported functionally graded nano-tube.
Comparisons of non-dimension natural frequencies () of an isotropic cylindrical shell with simply supported ends.
4.2 discussions of physical parameters
The formulation of the non-dimension frequency iswhere.The values of ρ 0 and E 0 are equivalent to 8166 kg/m3 and 201.04 GPa respectively. The effective properties of four types of material (SUS304, Si3N4, Ti-6Al-4V, ZrO2) are tabulated in Table. 1.
Comparisons of different beam models on non-dimension natural frequency for the tube. (Ri=0.8R0, R0=1nm, T=300K, μ=1nm, N1 = N2=1)
Within the results of Table. 4, the effect of slenderness ratio and respective beam models on non-dimension natural frequency for the tube can be illustrated as follows:
-
(i) The non-dimension natural frequency of the present model is close to that of Timoshenko model, but smaller than that of Reddy model and that of Euler model.
-
(ii) A higher slenderness ratio tends to waken the stiffness of the tube. In another word, with the slenderness ratio becoming large, the frequency gradually ascends, regardless of which model is adopted.
-
(iii) The difference between the answers of four beam models becomes prominently with increasing the natural frequency number. That is due to the fact that increasing the natural frequency number needs more degrees of freedom. However, among those beam models, only the present model takes two directions of transverse shear into account. So, the results of the present model are the smallest and close to the actual. The results of Euler-Bernoulli are the biggest, because it dosen’t consider any transverse shear and has the biggest stiffness of the tube. The difference between Timoshenko model and Reddy model is that Reddy model takes high-order shear deformation into consideration so that the results of Reddy model are higher than those of Timoshenko model.
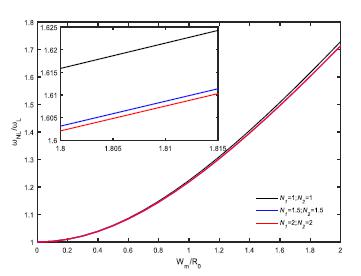
Effect of both volume indexes N1 and N2 on non-dimension natural frequency for the tube. (Ri=0.99R0,R0=1nm,L=20R0,T=300K, μ=1nm)
Results from Table. 5 distinctly reflects the influence of double material gradient indexes N 1 and N 2 on non-dimension natural frequency for the tube. Fig. 3 shows the different types of functionally graded nanotube. When both the content of SUS304 and Ti-6Al-4V increase, dimensionless natural frequency of the tube decreases continuously. Table. 6 gives comparisons on non-dimension natural frequency among various types of functionally graded tubes. It can be seen from this table that the non-dimension natural frequency of the tube consisted of functionally graded bi-semi-tubes is between that of conventional functionally graded tube(Si3N4/SUS304) and that of conventional functionally graded tube (ZrO2/Ti-6Al-4V) when material indexes(N) of different types of functionally graded tube are equal. Therefore, some frequencies that cannot be obtained by Type A and Type B but can be obtained by present type so long as by adequately moderating N-value. Besides, compared with conventional functionally graded tube, the tube with double volume indexes has a smaller adjusting step size to produce more frequencies in the same conditions thus results in more accurate frequency control. Therefore, results show that this design can satisfy the requirement of the natural frequency very well when dimensionless sizes of the tube are kept unchanged.
Effect of inner radius Ri to outer radius R0 ratio on non-dimension natural frequency for the tube.(T=300k,R0=1nm,μ=1nm, L=20R0, N1=N2=1)
The effect of the ratio of the inner radius R i to the outer radius R 0 on non-dimension natural frequencies of the tube has been listed in Table. 7. It reveals that as the thickness of the tube continues to reduce, the dimensionless natural frequencies of the tube decrease at first, then increase remarkably. In terms of this trait, the effect of the thickness of the tube should be considered in design of vibrating tubes.
Effect of nonlocal parameter μ on non-dimension natural frequency for the tube.(Ri=0.8R0, R0=1nm,T=300K,L=20R0,N1=N2=1)
As for the effect of the non-local parameter μ on non-dimension natural frequency for the tube, it can be observed from Table. 8 that the frequency is getting smaller when the value of parameter μ becomes larger and lager while other size parameters remain unchanged. Hence, we have demonstrated the non-local parameter μ has a tendency to reduce the non-dimensionless natural frequencies of the tube.
Effect of dimensionless temperature λT on non-dimension natural frequency for the tube.(Ri=0.8R0,R0=1nm,L=20R0,N1=N2=1, μ=1nm)
It can be calculated from Eq. (36) and Eq. (37) that if the value of dimensionless temperature λ T becomes large, the result of ω L will descend. Table. 9 indicates that with the non-dimension temperature elevating, the dimensionless frequencies of the tube subjected to uniform thermal environment diminish inversely.
Comparisons of different beam models on the amplitude-frequency of the studied tube made of SuS303, Si3N4, ZrO2 and Ti-6Al-4V. (Ri=0.8R0, R0=1nm, T=300K, μ=1nm, N1=N2=1)
Fig. 4 presents comparisons of different beam models on the amplitude-frequency of the tube made of SuS303, Si3N4, ZrO2 and Ti-6Al-4V. As could be seen in this figure, the results of present model are higher than those of other beam models and the results of Euler beam model is the lowest when L=10R 0. However, for large slenderness ratio(L/R 0≥30), all the resultsω NL/ω L become nearly the same value. In conclusion, transverse shear plays a crucial role in the vibration behavior of short tubes, whereas its effect on the vibration behavior of long enough tubes is neglectable.
The influence of non-local parameter μ with the amplitude-frequency of the tube. (R 0=1nm, T=300K, R i=0.8R 0, L=20R 0, N 1=N 2=1)
The influence of dimensionless temperature λT with respective to respective to the amplitude-frequency of the tube. (R 0=1nm, R i=0.8R 0, L=20R 0, N 1=N 2=1, μ=1nm)
Fig. 5 depicts the influence of non-local parameter μ on the relation of amplitude-frequency of the tube. These curves reveal that the ratio of the nonlinear frequency to linear frequency(RNFLF) of the tube can be remarkably improved by means of increasing the value of non-local parameter μ. Thus, the small-scale parameter μ plays an indispensable role in the nonlinear vibration problem.
Fig. 6 present the effect of non-dimension temperature on the relation of amplitude-frequency of the tube. It can be found that the RNFLF increases when the tube is exposed to a rising thermal environment. The results of Fig. 6 can be predicted from Eq. (36) and Eq. (37). The reason is that a higher dimensionless temperature λ T can result in lower denominator of the expression of ω NL /ω L.
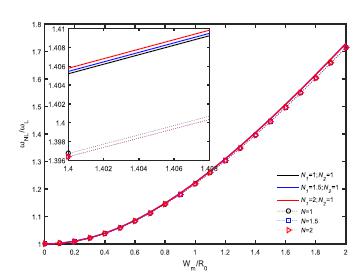
The influence of material index N2 and N1 with to the amplitude-frequency of the tube. (R0=1nm, T=300K, Ri=0.8R0, L=20R0, N1=1)
The influence of material index from different types of respective functionally graded tube on the amplitude-frequency. (R 0=1nm, T=300K, R i=0.8R 0, L=20R 0)
Fig. 7 shows the influence of material index N 2 and N 1 on the variation law of amplitude-frequency of the tube. From this figure, a conclusion can be drawn that with both material indexes N 1 and N 2 increasing, corresponding amplitude frequency curves become lower. In other words, as the content of SUS304 and Ti-6Al-4V continues to ascend, the nonlinear vibration frequencies reduce gradually.
Fig. 8 exhibits the difference between the tube consisted of functionally graded bi-semi-tubes and the tube made of functionally graded materials (Si3N4 and SuS304). Shown in this figure, the RNFLF of the former tube is larger than that of the later tube for the high value of the phase of SUS304.
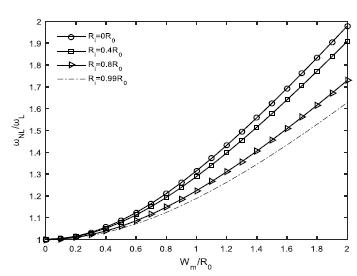
The influence of inner radius Ri above the amplitude frequency of the tube. (R0=1nm, T=300K, μ=1nm, Ri=0.8R0, N1=N2=1)
The influence of slenderness ratio above the amplitude frequency of the tube.(R0=1nm, T=300K, μ=1nm, L=20R0, N1=N2=1)
Fig. 9 describes the influence of inner radius R i above the amplitude frequency of the tube. It can be seen that when taking larger inner radius under the same outer radius, the nonlinear to linear frequencies ratio goes down.
Fig. 10 shows the influence of slenderness ratio above the amplitude frequency of the tube. The figure clearly plots that a bigger slenderness ratio leads to a smaller ω NL /ω L curve. That is due to the fact that a large slenderness is able to waken the stiffness of the studied tube.
5. Conclusions
This paper focuses on free vibration of nano-tubes formed by bonding together a Si3N4/SUS304 functionally graded upper semi-tube and a ZrO2/Ti-6Al-4V functionally graded lower semi-tube. Firstly, four types of material distribution of the FGM bi-semi-tubes were assumed. By using a two-steps perturbation method, the analytical solution was obtained to carry out a vibration analysis in detail. Finally, some important conclusions are outlined.
-
(1) The ascending of slenderness ratio can increase the natural frequencies, whereas the ascending of dimensionless temperature and non-local parameter μ can decrease the natural frequencies.
-
(2) The natural frequencies reduce with the increase of the content of SUS304 and Ti-6Al-4V.
-
(3) Compared with conventional functionally graded tube, obviously, the tube with two volume indexes results in more accurate frequency control in the same dimensionless size of tubes.
-
(4) The decrease of the thickness of the tube makes the natural frequencies firstly decline and then rise.
-
(5) The increment of dimensionless temperature λ T and non-local parameter μ can improve the RNFLF while the increase of slenderness ratio and the decrease of the thickness of tubes can make the RNFLF decline.
-
(6) The influence of double volume indexes on the relation of amplitude-frequency of bi-semi-tubes is more obvious than the influence of one volume index on the relation of amplitude-frequency of conventional functionally graded tubes.
References
- Adeli, M. M., Hadi, A., Hosseini, M., & Gorgani, H. H. (2017). Torsional vibration of nano-cone based on nonlocal strain gradient elasticity theory. European Physical Journal Plus, 132(9), 393.
- Cao, H. C., & Evans, A. G. (1989). An experimental study of the fracture resistance of bimaterial interfaces. Mechanics of Materials, 7(4), 295-304.
- Dai, H., Yue, X., Yuan, J., & Atluri, S. N. (2014). A time domain collocation method for studying the aeroelasticity of a two dimensional airfoil with a structural nonlinearity. Journal of Computational Physics, 270(3), 214-237.
- Djamaluddin, F., Abdullah, S., Ariffin, A. K., Nopiah, Z. M., Djamaluddin, F., & Abdullah, S., et al. (2015). Multi objective optimization of foam-filled circular tubes for quasi-static and dynamic responses. Latin American Journal of Solids & Structures, 12(6), 1126-1143.
- Dohmann, F., & Hartl, C. (1997). Tube hydroforming-research and practical application. Journal of Materials Processing Technology, 71(1), 174-186.
- Eringen, A. C. (1983). on differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. 54, 4703-4710. Journal of Applied Physics, 54(9), 4703-4710.
- Fan, P., Fang, Z. Z., & Guo, J. (2013). A review of liquid phase migration and methods for fabrication of functionally graded cemented tungsten carbide. International Journal of Refractory Metals & Hard Materials, 36(1), 2-9.
- Ghadiri, M., Rajabpour, A., & Akbarshahi, A. (2017). Non-linear forced vibration analysis of nanobeams subjected to moving concentrated load resting on a viscoelastic foundation considering thermal and surface effects. Applied Mathematical Modelling, 50, 676-694.
- Ghiasian, S. E., Kiani, Y., Sadighi, M., & Eslami, M. R. (2014). Thermal buckling of shear deformable temperature dependent circular/annular fgm plates. International Journal of Mechanical Sciences, 81(4), 137-148
- Gupta, A., & Talha, M. (2015). Recent development in modeling and analysis of functionally graded materials and structures. Progress in Aerospace Sciences, 79, 1-14.
- Hadi, A., Nejad, M. Z., & Hosseini, M. (2018). Vibrations of three-dimensionally graded nanobeams. International Journal of Engineering Science, 128, 12-23.
- Hall, K. C., Thomas, J. P., & Clark, W. S. (2002). Computation of unsteady nonlinear flows in cascades using a harmonic balance technique. Aiaa Journal, 40(5), 879-886.
- Hao, D., & Wei, C. (2016). Dynamic characteristics analysis of bi-directional functionally graded timoshenko beams. Composite Structures, 141, 253-263
- Hosseini, S. A. H., & Rahmani, O. (2016). Thermomechanical vibration of curved functionally graded nanobeam based on nonlocal elasticity. Journal of Thermal Stresses, 39(10), 1252-1267.
- Hosseini, M., Hadi, A., Malekshahi, A., & Shishesaz, M. (2018). A review of size-dependent elasticity for nanostructures, Journal of Computational Applied Mechanics, 49, 197-211.
- Hosseini, M., Shishesaz, M., Tahan, K. N., & Hadi, A. (2016). Stress analysis of rotating nano-disks of variable thickness made of functionally graded materials. International Journal of Engineering Science, 109, 29-53.
- Hosseini, M., Gorgani, H. H., Shishesaz, M., & Hadi, A. (2017). Size-dependent stress analysis of single-wall carbon nanotube based on strain gradient theory. International Journal of Applied Mechanics, 9(6), 1750087.
- Hsu, C., Hsu, W., & Hsu, C. (2000). A two-way membrane-type micro-actuator with continuous deflections. Journal of Micromechanics & Microengineering, 10(3), 387.
- Huang, B. W., Yu, P. P., Tseng, J. G., Huang, B. W., Yu, P. P., & Tseng, J. G. (2016). Dynamic properties of coupled tube-array structures with the axial loads. Lat.am.j.solids Struct, 13(12), 2220-2230.
- Huang, C. S., Cheng, Y. T., Chung, J., & Hsu, W. (2009). Investigation of ni-based thermal bimaterial structure for sensor and actuator application. Sensors & Actuators A Physical, 149(2), 298-304.
- Huang, Y., & Li, X. F. (2010a). Bending and vibration of circular cylindrical beams with arbitrary radial nonhomogeneity. International Journal of Mechanical Sciences, 52(4), 595-601
- Huang, Y., & Li, X. F. (2010b). Huang, y. and li,x.f. a new approach for free vibration of axially functionally graded beams with non-uniform cross-section. journal of sound and vibration, 329, 2291-2303. Journal of Sound & Vibration, 329(11), 2291-2303.
- Jha, D. K., Kant, T., & Singh, R. K. (2013). A critical review of recent research on functionally graded plates. Composite Structures, 96(4), 833-849.
- Kakar, R. (2013). Magneto-electro-viscoelastic torsional waves in aeolotropic tube under initial compression stress. Latin American Journal of Solids & Structures, 11(4), 580-597.
- Kiani, Y., & Eslami, M. R. (2013). Thermomechanical buckling oftemperature-dependent fgm beams. Latin American Journal of Solids & Structures, 10(2), 223-246.
- Koizumi, M. (1997). FGM activities in japan. Composites Part B Engineering, 28(1-2), 1-4.
- Le, J. L. (2011). General size effect on strength of bimaterial quasibrittle structures. International Journal of Fracture, 172(2), 151-160.
- Lei, Z. X., Zhang, L. W., & Liew, K. M. (2016). Buckling analysis of cnt-reinforced functionally graded laminated composite plates. Composite Structures, 152, 62-73.
- Liu, L., Dowell, E. H., & Hall, K. C. (2007). A novel harmonic balance analysis for the van der pol oscillator. International Journal of Non-Linear Mechanics, 42(1), 2-12.
- Lim, S. H., Choi, J., Horowitz, R., & Majumdar, A. (2005). Design and fabrication of a novel bimorph microoptomechanical sensor. Journal of Microelectromechanical Systems, 14(4), 683-690.
- Lü, C.F., C.W. Lim, & W.Q. Chen. (2009). Size-dependent elastic behavior of FGM ultra-thin films based on generalized refined theory. International Journal of Solids & Structures, 46(5), 1176-1185.
- Lü, C.F., W.Q. Chen, R.Q. Xu, & C.W. Lim. (2008). Semi-analytical elasticity solutions for bi-directional functionally graded beams. International Journal of Solids & Structures, 45(1), 258-275.
- Mook, D. & Nayfeh, A. Nonlinear Oscillations, John Wiley & sons, New York, 1979.
- Narendar, S. (2017). Nonlocal thermodynamic response of a rod. Journal of Thermal Stresses, 40(12), 1-11.
- Nazemnezhad, R., & Hosseini-Hashemi, S. (2014). Nonlocal nonlinear free vibration of functionally graded nanobeams. Composite Structures, 110(110), 192-199.
- Nejad, M. Z., & Hadi, A. (2016a). Non-local analysis of free vibration of bi-directional functionally graded euler-bernoulli nano-beams. International Journal of Engineering Science, 105, 1-11.
- Nejad, M. Z., & Hadi, A. (2016b). Eringen's non-local elasticity theory for bending analysis of bi-directional functionally graded euler-bernoulli nano-beams. International Journal of Engineering Science, 106, 1-9.
- Nejad, M. Z., Hadi, A., & Rastgoo, A. (2016). Buckling analysis of arbitrary two-directional functionally graded euler-bernoulli nano-beams based on nonlocal elasticity theory. International Journal of Engineering Science, 103, 1-10.
- Nemat-Alla, M. (2003). Reduction of thermal stresses by developing two-dimensional functionally graded materials. International Journal of Solids & Structures, 40(26), 7339-7356.
- Nguyen, D. K., Nguyen, Q. H., Tran, T. T., & Bui, V. T. (2017). Vibration of bi-dimensional functionally graded timoshenko beams excited by a moving load. Acta Mechanica, 228(1), 141-155.
- Noël, L., Miegroet, L. V., & Duysinx, P. (2016). Analytical sensitivity analysis using the extended finite element method in shape optimization of bimaterial structures. International Journal for Numerical Methods in Engineering, 107(8), 669-695.
- Pydah, A., & Sabale, A. (2017). Static analysis of bi-directional functionally graded curved beams. Composite Structures, 160(15), 867-876.
- Qiao, P., & Chen, F. (2008). An improved adhesively bonded bi-material beam model for plated beams. Engineering Structures, 30(7), 1949-1957.
- Rahmani, O., & Pedram, O. (2014). Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal timoshenko beam theory. International Journal of Engineering Science, 77(7), 55-70.
- Reddy, J. N., & Chin, C. D. (1998). Thermomechanical analysis of functionally graded cylinders and plates. Journal of Thermal Stresses, 21(6), 593-626.
- Salehipour, H., Shahidi, A. R., & Nahvi, H. (2015). Modified nonlocal elasticity theory for functionally graded materials. International Journal of Engineering Science, 90, 44-57.
- Shafiei, N., Kazemi, M., & Ghadiri, M. (2016a). On size-dependent vibration of rotary axially functionally graded microbeam. International Journal of Engineering Science, 101, 29-44.
- Shafiei, N., Kazemi, M., & Ghadiri, M. (2016b). Nonlinear vibration of axially functionally graded tapered microbeams. International Journal of Engineering Science, 102, 12-26.
- She, G. L., Yuan, F. G., Ren, Y. R., & Xiao, W. S. (2017a). On buckling and postbuckling behavior of nanotubes. International Journal of Engineering Science, 121, 130-142.
- She, G. L., Ren, Y. R., Yuan, F. G., & Xiao, W. S. (2018). On vibrations of porous nanotubes. International Journal of Engineering Science, 125(125C (2018)), 23-35.
- She, G. L., Yuan, F. G., & Ren, Y. R. (2017b). Thermal buckling and post-buckling analysis of functionally graded beams based on a general higher-order shear deformation theory. Applied Mathematical Modelling, 47.340-357.
- Shen, H. S., & Wang, Z. X. (2014). Nonlinear analysis of shear deformable fgm beams resting on elastic foundations in thermal environments. International Journal of Mechanical Sciences, 81(4), 195-206.
- Shishesaz, M., Hosseini, M., Tahan, K. N., & Hadi, A. (2017). Analysis of functionally graded nanodisks under thermoelastic loading based on the strain gradient theory. Acta Mechanica, 228, 1-28.
- Şimşek, M. (2015). Bi-directional functionally graded materials (BDFGMS) for free and forced vibration of timoshenko beams with various boundary conditions. Composite Structures, 133, 968-978.
- Soldatos, K. P., & Hadjigeorgiou, V. P. (1990). Three-dimensional solution of the free vibration problem of homogeneous isotropic cylindrical shells and panels. Journal of Sound & Vibration, 137(3), 369-384.
- Suhir, E. (2016). Bi-material assembly subjected to thermal stress: propensity to delamination assessed using interfacial compliance model. Journal of Materials Science Materials in Electronics, 27(7), 1-7.
- Thang, P. T., & Nguyen-Thoi, T. (2016). Effect of stiffeners on nonlinear buckling of cylindrical shells with functionally graded coatings under torsional load. Composite Structures, 153, 654-661.
- Thinh, T. I., Tu, T. M., Quoc, T. H., Long, N. V., Thinh, T. I., & Tu, T. M., et al. (2016). Vibration and buckling analysis of functionally graded plates using new eight-unknown higher order shear deformation theory. Lat.am.j.solids Struct, 13(3), 456-477.
- Tuna, M., & Kirca, M. (2016). Exact solution of eringen's nonlocal integral model for bending of euler-bernoulli and timoshenko beams. International Journal of Engineering Science, 105, 80-92.
- Zhang, P., & Fu, Y. (2013). A higher-order beam model for tubes. European Journal of Mechanics A/solids, 38(3), 12-19.
- Yang, T. Z., Ji, S., Yang, X. D., & Fang, B. (2014). Microfluid-induced nonlinear free vibration of microtubes. International Journal of Engineering Science, 76(4), 47-55.
- Zenkour, A. M., Abouelregal, A. E., K. A. Alnefaie, X. Zhang, & E. C. Aifantis. (2015). Nonlocal thermoelasticity theory for thermal-shocknanobeams with temperature-dependent thermal conductivity. Journal of Thermal Stresses, 38(9), 205-217.
- Zhang, D. G. (2013). Nonlinear bending analysis of fgm beams based on physical neutral surface and high order shear deformation theory. Composite Structures, 100(5), 121-126.
- Zhang, X., Wen, Z., & Zhang, H. (2014). Axial crushing and optimal design of square tubes with graded thickness. Thin-Walled Structures, 84(84), 263-274.
- Zheng, Y. (2012). Analysis of dual-beam asymmetrical torsional bi-material cantilever for temperature sensing applications. Physics. DOI: arXiv:1208.0939
- Zhong, J., Fu, Y., Wan, D., & Li, Y. (2016). Nonlinear bending and vibration of functionally graded tubes resting on elastic foundations in thermal environment based on a refined beam model. Applied Mathematical Modelling, 40(17-18), 7601-7614.
- Wang, J. F., Zhang, L. W., & Liew, K. M. (2016). A multiscale modeling of cnt-reinforced cement composites. Computer Methods in Applied Mechanics & Engineering, 309, 411-433.
Publication Dates
-
Publication in this collection
2019
History
-
Received
27 June 2018 -
Reviewed
09 Sept 2018 -
Accepted
13 Sept 2018

 Free vibration analysis of nano-tubes consisted of functionally graded bi-semi-tubes by a two-steps perturbation method
Free vibration analysis of nano-tubes consisted of functionally graded bi-semi-tubes by a two-steps perturbation method