Abstract
Gyroscopic systems and their properties have been extensively studied as Angular Momentum Devices (AMD), Control Moment Gyros (CMG) or Gyroscopes for various applications such as structure control, stability or energy storage. However, most of the works that have been done are theoretical and do not present experimental implementation. In this work we performed an experimental study of a gyroscope beam system (gyroelastic beam) focused systems on the deflection of cantilever beams or the control of flexural stresses. We first used a simple two-degree of freedom model to better understand the terms governing the design, construction and experimental evaluation of gyroelastic beam systems. We then performed experimental tests at different velocities of the gyroscopic actuator and measured the deflection of the system. The results showed that it is possible to have control of the deflection and the bending forces for this type of configurations which can be exported to helicopter blades or wind turbine blades.
Keywords
Cantilever beam; Gyroscopic moment; Gyroelastic systems
INTRODUCTION
The study of gyroscopic effects has arisen from the impulse and growth of the aeronautical industry. However, applications of gyroscopic effects have recently been found in biomedical science, robot control, vehicle dynamic control, clean energy, rotating structures, gyroelastic materials or as a means of suppressing vibrations for different structures, among other applications. All structures that present gyroscopic effects or contain one or more gyroscopes in their structure are called gyroscopic systems. Gyroscopic systems have been extensively studied due to their properties and applications as Angular Momentum Devices (AMD), Control Moment Gyros (CMG) or Gyroscopes (Meirovitch and Oz, 1980Meirovitch, L. and Oz, H. (1980). Modal-Space Control of Distributed Gyroscopic Systems. Journal of Guidance, Control, and Dynamics, Vol. 3, No. 2. pp. 140-150. http://dx.doi.org/10.2514/3.55961.
http://dx.doi.org/10.2514/3.55961...
; Meirovitch and Baruh, 1981Meirovitch, L. and Baruh, H. (1981). Optimal control of damped flexible gyroscopic systems. Journal of Guidance and Control, 4(2):157-163.). Nowadays, there are many mathematical models which have been developed with the purpose of studying the gyroscopic effects or gyroelasticity ranging from rotating beams to gyroelastic beam systems with several variants (Peck, 2004Peck, M. (2004). Practicable Gyroelastic Technology. 27th Annual AAS Guidance and Control Conference. Paper No. AAS 04-023. Breckenridge, CO.; Telli and Kopmaz, 2004Telli, S. and Kopmaz, O. (2004). On the Mathematical Modelling of Beams Rotating About A fixed Axis. Mathematical and Computational Applications 9 (3), 333-348. doi:10.3390/mca9030333.
https://doi.org/10.3390/mca9030333...
; Bai et al., 2008Bai, S., Tzvi, P., Zhou, Q. and Huang, X. (2008). Dynamic Modeling of a Rotating Beam Having a Tip Mass. IEEE International Workshop on Robotic and Sensors Environments. pp. 52-57.doi: 10.1109/ROSE.2008.4669180.
https://doi.org/10.1109/ROSE.2008.466918...
; Yamanaka et al., 1994Yamanaka, K., Heppler, G. R., Huseyin, K. (1994). The Stability of a Flexible Link with a Tip Rotor and a Comprehensive Tip Load. IEEE Transactions on Robotics and Automation, Vol. ICRA 1994: 1798-1803.) in order to analyze airplanes (Zhou et al., 2012Zhou, J., Zhang, J. and Meng, G. (2012). Gyroscopic effects on the engine rotor on the characteristics of wing bending-torsional flutter. Acta Aerodynamica Sinica. Issue 5. pp 578-582.), wind turbines (Hamdi et al., 2014Hamdi, H., Mrad, C., Hamdi, A. and Nasri, R. (2014). Dynamic response of a horizontal axis wind turbine blade under aerodynamic, gravity and gyroscopic effects. Applied Acoustics. Volume 86, Pages 154-164.http://dx.doi.org/10.1016/j.apacoust.2014.04.017.
http://dx.doi.org/10.1016/j.apacoust.201...
; Ma et al., 2015Ma, H., Lu, Y., Wu, Z., Tai, X., Li, H. and Wen, B. (2015). A new dynamic model of rotor-blade systems. Journal of Sound and Vibration, Volume 357, Pages 168-194.http://dx.doi.org/10.1016/j.jsv.2015.07.036.
http://dx.doi.org/10.1016/j.jsv.2015.07....
) or unmanned aerial vehicles (UAVs) (Shao et al., 2015Shao, P., Dong, W., Sun, X., Ding, T. and Zou, Q. (2015). Dynamic Surface Control To Correct For Gyroscopic Effect Of Propellers On Quadrotor . Information and Automation, IEEE International Conference on. pp. 2971-2976. doi: 10.1109/ICInfA.2015.7279797.
https://doi.org/10.1109/ICInfA.2015.7279...
). On the other hand, gyroscopic properties have been applied to the design of force sensors (Kurosu and Yamazaki, 2004Kurosu, S. and Yamazaki, T. (2004). Gyroscopic Force Measuring System -Theory and Applications. SICE Annual Conference in Sapporo, August 4-6,2004. Hokkaido Institute of Tecnology, Japan.), biomedical sensors (Nguyen et al., 2014Nguyen, T., Ranieri, M., DiGiovanna, J., Peter, O., Genovese, V., Pérez, A. and Micera S (2014). A real-time research platform to study vestibular implants with gyroscopic inputs in vestibular deficient subjects. IEEE Trans. Biomed. Circuits Syst., vol. 8, no. 4, pp. 474-484. doi: 10.1109/TBCAS.2013.2290089.
https://doi.org/10.1109/TBCAS.2013.22900...
) and cardiac stabilizers (Gagne et al., 2009Gagne, J., Laroche, E., Piccin, O. and Gangloff, J. (2009). An active cardiac stabilizer based on gyroscopic effect. Conf Proc IEEE Eng Med Biol Soc.6769-72. doi: 10.1109/IEMBS.2009.5332512.
https://doi.org/10.1109/IEMBS.2009.53325...
). The latter have been developed to compensate the movement of the heart at high frequencies and are also intended to aid surgeons and provide support to patients with locomotion difficulties (stability and walking balance) through human-robot interaction (Li and Vallery, 2012Li, D. and Vallery, H. (2012). Gyroscopic assistance for human balance. 12th IEEE International Workshop on Advanced Motion Control (AMC), pp. 1-6. doi: 10.1109/AMC.2012.6197144.
https://doi.org/10.1109/AMC.2012.6197144...
). In applications that seek mechanical stability as is the case of boats or aircrafts, bicycles and vehicles have been used for the reaction torque of a high-speed flywheel rotating around an axis (Jones and Peck, 2009Jones, L. and Peck, M. A. (2009). A generalized framework for linearly-constrained singularity-free control moment gyro steering laws. AIAA Guidance, Navigation, and Control Conference, 10-13. Aug 2009, Chicago, Illinois. http://dx.doi.org/10.2514/6.2009-5903.
http://dx.doi.org/10.2514/6.2009-5903...
; Yetkin et al. 2014Yetkin, H., Kalouche, S., Vernier, M., Colvin, G., Redmill, K. and Ozguner, U. (2014). Gyroscopic stabilization of an unmanned bicycle. American Control Conference (ACC) IEEE, pp. 4549-4554, 2014. doi: 10.1109/ACC.2014.6859392.
https://doi.org/10.1109/ACC.2014.6859392...
; Ha and Jung, 2015; Jin et al., 2016Jin, H. Wang, T., Yu, F., Zhu, Y., Zhao, J. and Lee, J. (2016). Unicycle Robot Stabilized by the Effect of Gyroscopic Precession and Its Control Realization Based on Centrifugal Force Compensation. IEEE/ASME Transactions on Mechatronics, vol. 21, no. 6, pp. 2737-2745. doi: 10.1109/TMECH.2016.2590020.
https://doi.org/10.1109/TMECH.2016.25900...
). Additionally, the damping properties of gyroscopic systems have been employed in Vehicle Dynamic Control. In some vehicles, gyroscopic properties have been used for energy storage (Flywheel energy storage systems or FESS) by means of a high-inertia rotor moving at high speed, especially in hybrid vehicles (Bitterly, 1997Bitterly, J. (1997). Flywheel Technology Past Present and 21 Century Projections. IECEC-97 Proceedings of the Thirty-Second Intersociety Energy Conversion Engineering Conference (Cat. No.97CH6203). pp. 2312-2315 vol.4. doi: 10.1109/IECEC.1997.658228.
https://doi.org/10.1109/IECEC.1997.65822...
; Pullen and Ellis, 2006Pullen, K. and Ellis, C. (2006). Kinetic Energy Storage for Vehicles. IET - The Institution of Engineering and Technology Hybrid Vehicle Conference. pp. 91-108. doi: 10.1049/cp:20060616.
https://doi.org/10.1049/cp:20060616...
). Mechanical batteries can outperform electric systems for many applications (Xiao et al. 2011Xiao, Y., Zhang, C., Zhu, K. and Ge, X. (2011). Suppression of gyroscopic rotation in flywheel energy storage systems. In Proc. Proceedings of the 2011 Chinese Control and Decision Conference. Pp. 3286-3289, Shenyang, China.;). Also, the damping properties of gyroscopic systems are used to design a means for suppressing vibrations in basic elements such as beams (Chu et al. 2007Chu, C., Wu, B. and Lin, Y. (2007). An experimental study on active micro-vibration suppression of a flexible beam mounted on an elastic base. Measurement Science and Technology, Volume 18, Number 7.; Ünker and Çuvalcý, 2015lÜnker, F. and Çuvalcý, O. (2015a). Vibration Control of a Column Using a Gyroscope. Procedia - Social and Behavioral Sciences. Volume 195, 3 July 2015, pages 2306-2315. https://doi.org/10.1016/j.sbspro.2015.06.182.
https://doi.org/10.1016/j.sbspro.2015.06...
a) or more complex structures such as passenger vehicles (Scheurich et al. 2015Scheurich, B., Koch, T., Frey, M. and Gauterin, F. (2015). Damping A Passenger Car With A Gyroscopic Damper System. SAE Int. J. Passeng. Cars - Mech. Syst. 8(2). Detroit, Michigan, USA. doi:10.4271/2015-01-1506 .
https://doi.org/10.4271/2015-01-1506...
) and in the control of seismic movements (Ünker and Çuvalcý, 2015bÜnker, F. and Çuvalcý, O. (2015b). Seismic Motion Control of a Column Using a Gyroscope. Procedia - Social and Behavioral Sciences 195:2316 - 2325.). Gyroscopic properties have also been used for the generation of clean energies by taking advantage of ocean waves (Wave Energy Converter or WEC). Incident waves activate the precession movement of a gyroscope and the output power is produced by damping the precession movement (Bracco et al. 2012Bracco, G., Giorcelli, E., Mattiazzo, G., Pastorelli, M. and Raffero, M. (2012). Testing of a Gyroscopic Wave Energy System. Renewable Energy Research and Applications (ICRERA), International Conference on. doi: 10.1109/ICRERA.2012.6477443.
https://doi.org/10.1109/ICRERA.2012.6477...
) or by generating their own energy which is used in Marine Vessels (Townsend 2016Townsend, N. (2016). Self-powered autonomous underwater vehicles: results from a gyroscopic energy scavenging prototype. IET Renewable Power Generation, Volume: 10, pp. 1078-1086. Issue: 8. doi: 10.1049/iet-rpg.2015.0210.
https://doi.org/10.1049/iet-rpg.2015.021...
). Even recently, the concept of gyroelastic materials has been introduced as a class of materials that have continuous distribution of mass, rotational inertia, elasticity, damping and gyricity. Gyroelasticity is the term used for a continuous distribution of angular momentum varying in time (Hassanpour and Heppler, 2014Hassanpour, S. and Heppler, G. (2014). Dynamics of micropolar gyroelastic materials. Proceedings of the 9th International Conference on Mechanics of Time-Dependent Materials. At Montreal, QC, Canada. doi: 10.13140/RG.2.1.1213.4169.
https://doi.org/10.13140/RG.2.1.1213.416...
). The theory or concept of gyroelasticity (D’Eleuterio and Hughes,1984D’Eleuterio, G. M. T. and Hughes, P. C. (1984). Dynamics of Gyroelastic Continua. J. Appl. Mech 51(2), 415-422. doi:10.1115/1.3167634.
https://doi.org/10.1115/1.3167634...
; D’Eleuterio and Hughes, 1987D’Eleuterio, G. M. T. and Hughes, P. C. (1987). Dynamics of Gyroelastic Spacecraft. J. Guid. Control Dyn., 10(4), pp. 401-405.http://dx.doi.org/10.2514/3.20231.
http://dx.doi.org/10.2514/3.20231...
) has given rise to studies on the control of beam structures with a single gyroscope (Hu and Zhang, 2015) and has extended to beams, chains and plates with multiple gyroscopes optimally distributed (Brocato and Capriz, 2009Brocato, M. and Capriz, G. (2009). Control of Beams and Chains Through Distributed Gyroscopes. AIAA Journal. Vol. 47, No. 2, pp. 294-302. http://dx.doi.org/10.2514/1.29250.
http://dx.doi.org/10.2514/1.29250...
; Hu et al. 2014Hu, Q., Jia, Y. and Xu, S. (2014). Dynamics and vibration suppression of space structures with control moment gyroscopes. Acta Astronautica. Volume 96, March-April 2014, Pages 232-245. doi:10.1016/j.actaastro.2013.11.032.
https://doi.org/10.1016/j.actaastro.2013...
; Chee and Damaren, 2015Chee, S. and Damaren, C. J. (2015). Optimal Gyricity Distribution for Space Structure Vibration Control. Journal of Guidance, Control, and Dynamics, Vol. 38, No. 7 (2015), pp. 1218-1228. https://doi.org/10.2514/1.G000293
https://doi.org/10.2514/1.G000293...
; Hassanpour and Heppler, 2016Hassanpour, S. and Heppler, G. R. (2016). Dynamics of 3D Timoshenko gyroelastic beams with large attitude changes for the gyros. Acta Astronautica, 118, pp.33-48. doi:10.1016/j.actaastro.2015.09.012
https://doi.org/10.1016/j.actaastro.2015...
). Thus, various applications of gyroscopic systems are important for industry and research. However, despite major advances in mathematical models of gyroscopic systems and gyroelastic systems, there are few experimental studies due to their complexity. Most of the experimental work focuses on position compensation taking advantage of the stability properties of gyroscopic systems, the main interest being the response of these systems to disturbances that may affect the performance of instruments, vehicles, robots and others. (Gagne et al. 2009, Yetkin et al. 2014, Ha, M. and Jung, S. 2015). The response of gyroscopic systems to a disturbance is a torque that compensates and counteracts the disturbance. This quality has been used experimentally to generate energy from sea waves (Bracco et al. 2012) or to suppress seismic movements (Ünker, F. and Çuvalcı, O. 2015). Regarding gyroelastic beams, no experimental work has been presented showing the results of modifying the dynamic properties (frequency, damping, modal coupling / decoupling) or the effect on cantilever beam deflection or flexural stress control.
In this work we performed an experimental study of a gyroscope-beam system (gyroelastic beam). The experimental tests were conducted at different speeds of the gyroscopic actuator while measuring the deflection of the system.
2 SIMPLE MATHEMATICAL MODEL OF A GYROSCOPE-BEAM SYSTEM
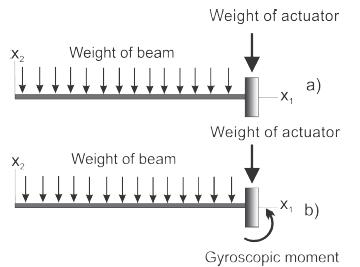
Consider the gyroscope-beam system (gyroelastic beam) shown in Figure 1. The physical model is composed of a beam of a rectangular uniform cross-section and a gyroscopic actuator. The beam rotates in a horizontal plane and a gyroscopic actuator of variable velocity is mounted on the free end (Hu and Zhang, 2015Hu, Q. and Zhang, J. (2015). Placement optimization of actuators and sensors for gyroelastic body. Adv.Mech.Eng.7(3). Pp 1-15. http://dx.doi.org/10.1177/1687814015573765.
http://dx.doi.org/10.1177/16878140155737...
). The beam rotates in a horizontal plane about the vertical axis x
2 . The actuator disc rotates in a plane perpendicular to the longitudinal axis of the beam. With this configuration it is possible to control the quantity of the system’s angular movement (h ) and consequently control the magnitude of the gyroscopic moment (Peck, 2004Peck, M. (2004). Practicable Gyroelastic Technology. 27th Annual AAS Guidance and Control Conference. Paper No. AAS 04-023. Breckenridge, CO.; Joubert et al. 2007Joubert, S., Fedotov, I., Pretorius, W. and Shatalov, M. (2007). On gyroscopic effects in vibrating and axially rotating solid and annular discs. International Conference - Days on Diffraction. St. Petersburg, pp. 89-94. 10.1109/DD.2007.4531995.
https://doi.org/10.1109/DD.2007.4531995...
).
The model has two degrees of freedom: the angular position around the axis x 2 and the vertical deflection of the beam. Figure 2 shows the forces and moments that act on the beam.
Loads and moments on the beam: (a) Nonrotating (static). (b) Rotating beam and gyroscopic actuator effect
The weight of the beam is represented as a uniformly distributed downward load. When the beam rotates around the vertical axis x 2 , tension is produced on the inside caused by centripetal forces (which in this work we now call inertial force) that keeps it attached to the axis of rotation (Simpkinson et al. 1948Simpkinson, S. H., Eatherton, L. J. and Millenson, M. B. (1948). Effect of Centrifugal Force On The Elastic Curve Of A Vibrating Cantilever Beam. NACA Report 914. Cleveland, Ohio.). As a result of this tension, the free end is raised a distance that is a function of the mass and length of the beam and its rotation speed or processional speed . In addition to the weight and the forces caused by the rotation of the beam, a gyroscopic moment acts on the free end of the beam. This moment is produced by the actuator which is mounted over the beam and rotating with constant angular velocity ) around the longitudinal axis of the beam (Figure 2). The gyroscopic moment is proportional to: i) the moment of inertia and the angular velocity of the actuator (), and ii) the angular speed of rotation of the beam around the vertical axis (). The directions of rotation of the beam and the actuator should be chosen so that the gyroscopic moment produces an elevation of the beam.
When the gyroscopic actuator and the beam are in motion, the forces and moments that act on the beam do not vary with time viewed from a fixed frame of reference. Thus, the relationship between the loads applied to the beam and the deformations that are produced can be studied by using static methods. There are three types of loads acting on the rotary beam: i) the weight of the beam and the gyroscopic actuator weight, ii) the inertial forces caused by the rotating beam and iii) the gyroscopic moment generated by the actuator.
The gyroelastic beam can be expressed through a simple two-degree-of-freedom model under the following assumptions: 1) the axes of the inertia of the beam coincide with the coordinate axes x
1 and x
2 (the angular momentum vector provided by the gyroscopic actuator is always directed to the neutral axis of the beam); 2) the mass of the beam is much smaller compared with the tip mass, 3); and the axial displacement of the beam is neglected in comparison to the transverse ones (Sinha et al., 2013Sinha, A., Bose, S., Nandi, A., Neogy, S. (2013). A precessing and nutating beam with a tip mass. Mechanics Research Communications,Volume 53, Pages 75-84,ISSN 0093-6413, https://doi.org/10.1016/j.mechrescom.2013.08.006.
https://doi.org/10.1016/j.mechrescom.201...
). This model enabled us to examine the terms of the equations of motion for their physical interpretation such as the following:
Where, is the beam mass, is the beam length is the weight of the gyro actuator, is the damping, is the Young's module, and is the angular momentum.
The above equations can be rewritten as:
The matrices from (Eq.3) are given by:
Where ,, represent the inertial, gyroscopic-damping, and stiffness matrices, respectively, and represents the vector of the external forces, which in this case is the weight of the gyroscopic actuator. represents the components of the acceleration vector, represents the components of the velocity vector and represents the vector components of beam deflection (displacement). The matrix contains a discrete mechanical damper (of damping coefficient c) and h that is the angular moment of beam; this matrix is also called the gyroscopic matrix (G ). Considering the gyroelastic beam system is not affected by external damping () Equations 1 and 2 can be expressed as:
As shown above, elements and couple the movement between both axes and therefore the equations, as is characteristic of gyroscopic systems. It is observed that deflection of the free end of the beam with respect to its no-load position is given only in the x 2 axle (see Figure 1); therefore, the axial displacement of the beam is neglected in comparison to the transverse ones. The main interest is to analyze the effects of the gyroscopic momentum on the axis of greater deflection. From Equations 4 and 5 only the terminus on the x 2 -axis is taken. Then these equations can be rewritten as:
Equation 6 represents the gyroscopic moment (). Similarly, first term in Equation 7 is the inertial o centrifugal moment (), while the second and last terms denote the moment of flexion and the moment generated by the weight of the gyroscopic actuator, respectively.
3 PARAMETER SELECTION IN THE DESIGN PROCESS
The magnitude of the gyroscopic moment generated by the gyroscopic actuator depends on the moment of inertia, the angular velocity of the actuator (ù) and the angular speed of the beam (precession speed) (). The goal in the design of a gyroscopic actuator is to produce the maximum gyroscopic moment with the lowest weight. Some design parameters such as the geometric and elastic properties as well as the location of the actuator along the beam do not affect the magnitude of the gyroscopic moment generated by the actuator. However, these determine the levels of deformation and stresses that occur in the beam. Equations 6 and 7 have been solved analytically in different ranges of ,, ù and . Using this information it is possible to determine the optimum values of these parameters. Such values were selected according to the desired beam length values as well as the elastic limit, angular velocity and weight of the actuator. The angular velocity of the gyroscopic actuator is important because the magnitude of the gyroscopic moment has a directly proportional variation to it. Figure 3 shows the simulation of the vertical static deflection of the beam as a function of its length under load conditions considered in the model. Curve (c) shows the beam is state of rest (Ω=0) and the gyroscopic actuator is disabled ( h=0 ); in Curve (b) the effects on the deflection of the beam caused by the inertial forces are shown (Ω≠0) and there are no gyroscopic moments (h=0 ) under these conditions; thus, the gyroscopic actuator behaves as a mass concentrated on the free end of the beam. The effects on the deflection of the beam caused by the inertial forces (Ω≠0) and the gyroscopic moment (h≠0 ) are shown in curve (a).
It can be observed that the maximum deflection of the beam in Curves (a) and (b) is smaller than at rest.
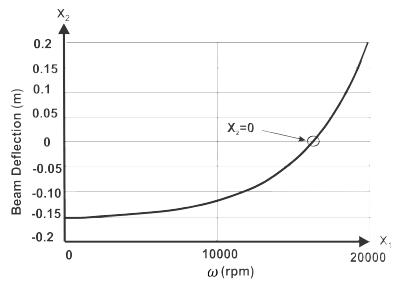
The experimental studies presented in Section 1 operate in the approximate range of 9000 - 20000 rpm. In this study the actuator angular velocities between 0 and 20000 rpm were considered in order to analyze the effects of the gyroscopic actuator on the deflection of the beam over a wide range. In all cases, the precession rate is assumed constant. From simulation results, the deflection on the free end of the beam as a rotational angular velocity function of the actuator is plotted in Figure 4. The rotation direction of the actuator was chosen in such a way that the moment generated by the gyroscopic actuator tended to bend the beam upward counteracting the effects of its weight. With the actuator deactivated at 0 rpm, the downward (negative) deflection is maximum when the speed of the actuator increases. The magnitude of gyroscopic moment counteracts this deflection, which is completely eliminated at close to 19000 rpm. The deflection is upward (positive) for velocities above this value.
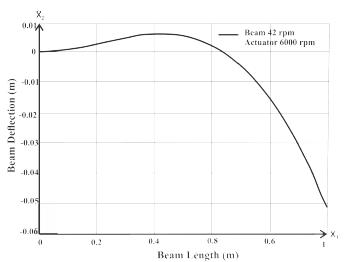
The results of the numerical solution show that the length of the beam is an important parameter in determining the effects of the gyroscopic moment. This is due to the bending moments caused by the weight of the actuator (the actuator is always connected to the free end of the beam) which varies linearly with the length of the beam. Such moments are decisive in determining its deflection. Figures 5 and 6 show that the deflection of the free end is upward in short beams. This is because in these beams the gyroscopic effects are predominant over the combined effects of other loads. The bending moments associated with weight increase as the length of the beam increases. For beams that are long enough, such moments produce a downward deflection, which could be countered by increasing the magnitude of the generated gyroscopic moment with the actuator, for example by increasing the angular velocity of the gyroscopic actuator.
Beam selection is important because a beam needs to have stiffness properties that enable observation of gyroscopic moments. Thus, if the beam is very rigid, the gyroscopic moments will become internal stresses with minor displacements; deformation in these displacements is difficult to detect by a position measuring system. In this study, a beam with geometry and dimensions that allows for the generation of a significant displacement was selected. The beam used for experimentation was 1.5 m in length; however, its length can vary by sliding over its support. Mainly, we worked with a length of 1 m in order to avoid working in the plastic region of the beam (Ha and Jung, 2015Ha, M. and Jung, S. (2015). Balancing control application using gyroscopic effect to a hand-carried one-wheel cart. IEEE International Conference on Advanced Intelligent Mechatronics (AIM), pp.1778-1782. doi: 10.1109/AIM.2015.7222804.; Hu and Zhang, 2015Hu, Q. and Zhang, J. (2015). Placement optimization of actuators and sensors for gyroelastic body. Adv.Mech.Eng.7(3). Pp 1-15. http://dx.doi.org/10.1177/1687814015573765.
http://dx.doi.org/10.1177/16878140155737...
; Chee and Damaren, 2015Chee, S. and Damaren, C. J. (2015). Optimal Gyricity Distribution for Space Structure Vibration Control. Journal of Guidance, Control, and Dynamics, Vol. 38, No. 7 (2015), pp. 1218-1228. https://doi.org/10.2514/1.G000293
https://doi.org/10.2514/1.G000293...
). The values obtained for the experimental design are shown in Table 1.
3.1 Gyroscopic actuator design
Based on the results obtained from the previous section, an initial gyroscopic actuator was constructed and coupled with a DC motor operating in an angular velocity ranging from 0 to 40,000 rpm. The actuator was used in the first experimental tests, where it was determined that the weight of the actuator causes excessive static deformation on the beam. In order to solve this problem, a second actuator was built with the purpose of reducing its weight and increasing its moment of inertia; however, it was only possible to increase the moment of inertia by keeping the same weight (Figure 7a). New alternatives to the gyroscopic actuator design were investigated in order to reduce their weight. The first point that was analyzed was the weight of the DC motor because a large part of it belonged to the gyroscopic actuator. Following this, the new gyroscopic actuator was designed and built (Figure 7b). This figure shows the final assembly of the gyroscopic actuator, which is composed of an inertial rotor, a pair of bearings and a link as a flexible shaft.
a) Explored design alternatives for the gyroscopic actuator, b)Final assembly of rigid beam actuator
3.2 Test Bench Construction
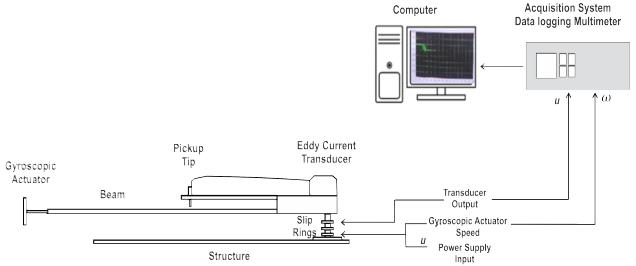
A solid structure is built in order to place a cantilever beam. This structure has to allow the beam to rotate in the horizontal plane and bending in the vertical plane. This is achieved by using a bench that supports a bearing flange and a rotating platform. Figure 8 shows the bench and its components. The rigid rotating platform is assembled to a shaft, over which some slip rings are placed. These slip rings are used to transmit electrical signals and supply electrical energy to the electric motor of the actuator (see Figure 8a). The Figure 8b shows the measurement detail in the gyroelastic beam system. The measurement process consists of an Eddy current transducer (TQ403 SKF System: range: 1.2 mm to 13.2 mm and sensitivity 1.33 mV/micron- displacement sensor) mounted on the beam (see Figure 9), an acquisition system (Fluke 289 with USB / RS232 interface for PC communications, which allows receiving, recording and performing data measurements over a long period of time with graphical visualization), a computer to display the results of the deflection in the beam and the velocity for gyroscopic actuator.
Figure 9 shows the block diagram and the function performed by each component of the gyroelastic system. In the system, u represents the voltage input, ù as stated above represents the motor speed of the gyroscopic actuator depending on the input voltage (u), h represents the gyroscopic momentum, which affects the deflection of the beam represented by x 2 . This deflection represents the output of the system, which is the variable of interest in this work.
The Figure 10 shows the schematic diagram of the measurement process where the input voltage defined by the operator (u) is used to regulate the speed of the gyroscopic actuator motor, thus allowing the control of the deflection of the beam (x 2 ). Deflection is captured through the displacement sensor through an acquisition system and a computer that displays the results of the deflection at the beam (x 2 ) and the speed of the gyro actuator (ù).
4 EXPERIMENTAL RESULTS
Tests were carried out using a flexible beam (see Figure 8) for two precession rates (Ω) (42 and 50 rpm) with five stages of gyroscopic actuator velocity ranging from 0 to 20000 rpm. Experimental values obtained for the deflection of the beam are shown on Figure 11. This Figure shows the beam deflection for some stages of the gyroscopic actuator velocity, with the following meanings:
Curve  represents the static deflection of the beam without a rotation effect or gyroscopic moment.
represents the static deflection of the beam without a rotation effect or gyroscopic moment.
Curve  represents the deflection of the beam when the beam is rotating; the beam is affected by the inertial force in its rotational speeds. The gyroscopic moment is not involved in this stage.
represents the deflection of the beam when the beam is rotating; the beam is affected by the inertial force in its rotational speeds. The gyroscopic moment is not involved in this stage.
Curve  represents the deflection affected by the inertial force and the gyroscopic moment at the free end of the beam.
represents the deflection affected by the inertial force and the gyroscopic moment at the free end of the beam.
From the previous figure, the values of the deflections are used to calculate the moments caused by the inertial force and the gyroscopic moments. Table 2 shows the magnitude of the gyroscopic moments with respect to the rotational speed of the beam and the rotational velocity of the gyroscopic actuator. Results for the five stages of the gyroscopic actuator speed with the beam’s rotational speed of 42 rpm and 50 rpm, respectively, are shown.
Magnitude of the gyroscopic moments with respect to the angular speed of the beam and the angular velocity of the gyroscopic actuator
As shown in Table 2, the magnitude of the gyroscopic moments generated under experimental conditions is small. Its greatest magnitude occurs when the condition of angular speed of the beam is 50 rpm and the angular velocity of the gyroscopic actuator is 20000 rpm. The magnitude of the gyroscopic moment is equivalent to 2.30 N.m; such magnitude is small, though it helps to counteract the bending moments, which are caused by actuator weight and the beam’s weight distribution.
In addition to the gyroscopic moments, inertial moments are also generated due to the inertial force when the gyroscope-beam system is in rotation. In Table 3, the inertial moments and the gyroscopic moments are compared with the gyroscopic moments registered during the steps of the actuator velocity.
The moments caused by inertial forces are constant during the rotation of the beam. It is important to observe that in the first two stages the moment caused by inertial force is greater than the gyroscopic moment. On other hand, in the last two stages the gyroscopic moment is greater than the moment caused by the inertial force.
5 DISCUSSION
The experimental results showed that in some stages the moments produced by the forces of inertia are greater than the gyroscopic moments generated by the actuator. However, these results do not occur in the later stages because the gyroscopic moments have greater magnitudes than the others, which help to counteract the deflection of the beam to around 55 percent of the initial deflection. The experimental results vary in comparison to the expected theoretical results (Figures 4, 5 and 6). Table 4 shows the variations in the results obtained.
This is because of considerations taken from the theoretical model shown in Section 2. The condition with the greatest effect on these results is the one that states that the axes of the inertia of the beam coincides with the coordinate axes x
1 and x
2 (the angular momentum vector provided by the gyroscopic actuator is always directed to the neutral axis of the beam). In the case of experimentation, the angular momentum vector moves approximately 2 cm parallel to the neutral axis of the beam and deviates 16° from the horizontal at maximum beam deflection. Therefore, a decomposition of the angular momentum vector into its vertical and horizontal components is presumed; thus, for theoretical calculation, the horizontal component was taken parallel to the neutral axis of the beam. In reality, due to the decomposition of the vector, the horizontal field of the vector is much better than the one considered theoretically. The discrepancy between theoretical and experimental results is mainly attributed to decomposition of the angular momentum vector. Li et al. (2000Li, L., Heppler, G. R. and Huseyin, K. (2000). Stability of a flexible link with an arbitrarily oriented tip rotor and a conservative tip load,” Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, 2000, pp. 1472-1477 vol.2. doi: 10.1109/ROBOT.2000.844805
https://doi.org/10.1109/ROBOT.2000.84480...
) propose a mathematical model that considers changes in the orientation of angular momentum vector in a flexible link with a tip rotor resulting in a very complex solution of the model, which was not our purpose. With the simple model we presented, we were able to plan the experimental stage and measure the components such as the gyroscopic actuator and the beam. It would certainly be of great interest in the future to develop a mathematical model that considers the decomposition of the angular momentum vector, in addition to the varying forces in time such as inertial and gravitational forces during experimentation. Other possible causes of the difference between theoretical and experimental results may be noise in the measurement signals generated by the use of slip rings.
6 CONCLUSIONS
The experimental behavior of a gyroelastic beam was investigated and presented in this work. Tests carried out using a flexible beam and a gyroscopic actuator where two precession rates (42 and 50 rpm) and five stages of gyroscopic actuator velocity ranging from 0 to 20000 rpm were analyzed. The maximum values obtained from the results of the gyroscopic moments were 2.21N.m and 2.3 N.m for each of the precession speeds. These moments helped to counteract the deflection of the beam to around 55 percent of the initial deflection. These results confirm the benefits of the use of the gyroscope actuator on cantilever beam systems. A simple mathematical model of a gyroscope beam system was used to obtain the design and construction parameters of the beam and the gyroscopic actuator. However, as an open problem, it would certainly be of great interest in the future to develop a more complete mathematical model that accurately represents the conditions presented in a gyroelastic beam system. Finally, in contrast with other works published in the literature, this study presents experimental evidence on the benefits of the gyroscopic actuator (CMG) as a viable alternative to reduce and control the magnitude bending stress through the control of deflection on cantilever beam systems (i.e. turbine blades or helicopter blades).
References
- Bai, S., Tzvi, P., Zhou, Q. and Huang, X. (2008). Dynamic Modeling of a Rotating Beam Having a Tip Mass. IEEE International Workshop on Robotic and Sensors Environments. pp. 52-57.doi: 10.1109/ROSE.2008.4669180.
» https://doi.org/10.1109/ROSE.2008.4669180 - Bitterly, J. (1997). Flywheel Technology Past Present and 21 Century Projections. IECEC-97 Proceedings of the Thirty-Second Intersociety Energy Conversion Engineering Conference (Cat. No.97CH6203). pp. 2312-2315 vol.4. doi: 10.1109/IECEC.1997.658228.
» https://doi.org/10.1109/IECEC.1997.658228 - Bracco, G., Giorcelli, E., Mattiazzo, G., Pastorelli, M. and Raffero, M. (2012). Testing of a Gyroscopic Wave Energy System. Renewable Energy Research and Applications (ICRERA), International Conference on. doi: 10.1109/ICRERA.2012.6477443.
» https://doi.org/10.1109/ICRERA.2012.6477443 - Brocato, M. and Capriz, G. (2009). Control of Beams and Chains Through Distributed Gyroscopes. AIAA Journal. Vol. 47, No. 2, pp. 294-302. http://dx.doi.org/10.2514/1.29250
» http://dx.doi.org/10.2514/1.29250 - Chee, S. and Damaren, C. J. (2015). Optimal Gyricity Distribution for Space Structure Vibration Control. Journal of Guidance, Control, and Dynamics, Vol. 38, No. 7 (2015), pp. 1218-1228. https://doi.org/10.2514/1.G000293
» https://doi.org/10.2514/1.G000293 - Chu, C., Wu, B. and Lin, Y. (2007). An experimental study on active micro-vibration suppression of a flexible beam mounted on an elastic base. Measurement Science and Technology, Volume 18, Number 7.
- D’Eleuterio, G. M. T. and Hughes, P. C. (1987). Dynamics of Gyroelastic Spacecraft. J. Guid. Control Dyn., 10(4), pp. 401-405.http://dx.doi.org/10.2514/3.20231
» http://dx.doi.org/10.2514/3.20231 - D’Eleuterio, G. M. T. and Hughes, P. C. (1984). Dynamics of Gyroelastic Continua. J. Appl. Mech 51(2), 415-422. doi:10.1115/1.3167634.
» https://doi.org/10.1115/1.3167634 - Gagne, J., Laroche, E., Piccin, O. and Gangloff, J. (2009). An active cardiac stabilizer based on gyroscopic effect. Conf Proc IEEE Eng Med Biol Soc.6769-72. doi: 10.1109/IEMBS.2009.5332512.
» https://doi.org/10.1109/IEMBS.2009.5332512 - Ha, M. and Jung, S. (2015). Balancing control application using gyroscopic effect to a hand-carried one-wheel cart. IEEE International Conference on Advanced Intelligent Mechatronics (AIM), pp.1778-1782. doi: 10.1109/AIM.2015.7222804.
- Hamdi, H., Mrad, C., Hamdi, A. and Nasri, R. (2014). Dynamic response of a horizontal axis wind turbine blade under aerodynamic, gravity and gyroscopic effects. Applied Acoustics. Volume 86, Pages 154-164.http://dx.doi.org/10.1016/j.apacoust.2014.04.017
» http://dx.doi.org/10.1016/j.apacoust.2014.04.017 - Hassanpour, S. and Heppler, G. (2014). Dynamics of micropolar gyroelastic materials. Proceedings of the 9th International Conference on Mechanics of Time-Dependent Materials. At Montreal, QC, Canada. doi: 10.13140/RG.2.1.1213.4169.
» https://doi.org/10.13140/RG.2.1.1213.4169 - Hassanpour, S. and Heppler, G. R. (2016). Dynamics of 3D Timoshenko gyroelastic beams with large attitude changes for the gyros. Acta Astronautica, 118, pp.33-48. doi:10.1016/j.actaastro.2015.09.012
» https://doi.org/10.1016/j.actaastro.2015.09.012 - Hu, Q. and Zhang, J. (2015). Placement optimization of actuators and sensors for gyroelastic body. Adv.Mech.Eng.7(3). Pp 1-15. http://dx.doi.org/10.1177/1687814015573765
» http://dx.doi.org/10.1177/1687814015573765 - Hu, Q., Jia, Y. and Xu, S. (2014). Dynamics and vibration suppression of space structures with control moment gyroscopes. Acta Astronautica. Volume 96, March-April 2014, Pages 232-245. doi:10.1016/j.actaastro.2013.11.032.
» https://doi.org/10.1016/j.actaastro.2013.11.032 - Jin, H. Wang, T., Yu, F., Zhu, Y., Zhao, J. and Lee, J. (2016). Unicycle Robot Stabilized by the Effect of Gyroscopic Precession and Its Control Realization Based on Centrifugal Force Compensation. IEEE/ASME Transactions on Mechatronics, vol. 21, no. 6, pp. 2737-2745. doi: 10.1109/TMECH.2016.2590020.
» https://doi.org/10.1109/TMECH.2016.2590020 - Jones, L. and Peck, M. A. (2009). A generalized framework for linearly-constrained singularity-free control moment gyro steering laws. AIAA Guidance, Navigation, and Control Conference, 10-13. Aug 2009, Chicago, Illinois. http://dx.doi.org/10.2514/6.2009-5903
» http://dx.doi.org/10.2514/6.2009-5903 - Joubert, S., Fedotov, I., Pretorius, W. and Shatalov, M. (2007). On gyroscopic effects in vibrating and axially rotating solid and annular discs. International Conference - Days on Diffraction. St. Petersburg, pp. 89-94. 10.1109/DD.2007.4531995.
» https://doi.org/10.1109/DD.2007.4531995 - Kurosu, S. and Yamazaki, T. (2004). Gyroscopic Force Measuring System -Theory and Applications. SICE Annual Conference in Sapporo, August 4-6,2004. Hokkaido Institute of Tecnology, Japan.
- Li, D. and Vallery, H. (2012). Gyroscopic assistance for human balance. 12th IEEE International Workshop on Advanced Motion Control (AMC), pp. 1-6. doi: 10.1109/AMC.2012.6197144.
» https://doi.org/10.1109/AMC.2012.6197144 - Li, L., Heppler, G. R. and Huseyin, K. (2000). Stability of a flexible link with an arbitrarily oriented tip rotor and a conservative tip load,” Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, 2000, pp. 1472-1477 vol.2. doi: 10.1109/ROBOT.2000.844805
» https://doi.org/10.1109/ROBOT.2000.844805 - Ma, H., Lu, Y., Wu, Z., Tai, X., Li, H. and Wen, B. (2015). A new dynamic model of rotor-blade systems. Journal of Sound and Vibration, Volume 357, Pages 168-194.http://dx.doi.org/10.1016/j.jsv.2015.07.036
» http://dx.doi.org/10.1016/j.jsv.2015.07.036 - Meirovitch, L. and Oz, H. (1980). Modal-Space Control of Distributed Gyroscopic Systems. Journal of Guidance, Control, and Dynamics, Vol. 3, No. 2. pp. 140-150. http://dx.doi.org/10.2514/3.55961
» http://dx.doi.org/10.2514/3.55961 - Meirovitch, L. and Baruh, H. (1981). Optimal control of damped flexible gyroscopic systems. Journal of Guidance and Control, 4(2):157-163.
- Nguyen, T., Ranieri, M., DiGiovanna, J., Peter, O., Genovese, V., Pérez, A. and Micera S (2014). A real-time research platform to study vestibular implants with gyroscopic inputs in vestibular deficient subjects. IEEE Trans. Biomed. Circuits Syst., vol. 8, no. 4, pp. 474-484. doi: 10.1109/TBCAS.2013.2290089.
» https://doi.org/10.1109/TBCAS.2013.2290089 - Peck, M. (2004). Practicable Gyroelastic Technology. 27th Annual AAS Guidance and Control Conference. Paper No. AAS 04-023. Breckenridge, CO.
- Pullen, K. and Ellis, C. (2006). Kinetic Energy Storage for Vehicles. IET - The Institution of Engineering and Technology Hybrid Vehicle Conference. pp. 91-108. doi: 10.1049/cp:20060616.
» https://doi.org/10.1049/cp:20060616 - Scheurich, B., Koch, T., Frey, M. and Gauterin, F. (2015). Damping A Passenger Car With A Gyroscopic Damper System. SAE Int. J. Passeng. Cars - Mech. Syst. 8(2). Detroit, Michigan, USA. doi:10.4271/2015-01-1506 .
» https://doi.org/10.4271/2015-01-1506 - Shao, P., Dong, W., Sun, X., Ding, T. and Zou, Q. (2015). Dynamic Surface Control To Correct For Gyroscopic Effect Of Propellers On Quadrotor . Information and Automation, IEEE International Conference on. pp. 2971-2976. doi: 10.1109/ICInfA.2015.7279797.
» https://doi.org/10.1109/ICInfA.2015.7279797 - Simpkinson, S. H., Eatherton, L. J. and Millenson, M. B. (1948). Effect of Centrifugal Force On The Elastic Curve Of A Vibrating Cantilever Beam. NACA Report 914. Cleveland, Ohio.
- Sinha, A., Bose, S., Nandi, A., Neogy, S. (2013). A precessing and nutating beam with a tip mass. Mechanics Research Communications,Volume 53, Pages 75-84,ISSN 0093-6413, https://doi.org/10.1016/j.mechrescom.2013.08.006
» https://doi.org/10.1016/j.mechrescom.2013.08.006 - Telli, S. and Kopmaz, O. (2004). On the Mathematical Modelling of Beams Rotating About A fixed Axis. Mathematical and Computational Applications 9 (3), 333-348. doi:10.3390/mca9030333.
» https://doi.org/10.3390/mca9030333 - Townsend, N. (2016). Self-powered autonomous underwater vehicles: results from a gyroscopic energy scavenging prototype. IET Renewable Power Generation, Volume: 10, pp. 1078-1086. Issue: 8. doi: 10.1049/iet-rpg.2015.0210.
» https://doi.org/10.1049/iet-rpg.2015.0210 - lÜnker, F. and Çuvalcý, O. (2015a). Vibration Control of a Column Using a Gyroscope. Procedia - Social and Behavioral Sciences. Volume 195, 3 July 2015, pages 2306-2315. https://doi.org/10.1016/j.sbspro.2015.06.182
» https://doi.org/10.1016/j.sbspro.2015.06.182 - Ünker, F. and Çuvalcý, O. (2015b). Seismic Motion Control of a Column Using a Gyroscope. Procedia - Social and Behavioral Sciences 195:2316 - 2325.
- Xiao, Y., Zhang, C., Zhu, K. and Ge, X. (2011). Suppression of gyroscopic rotation in flywheel energy storage systems. In Proc. Proceedings of the 2011 Chinese Control and Decision Conference. Pp. 3286-3289, Shenyang, China.
- Yamanaka, K., Heppler, G. R., Huseyin, K. (1994). The Stability of a Flexible Link with a Tip Rotor and a Comprehensive Tip Load. IEEE Transactions on Robotics and Automation, Vol. ICRA 1994: 1798-1803.
- Yetkin, H., Kalouche, S., Vernier, M., Colvin, G., Redmill, K. and Ozguner, U. (2014). Gyroscopic stabilization of an unmanned bicycle. American Control Conference (ACC) IEEE, pp. 4549-4554, 2014. doi: 10.1109/ACC.2014.6859392.
» https://doi.org/10.1109/ACC.2014.6859392 - Zhou, J., Zhang, J. and Meng, G. (2012). Gyroscopic effects on the engine rotor on the characteristics of wing bending-torsional flutter. Acta Aerodynamica Sinica. Issue 5. pp 578-582.
-
Available Online: June 20, 2018
Publication Dates
-
Publication in this collection
2018
History
-
Received
09 Jan 2018 -
Reviewed
01 June 2018 -
Accepted
14 June 2018