Abstract
In Brazil, the use of reinforced concrete waffle slab in multi-story buildings is widespread nowadays. These buildings are projected for different purposes such as fitness centers, supermarkets, parking garages, offices and residential units. Simple activities as walking, skipping and jumping can generate vibrations in these slabs. Vibrations can cause inconvenience in persons, questions about structure´s safety, and collapse risk that it is determined by its intensity of vibrations. The objective of this paper is evaluating the behavior of reinforced concrete waffle slabs due to the human rhythmic activities. Slabs are modeled by finite elements method using the SAP2000 program. The results are verified according to Brazilian and international codes. The waffle slabs are submitted to high-levels of acceleration and velocity generating discomfort in users.
Human actions; natural frequencies; human comfort; finite element method; NBR 6118:2003
Evaluation of dynamic behavior of waffle slab to gym center
Yuri Cláudio Vieira da Costa; Tereza Denyse de Araújo* * Autor e-mail: denyse@ufc.br
PEC - Programa de pós-graduação em engenharia civil: estruturas e construção civil. Universidade Federal do Ceará (UFC). Campus do Pici Bloco 710 2º. andar - 60455-760, Fortaleza. CE. Brazil
ABSTRACT
In Brazil, the use of reinforced concrete waffle slab in multi-story buildings is widespread nowadays. These buildings are projected for different purposes such as fitness centers, supermarkets, parking garages, offices and residential units. Simple activities as walking, skipping and jumping can generate vibrations in these slabs. Vibrations can cause inconvenience in persons, questions about structure´s safety, and collapse risk that it is determined by its intensity of vibrations. The objective of this paper is evaluating the behavior of reinforced concrete waffle slabs due to the human rhythmic activities. Slabs are modeled by finite elements method using the SAP2000 program. The results are verified according to Brazilian and international codes. The waffle slabs are submitted to high-levels of acceleration and velocity generating discomfort in users.
Keywords: Human actions, natural frequencies, human comfort, finite element method, NBR 6118:2003.
1 INTRODUCTION
Over the years, the multi-story buildings have become more slender and lighter, consequently more susceptible to vibrations (Middleton and Bownjohn, 2010). These vibrations are coming from different sources such as wind action, actions induced by people, and earthquakes.
The slab is the structural element that receives the main load of the building, being in direct contact with its occupants and so subjected to vibrations. One of most used slabs types currently in Brazil is the waffle slab, and its use is widespread in Fortaleza city, capital of Ceará´ state. The most commonly used type is two-way with ribbed inclined, being usually found in airports, parking garages, fitness center, commercial and industrial buildings, and residences. Its main advantages (Bocchi Jr, 1995; Silva, 2002; Stramandinoli, 2003; Araújo, 2005; Silva, 2005; Diógenes, 2006) are as follows: reducing costs and construction time; allows large spans (up to 7.5 m); and reduces the structure weight. In fact, flat slab can be an uneconomical option, because it requires high thicknesses to overcome longer spans, because part of its strength is used to withstand tension stresses due to its self- weight (Stramandinoli, 2003).
In nowadays, human activities such as walking, dancing, jumping, running and aerobic exercises are regarded the most severe excitation source in slab floors (Smith et al., 2007). Moreover, it can be said that people's behavior has been adapting to modern life being very common to use residential portable gym equipment like stationary bikes, mini elastic beds, among others. The dissemination of gym centers in shopping centers, in little commercial centers and even in residential buildings is spreading worldwide.
Therefore, there is a concern among researchers to evaluate the dynamic behavior of the waffle slab under the human activity effects, because these actions are considered like static load in structural design.
The human actions study on slabs gained impetus in the 80s, when the first mathematical formulations to model these actions emerged (Allen et al., 1985; Rainer and Pernica, 1986; Bachmann and Ammann, 1987; Rainer et al., 1988). These formulations are based on Fourier series and assuming that induced force by persons is periodic in time. Other formulations are proposed in the literature (Sachse et al., 2003) as for example the Hanning function (Faisca, 2003; Costa and Araújo, 2011).
These activities can be perceived by users, causing great discomfort in most of time. So, evaluating the human comfort has also been the study matter. These studies have shown that human activities can cause intolerable levels of acceleration peaks (Junges, 2010), often extrapolating the limits established by international codes (Almeida, 2008; Xuewei et al., 2008; Langer, 2009). According to Hechler et al. (2008), the perception of vibrations is an individual feeling that depends on age and people health, frequency and vibration magnitude, among other.
The waffle slab behavior is intermediary between plate (concrete slab), grillage of beams (ribbed), and shell behavior (diaphragm rigid and ribbed), which results in a difficult and complex analysis.
The NBR 6118 (ABNT, 2003) is the Brazilian code that gives the necessary requirements for design of simple, reinforced and prestressed concrete structures, except those which employ the lightweight concrete, heavy concrete or other special concrete. This code allows two-way waffle slabs are calculated statically like solid flat slabs (plate) with equivalent bending stiffness. However, this simplification disregards the torsional stiffness of ribbed. In this case, the results do not correspond to the real (Stramandinoli, 2003; Donin, 2007) and should be avoided.
In this way, the calculation of forces and displacements in these slab types can be done by grillage analogy method (Balendra and Shanmugam, 1985) or by plate's theory (Stramandinoli, 2003). Some authors (Bocchi Jr, 1995; Dias, 2003; Silva, 2005) believe that to use of first method is more advantageous than the second one, but these methods are established and both provide good results.
The finite element method (FEM) is now the most reliable analysis numerical tool to solve complex problems. It can be used in the application of the two aforementioned methods, in order to determine the natural frequencies and its respective mode shapes (Pavic et al., 2001; Reynolds and Pavic, 2003) as well as the displacement history in time due to loading (Howard and Hansen, 2003; Mello et al., 2008).
The aim of this job is to evaluate the reinforced concrete waffle slab behavior due to the rhythmic human actions. In this case, three slabs are modeled by finite element method, based on a real project of a gym slab located in a multi-story building built in Fortaleza-Ce. Three-dimensional analyses are performed using the computer program SAP 2000-v. 14 (CSI, 2008), in order to get the natural frequencies and mode shapes, as well as the displacements, velocities and accelerations when of dynamic loading application that simulates human rhythmic action. The natural frequencies and displacements are compared to requirements provided by NBR 6118 (ABNT, 2003), while the acceleration and velocity peaks are checked against the international codes for human comfort.
2 STRUCTURAL AND COMPUTATIONAL MODEL
The structural system of waffle slab consists of concrete slab, ribbed inclined, and board beams, which is analyzed in three different models of slab: model A, model B and model C (Figure 1). These models are different in the ratio of longer span (x-direction) to shorter span (y-direction) varying from 1 (model A) to 2 (model C). The model A corresponds to the real slab for the gym center, while the models B and C have the slab ratio of span that can be found in city buildings.
The three slab models have the following geometric characteristics (Figure 2): concrete slab thickness is 4 cm; thickness of ribbed is 7 cm at the bottom and 13 cm on the top; distance between ribs is 48 cm at the top and 54 cm on the bottom. The ribbed are bidirectional and inclined. The board beams have 14 cm of width and 50 cm of height (real dimensions), and are considered simply supported.
The real slab is constructed in reinforced concrete, whose mechanical properties are: characteristic compressive strength (fck) with 28 days curing is 35 MPa; Poisson coefficient (υ) is 0.2; and damping coefficient is 3% for all mode shapes, as recommended by NBR 6118 (ABNT, 2003). From this code is used the secant modulus of elasticity (Ecs), for the analysis, that is given by following equation:
The finite element mesh for each waffle slab and its respective board beam is done using three-dimensional solid element (Figure 3), whose number of elements of each model is shown in Table 1. This finite element was chosen to be faithful to real structure and get the natural eccentricity between the structural elements (concrete slab, ribbed, and board beams). The board beams are restricted in the support points to three translations (each of x-, y-, z- Cartesian axes). The analysis is realized considering the elastic-linear behavior of concrete. The model A, model B, and model C have the following masses: 17,515 kg, 21,896 kg, and 16,552 kg, respectively.
3 DYNAMIC LOADING
The design loads are classified in permanent (dead) loads and accidental loads. The permanent (dead) load is applied statically throughout design life of structure including the own weight of slab, beams and floor finish. The apparent specific for reinforced concrete weight value is 25 kN/m³ and for finish floor specific weight is 1 kN/m² (NBR 6120:1980). This last one load is applied only on slab surface.
The accidental load comprises loads which are not always acting but may exist at various times during the normal use of structure. These loads are resulting of occupation of a building and traffic on bridges (imposed loads), and wind loads (environmental loads), among others. The NBR 6120 (ABNT, 1980) recommends that this load type must be applied statically.
Aerobic activities are considered in this code like accidental load, however, in this work, they are applied like a dynamic load on the waffle slab. This load is represented by periodic mathematical functions decomposed in Fourier series. The function here used was suggested by Bachmann et al. (1995), that it is given by following expression:
where P(t) is the dynamic loading function in time (N); wp is the weight of the person considered as 800 N; ai is the Fourier coefficient of the i-th harmonic or dynamic load factor; fp is the activity rate (Hz); i is the number of i-th harmonic; n is total number of contributing harmonics; t is time (s); and ϕi is the phase lag of the i-th harmonic relative to the 1st harmonic.
Bachmann et al. (1995) suggest values for density of participants during activity (design density), for dynamic load factors (a) and phase lag (ϕ). These values are based in experimental researches and are shown in Table 2.
The frequency of excitation applied on slab models is 3 Hz and design density varies between 0.25 persons/m² and 0.5 persons/m². In this way, three slab models are submitted to four load models (Table 3): Loading 1 and Loading 2 are to normal activity rate and Loading 3 and Loading 4 to high activity rate (Figure 4).
These dynamic loads are applied as a distributed load in full of slab area (Figure 5), considering that participants of activity have total synchronization between each other. In other words, the synchronization is perfect that meaning the slabs are submitted to bigger efforts.
4 RESULTS AND DISCUSSION
Two types of dynamic analyses are performed: free vibration analysis for obtaining natural frequencies and mode shapes; and forced vibration analysis where the three models of ribbed slabs are subject to the four load models to obtain displacements in time, as well as peaks of acceleration and speed (human comfort).
4.1 Analysis of natural frequencies
The natural frequencies and its respective mode shapes are obtained through a free undamped vibration analysis of three slab models. The natural frequencies of each model are shown in Table 4. The mode shapes are coincident in all slab models which are presented in Figure 6 for model B.
In accordance with Figure 6, it is noticed that the first natural frequency is associated with first flexural mode; the second one corresponds to first torsional mode; the third one is related to the second bending mode; and fourth natural frequency refers to the second mode of torsion. Therefore, the lowest slab frequency is associated with the first mode shape in bending.
Among three models, the model A is more rigid, because its fundamental frequency is higher. When the ratio of spans increases of Model A to model B, the mass raises and the fundamental frequency is reduced. This is due to the length in x-axis direction is larger in model B (Figure 1). When the ratio of spans increases of model B for model C, the total mass is reduced and the fundamental frequency is increased. That can be explained because the length in direction y-axis of model C (Figure 1) is shorter, which increases the slab stiffness. Comparing model A with model C it is observed that model C is less rigid.
The NBR 6118 (ABNT, 2003) establishes values for critical frequencies allowed (Table 5). For slab of fitness center, the critical frequency value refers to gymnasium that is 8 Hz. This code still states that the fundamental frequency of the structure, with certain activity, may not be less than 20% the critical frequency (f1 > 1.2·fcrit). In other words, the fundamental frequency of gym floor (aerobic activities) must be greater than 9.6 Hz to ensure performance stability in Excessive Vibration Limit State (SLS-EV).
The fundamental frequencies of models B and C are 7.679 Hz and 9.443 Hz, respectively. These frequencies are below the critical frequency increased in 20% (9.6 Hz), while the model B still has its fundamental frequency below the critical frequency (8 Hz). The model A does not exceed these values (10.328 Hz).
4.2 Displacement analysis
The NBR 6118 (ABNT, 2003) determines limit values of displacements in order to avoid excessive deformation of structure. One of basic groups defined by this code is the acceptability sensorial that is characterized by unpleasant visual effect and undesirable vibrations. For unpleasant visual effect, the maximum vertical displacement is L/250, where L is the shorter length of slab; and for undesirable vibrations, the value limit is L/350. The first value is related to total displacement of structure and the second one is associated displacements from the accidental load only.
In this work, the maximum displacements of three models are compared with limit displacement value for unpleasant visual effect (2.588 cm for models A and B and 1.836 cm for model C). The maximum vertical displacements occur in the center of each slab model for each analysis (Table 6).
It is observed that none of maximum displacements allowed is exceeded. The Loading 4 generates the bigger displacements in the three models. This loading has high intensity and design density is in extreme situation (0.50 persons/m²), i.e. the unfavorable loading situation. Among all slabs analyzed, the model B presents the greatest displacements. This was expected since it has the largest spans (more flexible).
4.3 Human comfort analysis
The human body is sensitive to structures movements that oscillate in determined frequencies. These vibrations have different magnitudes that can cause different sensations which can vary of light discomfort to changes in health. The vibration levels that cause nuisance to humans are limited by technical codes.
According to the international code ISO 2631-1:1989, the humans may discriminate six different kinds of vibrations (three translational directions and three rotational directions - roll, pitch, yaw) that are given by the basicentric axis. This basicentric axis is oriented considering the body position with respect to gravity (Figure 7): sitting, standing, or recumbent.
The body sensitivity to vibrations along z-axis is different to vibrations along x- or y- axes. Individuals in standing position and vibration in the direction z-axis present greater sensitivity to acceleration in the frequency range of 4 to 8 Hz, which corresponds to the body resonance. In the x- and y- axes directions, the natural frequency range is 1 to 2 Hz. In the seating position, the fundamental frequency range is 4 to 6 Hz, for z-axis direction, and 1 to 3 Hz, for the x- and y- axes. The z-axis vibration is more important in the offices design and other workplaces, while all three axes are important in the design of residences and hotels where sleeping comfort should be considered (Naeim, 1991).
Building floors are exposed to excessive vibrations due dynamic forces induced by human activities that can cause annoyance and discomfort to the users (Saidi et al., 2007). The human discomfort is a concern and it must be avoided. The human comfort analysis can be made from accelerations and speeds generated by excitation in the structure considered. These accelerations and speeds are limited to maximum levels that guarantee comfort.
Bachmann et al. (1995) suggest limit values of accelerations and speeds that are shown in Table 7. According to those authors, these limit values are resulting of a data combination of many authors and there are a dispersion by a factor until two about values indicated. The human perception to vibrations is divided in four levels that ranging of just perceptible to intolerable. Thus, for an ideal comfort level, the peak acceleration shall be less than 3.4 cm/s2, for frequencies ranging of 1 to 10 Hz. If natural frequencies are above 10 Hz, the comfort level is evaluated by speed peaks being, in this case, imperceptible to values below 0.05 cm/s.
Other criteria are available in the literature for assessing human comfort, such as those proposed by DIN 4150-2:1999, by ISO 2631-1:1989, by Murray et al. (2003) and Goldman scale (1948 apud Goldman and Gierke, 1976). The Goldman scale (Figure 8) correlates acceleration peaks, as a function of gravity acceleration, with vibration frequencies and three levels of sensitivity (perception, unpleasant are possible in a frequency range of 1 to 50 cps.
In order to know the frequency range that slab models vibrate, it is necessary to do a spectral analysis of excitation loads (spectra obtained of SAP2000). The acceleration response spectrum of model C (Figure 9) for Loading 1 shows that the highest acceleration peak occurs in fundamental frequency 9.443 Hz (Table 4). However, there are still minor magnitude peaks whose frequency is lower than the fundamental (f01). These acceleration peaks is related to excitation frequency and its harmonics. This behavior is the same for models A and B, which they are not shown here (Costa, 2012). In other words, the response frequencies of these models are 10.328 Hz and 7.679 Hz, respectively.
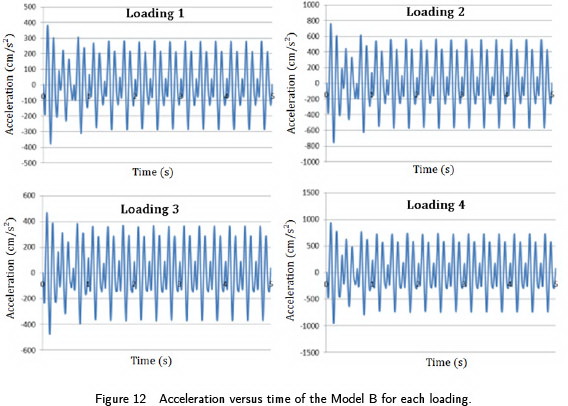
In the ribbed slabs here studied the maximum speeds and accelerations occur in the slab center for each one of excitation loads. Thus the graphics of speeds and acceleration versus time are shown in Figure 10 and Figure 11, respectively, for model A. The accelerations of models B and C are shown in Figure 12 and Figure 13, respectively. Notice that the highest acceleration and velocity peaks in three models occur for the Loading 4, because this loading represents the largest people concentration practicing aerobic activity (0.5 persons/m²).
About human comfort analysis, the fundamental frequency for model A is above 10 Hz. This model is evaluated by the speed peaks while models B and C are evaluated by the acceleration peaks. It is verified that speed peaks of model A are above 1.38 cm/s (Table 7) for all loadings, indicating an intolerable perception. The accelerations of models B (Figure 12) and C (Figure 13) are above 180 cm/s2 (Table 7), i.e. they are considered intolerable perception to all loads. Therefore, the four excitation loadings can generate discomfort to users. The same behavior happens when the slab models is analyzed using Goldman's scale (Figure 8).
The results of user perception to vibration are shown in Table 8. It can be observed that all models have high values of speed and acceleration in all excitation loads, i.e., these loadings cause discomfort for the users.
According to ISO 2631-1:1989, it should be noted that human sensitivity varies with frequency in each direction of orthogonal Cartesian axes. It has been said already, individuals in standing position and vibration in z-axis direction present greater sensitivity in frequency range of 4 to 8 Hz, which corresponds to body resonance. The model A has its fundamental frequency above that value. So, the discomfort feeling may not be so high to slab users (Table 8).
The vibration perception is different from person to person. Other factors in addition to the individual's position (standing, seated, and lay down) can influence this perception (Junges, 2010), such as: performed activity, age, humor, sex, damping, among others. However, the perception intensity depends only of displacements, acceleration and speed magnitudes, exposure time, and the vibration frequency (Bachmann et al., 1995).
The models B and C are subjected to acceleration peak values considered intolerable. Both models have the fundamental frequency (7.679 Hz and 9.443 Hz respectively) above of specified value in ISO 2631-1:1989 to maximum sensibility of person in standing position and vibration in the z-axis direction (4 to 8 Hz).
However, for Model C it is possible that uncomfortable sensation will be minimized. The third-harmonic frequency value of loading models (9 Hz) is closer to fundamental frequency value of this model and it presents less energy. I.e. this third-harmonic can be able to provide the resonance condition. In addition, it is important to recall that critical frequency (8 Hz) of model C satisfies the requirements of NBR 6118 (ABNT, 2003), but it does not satisfy the SLS-EV (9.6 Hz).
For model B there is no match with the harmonic frequencies of any loading, i.e. none of load models takes resonance of slab. In this way, it is possible the slab´s users will feel an unpleasant sensation if the ribbed slab is excited by any force similar to Loading 1, 2, 3 and 4 (Figure 4). However, this model B does not satisfy the requirements of NBR 6118 (ABNT, 2003) in relation the critical frequency and SLS-EV.
5 CONCLUSIONS
The objective of this work is to evaluate the dynamic behavior of reinforced concrete waffle slabs due to the rhythmic human actions. Three slab models are analyzed by finite element method, using the commercial program SAP 2000-v. 14 (CSI, 2008). The slab models are based on a real project of a ribbed slab for a fitness center that it was designed considering the human actions like a static load.
In relation frequency analysis, the first-mode shapes of the three slabs are equals and the fundamental frequency of each of them is associated with the bending vibration mode (Mode 1). It is verified, therefore, that raising ratio of longer span (x-direction) to shorter span does not modify the first modal forms of ribbed slab. This ratio only interferes on natural frequency values. So, it is important to take care in relation to slab fundamental frequency. This frequency do must not approach to the excitation frequencies to avoid a resonant state.
The forced vibration analysis shows that maximum displacement in all slab center are inferior to values allowed by NBR 6118 (ABNT, 2003), even for flexible slab (model B). Despite of this, the slab models are subjected to acceleration and speed peaks that exceed tolerable thresholds for the criteria adopted, generating discomfort on users. However, in all three models the discomfort can be minimized, because their fundamental frequencies are far from maximum frequency of human body sensitivity to standing position in z-axis direction.
On the other hand the dimensioning using only the static analysis of the real ribbed slab is not sufficient to ensure the user comfort. This indicates that a dynamic analysis is necessary to know the maximum accelerations of the waffle slab to minimize the human discomfort. It is important for further research compare the results of displacement and strength to both analyses, i.e., static and dynamic analysis. The first one load will be applied according to NBR 6120 (ABNT, 1980).
- ABNT - Brazilian Association of Technical Codes (1980). NBR 6120: Carga para o cálculo de estruturas de edificações. Rio de Janeiro, Brazil.
- ABNT - Brazilian Association of Technical Codes (2003). NBR 6118: Projetos de estruturas de concreto: procedimentos. Rio de Janeiro, Brazil.
- Allen, D.E., Rainer, J.H., Pernica, G., (1985). Vibration criteria for assembly occupancies. Canadian Journal of Civil Engineering, 12: 617 - 23.
- Almeida, R.R., (2008). Análise de vibrações em sistemas estruturais para pisos mistos com joists submetidos a atividades humanas rítmicas. Master of Science Dissertation (in Portuguese), University of Rio de Janeiro State, Brazil.
- Araújo, J.M., (2005). Considerações sobre a rigidez à torção das lajes nervuradas de concreto armado. Teoria e Prática na Engenharia Civil, 7: 1-8.
- Bachmann, H., Ammann, W., (1987). Vibration in structures induced by man and machines. IABSE Structural Engineering Document 3E, International Association for Bridges and Structural Engineering.
- Bachmann, H., Ammann, W.J., Deischl, F., Eisenmann, J., Floegl, I., Hirsch, G.H., Klein, G.H., Lande, G.J., Mahrenholtz, O., Natke, H.G., Nussbaumer, H., Pretlove, A., Rainer, J.H., Saemann, E., and Steinbeisser, L., (1995). Vibration problems in structures. Practical guidelines. Berlin:Birkhauser.
- Balendra, T., Shanmugam, N.E., (1985). Free vibration of plated structures by grillage method. Journal of Sound and Vibration, 99: 333-350.
- Bocchi Jr, C.F., (1995). Lajes nervuradas de concreto armado: projeto e execução. Master of Science Dissertation (in Portuguese), School of São Carlos Engineering, University of São Paulo, Brazil.
- Costa, Y.C.V., Araújo, T.D., (2011). Estudo paramétrico por elementos finitos de lajes nervuradas devido às ações humanas. Proceedings of the XXXII Iberian Latin American Congress on Computational Methods in Engineering (CILAMCE 2011), Ouro Preto, MG, Brazil, 1-20.
- Costa, Y.C.V., (2012). Análise paramétrica de vibrações em laje nervurada devido às ações humanas. Master of Science Dissertation (in Portuguese), Federal University of Ceará, Brazil.
- CSI - Computers and Structures Inc., (2008). Analysis reference manual for SAP2000, ETABS, and SAFE. Computers and Strutures, Berkeley.
- DIN 4150-2 (1999). Erschütterungenimbauwesen; einwirkungen auf menscher in gebäuden (Vibrations in building; influence on persons in buildings). Deutsches Institut für Normung, Berlin.
- Dias, R.H., (2003). Análise numérica de pavimentos de edifícios em lajes nervuradas. Master of Science Dissertation (in Portuguese), School of São Carlos Engineering, University of São Paulo, Brazil.
- Diógenes, B.H.N.O., (2006). Emprego de concreto armado da arquitetura de Fortaleza. Procedures of 48th Brazilian Congresso f Concrete (IBRACON), 1-18.
- Donin, C., (2007). Análise numérica de lajes nervuradas por meio do método dos elementos finitos. Master of Science Dissertation (in Portuguese), Federal University of Santa Maria, Brazil.
- Faisca, R.G., (2003). Caracterização de cargas dinâmicas geradas por atividades humanas. Ph.D. Thesis (in Portuguese) - Federal University of Rio de Janeiro, Brazil.
- Goldman, D.E., Gierke, H.E.V., (1976). The effects of shock and vibration on man. In: Harris, C.M., Crede, C.E. (eds.), Handbook of shock and vibration control, USA, Mcgraw-hill Book Company.
- Hechler, O., Feldmann, M., Heinemeyer, C., Galanti, F., (2008). Design guide for floor vibrations. Eurosteel 2008, Graz, Áustria, 1-6.
- Howard, C.Q., Hansen, C.H., (2003). Vibration analysis of waffles floors. Computers and structures, 81: 15-26.
- ISO 2631-1 (1989). Guide to the evaluation of human exposure to whole-body vibration.
- Junges, P., (2010). Análise de vibrações em uma laje mista de concreto e perfis de PRFV induzidas por atividades humanas. Master of Science of Dissertation (in Portuguese), Federal University of Santa Catarina, Brazil.
- Langer, N.A.S., (2009). Estudo do conforto humano em pisos mistos (aço-concreto) submetidos a ações humanas rítmicas. Master of Science of Dissertation (in Portuguese), University of Rio de Janeiro State, Brazil.
- Mello, A.V.A., Silva, J.G.S., Vellasco, P.C.G.S., Andrade, S. A.L., Lima, L.R.O., (2008). Dynamic analysis of composite systems made of concrete slabs and steel beams. Journal of Constructional Steel Research. 64: 1142 - 1151.
- Middleton, C.J., Brownjohn, J.M.W., (2010). Response of frequency floors: a literature review. Engineering Structures, 32: 337-352.
- Murray, T.M., Allen, D.E., Ungar, E.E., (2003). Floor vibration due to human activity, steel design guide series. Steel Design Guide 11, American Institute of Steel Construction.
- Naeim, F., (1991). Design practice to prevent floor vibration. Technical Information & Product Service, Structural Steel Educational Council.
- Pavic, A., Reynolds, P., Waldron, P., Bennet, K., (2001). Dynamic modeling of post-tensioned concrete floors using finite element analysis. Finite Elements in Analysis and Design, 37: 305-323.
- Rainer, J.H., Pernica, G., (1986). Vertical dynamic forces from footsteps. Canadian Acoustics, 14: 12-21.
- Rainer, J.H., Pernica, G., Allen, D.E., (1988). Dynamic loading and response of footbridges. Canadian Journal of Civil Engineering, 15: 66-71.
- Reynolds, P., Pavic, A., (2003). Effects of false floors on vibration serviceability of building floors. I: modal properties. Journal of Performance of Constructed Facilities, 17: 75-86.
- Sachse, R., Pavic, A., Reynolds, P., (2003). Human-structure dynamic interaction in civil engineering dynamics: a literature review. Shock and Vibration Digest, 35: 3-18.
- Saidi, I., Haritos, N., Gad, E.F., Wilson, J.L., (2007). Floor vibrations due to human excitation - damping perspective. Earthquake Engineering in Australia, Canberra 24-26 November.
- Silva, A.R., (2002). Análise comparativa de custos de sistemas estruturais para pavimentos de concreto armado. Master of Science of Dissertation (in Portuguese), Federal University of Minas Gerais, Brazil.
- Silva, M.A.F., (2005). Projeto e construção de lajes nervuradas de concreto armado. Master of Science of Dissertation (in Portuguese), Federal University of São Carlos, Brazil.
- Smith A.L., Hicks S.J., Devine P.J., (2007) Design of floors for vibration: A new approach (SCI P354). SCI, Ascot, Berkshire.
- Stramandinoli, J.S.B., (2003). Contribuições à análise de lajes nervuradas por analogia de grelha. Master of Science of Dissertation (in Portuguese), Federal University of Santa Catarina, Brazil.
- Xuewei, C., Xiaolei, H., Cheang, J., Weiqiu, H., Ji Jing, J., (2008). The research of time-history response analysis of floor vibration based on simulation of group walking. Proceedings of Fisrt International Conference on Modelling and Simulation. Nanjing, P. R. China, 214-220.
Publication Dates
-
Publication in this collection
13 Mar 2014 -
Date of issue
Dec 2014