Abstract
A solution procedure using the Green's function based finite element method (FEM) is presented for two-dimensional nonlinear steady-state seepage analysis with the presence of free surface in isotropic dams. In the present algorithm, an iteration strategy is designed to convert the over-specified free surface problem to a regular partial differential equation problem. Then, at each iteration step, the Green's function for isotropic linear seepage partial differential equation is employed to construct the element interior water head field, while the conventional shape functions are used for the independent element frame water head field. Then these two independent fields are connected by a double-variable hybrid functional to produce the final solving equation system. By means of the physical definition of Green's function, all two-dimensional element domain integrals in the present algorithm can reduce to one-dimensional element boundary integrals, so that versatile multi-node element is constructed to simplify mesh reconstruction during iteration. Finally, numerical results from the present Green's function based FEM with isotropic Green's function kernels are compared with other numerical results to verify and demonstrate the performance of the present method.
Keywords:
Seepage; free surface; isotropic dam; hybrid finite element method; Green's function
1 INTRODUCTION
During the treatment of water hazard, one of practical measures is to construct dams. So the drawdown seepage analysis is fatal for the security of dam subjected to water level change. One of the main difficulties is that the prediction of the free surface, which is usually over-specified.
Due to the complex boundary conditions and geometrical domain, numerical methods including FEM (Neuman, 1973Neuman, S.P., (1973). Saturated-unsaturated seepage by finite elements. Journal of the hydraulics division 99: 2233-2250.;Bathe and Khoshgoftaar, 1979Bathe, K.J., Khoshgoftaar, M.R., (1979). Finite element free surface seepage analysis without mesh iteration. International Journal for Numerical and Analytical Methods in Geomechanics 3: 13-22.;Bathe, 2006Bathe, K.J., (2006). Finite element procedures, Klaus-Jurgen Bathe.;Luo et al., 2008Luo, Z.J., Zhang, Y.Y., Wu, Y.X., (2008). Finite element numerical simulation of three-dimensional seepage control for deep foundation pit dewatering. Journal of Hydrodynamics, Ser. B 20: 596-602.) and boundary element method (BEM) (Brebbia and Chang, 1979Brebbia, C.A., Chang, O.V., (1979). Boundary elements applied to seepage problems in zoned anisotropic soils. Advances in Engineering Software 1: 95-105.;Chen et al., 1994Chen, J.T., Hong, H.K., Chyuan, S.W., (1994). Boundary element analysis and design in seepage problems using dual integral formulation. Finite Elements in Analysis and Design 17: 1-20.;Tsay et al., 1997Tsay, R.J., Chiou, Y.J., Cheng, T.C., (1997). Boundary element analysis for free surface of seepage in earth dams. Journal of the Chinese Institute of Engineers 20: 95-101.) are often used to analyze seepage problems of the dam with free surface. For example, Bath and Khoshgoftaar developed a FE solution procedure for nonlinear free surface seepage analysis without mesh iteration (Bathe and Khoshgoftaar, 1979Bathe, K.J., Khoshgoftaar, M.R., (1979). Finite element free surface seepage analysis without mesh iteration. International Journal for Numerical and Analytical Methods in Geomechanics 3: 13-22.). Luo et al. applied the FEM to establish three dimensional computational model of transient seepage for deep foundation pit dewatering in the Yangtze River Delta (Luo et al., 2008Luo, Z.J., Zhang, Y.Y., Wu, Y.X., (2008). Finite element numerical simulation of three-dimensional seepage control for deep foundation pit dewatering. Journal of Hydrodynamics, Ser. B 20: 596-602.). Brebbia and Chang established boundary element formulation for seepage problem in anisotropic soils (Brebbia and Chang, 1979Brebbia, C.A., Chang, O.V., (1979). Boundary elements applied to seepage problems in zoned anisotropic soils. Advances in Engineering Software 1: 95-105.). Chen et al. constructed boundary element formulation for seepage problems by introducing a dual integral equation with hypersingular integral (Chen et al., 1994Chen, J.T., Hong, H.K., Chyuan, S.W., (1994). Boundary element analysis and design in seepage problems using dual integral formulation. Finite Elements in Analysis and Design 17: 1-20.). In addition to the FEM and BEM mentioned above, meshless/meshfree methods including the method of fundamental solutions (MFS) (Young et al., 2006Young, D.L., Fan, C.M., Tsai, C.C., Chen, C.W., (2006). The method of fundamental solutions and domain decomposition method for degenerate seepage flownet problems. Journal of the Chinese Institute of Engineers 29: 63-73.;Chaiyo et al., 2011Chaiyo, K., Rattanadecho, P., Chantasiriwan, S., (2011). The method of fundamental solutions for solving free boundary saturated seepage problem. International Communications in Heat and Mass Transfer 38: 249-254.), the natural element method (NEM) (Jie et al., 2013Jie, Y.X., Liu, L.Z., Xu, W.J., Li, G.X., (2013). Application of NEM in seepage analysis with a free surface. Mathematics and Computers in Simulation 89: 23-37.), the hybrid boundary node method (Tan et al., 2010Tan, F., Deng, B., Zhang, D.M., Wang, Y.H., (2010). Solution of seepage problem with free surface by hybrid boundary node method. Rock and Soil Mechanics 31: 75-78.), the smoothed fixed grid finite element method (Kazemzadeh-Parsi and Daneshmand, 2012Kazemzadeh-Parsi, M.J., Daneshmand, F., (2012). Unconfined seepage analysis in earth dams using smoothed fixed grid finite element method. International Journal for Numerical and Analytical Methods in Geomechanics 36: 780-797.) and the scaled boundary finite-element method (Bazyar and Talebi, 2014Bazyar, M.H., Talebi, A., (2014). Transient seepage analysis in zoned anisotropic soils based on the scaled boundary finite-element method. International Journal for Numerical and Analytical Methods in Geomechanics, in press. DOI: 10.1002/nag.2291.
https://doi.org/10.1002/nag.2291...
) were recently developed for the numerical determination of the free surface in seepage problems.
Generally, the iteration procedure is necessary for the free surface problems. However, the mesh reconstruction during iteration increases extremely the difficulty of solution. To bypass this difficulty, development of super element (or multi-node large element) is desired. In this study, another numerical method different to the conventional FEM and BEM (Bathe, 2006Bathe, K.J., (2006). Finite element procedures, Klaus-Jurgen Bathe.;Qin, 1994Qin, Q.H., (1994). Hybrid Trefftz finite-element approach for plate bending on an elastic foundation. Applied Mathematical Modelling 18: 334-339.;1995Qin, Q.H., (1995). Hybrid-Trefftz finite element method for Reissner plates on an elastic foundation. Computer Methods in Applied Mechanics and Engineering 122: 379-392.;2003Qin, Q.H., (2003). Solving anti-plane problems of piezoelectric materials by the Trefftz finite element approach. Computational Mechanics 31: 461-468.;Qin and Mai, 2002Qin, Q.H., Mai Y.W., (2002). BEM for crack-hole problems in thermopiezoelectric materials. Engineering Fracture Mechanics 69: 577-588.), called the fundamental solution-based (or Green's function based) hybrid FEM (HFS-FEM), is formulated for solving such problems in two-dimensional isotropic dams and a multi-node element is developed to model the region close to the free surface for simplifying the mesh redefinition. The HFS-FEM was firstly presented by Wang and Qin for heat transfer analysis (Wang and Qin, 2009Wang, H., Qin, Q.H., (2009). Hybrid FEM with Fundamental Solutions as trial functions for Heat Conduction Simulation. Acta Mechanica Solida Sinica 22: 487-498.) and then was extended to analyze elastic stress field (Wang and Qin, 2010bWang, H., Qin, Q.H., (2010b). Fundamental-solution-based finite element model for plane orthotropic elastic bodies. European Journal of Mechanics-A/Solids 29: 801-809.;Wang and Qin, 2011aWang, H., Qin, Q.H., (2011a). Fundamental-solution-based hybrid FEM for plane elasticity with special elements. Computational Mechanics 48: 515-528.;Wang and Qin, 2012bWang, H., Qin, Q.H., (2012b). A new special element for stress concentration analysis of a plate with elliptical holes. Acta Mechanica 223: 1323-1340.), thermal properties of advanced functional/composite materials (Wang and Qin, 2011bWang, H., Qin, Q.H., (2011b). Special fiber elements for thermal analysis of fiber-reinforced composites. Engineering Computations 28: 1079-1097.;Wang et al., 2012Wang, H., Cao, L.L., Qin, Q.H., (2012). Hybrid graded element model for nonlinear functionally graded materials. Mechanics of Advanced Materials and Structures 19: 590-602.;Wang et al., 2013Wang, H., Han, M.Y., Yuan, F., Xiao, Z.R., (2013). Fundamental-solution-based hybrid element model for nonlinear heat conduction problems with temperature-dependent material properties. Mathematical Problems in Engineering 2013, ID 695457:8 pages.) and bioheat transfer in biological tissues (Wang and Qin, 2010aWang, H., Qin, Q.H., (2010a). FE approach with Green's function as internal trial function for simulating bioheat transfer in the human eye. Archives of Mechanics 62: 493-510.;Wang and Qin, 2012aWang, H., Qin, Q.H., (2012a). A fundamental solution-based finite element model for analyzing multi-layer skin burn injury. Journal of Mechanics in Medicine and Biology 12: 1250027.) with general/special elements to achieve the purpose of high accuracy and mesh reduction. It should be mentioned that convergence of the HFS-FEM was fully discussed in these works. Different to the conventional FEM, the HFS-FEM involves element boundary integrals only, and allows for constructing arbitrary n-sided polygonal elements and accurately calculating fields everywhere in the domain, due to the use of fundamental solutions. Besides, both the HFS-FEM and the BEM are dependent of fundamental solutions, however, the BEM seems more complicated for solving multi-material problems, because it requires separate boundary integral equation for each material domain and additional connective equations for satisfying the continuous conditions between adjacent material domains. In this study, the HFS-FEM was extended for solving two-dimensional nonlinear seepage problems with free surfaces. In the present hybrid FE algorithm, the linear combination of Green's function of isotropic seepage governing equation is employed to construct the element interior water head field by placing source points outside the physical boundary of the domain, as done in the classical MFS (Chen et al., 2008Chen, C.S., Karageorghis, A., Smyrlis, Y.S., (2008). The Method of Fundamental Solutions: A Meshless Method. Dynamic Publishers, Atlanta.), while the conventional shape functions are used for the element frame water head field, which is independent of the element interior field. Then these two fields are connected by a double-variable hybrid functional. Due to physical definition of the Green's function, the element interior field can naturally satisfy the isotropic seepage governing equation and thus, all element domain integrals in the functional are converted into nonsingular element boundary integrals, which have lower dimensions than domain integrals. Most importantly, one can flexibly construct large elements with more nodes and edges than the conventional plane elements for practical use. In the paper, a large multi-node element is designed to model the region nearby the free surface to alleviate difficulty of unavoidable mesh reconstruction during iteration procedures.
The outline of the present work is as follows: Details of the seepage boundary value problem are provided in Section 2, and the present Green's function based FEM is formulated in Section 3. Subsequently, numerical experiments are conducted by the present method in Section 4 and some conclusions are finally presented in Section 5.
2 MATHEMATICAL FORMULATIONS
2.1 Governing equation and boundary conditions
Generally, the governing partial differential equation of two-dimensional incompressible steady-state flow through isotropic dams can be described as:
where Ω is a bounded domain in two-dimensional space R2 refering to the rectangular coordinate (x1, x2). H is the unknown water head in the domain Ω, and k0 > 0 denotes isotropic hydraulic conductivity or permeability coefficient of materials.
According to the Darcy's law, the seepage velocity components qi (i = 1,2) can be written in terms of the hydraulic head H, that is,
Besides, generalized boundary conditions are of the type
where and
and are respectively the known boundary data on the boundary ΓH and Γq. q is the velocity in the direction normal to the boundary, and ni (i = 1,2) are the direction cosines of the normal with respect to the global coordinate system.
are respectively the known boundary data on the boundary ΓH and Γq. q is the velocity in the direction normal to the boundary, and ni (i = 1,2) are the direction cosines of the normal with respect to the global coordinate system.
For the convenience of following derivation, the normal velocity q is rewritten in matrix form as
with
Figure 1shows a two-dimensional seepage problem with free surface in a dam, in which the material is assumed to be isotropic. AE and DG are the boundaries with specified constant water heads H1 and H2, respectively. The bottom surface AD of the dam is assumed to be impermeable, that is q = 0. The curve EF is the free surface and F is the separation point. On the free surface EF, two boundary conditions should be satisfied simultaneously: H = x2 and q = 0, so EF is over-specified. On the seepage surface FG, there is a given water head in terms of the coordinate variable x2, i.e. H = x2. Since the water outflows the dam on this boundary, it should also satisfy the condition of q ≤ 0 on FG. In summary, the boundary sections AE, EF, FG, GD, and AD consist of the complete the boundary of the solution domain. For the sake of clarity, all boundary conditions related to the seepage shown inFigure 1are given as
2.2 Iteration of the free surface
Since the free surface problem is a nonlinear problem, it is inevitable to perform iteration in determining the location of the free surface displayed inFigure 1.
-
1
() Firstly, an initial guess of the location of free surface is assumed to start the computation. For example, a straight line of EF can be initially given by setting the separation point F as the midpoint of the line CG to determine the solution domain AEFDA (seeFigure 2).
-
2
() During iteration, only the condition q = 0 is specified on the free surface EF and the linear water condition H = x2 is given on the seepage surface FG.
-
3
() After each step of iteration, the water head at the nodes on the free surface can be obtained using the proposed numerical method.
-
4
() Examining the error norm defined by

-
where x2i are the nodal vertical coordinates on the free surface and Hi the nodal water heads on the free surface.
-
5
() Updating the nodal vertical coordinates x2i on the free surface by setting

-
6
() The polynomial interpolation of the vertical coordinates of nodal points on the free surface is used to determine the new location of the separation point F.
-
7
() Updating the nodal coordinates and linear water head boundary conditions on the seepage surface.
-
8
() The iteration process can be terminated if the error ε or the difference between εn at the nth iteration and εn+1) at the (n+1)th iteration is equal to or smaller than a given tolerance.
3 HYBRID FINITE ELEMENT FORMULATION
In the present Green's function based FE formulation, two independent element fields are separately defined and then are linked by a hybrid functional, from which the stiffness equation in terms of unknown nodal potential and the relationship of these two independent element fields can be obtained.
3.1 Hydraulic head within the element
In the interior of an element, say element e, the hydraulic head field can be approximated by a linear combination of Green's function as
where Ns is the number of source points locating outside the element domain. Cs (s = 1 → Ns ) present unknown interpolation coefficients and H*(P,Qs ) stands for the isotropic Green's function related to the field point P and the source point Qs , which locates outside the element to avoid the singularity of the Green's function, as done in the MFS (Chen et al. and Karageorghis et al., 2008Chen, C.S., Karageorghis, A., Smyrlis, Y.S., (2008). The Method of Fundamental Solutions: A Meshless Method. Dynamic Publishers, Atlanta.;Chaiyo et al. and Rattanadecho et al., 2011Chaiyo, K., Rattanadecho, P., Chantasiriwan, S., (2011). The method of fundamental solutions for solving free boundary saturated seepage problem. International Communications in Heat and Mass Transfer 38: 249-254.). Compared to the MFS, which employs the boundary discretization of the entire domain, the present method divides the entire domain into several small elements and in each element, the linear combination of Green's function is employed to represent the interior hydraulic head. Thus, the present method has better interpolation stability than the MFS and the location of the source points can be flexibly arranged outside the element domain (Wang and Qin, 2009Wang, H., Qin, Q.H., (2009). Hybrid FEM with Fundamental Solutions as trial functions for Heat Conduction Simulation. Acta Mechanica Solida Sinica 22: 487-498.;Wang and Qin, 2010aWang, H., Qin, Q.H., (2010a). FE approach with Green's function as internal trial function for simulating bioheat transfer in the human eye. Archives of Mechanics 62: 493-510.;Wang et al., 2013Wang, H., Han, M.Y., Yuan, F., Xiao, Z.R., (2013). Fundamental-solution-based hybrid element model for nonlinear heat conduction problems with temperature-dependent material properties. Mathematical Problems in Engineering 2013, ID 695457:8 pages.).
In Eq. (9), the vectors N and ce are respectively
And
Differentiating Eq. (9) yields the following normal seepage flow
where
with
The Green's function for a two-dimensional isotropic seepage problem is defined as
whose solution is
where
is an Euclidian distance between the field point P(x1, x2) and the source point Qs ( ,
, ), and d is the Dirac delta function.
), and d is the Dirac delta function.
Furthermore, the derivatives of the Green's function in terms of coordinate variables can be written as
Obviously, the assumed interior water head field (9) analytically satisfies the governing equation (1), and this feature will be used to simplify the hybrid functional.
3.2 Hydraulic head along the element boundary
In order to enforce conformity on inter-element boundary between two adjacent elements, the frame water field is independently prescribed in terms of element nodal hydraulic head de by
is independently prescribed in terms of element nodal hydraulic head de by
where Ñ is an interpolation shape function vector, in which the interpolation functions are chosen to be the conventional quadratic shape functions commonly used in the isoparametric quadratic line elements in the FEM (Bathe, 2006Bathe, K.J., (2006). Finite element procedures, Klaus-Jurgen Bathe.) and the BEM (Brebbia, 1982Brebbia, C.A., (1982). Boundary element methods in engineering, Springer, New York.).
3.3 Double-variable hybrid functional
For the particular element e, which occupying a sub-domain Ωe with boundary Γe, the hybrid functional in terms of H and is defined as (Qin, 2000Qin, Q.H., (2000). The Trefftz finite and boundary element method, WIT Press, Southampton.)
is defined as (Qin, 2000Qin, Q.H., (2000). The Trefftz finite and boundary element method, WIT Press, Southampton.)
Applying the Gauss theorem, one has
in which only element boundary integrals are involved.
The substitution of the interior field (9) and the frame field (19) into Eq. (21) yields
Subsequently, the minimization of the functional Πe with respect to the unknown vectors ce and de respectively gives
from which the optional relationship between ce and de
and the solving system of equations in terms of the nodal hydraulic head vector de
can be produced.
In Eq. (25), the symmetric and sparse coefficient matrix is written by
4 NUMERICAL EXPERIMENTS
4.1 Verification of the present method
To verify the accuracy of the present approach, let's consider a linear isotropic seepage problem in a rectangular dam by fixing the free surface. The rectangular dam is 24 m in height and 16 m in width. The upstream (left) water head is 24 m, and the downstream (right) water head is 4 m, as shown inFigure 3. The permeability coefficient is k0 = 1m/d. The free surface is assumed to be an inclined straight line connecting the points (0, 24) and (16, 14), which is the initial guess of the free surface in the next example.
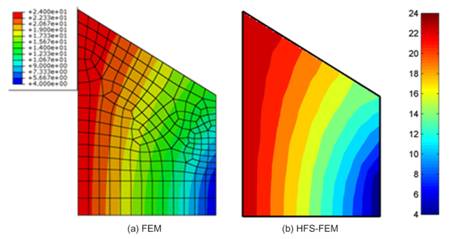
In the computation, the FE mesh shown inFigure 3is used to model the rectangular dam. In the meshing scheme, three 8-node general elements is used to model the bottom region of the dam and one 22-node super element is employed in the region close to the free boundary to provide more efficient remeshing process than the conventional FEM during iteration by updating only the locations of nodes on the free surface and the seepage surface. Besides, the use of large element is also beneficial to decrease the computation time, in contrast to the conventional FEM.
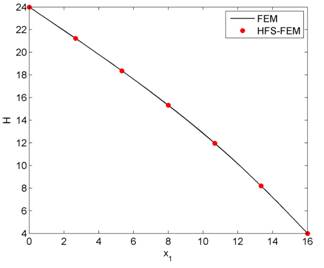
To demonstrate modeling efficiency and solution accuracy of the present method, numerical results from the conventional FEM implemented by ABAQUS are also provided.Figures 4and5respectively show the variation of the water head on the impermeable bottom surface and the straight-line free surface. It is observed that there is a good agreement between the present HFS-FEM and the FEM although much less elements are used in the proposed element model. It can be also seen fromFigure 5that there is an sudden jump of the water head at those points close to the seepage surface, due to the restriction of natural boundary condition at the separation point, so that curve fitting technology should be used to obtain a smooth free surface and to update the location of the separation point. Finally, the contour plots from the conventional FEM and the present method for the water head are presented inFigure 6, and similar distribution can be found for both methods. Therefore, the present method is efficient and accurate to simulate the distribution of the water head in the domain.
4.2 Isotropic seepage in a rectangular dam with size 24 m x 24 m
In this example, the rectangular dam in the first test is considered again to determine the final location of the free surface by mean of iteration approach. In order to start the iteration, the inclined straight line given inFigure 3is selected as an initial guess. The error tolerance in the iteration process is taken as 0.01.
The iteration results are shown inFigure 7. After 12 iterations, the iteration converges.Figure 8shows the converged configuration of the free surface from the present method. Also, the results from the BEM (Chen et al., 2007Chen, J.T., Hsiao, C.C., Chiu, Y.P., Lee, Y.T., (2007). Study of free-surface seepage problems using hypersingular equations. Communications in numerical methods in engineering 23: 755-769.) and the MFS (Chaiyo et al., 2011Chaiyo, K., Rattanadecho, P., Chantasiriwan, S., (2011). The method of fundamental solutions for solving free boundary saturated seepage problem. International Communications in Heat and Mass Transfer 38: 249-254.) are provided inFigure 8for comparison. We can see that there is no significant difference on the computation results between the present method and other methods. The small deviation at the separation point is mainly caused by different curve fitting techniques. In the developed algorithm, the cubic polynomial interpolation is employed. For the sake of clarity, the height of the separation point respectively predicted by the present HFS-FEM, the BEM, the MFS, and the FDM (Aitchison, 1972Aitchison, J., (1972). Numerical treatment of a singularity in a free boundary problem. Proceedings of the Royal Society of London. Series A 330: 573-580.) are listed inTable 1, and it's found that they agree very well. Finally, the converged shape of the dam and the corresponding contour plot for the water head are listed inFigure 9.
4.3 Isotropic seepage in a rectangular dam with size 6 m x 4 m
As another example in the literature (Jie et al., 2013Jie, Y.X., Liu, L.Z., Xu, W.J., Li, G.X., (2013). Application of NEM in seepage analysis with a free surface. Mathematics and Computers in Simulation 89: 23-37.), a rectangular dam with 4 m in width and 6 m in height is considered and its geometrical size is shown inFigure 10. The water levels upstream (left) and downstream (right) are 6 m and 1 m, respectively. The permeability coefficient is k0 = 0.1m/d. The error tolerance in the iteration process is taken as 0.01.
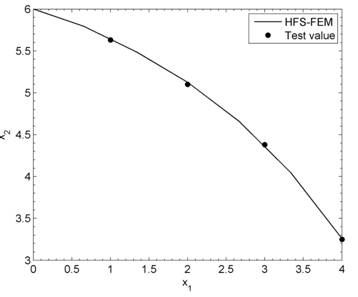
The example is analyzed by using the present HFS-FEM.Figure 11displays the initial computational mesh, in which three general 8-node hybrid elements and one 22-node hybrid element are employed to model the domain. After 11 iterations, the mesh of the computing domain is updated to a convergent configuration, which is displayed inFigure 11too.Figure 12plots the final location of the free surface predicted from the present method and the test (Jie et al., 2013Jie, Y.X., Liu, L.Z., Xu, W.J., Li, G.X., (2013). Application of NEM in seepage analysis with a free surface. Mathematics and Computers in Simulation 89: 23-37.), and it can be found that a good agreement is achieved between them. This dam has also been analyzed by Jie et.al. using the natural element method (NEM) (Jie et al., 2013Jie, Y.X., Liu, L.Z., Xu, W.J., Li, G.X., (2013). Application of NEM in seepage analysis with a free surface. Mathematics and Computers in Simulation 89: 23-37.). For the purpose of comparison, the heights of the separation point from different methods are tabulated inTable 2, from which it can be seen that the present method has smaller derivation to the test value.
5 CONCLUSIONS
As a kind of domain-type numerical methods, the present hybrid FEM with Green's function kernels needs only element boundary integrations and versatile element construction can be fulfilled in the HFS-FEM for your practical needs. Thus, the present HFS-FEM is more suitable for dealing with problems with moving boundaries than the conventional FEM. In this study, the HFS-FEM is formulated for the determination of the free surface and the height of the separation point in isotropic dams, and a large multi-node element is employed to model the region close to the free surface for the purpose of simplifying mesh reconstruction during iteration process, so that only nodes on the free surface and the seepage surface are updated during iterations. The numerical results demonstrate that the developed Green's function-based hybrid FEM is capable to calculate free surface with good accuracy and efficiency.
Acknowledgements
The support from the Natural Science Foundation of China (Grant no. 11102059; 11472099) and the Creative Talents Program of Universities in Henan Province (Grant no. 13HASTIT019) are fully acknowledged.
References
- Aitchison, J., (1972). Numerical treatment of a singularity in a free boundary problem. Proceedings of the Royal Society of London. Series A 330: 573-580.
- Bathe, K.J., (2006). Finite element procedures, Klaus-Jurgen Bathe.
- Bathe, K.J., Khoshgoftaar, M.R., (1979). Finite element free surface seepage analysis without mesh iteration. International Journal for Numerical and Analytical Methods in Geomechanics 3: 13-22.
- Bazyar, M.H., Talebi, A., (2014). Transient seepage analysis in zoned anisotropic soils based on the scaled boundary finite-element method. International Journal for Numerical and Analytical Methods in Geomechanics, in press. DOI: 10.1002/nag.2291.
» https://doi.org/10.1002/nag.2291 - Brebbia, C.A., (1982). Boundary element methods in engineering, Springer, New York.
- Brebbia, C.A., Chang, O.V., (1979). Boundary elements applied to seepage problems in zoned anisotropic soils. Advances in Engineering Software 1: 95-105.
- Chaiyo, K., Rattanadecho, P., Chantasiriwan, S., (2011). The method of fundamental solutions for solving free boundary saturated seepage problem. International Communications in Heat and Mass Transfer 38: 249-254.
- Chen, C.S., Karageorghis, A., Smyrlis, Y.S., (2008). The Method of Fundamental Solutions: A Meshless Method. Dynamic Publishers, Atlanta.
- Chen, J.T., Hong, H.K., Chyuan, S.W., (1994). Boundary element analysis and design in seepage problems using dual integral formulation. Finite Elements in Analysis and Design 17: 1-20.
- Chen, J.T., Hsiao, C.C., Chiu, Y.P., Lee, Y.T., (2007). Study of free-surface seepage problems using hypersingular equations. Communications in numerical methods in engineering 23: 755-769.
- Jie, Y.X., Liu, L.Z., Xu, W.J., Li, G.X., (2013). Application of NEM in seepage analysis with a free surface. Mathematics and Computers in Simulation 89: 23-37.
- Kazemzadeh-Parsi, M.J., Daneshmand, F., (2012). Unconfined seepage analysis in earth dams using smoothed fixed grid finite element method. International Journal for Numerical and Analytical Methods in Geomechanics 36: 780-797.
- Luo, Z.J., Zhang, Y.Y., Wu, Y.X., (2008). Finite element numerical simulation of three-dimensional seepage control for deep foundation pit dewatering. Journal of Hydrodynamics, Ser. B 20: 596-602.
- Neuman, S.P., (1973). Saturated-unsaturated seepage by finite elements. Journal of the hydraulics division 99: 2233-2250.
- Qin, Q.H., (1994). Hybrid Trefftz finite-element approach for plate bending on an elastic foundation. Applied Mathematical Modelling 18: 334-339.
- Qin, Q.H., (1995). Hybrid-Trefftz finite element method for Reissner plates on an elastic foundation. Computer Methods in Applied Mechanics and Engineering 122: 379-392.
- Qin, Q.H., (2000). The Trefftz finite and boundary element method, WIT Press, Southampton.
- Qin, Q.H., (2003). Solving anti-plane problems of piezoelectric materials by the Trefftz finite element approach. Computational Mechanics 31: 461-468.
- Qin, Q.H., Mai Y.W., (2002). BEM for crack-hole problems in thermopiezoelectric materials. Engineering Fracture Mechanics 69: 577-588.
- Tan, F., Deng, B., Zhang, D.M., Wang, Y.H., (2010). Solution of seepage problem with free surface by hybrid boundary node method. Rock and Soil Mechanics 31: 75-78.
- Tsay, R.J., Chiou, Y.J., Cheng, T.C., (1997). Boundary element analysis for free surface of seepage in earth dams. Journal of the Chinese Institute of Engineers 20: 95-101.
- Wang, H., Cao, L.L., Qin, Q.H., (2012). Hybrid graded element model for nonlinear functionally graded materials. Mechanics of Advanced Materials and Structures 19: 590-602.
- Wang, H., Han, M.Y., Yuan, F., Xiao, Z.R., (2013). Fundamental-solution-based hybrid element model for nonlinear heat conduction problems with temperature-dependent material properties. Mathematical Problems in Engineering 2013, ID 695457:8 pages.
- Wang, H., Qin, Q.H., (2009). Hybrid FEM with Fundamental Solutions as trial functions for Heat Conduction Simulation. Acta Mechanica Solida Sinica 22: 487-498.
- Wang, H., Qin, Q.H., (2010a). FE approach with Green's function as internal trial function for simulating bioheat transfer in the human eye. Archives of Mechanics 62: 493-510.
- Wang, H., Qin, Q.H., (2010b). Fundamental-solution-based finite element model for plane orthotropic elastic bodies. European Journal of Mechanics-A/Solids 29: 801-809.
- Wang, H., Qin, Q.H., (2011a). Fundamental-solution-based hybrid FEM for plane elasticity with special elements. Computational Mechanics 48: 515-528.
- Wang, H., Qin, Q.H., (2011b). Special fiber elements for thermal analysis of fiber-reinforced composites. Engineering Computations 28: 1079-1097.
- Wang, H., Qin, Q.H., (2012a). A fundamental solution-based finite element model for analyzing multi-layer skin burn injury. Journal of Mechanics in Medicine and Biology 12: 1250027.
- Wang, H., Qin, Q.H., (2012b). A new special element for stress concentration analysis of a plate with elliptical holes. Acta Mechanica 223: 1323-1340.
- Young, D.L., Fan, C.M., Tsai, C.C., Chen, C.W., (2006). The method of fundamental solutions and domain decomposition method for degenerate seepage flownet problems. Journal of the Chinese Institute of Engineers 29: 63-73.
Publication Dates
-
Publication in this collection
Oct 2015
History
-
Received
24 Nov 2014 -
Reviewed
23 Apr 2015 -
Accepted
08 May 2015

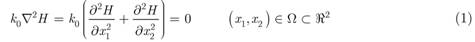








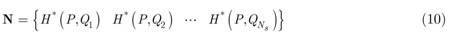






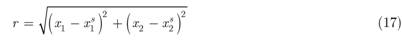




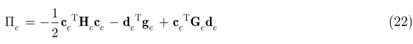















 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail