Abstract
Here In this study, the composite laminates subjected to transverse impact with consideration interlaminar and intralaminar damage based on Cohesive Zone Model (CZM) and Progressive Damage Model (PDM) are investigated by numerical analysis using ABAQUS commercial finite element code. The delamination in stacking ply with the same fiber orientation is considered as interlaminar damage and the delamination in an inner layer of any cluster is ignored. Hashin criterion is used for intralaminar damage initiation and evolution without using any subroutine. First, the appropriate procedure for delamination on composite specimen was suggested based on CZM approach in double cantilever beam to verify the intralaminar damage simulation. Then by considering several case studies with different impact energies, the results of present simulation is verified with the relevant and available experimental results and numerical references in the existing literature. According to the available experimental results the present simulation results are more acceptable and accurate than the results of similar numerical works, especially in higher impactor velocity.
Keywords
Polymer-matrix composites (PMCs); Finite element analysis (FEA); Damage evolution; Impact behaviour
1 INTRODUCTION
Composite structures are widely used in many industrial applications like aerospace and defence industry due to their inherently high specific mechanical properties. In many situations, these composite structures are subjected by high and low velocity impact. Composite structures are very sensitive to non-visual damage that strongly influence their residual load bearing capability. Lack of knowledge of the impact effects on composite structures is a factor in limiting the use of composite materials ( Abrate, 1998 Abrate, S. (1998). Impact on composite structure, Cambridge University Press, New York, USA. ). To understand the responses of composite structures under high velocity projectile impacts, various experimental and numerical studies have been conducted. Cantwell and Morton (1989) Cantwell, W. J., and Morton, J. (1989). Comparison of the low and high velocity impact response of CFRP. Composites, 20: 545-551. examined the initiation and development of damage in composite structures with a series of low and high velocity impact tests. Guoqi et al., (1992) Guoqi, Z., Goldsmith, W., and Dharan, C. H. (1992). Penetration of laminated Kevlar by projectiles—I. Experimental investigation. International Journal of Solids and Structures, 29(4), 399-420. investigated experimentally the response of woven Kevlar/polyester laminates of varying thicknesses to quasi-static and dynamic penetration by projectiles. Cheng et al., (2003) Cheng, W. L., Langlie, S., and Itoh, S. (2003). High velocity impact of thick composites. International journal of impact engineering, 29: 167-184. developed a model based on hydrodynamic finite element code for high velocity impact on thick composites. This model was based on a continuum approach which was built on the basis of an orthotropic constitutive behaviour with stress-based failure criteria and a simplified degradation model of the failure of composites. Silva et al., (2005) Silva, M. A., Cismaşiu, C., and Chiorean, C. G. (2005). Numerical simulation of ballistic impact on composite laminates. International Journal of Impact Engineering, 31: 289-306. investigated experimental and numerical simulation of ballistic impact on Composite structures made of Kevlar-29. Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari presented a numerical simulation of delamination in composite materials under static and fatigue loading by cohesive zone models. Zhao et al., (2010) Zhao, G., Cho, C., Lu, S., et al., (2010). Experimental study on impact resistance properties of T300/epoxy composite laminates. Journal of composite materials, 44: 857-870. experimentally reported the failure modes of T300/epoxy composite laminates at different impactor velocities of 10-300 m/s on the different stacking sequence. Khalili et al., (2011) Khalili, S. M. R., Soroush, M., Davar, A., et al., (2011). Finite element modeling of low-velocity impact on laminated composite plates and cylindrical shells. Composite Structures, 93: 1363-1375. proposed a verified finite element model using ABAQUS finite element for composite laminates and shell structures subjected to low-velocity impact. Gonzalez (2011) Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari investigated the damage induced in composite plates under drop-weight impact loading by analytical description and experimental test plan for assessment of the virtual test performance by finite element simulation. Ramadhan et al., (2013) Ramadhan, A. A., Talib, A. A., Rafie, A. M., et al., (2013). High velocity impact response of Kevlar-29/epoxy and 6061-T6 aluminum laminated panels. Materials & Design, 43: 307-321. investigated the high velocity impact response of composite laminated plates, both experimentally and numerically.
Simulation of damage induced in composite laminates has been performed with macro, meso and micro-scale of modelling. Investigating the overall response of the composite laminate with treating the composite as fully homogenized is called marco-scale analysis. In the meso-scale approach the composite treated as effective anisotropic materials while involving the analysis of the composite to the scale of the constituents is called micro-scale approach. Although the finite element method could be used to simulate the composite laminate damage induced in all the mentioned scale modelling, extremely computational efficient method in macro-scale approach. The complex damage mechanisms of composite laminates, could be divided in intralaminar and interlaminar damage. The intralaminar damage mechanisms correspond to fiber fracture and matrix cracking, while the other correspond to the delamination of the plies.
Progressive Damage Model (PDM) was first used by Chou et al., (1977) Chou, S. C., Orringer, O., and Rainey, J. H. (1977). Post-Failure Behavior of Laminates: II—Stress Concentration. Journal of Composite Materials, 11: 71-78. to analyse post-failure of composite materials. Continuum Damage Mechanics (CDM) has been employed by many researchers for progressive damage analyses of composite laminates. In macro-scale analysis of composite laminate, the CDM has been used and proposed by many researchers such as Maimí et al., (2007) Maimí, P., Camanho, P. P., Mayugo, J. A., et al., (2007). A continuum damage model for composite laminates: Part I–Constitutive model. Mechanics of Materials, 39: 897-908. , Camanho et al., (2007) Camanho, P. P., Maimí, P., and Dávila, C. G. (2007). Prediction of size effects in notched laminates using continuum damage mechanics. Composites science and technology, 67: 2715-2727. , Zou et al., (2002) Zou, Z., Reid, S. R., Li, S., and Soden, P. D. (2002). Modelling interlaminar and intralaminar damage in filament-wound pipes under quasi-static indentation. Journal of composite materials, 36: 477-499. for the prediction of the onset and evolution of the intralaminar damage. The continuum damage model is the most accurate technique to predict size effects in composites and is applicable to general geometries and boundary conditions. In addition, it doesn't require any calibration ( Camanho et al., 2007 Camanho, P. P., Maimí, P., and Dávila, C. G. (2007). Prediction of size effects in notched laminates using continuum damage mechanics. Composites science and technology, 67: 2715-2727. ). Also a progressive damage method -which builds nonlinear mechanics models for composite materials and has capacity of accurately simulating the structural failure process from initial damage to ultimate failure- attracts wide spread attention in composite structure analyses ( Tan, 1991 Tan, S. C. (1991). A progressive failure model for composite laminates containing openings. Journal of Composite Materials, 25: 556-577. ; Shokrieh, 1996 Shokrieh, M. M., (1996). Progressive fatigue damage modeling of composite materials. Ph.D. Thesis, McGill University, Montreal ; Camanho and Matthews, 1999 Camanho, P. P., and Matthews, F. L. (1999). A progressive damage model for mechanically fastened joints in composite laminates. Journal of Composite Materials, 33: 2248-2280. ). In order to use PDM additional material testing is required to adjust the empirical evolutions laws. Moreover, PDM is suitable for structural analysis and its parameters could be determined by experiment test ( Shokrieh, 1996 Shokrieh, M. M., (1996). Progressive fatigue damage modeling of composite materials. Ph.D. Thesis, McGill University, Montreal ).
Delamination or interfacial cracking between composite layers, is one of the most common types of damage in composite laminates due to their relatively weak interlaminar strengths. The FE simulation of delamination is normally performed by means of the Virtual Crack Closure Technique (VCCT), or cohesive finite elements ( Turon et al., 2007 Turon, A., Davila, C. G., Camanho, P. P., et al., (2007). An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Engineering fracture mechanics, 74: 1665-1682. ). The formulation of the cohesive finite elements is based on the Cohesive Zone Model (CZM) approach and was originally introduced by Barenblatt and Dugdale ( Barenblatt, 1962 Barenblatt, G. I. (1962). The mathematical theory of equilibrium cracks in brittle fracture. Advances in applied mechanics, 7: 55-129. ; Dugdale, 1960 Dugdale, D. S. (1960). Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids, 8: 100-104. ). CZM in the computational framework of FEM was first implemented by Hillerborg et al., (1976) Hillerborg, A., Modéer, M., and Petersson, P. E. (1976). Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and concrete research, 6: 773-781. . The CZM approach is one of the most commonly used tools to investigate interfacial fracture. It is based on the Griffith's theory of fracture and assumed a cohesive damage zone developed near the crack tip and described the crack propagation in perfectly brittle materials ( Turon et al., 2007 Turon, A., Davila, C. G., Camanho, P. P., et al., (2007). An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Engineering fracture mechanics, 74: 1665-1682. ; Barenblatt, 1962 Barenblatt, G. I. (1962). The mathematical theory of equilibrium cracks in brittle fracture. Advances in applied mechanics, 7: 55-129. ). The CZM approach was developed in a continuum damage mechanics framework and resulted in improving its applicability by using fracture mechanics concepts. The cohesive zone model combines a strength-based failure criterion to predict the damage initiation, and a fracture mechanics-based criterion to determine the damage propagation ( Khoramishad et al., 2010 Khoramishad, H., Crocombe, A. D., Katnam, K. B., et al., (2010). Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. International Journal of fatigue, 32: 1146-1158. ).
The earlier work ( Khalili et al., 2011 Khalili, S. M. R., Soroush, M., Davar, A., et al., (2011). Finite element modeling of low-velocity impact on laminated composite plates and cylindrical shells. Composite Structures, 93: 1363-1375. ) proposed a verified and low-cost finite element model using ABAQUS for composite laminates and shell structures subjected to low-velocity impact without damage consideration. The element type, solution method, impactor modelling method, meshing pattern and contact modelling are investigated and verified with several case studies with various conditions. It is significant to understand the dynamic behaviour of composite laminates and the induced damage mechanisms in order to use the composite effectively.
According to the abovementioned work ( Khalili et al., 2011 Khalili, S. M. R., Soroush, M., Davar, A., et al., (2011). Finite element modeling of low-velocity impact on laminated composite plates and cylindrical shells. Composite Structures, 93: 1363-1375. ), the purpose of this study is to introduce a reliable, low-cost and simple method based on ABAQUS commercial finite element code and by considering damage in composite laminates under transverse impact loadings. In fact the main objective is to provide a general solution for the modelling of dynamic simulation of the impact on composite plate based on PDM and CZM techniques that are available in ABAQUS without using any subroutine. In order to achieve the mentioned goals, the valid experimental and numerical examples are selected for validating the proposed FEM approach. First, a valid reference is chosen to verify the CZM technique. Then, several case studies of the impact loading on the composite laminates by considering intralaminar and interlaminar damage are chosen to verify the proposed finite element simulation procedure.
2 SIMULATION OF DELAMINATION ON DCB COMPOSITE SPECIMEN BASED ON CZM
In this section, the valid experimental and numerical reference are used to verify the proposed simulation approach. The results of the present simulation are compared with the experimental and numerical results reported by Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari . Consequently, the appropriate procedure was suggested for delamination on composite specimen based on CZM approach. An unidirectional 24-ply Graphite/Epoxy composite laminates are considered with the dimensions of 140×20 mm, total thickness of 3.24 mm, laminate configuration [011/-5/5/011] and initial crack length. The DCB (Double Cantilever Beam) test is one of the most common tests used to evaluate the mode I interlaminar fracture toughness in a composite laminate. In fact, the test considers a composite beam with a cohesive layer of thickness t = 0.02 mm and an initial delamination crack of 50 mm length. As shown in the Figure 1 the initial delamination is forced to open by applying a displacement that pull the two beams of the specimen away from each other. The material properties given for composite plies of DCB specimen and cohesive interface are indicated in Table 1 and 2 ( Cerioni, 2009 Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari ).
2.1 Material failure modelling
As indicated in Figure 2 , the cohesive zone model, as shown combines an initially linear elastic behaviour with strength-based failure criterion to predict the damage initiation and a fracture mechanics-based criterion to determine the damage evolution. The elastic behaviour is written in terms of an elastic constitutive matrix that connect cohesive surface tractions (t) to displacement (δ) at the interface. The initial stiffness of CZM ( Figure 2 , E0) defined as traction divided by separation, (units N/m3) should be chosen as high as possible to provide a reasonable stiffness. But from a numerical perspective, it cannot be infinitely large; otherwise, it leads to numerical ill-conditioning ( Turon et al., 2007 Turon, A., Davila, C. G., Camanho, P. P., et al., (2007). An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Engineering fracture mechanics, 74: 1665-1682. ; Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. )
Many researchers have suggested various guidelines for selecting the stiffness of the interface. For instance, Camanho and Matthews (1999) Camanho, P. P., and Matthews, F. L. (1999). A progressive damage model for mechanically fastened joints in composite laminates. Journal of Composite Materials, 33: 2248-2280. obtained predictions for graphite/epoxy specimens by using a value of 106 N/mm 3. Zou et al., (2002) Zou, Z., Reid, S. R., Li, S., and Soden, P. D. (2002). Modelling interlaminar and intralaminar damage in filament-wound pipes under quasi-static indentation. Journal of composite materials, 36: 477-499. proposed a value for the interface stiffness between 104 and 107 times of the interfacial strength value per unit length. Turon et al., (2007) Turon, A., Davila, C. G., Camanho, P. P., et al., (2007). An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Engineering fracture mechanics, 74: 1665-1682. proposed equation (1) in order to estimate the stiffness of the interface and declared that the equation is more appropriate than the other works. In this equation, E3 is the elastic modulus through-the-thickness of the composite materials t is the laminate thickness adjoining to the cohesive interface, and α is an increasing parameter normally taken about 50.
As Shown in Figure 2 , the point t0 refers to the beginning of materials response degradation. The t0 represents the peak values of the traction that correspond to the δ 0 when the deformation is purely normal to the interface. The process of degradation begins when the traction or separation satisfies certain damage initiation criteria. Several damage initiation criteria such as maximum nominal stress (MAXE Damage) and quadratic nominal stress (QUADS Damage) are available in the ABAQUS ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ). Each damage initiation criterion also has an output variable associated with it in order to indicate whether the criterion is met. Perillo et al., (2012) Perillo, G., Vedvik, N. P., and Echtermeyer, A. T. (2012). Numerical analyses of low velocity impacts on composite. Advanced modelling techniques. In Proceedings of the Simulia customer conference. have reached a better agreement between experimental results and the finite element results by using the QUADS initiation criterion.
The Quadratic nominal stress criterion is assumed to initiate when a quadratic interaction function reaches a value of one. This criterion can be represented as equation (2) . In three-dimensional problems, the index n refers to normal traction and the index s and t refer to two shear traction. The Macaulay bracket (‹ ›) are used to signify that a pure compressive deformation or stress state does not initiate damage. Under single-mode loading, interface damage initiates when the traction reaches the maximum nominal interfacial strength (t0) ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ).
According to the strength-based failure criterion, the damage evolution would be initiated once the damage initiation condition has been met. Several constitutive models that have been proposed by the researchers for the damage evolution schemes, linear softening behaviour is usually implemented ( Camanho et al., 2003 Camanho, P. P., Davila, C. G., and De Moura, M. F. (2003). Numerical simulation of mixed-mode progressive delamination in composite materials. Journal of composite materials, 37: 1415-1438. ). The damage evolution law describes the rate at which the material stiffness is degraded once the corresponding initiation criterion is reached. A scalar damage variable, D, represents the overall damage in the material. It initially has a value of 0 and then monotonically evolves from 0 to 1 upon further loading. The stress components of the traction-separation model are affected by the damage. According to equation (3) , is the stress components predicted by the elastic traction-separation behaviour for the current strains without damage ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ). As shown in Figure 2 , a value of 1 of the SDEG (Overall value of the scalar damage variable D), indicates that the initiation criterion has been met at the end of the damage evolution area which corresponds to the δm. Camanho et al., (2003) Camanho, P. P., Davila, C. G., and De Moura, M. F. (2003). Numerical simulation of mixed-mode progressive delamination in composite materials. Journal of composite materials, 37: 1415-1438. proposed equation (4) in order to define the effective displacement (δm) to describe the evolution of damage under a combination of normal and shear deformation across the interface.
Damage evolution can be defined based on the energy that is dissipated as a result of the damage process. The area under the traction-separation relation (the area that shaded in Figure 2 ) is equal to the fracture toughness energy, Gc. Although the scalar damage variable (D) is derived from this parameter, the fracture energy (Gc ) is the most important parameter which can be determined by means of some standard experimental tests.
2.2 Solution method
The simulation of delamination based on CZM approach, is possible to be solved by an explicit or implicit algorithm available in ABAQUS. The ABAQUS/Standard general-purpose solver uses a traditional implicit integration scheme to solve finite element analyses. On the other hand, the ABAQUS/Explicit which uses an explicit central-difference time integration rule applies an explicit integration scheme to solve highly nonlinear transient dynamic and quasi-static analyses. The simulation of delamination based on CZM approach is involves softening in the material response, and lead to convergence difficulties in an implicit solution procedure in ABAQUS/Standard. Convergence difficulties may also occur during unstable crack propagation when the available energy is higher than the fracture toughness of the material ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ).
Khoramishad et al. (2010) Khoramishad, H., Crocombe, A. D., Katnam, K. B., et al., (2010). Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. International Journal of fatigue, 32: 1146-1158. uses standard solver of ABAQUS to simulate the single lap joints according to the CZM approach. Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari offers explicit solver in order to obtain the finite element solution for avoiding convergence problems and numerical instabilities. In the earlier work ( Khalili et al., 2011 Khalili, S. M. R., Soroush, M., Davar, A., et al., (2011). Finite element modeling of low-velocity impact on laminated composite plates and cylindrical shells. Composite Structures, 93: 1363-1375. ), it was found that in an explicit scheme, the analysis cost rises only linearly with problem size, whereas the cost of solving the nonlinear equations associated with implicit integration rises more rapidly than linearly with problem size. Therefore, ABAQUS/Explicit is attractive for very large problems.
2.3 Type of elements
Based on plane strain assumption, the simulation of delamination on DCB composite could be analysis with two-dimensional elements. Mi et al., (1998) Mi, Y., Crisfield, M. A., Davies, G. A. O., and Hellweg, H. B. (1998). Progressive delamination using interface elements. Journal of composite materials, 32: 1246-1272. applied a three-dimensional analysed and indicated that the 2D plane strain formulation gave a very reasonable approximation versus three-dimensional analysis. While Alfano and Crisfield (2001) Alfano, G., and Crisfield, M. (2001). Finite element interface models for the delamination analysis of laminated composites: mechanical and computational issues. International journal for numerical methods in engineering, 50: 1701-1736. strictly declared that a 3D analysis would be needed since the delamination front was not precisely a straight line.
Conventional shell, continuum shell and solid elements are available options in ABAQUS for modelling the composite structures. While cohesive behaviour is used in conjunction with stacked conventional shell elements, the specialized contact formulation may lead to approximate normal contact forces. This may induce approximate transverse shear behaviour in the stacked shells which affect the bending behaviour of the stack. Continuum shells should be used instead of conventional shells in such modelling scenarios ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ).
2.4 Cohesive surfaces versus cohesive elements
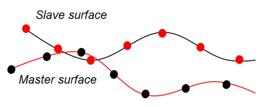
Similar to cohesive surfaces, cohesive elements could be used in CZM approach simulation in ABAQUS. The formulation used for surface-based cohesive, is very similar to that of cohesive elements with traction-separation response. For cohesive surfaces, the cohesive constraint is enforced at each slave node while in cohesive elements, the cohesive constraints are calculated at the material points. Hence for cohesive surfaces, refining the slave surface as compared to the master surface will likely lead to improved constraint satisfaction and more accurate results ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ).
Some researchers like Turon et al., (2007) Turon, A., Davila, C. G., Camanho, P. P., et al., (2007). An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Engineering fracture mechanics, 74: 1665-1682. used cohesive elements in CZM approach, but others like Gonzalez (2011) Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari , used both of cohesive elements and cohesive surfaces in CZM approach and concluded that the use of cohesive surfaces resulted in improving the runtime of the analysis. On the other hand, it can yield to large runtime analysis because contact algorithms are computationally heavy especially when the connected mesh are highly refined.
2.5 Verification and discussion on simulation method
This section briefly describes the finite element (FE) simulation of the delamination on DCB composite specimen based on CZM approach. In this study, the FE simulation, has been done with the finite element package ABAQUS version 2016 and is performed on a computer with 3.2 GHz Intel® Corei7, with 8.00 GB RAM.
According to Table 1 , the material modelling of composite ply in the present FE simulation has been done by linear elastic with engineering constant option that is available in ABAQUS. The CZM approach is used to simulate the interface failure modelling of cohesive layer between two beams of the specimen. According to Table 2 , the magnitude of the initial stiffness of the cohesive element ( Figure 2 , E0) has been imported to the ABAQUS and it does not need to be divided by the cohesive thickness. For defining the quadratic nominal stress (QUADS Damage) criterion, the S and T which are taken from Table 2 are considered as the maximum nominal interfacial strength (t0) in the two directions (normal and shear). Also according to Table 2 , the fracture energies GIC, and GIIC are imported to ABAQUS to define the modes I and II for simulation of the interlaminar fracture toughness in cohesive interface.
The 4 nodes, two-dimensional continuum plane strain elements (CPE4R) and the 4 nodes, two-dimensional cohesive elements (COH2D4) are used in the FE simulation of the composite specimens and the cohesive interface. A very refined mesh using an element length of 0.25 mm was used for both solid and cohesive elements and is constant for all the models (6720 elements of type CPE4R and 360 elements of type COH2D4). This element length is recommended by Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari and as shown in Figure 3 , only one cohesive element in the cohesive interface was put.
Here, a double cantilever beam has been simulated under displacement control. As shown in Figure 4 , the movement of the opening edge in the vertical direction of the composite specimens is applied by the displacement control and is restrained in horizontal direction. Also, the last node of the bottom of the lower composite specimen has been restrained in vertical direction.
In this case study, the present simulation results gained by standard solver of ABAQUS are compared with the available experimental and numerical results by the Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari . As shown in Figure 5 , there is a good correspondence between the elastic branches of the three curves. Also, the prediction of the onset of the delamination looks adequate. But some mismatch was observed between the present simulation and the results of reference ( Cerioni, 2009 Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari ) in onset of the delamination. Furthermore, there is a difference in the propagation branch of the simulation model stiffness which has been decreased more quickly in respect of the experimental results. In addition, better correspondence was observed with experimental results in the present simulation versus simulation of Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari .
Comparison of contact force variation as a function of displacement for delamination on DCB composite specimen between the present FE simulation and the results of Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari
In Figure 6 , the present simulation results gained by the explicit solver of ABAQUS are compared with the available experimental and numerical results by the Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari . As indicated in Figure 6 , the mismatch in onset of delamination gained by standard solver of ABAQUS ( Figure 5 ) is eliminated. Also better results correspondence was observed in explicit solver than standard solver.
Comparison of contact force variation as a function of displacement for delamination on DCB composite specimen between the present FE simulation with explicit solver and the results of Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari
As mentioned earlier in section 2.3, a 3D analysis would be needed since the delamination front is not precisely a straight line ( Alfano and Crisfield, 2001 Alfano, G., and Crisfield, M. (2001). Finite element interface models for the delamination analysis of laminated composites: mechanical and computational issues. International journal for numerical methods in engineering, 50: 1701-1736. ). In this study the composite specimen uses the SC8R element for investigation the effect of 3D modelling in delamination. According to the earlier work ( Khalili et al., 2011 Khalili, S. M. R., Soroush, M., Davar, A., et al., (2011). Finite element modeling of low-velocity impact on laminated composite plates and cylindrical shells. Composite Structures, 93: 1363-1375. ), SC8R elements should be used in thick plates and shells. The SC8R or S4R elements are an eight-node continuum shell and four-node conventional shell elements with reduced integration, respectively.
In case of modelling, cohesive behaviour is possible to be used in conjunction with stacked conventional shell elements. Depending on the load case, the specialized contact formulation may lead to approximate normal contact forces, which in turn may induce the approximate transverse shear behaviour in the stacked shells and consequently affect the bending behaviour of the stack. For increasing accuracy in such modelling scenarios, continuum shells should be used instead of conventional shells ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ).
As mentioned earlier in section 2.4, cohesive surfaces like cohesive elements could be used in CZM approach simulation. Also unlike to 2D modelling, the 3D modelling leads to large runtime analysis. Therefore the cohesive surfaces should be uses in 3D modelling in order to improve the analysis runtime.
In the cohesive surface method, the initial stiffness magnitude of the cohesive surface that should be imported to the ABAQUS is different from the magnitude for the cohesive element. In addition it should be divided by the cohesive thickness and does not need to multiply to 50, according to the equation (1).
As indicated in Figure 7 , the force variation as a function of displacement for delamination on DCB composite specimen by using SC8R elements (3D modelling) is similar to Figure 6 , in which explicit solver is also used. But the fluctuation in the force history of the 3D modelling versus 2D modeling is considerable. The non-symmetric pattern of the displacement contour which is shown in Figure 8 , leads to the fluctuation of force history. Therefore unlike to the 2D modeling, the fluctuation of force history is considerable in the 3D modelling because the delamination is not precisely a straight line.
Comparison of force variation as a function of displacement for delamination on DCB composite specimen between the present FE simulation with explicit solver and 3D modelling and the results of Cerioni (2009) Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari
3 SIMULATION OF IMPACT ON LAMINATED COMPOSITE PLATES BASED ON CZM AND PDM
By applying the appropriate procedure for delamination based on CZM method mentioned in section 2; here, the impact FE simulation process of composite plates is briefly described regarding CZM and PDM approach. To verify the proposed simulation approach, the results of the present simulation are compared with the valid experimental and numerical results reported by Gonzalez (2011) Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari . And finally, the appropriate procedure for impact on composite laminated plates is suggested by regarding intralaminar and interlaminar damage. A plate is considered with the dimensions of 150×100 mm2 made of Hexply AS4/8552 carbon-epoxy unidirectional pre-preg composite with laminate configuration [454/04/-454 /904]s. In Figure 9 ( Gonzalez, 2011 Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari ), the test specimen and fixture base with details of support area and clamping points of the specimen are indicated. The material failure properties assumed for AS4/8552 plies and cohesive interface are demonstrated in Tables 3 and 4 ( Gonzalez, 2011 Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari ). It should be mentioned that the ʋ12 is 0.35, the mass density of the plate is 1.590 kg/m3, and the ply thickness is 0.18125 mm. The plate is subjected to transverse impact by a steel sphere impactor of 16 mm diameter with the mass of 5 kg.
(a) Test specimen and fixture base and (b) detail of support area and clamping points of the specimen
3.1 Material failure modelling
In this study, the material failure modelling is based on the progressive damage model that is used mainly to obtain the overall response of the composite laminates. A typical PDM consists of three steps: linear elastic stress analysis, failure analysis, and property-degrading material state variable. There are many material models that can be used to predict the behaviour of composite laminates. Progressive damage model in ABAQUS is assumed to be linearly elastic. It is intended that the model predicts the behaviour of composite laminates for damage which can be initiated without a large amount of plastic deformation. The initiation criteria are used to predict the onset of damage and the damage evolution law is based on the energy dissipated during the damage process and linear material softening ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ).
The ABAQUS anisotropic damage model is based on the work of Hashin and Rotem (1973) Hashin, Z., and Rotem, A. (1973). A fatigue failure criterion for fiber reinforced materials. Journal of composite materials, 7: 448-464. , Hashin (1981) Hashin, Z. (1981). Fatigue failure criteria for unidirectional fiber composites. ASME, Transactions, Journal of Applied Mechanics, 48: 846-852. and Camanho et al., (2003) Camanho, P. P., Davila, C. G., and De Moura, M. F. (2003). Numerical simulation of mixed-mode progressive delamination in composite materials. Journal of composite materials, 37: 1415-1438. . In ABAQUS, the damage initiation criteria for fiber composite laminates are based on Hashin's theory. There are four different damage initiation criteria in ABAQUS ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ) as follows:
-
fiber rupture in tension
-
fiber buckling and kinking in compression
-
matrix cracking under transverse tension and shearing
-
matrix crushing under transverse compression and shearing
The equations for these damage initiation criteria are listed in the following equations (5 - 8 ). Tensile or compressive damage can be initiated in the fiber or the matrix when the respective F equals one.
In the above equations, , , , , and denotes the longitudinal tensile strength, the longitudinal compressive strength, the transverse tensile strength, the transverse compressive strength, the longitudinal shear and transverse shear strength respectfully. Also, is a coefficient that determines the contribution of the shear stress to the fiber tensile initiation criterion. In addition are components of the effective stress tensor which is used to evaluate the initiation criteria. The initiation criteria presented above can be specialized to obtain the model proposed in Hashin and Rotem (1973) Hashin, Z., and Rotem, A. (1973). A fatigue failure criterion for fiber reinforced materials. Journal of composite materials, 7: 448-464. by setting and , or the model proposed in Hashin (1981) Hashin, Z. (1981). Fatigue failure criteria for unidirectional fiber composites. ASME, Transactions, Journal of Applied Mechanics, 48: 846-852. by setting .
Prior to damage initiation, the material in ABAQUS Progressive damage modelling is linearly elastic with the stiffness matrix of a plane stress orthotropic material. Thereafter, the effect of damage is taken into account by reducing the value of stiffness coefficients. If any of the damage variables become one, stress can no longer be supported in the respective direction because the stiffness goes to zero. The response of the material is computed by the equation (9) , where is the strain and is the damaged elasticity matrix ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ).
In a damage evolution model in ABAQUS PDM, it's required to predict the material response in each of the four failure modes as loading increases or unloading. As it's indicated in Figure 10 , these should be beyond the point of initial damage as linear damage evolution. Prior to damage initiation the positive slope of the stress-displacement curve corresponds to linear elastic material behavior. Whereas the negative slope is achieved by evolution of the respective damage variables after damage initiation. To relieve mesh dependency during material softening, ABAQUS introduces a characteristic length into the formulation. So the damage evolution is expressed as a stress-displacement relation. In Figure 10 , (initial equivalent displacement) intersected (initial equivalent stress) at the point A. This point is the damage initiation criterion which met for each failure mode. is the displacement at which the material is fully damaged.
For each failure mode, the energy dissipated should be specified due to failure ( ), which corresponds to the area of the triangle OAC in Figure 10 . The values of for the various modes depend on the respective values. Thereafter the damage initiated, unloading from a partially damaged state such as point B in Figure 10 , occurs along a linear path toward the origin with degraded stiffness and strength due to damage induced.
3.2 Solution method
As mentioned in the earlier work ( Khalili et al., 2011 Khalili, S. M. R., Soroush, M., Davar, A., et al., (2011). Finite element modeling of low-velocity impact on laminated composite plates and cylindrical shells. Composite Structures, 93: 1363-1375. ), the simulation of impact on composite laminates, is possible to be solved by both explicit and implicit solver of ABAQUS, but the ABAQUS/Explicit is the appropriate choice to solve highly nonlinear transient dynamic and progressive damage modelling ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ). Also as it is mentioned in section 2.2, the ABAQUS/Explicit is attractive for very large problems.
3.3 Contact modelling
Hard contact law is one of the contact laws that is available in ABAQUS. In this contact method, the contact constraint is applied when the clearance between two surfaces becomes zero. There is no limit in the contact formulation on the magnitude of contact pressure which can be transmitted between the surfaces. The surfaces are separated when the contact pressure between them becomes zero or negative, then the constraint is removed. The contact force is a function of the penetration distance. And it is applied to the slave nodes to oppose the penetration while equal and opposite forces act on the master surface at the penetration point. When using hard contact, it is still possible to make master surface penetrate into the slave surface by pure master-slave algorithm as indicated in Figure 11 ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ).
Both the pure master-slave and the balanced master-slave contact algorithms are available in ABAQUS/Explicit. By default, ABAQUS/Explicit will decide which algorithm to be used for any given contact pair based on the nature of the two surfaces forming the contact pair and also applying kinematic or penalty enforcement of contact constraints. ABAQUS/Explicit uses the pure master-slave in kinematic contact algorithm as a rigid surface contacts a deformable surface. If the penalty contact algorithm is specified, ABAQUS/Explicit chooses balanced master-slave weighting as two element-based surfaces contact each other. Balanced master-slave weighting means that the corrections produced by both sets of contact calculations are weighted equally. The penalty contact algorithm for balanced master-slave contact surfaces computes contact forces that are linear combinations of the calculated pure master-slave forces. One set of forces is calculated by considering one surface as the master surface, and the other forces are calculated by considering the same surface as the slave surface ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ). As mentioned in section 2.4, it is possible to use both cohesive element and cohesive surfaces for defining cohesive behaviour between tow laminates of composite plate. But in the 3D modelling, cohesive surfaces are preferable due to their low-cost analysis.
3.4 Type of elements and mesh convergence study
Conventional shell, continuum shell and solid elements are available options in the modelling of the composite laminates in ABAQUS. The choice of an element type used for the plates or shells as target structures depends on their side to thickness ratio as well as the impactor velocity. Increasing the thickness of target and impactor velocity lead to increase in the shear deformation.
In order to obtain the optimum number of elements, an analysis of the number of elements sensitivity is performed. In Figure 12 mesh pattern of the circular area surrounding the contact region and the convergence study of the number of elements are shown. This study indicated that the element number of 15 in edges of circular impact area is the optimum number of elements.
Convergence study of element numbers (a) mesh pattern of the circular area surrounding the contact region (b) variation of maximum contact force vs. number of element
3.5 Verification and discussion on simulation method
Similar to the section 2 of this study, the ABAQUS version 2016 is used for simulation of the impact on laminated composite plates. The simulation is performed on the same computer mentioned in the previous section.
The material modelling of composite ply has been done by linear elastic with lamina option that is available in ABAQUS. Due to the plane stress condition that is used for SC8R elements, only the values of , , ʋ12, , and are required to define an orthotropic material ( Dssault System’s Simulia Corp, 2016 Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA. ). Therefore based on Table 3 of the present FE simulation, the requared materials properties are defined assuming is equal to and is equal to .
As mentioned earlier in section 3.1, Hashin's damage initiation criteria parameters are required in the PDM approach that is used for intralaminar failure modelling of laminated composite. According to the Table 3 , the mentioned parameters are defined as damage initiation, assuming is equal to . In order to model progressive damage, the energy dissipated due to failure ( ) of each failure mode should be imported to ABAQUS. The and are taken from Table 3 , as fracture energy in the fiber and matrix in tension and compression mode.
According to Table 4 , the interlaminar failure properties of interfaces are defined. Also the procedure that is used in this section is similar to section 2.5 for cohesive zone modelling. In order to modelling the interlaminar failure of interfaces in the present laminate configuration [454 /04/-454/904]s the clustering ply was chosen. Therefore the delamination in stacking ply with the same fiber orientation (clustering) is considered and the interlaminar failure in inner layer of any cluster is ignored. As indicated in Figure 13 , seven cohesive surfaces duo to low-cost analysis are modelled according to the CZM procedure by using the properties of Table 4 .
Based on the preferences of explicit solver mentioned earlier in section 3.2, ABAQUS/Explicit is used in this study for simulating the impact phenomena. The hard contact law is chosen for being applied as the clearance between two surfaces becomes zero. The impactor and the target are set as the master and slave surfaces, respectively with penalty contact algorithm of balanced master-slave contact surfaces. The impactor was modelled as deformable body with element of C3D8R and the laminated composite are meshed using SC8R elements. As mentioned earlier in section 3.4, the optimum number of elements (12224 elements of type SC8R and 4025 elements of type C3D8R) are obtained based on the mesh convergence study,
According to section 3, three case studies with different level of impact energies were chosen to verify the present FE simulation procedure. Therefore, impactor with initial velocities of 3.93, 3.38 and 2.78 m/s were simulated.
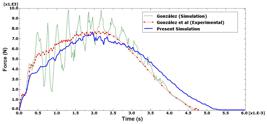
The results of impact with impactor velocity of 2.78 m/s and kinetic energy of 19.3 J were compared with experimental and numerical results those presented by Gonzalez (2011) Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari . The comparison of the results for the contact force history was indicated in Figure 14 . As it is observed, there is appropriate correspondence between the results. Also unlike to the simulation results that presented by Gonzalez the fluctuations of contact force are decreased in the present FE simulation. In Figure 15 , the FE simulation and experimental variation of energy dissipation of impactor is demonstrated as a function of time for laminated composite plate. The results indicated that the energy absorption by laminated composite plate of the present simulation has less discrepancies than simulation results presented by Gonzalez. In addition, in Figure 16 , the comparison of contact force is indicated as a function of impactor displacement for a composite plate under impact kinetic energy of 19.3 J and appropriate correspondence is observed.
FE Simulation and Experimental contact force variation as a function of time for a composite plate under impact kinetic energy of 19.3 J
FE Simulation and Experimental energy dissipation variation of impactor as a function of time for a composite plate under impact kinetic energy of 19.3 J
The comparison of contact force variation as function of impactor displacement for a composite plate under impact kinetic energy of 19.3 J
The present results for the contact force history with impactor velocity of 3.38 m/s and kinetic energy of 28.6 J is shown in Figure 17 , and compared with experimental and numerical results of Gonzalez (2011) Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari . It should be mentioned Gonzalez (2011) Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari has only reported the contact force history for this level of impact energy.
FE Simulation and Experimental contact force variation as a function of time for a composite plate under impact kinetic energy of 28.6 J
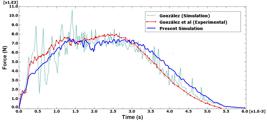
The comparison of the results for the contact force history, energy absorption and contact force as a function of the impactor displacement is shown in Figure 18 , Figure 19 and Figure 20 respectively in case of impactor velocity is 3.93 m/s and kinetic energy is 38.6 J. Here, appropriated correspondence is observed. The comparison of contact force history of three case studies ( Figure 14 , Figure 17 and Figure 18 ) is indicated that unlike to the present simulation, increasing impactor velocity leads to increasing the discrepancy between simulation and experimental results of Gonzalez (2011) Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari . Therefore the validity of the present impact simulation procedure is not dependent on the impactor velocity. In addition as indicated in Figure 18 , the maximum contact force that reported by Gonzalez experimentally (point A) is equal to 8.66 kN. The discrepancy in contact force (point A) is equal to 13.43% and 25.24% for the present and Gonzalez simulation respectively. Therefore, the accuracy of the present impact simulation is prefer than the Gonzalez simulation especially in higher impactor velocity.
FE Simulation and Experimental contact force variation as a function of time for a composite plate under impact kinetic energy of 38.6 J
FE Simulation and Experimental energy dissipation variation of impactor as a function of time for a composite plate under impact kinetic energy of 38.6 J
The comparison of contact force variation as a function of displacement of impactor for a composite plate under impact kinetic energy of 38.6 J
4 CONCLUSION
In this study, a reliable, low-cost and simple method is provided based on ABAQUS/Explicit package by considering damage in laminated composite plates under transverse impact loadings. The best procedure is proposed which can serve as benchmark method in damage modeling of composite structures under high velocity impact for future investigations. First, the simulation of delamination on DCB composite specimen is verified based on CZM approach. In addition, materials model, solution method, element type and method of cohesive definition are considered. It is observed that, less CPU run-time is required for simulation of delamination problems 2D modelling. Furthermore, cohesive surface rather than cohesive element should be used in 3D modelling for improving the analysis runtime. Contrary to cohesive surface, there is no need to divide the initial stiffness of the cohesive element -which should be imported to the ABAQUS- by the cohesive thickness
It can be declared that, explicit solver of ABAQUS is the appropriate choice for modelling progressive damage and cohesive zone. In addition ABAQUS/Explicit is capable to solve highly nonlinear transient dynamic and it is attractive for very large problems.
In this study, the simulation of impact on laminated composite plates based on CZM and PDM are verified by the experimental and numerical results available in the literature.
By considering damage evolution behaviours of matrix and fiber cracking and interface delamination in three case studies with different levels of impact energies, our simulation results have an appropriate correspondence with the results of similar works especially in the aspect of force-time, force-displacement and energy time histories curves. According to the simulation results, the delamination in clustering ply is significant but the interlaminar failure in an inner layer of any cluster could be ignored.
Like to Gonzalez (2011) Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari , we have used ABAQUS finite element simulation; unlike to him, our simulation results are more accurate -about 12 percent better correspondence in maximum contact force- than his simulation results especially in higher impactor velocity. On the other hand, our results correspond to his experimental results appropriately. Finally, the proposed method can serve as a benchmark for simple impact simulation of composite structures based on CZM and PDM in the future investigations, such as optimization study and engineering application of composite laminates under impact.
References
- Abrate, S. (1998). Impact on composite structure, Cambridge University Press, New York, USA.
- Cantwell, W. J., and Morton, J. (1989). Comparison of the low and high velocity impact response of CFRP. Composites, 20: 545-551.
- Guoqi, Z., Goldsmith, W., and Dharan, C. H. (1992). Penetration of laminated Kevlar by projectiles—I. Experimental investigation. International Journal of Solids and Structures, 29(4), 399-420.
- Cheng, W. L., Langlie, S., and Itoh, S. (2003). High velocity impact of thick composites. International journal of impact engineering, 29: 167-184.
- Silva, M. A., Cismaşiu, C., and Chiorean, C. G. (2005). Numerical simulation of ballistic impact on composite laminates. International Journal of Impact Engineering, 31: 289-306.
- Cerioni, A. (2009). Simulation of delamination in composite materials under static and fatigue loading by cohesive zone models, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari
- Zhao, G., Cho, C., Lu, S., et al., (2010). Experimental study on impact resistance properties of T300/epoxy composite laminates. Journal of composite materials, 44: 857-870.
- Khalili, S. M. R., Soroush, M., Davar, A., et al., (2011). Finite element modeling of low-velocity impact on laminated composite plates and cylindrical shells. Composite Structures, 93: 1363-1375.
- Gonzalez, E.V., (2011). Simulation of interlaminar and intralaminar damage in polymer-based composites for aeronautical applications under impact loading, Ph.D. Thesis, Universita'degli Studi di Cagliari, Cagliari
- Ramadhan, A. A., Talib, A. A., Rafie, A. M., et al., (2013). High velocity impact response of Kevlar-29/epoxy and 6061-T6 aluminum laminated panels. Materials & Design, 43: 307-321.
- Chou, S. C., Orringer, O., and Rainey, J. H. (1977). Post-Failure Behavior of Laminates: II—Stress Concentration. Journal of Composite Materials, 11: 71-78.
- Maimí, P., Camanho, P. P., Mayugo, J. A., et al., (2007). A continuum damage model for composite laminates: Part I–Constitutive model. Mechanics of Materials, 39: 897-908.
- Camanho, P. P., Maimí, P., and Dávila, C. G. (2007). Prediction of size effects in notched laminates using continuum damage mechanics. Composites science and technology, 67: 2715-2727.
- Zou, Z., Reid, S. R., Li, S., and Soden, P. D. (2002). Modelling interlaminar and intralaminar damage in filament-wound pipes under quasi-static indentation. Journal of composite materials, 36: 477-499.
- Tan, S. C. (1991). A progressive failure model for composite laminates containing openings. Journal of Composite Materials, 25: 556-577.
- Shokrieh, M. M., (1996). Progressive fatigue damage modeling of composite materials. Ph.D. Thesis, McGill University, Montreal
- Camanho, P. P., and Matthews, F. L. (1999). A progressive damage model for mechanically fastened joints in composite laminates. Journal of Composite Materials, 33: 2248-2280.
- Turon, A., Davila, C. G., Camanho, P. P., et al., (2007). An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Engineering fracture mechanics, 74: 1665-1682.
- Barenblatt, G. I. (1962). The mathematical theory of equilibrium cracks in brittle fracture. Advances in applied mechanics, 7: 55-129.
- Dugdale, D. S. (1960). Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids, 8: 100-104.
- Hillerborg, A., Modéer, M., and Petersson, P. E. (1976). Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and concrete research, 6: 773-781.
- Khoramishad, H., Crocombe, A. D., Katnam, K. B., et al., (2010). Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. International Journal of fatigue, 32: 1146-1158.
- Dssault System’s Simulia Corp (2016). ABAQUS 2016 User's Manual. Providence. RI. USA.
- Camanho, P. P., Davila, C. G., and De Moura, M. F. (2003). Numerical simulation of mixed-mode progressive delamination in composite materials. Journal of composite materials, 37: 1415-1438.
- Perillo, G., Vedvik, N. P., and Echtermeyer, A. T. (2012). Numerical analyses of low velocity impacts on composite. Advanced modelling techniques. In Proceedings of the Simulia customer conference.
- Mi, Y., Crisfield, M. A., Davies, G. A. O., and Hellweg, H. B. (1998). Progressive delamination using interface elements. Journal of composite materials, 32: 1246-1272.
- Alfano, G., and Crisfield, M. (2001). Finite element interface models for the delamination analysis of laminated composites: mechanical and computational issues. International journal for numerical methods in engineering, 50: 1701-1736.
- Hashin, Z., and Rotem, A. (1973). A fatigue failure criterion for fiber reinforced materials. Journal of composite materials, 7: 448-464.
- Hashin, Z. (1981). Fatigue failure criteria for unidirectional fiber composites. ASME, Transactions, Journal of Applied Mechanics, 48: 846-852.
Publication Dates
-
Publication in this collection
02 July 2018 -
Date of issue
2018
History
-
Received
23 Oct 2017 -
Reviewed
27 Apr 2018 -
Accepted
30 Apr 2018