Abstract
This problem deals with the thermo-elastic interaction due to step input of temperature on the stress free boundaries of a homogeneous visco-elastic orthotropic spherical shell in the context of a new consideration of heat conduction with fractional order generalized thermoelasticity. Using the Laplace transformation, the fundamental equations have been expressed in the form of a vector-matrix differential equation which is then solved by eigen value approach and operator theory analysis. The inversion of the transformed solution is carried out by applying a method of Bellman et al (1966). Numerical estimates for thermophysical quantities are obtained for copper like material for weak, normal and strong conductivity and have been depicted graphically to estimate the effects of the fractional order parameter. Comparisons of the results for different theories (TEWED (GN-III), three-phase-lag model) have also been presented and the effect of viscosity is also shown. When the material is isotropic and outer radius of the hollow sphere tends to infinity, the corresponding results agree with that of existing literature.
Generalized thermo-visco-elasticity; Three-phase-lag model; Fractional order heat equation; Eigen value approach; Vector-matrix differential equation; Step input temperatures
Fractional heat conduction with finite wave speed in a thermo-visco-elastic spherical shell
A. Sur; M. Kanoria* * Author e-mail: k_mri@yahoo.com
Department of Applied Mathematics, University of Calcutta, India
ABSTRACT
This problem deals with the thermo-elastic interaction due to step input of temperature on the stress free boundaries of a homogeneous visco-elastic orthotropic spherical shell in the context of a new consideration of heat conduction with fractional order generalized thermoelasticity. Using the Laplace transformation, the fundamental equations have been expressed in the form of a vector-matrix differential equation which is then solved by eigen value approach and operator theory analysis. The inversion of the transformed solution is carried out by applying a method of Bellman et al (1966). Numerical estimates for thermophysical quantities are obtained for copper like material for weak, normal and strong conductivity and have been depicted graphically to estimate the effects of the fractional order parameter. Comparisons of the results for different theories (TEWED (GN-III), three-phase-lag model) have also been presented and the effect of viscosity is also shown. When the material is isotropic and outer radius of the hollow sphere tends to infinity, the corresponding results agree with that of existing literature.
Keywords: Generalized thermo-visco-elasticity, Three-phase-lag model, Fractional order heat equation, Eigen value approach, Vector-matrix differential equation, Step input temperatures.
1 INTRODUCTION
Linear viscoelasticity has been an important area of research since the period of Maxwell, Boltzman, Voigt and Kelvin. Valuable information regarding linear viscoelasticity theory may be obtained in the books of Gross (1953), Staverman and Schwrzl, Alfery and Gurnee, Ferry, Bland and Lakes. Many researchers like Biot (1954, 1955), Gurtin and Sternberg, Liioushin and Pobedria, Tanner, Huilgol and Phan-Thein have contributed notably on thermoviscoelasticity. Freudenthal has pointed out that most of the solids, when subjected to dynamic loading, exhibit viscous effects.
The Kelvin-Voigt model is one of the macroscopic mechanical models often used to describe the viscoelastic behavior of a material. The model represents the delayed elastic response subjected to stress when the deformation is time dependent but recoverable. The dynamic interaction of thermal and mechanical fields in solids has great practical applications in modern aeronautics, astronautics, Nuclear reactors and high-energy particle accelerators. Several researchers are working in this field. A problem involving Two-Temperature Magneto-Viscoelasticity with thermal Relaxation time in Perfect conducting medium have been solved by Ezzat and El-Karamany (2009). A two temperature thermo-electro-viscoelastic problem subjected to modified Ohm's and Fourier's Laws have been solved by Ezzat et al. (2012).
The classical theories of thermoelasticity involving infinite speed of propagation of thermal signals, contradict physical facts. During the last five decades, non-classical theories involving finite speed of heat transportation in elastic solids have been developed to remove the paradox. In contrast with the conventional coupled thermoelasticity theory, which involves a parabolic-type heat transport equation, these generalized theories involving a hyperbolic-type heat-transport equation are supported by experiments exhibiting the actual occurrence of wave-type heat transport in solids, called second sound effect. The first generalization to this theory is due to Lord and Shulman (1967) who formulated the generalized thermoelasticity theory involving one thermal relaxation time, which is known as extended thermo-elasticity theory (ETE). The second generalization to the coupled thermoelasticity theory due to Green and Lindsay (1972), involves two relaxation times.
The third generalization to the coupled thermoelasticity theory is known as low-temperature thermoelasticity introduced by Hetnarski and Ignaczak called the H-I theory. This model is characterized by a system of non-linear field equations.
The fourth generalization in concerned with the thermo-elasticity without energy dissipation (TEWOED) and thermoelasticity with energy dissipation (TEWED) introduced by Green and Naghdi (1991, 1992, 1993) and provide sufficient basic modifications in the constitutive equations that permit treatment of a much wider class of heat flow problems, labeled as types I, II, III. The natures of these three types of constitutive equations are such that when the respective theories are linearized, type-I is same as the classical heat equation (based on Fourier's law) whereas types II and III permit propagation of thermal signals at a finite speed. When Fourier conductivity is dominant the temperature equation reduces to classical Fourier's law of heat conduction and when the effect of conductivity is negligible, the equation has undamped thermal wave solutions without energy dissipation. Applying the above theories of generalized thermoelasticity, several problems have been solved by Mallik and Kanoria (2008), Kar and Kanoria (2009), Islam and Kanoria (2011), Ghosh and Kanoria (2010), Banik and Kanoria (2011).
Recently Roychoudhury (2007) has established a generalized mathematical model of a coupled thermoelasticity theory that includes three-phase lags in the heat flux vector, the temperature gradient and in the thermal displacement gradient. The more general model established reduces to the previous models as special cases. According to this model  , where
, where  is the thermal displacement gradient and
is the thermal displacement gradient and  is the additional material constant. To study some practical relevant problems, particularly in heat transfer problems involving very short time intervals and in the problems of very high heat fluxes, the hyperbolic equation gives significantly different results than the parabolic equation. According to this phenomenon the lagging behavior in the heat conduction in solid should not be ignored particularly when the elapsed times during a transient process are very small, say about
is the additional material constant. To study some practical relevant problems, particularly in heat transfer problems involving very short time intervals and in the problems of very high heat fluxes, the hyperbolic equation gives significantly different results than the parabolic equation. According to this phenomenon the lagging behavior in the heat conduction in solid should not be ignored particularly when the elapsed times during a transient process are very small, say about  s or the heat flux is very much high. Three-phase-lag model is very useful in the problems of nuclear boiling, exothermic catalytic reactions, phonon-electron interactions, phonon-scattering etc., where the delay time
s or the heat flux is very much high. Three-phase-lag model is very useful in the problems of nuclear boiling, exothermic catalytic reactions, phonon-electron interactions, phonon-scattering etc., where the delay time  captures the thermal wave behavior (a small scalar response in time), the phase-lag
captures the thermal wave behavior (a small scalar response in time), the phase-lag  captures the effect of phonon-electron interactions (a microscopic response in space), the other delay time
captures the effect of phonon-electron interactions (a microscopic response in space), the other delay time  is effective since, in the three-phase-lag model, the thermal displacement gradient is considered as a constitutive variable whereas in the conventional thermoelasticity theory temperature gradient is considered as a constitutive variable. Banik and Kanoria (2012) have solved the effect of three-phase-lag in an infinite medium with a spherical cavity. The magneto-thermo-elastic responses in a perfectly conducting medium under three-phase-lag model have been studied by Das and Kanoria (2012).
is effective since, in the three-phase-lag model, the thermal displacement gradient is considered as a constitutive variable whereas in the conventional thermoelasticity theory temperature gradient is considered as a constitutive variable. Banik and Kanoria (2012) have solved the effect of three-phase-lag in an infinite medium with a spherical cavity. The magneto-thermo-elastic responses in a perfectly conducting medium under three-phase-lag model have been studied by Das and Kanoria (2012).
However, over the last few decades, anisotropic materials have been increasingly used. There are materials which have natural anisotropy such as zinc, magnesium, sapphire, wood, some rocks and crystals, and also there are artificially manufactured materials such as fiber-reinforced composite materials which exhibit anisotropic character. The advantage of composite materials over the traditional materials lies on their valuable strength, elastic and other properties (1980). A reinforced material may be regarded to some order of approximation, as homogeneous and anisotropic elastic medium having a certain kind of elastic symmetry depending on the symmetry of reinforcement. Some glass fibre reinforced plastics may be regarded as transversely isotropic. Thus, problems of solid mechanics should not be restricted to the isotropic medium only. Increasing use of an anisotropic media demand that the study of elastic problems should be extended to anisotropic medium also.
Differential equations of fractional order have been the focus of many studies due to their frequent appearance in various applications in fluid mechanics, viscoelasticity, biology, physics and engineering. The most important advantage of using fractional differential equations in these and other applications is their non-local property. It is well known that the integer order differential operator is a local operator but the fractional order differential operator is non-local. This means that the next state of a system depends not only upon its current state but also upon all of its historical states. This is more realistic, and this is one reason why fractional calculus has become more and more popular (1967, 1997, 1999).
Fractional calculus has been used successfully to modify many existing models of physical processes. One can state that the whole theory of fractional derivatives and integrals was established in the second half of the nineteenth century. The first application of fractional derivatives was given by Abel who applied fractional calculus in the solution of an integral equation that arises in the formulation of the Tautochrone problem. The generalization of the concept of derivative and integral to a non-integer order has been subjected to several approaches, and some various alternative definitions of fractional derivatives appeared in Refs. (1974, 1997, 2000). In the last few years, fractional calculus was applied successfully in various areas to modify many existing models of physical processes, e.g., chemistry, biology, modeling and identification, electronics, wave propagation and viscoelasticity (1971, 1974, 1983, 1984, 1997). One can refer to Padlubny (1999) for a survey of applications of fractional calculus.
Recently, a considerable research effort is expended to study anomalous diffusion, which is characterized by the time-fractional diffusion-wave equation by Kimmich (2002) as follows
where  is the mass density,
is the mass density,  is the concentration,
is the concentration,  is the diffusion conductivity,
is the diffusion conductivity,  the coordinate symbol, which takes the value 1, 2, 3. The notation
the coordinate symbol, which takes the value 1, 2, 3. The notation  is the Riemann-Liouville fractional integral, introduced as a natural generalization of the well-known n-fold repeated integral
is the Riemann-Liouville fractional integral, introduced as a natural generalization of the well-known n-fold repeated integral  written in a convolution-type form as in (2000).
written in a convolution-type form as in (2000).
Youssef (2010) introduced another formula of heat conduction in the following form
and a uniqueness theorem has also been proved.
Ezzat established a new model of fractional heat conduction equation by using the new Taylor series expansion of time-fractional order, developed by Jumarie (2010) as
El-Karamany and Ezzat (2011) introduced two general models of fractional heat conduction law for a non-homogeneous anisotropic elastic solid. Uniqueness and reciprocal theorems are proved, and the convolutional variational principle is established and used to prove a uniqueness theorem with no restriction on the elasticity or thermal conductivity tensors except symmetry conditions. For fractional thermoelasticity not involving two-temperatures, El-Karamany and Ezzat (2011) established the uniqueness, reciprocal theorems and convolution variational principle. The dynamic coupled and Green-Naghdi thermoelasticity theories result as limit cases. The reciprocity relation in case of quiescent initial state is found to be independent of the order of differintegration. Fractional order theory of a perfect conducting thermoelastic medium not involving two temperatures was investigated by Ezzat and El-Karamany (2011). Thermal wave propagation in an infinite half-space under fractional order Green-Naghdi theory was studied by Sur and Kanoria (2012).
To the authors' knowledge, under three-phase-lag effect, no solution of visco-elastic orthotropic materials for fractional heat conduction equation has been reported. With this motivation in mind the present analysis is to study the thermoelastic stresses, displacement and temperature distribution in a orthotropic hollow sphere in the context of GN-III and three-phase-lag model of generalized thermoelasticity where the heat equation consists of some non-local fractional operator signifying not only the present state, but also the previous states due to sudden temperature change on the stress-free boundaries. The governing equations are formed in Laplace transform domain which is then solved by eigen-value approach and operator theory analysis. The inversion of the transformed solution are carried out numerically applying the method of Bellman et al. A comprehensive analysis of the result have been presented for 3P model and GN-III model for both viscous and non-viscous isotropic materials. The effect of the fractional order parameter is also discussed.
2 FORMULATION OF THE PROBLEM
We consider a homogeneous orthotropic thermo-visco-elastic spherical shell of inner radius  and outer radius
and outer radius  in an undisturbed state and initially at uniform temperature
in an undisturbed state and initially at uniform temperature  . We introduce spherical polar coordinates
. We introduce spherical polar coordinates  with the center of the cavity at the origin as shown in Figure a.
with the center of the cavity at the origin as shown in Figure a.
We consider spherically symmetric thermal problem so that the displacement component  and the temperature
and the temperature  are assumed to be functions of
are assumed to be functions of  and
and  only.
only.
The stress-strain-temperature relations in the present problem are (Kelvin-Voigt type)
and the generalized heat conduction equation for fractional order three-phase-lag model is
where  are the stress tensor,
are the stress tensor,  is the temperature increase over the reference temperature
is the temperature increase over the reference temperature  ,
,  are the elastic constants,
are the elastic constants,  are the thermal moduli,
are the thermal moduli,  is the coefficient of thermal conductivity along the radial direction,
is the coefficient of thermal conductivity along the radial direction,  is the additional material constant along the radial direction,
is the additional material constant along the radial direction,  is the mass density,
is the mass density,  is the specific heat of the solid at constant strain,
is the specific heat of the solid at constant strain,  is the mechanical relaxation time,
is the mechanical relaxation time,  and
and  are the phase-lag of temperature gradient and the phase-lag of the heat flux respectively. Also
are the phase-lag of temperature gradient and the phase-lag of the heat flux respectively. Also  where
where  is the phase-lag of thermal displacement gradient.
is the phase-lag of thermal displacement gradient.
In the case  and
and  we arrive at the thermo-elasticity equations with energy dissipation (TEWED(GN-III)).
we arrive at the thermo-elasticity equations with energy dissipation (TEWED(GN-III)).
The stress equation of motion in spherical polar co-ordinate is given by
Introducing the following non-dimensional quantities
Equations (4)-(8) become
and
where
and
Also,  and
and  are dimensionless constants,
are dimensionless constants,  being the thermoelastic coupling constant. Where
being the thermoelastic coupling constant. Where  is the non-dimensional thermal wave velocity and
is the non-dimensional thermal wave velocity and  is the damping co-efficient.
is the damping co-efficient.
The boundary conditions are given by
where  and
and  are dimensionless constants, and
are dimensionless constants, and  is the Heaviside unit step function. The above condition indicate that for time η P η10 there is no temperature
is the Heaviside unit step function. The above condition indicate that for time η P η10 there is no temperature  on the inner boundary and for η # 0 there is no temperature
on the inner boundary and for η # 0 there is no temperature  on the outer boundary. Thermal shocks are given on the boundaries of the shell
on the outer boundary. Thermal shocks are given on the boundaries of the shell  Thermal stresses in the elastic medium due to the application of these thermal shocks are calculated. We assume that the medium is at rest and undisturbed initially.
Thermal stresses in the elastic medium due to the application of these thermal shocks are calculated. We assume that the medium is at rest and undisturbed initially.
The initial and the regularity conditions can be written as
3 METHOD OF SOLUTION
Let
with  denote the Laplace transform of
denote the Laplace transform of  and
and  respectively.
respectively.
Since we have
On taking Laplace transform, equations (12) and (13) reduce to
and
where
 and assuming
and assuming 
Differentiating equation (21) with respect to  and using equation (22), we get
and using equation (22), we get
Equations (22) and (23) can be written in the form
and
where, we assume that
 is the thermo-elastic coupling constant and
is the thermo-elastic coupling constant and
From equations (24) and (25), we have the vector-matrix differential equation as follows
where
and
4 EIGEN VALUE APPROACH
Let
where  is a scalar,
is a scalar,  is a vector depending on
is a vector depending on  and
and  is a non-trivial solution of the scalar differential equation
is a non-trivial solution of the scalar differential equation
Let  . Therefore, from equation (30) we have
. Therefore, from equation (30) we have
The solution of equation (30) is
Using equation (29) and (30) into equation (27) we get
where  is the eigen vector corresponding to the eigen value
is the eigen vector corresponding to the eigen value  .
.
The characteristic equation corresponding to  can be written as
can be written as
The roots of the characteristic equation (37) are of the form  and
and  , where
, where
Equation (34) can be written as
Therefore, the positive roots of the equation (36) are
where
Therefore,  and
and  are real positive quantities.
are real positive quantities.
The eigen vectors  corresponding to the eigen values
corresponding to the eigen values  can be calculated as
can be calculated as
Therefore, from equation (29) and using equation (28) we get
and
where  and
and  are the modified Bessel functions of order
are the modified Bessel functions of order  of first and second kind respectively.
of first and second kind respectively.  's and
's and  's
's  are independent of
are independent of  but dependent of
but dependent of  and are to be determined from the boundary conditions.
and are to be determined from the boundary conditions.
Using the recurrence relations of modified Bessel functions we obtain from equation (41)
since
where  . Taking Laplace transform on the equations (9), (10) and (11) we get
. Taking Laplace transform on the equations (9), (10) and (11) we get
where  Using the boundary conditions
Using the boundary conditions  on
on  and
and  on
on  , where
, where  ,
,  on
on 
Using the recurrence relations (Watson, 1980) from equations (42) and (44) we obtain
and
where  for
for 
 for
for  and
and 
From (44), the values of ,
, ,
, and
and  are given as
are given as
5 SPECIAL CASES
For the homogeneous and transversely isotropic material
 and
and  Therefore from (9) and (10),
Therefore from (9) and (10),  Hence, from (45) and (46), we can write
Hence, from (45) and (46), we can write
Also for an isotropic material,  and
and  and for a non-viscous material, we have
and for a non-viscous material, we have  Hence,
Hence,  Thus, for an isotropic material, equations (45) and (46) reduce to
Thus, for an isotropic material, equations (45) and (46) reduce to
Moreover, for large value of  i.e., for large value of
i.e., for large value of  ,
,  and
and  tend to zero. Thus we have
tend to zero. Thus we have
Hence for large value of , the asymptotic expressions of
, the asymptotic expressions of  and
and  are given as
are given as
and
Therefore, for an infinitely extended body
where
The results agree with those of Kar and Kanoria (2007) for GN III model.
6 OPERATOR THEORY ANALYSIS
Equations (12) and (13) can be expressed in the following form
with  and
and
where
 and
and 
Taking the Laplace transform, we have
and
Where  and
and 
Operating  on (64) and using (65) we have
on (64) and using (65) we have
Similarly, operating  on (65) and using (64) we have
on (65) and using (64) we have
where  and
and  are the two operators and
are the two operators and  and
and  are the roots of the quadratic equation in
are the roots of the quadratic equation in  given by
given by
As the solution of equation (66) and (67) we have
and
Where  and
and  are the modified Bessel functions of order
are the modified Bessel functions of order  of first and second kind respectively;
of first and second kind respectively;  ,
, ,
, and
and  are independent of
are independent of  but dependent on
but dependent on 
Therefore, substituting the expressions of  and
and  in equation (65), we get
in equation (65), we get
and
Therefore
Equations (73) and (74) are the same as that of equations (40) and (42) (i.e., the solutions obtained by Eigen-value approach).
7 NUMERICAL RESULTS AND DISCUSSIONS
To get the solutions for displacement, temperature distribution and stresses in the space-time domain we have to apply Laplace inversion formula to the equations (40), (42), (44) and (45) respectively, which have been done numerically using the method of Bellman et al. (1966) for fixed value of the space variable and for  ,
,  , where
, where  's are computed from roots of the shifted Legendre polynomial of degree 7 (see Appendix
Appendix
) with
's are computed from roots of the shifted Legendre polynomial of degree 7 (see Appendix
Appendix
) with  The computations for the state variables are carried out for different values of
The computations for the state variables are carried out for different values of  and values of
and values of 
 The materials chosen for numerical evaluation are copper material. The physical data for orthotropic material are (2009)
The materials chosen for numerical evaluation are copper material. The physical data for orthotropic material are (2009)
and the hypothetical values of the relaxation time parameters are taken as
Here, in this article we have considered three-phase-lag model. Now, for this model, the solution of heat conduction is stable if  where
where  i.e., the stability condition of Quintanilla and Racke is verified (2008).
i.e., the stability condition of Quintanilla and Racke is verified (2008).
Also, for an isotropic material, the physical data are taken as (www.matweb.com).
In case of GN theory,  is an additional material constant depending on the material. For copper like material, we take
is an additional material constant depending on the material. For copper like material, we take 
The results of the numerical evaluation of the thermo-elastic stress variations and temperature distribution are illustrated in figures 1-8 for both large time  and small time
and small time  for weak conductivity
for weak conductivity , normal conductivity
, normal conductivity  and strong conductivity
and strong conductivity  respectively for 3P and GN III models. In these figures, the magnitudes of the variation of stresses and temperature are observed for viscous material when the step-input temperatures are applied on the inner boundary
respectively for 3P and GN III models. In these figures, the magnitudes of the variation of stresses and temperature are observed for viscous material when the step-input temperatures are applied on the inner boundary  and outer boundary
and outer boundary  of the hollow sphere. Figures 1 and 2 depict the variation of the radial stress against the radial distance
of the hollow sphere. Figures 1 and 2 depict the variation of the radial stress against the radial distance  of the sphere. From the figures it is observed that the radial stress
of the sphere. From the figures it is observed that the radial stress  vanishes at the inner boundary
vanishes at the inner boundary  and the outer boundaries
and the outer boundaries  of the shell which satisfy our theoretical boundary conditions. The magnitude of the radial stress is maximum near
of the shell which satisfy our theoretical boundary conditions. The magnitude of the radial stress is maximum near  for a strong conductive material and for GN III model. Also, for three-phase-lag model, the oscillatory nature is observed. This is due to the presence of the oscillation term in the heat equation of three-phase-lag model. For weak conductivity
for a strong conductive material and for GN III model. Also, for three-phase-lag model, the oscillatory nature is observed. This is due to the presence of the oscillation term in the heat equation of three-phase-lag model. For weak conductivity , the oscillatory nature is also seen for GN III model.
, the oscillatory nature is also seen for GN III model.
Figure 2 represents the variation of  for
for  and
and  respectively. It is seen that
respectively. It is seen that  vanishes at the boundaries of the shell where there are thermal sources which agree with our theoretical boundary conditions. As may seen from the figure, the stress wave is compressive in nature near both the boundaries. Also, at earlier stage of wave propagation, both the models give close results, whereas with advancement of time time, the stress wave is propagating with different speeds. For
vanishes at the boundaries of the shell where there are thermal sources which agree with our theoretical boundary conditions. As may seen from the figure, the stress wave is compressive in nature near both the boundaries. Also, at earlier stage of wave propagation, both the models give close results, whereas with advancement of time time, the stress wave is propagating with different speeds. For , the effect of
, the effect of  is very prominent inside the shell, whereas, for
is very prominent inside the shell, whereas, for  and
and , the radial stress vanishes for
, the radial stress vanishes for  and
and  respectively, which is physically plausible.
respectively, which is physically plausible.
Figures 3 and 4 are plotted to show the variation of the stress  along the radius of the sphere for different values of the non-local fractional parameter
along the radius of the sphere for different values of the non-local fractional parameter  and for
and for  respectively. In figure 3, variation of
respectively. In figure 3, variation of  is shown for larger time
is shown for larger time  for same set of parameters. As seen from the figure,
for same set of parameters. As seen from the figure,  attains the maximum magnitude near the inner boundary of the shell. The magnitude of
attains the maximum magnitude near the inner boundary of the shell. The magnitude of  for
for  is larger than that of
is larger than that of  which is again larger than that of
which is again larger than that of  when
when  and the rate of decay in magnitude of
and the rate of decay in magnitude of  for
for  is faster than that of
is faster than that of  which is again faster than that obtained for
which is again faster than that obtained for  .
.
In both cases, the stress corresponding to each model and for different nonlocal fractional parameter , the stress propagates for
, the stress propagates for  For small time, the stress is compressive in nature near the inner boundary of the shell. Here also, for
For small time, the stress is compressive in nature near the inner boundary of the shell. Here also, for  the stress component almost disappears for
the stress component almost disappears for  and for
and for  , it vanishes for
, it vanishes for  . For
. For  ,i.e., the region equidistant from the boundaries
,i.e., the region equidistant from the boundaries  vanishes in earlier situations for normal conductivity and strong conductivity of the materials.
vanishes in earlier situations for normal conductivity and strong conductivity of the materials.
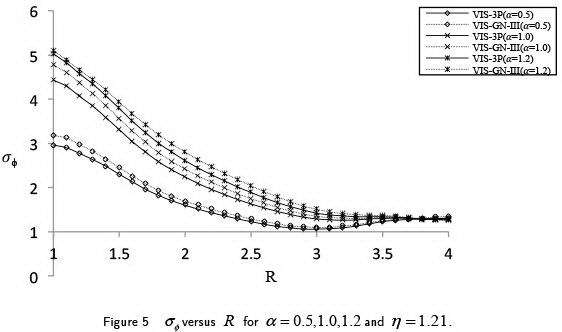
Figures 5 and 6 are plotted to show the variation of the stress component  for different fractional parameter
for different fractional parameter  From the figure 5, it is seen that when
From the figure 5, it is seen that when  the magnitude of
the magnitude of  is maximum near the inner boundary of the shell. Also it is observed that increase in the nonlocal fractional parameter
is maximum near the inner boundary of the shell. Also it is observed that increase in the nonlocal fractional parameter  also increases the magnitude of the stress component
also increases the magnitude of the stress component  For
For  and
and  the decay in magnitude of
the decay in magnitude of  is more rapid compared to that of
is more rapid compared to that of  As may seen from the figure,
As may seen from the figure,  is compressive near the inner boundary of the shell and the similar qualitative behavior is seen in the variation of
is compressive near the inner boundary of the shell and the similar qualitative behavior is seen in the variation of  as that in figure 4.
as that in figure 4.
Figures 7 and 8 depict the variation of the temperature  along the radius of the sphere
along the radius of the sphere  for different values of
for different values of  It is seen that whenever
It is seen that whenever  (i.e., for
(i.e., for  ) the inner boundary of the shell is kept at zero temperature whereas for
) the inner boundary of the shell is kept at zero temperature whereas for  the inner boundary is maintained the fixed temperature value
the inner boundary is maintained the fixed temperature value  while in both situations, outer boundary maintains the same step-input-temperature
while in both situations, outer boundary maintains the same step-input-temperature  For larger time,
For larger time,  attains the maximum magnitude near
attains the maximum magnitude near  for GN III model. Whereas in the earlier situations, the magnitude of
for GN III model. Whereas in the earlier situations, the magnitude of  decays sharply near the inner boundary of the shell for
decays sharply near the inner boundary of the shell for  compared to that of
compared to that of  and
and  The rise in magnitude near the outer boundary is rapid also. For
The rise in magnitude near the outer boundary is rapid also. For  and for
and for  , the magnitude of the temperature almost disappears for
, the magnitude of the temperature almost disappears for 
Figures 9-16 are plotted to show the effect of viscosity for two set of times for weak conductive materials. Form figures 9-10 it is seen that  satisfies our theoretical boundary conditions. As may seen from figure 10, it is seen that
satisfies our theoretical boundary conditions. As may seen from figure 10, it is seen that  attains the maximum value for non-viscous material for both models near the inner boundary of the shell.
attains the maximum value for non-viscous material for both models near the inner boundary of the shell.
Figures 11-12 are plotted to show the variation of  versus
versus  from these figures it is seen that the effect of viscosity is more prominent in GN III model compared to that of 3P lag model for a large time when
from these figures it is seen that the effect of viscosity is more prominent in GN III model compared to that of 3P lag model for a large time when  Whereas, for earlier situations, the effect of viscosity for GN III model is very prominent near the boundaries of the shell compared to the interior of the shell.
Whereas, for earlier situations, the effect of viscosity for GN III model is very prominent near the boundaries of the shell compared to the interior of the shell.
From figures 13-14, the similar qualitative nature is seen in the variation of  for both viscous and non-viscous materials.
for both viscous and non-viscous materials.
Figures 15 and 16 are plotted to show the effect of viscosity on temperature  for two sets of time. For both viscous and non-viscous material, the temperature satisfies our thermal boundary conditions. Also, the effect of viscosity is very prominent in earlier situations than latter. As may seen from the figures, when
for two sets of time. For both viscous and non-viscous material, the temperature satisfies our thermal boundary conditions. Also, the effect of viscosity is very prominent in earlier situations than latter. As may seen from the figures, when  , for 3P lag model, the magnitude of
, for 3P lag model, the magnitude of  is larger for viscous material compared to the non-viscous material. Whereas for
is larger for viscous material compared to the non-viscous material. Whereas for  , the magnitude is larger for non-viscous material compared to the viscous material.
, the magnitude is larger for non-viscous material compared to the viscous material.
Figures 17-19 are plotted to show the variations of  ,
, and
and  respectively against the time
respectively against the time  whenever
whenever  and
and  From these figures, it is seen that at the beginning of time, oscillatory natures are seen in the propagation of the stress components. Finally they reach to a steady state which supports the physical fact.
From these figures, it is seen that at the beginning of time, oscillatory natures are seen in the propagation of the stress components. Finally they reach to a steady state which supports the physical fact.
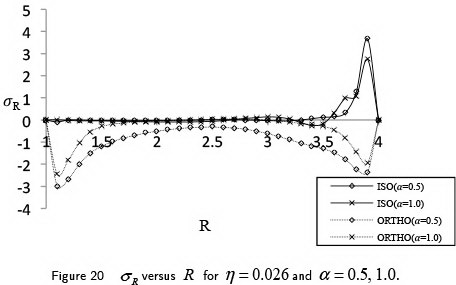
Figures 20-22 are plotted to draw the comparison between isotropic and orthotropic material for  and for
and for  for viscous material. From figure 20, it is seen that for orthotropic material, the stress waves are reflected from either boundary whereas for isotropic material, the propagation of each of the waves are found to occur. Also, amplitude of
for viscous material. From figure 20, it is seen that for orthotropic material, the stress waves are reflected from either boundary whereas for isotropic material, the propagation of each of the waves are found to occur. Also, amplitude of  decreases with the increase of the non-local fractional parameter
decreases with the increase of the non-local fractional parameter .
.
Figure 21 depicts the variation of  versus
versus  for isotropic and orthotropic materials. As may be seen from the figure that for an isotropic material, the oscillatory nature is observed due to the reflection as mentioned earlier. However, the magnitude of
for isotropic and orthotropic materials. As may be seen from the figure that for an isotropic material, the oscillatory nature is observed due to the reflection as mentioned earlier. However, the magnitude of  is maximum near the outer boundary of the shell for an isotropic material.
is maximum near the outer boundary of the shell for an isotropic material.
8 CONCUSIONS
The problem of investigating the radial stress, hoop stress, temperature in a homogeneous isotropic viscoelastic spherical shell is studied in the light of three-phase-lag model and GN-III model in the context of space-fractional heat conduction equation. The method of Laplace Transform is used to write the basic equations in the form of a vector-matrix differential equation which is then solved by eigen-value approach. The numerical inversion of Laplace Transform is computed by the method of Bellmen. The analysis of the result permits some concluding remarks:
(i) When the time is small,
, i.e., at early stage of wave propagation, both the models give close results, whereas for comparatively large time
, significant differences are observed for weak, normal and strong conductivities
respectively. Also, in the earlier situations, maximum magnitude occurs for weak conductivity whereas for large time, magnitudes are maximum when conductivity is high inside the body.
(ii) It is observed that maximum magnitude of stresses will occur for viscous material and for strong conductivity
.
(iii) For an isotropic material, the maximum temperature occurs near the boundaries of the shell and it almost disappears in the interior of the shell.
(iv) The effect of
is more prominent near the inner boundary for orthotropic material compared to that of an isotropic material.
Acknowledgements We are grateful to Professor S. C. Bose of the Department of Applied mathematics, University of Calcutta, for his kind help and guidance in preparation of the paper. We also express our sincere thanks to the reviewer for his valuable suggestions for the improvement of the paper.
Appendix
Let the Laplace transform of  be given by
be given by
We assume that  is sufficiently smooth to permit the use of the approximate method to apply.
is sufficiently smooth to permit the use of the approximate method to apply.
Substituting  in equation (A.1) we obtain
in equation (A.1) we obtain
where
Applying the Gaussian quadrature rule to (A.2) we obtain the approximate relation
where  's
's are the roots of the shifted Legendre polynomial and
are the roots of the shifted Legendre polynomial and  's
's  are the corresponding weights and
are the corresponding weights and 
Thus, we have
Therefore
As the matrix is the product of  multiplied by Vander monde matrix, it can be shown that the matrix is non-singular.
multiplied by Vander monde matrix, it can be shown that the matrix is non-singular.
Hence,  are known. For
are known. For  we have
we have
From equations in (A.5) we can calculate the discrete values of  i.e.,
i.e., 
 and finally using interpolation, we obtain the stress components
and finally using interpolation, we obtain the stress components 
- Bagley, R. L.; Torvik, P. J. A theoretical basis for the application of fractional calculus to viscoelasticity. J Rheol, v.27, p. 201-210, 1983.
- Banik, S.; Kanoria, M. Two temperature generalized thermoelastic interactions in an infinite body with a spherical cavity. Int J Thermophysics, v. 32, p. 1247-1270, 2011.
- Banik, S.; Kanoria, M. effects of three-phase-lag on two-temperature generalized thermoelasticity for infinite medium with spherical cavity. Applied Mathematics and Mechanics, v. 33(4), p. 483-498, 2012.
- Bellman, R.; Kolaba, R. E.; Lockette, J. A. Numerical Inversion of the Laplace Transform. American Elsevier Publishing Company, New York 1966.
- Biot, M. A. Theory of stress-strain relations in an isotropic viscoelasticity and relaxation phenomena. J Appl Phys, v. 25(11), p. 1385-1391, 1954.
- Biot, M. A. Variational principal in irreversible thermodynamics with application to viscoelasticity. Phys Rev, v. 97(6), p. 1463-1469, 1955.
- Caputo, M. Linear models of dissipation whose Q is almost frequently independent II. Geophys J R Astron Soc , v. 13, p. 529-539, 1967.
- Caputo, M.; Mainardi, F. Linear model of dissipation in anelastic solids. Rivis Ta El Nuovo Cimento , v. 1, p. 161-198, 1971.
- Caputo, M. Vibrations of an infinite viscoelastic layer with a dissipative memory. J Acous Soc Am, v. 56, p. 897-904, 1974.
- Das, P.; Kanoria, M. Magneto-thermo-elastic response in a perfectly conducting medium with three-phase-lag effect. Acta Mechanica, v. 223, p. 811-828, 2012.
- El-Karamany, A. S.; Ezzat, M. A. Convolutional variational principle, reciprocal and uniqueness theorems in linear fractional two-temperature thermoelasticity. Journal of Thermal Stresses, v. 34(3), P. 264-284, 2011.
- El-Karamany, A. S.; Ezzat, M. A. On the fractional Thermoelasticity. Mathematics and Mechanics of Solids , v. 16, p. 334-346, 2011.
- El-Karamany, A. S.; Ezzat, M. A. Fractional order theory of a prefect conducting thermoelastic medium. Can J Phys, v. 89(3), p. 311-318, 2011.
- Ezzat, M. A.; El-Karamany, A. S. State Space Approach of Two-Temperature Magneto-Viscoelasticity Theory with Thermal Relaxation in a Medium of Perfect Conductivity. Journal of Thermal Stresses, v. 32, p. 819-838, 2009.
- Ezzat, M. A.; Zakaria, M.; El-Bary, A. A. Two-Temperature theory in thermo-electric viscoelastic material subjected to modified Ohm's and Fourier's Laws. Mech of Advanced Mater and Struct, v. 19, p. 453-464, 2012.
- Ghosh, M. K.; Kanoria, M. Study of dynamic response in a functionally graded spherically isotropic hollow sphere with temperature dependent elastic parameters. Journal of Thermal Stresses, v.33, p. 459-484, 2010.
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Orders. Fractals and Fractional Calculus in Continuum Mechanics. Springer, Wien, 1997.
- Green, A. E.; Lindsay, K. A. Thermoelasticity. J Elasticity, v. 2, p. 1-7, 1972.
- Green, A. E.; Naghdi, P. M. A re-examination of the basic postulate of thermo-mechanics. Proc Roy Soc Lond , v. 432, p. 171-194, 1991.
- Green, A. E.; Naghdi, P .M. An undamped heat wave in an elastic solid. Journal of Thermal Stresses, v. 15, p. 253-264, 1992.
- Green, A. E.; Naghdi, P. M. Thermoelasticity without energy dissipation. J Elasticity, v. 31, p. 189-208, 1993.
- Gross, B. Mathematical structure of the theories of Viscoelasticity. Hermann, Paris 1953.
- Hilfer, R. Application of Fraction Calculus in Physics. World Scientific, Singapore, 2000.
- Islam, M.; Kanoria, M. Study of dynamical response in a two dimensional transversely isotropic thick plate due to heat source. Journal of Thermal Stresses, v. 34, p. 702-723, 2011.
- Jumarie, G. Derivation and solutions of some fractional Black-Scholes equations in coarse-grained space and time. Application to Merton's optimal portfolio. Comput Math Appl, v. 59, p. 1142-1164, 2010.
- Kar, A,; Kanoria, M.: Thermoelastic interaction with energy dissipation in an unbounded body with a spherical hole. Int. J. Solids. Struct., v. 44, p. 2961-2971, 2007.
- Kar, A.; Kanoria, M. Generalized thermoelastic functionally graded orthotropic hollow sphere under thermal shock with three-phase-lag effect. European Journal of Mechanics A/Solids, v. 28, p. 757-767, 2009.
- Kimmich, R. Strange Kinetics, porous media, and NMR. J Chem Phys, v. 284,. p. 243-285, 2002.
- Koeller, R. C. Applications of fractional calculus to the theory of viscoelasticity. Trans ASME-J Appl Mech , v. 51, p. 299-307, 1984.
- Lekhnitskii, S. G. Theory of Elasticity of an anisotropic body. Mir. Moscow
- Lord, H.; Shulman, Y. A. generalized theory of thermoelasticity. J Mech Phys Solid, v. 15, p. 299-309, 1967.
- Mainardi, F. Fractional calculus: some basic problems in continuum and statistical mechanics. In: A. Carpinteri, F. Mainardi, (eds.) Fractals and Fractional calculus in Continuum Mechanics. Springer, New York, p. 291-348, 1997.
- Mainardi, F.; Gorenflo, R. On Mittag-Lettler-type function in fractional evolution processes. J Comput Appl Math , v.118, p. 283-299, 2000.
- Mallik, S. H.; Kanoria, M. A two-dimensional problem for a transversely isotropic generalized thick plate with spatially varying heat sources. European Journal of Mechanics A/Solids, v. 27, p. 607-621, 2008.
- Oldham KB, Spanier J. The Fractional Calculus. Academic Press, New York, 1974.
- Podlubny, I. Fractional Differential Equations. Academic Press, New York 1999.
- Quintanilla, R.; Racke, R.: A note on stability in three-phase-lag heat conduction. Int. J. Heat Mass Transfer, v. 51, p. 24-29, 2008.
- Rossikhin, Yu. A.; Shitikova, M. V.; Applications of fractional calculus to dynamic problems of linear and nonlinear heredity mechanics of solids. Appl Mech Rev, v. 50, p. 15-67, 1997.
- Roychoudhuri, S. K. On a thermoelastic three-phase-lag model. Journal of Thermal Stresses, v. 30, p. 231 - 238, 2007.
- Sur, A.; Kanoria, M. Fractional order two-temperature thermoelasticity with finite wave speed. Acta Mechanica, v. 223(12), p. 2685-2701, 2012.
- Youssef, H. Theory of fractional order generalized thermoelasticity. J Heat Transfer, v. 132, p. 132:1-7, 2010.
Appendix
Publication Dates
-
Publication in this collection
13 Mar 2014 -
Date of issue
Dec 2014