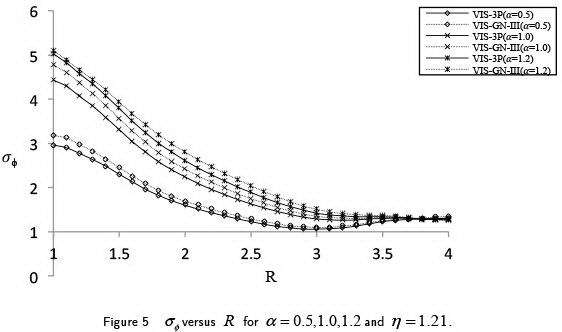
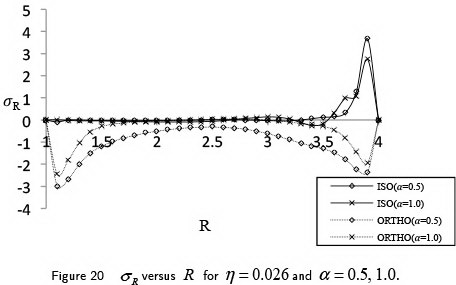
This problem deals with the thermo-elastic interaction due to step input of temperature on the stress free boundaries of a homogeneous visco-elastic orthotropic spherical shell in the context of a new consideration of heat conduction with fractional order generalized thermoelasticity. Using the Laplace transformation, the fundamental equations have been expressed in the form of a vector-matrix differential equation which is then solved by eigen value approach and operator theory analysis. The inversion of the transformed solution is carried out by applying a method of Bellman et al (1966). Numerical estimates for thermophysical quantities are obtained for copper like material for weak, normal and strong conductivity and have been depicted graphically to estimate the effects of the fractional order parameter. Comparisons of the results for different theories (TEWED (GN-III), three-phase-lag model) have also been presented and the effect of viscosity is also shown. When the material is isotropic and outer radius of the hollow sphere tends to infinity, the corresponding results agree with that of existing literature.
Generalized thermo-visco-elasticity; Three-phase-lag model; Fractional order heat equation; Eigen value approach; Vector-matrix differential equation; Step input temperatures