Abstract
The main goal of this research is to extract a suitable continuum modeling of buckyball-C60. For this purpose, firstly the lattice structure of buckyball-C60 is modelled and subsequently a spherical structure equivalent to fullerene structure is considered. The fullerene structure modeled with shell elements is under internal pressure and in the continuum shell modeling process. The results of simulation demonstrate that the fullerene structure can be modelled using spherical structure. The comparison between strain energies of the equivalent fullerene spherical model and molecular mechanics model under radial displacement, shows that C60-fullerene spherical structures can be modeled using a shell with 0.665 Å thickness, 5.07 TPa elastic modulus and 0.165 Poisson's ratio or a shell with 0.75 Å thickness, 4.84 TPa elastic modulus and 0.19 Poisson's ratio. Moreover, the applied elliptical strain is used to demonstrate that the performance of the continuum spherical shell model of C60 is faultless.
Keywords:
Fullerene; Continuum shell model; Molecular mechanics; Elastic modulus
1 INTRODUCTION
Fullerenes (Kroto et al., 1985Kroto, H.W., Heath, J.R., O'Brien, S.C., Curl, R.F., Smalley, R.E. (1985). C60: buckminsterfullerene. Nature 318: 162-163.), graphene sheets (Stankovich et al., 2006Stankovich, S., Dikin, D.A., Dommett, G.H.B., Kohlhaas, K.M., Zimney, E.J., Stach, E.A., Piner, R.D., Nguyen, S.T., Ruoff, R.S. (2006). Graphene-based composite materials. Nature 442: 282-286.) and nanotubes (Iijima, 1991Iijima, S. (1991). Helical microtubules of graphitic carbon. Nature 354: 56-58.) are common nano-structures. Nano-structures can be defined as a system where at least one dimension is less than 100 nm (Lieber, 1998Lieber, C.M. (1998). One-dimensional nanostructures: chemistry, physics & applications. Solid State Communications 107: 607-616.). These materials are expected to possess numerous properties which are interesting for their potential application in technological fields (Cornwell et al., 1997Cornwell, C.F., Wille, L.T. (1997) Elastic properties of single-walled carbon nanotubes in compression. Solid State Communications 101: 555-558.). The ground state of an infinitely large array of sp2 bonded carbons is the planar graphene configuration. For the finite arrays of carbons, such as fullerene, the situation is different. The non-saturated bonds at the edges increase the energy of the system significantly, and bending back and closure of the surface become energetically favorable. The energy per area of such closed surfaces as, e.g., fullerenes and carbon nanotubes is still higher than the energy of graphene (Holec et al., 2010Holec, D., Hartmann, M.A., Fischer, F.D., Rammerstorfer, F.G., Mayrhofer, P.H., Paris, O. (2010). Curvature-induced excess surface energy of fullerenes: density functional theory and Monte Carlo simulations. Physical Review B 81: 235403.).
In contrast to graphene and carbon nanotubes which have pure hexagonal atomic structures, each fullerene accommodates exactly 12 pentagonal rings beside hexagon rings. Some fullerenes have spherical structures which is also called "buckyball" and recognized with symbol CNo. (No. is the number of carbon atoms in buckyball structure) (Todt et al., 2013Todt, M., Rammerstorfer, F.G., Hartmann, M.A. (2013). Continuum shell models for closed cage carbon nanoparticles. Shell Structures: Theory and Applications 3: 149-152.).
There are several methods for the modeling of nano-structures (graphene and carbon nanotube), one of the important techniques for this modeling is molecular dynamics simulations. (Lu, 1997Lu, J.P. (1997). Elastic properties of carbon nanotubes and nanoropes. Physical Review Letters 79: 1297-1230.) and (Yakobson et al., 1996Yakobson, B.I., Brabec, C.J., Bernholc, J. (1996). Nanomechanics of carbon tubes: instabilities beyond linear response. Physical Review Letters 76: 2511-2514.) evaluated the mechanical properties of graphene sheet by using this method. (Kang et al., 2010Kang, Z., Li, M., Tang, Q. (2010). Buckling behavior of carbon nanotube-based intramolecular junctions under compression: Molecular dynamics simulation and finite element analysis. Computational Materials Science 50: 253-259.) investigated the buckling behavior of carbon nanotubes based intramolecular junctions (IMJ's) under axial compression by conducting finite element analysis and molecular dynamics simulations. (Chen and Cao, 2006Chen, X., Cao, G. (2006). A structural mechanics approach of single-walled carbon nanotubes generalized from atomistic simulation. Nanotechnology 17: 1004-1015.) studied the mechanical behavior of single-walled carbon nanotubes by molecular dynamics simulation and continuum shell modeling. Nanotubes are modeled with space frame elements and the properties of these elements generalized by molecular dynamics simulation base on ab-initio force field. In other studies, (Kudin et al., 2001Kudin, K.N., Scuseria, G.E., Yakobson, B.I. (2001). C 2 F, BN, and C nanoshell elasticity from ab initio computations. Physical Review B 64: 235406.) and (Wang et al., 2005Wang, L., Zheng, Q., Liu, J.Z., Jiang, Q. (2005). Size dependence of the thin-shell model for carbon nanotubes. Physical review letters 95: 105501-105504.) evaluated the mechanical properties of carbon nanotubes by using ab-intio method. Continuum mechanics is one of the important ones that have been used for modeling of important nano-structures such as graphene and carbon nanotube (Vodenitcharova et al., 2007Vodenitcharova, T., Mylvaganam, K., Zhang, L.C. (2007). Effective wall thickness of a single-walled carbon nanotube. Journal of Materials Science 42: 4935-4941.; Pantano et al., 2004Pantano, A., Parks, D.M., Boyce, M.C. (2004). Mechanics of deformation of single-and multi-wall carbon nanotubes. Journal of the Mechanics and Physics of Solids 52: 789-821.; Goupalov, 2005Goupalov, S.V. (2005). Continuum model for long-wavelength phonons in two-dimensional graphite and carbon nanotubes. Physical Review B 71: 085420.). (Huang et al., 2006Huang, Y., Wu, J., Hwang, K.C. (2006). Thickness of graphene and single-wall carbon nanotubes. Physical Review B 74: 245413.) established an analytical approach to bypass atomistic simulations and determine the thickness and elastic properties of graphene. Molecular mechanics is another method for modeling of nano-structures. Li and Chou were the first researchers used this method (2003Li, C., Chou, T.W. (2003). A structural mechanics approach for the analysis of carbon nanotubes. International Journal of Solids and Structures 40: 2487-2499.). Fundamental to the proposed concept was that the primary bonds between two nearest-neighboring atoms act like load-bearing beam members, whereas an individual atom acts as the joint of the related load-bearing beam members. By establishing a linkage between structural mechanics and molecular mechanics, the sectional and mechanical properties of these beam members were obtained (Kalamkarov et al., 2006Kalamkarov, A.L., Georgiades, A.V., Rokkam, S.K., Veedu, V.P., Ghasemi-Nejhad, M.N. (2006). Analytical and numerical techniques to predict carbon nanotubes properties. International Journal of Solids and Structures 43: 6832-6854.; Hu et al., 2007Hu, N., Nunoya, K., Pan, D., Okabe, T., Fukunaga, H. (2007). Prediction of buckling characteristics of carbon nanotubes. International Journal of Solids and Structures 44: 6535-6550.). (Sakhaee-pour, 2009Sakhaee-Pour, A. (2009). Elastic properties of single-layered graphene sheet. Solid State Communications 149: 91-95.) adopted an atomistic simulation method to investigate the elastic characteristics of defect-free single-layered graphene sheet. In this regard, the equivalent structural beam was employed to model interatomic forces of the covalently bonded carbon atoms. The beam properties were computed by considering the covalent bond stiffness. In recent years, structural mechanics method has been developed for evaluation of the mechanical properties.
Some researchers have used several specific methods for studying the properties of the nano-structures. In this regards (Tu and Ou-yang, 2002Tu, Z.C., Ou-Yang, Z.C. (2002). Single-walled and multiwalled carbon nanotubes viewed as elastic tubes with the effective Young's moduli dependent on layer number. Physical Review B 65: 233407.) investigated the Young's modulus and thickness of nanotubes by using local density approximation method. Accordingly, Ring theory continuum mechanics was used by (Vodenitcharova and Zhang, 2003Vodenitcharova, T., Zhang, L.C. (2003). Mechanical interaction between single-walled carbon nanotubes during the formation of a bundle. Physical Review B 68: 165401.). (Hernández et al., 1998Hernández, E., Goze, C., Bernier, P., Rubio, A. (1998). Elastic properties of C and BxCyNz composite nanotubes. Physical Review Letters 80: 4502-4505.) used tight binding molecular dynamics for investigation of the carbon nanotube mechanical properties. (Arroyo and Belytschko, 2004Arroyo, M., Belytschko ,T. (2004). Finite crystal elasticity of carbon nanotubes based on the exponential Cauchy-Born rule. Physical Review B 69: 115415.) presented a finite deformation continuum theory that was derived from interatomic potentials for the analysis of the mechanics of carbon nanotubes. This nonlinear elastic theory was based on an extension of the Cauchy-Born rule called the exponential Cauchy-Born rule. The continuum object replacing the graphene sheet was a surface without thickness. The method systematically addressed both the characterization of the small strain elasticity of nanotubes and the simulation at large strains. (Ghavamian et al., 2012Ghavamian, A., Rahmandoust, M., Ochsner, A. (2012). A numerical evaluation of the influence of defects on the elastic modulus of single and multi-walled carbon nanotubes. Computational Materials Science 62: 110-116.) studied the influence of the vacancy defects on the elastic modulus of single and multi-walled carbon nanotubes by using numerical method.
For exploring the mechanical properties of fullerenes some researchers utilized the mechanical properties of graphene for introducing a continuum model for fullerene (Todt et al., 2013Todt, M., Rammerstorfer, F.G., Hartmann, M.A. (2013). Continuum shell models for closed cage carbon nanoparticles. Shell Structures: Theory and Applications 3: 149-152.; Ahmad, 2002Ahmad, S. (2002). Continuum elastic model of fullerenes and the sphericity of the carbon onion shells. The Journal of Chemical Physics 116: 3396-3400.). Mechanical properties of fullerenes and carbon nanotubes have a relation with graphene properties. Thus, for investigation of fullerenes' properties, studying the mechanical properties of graphene is unavoidable.
(Todt et al., 2013Todt, M., Rammerstorfer, F.G., Hartmann, M.A. (2013). Continuum shell models for closed cage carbon nanoparticles. Shell Structures: Theory and Applications 3: 149-152.) investigated the mechanical properties of fullerenes by using continuum shell models and Monte Carlo (MC) simulation. They presented an effective modulus and thickness for a reprehensive continuum shell that has a good agreement with MC simulation results.
(Ahmad, 2002Ahmad, S. (2002). Continuum elastic model of fullerenes and the sphericity of the carbon onion shells. The Journal of Chemical Physics 116: 3396-3400.) described a continuum elastic model of fullerenes by utilizing the analogy between the closed carbon cages and elastic shells. The author presented expressions for the curvature-related strain energies of the pentagonal protrusions and proposed to explain the observed sphericity of the carbon onion shells as opposed to the predicted protrusions around the pentagonal defects on the basis of continuum elastic model of fullerenes.
In the case of carbon onions, (Todta et al., 2011Todta, M., Rammerstorfer, F.G., Fischer, F.D., Mayrhofer, P.H., Holec, D., Hartmann, M.A. (2011). Continuum modeling of van der waals interactions between carbon onion layers. Carbon 49: 1620-1627.) presented a continuum formulation of the van der Waals interactions between carbon onion layers in form of pressure/radius relations. The relations were derived analytically considering the doubly-curved geometry of carbon onion layers. For finite layer radii it was shown that the van der Waals induced pressures on opposing faces of two adjacent onion layers were not equal and depended on both layer radii. (Zerenturk and Berber, 2012Zerenturk, A., Berber, S. (2012). Hydrogen migration on the C60 fullerene. Solid State Communications 152: 1522-1525.) investigated the migration barriers, transition states, and optimum migration paths of hydrogen on the C60-fullerene using the ab-initio density functional theory. However, empirical evidence suggests that calculated energy barriers tend to be higher for non-local exchange-correlation functional.
In another study, (Murmu et al., 2011Murmu, T., Adhikari, S., Wang, C.Y. (2011). Torsional vibration of carbon nanotube-buckyball systems based on nonlocal elasticity theory. Physica E 43: 1276-1280.) conducted torsional vibration analysis of single-walled carbon nanotube-buckyball systems. In this work, the buckyball was attached to one end a single-walled carbon nanotube, while its other end was fixed. Such nano-structures are thus promising for applications in tunable nanoresonators, whose frequency can be altered by attaching different buckyballs.
(Adhikari and Chowdhury, 2011Adhikari, S., Chowdhury, R. (2011). Vibration spectra of fullerene family. Physics Letters A 375: 2166-2170.) considered a molecular mechanics approach for the vibration spectra analysis of fullerenes, examining sixteen different fullerenes, ranging from C20 to C720. Here, the universal force field potential was used for the molecular mechanics approach. The authors proposed an analytical expression based on the elastic shell theory, aiming to explain the variation of the natural frequencies across the entire family. In a similar work, (Prasanthi et al., 2014Prasanthi, P., Sambasiva Rao, G., Umamaheswar Gowd, B. (2014). Effectiveness of buckminster fullerene reinforcement on mechanical properties of FRP composites. Procedia Materials Science 6: 1243-1252.) performed a micromechanical study to evaluate the longitudinal and transverse properties of nano-based composite materials. Their analysis was based on selecting two different fibers (T-300, Boron), which were reinforced in nano-based matrix. The nano-sized reinforcement considered for the present work was buckminster fullerene, which was idealized as a hollow sphere of uniform thickness and the analysis was performed in two stages. In the first stage, the buckminster fullerene reinforced composite material properties were obtained using continuum approach. In the second stage, the analysis was extended by reinforcing the T-300, Boron fiber in buckminster fullerene reinforced composite to characterize the mechanical behavior. The finite element method was used to perform the micromechanical analysis of the composite material. The results indicated that better enhancement in the transverse properties of the composite material are obtained for buckminster fullerene in FRP composites. (Cavalcante and Furtado, 2014Cavalcante, E., Furtado, C. (2014). Geometric model of a fullerene molecule in the presence of Aharonov-Bohm flux. Journal of Physics and Chemistry of Solids 75: 1265-1268.) described a geometric model of a fullerene molecule with lh symmetry. In their work, the authors combined the well-known non-Abelian monopole approach and the geometric theory of defects, where every topological defect was associated with curvature and torsion, to describe a fullerene molecule.
(Moradi, 2014Moradi, A. (2014). Extinction properties of an isolated C60 molecule. Solid State Communications 192: 24-26.) investigated the extinction spectra of an isolated C60 molecule, within the framework of the vector wave function method. Electronic excitations on the C60 molecule surface were modeled by an infinitesimally thin spherical layer of the σ and π electrons, which was described by means of the two-dimensional two-fluid model. Molecular mechanics method is one of the most common approaches for modeling the behavior of nano-structures in nano- and micro-phases. However, in upper phase such as messo and macro because of the increased elements (beam element) and the consequent increase in the volume of computing and time, this solution method is not suitable. In this case, the continuum modeling using shell elements is an alternative for modeling nano-structures.
Based on literature survey most of the modeling of nano-structures is in case of graphene and nanotube, so in this paper, a continuum shell model is proposed for buckyball-C60 (thin-walled sphere). For this purpose, as a first step, fullerene real structure of C60 is modeled and, subsequently, an equivalent spherical structure is suggested to simulate fullerene structure. Two groups including spherical and elliptical strain examination are established to investigate the accuracy of proposed model for the fullerene simulation, while molecular mechanics modeling is used to verify the results of the continuum model.
2 MODELING OF BUCKYBALL-C60
In this section, the process of modeling the buckyball-C60 structure is explained. Three methodologies are considered for numerical modeling of the fullerene structure. In the first model, continuum finite element shell structure is used in which elements filling the gaps between carbon atoms in C60 structure, Figure 1. In the second method, the elements of first method are mapped on an equivalent sphere. The spherical model for simulation the fullerene structure is shown in Figure 2. The third method, taking into account lattice structure of buckyball, carbon atoms are connected using beam elements. Thus, a discrete structure of buckyball is modeled by molecular mechanics method. Considered as material points and the forces are modeled using beam model, Figure 3. It should be noted that the third method is used to verify the proposed methodology.
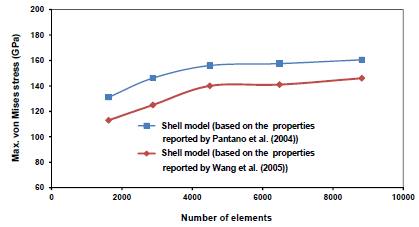
Since the results of a finite element model are sensitive to the number of elements; a mesh sensitivity analysis has been carried out to make sure that the solution is meshing independent. For this purpose two sets of properties based on (Pantano et al., 2004Pantano, A., Parks, D.M., Boyce, M.C. (2004). Mechanics of deformation of single-and multi-wall carbon nanotubes. Journal of the Mechanics and Physics of Solids 52: 789-821.) and (Wang et al., 2005Wang, L., Zheng, Q., Liu, J.Z., Jiang, Q. (2005). Size dependence of the thin-shell model for carbon nanotubes. Physical review letters 95: 105501-105504.) observations are selected and the sensitivity analysis performed to spherical structure of buckyball-C60 with a radial displacement showed a good convergence tendency as shown in Figure 4. Based on that curve, the number of elements selected is 4500 in the simulation process.
In the next section, shell element parameters that used in the model are carefully chosen by investigating a radial displacement subjected to mapped and faceted C60 structure.
3 MECHANICAL PROPERTIES OF BUCKYBALL-C60
This section presents the modeling strategy of C60-fullerene using shell model of faceted and spherical mapped subjected to internal hydrostatic pressure for determining the mechanical properties. For this purpose, a continuum thin-walled sphere of radius r consists of shell elements with thickness t and modulus E is analyzed by considering five different cases under internal pressure. Due to symmetry, tangential (wall) stresses are equal to each other in all the directions. Note that in thin-walled sphere the radial stresses have been neglected. In order to determine this stress, the equilibrium is considered in half of the sphere:
where σ θ is the tangential stress; ε θ is tangential strain; P is internal hydrostatic pressure; t is thickness of continuum model of fullerene; r is the radius of continuum mapped and average radius of faceted model; ν is Poisson's ratio of sphere and E is Young's modulus of continuum model.
By defining the parameter λ as: λ=(1-ν)/E, Eq. (1) becomes
Note that the parameter λ describes the Young's modulus and Poisson's ratio of the shell models which is different from Young's modulus and Poisson's ratio of shell elements. In the calculations, the radius of the C60-fullerene spherical structure is given by r=3.55 Å (Todt et al., 2013Todt, M., Rammerstorfer, F.G., Hartmann, M.A. (2013). Continuum shell models for closed cage carbon nanoparticles. Shell Structures: Theory and Applications 3: 149-152.).
For graphene and carbon nanotubes different values for Young's modulus, layer thickness and Poisson's ratio are presented in the literature according to various methods, so that these values can be used to simulate the real structure and equivalent spherical structure of fullerene. In all studies clearly indicate that despite the different values of Young's modulus and thickness, the multiplication of modulus and thickness, namely E×t, has consistently been reported as an average value of about 3.3 TPaÅ. This expression shows that for correct modeling of the fullerene, this parameter should be considered. Young's modulus, thickness and Poisson's ratio for five types of shell elements in C60 structure simulation according to available data in the literature are listed in Table 1.
Five different structures of fullerene are modelled using the parameters given in Table 1. And all sets are exposed to internal hydrostatic pressure regarding their ability to predict the mechanical behavior of C60 buckyball.
In order to simulate the hydrostatic pressure, displacement boundary condition is applied on the points (carbon atoms). By applying a radial displacement on the models which is actually tangential strain, the resultant forces are determined and subsequently pressure is extracted. Thus, the parameter λ is calculated from Eq. (2) using known amounts.
In the following step, strain energy obtained due to mapping of equivalent spherical C60 structure on different elliptical shapes are analyzed using two different models, namely, shell model of elliptical mapped and lattice structure composed of beam elements. In this stage, the equivalent spherical model and molecular mechanics model are mapped on the different ellipses. In order to map the fullerene structure on the ellipses, relevant elliptical parameters shown in Figure 5 are used. The fullerene structure mapped on an ellipse is shown in Figure 6. Here, it should be noted that using different elliptical parameters, various mappings of fullerene structure for C60 are obtained.
4 RESULTS AND DISCUSSION
The main goal of this research is to introduce an equivalent sphere for C60 based on continuum modeling, but the C60 is not a complete sphere, so the real geometries of this structure (faceted model) should be studied too. The results of parameter λ in the simulation of the real structure (faceted) and equivalent spherical of fullerenes (mapped) for overall cases C1-C5 is presented in Table 2. According to these results, the fullerene elastic modulus is calculated and listed in Table 3. It should be noted that equivalent Poisson's ratio from an average of the Poisson's ratio of shell elements in C1 to C5 is used.
Parameter λ obtained using faceted and spherical mapped model for modelling C60 fullerene structure.
It can be seen in Table 3 that the elastic modulus for C60 structure, obtained using faceted model and spherical mapped model are in the range of 4.46-5.96 TPa and 3.77-5.15 TPa, respectively. These results are comparable to the ones considered by different researchers (Yakobson et al., 1996Yakobson, B.I., Brabec, C.J., Bernholc, J. (1996). Nanomechanics of carbon tubes: instabilities beyond linear response. Physical Review Letters 76: 2511-2514.; Kudin et al., 2001Kudin, K.N., Scuseria, G.E., Yakobson, B.I. (2001). C 2 F, BN, and C nanoshell elasticity from ab initio computations. Physical Review B 64: 235406.; Vodenitcharova and Zhang, 2003Vodenitcharova, T., Zhang, L.C. (2003). Mechanical interaction between single-walled carbon nanotubes during the formation of a bundle. Physical Review B 68: 165401.; Pantano et al., 2004Pantano, A., Parks, D.M., Boyce, M.C. (2004). Mechanics of deformation of single-and multi-wall carbon nanotubes. Journal of the Mechanics and Physics of Solids 52: 789-821.; Wang et al., 2005Wang, L., Zheng, Q., Liu, J.Z., Jiang, Q. (2005). Size dependence of the thin-shell model for carbon nanotubes. Physical review letters 95: 105501-105504.) for graphene layers based on different thickness and elastic modulus.
The different structures of faceted an mapped models cause some differences between predictive modules. In the faceted model the pentagonal protrusions affected the system by concentrating the stress so because of this reason, the average predictive modulus in faceted model increases in comparison to mapped model.
The radial displacement contours of faceted and mapped models under a same strains for case C4 are shown in Figure 7 and 8. Both models are achieved the average strain 8%. The difference of contours is because of the deference of the nature of the models' structures(mapped and faceted). Based on these results, the strain energy is generated. It should also be noted that similar behavior has been observed in the displacement domain for all models, so, only the results for case C4 is presented.
In the following, using the radial strain results obtained from the shell model of spherical mapped and faceted C60, the proper thickness is set to determine the modulus for the continuum layer representing fullerene. As an approved and accepted method is needed for verification of the obtained results, molecular mechanics method presented by (Li and Chou, 2003Li, C., Chou, T.W. (2003). A structural mechanics approach for the analysis of carbon nanotubes. International Journal of Solids and Structures 40: 2487-2499.) is adopted. In this method, the atomic bonds between carbon atoms are modeled as a circular beam with length 1.42 and radius 0.73 Å. Since the C60 structure consists of 90 atomic bonds, 90 beam elements are used for modeling this structure in the molecular mechanics method. The mechanical properties of this beam are presented in Table 4.
Figure 9 shows the molecular model representing C60-fullerene structure in which beam element is used to model the covalent bond between carbon atoms.
In order to calculate the fullerene strain energy, radial displacement is applied on all shell models, in addition to employing the model composed of beam elements (molecular mechanics method).
The C60 strain energy results (for strain=8%) obtained by shell faceted and spherical mapped models are compared in Table 5 for cases C1-C5. Simulation results indicated that, in comparison with the molecular mechanics model results, the C4 and C5 are the best shell model representing C60-fullerene structure.
Comparison between C60-fullerene strain energy obtained from shell faceted and spherical mapped models and lattice structure (for strain=8%).
Based on the results obtained for different thicknesses, it can be seen that the spherical mapped model for C60 correlates well with the results obtained from the model composed of beam elements in the cases C4 and C5 (with an error of about 2%). Therefore, it can be assumed in the future analyses that the C60-fullerene is a complete sphere. Hence, these structures can be modelled using a shell of 0.665 Å thickness, 5.07 TPa elastic modulus and 0.165 Poisson's ratio or a shell of 0.75 Å thickness, 4.84 TPa elastic modulus and 0.19 Poisson's ratio.
Contour of the fullerene strain energy for the model composed of shell and beam elements are shown in Figure 10 and 11. These contours present the strain energy of each elements in models. In order to simulate the strain energy, the displacement is applied on points (carbon atoms) of all models. The results show the strain energy of each element for 8% strain. The total strain energy in models is equal to the sum of the strain energy value of each element (4500 shell elements and 90 beam elements), as listed in Table 5. For the continuum shell model, it should be noted that for achieving the 8% strain, displacements are applied to 60 points. In this way, the model has this amount of strain totally, while the strains values correspond to these 60 points are not considered in calculations. The results in Figure 10-a and 10-b present the strain energy of elements on faceted and mapped models for case C4 based on the radial displacement (strain 8%), respectively. Figure 11 also presents the resulting strain energy of elements on molecular mechanic model under strain 8%.
In order to provide further verification of the results obtained thus far, the elliptical displacement is applied to the spherical continuum shell model based on parameter values mentioned in the cases C4 and C5. Figure 12 shows an example of the displacement contour results on the shell model that has been compared with the beam element results based on the same elliptical strain. As can be seen, there is a good agreement between the two approaches. Note that a little difference in the maximum and minimum values is due to the type and size of elements in continuum shell model and molecular model (90 beam elements and 4500 shell elements). In the process of mapping using shell elements the simulation of curvature at the ends of model is accurate than the beam elements.
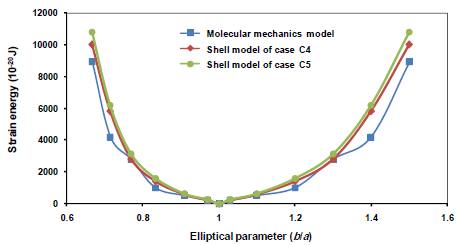
The strain energy obtained of shell models for the cases C4 and C5 and the beam element model based on different parameters of elliptical displacement is shown in Figure 13. The results show that for 0.9<elliptical parameter<1.1, the strain energies obtain from shell models and molecular model are fully matched. By varying the value of elliptical parameter, less than 0.9 and more than 1.1, the strain energies of shell models and molecular mechanics model diverge from each other. The large displacement is the main reason for this phenomenon.
5 CONCLUSIONS
This paper presents an equivalent thin-walled sphere for buckyball-C60 based on continuum mechanics modelling instead of molecular dynamics simulation and molecular structural mechanic modeling. Since this structure is almost spherical, at the first place, it is attempted to model the exact geometry of fullerene and then mapping it on the complete sphere. Exact fullerene structure and mapped structure is modelled by shell elements. The properties of shell elements is adopted from graphene sheets, so five cases of properties is selected for this purpose, where multiplying of the elastic modulus and thickness (E×t) for different cases are equal. Two groups including spherical and elliptical strain examination are used for investigation of the accurate shell element properties for fullerene modeling. In addition, molecular mechanics modeling is used for verification the results.
In the first by comparison of strain energy of molecular mechanics model and continuum model consist of shell element by different properties in radial displacement, two series of properties is suggested for using in fullerene modeling. The properties for the first chosen case is 0.665 Å thickness, 5.07 TPa elastic modulus and 0.165 Poisson's ratio and for another one is 0.75 Å thickness, 4.84 TPa elastic modulus and 0.19 Poisson's ratio.
Finally for further verification for these selected elements properties, elliptical displacement is used. The elliptical displacement makes different displacements for each element. By comparing between strain energy of equivalent spherical fullerene model and the fullerene model composed of beam elements under elliptical strains for 0.9<elliptical parameter<1.1 the same behavior is observed, but outside of mentioned elliptical parameter domain because of the large values of the radial displacements, a gap between the results of continuum shell model and molecular model is appeared. So, the result indicates that the proposed model is suitable for fullerene simulation under small displacement such as linear domain.
REFERENCES
- Adhikari, S., Chowdhury, R. (2011). Vibration spectra of fullerene family. Physics Letters A 375: 2166-2170.
- Ahmad, S. (2002). Continuum elastic model of fullerenes and the sphericity of the carbon onion shells. The Journal of Chemical Physics 116: 3396-3400.
- Arroyo, M., Belytschko ,T. (2004). Finite crystal elasticity of carbon nanotubes based on the exponential Cauchy-Born rule. Physical Review B 69: 115415.
- Cavalcante, E., Furtado, C. (2014). Geometric model of a fullerene molecule in the presence of Aharonov-Bohm flux. Journal of Physics and Chemistry of Solids 75: 1265-1268.
- Chen, X., Cao, G. (2006). A structural mechanics approach of single-walled carbon nanotubes generalized from atomistic simulation. Nanotechnology 17: 1004-1015.
- Cornwell, C.F., Wille, L.T. (1997) Elastic properties of single-walled carbon nanotubes in compression. Solid State Communications 101: 555-558.
- Ghavamian, A., Rahmandoust, M., Ochsner, A. (2012). A numerical evaluation of the influence of defects on the elastic modulus of single and multi-walled carbon nanotubes. Computational Materials Science 62: 110-116.
- Goupalov, S.V. (2005). Continuum model for long-wavelength phonons in two-dimensional graphite and carbon nanotubes. Physical Review B 71: 085420.
- Hernández, E., Goze, C., Bernier, P., Rubio, A. (1998). Elastic properties of C and BxCyNz composite nanotubes. Physical Review Letters 80: 4502-4505.
- Holec, D., Hartmann, M.A., Fischer, F.D., Rammerstorfer, F.G., Mayrhofer, P.H., Paris, O. (2010). Curvature-induced excess surface energy of fullerenes: density functional theory and Monte Carlo simulations. Physical Review B 81: 235403.
- Hu, N., Nunoya, K., Pan, D., Okabe, T., Fukunaga, H. (2007). Prediction of buckling characteristics of carbon nanotubes. International Journal of Solids and Structures 44: 6535-6550.
- Huang, Y., Wu, J., Hwang, K.C. (2006). Thickness of graphene and single-wall carbon nanotubes. Physical Review B 74: 245413.
- Iijima, S. (1991). Helical microtubules of graphitic carbon. Nature 354: 56-58.
- Kalamkarov, A.L., Georgiades, A.V., Rokkam, S.K., Veedu, V.P., Ghasemi-Nejhad, M.N. (2006). Analytical and numerical techniques to predict carbon nanotubes properties. International Journal of Solids and Structures 43: 6832-6854.
- Kang, Z., Li, M., Tang, Q. (2010). Buckling behavior of carbon nanotube-based intramolecular junctions under compression: Molecular dynamics simulation and finite element analysis. Computational Materials Science 50: 253-259.
- Kroto, H.W., Heath, J.R., O'Brien, S.C., Curl, R.F., Smalley, R.E. (1985). C60: buckminsterfullerene. Nature 318: 162-163.
- Kudin, K.N., Scuseria, G.E., Yakobson, B.I. (2001). C 2 F, BN, and C nanoshell elasticity from ab initio computations. Physical Review B 64: 235406.
- Li, C., Chou, T.W. (2003). A structural mechanics approach for the analysis of carbon nanotubes. International Journal of Solids and Structures 40: 2487-2499.
- Lieber, C.M. (1998). One-dimensional nanostructures: chemistry, physics & applications. Solid State Communications 107: 607-616.
- Lu, J.P. (1997). Elastic properties of carbon nanotubes and nanoropes. Physical Review Letters 79: 1297-1230.
- Moradi, A. (2014). Extinction properties of an isolated C60 molecule. Solid State Communications 192: 24-26.
- Murmu, T., Adhikari, S., Wang, C.Y. (2011). Torsional vibration of carbon nanotube-buckyball systems based on nonlocal elasticity theory. Physica E 43: 1276-1280.
- Pantano, A., Parks, D.M., Boyce, M.C. (2004). Mechanics of deformation of single-and multi-wall carbon nanotubes. Journal of the Mechanics and Physics of Solids 52: 789-821.
- Prasanthi, P., Sambasiva Rao, G., Umamaheswar Gowd, B. (2014). Effectiveness of buckminster fullerene reinforcement on mechanical properties of FRP composites. Procedia Materials Science 6: 1243-1252.
- Sakhaee-Pour, A. (2009). Elastic properties of single-layered graphene sheet. Solid State Communications 149: 91-95.
- Stankovich, S., Dikin, D.A., Dommett, G.H.B., Kohlhaas, K.M., Zimney, E.J., Stach, E.A., Piner, R.D., Nguyen, S.T., Ruoff, R.S. (2006). Graphene-based composite materials. Nature 442: 282-286.
- Todt, M., Rammerstorfer, F.G., Hartmann, M.A. (2013). Continuum shell models for closed cage carbon nanoparticles. Shell Structures: Theory and Applications 3: 149-152.
- Todta, M., Rammerstorfer, F.G., Fischer, F.D., Mayrhofer, P.H., Holec, D., Hartmann, M.A. (2011). Continuum modeling of van der waals interactions between carbon onion layers. Carbon 49: 1620-1627.
- Tu, Z.C., Ou-Yang, Z.C. (2002). Single-walled and multiwalled carbon nanotubes viewed as elastic tubes with the effective Young's moduli dependent on layer number. Physical Review B 65: 233407.
- Vodenitcharova, T., Mylvaganam, K., Zhang, L.C. (2007). Effective wall thickness of a single-walled carbon nanotube. Journal of Materials Science 42: 4935-4941.
- Vodenitcharova, T., Zhang, L.C. (2003). Mechanical interaction between single-walled carbon nanotubes during the formation of a bundle. Physical Review B 68: 165401.
- Wang, L., Zheng, Q., Liu, J.Z., Jiang, Q. (2005). Size dependence of the thin-shell model for carbon nanotubes. Physical review letters 95: 105501-105504.
- Yakobson, B.I., Brabec, C.J., Bernholc, J. (1996). Nanomechanics of carbon tubes: instabilities beyond linear response. Physical Review Letters 76: 2511-2514.
- Zerenturk, A., Berber, S. (2012). Hydrogen migration on the C60 fullerene. Solid State Communications 152: 1522-1525.
Publication Dates
-
Publication in this collection
May 2016
History
-
Received
03 Oct 2015 -
Reviewed
11 Jan 2016 -
Accepted
16 Feb 2016