Abstract
An axial follower force acting on the free end of a beam-column is known to remain tangential to its elastica at that point. Elastic beam-columns exhibit infinitely high buckling resistance to static compressive follower load. Loss of their dynamic stability is known to occur at critical follower loads, by flutter characterized by vanishing lateral displacement and infinitely high natural frequency. Classical theory deals with physically linear nonconservative beam-columns. Physical nonlinearity exhibited by concrete beam-columns under service loads is caused by the closing and reopening of the extant transverse cracks. In this Paper, analytical expressions for the lateral displacement and lateral stiffness of such concrete beam-columns are derived. Using these expressions, the stability of physically nonlinear elastic flanged concrete beam-columns under the action of a follower compressive axial force and a lateral force is investigated. The significance of the analytical approach and the theoretical predictions is discussed.
Concrete beam-columns; tangential follower load; flutter; divergence; snap-through
Stability of concrete beam-columns under follower forces
Mamta R. SharmaII; Arbind K. SinghI; Gurmail S. BenipalI,** Author email: gurmail@civil.iitd.ernet.in
IAssociate Professor, Department of Civil Engineering, I IT Guwahati
IIResearch Scholar, Department of Civil Engineering, I IT Delhi
ABSTRACT
An axial follower force acting on the free end of a beam-column is known to remain tangential to its elastica at that point. Elastic beam-columns exhibit infinitely high buckling resistance to static compressive follower load. Loss of their dynamic stability is known to occur at critical follower loads, by flutter characterized by vanishing lateral displacement and infinitely high natural frequency. Classical theory deals with physically linear nonconservative beam-columns. Physical nonlinearity exhibited by concrete beam-columns under service loads is caused by the closing and reopening of the extant transverse cracks. In this Paper, analytical expressions for the lateral displacement and lateral stiffness of such concrete beam-columns are derived. Using these expressions, the stability of physically nonlinear elastic flanged concrete beam-columns under the action of a follower compressive axial force and a lateral force is investigated. The significance of the analytical approach and the theoretical predictions is discussed.
Keywords: Concrete beam-columns, tangential follower load, flutter, divergence, snap-through
1 INTRODUCTION
Like dead loads, many types of live or imposed loads acting on the structures are gravitational forces. During the deformation of the structures, the points of action of such loads do not shift and their directions also remain same. The stiffness matrix of structures under such loads is symmetric. The energy is unique path-independent reversible additive function of the state variables and is conserved during closed load cycles. Such conservative forces are also called gradient or potential forces because they can be derived as gradients of a potential in the space of state variables. Energy theorems are valid for these conservative or self-adjoint structures.
In contrast, the fluid-structure interactions impose some nonconservative forces on the structures. Either the point of action of these forces shifts on the structures during their deformation or motion, or their direction of action does not remain invariant. For example, the line of action of a follower force remains parallel to the deformed centroidal axis of a beam-column. Viscous fluids flowing past a surface of a deformable structure impose a tangential drag force on it. Examples of follower forces include a fluid-conveying cantilevered pipe, rocket thrust caused by solid propellant fuel, powered jets, rockets or missiles, etc. Aeroplane wing flutter caused by aeroelastic follower forces is well known in aeronautical engineering (Bazant and Cedolin, 2010; Bolotin, 1964; Chen, 1976; Thomsen, 2003; Leipholz, 1978; Sugiyama, et al, 1999). Follower forces are also encountered, though as yet not recognized as such, even in the machine foundations and structures supporting rotating or reciprocating machinery (Srinivasulu and Vaidyanathan, 1976). A cantilever type beam-column supporting a rotating machine at the top end can also be considered to be under the action of pulsating tangential and transverse follower forces. As a special case, two motors with opposite direction of motion result only in sinusoidal tangential follower force. Long- span cable-stayed and suspension bridges are shown to be vulnerable to flutter instability at critical wind velocities (Kreis and Andre, 2005). The extensive literature available till that time on the theoretical and experimental studies on the dynamic stability of columns subjected to follower forces has been evaluated (Langthjem and Sugiyama, 2000).
The stiffness matrix of the nonconservative structures being asymmetric, the work done by these forces is not a unique function of the state variables. Instead, it is path-dependent resulting in energy deficit or excess in the closed load cycles. Invalidity of the principle of conservation of energy implies the invalidity of energy theorems for structural analysis. To be specific, theorems of Maxwell, Betti and Castigliano as well as principle of minimum potential energy are invalid. Euler's method of buckling of elastic structures is equivalent to the energy-based methods. Hence, it is valid only for investigating the stability of conservative structures. For example, the critical buckling load of a column under a follower force is predicted by the Euler method to be infinitely high. This implies that column under a follower force is always stable. However, Euler method can only determine states of static equilibrium adjacent to the given equilibrium state. For determining the alternative states of dynamic equilibrium, the methods of dynamic stability analysis have to be employed. Indeed, the elastic columns have been observed to lose their dynamic stability by flutter. Such stability analysis has proved to be useful in the design of many types of structures like aeroplanes (Bazant and Cedolin, 2010; Bolotin, 1964; Chen, 1976; Thomsen, 2003; Leipholz, 1976; Sugiyama, et al, 1999; Langthjem and Sugiyama, 2000). Interestingly, even in the presence of abundant literature dealing with the stability of structures under follower forces published in the past few decades, the admissibility of the concept of static follower force has recently been questioned on operational grounds (Elishakoff, 2005; Sugiyama, et al, 1999).
With increase in applied loads, concrete structures exhibit cracking of concrete, yielding and debonding of reinforcement, crushing of concrete, etc., prior to failure. Being design-oriented, the popular methods of concrete structural analysis attempt to incorporate the effect of all the above factors (Chopra, 2007). Such is also the case with stability analysis of concrete columns and beam- columns subjected to conservative loads. To the best of Authors' knowledge, stability of nonconservative concrete structures has not yet been analysed. Exceptionally, Aristizabal-Ochoa has emphasized the significance of investigating the behaviour of beam-column connections undergoing finite rotations under the action of tangential follower forces (Aristizabal-Ochoa, 2004, 2005). Need has been felt for carrying out more accurate analysis of concrete structures including the effects of material and geometric nonlinearity (Nogueira et al, 2013). Stiffness degradation caused by fire (Caldas et al, 2014) can render such concrete structures vulnerable to static and dynamic instabilities. Concrete structures are cracked in flexural tension even under service loads. Fully cracked concrete structures undergoing small deformations exhibit physically nonlinear elastic behaviour. Conventional stability analysis generally deals with physically linear structures. Static and dynamic stability of fully cracked concrete columns and beam-columns subjected to conservative loads has been earlier investigated by the Authors. Two values of the critical axial and lateral loads are identified for the concrete beam-columns in the form of cantilever. Concrete beam- columns are predicted to fail by brittle mode at peak axial loads and small lateral displacements. For constant lateral load, quite complex axial load-lateral displacement behaviour is exhibited. For lesser lateral loads, two equilibrium displacements are possible, out of which the one with lesser displacement is dynamically stable while the other is dynamically unstable. In this latter case, the loss of dynamic stability occurs by divergence. At two critical axial loads, the loss of stability occurs by vanishing natural frequency. The load space and the phase plane of initial conditions are partitioned into stable and unstable regions (Sharma et al. 2010; 2012a; 2012b).
The objective of the present Paper is to investigate the elastic stability of such beam-columns under the action of a conservative lateral force and a tangential follower force. Expressions for the lateral displacement and lateral stiffness are derived and the nonlinear differential equation of motion is formulated. The theoretical predictions using the analytical-computational methodology are discussed.
2 THEORETICAL FORMULATION
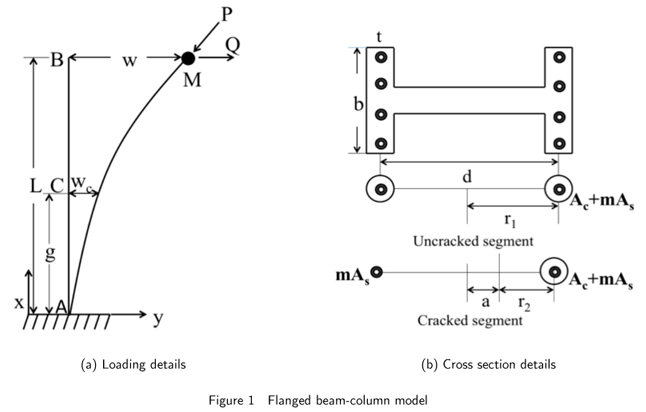
Consider a fully cracked flanged concrete beam-column in the form of a vertical cantilever under the action of an tangential follower force P and a conservative lateral force Q. The cross section has equal reinforced flanges with concentrated areas of concrete and reinforcement as shown in Fig. 1. For some load combinations, the upper segment BC of the beam-column can have existing cracks in the closed state, while the tension flange of the lower segment AC has cracks in the open state.
Here, these upper 'uncracked' and lower 'cracked' segments and their section properties, like moments of inertia and the location of the centroids, are denoted by subscripts 1 and 2 respectively. As in the earlier derivations (Bolotin, 1964 ; Bazant and Cedolin, 2010), the tangential follower force P is resolved into vertical and horizontal components. Assuming the slope θ of the elastica at the free end to be small, these components turn out to be P and (Pθ) respectively.
In this Paper, the moments of inertia of the uncracked as well as cracked sections are determined in reference to their respective elastic centroids. Also, the same centroidal axes play the role of the reference axes for measuring the eccentricity of vertical load component for determining the flexural moment introduced by it. The flexural moment at any section in the uncracked segment BC yields the following second order differential equation:
Or equivalently,
Here, the prime denotes differentiation with respect to space coordinate x. Also,  ,
,  ,
,  ,
,  . Similarly, y(L) = w and y'(L) = θ. The general solution for the above differential equation (2c) is of the form:
. Similarly, y(L) = w and y'(L) = θ. The general solution for the above differential equation (2c) is of the form:
Using equations (2), the boundary conditions at the free end (y"(L) = 0 and y"'(L) = - ) yields the following expressions:
) yields the following expressions:
Similarly, the differential equation of flexural equilibrium in the cracked segment AC is stated as
Or equivalently,
The general solution is obtained as
The boundary conditions at the fixed end (y(0) = 0 and y'(0) = 0) yields the following expressions
The following two more equations are obtained by using continuity conditions for displacement and slope at C (x=g):
Elementary structural mechanics requires that, for nil strain in the 'tension' flange, the moment at C in CB and CA segments must amount to Pr1 and Pr2 respectively. In view of this, equations (2a) and (6a) respectively yield the following expressions:
Similarly, the equations (2b) and (6b) respectively yield the following expressions
One obtains the equality
Using equations (4), (8), (9), (11) and (13), the unknown coefficients are determined as
 ,
,  ,
,  ,
, 
X1 = (B cos k2g + 1 B) sin k1 (L g) + sin k2g cos k1 (L g)
sin k2g cos k1 (L g)
X1 = cos k2g cos k1 (L g)  sin k2g sin k1 (L g)
sin k2g sin k1 (L g)
X1 = sin k2g cos k1 (L g) + cos k2g sin k1 (L g)
cos k2g sin k1 (L g)
Thus, the expression for the lateral displacement w, rotation θ and the lateral stiffness K are determined as follows:
Another useful expression in terms of loads is obtained from equation (10a) for determining the length 'g' of the cracked segment AC as
When the cracks at all the sections are closed, the expressions for the lateral displacement and lateral stiffness for such uncracked concrete beam-columns are obtained as
These expressions derived for physically linear beam-columns are identical to the well-known expressions for the physically linear columns under the action of the axial follower force (Bolotin, 1963; Bazant and Cedolin, 2010). Clearly, the lateral stiffness of the physical linear beam-columns is independent of the magnitude of the lateral force. The flutter loads for the fully uncracked beam-columns can be obtained using the conventional theory as 20.19 , while for the fully uncracked state, the corresponding flutter loads are B times lower.
, while for the fully uncracked state, the corresponding flutter loads are B times lower.
For this SDOF nonlinear dynamical system, the stiffness and damping coefficients are vibration amplitude-dependent. The instantaneous values of the natural frequency ωn and the damping coefficient C depend upon the instantaneous stiffness coefficient K and the constant mass M lumped at the free end as
where ξ is the damping ratio.
Thus, the second order nonlinear differential equation of motion of the SDOF partly-cracked beam-column subjected to forcing function F(t) is stated as
The above analysis is intended for cracked concrete flanged beam-columns is also valid for flanged beam-columns composed of bimodular solids. Concrete or ferrocement with distributed reinforcement can be modelled as bimodular solids. Let the bimodular ratio c be defined as  where Et and Ec denote the values of Young's moduli of elasticity in tension and compression respectively. This bimodular ratio c is related to the parameter B as B(1 + c) = 2c.
where Et and Ec denote the values of Young's moduli of elasticity in tension and compression respectively. This bimodular ratio c is related to the parameter B as B(1 + c) = 2c.
3 STABILITY ANALYSIS
The theoretical predictions presented below pertain to a particular concrete beam-column with following numerical details:
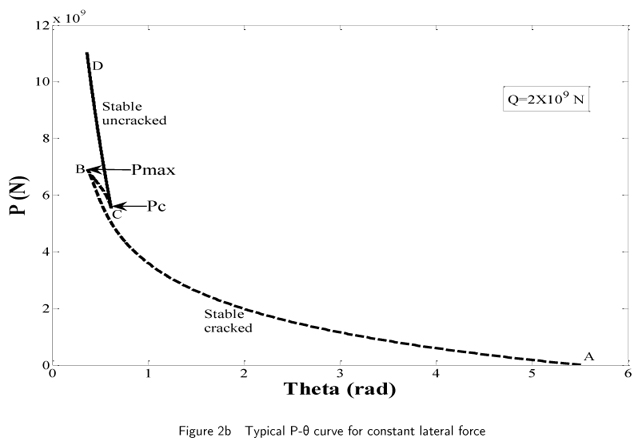
The results apply to a bimodular ratio of 0.099. The adopted computational algorithm is based upon average acceleration Newmark-Beta method. When only the lateral force Q is acting, the concrete beam-columns are cracked all through their length. Application of an axial follower force P results in the closure of extant cracks in the upper segment. The lateral force remaining constant, the typical axial-load lateral displacement (P w) and axial load-end rotation (P θ) curves are shown in Fig. 2. With increase in axial force, the lateral displacement initially decreases. With further increase in axial load, quite complex response is predicted. Segment AB of the (P w) curve is associated with an increase in axial load upto Pmax and a decrease in the length 'g' of the cracked segment of the concrete beam-column from its length L to a certain value. To be specific, cracks at all the sections do not close up at Pmax. Further decrease in 'g' along segment BC of (P w) curve is accompanied by a decrease in axial load from Pmax to Pc. Here, Pc signifies the magnitude of axial load corresponding to vanishing 'g'as per Eq. (17). The segment CD of the P w curve pertains to uncracked beam-columns.
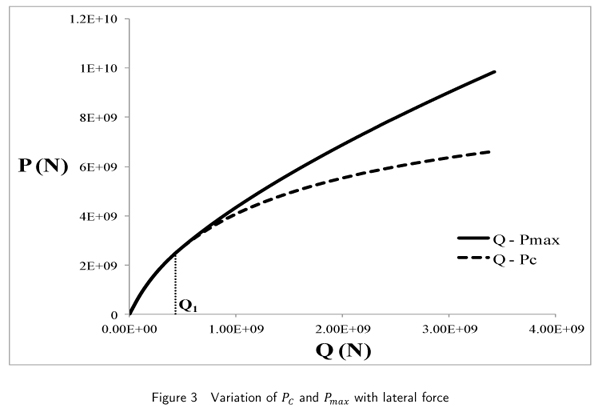
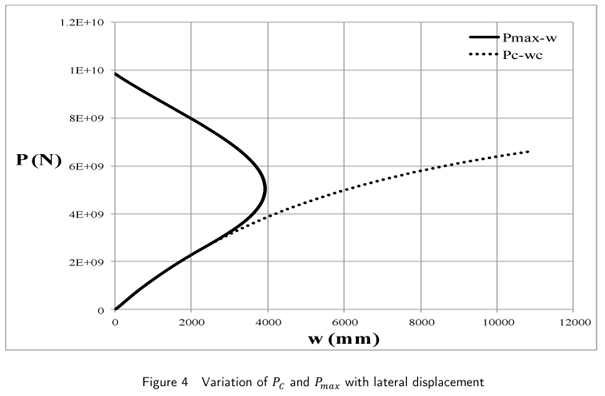
The variation of end rotation with P resembles that of the lateral displacement. The variation of Pmax and Pc with Q is shown in Fig.3. Equation (17) gives an expression for Pc in terms of Q, while Pmax has been determined by numerical computations. It can be observed that Pmax exists only for lateral load exceeding Q1. For this particular case the magnitude of Q1 turns out to be 0.437x109 N with the corresponding value of Pc as 2.352x109 N. Systematically varying the magnitude of the lateral force, the variation of Pmax and Pc with their corresponding lateral displacements is plotted in Fig.4. With increase in Q, both Pmax and Pc are predicted to increase. Similarly, Pc increases monotonically with wc. The displacement wm corresponding to the peak load Pmax first increases, but reaches a maximum value at Q = 1.34x109N before decreasing with further increase in Q. The lateral displacement vanishes when Q attains the magnitude Q2 given by 3.014 109N. For higher values of Q the lateral displacements can be negative as discussed later.
From the enlarged view of the P w curve in Fig.2 presented in Fig.5, it can observed that for P < Pc and for P > Pmax, the concrete beam-columns are predicted to exhibit unique response. However, for Pc< P < Pmax, three equilibrium states with different lateral displacements are possible. Corresponding to the segments AB, BC and CD of the P w curve discussed in Fig.2 above, these three displacements are denoted as w1, w2 and w3 respectively. For a particular load set (P = 6.2Sx109N, Q = 2x109N) the above three equilibrium displacements turn out to be 3793 mm, 5433.5 mm and 6646.7 mm respectively. Further, the dynamic stability of these three alternative equilibrium states is studied. This is achieved by analysing the phase plane representations of the dynamic response of concrete beam-columns taking the above equilibrium displacements as the initial displacements in different cases. In all these investigations, vanishing initial velocity is assumed. Phase plane plots shown in Fig.6 reveal that, irrespective of the particular initial displacement for each case, the lateral displacement asymptotically attains the same value w2. It can be observed that the trajectories originating from the other equilibrium displacements w1 and w3 diverge, i.e., are repelled away. It implies that the equilibrium states corresponding to displacements w1 and w3 are dynamically unstable. Such a dynamic instability is called divergence. It has been verified, but not presented here, that the above conclusion deduced for a particular case is valid for other magnitudes of the axial and lateral loads as well.
It is worth mentioning here that purely static structural response is a theoretical construct. In fact, under 'static' load variations, structures exhibit quasi-static behaviour. Real structures located in the natural environment as well as the structural models in the laboratory are subjected to small perturbations. Obviously, the dynamically unstable equilibrium states are de facto inaccessible to measurement and the structures are observed to exhibit only dynamically stable 'static' response. In view of this argument, the P w curve discussed above can be reinterpreted. Fig.7 depicts the observed static response of a concrete beam-column subjected to a constant lateral force and a monotonically increasing axial follower force. Here, the observed P w curve is identified as AcCBbD. As the axial load is increased upto Pc, the segment Ac of the curve depicts the stable structural response. When the axial load slightly exceeds Pc, a sudden increase cC in the lateral displacement is predicted. For Pc < P < Pmax, only the segment CB of the curve is relevant. Another sudden increase Bb in lateral displacement occurs as the axial load crosses Pmax.
For P > Pmax, the structure again exhibits unique mechanical response. Such also happens to be the case when the constant lateral force exceeds a value (3.0134x 109N). For lower magnitudes of constant lateral force, slightly different P w curve is obtained. As shown in Fig.8, jump phenomenon in the form of sudden changes in the response at Pc and Pmax are predicted in this case as well. Here, again the observed P w curve is AcCBbD. However, in this case, there is a sudden decrease cC in larteral displacement occurs at Pc. It can be observed from Fig. 2 that the sudden increase/decrease in the lateral displacement is accompanied by the sudden increase/decrease in the rotation at the free end of the beam-column.
Fig.9 shows the P w curves for the special case of the fully uncracked concrete beam-column subjected to different lateral forces. The magnitudes of the axial force corresponding to vanishing lateral displacements are denoted by P1uc < P2uc < P3uc, etc. For fully uncracked beam-columns the values of P1uc and P2uc are respectively obtained as 20.036x109N and 60.189x109N. The corresponding values of the follower forces for the fully cracked beam-column turn out to be B times the values for the uncracked beam-columns. These values of axial follower force are independent of the magnitude of the constant lateral force. In the classical theory of columns under the action of an axial follower force, vanishing lateral displacement is interpreted to imply infinitely high lateral stiffness and so infinitely high natural frequency. Such a dynamic instability is called flutter. For P < Pluc, the positive natural frequency implies dynamic stability of the system. When P1uc < P < P2uc, the lateral stiffness assumes negative values implying dynamic instability. This system again exhibits dynamically stable behaviour when axial load P is in the range P2uc P3uc, and so on.
To recapitulate, for P < Pmax, the lateral displacement of partly cracked concrete beam- columns do not vanish at lower magnitudes of the constant lateral force. When the lateral force exceeds a particular value Q2 = 3.014x 109N, displacement vanishes at two values P1 and P2 of the axial follower force. Fig.10 shows the P-w curve for a particular case when P1 and P2 are obtained as 4.987x 109 N and 9.888x 109 N respectively. It can be observed that these values of the flutter loads for the partly cracked concrete beam-columns lie between their corresponding values for the two limiting cases of fully uncracked and fully cracked concrete beam-columns discussed above. When the axial load is increased beyond Pmax, the lateral displacement also vanishes as and when the flutter loads (P3, etc.) for the fully uncracked concrete beam-columns are reached.
The corresponding variation of the lateral stiffness of concrete beam-columns with the axial follower force is plotted in Fig. 11. Here, the flutter loads P3 is the same as the lowest flutter load of the uncracked beam-columns. For P < P1, the stiffness increases with increase in the axial force. As the axial force reaches P1, the stiffness, as expected, attains infinitely high values. When axial force crosses P1 or P3, the stiffness is expected to change discontinuously form infinitely high positive values to infinitely high negative values. Such indeed happens to be the case here as well. However, the stiffness of concrete beam-columns is predicted to vary in complex manner when the axial force varies in the range P1 P3.
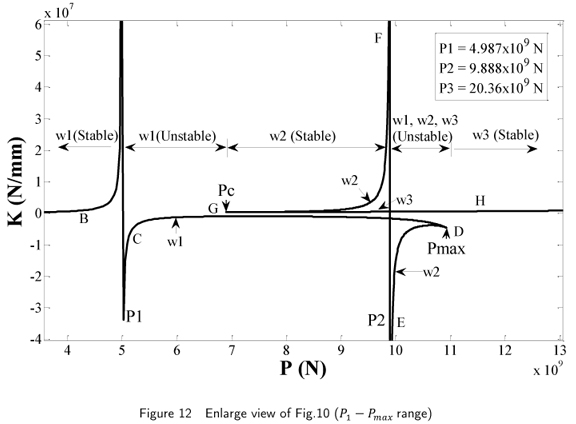
An enlarged view of Fig. 11 around P2 is presented in Fig.12. For proper interpretation of this plot, it must be remembered that the points D and G marked on the K P curve correspond to axial forces Pmax and Pc respectively. Thus, the flutter load P2 lies within the range Pc Pmax. In this range, there are three values of stiffness corresponding to the three equilibrium lateral displacements. As the axial force is increased from P1 to Pmax along CD, the lateral stiffness increases from infinitely high negative value to a certain negative but finite value. From this finite negative value, the stiffness decreases along DE again to infinitely high negative value as the axial load decreases from Pmax to P2. When the decreasing load crosses P2, the stiffness increases from infinitely high negative values to an infinitely high positive value. On decreasing the axial force further blow P2 upto Pc along FG, the stiffness decreases from infinitely high positive value to a certain positive finite value at Pc. When axial force is increased along GH from Pc to P3, the stiffness again increases to infinitely high positive value. Thus, contrary to expectations, as axial force increases across P2, the stiffness varies from infinitely high positive value to infinitely high negative value.
Further, the dynamic stability of concrete beam-columns is investigated in reference to magnitude of the axial follower force relative to the flutter loads P1, P2, P3, etc. This is achieved by analysing their dynamic response on being perturbed from their equilibrium state. The forcing function F(t) has been assumed to equal constant lateral force Q. When the axial force lies outside the range Pc Pmax, there is only one equilibrium state. However, within this range of axial force, there exist three equilibrium lateral displacements. The segments ABCD, DEFG and GHIJK of the K-P curve pertain respectively to the lateral displacements w1, w2 and w3.
For appreciating the following dynamic stability analysis, the relative magnitudes of follower loads for this particular case should be noted: P1 < Pc < P2 < Pmax < P3. From the analysis of dynamic stability of equilibrium states, the following conclusions can be drawn: For P < P1, the unique equilibrium state (w = w1) corresponds to the positive stiffness and hence is stable. This equilibrium state is rendered dynamically unstable because of negative lateral stiffness in the range P1 Pc. It has been discussed earlier that, of the three equilibrium displacements within the range Pc Pmax, only that corresponding to displacement w2 is stable. Such happens to be the case here as well as in range Pc P2 because of the corresponding positive stiffness. Negative stiffness in the range P2 Pmax even destabilizes this one otherwise stable equilibrium state. It implies that in the ranges P1 Pc and P2 Pmax of the tangential follower force, there are no dynamically stable equilibrium states. Of course, Pmax P3, the unique equilibrium state (w = w3) continues to be stable. As expected, there exist other dynamically unstable and stable states of the uncracked beam-columns at higher follower loads. It can be concluded that cracking lowers the magnitude of the flutter loads for the concrete beam-columns.
Based upon the above results, the load space is shown to be partitioned into dynamically stable and unstable regions in Fig.13. Here, the variation of various flutter loads, Pc and Pmax with Q is plotted. While the flutter loads P1uc = P3 for the uncracked structures remains constant, the flutter loads for the partly cracked structures vary with Q > Q2. Specifically, the lower flutter load P1 decreases with Q to asymptotically reach the flutter load BP1uc for the fully cracked structures. The higher flutter load P2 increases with Q while the flutter load P3 equals that P1ucfor the uncracked structure. For Q < Q2, no flutter occurs for P < P1. Based upon their vulnerability to flutter instability, the ranges P1 Pc and P2 Pmax of the follower force corresponds to dynamically unstable equilibrium states. In contrast, the ranges Pc P2 as well as Pmax P3 represent dynamically stable behaviour. Within the range Q1 Q2 of the lateral force, Pmax exceeds Pc. In this range, out of the three equilibrium states, only one w2 is dynamically stable. As discussed earlier, snap-through-like discontinuities in the P w curves are predicted in this range as and when P equals either Pc or Pmax. Thus, based upon the vulnerability to divergence instability, in the load space bounded by Pc < P < Pmax and Q1 < Q < Q2 is also dynamically unstable. It can be observed that for Q ≳ Q1, Pc and Pmax are below even the lowest flutter load BP1uc for the fully cracked concrete beam-columns.
4 DISCUSSION
To recapitulate, the classical theory deals with physically linear beam-columns subjected to tangential follower force only. In contrast, the present Paper deals with the physically nonlinear beam-columns subjected to lateral force in addition to the follower force. Concrete beam-columns cracked a priori at all the sections exhibit such physical nonlinearity. Beam-columns composed of bimodular solids with Young's modulus of elasticity in tension being smaller than that in compression constitute another example. Thus, in this Paper, the conventional theory of beam- columns is extended by incorporating the effect of physical nonlinearity. In this respect, this Paper can claim to constitute a definite significant contribution to structural stability theory. However, the hypothesis of small end rotations at the basis of the classical theories as well as the proposed theory does not seem to hold specifically at lower magnitudes of the follower force.
The predicted behaviour of concrete beam-columns turns out to be quite interesting as discussed below:
Conventional beam-columns subjected to tangential follower force only are known to exhibit infinitely high resistance to static buckling. In contrast, when subjected to lateral forces exceeding Q1, concrete beam columns exhibit finite resistance to quasi-static follower force. The jump phenomenon resembles static instability called snap-through and occurs at follower forces lower than the lowest flutter load for the fully cracked beam-columns.
When the concrete beam-columns are either uncracked or cracked all through their length, their axial load-lateral displacement curves are qualitatively similar to those of the conventional beam-columns. However, in the latter case, the magnitudes of the flutter loads are not affected by the magnitude of the lateral force, even through the P-w curves depend upon it. Generally, the concrete beam-columns are partly cracked. When Q < Q2, even these physically nonlinear beam- columns have the same flutter loads as the fully uncracked beam-columns. Otherwise, the two more values of the flutter loads are predicted. These values lie between the lowest values of the flutter loads for fully uncracked and fully cracked concrete beam-columns. These flutter loads are in addition to those for the fully uncracked case. In other words, cracking reduces the magnitudes of the flutter loads for concrete beam-columns under sufficiently high lateral loads. From the design point of view, when the lateral force is lesser than Q2, the lowest flutter load equals P1ucwhile, for higher lateral forces, it reduces to BP1uc. However, snap-through like jump phenomenon can occur even at lower loads for the lateral force in the range Q1 Q2.
As discussed above, concrete beam-columns supporting machine foundations are subjected to sinusoidal tangential follower forces. The scope of the present Paper is restricted to constant follower forces. Also, the theoretical predictions have not yet been empirically validated. Typical qualitative predictions of the concrete beam-columns subjected to a tangential follower force and a lateral force are presented in this Paper. The theory of concrete beam-columns presented here has to be extended further and validated before it can be of any relevance to structural design.
5 CONCLUSION
In this Paper, motivated by cracked concrete beam-columns, the stability of physically nonlinear elastic beam-columns subjected to a tangential follower force and a conservative lateral force is investigated. Analytical expressions for the lateral displacement and stiffness are derived. For certain range of follower loads lesser than the lowest flutter load for the uncracked structures, the beam-columns are predicted to exhibit three equilibrium states out of which only one is dynamically stable. The loss of dynamic stability of the remaining two equilibrium states is of divergence type. Consequently, snap-through type behaviour of static instability is predicted under quasi-static increase of the follower axial force. Such instabilities are predicted to occur even below the lowest flutter load for the fully cracked concrete beam-columns. Quite complex flutter instability response is exhibited. For higher values of the lateral force, the flutter loads turn out to be lesser than those for the uncracked beam-columns. The load space is partitioned into flutter-based dynamically stable and unstable regions. The proposed theory is shown to be valid for bimodular beam-columns as well.
Received in 02 Mar 2013
In revised form 11 Jul 2013
- Aristizabal-Ochoa, J. D., "Static stability of beam-columns under combined conservative and nonconservative end forces: Effect of semi rigid connections", Journal of Engineering Mechanics, Vol. 133(5), pp. 473-484 (2005).
- Aristizabal-Ochoa, J. D., "Large deflection stability of slender beam-columns with semi rigid connections: Elastica Approach", Journal of Engineering Mechanics, Vol. 130(3), pp. 274-282 (2004).
- Bolotin, V.V., "Nonconservative Problems in the Theory of Elastic Stability", Pergamon Press, New York, (1964).
- Bazant Z. P. and Cedolin, L., "Stability of Structures: Elastic, Inelastic, Fracture and Damage Theories", Word Scientific Pub. Co., Singapore, (2010).
- Caldas, R. B., Fakury, R. H. and Sousa Jr., J. B. M., "Finite element implementation for the analysis of 3D steel and composite frames subjected to fire", Latin American Journal of Solids and Structures, Vol. 11, pp. 001-018 (2014).
- Chen, W. F., "Theory of Beam-Columns", McGraw-Hill, New York, (1976).
- Chopra, Anil K., "Dynamics of Structures: Theory and Applications to Earthquake Engineering" Pearson Education, (2007).
- Elishakoff, Isaac, "Controversy associated with the so-called "Follower Forces": Critical overview", Applied Mechanics Reviews, Vol.58, pp. 117- 142 (2005).
- Kreis, E. S. and Andre J. C., "A numerical inquiry into the flutter phenomenon in long-span bridges", Latin American Journal of Solids and Structures, Vol. 2, pp. 321-337 (2005).
- Langthjem, M. A. and Sugiyama, Y., "Dynamic stability of columns subjected to follower loads: A Survey", Journal of sound and vibration, Vol. 238 (5), pp.809-851 (2000).
- Leipholz, H.H.E., "Stability of Elastic Structures", Springer Verlag, Wien, (1978).
- Nogueira, C. G., Venturini, W. S. and Coda, H. B., "Material and geometric nonlinear analysis of reinforced concrete frame structures considering the influence of shear strength complementary mechanics", Latin American Journal of Solids and Structures, Vol. 10, pp. 953-980 (2013).
- Sharma, Mamta R., Singh, Arbind K., and Benipal, Gurmail S., "Elastic stability analysis of flanged concrete columns", Proc., 55 Congress of Indian Society of Theoretical and Applied Mechanics December 18-21, NIT Hamirpur, (India), pp. 169-175 (2010).
- Sharma, Mamta R., Singh, Arbind K. and Benipal Gurmail S., "Elastic stability of concrete beam-columns", Part I: Static stability, Communicated to International Journal of Structural Stability and Dynamics (IJSSD), July 2012a.
- Sharma, Mamta R., Singh, Arbind K. and Benipal Gurmail S., "Elastic stability of concrete beam-columns", Part II: Dynamic stability, Communicated to International Journal of Structural Stability and Dynamics (IJSSD), July 2012b.
- Srinivasulu, P. and Vaidyanathan, V., "Handbook of Machine Foundations", Tata McGraw-Hill Publishing Company Limited, (1976).
- Sugiyama, Y., Langthjem, M.A. and Ryu, B. J., "Realistic follower forces", Journal of Sound and Vibration, Vol. 225, pp.779-782 (1999).
- Thomsen, J.J., "Vibrations and Stability: Advanced Theory, Analysis and Tools", 2nd Edition, Springer (India) Private Limited, New Delhi (2003).
Publication Dates
-
Publication in this collection
03 Feb 2014 -
Date of issue
Oct 2014
History
-
Received
02 Mar 2013 -
Accepted
11 July 2013