Abstract
In this paper, the Homotopy Analysis Method (HAM) with two auxiliary parameters and Differential Transform Method (DTM) are employed to solve the geometric nonlinear vibration of Euler-Bernoulli beams subjected to axial loads. A second auxiliary parameter is applied to the HAM to improve convergence in nonlinear systems with large deformations. The results from HAM and DTM are compared with another popular numerical method, the shooting method, to validate these two analytical methods. HAM and DTM show excellent agreement with numerical results (the maximum errors in our calculations are about 0.002%), and they additionally provide a simple way to conduct a parametric analysis with different physical parameters in Euler-Bernoulli beams. To show the benefits of this method, the effect of different physical parameters on the amplitude is discussed for a cantilever beam with a cyclically varying axial load.
Keywords:
Nonlinear vibration; Euler-Bernoulli beam; Homotopy Analysis Method (HAM); Two auxiliary parameters; Differential Transform Method (DTM)
1 INTRODUCTION
The governing equations of beam vibration are generally non-linear making it difficult to solve the nonlinear problem via analytical methods. Because of this, many researchers use numerical methods to solve these equations. In recent years, some approximate analytical solutions have been offered to investigate these non-linear equations. (Wu and Liu, 1999Wu, T. Y., Liu, G. R., (1999). A Differential Quadrature as a numerical method to solve differential equations. Computational Mechanics, 24:197-205.) used differential quadrature to solve the single-span Bernoulli-Euler beam's buckling equation. (He, 2006He, J. H., (2006). Some asymptotic methods for strongly nonlinear equations. International Journal of Modern Physics B, 20:1141-1199.) suggested that the Parameterized-Perturbation Method (PPM) be used to solve strongly nonlinear equations. (Qaisi, 1993Qaisi, M. I., (1993). Application of the harmonic balance principle to the nonlinear free vibration of beams. Applied Acoustics, 40:141-151.) determined the vibration modes of geometrically nonlinear beams under the various edge conditions by the harmonic balance principle. (Moeenfard et al., 2011Moeenfard, H., Mojahedi, M., Ahmadian, M., (2011). A homotopy perturbation analysis of nonlinear free vibration of Timoshenko microbeams. Journal of Mechanical Science and Technology, 25:557-565.) developed the homotopy perturbation method (HPM) to analyze the nonlinear free vibration of Timoshenko beams. They also converted the nonlinear partial differential governing equation to a non-linear ordinary differential equation using Galerkin's projection method. (Sfahani et al., 2011Sfahani, M. G., Barari, A., Omidvar, M., Ganji, S. S., Domairry, G., (2011). Dynamic Response of Inextensible Beams by Improved Energy Balance Method. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 225:66-73.) used the energy balance method (EBM) to study the dynamic response of inextensible beams (neutral axis length is preserved during vibration). (Barari et al., 2010Barari, A., Kimiaeifar, A., Domairry, G., Moghimi, M., (2010). Analytical evaluation of beam deformation problem using approximate methods. Songklanakarin Journal of Science and Technology, 32:207-326.) used the Homotopy-Perturbation method to analyze the beam deformation. (Pillai and Rao, 1992Pillai, S. R. R., Nageswara Rao, B., (1992). On nonlinear free vibrations of simply supported uniform beams. Journal of Sound and Vibration, 159:527-531.) applied several methods to study the large amplitude free vibrations of simply supported prismatic beams with fixed ends. The methods that they used in their study consist of the elliptic function method, harmonic balance method and methods considering simple harmonic oscillations. (Kopmaza and Gündogdub, 2003Kopmaza, O., Gündogdub, Ö., (2003). On the curvature of an Euler-Bernoulli beam. International Journal of Mechanical Engineering Education, 31:2.) developed the relation between curvature of an Euler-Bernoulli beam and bending moment. (Soldatos and Selvadurai, 1985Soldatos, K. P., Selvadurai, A. P. S., (1985). Flexure of beams resting on hyperbolic elastic foundations. International journal of solids and structures, 21:373-388.) used a perturbation method to survey the static flexure of a Bernoulli-Euler beam resting on a nonlinear Winkler-type foundation. (Ahmadi et al., 2014Ahmadi, M., Hashemi, G., Asghari, A., (2014). Application of iteration perturbation method and Hamiltonian approach for nonlinear vibration of Euler-Bernoulli beams. Latin American Journal of Solids and Structures, 11:1049-1062.) devoted to the new classes of analytical techniques called the Iteration Perturbation Method (IPM) and Hamiltonian Approach (HA) for solving the equation of motion governing the nonlinear vibration of Euler-Bernoulli beams. (Liu and Gurram, 2009Liu, Y., Gurram, C. S., (2009). The use of He's variational iteration method for obtaining the free vibration of an Euler-Bernoulli beam. Mathematical and Computer Modelling, 50:1545-1552.) employed He's Variational Iteration Method (VIM) to solve free vibration problems for an Euler-Bernoulli beam with various supporting conditions. They compared VIM results with Adomian decomposition method results. They concluded that VIM is accurate and it provides a simple and efficient approach for solving vibration of uniform Euler-Bernoulli beams. (Rashidi et al., 2012Rashidi, M. M., Shooshtari, A., Anwar Bég, O., (2012). Homotopy perturbation study of nonlinear vibration of Von Karman rectangular plates. Computers & Structures, 106-107:46-55.) derived the equations of the motion for a rectangular isotropic plate. They considered the effect of shear deformation and rotary inertia and used the Homotopy Perturbation Method (HPM) to solve the nonlinear equation.
In 1992, (Liao, 1992Liao, S. (1992). The proposed homotopy analysis technique for the solution of nonlinear problems. Ph. D. Thesis, Shanghai Jiao Tong University, China.) proposed the homotopy analysis method (HAM) to solve nonlinear equations. Many researchers used HAM to solve various nonlinear problems. (Hoseini et al., 2008Hoseini, S. H., Pirbodaghi, T., Asghari, M., Farrahi, G. H., Ahmadian, M. T., (2008). Nonlinear free vibration of conservative oscillators with inertia and static type cubic nonlinearities using homotopy analysis method. Journal of Sound and Vibration, 316:263-273.) studied the nonlinear free vibration of a conservative oscillator via HAM. They showed that the HAM leads to an accurate analytical solution, which is valid for a wide range of system parameters. (Mohammadpour et al., 2012Mohammadpour, A., Rokni, E., Fooladi, M., Kimiaeifar, A., (2012) Approximate analytical solution for bernoulli-euler beams under different bpundary conditions with non-linear winkler type foundation. Journal of Theoretical and Applied Mechanics, 50:339-355.) studied deflection of beams with nonlinear Winkler type foundations using HAM. They showed that the HAM improves convergence of nonlinear problems.
The Differential Transform Method (DTM) was developed by Taylor's series expansion. DTM applied to solve linear and nonlinear differential equations. This method can be used for solution of ordinary and partial differential equations. (Ayaz, 2003Ayaz, F., (2003). On the two-dimensional differential transform method. Applied Mathematics and Computation, 143:361-374.) solved the initial value problem for partial differential equations (PDE) using a two-dimensional differential transform method. Using this method reduces computational time. (Ayaz, 2004Ayaz, F., (2004). Solutions of the system of differential equations by differential transform method. Applied Mathematics and Computation, 147:547-567.) studied PDE by a three-dimensional differential transform method. (Hassan, 2002) solved eigenvalue problems by the DTM method. (Kuang Chen and Shin Chen, 2004Chen, C. O.-K., Chen, S.-S., (2004). Application of the differential transformation method to a non-linear conservative system. Applied Mathematics and Computation, 154:431-441.) applied DTM to solve the free vibrations of a conservative oscillator and also compared the results with the Runge-Kutta method. In addition, (Shin Chen and Kuang Chen, 2009Chen, S.-S., Chen, C. O.-K., (2009). Application of the differential transformation method to the free vibrations of strongly non-linear oscillators. Nonlinear Analysis: Real World Applications, 10:881-888.) investigated the free vibrations of strongly non-linear oscillators by DTM and proposed this method to solve the non-linear problem because of DTMs improved accuracy.
In this paper, two new analytical methods are proposed to solve the nonlinear vibration of an Euler-Bernoulli beam. First, the governing equation is obtained, and then the Galerkin Method is used to obtain the corresponding ordinary differential equation. Then, the HAM with two auxiliary parameters and DTM are employed to solve this equation. Finally, the results of HAM and DTM are compared with numerical method results and good agreement is achieved.
2 GOVERNING EQUATION
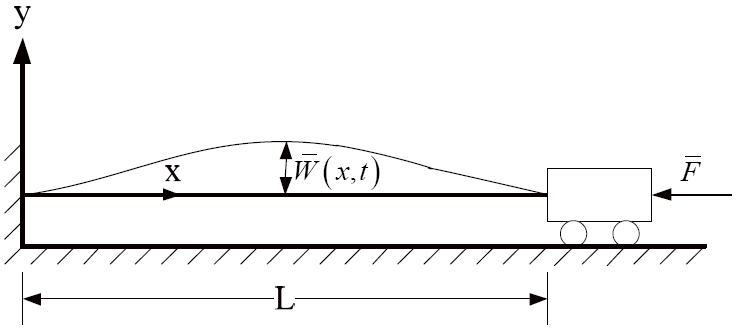
In order to obtain the governing equation, we consider three assumptions: the plane deformation is negligible so it is neglected, transverse shear strains are small so they are neglected, and rotation of the cross section is only due to bending. The schematic of Euler-Bernoulli beam subjected to the axial loading is shown in Fig. 1.
The equation of motion including the effects of mid-plane stretching is introduced as (Rao, 2007Rao, S. S. (2007). Vibration of continuous systems. New Jersey: John Wiley & Sons.):
where L is the length of beam, Ab
is the cross-sectional area, I is the moment of inertia, E is the young modulus, mb
is the mass per unit length of beam and . . is magnitude of axial force. For simplification, the following non-dimensional variables are used:
. is magnitude of axial force. For simplification, the following non-dimensional variables are used:
where R = Eq. 1) can be written as follows: is the radius of gyration of the cross-section. Therefore, (
is the radius of gyration of the cross-section. Therefore, (
Assuming that W(X, t) = T(t) w(X), where w(X) is the first Eigen-mode of the beam. By applying the Galerkin method, the equation of motion is obtained as follows:
where β = β 1 + Fβ 2. The above equation is the governing equation of nonlinear vibration of Euler-Bernoulli beams. The β 1, β 2 and λ parameters are as follows:
The center of the beam are subjected to the following initial conditions:
where A denotes the non-dimensional maximum amplitude of oscillation.
3 APPLICATION OF HAM
Consider the suitable initial approximation, in order to solve (Eq. 4). (for more information about HAM steps, see Refs. ((Abolbashari et al., 2014Abolbashari, M. H., Freidoonimehr, N., Nazari, F., Rashidi, M. M., (2014). Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technology, 267:256-267.), (Abolbashari et al., 2015Abolbashari, M. H., Freidoonimehr, N., Nazari, F., Rashidi, M. M., (2015). Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Advanced Powder Technology, 26:542-552.), (Jafari and Freidoonimehr, 2015Jafari, S. S., Freidoonimehr, N., (2014). Second law of thermodynamics analysis of hydro-magnetic nano-fluid slip flow over a stretching permeable surface. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 37:1245-1256.)):
where α is the secondary auxiliary parameter, which is used to accelerate the convergence of the series. The auxiliary linear operator ℒT (T) becomes:
which the following relation is satisfied
where c 1 and c 2 are the arbitrary constants. According to the (Eq. 4), the nonlinear operator is introduced as:
The zero-order deformation equation is introduced as:
where p is an embedded parameter and ħT is an auxiliary nonzero parameter. The auxiliary functions are introduced as:
Due to the boundary conditions
By Taylor's theorem, we have
Where
Consider that ħT is chosen such that the Taylor series expansion of (Eq. 14) has converged at p = 1:
where
and
The mth order deformation equations ((Eq. 17)) were solved using MATHEMATICA software. The result of first order solution of HAM is determined as:
It is important to select a proper value of auxiliary parameter to control the speed of convergence of the approximation series by the help of the so-called ħT - curve. The optimal values of ħT are selected from the valid region in straight line. The ħT - curve of T"(0) obtained by the different order of approximation is shown in Fig. 2. The averaged residual error is introduced as (Eq. 21):
The ħT - curve of T"(0) obtained by different orders of approximation of HAM when A = 2, β = 1, λ = 1 and α = 1.8.
In order to select the optimal value of the auxiliary parameter, the averaged residual error (for more details, see Refs. ((Liao, 2010Liao, S., (2010). An optimal homotopy-analysis approach for strongly nonlinear differential equations. Communications in Nonlinear Science and Numerical Simulation, 15:2003-2016.), (Rashidi and Abbasbandy, 2011Rashidi, M. M., Abbasbandy, S., (2011). Analytic approximate solutions for heat transfer of a micropolar fluid through a porous medium with radiation. Communications in Nonlinear Science and Numerical Simulation, 16:1874-1889.)) is defined as:
where Δx = 5/K and K = 10. For a given order of approximation m the optimal value of ħT is given by the minimum of Δm corresponding to nonlinear algebraic equations
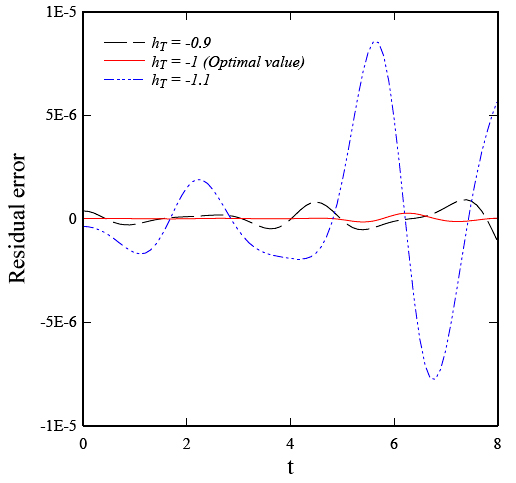
In order to check the accuracy of the HAM method with two auxiliary parameters, the residual errors for 5th order HAM solutions of (Eq. 21) is shown in Fig. 3.
The residual error for (Eq. 21) using 5th-order of approximations when A = 1, β = 0.5 and λ = 0.1.
4 APPLICATION OF DTM
Taking the differential transform of (Eq. 4), one can obtain (for more details, see Refs. ((Freidoonimehr, 2015Freidoonimehr, N., Rashidi, M. M., Jalilpour, B., (2015). MHD stagnation-point flow past a stretching/shrinking sheet in the presence of heat generation/absorption and chemical reaction effects. Journal of the Brazilian Society of Mechanical Sciences and Engineering:1-10.), (Rashidi et al., 2015Rashidi, M. M., Freidoonimehr, N., Momoniat, E., Rostami, B., (2015). Study of nonlinear MHD tribological squeeze film at generalized magnetic reynolds numbers using DTM. PloS one, 10: e0135004.), (Rashidi and Freidoonimehr, 2014Rashidi, M. M., Mehr, N. F., (2014). Series solutions for the flow in the vicinity of the equator of an MHD boundary-layer over a porous rotating sphere with heat transfer. Thermal Science, 18:527-537.)):
where T(k) is the differential transforms of T(t) and displayed as:
(Eq. 26) provides the transformed boundary conditions. By substituting (Eq. 26) into (Eq. 24) and combining with (Eq. 25), the recursive method yields the values of T(t)
It is important to note that the number of required terms is determined by the convergence of the numerical values up to one's desired accuracy.
5 RESULTS AND DISCUSSIONS
First of all, comparisons have been done between the results of the current study; the results of numerical solution via the shooting method are used to validate the proposed analytical methods (HAM & DTM) in Fig. 4. Excellent agreement can be observed between them.
Deflection versus time results comparing HAM, DTM, and a numerical method at A = 0.0001, β = 1and λ = 0.01.
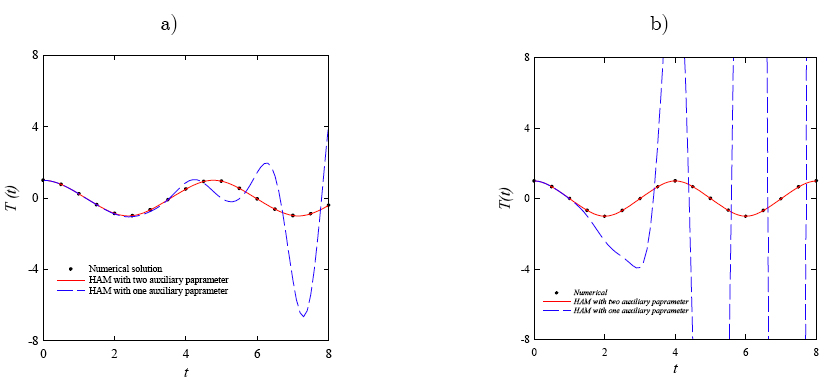
Fig. 5 displays the result of HAM solution with and without considering the second auxiliary parameter. As mentioned previously, the second auxiliary parameter is used to increase the convergence performance of the HAM. Thus, the HAM with two auxiliary parameters provides solutions that have good agreement with the numerical solution. In addition, it is obvious that by increasing the value of λ, which represents the value of non-linearity of the Eq. 4, the HAM with one auxiliary parameter diverge faster. Thus for large values of the non-linear parameter, the HAM with two auxiliary parameter must be applied to ensure the series convergence. Tables 1-3 present the comparison between the HAM results with one and two auxiliary parameters with the numerical method results for the various values of the amplitude, β, λ and time. As it is obvious form these tables, good agreement can be seen between the results of the HAM with two auxiliary parameters and the numerical method results.
Amplitude oscillation comparison of HAM and numerical solution for the one and two auxiliary parameters at A = 1, β = 1 a) λ = 1 and b) λ = 2.
Comparison between HAM I & HAM II with numerical method for various amplitude (A) and time at β = 0.5 and λ = 0.5.
Comparison between HAM I & HAM II with numerical method for various β and time at A = 1 and λ = 0.5.
Comparison between HAM I & HAM II with numerical method for various λ and time at A = 1 and β = 0.5.
A parametric study was conducted on a cantilever beam with cyclically varying axial load. The nonlinear vibration analysis of deflection T(t) is shown in Figs. 6-7 for a wide range of amplitudes (A) and time (t) and different values of the constant physical parameters via two auxiliary parameter of HAM solution. The difference between these two figures is in their physical constant β and λ where in Fig. 6 β = π, λ = 0.15, B = 0.15 and λ = 0.5 in Fig. 7.
3D plot of deflection T(t) for a wide range of amplitude (A) and time (t) where β = π and λ = 0.15.
3D plot of deflection T(t) for a wide range of amplitude (A) and time (t), where β = 0.15 and λ = 0.5.
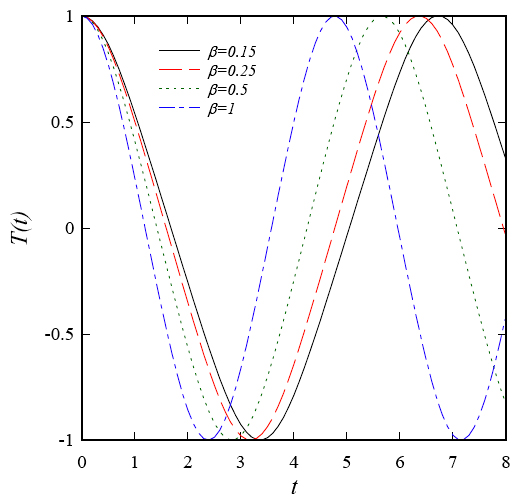
Influence of λ on T(t) behavior is demonstrated in Fig. 8, where A and β are equal to 1. Also, the effect of β on the behavior of T(t) is shown in Fig. 9, where A and λ are equal to 1. It is worth mentioning that the two auxiliary parameters of HAM solution are used in Figs. 8-9.
The DTM response depends on the order of solutions. The DTM response at A =0.0001 β = 0.5 and λ = 0.5 is shown in Fig. 10 for different orders of solutions. According to Fig. 10 there is good agreement with numerical results at the 20th order of solution. The solutions based on HAM, DTM and numerical method for t = 1 are compared in Table. 4. In this table, the values of the λ and β are equal to 0.5. It can be observed that the maximum errors of HAM and DTM solutions with numerical results are less than 0.002%.
The T(t) behavior at A = 0.0001 β = 0.5 and λ = 0.5, based on DTM for different order of solutions.
Comparison between DTM & HAM with numerical method for various amplitude (A) at t = 1(s), β = 0.5 and λ = 0.5.
6 CONCLUSIONS
In this paper, nonlinear vibration of an Euler-Bernoulli beam subjected to a cyclically varying axial load is investigated by analytical methods. The governing equation of nonlinear vibration of the beam is in the form of a partial differential equation. The Galerkin method is employed to reduce the governing equation to ordinary differential equation. The homotopy analysis method (HAM) with two auxiliary parameters and differential transform method (DTM) are used to express the response of the axially loaded beam. In this problem, the second auxiliary parameter is used to accelerate the convergence of the Taylor series expansion, and it was shown that this parameter improves the analysis of highly nonlinear systems. Excellent agreement was found in comparing the HAM, DTM and numerical solution results.
References
- Abdel-Halim Hassan, I. H., (2002). On solving some eigenvalue problems by using a differential transformation. Applied Mathematics and Computation, 127:1-22.
- Abolbashari, M. H., Freidoonimehr, N., Nazari, F., Rashidi, M. M., (2014). Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technology, 267:256-267.
- Abolbashari, M. H., Freidoonimehr, N., Nazari, F., Rashidi, M. M., (2015). Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Advanced Powder Technology, 26:542-552.
- Ahmadi, M., Hashemi, G., Asghari, A., (2014). Application of iteration perturbation method and Hamiltonian approach for nonlinear vibration of Euler-Bernoulli beams. Latin American Journal of Solids and Structures, 11:1049-1062.
- Ayaz, F., (2003). On the two-dimensional differential transform method. Applied Mathematics and Computation, 143:361-374.
- Ayaz, F., (2004). Solutions of the system of differential equations by differential transform method. Applied Mathematics and Computation, 147:547-567.
- Barari, A., Kimiaeifar, A., Domairry, G., Moghimi, M., (2010). Analytical evaluation of beam deformation problem using approximate methods. Songklanakarin Journal of Science and Technology, 32:207-326.
- Chen, C. O.-K., Chen, S.-S., (2004). Application of the differential transformation method to a non-linear conservative system. Applied Mathematics and Computation, 154:431-441.
- Chen, S.-S., Chen, C. O.-K., (2009). Application of the differential transformation method to the free vibrations of strongly non-linear oscillators. Nonlinear Analysis: Real World Applications, 10:881-888.
- Freidoonimehr, N., Rashidi, M. M., Jalilpour, B., (2015). MHD stagnation-point flow past a stretching/shrinking sheet in the presence of heat generation/absorption and chemical reaction effects. Journal of the Brazilian Society of Mechanical Sciences and Engineering:1-10.
- He, J. H., (2006). Some asymptotic methods for strongly nonlinear equations. International Journal of Modern Physics B, 20:1141-1199.
- Hoseini, S. H., Pirbodaghi, T., Asghari, M., Farrahi, G. H., Ahmadian, M. T., (2008). Nonlinear free vibration of conservative oscillators with inertia and static type cubic nonlinearities using homotopy analysis method. Journal of Sound and Vibration, 316:263-273.
- Jafari, S. S., Freidoonimehr, N., (2014). Second law of thermodynamics analysis of hydro-magnetic nano-fluid slip flow over a stretching permeable surface. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 37:1245-1256.
- Kopmaza, O., Gündogdub, Ö., (2003). On the curvature of an Euler-Bernoulli beam. International Journal of Mechanical Engineering Education, 31:2.
- Liao, S. (1992). The proposed homotopy analysis technique for the solution of nonlinear problems. Ph. D. Thesis, Shanghai Jiao Tong University, China.
- Liao, S., (2010). An optimal homotopy-analysis approach for strongly nonlinear differential equations. Communications in Nonlinear Science and Numerical Simulation, 15:2003-2016.
- Liu, Y., Gurram, C. S., (2009). The use of He's variational iteration method for obtaining the free vibration of an Euler-Bernoulli beam. Mathematical and Computer Modelling, 50:1545-1552.
- Moeenfard, H., Mojahedi, M., Ahmadian, M., (2011). A homotopy perturbation analysis of nonlinear free vibration of Timoshenko microbeams. Journal of Mechanical Science and Technology, 25:557-565.
- Mohammadpour, A., Rokni, E., Fooladi, M., Kimiaeifar, A., (2012) Approximate analytical solution for bernoulli-euler beams under different bpundary conditions with non-linear winkler type foundation. Journal of Theoretical and Applied Mechanics, 50:339-355.
- Pillai, S. R. R., Nageswara Rao, B., (1992). On nonlinear free vibrations of simply supported uniform beams. Journal of Sound and Vibration, 159:527-531.
- Qaisi, M. I., (1993). Application of the harmonic balance principle to the nonlinear free vibration of beams. Applied Acoustics, 40:141-151.
- Rao, S. S. (2007). Vibration of continuous systems. New Jersey: John Wiley & Sons.
- Rashidi, M. M., Abbasbandy, S., (2011). Analytic approximate solutions for heat transfer of a micropolar fluid through a porous medium with radiation. Communications in Nonlinear Science and Numerical Simulation, 16:1874-1889.
- Rashidi, M. M., Freidoonimehr, N., Momoniat, E., Rostami, B., (2015). Study of nonlinear MHD tribological squeeze film at generalized magnetic reynolds numbers using DTM. PloS one, 10: e0135004.
- Rashidi, M. M., Mehr, N. F., (2014). Series solutions for the flow in the vicinity of the equator of an MHD boundary-layer over a porous rotating sphere with heat transfer. Thermal Science, 18:527-537.
- Rashidi, M. M., Shooshtari, A., Anwar Bég, O., (2012). Homotopy perturbation study of nonlinear vibration of Von Karman rectangular plates. Computers & Structures, 106-107:46-55.
- Sfahani, M. G., Barari, A., Omidvar, M., Ganji, S. S., Domairry, G., (2011). Dynamic Response of Inextensible Beams by Improved Energy Balance Method. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 225:66-73.
- Soldatos, K. P., Selvadurai, A. P. S., (1985). Flexure of beams resting on hyperbolic elastic foundations. International journal of solids and structures, 21:373-388.
- Wu, T. Y., Liu, G. R., (1999). A Differential Quadrature as a numerical method to solve differential equations. Computational Mechanics, 24:197-205.
Publication Dates
-
Publication in this collection
July 2016
History
-
Received
06 Sept 2015 -
Reviewed
05 Mar 2016 -
Accepted
06 Mar 2016