Abstract
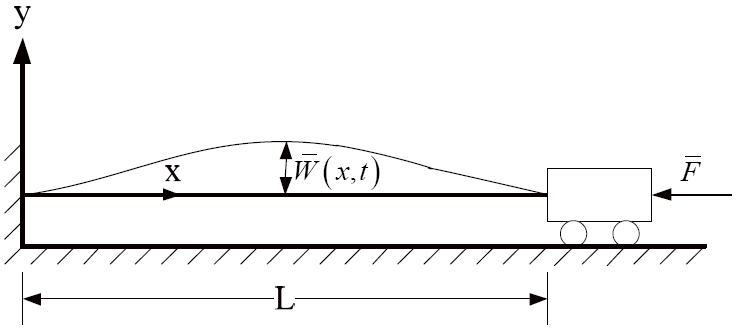
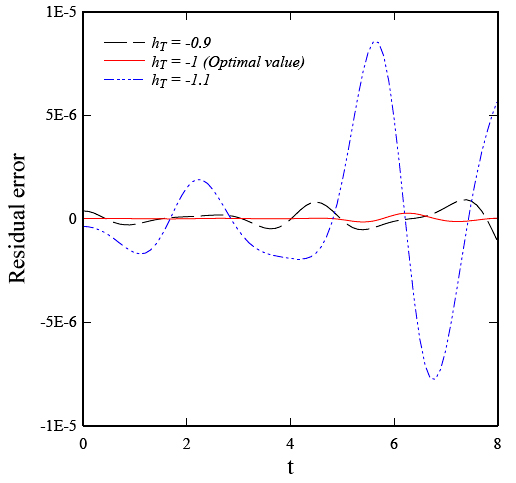
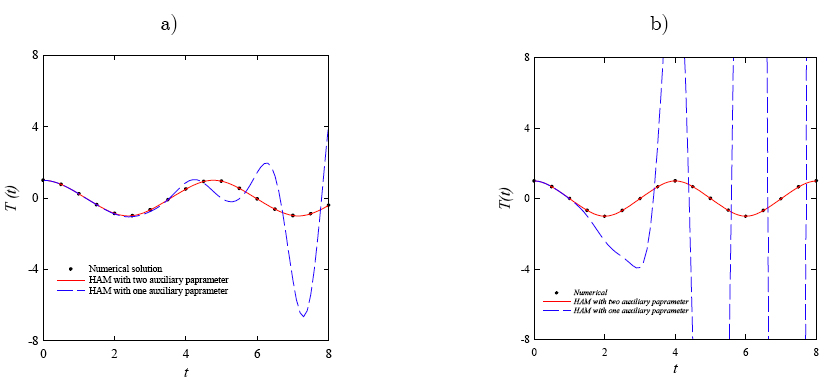
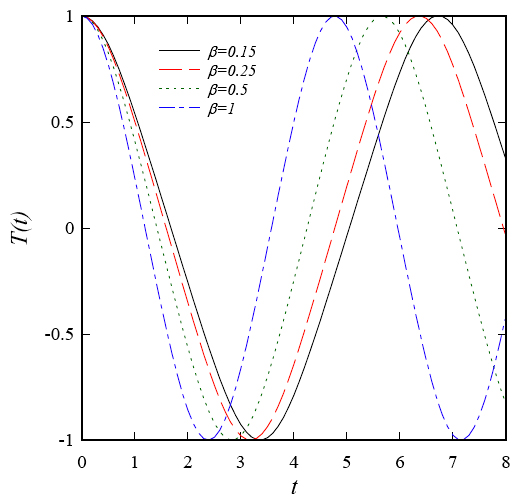
In this paper, the Homotopy Analysis Method (HAM) with two auxiliary parameters and Differential Transform Method (DTM) are employed to solve the geometric nonlinear vibration of Euler-Bernoulli beams subjected to axial loads. A second auxiliary parameter is applied to the HAM to improve convergence in nonlinear systems with large deformations. The results from HAM and DTM are compared with another popular numerical method, the shooting method, to validate these two analytical methods. HAM and DTM show excellent agreement with numerical results (the maximum errors in our calculations are about 0.002%), and they additionally provide a simple way to conduct a parametric analysis with different physical parameters in Euler-Bernoulli beams. To show the benefits of this method, the effect of different physical parameters on the amplitude is discussed for a cantilever beam with a cyclically varying axial load.
Keywords:
Nonlinear vibration; Euler-Bernoulli beam; Homotopy Analysis Method (HAM); Two auxiliary parameters; Differential Transform Method (DTM)