Abstract
This paper introduces a hybrid approach for obtaining S-N curves with reduced number of tests associated to statistically simulated data. In order to validate the proposal, two validation process were developed. One using a methodology to generate S-N curves based on Monte Carlo simulations and other using actual data according Zhao et al. (1998), allowing to compare the hybrid approach with the experimental curve S-N obtained with high replication. In both validation process, a good accuracy was verified. Subsequently, the fatigue analysis of a fillet welded joint was carried out using finite element analysis to evaluate the cumulative damage and fatigue life, enabling comparison between the proposed method and standard NBR 8800 (2008)NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards.. The results obtained with the proposed methodology allowed more accuracy results and less conservative than standard for the same weld detail class, both for fatigue life and for cumulative fatigue damage evaluations.
Keywords
Wöhler curves; Monte Carlo method; fatigue test; fillet welded joint; fatigue material properties
1 INTRODUCTION
In the fatigue design of components and structures, it is imperative to know the fatigue properties of the used materials, whether welded or not. Several studies have been carried out to determine the fatigue properties of the materials, seeking to combine a high degree of confidence with a reduced number of specimens, since fatigue tests are expensive and time consuming.
Many studies focused on fatigue properties were and still are being developed, such as Shen (1994Shen, C. (1994). The Statistical Analysis of Fatigue Data, Ph.D. Dissertation, University of Arizona, Tucson.), Pascual and Meeker (1997Pascual, F.G. and Meeker, W.Q. (1997), Estimating fatigue curves with the random fatigue-limit model. Technometrics, 41(4): 277-289.), Gope (1999Gope, P.C. (1999). Determination of sample size for estimation of fatigue life by using Weibull or log-normal distribution. International Journal of Fatigue, 21(8): 745-752., 2002Gope, P.C. (2002). Determination of minimum number of specimens in SN testing. Journal of Engineering Materials and Technology, 124(4): 421-427.), Pinto et al. (2002Pinto, J.M.A., et al. (2002), Fatigue test plan to obtain SN curves. ASME 2002 Pressure Vessels and Piping Conference-American Society of Mechanical Engineers, Vancouver, Canada, August.), Pascual (2003)Pascual, F. G. (2003), Theory for optimal test plans for the random fatigue-limit model. Technometrics, 45(2): 130-141., Lorén and Lundström (2005Lorén, S. and Lundström, M. (2005). Modelling curved S-N curves. Fatigue & Fracture of Engineering Materials & Structures, 28(5): 437-443.), Paolino, Chiandussi and Rossetto (2013Paolino, D. S., Chiandussi, G. and Rossetto M. (2013). A unified statistical model for S-N fatigue curves: probabilistic definition. Fatigue & Fracture of Engineering Materials & Structures, 36(3): 187-201.), Pang et al (2014Pang, J. C., Li, S. X., Wang, Z. G., & Zhang, Z. F. (2014). Relations between fatigue strength and other mechanical properties of metallic materials. Fatigue & Fracture of Engineering Materials & Structures, 37(9): 958-976.), Strzelecki and Sempruch (2016aStrzelecki, P., Sempruch, J. (2016a). Experimental method for plotting SN curve with a small number of specimens. Polish Maritime Research, 23(4): 129-137., 2016bStrzelecki, P., Sempruch, J. (2016b). Verification of analytical models of the S-N curve within limited fatigue life. Journal of Theoretical and Applied Mechanics, 54(1): 63-73.), Strzelecki and Tomaszewski (2016)Strzelecki, P., Tomaszewski, T. (2016), “Application of Weibull distribution to describe SN curve with using small number specimens”. AIP Conference Proceedings, October. and Paolino et al (2018)Paolino, D. S., Tridello, A., Chiandussi, G., & Rossetto, M. (2018). Estimation of P‐S‐N curves in very‐high‐cycle fatigue: Statistical procedure based on a general crack growth rate model. Fatigue & Fracture of Engineering Materials & Structures, 41(4): 718-726.. In these researches, different practices and experimental plans were studied to obtain the S-N curves, as well as probabilistic methods were employed. The Monte Carlo simulation is an important statistical tool to analyze fatigue data, since fatigue life is probabilistic and not deterministic. Several studies were conducted based on Monte Carlo Method, such as Bai et al. (2017Bai, X., Xie, L., Zhang, R., Guan, R., Tong, A., & Bai, E. (2017). Measurement and estimation of probabilistic fatigue limits using Monte-Carlo simulations. International Journal of Fatigue, 95: 229-235.), Cetin, Härkegård and Naess (2013Cetin, A., Härkegård, G., & Naess, A. (2013). The fatigue limit: An analytical solution to a Monte Carlo problem. International Journal of Fatigue, 55: 194-201.) and Sanches et al. (2015Sanches, R. F., de Jesus, A. M., Correia, J. A., Da Silva, A. L. L., & Fernandes, A. A. (2015). A probabilistic fatigue approach for riveted joints using Monte Carlo simulation. Journal of Constructional Steel Research, (110): 149-162.).
Some authors already used the term “hybrid approach” for developed methods that use mixed analytics and experimental data. For example, one can refer to Strzelecki and Sempruch (2016aStrzelecki, P., Sempruch, J. (2016a). Experimental method for plotting SN curve with a small number of specimens. Polish Maritime Research, 23(4): 129-137., 2016bStrzelecki, P., Sempruch, J. (2016b). Verification of analytical models of the S-N curve within limited fatigue life. Journal of Theoretical and Applied Mechanics, 54(1): 63-73.) and Szala and Ligaj (2016Szala, G., Ligaj, B. (2016). Application of hybrid method in calculation of fatigue life for C45 steel (1045 steel) structural components. International Journal of Fatigue, 91: 39-49.). The hybrid approach proposed by Strzelecki and Sempruch (2016aStrzelecki, P., Sempruch, J. (2016a). Experimental method for plotting SN curve with a small number of specimens. Polish Maritime Research, 23(4): 129-137., 2016bStrzelecki, P., Sempruch, J. (2016b). Verification of analytical models of the S-N curve within limited fatigue life. Journal of Theoretical and Applied Mechanics, 54(1): 63-73.) consists of setting the fatigue properties using an analytical method, and then correcting the accuracy of life determination by carrying out a “simplified” experiment. This simplified experiment is based on determining an experimental point within the limited life range for the fatigue strength corresponding to 105 cycles based on the analytical characteristics. Szala and Ligaj (2016) propose a hybrid method that involves an assumption that cyclic properties of steel in the range of low cycle fatigue are defined by a strain based approach (Manson-Coffin diagram), whereas in the high cycle fatigue range, cyclic properties of steel are described with Wöhler diagram in stress based approach.
The most accurate way to obtain the fatigue properties of the material is by the experimental tests, conducted according to standards such as ASTM E739 (2015)ASTM E739 (2015). Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (SN) and Strain-Life. American Society for Testing and Materials., JSME S 002 (1994)JSME S 002 (1994). Standard Method of Statistical Fatigue Testing, Japan Society of Mechanical Engineers. and ISO 12107 (2012)ISO 12107 (2012). Metallic Materials-Fatigue Testing-Statistical Planning and Analysis of Data. International Organization for Standardization., which specify the minimum number of specimens required in fatigue tests according to the type of application. However, in some design situations, obtaining the fatigue properties of the materials only with tests, i.e. an experimental S-N curve, is very difficult due to time and costs, justifying the use of procedures based on the design codes or a hybrid method, such as the method proposed here.
The aim of this article was to propose and validate a hybrid approach for obtaining S-N curves with a reduced number of tests, balancing time and costs to get a S-N curve for the design of a component.
2 PROCEDURES FOR OBTAINING S-N CURVES
In the fatigue life evaluation, the S-N curve method in the high cycle fatigue region is commonly used and has great acceptance in the design of components or structures that are exposed to cyclic loads. Several mathematical models have been proposed over the years to describe the relationship between cyclic stresses and number of cycles to failure (S-N curve). One that has great acceptance and is frequently used in fatigue design codes is shown in Equation 1 (Maddox, 2014Maddox, S. J. (2014). Fatigue strength of welded structures. Woodhead publishing.), which is based on the stress range , number of cycles to failure and the fatigue proprieties of material and .
In Equation 1, the slope and fatigue constant can be obtained by experimental or standards-based procedures. The form presented in Equation 1 defines the relation between stress range and number of cycles for the finite-life region, where is the slope of the straight line in log-log scale and can be related to the parameter by the equation . Figure 1 shows a schematic representation of an S-N curve for steels with the main parameters involved and the main regions of the curve.
Schematic representation of an S-N curve for steels (Lee, 2005Lee, Y.-L. (2005). Fatigue Testing and Analysis: Theory and Practice, Burlington: Butterworth-Heinemann.).
2.1 Procedures for determining the S-N curve based on Design Standards
During the development of a new machine component or structure, which is subject to time-varying loads, the fatigue properties of the material or component must be available or obtained. A rapid method for determining the S-N curve in limited life region, and widely used in the design phase, is the use of codes according to the structure type. A list of some standards is presented in Table 1.
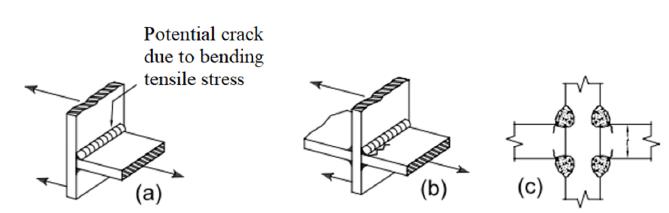
In this article, the Brazilian standard NBR 8800 (2008)NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards. was used, which is similar to AISC (2016)AISC 360-16 (2016). Specification for structural steel buildings. American National Standard. and both standards define the properties for welded structural details according to a fatigue category for nominal stress. For the fillet welded joint studied in this work, the fatigue category is presented in Figure 2, which corresponds to stress category C according with NBR 8800, with constant and =69 MPa for 95% of reliability (see Appendix K in the NBR 8800 for all fatigue categories). For others values of the reliability, the constant must be adjusted. For comparison purposes with others results obtained by experimental and hybrid approach in Section 3, the adjusted constant is for 50% of reliability.
NBR 8800 (2008)NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards. must be applied to members and connections subject to high cycle loading within the elastic range of stresses of frequency and magnitude sufficient to initiate cracking and progressive failure, which defines the limit state of fatigue, and is applied to stresses calculated on the basis of service loads with the maximum permitted stress due to service loads of 0.66S y. No evaluation of fatigue resistance is required if the live load stress range is less than the threshold allowable stress range and for sections or plates if the number of cycles of application of live load is less than 20000 cycles. For welded joints the range of stress at service loads shall not exceed the allowable stress range () computed for stress categories A, B, B’, C, D, E and E’, shall be determined by Equation 2:
where the stress category is defined by the detail type according Tables K.1 e K2 of the NBR 8800. The constant and is found in Table K.1.
2.2 Procedures for determining the S-N curve based on experimental tests
Several statistical schemes for obtaining an S-N curve are available, some methods are presented by JSME S 002 (1994)JSME S 002 (1994). Standard Method of Statistical Fatigue Testing, Japan Society of Mechanical Engineers., Nakazawa and Kodama (1987Nakazawa, H., Kodama, S. (1987), Statistical S-N testing method with 14 specimens: JSME standard method for determination of S-N curves. In Statistical Research on Fatigue and Fracture: Current Japanese Materials Research, pp. 59-69.), ASTM E739 (2015)ASTM E739 (2015). Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (SN) and Strain-Life. American Society for Testing and Materials., Shen (1994Shen, C. (1994). The Statistical Analysis of Fatigue Data, Ph.D. Dissertation, University of Arizona, Tucson.), Wirsching (1983Wirsching, P. H. (1983). Statistical summaries of fatigue data for design purposes. NASA CR-3697, NASA, Lewis.), and Kececioglu (2003Kececioglu, D. (2003). Robust engineering design-by-reliability with emphasis on mechanical components & structural reliability (Vol. 1). DEStech Publications, Inc, pp. 185-218.), which are widely used for experimental planning of fatigue tests. A brief definition of the standard ASTM E739 (2015)ASTM E739 (2015). Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (SN) and Strain-Life. American Society for Testing and Materials., that suggests a procedure for statistical treatment of data in the generation of fatigue curves, which was employed to analyze the experimental fatigue data generated in the present work.
ASTM E739 (2015) recommends that more than one specimen should be tested at each stress level, otherwise, the evaluating of variability would not be possible. Percent replication (PR) depends on the total number of specimens tested and the number of stress levels used during the tests, as defined by Equation 3. In other words, PR indicates the portion of the total number of specimens tested that may be used to obtain an estimate of the variability of the replication tests. This standard defines a minimum percentage of replication depending on the test purpose. Table 2 shows that the sample size and the percentage of replication required in the S-N testing, depending on the type of test program conducted.
Minimum sample size and percentage of replication according to ASTM E739 (2015)ASTM E739 (2015). Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (SN) and Strain-Life. American Society for Testing and Materials..
2.3 Hybrid approach proposed to obtain the S-N curve
This section introduces a new hybrid approach, which consists of defining an S-N curve with reduced tests associated to simulated data based on statistical distributions of slope available in the literature. The objective of the proposed methodology is to improve the estimation of the fatigue life with lower costs and reduced time, however enabling better results compared to the design codes, which sometimes are very conservative. The proposed methodology enables lower costs and time, once the number of specimens tested is considerably smaller than that required in case of purely experimental method as per ASTM E739 (2015)ASTM E739 (2015). Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (SN) and Strain-Life. American Society for Testing and Materials.. Strzelecki and Sempruch (2016bStrzelecki, P., Sempruch, J. (2016b). Verification of analytical models of the S-N curve within limited fatigue life. Journal of Theoretical and Applied Mechanics, 54(1): 63-73.) performed a study that takes into account error in fatigue life determination and time for the experiment execution, whereby it was concluded that the use of a hybrid approach is preferred to determine the fatigue life when aspects of cost and time are limited.
The proposed methodology is presented in the flowchart of Figure 3 and explained step by step below.
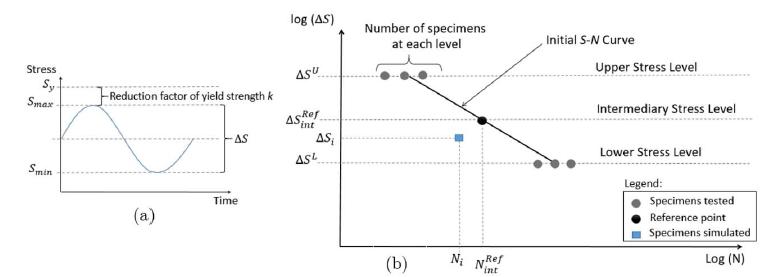
Step 1: Provide the necessary input parameters, which are presented in Table 3, along with the values used in the studies of this work. Two study cases were developed according to Table 3, one for a stress ratio R=0.1 and other with R=-1. The main objective of these two setups was to evaluate the influence of the fatigue life range of tested specimens, considering that the S-N approach is only valid for elastic stresses. For Case 1 (R=0.1), the range of tested fatigue life is limited for specimens with longer lives ( to cycles), since a high value of the stress range would lead to maximum stress of the cycle above the yield strength of the material. On the other hand, for Case 2 (R=-1), higher values of the stress range are possible, and the fatigue life range of tested specimens is to cycles, i.e. a totally different range from the one of Case 1, which may influence the results. is a reduction factor of the yield strength of material, necessary to define the maximum stress of the load cycle according to Figure 4.
Step 2: Perform the experimental fatigue tests with reduced number of specimens at the two stress levels chosen, with the number of tests chosen in Step 1. represent the number of specimens to be tested at each stress level. A scheme is shown in Figure 4.
Schematic representation of the (a) load cycle and (b) preliminary tests for the proposed methodology.
Step 3: After the tests, the initial fatigue properties of the material are estimated through the use of minimum squares and linear regression, obtaining the fatigue properties, called and .
Step 4: Using the initial fatigue properties estimated in Step 3, determine the average number of cycles for the intermediate stress level (see Figure 4), which will serve as the initial reference for the test simulations starting at the Step 5. An intermediate stress level was chosen because the relative error in this levels are smaller than in the upper and lower levels.
Step 5: Randomly select a value from exponent m within the limits desired according to experience or as available in the literature, which is called , where i represents the number of specimens to be simulated. In the present work, the probability distribution used was developed by the authors using a 3-parameters Weibull distribution to describe the relative occurrence frequency of the exponent m for 31 fillet welded joint made of steels, according to Figure 5.
Step 6: Using the stress range at the intermediate level as a reference, the number of cycles obtained in Step 4, the value of chosen at random in Step 5, a new value is estimated for the fatigue coefficient, denoted by , according Equation 4.
Step 7: Using a uniform probability distribution, one should randomly choose a new stress value that will be within the stress limits of the upper and lower levels chosen in Step 1, which is called and will be used as reference to generate the first specimen simulated in Step 8.
Step 8: In this step the first virtual specimen is generated, determining the number of cycles using the Equation 5 with the values of (Step 6), (Step 5) and (Step 7). As can be seen in Figure 4, a simulated specimen is generated with the Stress and the number of cycles . The steps 5 through 8 are repeated i times, generating i virtual specimens through statistical simulations.
Step 9: After the generation of all the simulated specimens according to the input data, all real and virtual specimens are grouped to allow the estimation of the adjusted hybrid S-N curve applying the method of least squares and linear regression.
3 EVALUATION OF THE PROPOSED METHOD
For performance evaluation of the proposed method, two studies were carried out to determinate the fatigue life and accumulated damage using the available fatigue test data from the literature (Figure 6) of a welded joint presented by Zhao et al. (1998Zhao, Y.-X.; Gao, Q.; Sun, X.-F. (1998), A statistical investigation of the fatigue lives of Q235 steel-welded joints. Fatigue & Fracture of Engineering Materials & Structures, 21(7): 781-790.). The first study is based in Monte Carlo simulations according shown in the Figure 7 (results in Section 3.1). The second study was performed through the algorithm presented in Figure 3, only modifying Step 2, in which originally should be tested specimens in real tests, in this section these specimens were randomly chosen in two stress levels already tested by Zhao et al. (1998) and already presented in Table 4. The stress levels tested by Zhao et al. (1998) were 254.8 MPa (11 specimens), 215.6 MPa (10 specimens), 176.4 MPa (10 specimens) and 137.2 MPa (10 specimens), where the stress values represent the stress range ΔS. The levels chosen for the studies were 254.8 MPa and 176.4 MPa, and randomly selected two specimens per level to run Step 2 of the proposed methodology. In addition to the four tested specimens chosen to obtain the initial curve, two more specimens were randomly chosen at the stress level of 137.2 MPa for use in the validation process, i.e., this stress level will be used to verify the proposed method (results in Section 3.2).
Figure 6 shows the S-N curve and the dimensions of the specimens tested by Zhao et al. (1998Zhao, Y.-X.; Gao, Q.; Sun, X.-F. (1998), A statistical investigation of the fatigue lives of Q235 steel-welded joints. Fatigue & Fracture of Engineering Materials & Structures, 21(7): 781-790.). Table 4 presents the fatigue test results of a welded joint made of steel Q235. The welding procedure was a manual electric arc with a wire diameter of 4 or 5 mm. The chemical composition of the weld metal was 0.14 C, 0.25 Mn, 0.03 Si, 0.018 P, and 0.03 S. The remainder was ferrite. The local dimensions of the welded joints were in accordance with the Chinese code-GB. The experiments were at room temperature with four-point bending, sine-wave loading, and a stress ratio of R = 0.1. The loading frequency was approximately 80-120 Hz. The percent replication of this fatigue test is RP=90%, with reliability data, thereby being chosen as a reference in the studies. Table 5 shows the information regarding the material used.
Different methodologies for obtaining S-N curves were compared: using the Brazilian standard NBR 8800 (2008)NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards., the initial S-N curve generated with reduced sample size and the corrected S-N curve obtained by proposed hybrid methodology.
S-N curve used as reference to the statistics simulations. (Zhao et al., 1998Zhao, Y.-X.; Gao, Q.; Sun, X.-F. (1998), A statistical investigation of the fatigue lives of Q235 steel-welded joints. Fatigue & Fracture of Engineering Materials & Structures, 21(7): 781-790.).
Real fatigue data of a welded joint made of steel Q235 (Zhao et al., 1998Zhao, Y.-X.; Gao, Q.; Sun, X.-F. (1998), A statistical investigation of the fatigue lives of Q235 steel-welded joints. Fatigue & Fracture of Engineering Materials & Structures, 21(7): 781-790.).
Table 5 presents the fatigue properties of the welded joint and static strength of base material (steel Q235), where constant C and slope m are fatigue properties and S y and S ut are static properties of the material.
A statistical simulation procedure of S-N curves based on the Monte Carlo method developed by the authors was used to verify the performance of the method proposed in Section 2.3. Figure 7 presents a basic scheme used for data generation, which replace the actual data in the Step 2 of Figure 3 (Section 2.3) by simulated data based on a normal distribution with mean and standard deviation from the actual tests (in this study according Zhao et al. (1998Zhao, Y.-X.; Gao, Q.; Sun, X.-F. (1998), A statistical investigation of the fatigue lives of Q235 steel-welded joints. Fatigue & Fracture of Engineering Materials & Structures, 21(7): 781-790.)) to obtain the initial curve with reduced size sample. This procedure was used to allow the statistical evaluation of the proposed method, since with the procedure adopted by the authors, it is possible to generate several fatigue curves, which experimentally would be impracticable due to the time and costs involved. In the studies described in this section, 100 fatigue curves were simulated using the procedure for generation of S-N curves of the Figure 7 (for both cases of Table 3), allowing a more consistent evaluation of the performance of the proposed method.
The flowchart of Figure 7 is detailed as follows:
Step 1: Provide the additional input parameters required for the simulation of fatigue data assuming a normal distribution. In addition to the input data already presented in Table 3, it is necessary to provide the number of curves to be simulated, and which are fatigue material properties through which the average curve is determined and the standard deviation (STD). In this work, a fixed standard deviation equal to 0.17 was considered. According to Eriksson et al. (2003Eriksson, Å., Lignell, A., Olsson, C., & Spennare, H. (2003). Weld evaluation using FEM: a guide to fatigue-loaded structures. Översättning: Teknikytex AB: Industrilitteratur.), one standard deviation to log N for the welded specimens is 0.16-0.18. Meanwhile, according to Lotsberg (2016Lotsberg, I. (2016). Fatigue design of marine structures. Cambridge University Press.), it is 0.20.
Step 2: Isolating N in Equation 1, the average life for each stress level can be determined according to Equation 6 for the material under consideration, using the fatigue properties provided in Step 1 in this section.
Step 3: Start the fatigue data simulation process (100 initial curves were simulated in this work) by randomly selecting samples, based on a normal distribution with mean life equal to defined by Equation 6 and standard deviation (STD). Equation 7 was used to generate random numbers for each stress level.
RN is the random number selected for each stress level with the number of simulated specimens equal to the number of test specimens defined in Step 1 of Section 2.3.
Step 4: This step consists of applying the flowchart defined in Figure 3 for each simulated curve.
Step 5: For each simulation (Step 3 through 6 in Figure 7) to qualitatively verify the differences between the curves studied, the simulated initial, hybrid, standard NBR 8800 and S-N reference curves are plotted together with the simulated test data.
Step 6: At the end of each loop the relative percentage difference in the life prediction and fatigue damage are calculated in relation to the reference curve, allowing a quantitative comparison of the results. The main output data verified in the present work were the maximum relative errors and the comparison of the accumulated damage using the average curves (50% of reliability), applying the Miner damage rule (Equation 9) with stress spectra according to DIN 15018 (1984)DIN 15018 (1984). Cranes; steel structures; verification and analyses. Beuth Verlag GmbH., which are based on maximum stress range and are widely applied in the design of structures, such as cranes. Equation 8 shows how the relative percentage difference (RPD) was evaluated for each simulation.
where is obtained with Equation 1 using the properties of the reference material and the value of stress range in each stress level considered. is the life obtained with the properties of the material obtained according to the method considered for estimating the properties. The Miner damage rule is defined by Equation 9. In the present work the number of cycles was defined based on the spectrum of DIN 15018 (1984)DIN 15018 (1984). Cranes; steel structures; verification and analyses. Beuth Verlag GmbH., as also used by Pravia (2003Pravia, Z. M. (2003). Stability of steel bridges structures with fractures. Ph.D. Thesis (in Portuguese). Federal University of Rio De Janeiro, Rio de Janeiro.).
Table 6 shows damage (D) for the reference curve using the spectrum according to DIN 15018 (1984)DIN 15018 (1984). Cranes; steel structures; verification and analyses. Beuth Verlag GmbH.. The number of cycles was set to get D equal 1 for the reference curve. The values of the stress range and number of cycles used to calculate the damage are presented in Table 6. The damage obtained using the simulated hybrid curves is presented in Section 3.1, after the generation of the curves according to the methodologies depicted in Figure 3 and Figure 7.
Stress spectrum according to DIN 15018 (1984)DIN 15018 (1984). Cranes; steel structures; verification and analyses. Beuth Verlag GmbH. for reference curve.
3.1 Results of Monte Carlo simulation for evaluation of the proposed method
Using Monte Carlo simulations, 100 curves were generated for the evaluation of the proposed method, as described in Section 3 for the studied welded joint. Figure 8 shows the experimental reference curve (obtained using actual data) and the S-N curve defined according to NBR 8800 overlaid with the 100 simulated initial and hybrid S-N curves for the Cases 1 and 2 of Table 3, enabling a qualitative assessment of the results. It is noted that the slopes of the curves (in log-log scale) obtained using the Hybrid Approach do not vary as much as the ones from the initial curves, keeping the hybrid curves within a narrow band that have physical meaning for the welded joint according to data available on the literature, getting more accuracy on the fatigue results.
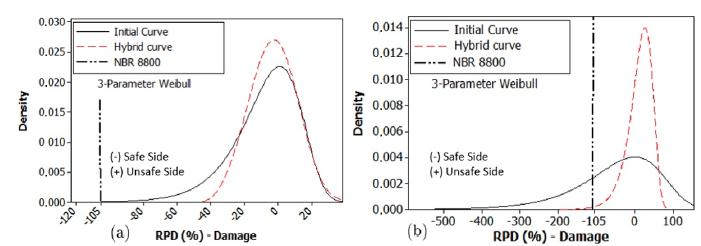
The quantitative resume of results is shown in the Table 7, for Cases 1 and 2. Figures 9 and 10 have complementary results for initial curve and hybrid approach, presenting a probability density for relative percentage difference of the damage and fatigue life, respectively.
Comparing the proposed method with the S-N curve according to NBR 8800 (2008)NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards., for the estimated damage (see Figure 9), the relative percentage difference RPD for both study cases is smaller when the Hybrid Approach is considered. Note that for NBR 8800 curve the RPD is -105% (Safe Side - SS), whereas for the hybrid method for Case 1, the RPD is -30% (SS) to 25% (Unsafe Side - US) and for Case 2 it is -66 to 62%, both considering 95% of probability of occurrence. Too can be conclude that when is used the Hybrid Approach, for the Case 1, the probability of exceeding the RPD obtained by NBR 8800 is negligible, and for Case 2, the probability of exceeding is 0.52%, in both cases very small.
About the fatigue life (see Figure 10), the RPD of NBR 8800 curve for both study cases is within the probability distribution for the hybrid curve. The Hybrid Approach has 17.9% (Case 1) and 12.7% (Case 2) of probability of exceeding the RPD obtained using the NBR 8800 curve, as can be seen in the Figure 10 (hatched areas). Note that fatigue life the RPD for NBR 8800 is 53% (SS), whereas for the hybrid method for Case 1 is -140% (US) to 90.2% (SS) and for Case 2 it is -201% (US) to 88% (SS), both considering 95% of probability of occurrence.
It can be concluded that the advantage of the proposed method is associated with the fact that even the RPD range to be larger for life estimations, the results for damage using Hybrid Approach present a considerable reduction of RPD. Therefore, for projects that considers finite life criteria for fatigue damage analysis, the proposed method is indicated. It can be noticed that in both Hybrid and NBR 8800 approaches, mean curve (i.e. the curve with reliability of 50%) is used. For design applications, an S-N design curve must be used, which corresponds to a lower limit S-N curve, obtained by adjusting the mean curve for the probability of failure and the confidence level. This procedure was not presented in this article, being the next step in the improvement of the methodology.
3.2 Results of the proposed method using actual data
In this section, the algorithm presented in Figure 3 was used, only modifying Step 2. In this step, originally, actual specimens should be tested, however, in this section experimental data obtained by Zhao et al. (1998Zhao, Y.-X.; Gao, Q.; Sun, X.-F. (1998), A statistical investigation of the fatigue lives of Q235 steel-welded joints. Fatigue & Fracture of Engineering Materials & Structures, 21(7): 781-790.) were employed for validation of the proposed hybrid methodology. A reduced number of experimental data (two specimens) were randomly selected among the results presented by Zhao at each stress level (already listed in Table 4). These initial random specimens are presented in Table 8 for each stress level considered, allowing to compare the hybrid approach with the experimental curve S-N obtained with high replication.
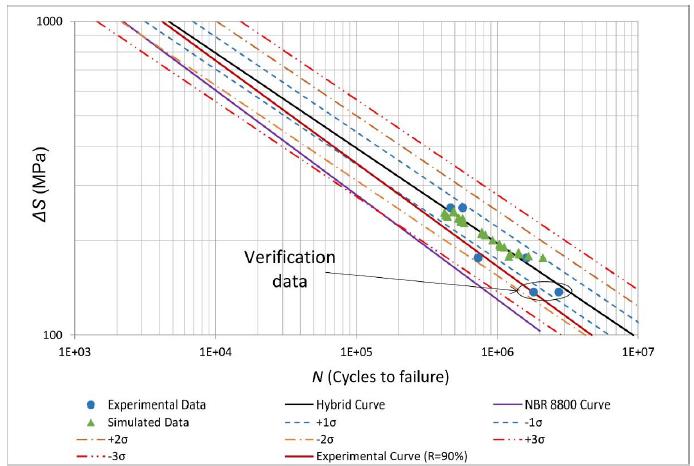
The validation criterion is to evaluate whether the verification data are within the 3σ interval of the mean hybrid curve, where σ is the standard deviation equal to 0.17 according Eriksson, Lignell, Olsson, & Spennare (2003Eriksson, Å., Lignell, A., Olsson, C., & Spennare, H. (2003). Weld evaluation using FEM: a guide to fatigue-loaded structures. Översättning: Teknikytex AB: Industrilitteratur.).
It can be seen in Figure 11 that the verification experimental data are within the range of 2σ, approving the proposed method according to the established criterion, which has already been used by Marin and Nicoletto (2009Marin, T., & Nicoletto, G. (2009). Fatigue design of welded joints using the finite element method and the 2007 ASME Div. 2 Master curve. Frattura ed Integrità Strutturale, 3(9), 76-84.). Note that all experimental data (six specimens tested) are within the curves shifted of the hybrid. Therefore, based on the results of Figure 11, it is concluded that the hybrid approach presents a good approximation, especially considering the time required to obtain a fully experimental S-N curve.
Comparative chart for verification of the proposed method using data of Zhao et al. (1998Zhao, Y.-X.; Gao, Q.; Sun, X.-F. (1998), A statistical investigation of the fatigue lives of Q235 steel-welded joints. Fatigue & Fracture of Engineering Materials & Structures, 21(7): 781-790.).
4 APPLICATION - FATIGUE LIFESPAN OF A FILLET WELDED JOINT BASED ON FEM MODEL
In this section, an application of the proposed method is described for the fatigue analysis of a fillet welded joint tested by the authors is described. The application is depicted in the flowchart of Figure 12, where a finite element model was employed to obtain the stresses of the tested joint for posteriori evaluation of its fatigue lifespan. The software used for preprocessing and solver steps was Ansys 19. For post-processing step, the same methodology presented in Step 6 of the Section 3 was used, implemented in MatLab software.
The geometry of the tested joint and its dimensions are shown in Figure 13(a). The welded joint is made of Steel LNE-380 with S y=408 MPa and S ut=500 MPa obtained from single-tensile test. The fatigue properties were determined using the Hybrid Approach, with values of input parameters according Tables 9 and 10. The experiments were carried out at room temperature with three-point bending, sine-wave loading, stress ratio of R=-1. The loading frequency was 1-4 Hz and 2 specimens were tested at each level for two stress levels. Figure 13(b) show the fatigue test setup using a servo-hydraulic testing machine from the manufacturer Shimadzu with a load capacity of 100 kN.
The numerical model was developed with software Ansys 19, using modeling techniques already used by Silveira, Mezzomo, Goedel (2017Silveira, J. A., Mezzomo, G. P., Goedel, F. (2017). Evaluation of structural stress method and master curve for fatigue life prediction of a welded joint. Revista Internacional de Metodos Numericos para Calculo Y Diseno En Ingenieria, 33(3-4), 318-328.), where several techniques of representation of the weld were analyzed. In this work, the chosen technique to model the weld was the increased thickness suggest by Niemi (1995Niemi, E. (1995). Stress determination for fatigue analysis of welded components. The International Institute of Welding (IIW): Woodhead Publishing.), which consists in increasing the element thickness in the region of the weld. Eriksson, Lignell, Olsson, & Spennare (2003Eriksson, Å., Lignell, A., Olsson, C., & Spennare, H. (2003). Weld evaluation using FEM: a guide to fatigue-loaded structures. Översättning: Teknikytex AB: Industrilitteratur.) suggests the scheme illustrated in Figure 14. The load spectra are equal to the one in Section 3 (Step 6) according to DIN 15018 (1984)DIN 15018 (1984). Cranes; steel structures; verification and analyses. Beuth Verlag GmbH. and shown in Table 6. For obtaining the NBR 8800 curve, the same class for the joint detail was employed, according to Figure 2(a).
The geometry modeled using the technique exhibited in Figure 14 and the employed mapped finite element mesh for the tested welded joint are shown in Figure 15. The mesh was built using 8-node shell elements with maximum element size of 12.5mm. The choice of 8-node shell elements was made according to Niemi (1995Niemi, E. (1995). Stress determination for fatigue analysis of welded components. The International Institute of Welding (IIW): Woodhead Publishing.), in general, these shell element provides best results for this type of detail joint. The size of elements was defined for convergence reasons. The distance between supports is 285mm. The boundary conditions are also depicted in the Figure 15a, where d stands for translation and r represents rotation.
The specimens were machined and prepared using a robotic welding procedure, welding wire ER70S-6 with gas protective welding containing two-component mixture comprising 82% argon and 18% carbon dioxide. The chemical composition of the welding wire ER70S-6 is 0.09%C, 1.63%Mn, 0.007%S, 0.9%Si, 0.007%P, 0.20%Cu, 0.05%Cr, 0.05%Ni, 0.05%Mo and 0.05%V, which is adequate for base material. Welding parameters are a pulsed current of 300A, a voltage of 29V and a speed of 40 cm/min and gas input of 15 l/min.
Modeling of the fillet weld with shell elements using increased thickness at the weld region (Eriksson, Lignell, Olsson, & Spennare, 2003Eriksson, Å., Lignell, A., Olsson, C., & Spennare, H. (2003). Weld evaluation using FEM: a guide to fatigue-loaded structures. Översättning: Teknikytex AB: Industrilitteratur.).
(a) Geometry and boundary conditions and (b) finite element mesh of the tested welded joint.
4.1 Results of the estimation of the fatigue lifespan for the tested joint
Initially, the results of the fatigue properties of the tested welded joint obtained using the proposed Hybrid Approach are presented. Two specimens were tested in two stress levels (4 specimens) in order to generate the initial S-N curve according to Step 2 (Figure 3), which are listed in Table 9. The stress range values at the stress levels used to generate the initial data were 700 and 450 MPa. Others two specimens were tested at 380 MPa for use in the validation process.
Table 10 shows the input data used to generate a Hybrid S-N curve based on the flowchart of Figure 3.
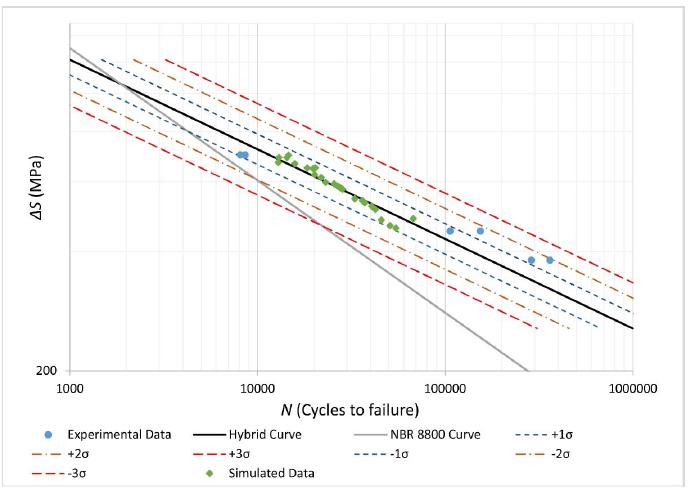
Using the flowchart of Figure 3 and data of Tables 9 and 10, it was possible to obtain the fatigue properties of the joint material using the proposed methodology with a reduced number of tests added to improve the quality of simulated specimens. The fatigue properties obtained with Hybrid Approach were C= 2. 04133E+16 and m=4.3 for 50% of reliability. Figure 15 exhibits plots of the experimental data, the S-N curve according to NBR 8800 (2008)NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards. and the hybrid curve (including the mean curve and the curves corresponding to , and ). Two specimens at the lower stress level were tested for verification of the Hybrid Approach (identified in Figure 16).
It can be seen from Figure 16 that the verification experimental data are within the range of 2σ, approving the proposed method according to the established criterion, as previously discussed. Note that all experimental data based (six specimens tested) shown in Table 9 are within the curves shifted of the hybrid. Therefore, based on the results of Figure 16, it is concluded that the hybrid approach presents a good approximation.
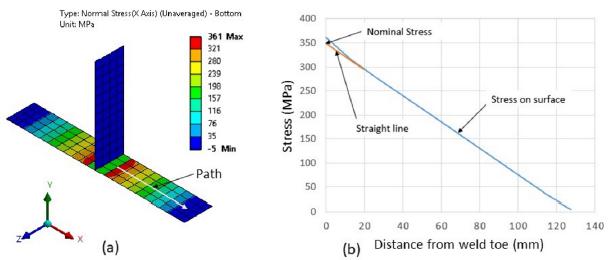
The FEM results are shown in Figure 17. In Figure 17(a), a contour plot of the normal stress in the x direction is shown. The highlighted path was used to plot the stresses, starting at the weld toe and extending perpendicularly to the weld (because the maximum principal stress occurs in this direction). Figure 17(b) shows the extrapolation method used according Eriksson, Lignell, Olsson, & Spennare (2003Eriksson, Å., Lignell, A., Olsson, C., & Spennare, H. (2003). Weld evaluation using FEM: a guide to fatigue-loaded structures. Översättning: Teknikytex AB: Industrilitteratur.) to obtain the nominal stress at the weld toe. The maximum nominal stress of the fatigue load cycle is 350 MPa, for the upper stress level.
The next step is to perform the fatigue analysis to obtain the damage and fatigue life using the S-N curve based on Hybrid Approach and NBR 8800 (2008)NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards.. The results for the tested joint are presented in Table 11.
According Table 11, the Hybrid Approach lead to accuracy results like seen previously in the Section 3.1 and 3.2. Evaluating the strength for 103 cycles, it is verified that the two approaches are very close. For 106 cycles, the relative difference between the approaches is bigger. The strength by NBR 8800 is fifty percent less than the strength by the Hybrid Approach for 106 cycles.
Evaluating the damage, the relative percentage difference is even greater, being that the damage according NBR 8800 is 336.7% bigger than the Hybrid Approach, and can be seen that the Hybrid Approach allow more accuracy results and less conservative than NBR 8800. According mentioned by Eriksson, Lignell, Olsson, & Spennare (2003Eriksson, Å., Lignell, A., Olsson, C., & Spennare, H. (2003). Weld evaluation using FEM: a guide to fatigue-loaded structures. Översättning: Teknikytex AB: Industrilitteratur.), the design codes and reality are not the same thing, once the design codes are often very general, allowing a little room for innovative approaches, and for structural applications they give are normally “on safe side”.
5 SUMMARY AND CONCLUSIONS
This work introduced a hybrid approach to obtain the S-N curve, which combines statistical simulated data to a fatigue actual fatigue test data obtained with a reduced number of specimens. Initially using an own methodology based on the Monte Carlo Method that enables to generate several S-N curves based on the fatigue properties of the reference material (mean curve with 50% reliability) and standard deviation, it was possible to evaluate the performance of the proposed method for obtaining S-N curves with good accuracy and lower costs. Subsequently the hybrid approach was applied in a real case (a fillet welded joint) in order to obtain the S-N curve using only four specimens as initial experimental data and therefore assess its fatigue lifespan and cumulative fatigue damage. FEM was employed to obtain the stresses ate the weld toe, and Miner's rule and load spectra from DIN 15018 (1984)DIN 15018 (1984). Cranes; steel structures; verification and analyses. Beuth Verlag GmbH. were used for the damage estimation. The results obtained for the real case show that the proposed approach improved the accuracy comparing with the S-N curve obtained by standard NBR 8800 (2008)NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards. for the same detail class, both for fatigue life and for damage calculation. Some additional comments can be made about the hybrid approach:
-
The proposed methodology present a balanced cost-benefit;
-
The proposed methodology provides quantification of cumulative fatigue damage with greater accuracy.
-
Whenever possible, when working with finite fatigue life, it is a good practice to perform the tests for higher numbers of life cycles, since the in actual work conditions of several equipment, the number of cycles that occurs in this region is bigger and it is possible to reduce the associated errors in the fatigue life and damage. However, even when testing specimens with low/medium number of life cycles, the proposed methodology proved to be satisfactory, achieving better results than the other methods used for comparison;
-
In the present work, the mean S-N curves were used in the analyses, i.e. the curve with reliability of 50%. For design applications, an appropriate coefficient must be used to adjust a proposed curve for the desired failure probability and confidence level. This procedure was not presented in this article, being the next step in the improvement of the methodology;
-
The accuracy of the hybrid approach is linked to the distribution probabilities of the slope m, which must be obtained taking into account the weld detail and loading types. Several data are available in the literature, being necessary a search to compile this data and subsequently perform a statistical analysis;
-
The present methodology will be validated for other types of welded joints, making it possible to generalize its application.
References
- AISC 360-16 (2016). Specification for structural steel buildings. American National Standard.
- ASTM E739 (2015). Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (SN) and Strain-Life. American Society for Testing and Materials.
- Bai, X., Xie, L., Zhang, R., Guan, R., Tong, A., & Bai, E. (2017). Measurement and estimation of probabilistic fatigue limits using Monte-Carlo simulations. International Journal of Fatigue, 95: 229-235.
- Cetin, A., Härkegård, G., & Naess, A. (2013). The fatigue limit: An analytical solution to a Monte Carlo problem. International Journal of Fatigue, 55: 194-201.
- DIN 15018 (1984). Cranes; steel structures; verification and analyses. Beuth Verlag GmbH.
- Eriksson, Å., Lignell, A., Olsson, C., & Spennare, H. (2003). Weld evaluation using FEM: a guide to fatigue-loaded structures. Översättning: Teknikytex AB: Industrilitteratur.
- Gope, P.C. (1999). Determination of sample size for estimation of fatigue life by using Weibull or log-normal distribution. International Journal of Fatigue, 21(8): 745-752.
- Gope, P.C. (2002). Determination of minimum number of specimens in SN testing. Journal of Engineering Materials and Technology, 124(4): 421-427.
- ISO 12107 (2012). Metallic Materials-Fatigue Testing-Statistical Planning and Analysis of Data. International Organization for Standardization.
- JSME S 002 (1994). Standard Method of Statistical Fatigue Testing, Japan Society of Mechanical Engineers.
- Kececioglu, D. (2003). Robust engineering design-by-reliability with emphasis on mechanical components & structural reliability (Vol. 1). DEStech Publications, Inc, pp. 185-218.
- Lee, Y.-L. (2005). Fatigue Testing and Analysis: Theory and Practice, Burlington: Butterworth-Heinemann.
- Lorén, S. and Lundström, M. (2005). Modelling curved S-N curves. Fatigue & Fracture of Engineering Materials & Structures, 28(5): 437-443.
- Lotsberg, I. (2016). Fatigue design of marine structures. Cambridge University Press.
- Maddox, S. J. (2014). Fatigue strength of welded structures. Woodhead publishing.
- Marin, T., & Nicoletto, G. (2009). Fatigue design of welded joints using the finite element method and the 2007 ASME Div. 2 Master curve. Frattura ed Integrità Strutturale, 3(9), 76-84.
- Nakazawa, H., Kodama, S. (1987), Statistical S-N testing method with 14 specimens: JSME standard method for determination of S-N curves. In Statistical Research on Fatigue and Fracture: Current Japanese Materials Research, pp. 59-69.
- Niemi, E. (1995). Stress determination for fatigue analysis of welded components. The International Institute of Welding (IIW): Woodhead Publishing.
- NBR 8800 (2008). Design of steel and composite structures for buildings. Brazilian Association of Technical Standards.
- Pang, J. C., Li, S. X., Wang, Z. G., & Zhang, Z. F. (2014). Relations between fatigue strength and other mechanical properties of metallic materials. Fatigue & Fracture of Engineering Materials & Structures, 37(9): 958-976.
- Paolino, D. S., Chiandussi, G. and Rossetto M. (2013). A unified statistical model for S-N fatigue curves: probabilistic definition. Fatigue & Fracture of Engineering Materials & Structures, 36(3): 187-201.
- Paolino, D. S., Tridello, A., Chiandussi, G., & Rossetto, M. (2018). Estimation of P‐S‐N curves in very‐high‐cycle fatigue: Statistical procedure based on a general crack growth rate model. Fatigue & Fracture of Engineering Materials & Structures, 41(4): 718-726.
- Pascual, F.G. and Meeker, W.Q. (1997), Estimating fatigue curves with the random fatigue-limit model. Technometrics, 41(4): 277-289.
- Pascual, F. G. (2003), Theory for optimal test plans for the random fatigue-limit model. Technometrics, 45(2): 130-141.
- Pinto, J.M.A., et al. (2002), Fatigue test plan to obtain SN curves. ASME 2002 Pressure Vessels and Piping Conference-American Society of Mechanical Engineers, Vancouver, Canada, August.
- Pravia, Z. M. (2003). Stability of steel bridges structures with fractures. Ph.D. Thesis (in Portuguese). Federal University of Rio De Janeiro, Rio de Janeiro.
- Sanches, R. F., de Jesus, A. M., Correia, J. A., Da Silva, A. L. L., & Fernandes, A. A. (2015). A probabilistic fatigue approach for riveted joints using Monte Carlo simulation. Journal of Constructional Steel Research, (110): 149-162.
- Shen, C. (1994). The Statistical Analysis of Fatigue Data, Ph.D. Dissertation, University of Arizona, Tucson.
- Silveira, J. A., Mezzomo, G. P., Goedel, F. (2017). Evaluation of structural stress method and master curve for fatigue life prediction of a welded joint. Revista Internacional de Metodos Numericos para Calculo Y Diseno En Ingenieria, 33(3-4), 318-328.
- Szala, G., Ligaj, B. (2016). Application of hybrid method in calculation of fatigue life for C45 steel (1045 steel) structural components. International Journal of Fatigue, 91: 39-49.
- Strzelecki, P., Sempruch, J. (2016a). Experimental method for plotting SN curve with a small number of specimens. Polish Maritime Research, 23(4): 129-137.
- Strzelecki, P., Sempruch, J. (2016b). Verification of analytical models of the S-N curve within limited fatigue life. Journal of Theoretical and Applied Mechanics, 54(1): 63-73.
- Strzelecki, P., Tomaszewski, T. (2016), “Application of Weibull distribution to describe SN curve with using small number specimens”. AIP Conference Proceedings, October.
- Zhao, Y.-X.; Gao, Q.; Sun, X.-F. (1998), A statistical investigation of the fatigue lives of Q235 steel-welded joints. Fatigue & Fracture of Engineering Materials & Structures, 21(7): 781-790.
- Wirsching, P. H. (1983). Statistical summaries of fatigue data for design purposes. NASA CR-3697, NASA, Lewis.
-
Available online September 18, 2018
Publication Dates
-
Publication in this collection
2018
History
-
Received
18 July 2018 -
Reviewed
04 Sept 2018 -
Accepted
17 Sept 2018