Experimental study of brass properties through perforation tests using a thermal chamber for elevated temperatures

Abstract

Experimental analysis on standard brass alloy has been carried out using a high pressure gas gun. Perforation tests have been performed for a variety of impact velocities from 40 to 120 m/s in order to study the material behaviour and to define failure modes.

The main aim of the study has been to provide results using an innovative thermal chamber that allows to heat specimens before impact. The range of available temperatures is from the room temperature up to 260 ˚C.

The experimental study has allowed to discuss the ballistic properties of the structure. The ballistic resistance of sheet plates is strongly dependent on the material behaviour under dynamic loading and changes with temperature. The ballistic properties are also intensely related to interaction between the projectile and thin brass target. The results in terms of the ballistic curve VR (residual velocity) versus V0 (initial velocity) have shown the temperature effect on the residual kinetic energy and thus on the energy absorbed by the plate, revealing a thermal softening of the brass. The ballistic limit corresponding to the maximum impact velocity without complete perforation has decreased by 5-7% for the highest temperature considered.

A changing failure pattern is observed. The number of petals varies as a function of impact velocity and temperature. It can be concluded based on experimental observations that thermal softening is a key point on the process of perforation.

Preliminary temperature records have been provided using a thermal imaging camera.

Keywords
Gas gun experimental technique; high rates of loading; high-performance thermal chamber; brass properties

1 INTRODUCTION

Few experimental data are available in the international literature in which specimens are subjected to impact loading at elevated temperatures. The main reason is due to the non-coupling of standard gas gun to a thermal chamber. The usual approach is to carry out perforation tests at room temperature and to extrapolate results using numerical simulations at high temperatures knowing the constitutive relation.

Many authors dealt with perforation analysis, from theoretical approaches such as discussed in [¹-²] to more practical considerations as reported in [³-⁵]. However, no direct data concerning perforation failure modes at high temperatures were reported or published. The thermal softening of the material was usually tested using quasi-static experiments and its extrapolation to high strain rates was often a rough simplification. The idea of carrying out dynamic tests using thermal chamber is a solution to the problem.

In this work, a new high-performance thermal chamber is used to heat up metallic thin plate specimens and to impose an initial temperature higher than the room temperature. The maximum temperature reached with this original device is 260 ˚C. This level is efficient to explore structure behaviour where thermal softening effect is observed. Brass alloy has been selected in this work since the strain rate sensitivity may be assumed as negligible [⁶]. In this case, it is possible to consider only one dependency on the material behaviour, i.e. the temperature sensitivity. Experimental results obtained have been compared with available literature data [⁷].

2 PERFORATION TESTS

A number of dynamic perforation tests were conducted at high impact velocity in order to understand the thermo-mechanical behaviour of metals such as brass and to evaluate its mechanical properties. These experimental results are necessary to complete 1D tests (tension, compression and others) allowing to estimate the material constants and to ensure accurate FE simulations. However, no data were available for perforation tests carried out at elevated temperatures. Most authors assumed a thermal behaviour according to the constitutive relations based on the function describing the temperature sensitivity obtained from compression or tensile tests in quasi-static conditions.

Experimental and analytical investigations have been carried out to analyze in details the perforation process [¹]. A wide range of impact velocities from 40 to 120 m/s has been covered during the tests. Two projectiles shapes have been used: a conical projectile with an angle of 72° and a blunt-shaped one, both with 11.5 mm in diameter. The target plate is 1.0 mm thick with a size of 130 x 130 mm which is clamped along its perimeter to provide a perfect fixation and to avoid sliding. The gas gun set-up is shown in Fig. 1 and the specimen and the projectiles dimensions are presented in Fig. 2.

Figure. 1
Gas gun set-up used for perforation tests at high impact velocities and temperatures, a/ general scheme b/ photo of the system with the thermal chamber installed

Figure 2
Dimensions of the plate used for perforation and projectiles shapes with a constant mass

The apparatus is also equipped with a thermal chamber in which a specimen is fixed. The temperature is changed from room temperature to a maximum temperature of 260 ˚C.

The air flows inside the system through to a ventilator. A sarcophagus is used around the plate specimen to keep a uniform temperature distribution. Therefore, the two sides of the specimen are heated up in the same time. Due to conductivity the entire specimen reaches the initial temperature imposed to the specimen and regulated by the controller.

A schematic description of the oven used during perforation and the heat airflow is reported in Fig. 3. The electronic heat controller (PID type) permits to set the required temperature and to control the temperature increase. The temperature values in the thermal chamber and in the specimen are measured by two thermocouples. The built-in thermocouple measures continuously the temperature inside the chamber. Then, a special calibration specimen with the thermocouple is used to measure the temperature evolution in the specimen itself.

The temperature imposed by the user and regulated by the controller does not exactly match the temperature in the specimen. A difference is observed between these two measurements due to the heat loss by conductivity along the device. It is corresponding to 28-30% of the temperature assumed. This effect is reported, Fig. 4. Therefore, a waiting time ${\text{t}}_{\text{waiting}}\approx 20\text{min}$ is necessary to obtain a uniform required temperature distribution along the specimen. The procedure of calibration must be repeated if the material is changed or if the thickness of the material studied is modified.

Figure. 3
Thermal chamber for heating up the target plate specimens, a/ schematic representation of the process of air mixing b/ general view of the thermal chamber

Figure. 4
Calibration of the system - thermocouples records inside thermal chamber and on specimen surface for different imposed temperatures

The projectile is launched using a pneumatic gas gun, it accelerates in the tube to reach an initial impact velocity ${\text{V}}_0$. Then, the projectile impacts the brass plate with partial or complete perforation depending on the quantity of kinetic energy transferred to the tested plate. The residual velocity ${\text{V}}_{\text{R}}$ of the projectile is measured after perforation. A pair of laser sensors are used to measure the initial impact velocity and a laser barrier is fixed behind the plate to measure the residual velocities. The projectile mass is equal to 30 g. The material used for machining the projectile is a maraging steel with a heat treatment to reach a yield stress close to 2 GPa. Therefore, the projectile has no visible permanent deformation during the process of perforation. The residual velocity of the projectile ${\text{V}}_{\text{R}}$ can be estimated using the following equation proposed by Ipson and Recht [²], calibrating the shape parameter $\kappa$ and knowing the ballistic limit velocity ${\text{V}}_{\text{B}}$:

${\text{V}}_{\text{R}}={\left({\text{V}}_0{}^{}-{\text{V}}_{\text{B}}{}^{}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$$}\right.}$ (1)

where ${\text{V}}_0$ is the initial velocity. In the above equation ${\text{V}}_{\text{B}}$ is equal to 40 m/s and $\kappa$ is varying from 1.85 at T=20˚C to 2.29 at T=260˚C. The parameters of Eq. 1 are calculated using the least squares method-based on experimental results. The energy absorbed by the plate ${\text{E}}_{\text{d}}$ can be calculated using the following equation:

${\text{E}}_{\text{d}}=\frac{{\text{m}}_{\text{p}}}{2}\left({\text{V}}_0{}^2-{\text{V}}_{\text{R}}{}^2\right)$ (2)

where ${\text{m}}_{\text{p}}$ is the projectile mass.

The difference of the initial and residual kinetic energy can be calculated using the experimental data, then based on the Recht-Ipson approximation, so the energy absorbed by the plate can be derived [², ⁸].

3 ANALYSIS OF RESULTS

The failure modes observed depends on both impact velocity and initial temperature value. For a conical projectile, a failure mode by petaling occurs inducing radial necking due to a process of piercing [⁵, ⁹, ¹⁰, ¹¹]. The conical projectile perforates the target plate and the plastic strain is localized at the extremities of the petals. Analytical predictions discussed in [¹²] are fully confirmed at room temperature, whereas more discrepancy in petals number is reported at higher temperatures.

The usual failure mode is by petaling with 3 or 4 petals. Up to 6 petals have been observed at lower impact velocities (close to the ballistic limit) and at higher temperatures. The failure modes observed during experiments are presented, Fig. 5.

According to the theoretical considerations of Landkof and Goldsmith in [¹²], the number of petals strongly depends on the failure deformation parameter. This parameter changes with temperature, i.e. the elongation of the material is more substantial at higher temperatures which directly leads to the number of petals increase. This is confirmed in this study: 5 and 6 petals have been observed for temperatures over 200 ˚C, whereas 3 or 4 petals have been usually observed at lower temperatures.

The nose angle of the conical projectile also has a direct influence on the failure mode [¹²], however this parameter is kept as constant in this study.

Figure 5
Initial temperature effect and impact velocity during perforation. Experimental observations of petaling failure mode, a/ 3 petals at T=20˚C and V0=120.18 m/s, b/ 4 petals at T=100˚C and V0=65.27 m/s, c/ 5 petals at T=200˚C and V0=54.94 m/s, d/ 6 petals at T=260˚C and V0=44.88 m/s

In general, the failure strain level which follows the process of instability is related to the hardening parameter. This is why in dynamic, due to adiabatic heating, the parameter n decreases and trigger instability. However, in this study the Johnson-Cook constitutive relation is only discussed (see chapter 4 hereafter) which imposes the n value as constant. It could be interesting to improve a material definition by introducing the n(T) function. It can be anticipated this would reflect more precisely the phenomenon of multi-petaling (5 or 6) at higher temperatures.

Another important observation is made by a juxtaposition of initial and residual velocities of the projectile at different rates of loading and for different temperatures. In Fig. 6, it has been shown that the residual velocity increases with temperature. It is more evident for high impact velocities (approx. 120 m/s corresponding to the gas gun pressure of 5.0 bars). It reflects a softening of the material with the temperature increase; in case of brass the softening process starts above 200 ˚C.

Figure 6
Initial vs residual velocity of projectiles at different rates of loading and for different temperatures; case of conical projectile

A different failure pattern has been observed for a blunt projectile. A process of high speed cutting due to intensive shearing takes place inducing a plug ejection. No perforation results are seen in Figs 7a and 7b in the form of a typical dishing is observed. At V0=60 m/s (Fig. 7b), a plug starts to separate. Two target plates perforation modes are presented in the next figures, namely Fig. 7c and Fig. 7d. A plug is either not separated completely (metal is locally bent and torn) or it is completely ejected.

For high velocities, a high localization of the plastic strain appears in a very small shear zone, the plastic deformation is limited to the near vicinity of the impacted point (Fig. 8b). Similar conclusions were made in [¹³]. However, for impact velocities close to the ballistic limit (no complete perforation), a plastic deformation of the whole active zone is observed (Fig. 8a). For comparative reasons, this phenomenon is shown for the conical projectile (Fig. 8c) where a more localized plastic deformation is observed.

Figure 9 reports a comparison between experimental results at room temperature and for a temperature of 260 ˚C. It can be noticed that increasing the initial temperature of the specimen shifts the ballistic limit (state of no perforation) to lower values: the ballistic limit obtained is approximately 43 m/s (20 ˚C) and 40 m/s (260 ˚C) for the conical projectile. The Recht-Ipson estimation would suggest a slightly lower ballistic limit for 260 ˚C, i.e. approximately 37 m/s. For the blunt projectile, the ballistic limit is equal to 63 m/s (20 ˚C) and 60 m/s (260 ˚C), respectively. The other measured points are also shifted when higher residual velocities VR are measured for elevated temperatures. All experimental data are reported in Table 1.

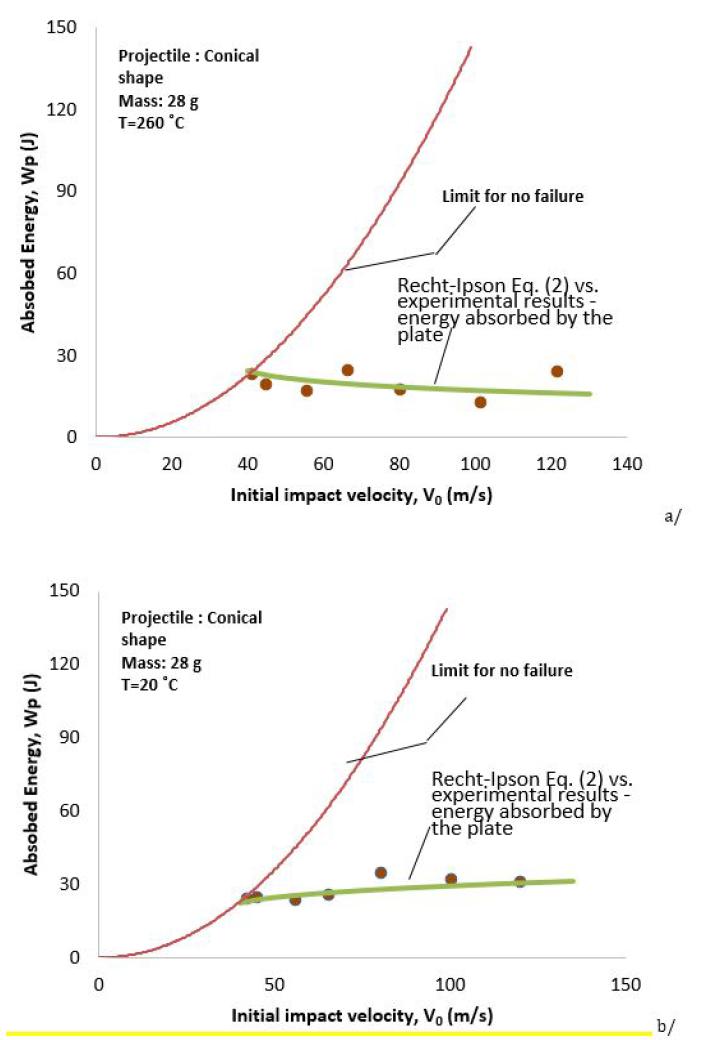
The energy absorbed during the impact does not change considerably with the impact velocity, this is presented in Fig. 10. Experimental results stay in accordance with analytical predictions using Eq. (1) [²].

Figure 7
Experimentally observed failure patterns for blunt-shaped projectile a/ dishing at T=20˚C and V0=52.85m/s, b/ plug starting to form at T=20˚C and V0=60.39m/s, c/ plug not-separated at T=20˚C and V0=74.18m/s, d/ plug ejected at T=20˚C and V0=93.28m/s

Figure 8
Overal deformation of the active zone of the target plates a/ no perforation using a blunt-shaped projectie, b/ perforation with a blunt projectile, c/ perforation in form of petals obtained with a conical projectile

Figure 9
Initial impact velocity V0 vs residual velocity VR - experimental results for T=20˚C and T=260˚C; a/ conical projectile, b/ blunt-shaped projectile

Table 1
Experimental results - initial impact velocity V0 vs residual velocity VR

Conical projectile				Blunt-shaped projectile
T=20˚C		T=260˚C		T=20˚C		T=260˚C
V0 (m/s)	VR (m/s)	V0 (m/s)	VR (m/s)	V0 (m/s)	VR (m/s)	V0 (m/s)	VR (m/s)
43.00 44.74 55.93 65.28 80.02 100.00 119.91	0 14.37 37.45 48.84 62.11 87.75 110.22	40.00 44.54 55.37 66.14 79.87 101.01 121.07	0 23.83 42.68 51.11 71.43 96.34 113.64	60.00 74.40 93.28 112.11	0 29.41 79.36 102.04	56.00 65.62 75.30 95.06 113.12	0 30.12 56.82 83.83 104.17

Perforation process causes an instantaneous increase of the temperature localized in the perforated zone. Plastic deformation energy dissipated during the perforation process is transformed into thermal energy and provokes a considerable increase of the temperature along the petals. Some results using thermal imaging camera are displayed in Fig. 11. The analysis has been made for a specimen at room temperature. The observed temperature increase is close to 33-48 ˚C and it confirms a transient, adiabatic nature of the process.

Figure 10
Energy absorbed by the plate during impact test, a/ T=20 ˚C, b/ T=260 ˚C; case of conical projectile

Figure 11
Thermal heating during perforation process captured by thermal imaging camera. Initial temperature = 20 °C; impact velocities: a/ V0 = 89.1 m/s, b/ 90.4 m/s; maximum temperature increase recorded: 48 °C (darker parts indicate local temperature increase); legend displayed in °C

4 PROPOSED CONSTITUTIVE RELATION

Brass is a substitutional alloy composed mainly of two main pure elements which is copper and zinc. Changing the proportions of copper and zinc vary the properties of the alloy. In this study, a common industrial alloy has been used to carry out the tests. This material reveals no or insignificant strain rate sensitivity at room temperatures. Different phenomenological constitutive relations have been considered to model the material behaviour [⁷, ¹⁴, ¹⁵].

The parameters of the Johnson-Cook model [¹⁴] has been proposed for brass to be used later in numerical simulations of perforation tests. The thermo-viscoplastic behaviour of brass alloy is described as follows:

$\mathrm{\sigma }=\left(\mathrm{A}+\mathrm{B}{\mathrm{\epsilon }}_{\mathrm{p}\mathrm{l}}^{\mathrm{n}}\right)\left(1+\mathrm{C}\ln \frac{{\dot{\mathrm{\epsilon }}}_{\mathrm{p}\mathrm{l}}}{{\dot{\mathrm{\epsilon }}}_0}\right)\left(1-{{\mathrm{T}}^{\mathrm{*}}}^{\mathrm{m}}\right)$ (3)

where $\text{A}$ is the yield stress, $\text{B}$ and $\text{n}$ are the strain hardening coefficients, $\text{C}$ is the strain rate sensitivity coefficient, ${\dot{\mathrm{\epsilon }}}_0$ is strain rate reference value and $\text{m}$ is the temperature sensitivity parameter. The non-dimensional temperature ${\text{T}}^{\text{*}}$ for the temperature in range between ${\text{T}}_0$ and ${\text{T}}_{\text{m}}$ is defined in the following form:

${\text{T}}^{\text{*}}=\frac{\text{T}-{\text{T}}_0}{{\text{T}}_{\text{m}}-{\text{T}}_0}$ (4)

where ${\text{T}}_0$ is the reference room temperature and ${\text{T}}_{\text{m}}$ is the melting temperature. The constants have been taken from the international literature [⁷] and compared to existing data [⁶, ¹⁶, ¹⁷] as no data are available from own compression/tension tests. They are presented in Table 2.

Table 2
Material parameters for Johnson-Cook model [⁷]

A (MPa)	B (MPa)	n (-)	C (-)	m (-)
403.5	674.6	0.7374	0	1.132

To define the failure mode, the classical Johnson-Cook failure model [¹⁸] is discussed, Eq. 5:

${\mathrm{\epsilon }}_{\mathrm{f}}^{\mathrm{p}\mathrm{l}}=\mathrm{}\left[{\mathrm{d}}_1+{\mathrm{d}}_2\mathrm{}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\mathrm{d}}_3\right)\right]\left[1+{\mathrm{d}}_4\mathrm{}\mathrm{l}\mathrm{n}\left(\frac{{\dot{\mathrm{\epsilon }}}^{\mathrm{}}}{{\dot{\mathrm{\epsilon }}}_0}\right)\right]\left(1+{\mathrm{d}}_5{\mathrm{T}}^{\mathrm{*}}\right)$ (5)

where ${\text{d}}_1$, ${\text{d}}_2$, ${\text{d}}_3$, ${\text{d}}_4$, ${\text{d}}_5$ are material parameters, $\eta$ is the stress triaxiality factor, ${\dot{\mathrm{\epsilon }}}_0$ is the reference strain rate and ${\text{T}}^{\text{*}}$ is the non-dimensional temperature defined by Eq. 4. The first square bracket in Eq. 5 is related to the stress triaxiality effect on the value of strain at failure${\text{ε}}_{\text{f}}^{\text{pl}}$. The second square bracket represents the influence of strain rate on that value, while the third bracket represents the thermal softening effect.

A more sophisticated approach to define failure, i.e. damage initiation deformation ${\text{ε}}_{\text{Y}}$, has been recently developed in [¹⁹]. Two functions with four constants H, I, J and K are determined using an optimization method.

${\mathrm{\epsilon }}_{\mathrm{Y}}\left(\dot{\mathrm{\epsilon }}\right)=\left\{\begin{array}{c}H{\mathrm{e}}^{\left(\mathrm{I}\mathrm{}{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left(\dot{\mathrm{\epsilon }}\right)\right)}\dot{\mathrm{\epsilon }}\le {\dot{\mathrm{\epsilon }}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\\ J-\left(K{\mathrm{e}}^{\mathrm{}{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left(\dot{\mathrm{\epsilon }}\right)}\right)\dot{\mathrm{\epsilon }}\ge {\dot{\mathrm{\epsilon }}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\end{array}\right.$ (6)

where ${\dot{\mathrm{\epsilon }}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$= 1 1/s.

As far as failure models are concerned, both models have provided similar results in preliminary numerical simulations in terms of failure mode form and temperature response. It must be noted, however, that they both lack a temperature dependence and this simplification should be eliminated in the next step of analysis.

5 CONCLUDING REMARKS

The principal aim of the study was to check the effectiveness of the new experimental technique in which perforation tests have been performed within a wide range of temperatures, starting from the ambient one and reaching 260 ˚C. The points of main focus were:

• repeatability of experimental results with heated specimens (stabilization of temperature in the thermal chamber),

• failure pattern observations during perforation connected with thermal softening of brass,

It can be concluded the thermal chamber set-up has proved its designed performances and opened new perspectives to carry out perforation tests in the wide range of temperatures. This innovative testing methodology allows to verify material behaviour in conditions which could be so far only analyzed numerically or analytically.

Important results have been obtained for brass heated to elevated temperatures. The failure mode for the conical projectile in form of petals have confirmed analytical considerations in which the petals number varied from 3 to 6. The studies on initial impact velocity and residual impact velocities have reproduced typical behaviour of material. The energy absorbed during perforation is quasi-constant for the studied range of velocities (up to 120 m/s). For the conical projectile the average value has been 31.2 J at room temperature and it has decreased to the average of 20.9 J at 260 ˚C.

The ballistic limit is a function of the projectile shape and temperature. For the conical projectile the value measured is equal to 43 m/s at room temperature and it has diminished to 40 m/s at 260 ˚C. For the blunt-shaped projectile, the ballistic limit has evolved from 63 m/s to 60 m/s for the same temperature conditions.

Thermal imaging camera has permitted to observe local heating during perforation using the conical projectile. The maximum temperature increase recorded has been 48 ˚C.

These results will be, in the next step, extended and completed using dynamic compression experimental analysis at high temperatures. The proposed application of Johnson-Cook approach for the material description in terms of resistance properties (stress-strain characteristic) as well as in failure criterion will be suitable for brass in further numerical simulations. The 3D solid elements model shall be proposed to optimally reflect a failure pattern in form of petaling and plugging.

Acknowledgements

The study was possible due to the technical support provided by Tomasz Libura from the Institute of Fundamental Technological Research of the Polish Academy of Sciences. The assistance of Piotr Sielicki during the use of the thermal imaging camera at Poznan University of Technology is highly acknowledged.

The patent of the thermal chamber has been submitted to OMPIC (Morocco) on 31st October 2017 under the reference number 41383.

References

• ^[1]
  T. Børvik, O.S. Hopperstad, M. Langseth, K.A. Malo, (2003), Effect of target thickness in blunt projectile penetration of Weldox 460 E steel plates, International Journal of Impact Engineering, 28 (4), pp. 413-464.
• ^[2]
  R.F. Recht, T.W. Ipson (1963), Ballistic perforation dynamics, Journal of Applied Mechanics, 30 (3), pp. 384-390.
• ^[3]
  F.H. Abed, F. H., G. Voyiadjis (2007), Adiabatic Shear Band Localizations in BCC Metals at High Strain Rates and Various Initial Temperatures, Int. J. Multiscale Comput. Eng., 5 (3-4), pp. 325-349.
• ^[4]
  T. Jankowiak, A. Rusinek, K.M. Kpenyigba, R. Pesci (2014), Ballistic behaviour of steel sheet subjected to impact and perforation. Steel and Composite Structures, 16 (6), pp. 595-609.
• ^[5]
  T. Jankowiak, A. Rusinek, P. Wood, (2015), A numerical analysis of the dynamic behaviour of sheet steel perforated by a conical projectile under ballistic conditions. Finite Elements in Analysis and Design, 65, pp. 39-49.
• ^[6]
  R. Julien, T. Jankowiak, A. Rusinek, P. Woo, P., (2016) Taylor’s Test Technique for Dynamic Characterization of Materials: Application to Brass, Exp. Tech., 40, pp. 347-355.
• ^[7]
  F. Abed, T. Jankowiak, A. Rusinek, (2015), Verification of a Thermoviscoplastic Constitutive Relation for Brass Material Using Taylor’s Test. Journal of Engineering Materials and Technology, 137, pp. 1-11.
• ^[8]
  T. Jankowiak, (2016), The use of experimental methods and computer simulations to determine the properties of materials under high strain rates conditions (in Polish), Poznan: Publishing House of Poznan University of Technology, s. 161
• ^[9]
  M. Rodríguez Millán. A. Vaz-Romero, A. Rusinek, A. Arias, (2014), Experimental Study on the Perforation Process of 5754-H111 and 6082-T6 Aluminium Plates Subjected to Normal Impact by Conical, Hemispherical and Blunt Projectiles, Experimental Mechanics 54(5), pp. 729-742.
• ^[10]
  X. Shuang-x, W. Wei-guo, L. Xiao-bin, H. Yan-ling, (2010), Petal failure characteristics of a conical projectile penetrating a thin plate at high oblique angle, Journal of Shanghai Jiaotong University (Science) 15(4), pp. 434-440.
• ^[11]
  Q.-B. Yu, H.-G. Guo, T.-Y. Zhang, Dynamic Behavior of Non-Deformable Projectiles with Different Nose Shape Penetrating Steel Plate, (2017) Beijing Ligong Daxue Xuebao/Transaction of Beijing Institute of Technology 37(4), pp. 331-336.
• ^[12]
  B. Landkof, W. Goldsmith (1993), Petaling of thin metallic plates during penetration by cylindro-conical projectiles, International Journal of Solids and Structures, 21, pp. 245-266.
• ^[13]
  K.M. Kpenyigba, T. Jankowiak, A. Rusinek, R. Pesci (2013), Influence of projectile shape on dynamic behaviour of steel sheet subjected to impact and perforation. Thin-Walled Structures, 65, pp. 93-104.
• ^[14]
  G.R. Johnson, W.H. Cook (1983), A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, Vol. 21, pp. 541-547.
• ^[15]
  U. F. Kocks, (2001), Realistic Constitutive Relations for Metal Plasticity, Mater. Sci. Eng. A, 317(1-2), pp. 181-187.
• ^[16]
  Y. Wang, Y. Zhou, Y. Xia, (2004), A constitutive description of tensile behaviour for brass over a wide range of strain rates. Materials Science and Engineering: A, 372, Issues 1-2, pp. 186-190.
• ^[17]
  Y. Wang, Y. Xia, (2003), Modeling of mechanical behaviour of brass at high strain rates Journal of Materials Science Letters, 22, pp. 1393-1394.
• ^[18]
  G. R. Johnson, W. H. Cook, (1985), Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Engineering Fracture Mechanics, 21(1), pp. 31-48.
• ^[19]
  A. Bendarma, T. Jankowiak, T. £odygowski, A. Rusinek, M. Klósak (2016), Experimental and numerical analysis of the aluminum alloy AW5005 behaviour subjected to tension and perforation under dynamic loading, Journal of Theoretical and Applied Mechanics, 55 (4), pp. 1219-1233.

• Available online: February 05, 2018

Publication Dates

• Publication in this collection
  2018

History

• Received
  01 Aug 2017
• Reviewed
  04 Jan 2018
• Accepted
  26 Jan 2018