Abstract
This paper analyses the non-stationary free vibration and nonlinear dynamic behavior of the viscoelastic nano-plates. For this purpose, a size-dependent theory is developed in the framework of the consistent couple stress theory for viscoelastic materials. The previously presented modified couple stress theory was based on some consideration making it partially doubtful to apply. This paper uses the recent findings for the mentioned problem and develops it to analyze the nonlinear dynamic behavior of nano-plates with nonlinear viscoelasticity. The material is supposed to follow the Leaderman integral nonlinear constitutive relation. In order to capture the geometrical nonlinearity, the von-Karman strain displacement relation is used. The viscous parts of the size-independent and size-dependent stress tensors are calculated in the framework of the Leaderman integral and the resultant virtual work terms are obtained. The governing equations of motion are derived using the Hamilton principle in the form of the nonlinear second order integro-partial differential equation with coupled terms. These coupled size-dependent viscoelastic equations are solved using the forth-order Runge-kutta and Harmonic balance method after simplifying by the expansion theory. The short-time Fourier transform is performed to examine the system free vibration. In addition, frequency- and force-responses of the nanosystem subjected to distribute harmonic load are presented. The obtained results show that the viscoelastic model-based vibration is non-stationary unlike the elastic model. Moreover, the damping mechanism of the viscoelasticity is amplitude dependent and the contribution of the viscoelastic damping terms at higher forcing conditions becomes noticeable.
Keywords
nonlinear viscoelastic; consistent couple stress; Harmonic balance method; nonlinear dynamic; nano-plate
1 INTRODUCTION
Micro-nano elements are extensively used in tiny bio-structural and mechanical applications (Pandey et al. 2009Pandey, J., Chu, W., Kim, C., Lee, C. and Ahn, S. (2009). Bio-nano reinforcement of environmentally degradable polymer matrix by cellulose whiskers from grass. Composites Part B: Engineering 40: 676-680.,Feng et al. 2012Feng, L., Wu, L., Wang, J., Ren, J., Miyoshi, D., Sugimoto, N. and Qu, X. (2012). Detection of a Prognostic Indicator in Early‐Stage Cancer Using Functionalized Graphene‐Based Peptide Sensors. Advanced Materials 24: 125-131.,Murmu and Adhikari 2012Murmu, T. and Adhikari, S. (2012). Nonlocal frequency analysis of nanoscale biosensors. Sensors and Actuators A: Physical 173: 41-48.,Xiao et al. 2017Xiao, Y., Huang, W., Tsui, C.P., Wang, G., Tang, C.Y. and Zhong, L. (2017). Ultrasonic atomization based fabrication of bio-inspired micro-nano-binary particles for superhydrophobic composite coatings with lotus/petal effect. Composites Part B: Engineering 121: 92-98.). Micro-nanomechanical resonators that can reach to very high frequencies up to GHz (Husain et al. 2003Husain, A., Hone, J., Postma, H.W.C., Huang, X., Drake, T., Barbic, M., Scherer, A. and Roukes, M. (2003). Nanowire-based very-high-frequency electromechanical resonator. Applied Physics Letters 83: 1240-1242.,Huang et al. 2005Huang, X., Feng, X., Zorman, C., Mehregany, M. and Roukes, M. (2005). VHF, UHF and microwave frequency nanomechanical resonators. New Journal of Physics 7: 247.,Baghelani 2016Baghelani, M. (2016). Design of a multi-frequency resonator for UHF multiband communication applications. Microsystem Technologies 22: 2543-2548.) are very important types of these elements highlighted due to their exemplary characteristics. In order to tune the resonators for better sensing performance, one should recognize their dynamic characteristics, carefully (Ekinci et al. 2004Ekinci, K., Huang, X. and Roukes, M. (2004). Ultrasensitive nanoelectromechanical mass detection. Applied Physics Letters 84: 4469-4471.,Braun et al. 2005Braun, T., Barwich, V., Ghatkesar, M.K., Bredekamp, A.H., Gerber, C., Hegner, M. and Lang, H.P. (2005). Micromechanical mass sensors for biomolecular detection in a physiological environment. Physical Review E 72: 031907.,Tajaddodianfar et al. 2017Tajaddodianfar, F., Yazdi, M.R.H. and Pishkenari, H.N. (2017). Nonlinear dynamics of MEMS/NEMS resonators: analytical solution by the homotopy analysis method. Microsystem Technologies 23: 1913-1926.). Hence, analyzing the dynamic characteristics of these elements is a critical issue to improve their performance. The mentioned resonators are often made from micro-nano plate and shell elements. The experimental results for instance, in polymers and metals showed that the mechanical behaviors of the micro-nano structures have considerable amount of size effects (Poole et al. 1996Poole, W., Ashby, M. and Fleck, N. (1996). Micro-hardness of annealed and work-hardened copper polycrystals. Scripta Materialia 34: 559-564.,Lam et al. 2003Lam, D.C., Yang, F., Chong, A., Wang, J. and Tong, P. (2003). Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids 51: 1477-1508.). It is worth noting that in classical continuum theories, CT, the size effects are not considered. Hence, the material length-scale parameter is not considered in these theories. In order to compensate this shortage, some non-classical elasticity theories were developed (Mindlin and Tiersten 1962Mindlin, R. and Tiersten, H. (1962). Effects of couple-stresses in linear elasticity. Archive for Rational Mechanics and analysis 11: 415-448., Koiter 1964Koiter, W. (1964). Couple-stress in the theory of elasticity, North Holland Pub, Eringen and Edelen 1972Eringen, A.C. and Edelen, D. (1972). On nonlocal elasticity. International Journal of Engineering Science 10: 233-248., Yang et al. 2002Yang, F., Chong, A., Lam, D.C.C. and Tong, P. (2002). Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures 39: 2731-2743., Lam et al. 2003). In this regard, Mindlin and Tiersten (1962) and Koiter (1964), developed a couple stress theory for elastic models based on the rotation vector as a curvature tensor. However, this theory suffers from some problems: first, the spherical part of the couple-stress tensor is indeterminate and second, the body couple appears in the constitutive relation of the force-stress tensor. Therefore, its original form has not been used widely. In order to compensate the mentioned problems, the modified couple stress theory (MCST) was developed by Yang et al. (2002). According to the MCST, when the resultant vectors of couples, moments of couples and applied forces become zero, the system is in equilibrium. In this theory, true continuum representations of deformation has been used. However, the obtained equations were not consistent with proper boundary conditions and the virtual work principle energy conjugacy Hadjesfandiari and Dargush (2011Hadjesfandiari, A.R. and Dargush, G.F. (2011). Couple stress theory for solids. International Journal of Solids and Structures 48: 2496-2510.). In addition, the resulting couple-stress and stress tensors are symmetric and this contrasts with the original form of the couple stress theory, specifically for the couple stress tensor. Recently, Hadjesfandiari and Dargush developed a new theory based on the original theory by using true continuum kinematical displacement and rotation and found a reasonable solution for the associated problems (Hadjesfandiari and Dargush 2011Hadjesfandiari, A.R. and Dargush, G.F. (2011). Couple stress theory for solids. International Journal of Solids and Structures 48: 2496-2510., 2013Hadjesfandiari, A.R. and Dargush, G.F. (2013). Fundamental solutions for isotropic size-dependent couple stress elasticity. International Journal of Solids and Structures 50: 1253-1265., Hadjesfandiari et al., 2013Hadjesfandiari, A.R., Dargush, G.F. and Hajesfandiari, A. (2013). Consistent skew-symmetric couple stress theory for size-dependent creeping flow. Journal of Non-Newtonian Fluid Mechanics 196: 83-94.). Their new size-dependent theory is called the consistent couple stress theory (CCST). In their theory, the couple-stress tensor becomes skew-symmetric while the skew-symmetric components of the rotation vector gradient are considered as a consistent curvature tensor. The two skew-symmetric tensors are conjugate with each other in calculation of the virtual work Hadjesfandiari and Dargush (2011)Hadjesfandiari, A.R. and Dargush, G.F. (2011). Couple stress theory for solids. International Journal of Solids and Structures 48: 2496-2510.. In the current paper, for the first time, the recent theory that (CCST) is developed for the viscoelastic model to study non-stationary free vibration and nonlinear dynamic behavior of a viscoelastic nanoplate subjected to harmonic load.
Recently, some experiments have discovered that the viscoelasticity widely present in materials of NEMS and MEMS such as silicon Elwenspoek and Jansen (2004Elwenspoek, M. and Jansen, H.V. (2004). Silicon micromachining, Cambridge University Press), polysilicon Teh and Lin (1999Teh, K.S. and Lin, L. (1999). Time-dependent buckling phenomena of polysilicon micro beams. Microelectronics journal 30: 1169-1172.) and gold films Yan et al. (2009Yan, X., Brown, W., Li, Y., Papapolymerou, J., Palego, C., Hwang, J. and Vinci, R. (2009). Anelastic stress relaxation in gold films and its impact on restoring forces in MEMS devices. Journal of Microelectromechanical Systems 18: 570-576.). Furthermore, the experimental investigations conducted by Su et al. (2012Su, Y., Wei, H., Gao, R., Yang, Z., Zhang, J., Zhong, Z. and Zhang, Y. (2012). Exceptional negative thermal expansion and viscoelastic properties of graphene oxide paper. Carbon 50: 2804-2809.) revealed that the viscoelastic phenomena exist in graphene oxide sheets. The tensile tests on this specimen displayed clear hysteresis loops, indicating the viscoelasticity of the graphene oxide. Furthermore, the viscoelastic properties can exhibit at some nanostructures (Karlièiæ et al. 2014Karlièiæ, D., Koziæ, P. and Pavloviæ, R. (2014). Free transverse vibration of nonlocal viscoelastic orthotropic multi-nanoplate system (MNPS) embedded in a viscoelastic medium. Composite Structures 115: 89-99.,Mohammadimehr et al. 2015Mohammadimehr, M., Navi, B.R. and Arani, A.G. (2015). Free vibration of viscoelastic double-bonded polymeric nanocomposite plates reinforced by FG-SWCNTs using MSGT, sinusoidal shear deformation theory and meshless method. Composite Structures 131: 654-671.,Khaniki and Hosseini-Hashemi 2017Khaniki, H.B. and Hosseini-Hashemi, S. (2017). Dynamic response of biaxially loaded double-layer viscoelastic orthotropic nanoplate system under a moving nanoparticle. International Journal of Engineering Science 115: 51-72.). Zhang et al. (2016Zhang, Y., Pang, M. and Fan, L. (2016). Analyses of transverse vibrations of axially pretensioned viscoelastic nanobeams with small size and surface effects. Physics letters A 380: 2294-2299.) studying the vibration of nanobeams. Wang et al. (2015Wang, Y., Li, F.-M. and Wang, Y.-Z. (2015). Nonlinear vibration of double layered viscoelastic nanoplates based on nonlocal theory. Physica E: Low-dimensional Systems and Nanostructures 67: 65-76.) and Ebrahimi and Hosseini (2016Ebrahimi, F. and Hosseini, S. (2016). Thermal effects on nonlinear vibration behavior of viscoelastic nanosize plates. Journal of Thermal Stresses 39: 606-625.) examined the nonlinear vibration of viscoelastic nanoplates. In addition, Hashemi et al. (2015) investigated the free vibration of viscoelastic nano graphene sheets.
Generally, in a structure made from viscoelastic material, a quota of energy of deformation is recoverable and the other quota is irrecoverable. Mainly, in the viscoelastic materials, the stress-strain relations cause the equations of motion to become in integro-differential type. As a result, the dynamic behavior of the viscoelastic nanoplates are more complicated than their elastic counterparts.
Viscoelastic models have been used for dynamic/statics analyses of macro-scale plates. For instance, nonlinear vibration of viscoelastic thin plates subjected to transverses harmonic force was discussed at the first resonances Amabili (2016Amabili, M. (2016). Nonlinear vibrations of viscoelastic rectangular plates. Journal of Sound and Vibration 362: 142-156.). Dynamic stability of the viscoelastic plates with longitudinally varying tensions subjected to axial acceleration was studied by Tang et al. (2016Tang, Y., Zhang, D., Rui, M., Wang, X. and Zhu, D. (2016). Dynamic stability of axially accelerating viscoelastic plates with longitudinally varying tensions. Applied Mathematics and Mechanics 37: 1647-1668.). In addition, An and Chen (2016An, F. and Chen, F. (2016). Bifurcations and chaos of the nonlinear viscoelastic plates subjected to subsonic flow and external loads. Chaos, Solitons & Fractals 91: 78-85.) studied the nonlinear dynamic behavior of the viscoelastic plates subjected to external force and subsonic flow. They found the critical conditions that chaos could take place. Furthermore, Chen and Cheng (2005)Chen, L.-Q. and Cheng, C.-J. (2005). Instability of nonlinear viscoelastic plates. Applied Mathematics and computation 162: 1453-1463. discussed the instability problem of an isotropic, homogeneous, rectangular plate made from viscoelastic material subjected to a prescribed periodic in-plane load. Cveticanin et al. (2012Cveticanin, L., KalamiYazdi, M., Askari, H. and Saadatnia, Z. (2012). Vibration of a two-mass system with non-integer order nonlinear connection. Mechanics Research Communications 43: 22-28.) studied the vibration of the two-mass system with viscoelastic connection. However, the large amount of previous studies in the literature on the static/dynamic deformation of the micro-nanostructures considered only the elastic models of the systems (Jomehzadeh et al. 2011Jomehzadeh, E., Noori, H. and Saidi, A. (2011). The size-dependent vibration analysis of micro-plates based on a modified couple stress theory. Physica E: Low-dimensional Systems and Nanostructures 43: 877-883.,Farajpour et al. 2012Farajpour, A., Shahidi, A., Mohammadi, M. and Mahzoon, M. (2012). Buckling of orthotropic micro/nanoscale plates under linearly varying in-plane load via nonlocal continuum mechanics. Composite Structures 94: 1605-1615.,Ke et al. 2012Ke, L.-L., Wang, Y.-S., Yang, J. and Kitipornchai, S. (2012). Free vibration of size-dependent Mindlin microplates based on the modified couple stress theory. Journal of Sound and Vibration 331: 94-106.). For example, Ke et al. (2013)Ke, L., Yang, J., Kitipornchai, S., Bradford, M. and Wang, Y. (2013). Axisymmetric nonlinear free vibration of size-dependent functionally graded annular microplates. Composites Part B: Engineering 53: 207-217. employed the MCST to investigate free vibration of functionally graded (FG) axisymmetric Mindlin microplates with von-Karman nonlinearity. Asghari (2012Asghari, M. (2012). Geometrically nonlinear micro-plate formulation based on the modified couple stress theory. International Journal of Engineering Science 51: 292-309.) derived the size-dependent motion equations for geometrically nonlinear microplates with arbitrary shapes by means of the MCST. Moreover, Lou and He (2015Lou, J. and He, L. (2015). Closed-form solutions for nonlinear bending and free vibration of functionally graded microplates based on the modified couple stress theory. Composite Structures 131: 810-820.) examined the free vibration and nonlinear bending responses of a FGM Kirchhoff and Mindlin microplate resting on an elastic substrate by means of the MCST.
Recently, in some research studies, the viscoelasticity effects on the static/dynamic behavior of the micro-nanostructures were studied (Hashemi et al. 2015Hashemi, S.H., Mehrabani, H. and Ahmadi-Savadkoohi, A. (2015). Exact solution for free vibration of coupled double viscoelastic graphene sheets by viscoPasternak medium. Composites Part B: Engineering 78: 377-383.,Wang et al. 2015Wang, Y., Li, F.-M. and Wang, Y.-Z. (2015). Nonlinear vibration of double layered viscoelastic nanoplates based on nonlocal theory. Physica E: Low-dimensional Systems and Nanostructures 67: 65-76.,Tang et al. 2016Tang, Y., Zhang, D., Rui, M., Wang, X. and Zhu, D. (2016). Dynamic stability of axially accelerating viscoelastic plates with longitudinally varying tensions. Applied Mathematics and Mechanics 37: 1647-1668.,Khaniki and Hosseini-Hashemi 2017Khaniki, H.B. and Hosseini-Hashemi, S. (2017). Dynamic response of biaxially loaded double-layer viscoelastic orthotropic nanoplate system under a moving nanoparticle. International Journal of Engineering Science 115: 51-72.). For instance, Liu et al. (2017Liu, J., Zhang, Y. and Fan, L. (2017). Nonlocal vibration and biaxial buckling of double-viscoelastic-FGM-nanoplate system with viscoelastic Pasternak medium in between. Physics letters A 381: 1228-1235.) discussed the vibration of a double-viscoelastic FGM nanoplate, and Pouresmaeeli et al. (2013Pouresmaeeli, S., Ghavanloo, E. and Fazelzadeh, S. (2013). Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Composite Structures 96: 405-410.) found a closed-form solution for the vibration of viscoelastic orthotropic nanoplates resting on viscoelastic substrate in the framework of the nonlocal plate theory. In their study, the Kelvin-Voigt model was used to model the medium. In another research, Jamalpoor et al. (2017Jamalpoor, A., Bahreman, M. and Hosseini, M. (2017). Free transverse vibration analysis of orthotropic multi-viscoelastic microplate system embedded in visco-Pasternak medium via modified strain gradient theory. Journal of Sandwich Structures & Materials 1099636216689384.) used the Hamilton's principle and found an analytical solution for out-of-plane vibration of multi-viscoelastic Kirchhoff microplates with free-chain and clamped-chain boundary conditions in the framework of the modified strain gradient theory. In addition, Farokhi and Ghayesh (2017Farokhi, H. and Ghayesh, M.H. (2017). Viscoelasticity effects on resonant response of a shear deformable extensible microbeam. Nonlinear Dynamics 87: 391-406.) studied the effects of the viscoelasticity on dynamic response of a shear deformable microbeam in the framework of the MCST. In another study, the size-dependent instability and forced vibration of a viscoelastic sinusoidal shear deformation micro-plate with axially moving condition is examined based on the MCST Ghorbanpour Arani and Haghparast (2017Ghorbanpour Arani, A. and Haghparast, E. (2017). Size-dependent vibration of axially moving viscoelastic micro-plates based on sinusoidal shear deformation theory. International Journal of Applied Mechanics 9: 1750026.). In all above investigations, the Kelvin-Vigot model was used enabling modeling the linear viscoelastic materials. However, large amount of the viscoelastic materials are not linear and in order to have accurate solutions for the behavior of viscoelastic structures, the nonlinearity of these materials should be modeled. A comparative research study Smart and Williams (1972Smart, J. and Williams, J. (1972). A comparison of single-integral non-linear viscoelasticity theories. Journal of the Mechanics and Physics of Solids 20: 313-324.) discovered that when prediction and simplicity become important the Leaderman integral model Leaderman (1962Leaderman, H. (1962). Large longitudinal retarded elastic deformation of rubberlike network polymers. Transactions of the Society of Rheology 6: 361-382.) is one of the useful representations of the nonlinear viscoelastic properties. Thus, this model is used in this paper. In addition, in all the mentioned studies, the governing motion equations were achieved but the solutions of the nonlinear dynamic characteristics were not provided.
According to the descriptions in the previous paragraphs, all of the studies performed analysis on the elastic or linear viscoelastic nano-mico structures. This paper, for the first time, studies the non-stationary free vibration and nonlinear dynamic behavior of a nanoplate with nonlinear viscoelasticity by means of the CCST. This paper used the CCST and developed it to analyze the nonlinear dynamic characteristics of a nanoplate with nonlinear viscoelasticity. The material is supposed to follow the Leaderman integral nonlinear relation. Additionally, in many applications, such as resonators (Ghayesh et al. 2013aGhayesh, M.H., Farokhi, H. and Amabili, M. (2013a). Nonlinear behaviour of electrically actuated MEMS resonators. International Journal of Engineering Science 71: 137-155., bGhayesh, M.H., Farokhi, H. and Amabili, M. (2013b). Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Composites Part B: Engineering 50: 318-324.), the nanoplate undergoes large-amplitude deformations. Therefore, it is necessary to employ a nonlinear strain-displacement relation. Therefore, in this study, the von-Karman relation is used to capture the geometrical nonlinearity. The viscous parts of the size-independent and size-dependent stress tensors are derived by means of the Leaderman integral and their virtual work terms are obtained. The governing equations of motion are derived using the Hamilton's principle in the form of the nonlinear second-order integro-partial differential equation with coupled terms. The nonlinear vibration equations are solved previously with Hamiltonian approach, He's variational approach, global error minimization and Jacobi collocation method (Askari et al. 2013Askari, H., Nia, Z.S., Yildirim, A., Yazdi, M.K. and Khan, Y. (2013). Application of higher order Hamiltonian approach to nonlinear vibrating systems. Journal of Theoretical and Applied Mechanics 51: 287-296.,Yazdi and Tehrani 2015Yazdi, M. and Tehrani, P. (2015). The energy balance to nonlinear oscillations via Jacobi collocation method. Alexandria Engineering Journal 54: 99-103.,Yazdi 2016Yazdi, M. (2016). Approximate solutions to nonlinear oscillations via an improved He's variational approach. Karbala International Journal of Modern Science 2: 289-297.,Yazdi and Tehrani 2016Yazdi, M.K. and Tehrani, P.H. (2016). Frequency analysis of nonlinear oscillations via the global error minimization. Nonlinear Engineering 5: 87-92.). In this paper, the size-dependent viscoelastically coupled equations are solved with incorporating the expansion theory and Harmonic balance method, HBM,. Frequency- and force- responses of the nanosystem subjected to distributive harmonic load are obtained and validated with the forth-order Runge-kutta method. The effects of the initial excitation values and length-scale amounts as well as the viscoelastic parameter on the system vibration are also examined. In the following, the viscoelastic model and elastic model with linear damping resonance frequency are compared with each other. Furthermore, the short-time Fourier transform is performed to investigate the system free vibration.
2 Viscoelastically size-dependent coupled nonlinear models
In the CCST, the equilibrium equations are formulated as Hadjesfandiari and Dargush (2013Hadjesfandiari, A.R., Dargush, G.F. and Hajesfandiari, A. (2013). Consistent skew-symmetric couple stress theory for size-dependent creeping flow. Journal of Non-Newtonian Fluid Mechanics 196: 83-94.):
In the above equations, σji and µji are the force and couple-stress tensors while f i and 𝜀 ijk are the body force per volume unit and the permutation tensor. The µji equals to zero for the classical continuum mechanics. According to Hadjesfandiari and Dargush, in materials with couple stresses, body couples can be converted to a surface traction and equivalent body force Hadjesfandiari and Dargush (2013)Hadjesfandiari, A.R. and Dargush, G.F. (2013). Fundamental solutions for isotropic size-dependent couple stress elasticity. International Journal of Solids and Structures 50: 1253-1265.. Particularly, as mentioned before, they showed that the couple-stress tensor is skew-symmetric. Therefore, the force-stress tensor can be divided into the skew-symmetric and symmetric parts:
In the above equation, and are the skew-symmetric and symmetric components of the force-stress tensor.
In this paper, the continuum mechanic kinematics is defined based on the infinitesimal deformation. Thus, the gradient of displacement vector is divided into skew-symmetric and symmetric components
where
where εij and ωij are symmetric strain and skew-symmetric rotation tensors. The rotation vector is defined as
Decomposing the rotation vector gradient into two components results in:
where the 𝜒ij and 𝜅ij are symmetric and skew-symmetric tensors obtained from applying the strain and rotation operators to the rotation vector.
According to the couple stress theory, the symmetric tensor 𝜒ij, as curvature tensor, is an important part in calculating strain energy. However, this tensor denotes the pure twists along the principal axes. Consequently, this symmetric tensor cannot participate as a fundamental element in measuring deformation in continuum mechanics Hadjesfandiari and Dargush (2013Hadjesfandiari, A.R. and Dargush, G.F. (2013). Fundamental solutions for isotropic size-dependent couple stress elasticity. International Journal of Solids and Structures 50: 1253-1265.). However, in the CCST the skew-symmetric tensor is assumed as a fundamental curvature tensor. The vectorial form of the curvature tensor is formulated as:
After defining the kinematic parameters, the force- and couple-stresses can be formulated. For the elastic isotropic materials, Hadjesfandiari and Dargush (2013Hadjesfandiari, A.R. and Dargush, G.F. (2013). Fundamental solutions for isotropic size-dependent couple stress elasticity. International Journal of Solids and Structures 50: 1253-1265.) demonstrated that the couple stress can be defined as:
Furthermore, the skew-symmetric and symmetric components of the force-stress tensor are formulated as Hadjesfandiari and Dargush (2013Hadjesfandiari, A.R. and Dargush, G.F. (2013). Fundamental solutions for isotropic size-dependent couple stress elasticity. International Journal of Solids and Structures 50: 1253-1265.).
where l is the material length-scale parameter and the constant is the difference between the classic theory and CCST. Moreover, λ and μ are the time-dependent Lame's constants and is Kroncker delta.
Therefore, according to the CCST, the strain energy for an isotropic material with volume V can be formulated as:
As mentioned before, the material of the nanoplate is assumed to have nonlinear viscoelasticity and follows from the nonlinear Leaderman's integral relation. According to this relation, Christensen and Freund (1971Christensen, R.M. and Freund, L. (1971). Theory of viscoelasticity. Journal of Applied Mechanics 38: 720.), for a viscoelastic structure the components of the couple-stress and force-stress tensors can be written as
whereis the convolution operator defined as:
Based on the definition in Eq. (17), the Eqs. (14-16) can be rewritten as
where λ0 and μ0 are the Lame's constants in time zero and .In addition, E (t) and G(t) are relaxation function and modulus of rigidity and ν is the time-independent Poisson ratio. The over dot (·) represents the derivative with respect to time. Therefore, due to the Eqs.(18-19) the stress tensor σ and couple stress tensor µ can be divided into two components.
Considering the Cartesian system (x, y, z) where xy-plane is coincident with the geometrical mid-plane of the undeformed nanoplate, the displacement field according to the Kirchhoff’s plate theory JE. (1989JE., L. (1989). Boundary stabilization of thin plates, SIAM (Philadelphia).) can be formulated as:
The variables u, v and w are the time-dependent displacements of the mid-surface in the x, y and z directions, respectively. Considering of the von-Karman non-linearity, the strain components of any point in the nanoplate are expressed as
where 𝜀ij (i,j= x, y, z) are strain components.
By substituting Eq. (20) in Eq. (5), the component of the rotation tensors are obtained as
Similarly, from Eqs. (8) and (20), one can write
Replacing Eq. (21) into Eq. (18), the symmetrical stress components can be written as
Similarly, after substituting Eq. (23) into Eq. (19), the skew-symmetric couple stress can be written as
In order to derive the governing motion equations of the viscoelastic nanoplate, the well-known Hamilton's principle is used
where, δ is the variational operator, U and W are the kinetic energy, elastic strain energy and non-conservative forces such as viscous dissipation or virtual work of external forces, respectively. Therefore, the virtual work of the non-conservative forces can be decomposed into the virtual work of external forces δWext and the virtual work of viscous dissipative forces δWvis. Hence, we get
Replacing Eq. (27) into Eq. (26), the generalized Hamilton's principle can be rewritten as
According to the CCST, the first variational of elastic strain energy is obtained from Eq. (29)
Integration on volume for homogenous rectangular nanoplate can be written as
Substituting Eqs. (30), (21) and (23) into Eq. (29), integrating by parts and after some algebraic processes, the Eq. (29) can be written as Eq. (31)
where
By integrating stress and couple along the thickness of the nanoplate, the resultants are obtained as
Similarly, the first variational of virtual work of the viscous dissipative forces can be defined as
Substituting Eqs. (30), (21) and (23) into Eq. (34), and integrating by parts results in the Eq. (35)
where
Similarly, the viscous stress and couple of resultants can be defined as
The first variational of kinetic energy is given as
In the Eq. (38) and throughout this paper, the overhead “·” and“··” denote, respectively, the first and second time derivatives. In addition, ρ is the mass density of the nanoplate. Derivation of Eq. (20) with respect to the time and replacing in Eq. (27) gives Eq.(39)
Where
From the general expression of the external forces work in the CCST Hadjesfandiari and Dargush (2013Hadjesfandiari, A.R. and Dargush, G.F. (2013). Fundamental solutions for isotropic size-dependent couple stress elasticity. International Journal of Solids and Structures 50: 1253-1265.), the first variational of virtual work performed by the applied forces on the viscoelastic nanoplate in the time interval [0, T] can be calculated as Ma et al. (2011Ma, H., Gao, X.-L. and Reddy, J. (2011). A non-classical Mindlin plate model based on a modified couple stress theory. Acta mechanica 220: 217-235.)
where Γ is the the middle surface boundary of the nanoplate Reddy and Kim (2012Reddy, J. and Kim, J. (2012). A nonlinear modified couple stress-based third-order theory of functionally graded plates. Composite Structures 94: 1128-1143.). In addition, (fx ,f y , f z) and the (c x , c y , c z) are, respectively, the body forces and the body couples, and (q x , q y , q z), (t x , t y , t z) and (s x , s y , s z) are, respectively, the tractions applied on Γ, the surface couple and Cauchy traction applied on A. In this paper, it is assumed that the nanoplate is only subjected to transverse force.
Replacing the expressions for δU, δW vis, δK and δW ext from the Eqs. (31), (35), (39) and (41) into Eq. (3) and integrating by parts, the size-dependent viscoelastically coupled governing equations of the motion based on the CCST can be obtained as Eq. (42)
where , , and .
The Equation (42) is the system of nonlinear integral-differential partial equations for a viscoelastic nanoplate based on the CCST. Proposed model includes an added length-scale parameter. As expected, the added material constant affects both of the current and the past history conditions, simultaneously. Additionally, with ignoring the past history term, the Eq. (42) is abridged into the size-depended CCST for elastic nanoplate, and with ignoring the size effect, namely l=0, it is abridged into the macro scale viscoelastic plate model. These facts clearly reveal the accuracy of our calculations during the derivation of governing equations.
The motion equations can be presented in the displacement terms (u,v,w) as
Where
For homogenous rectangular nanoplate, I 1 becomes zero.
The large amount of experimental results (Lee et al. 2005Lee, H.-J., Zhang, P. and Bravman, J.C. (2005). Stress relaxation in free-standing aluminum beams. Thin Solid Films 476: 118-124.,Yan et al. 2009Yan, X., Brown, W., Li, Y., Papapolymerou, J., Palego, C., Hwang, J. and Vinci, R. (2009). Anelastic stress relaxation in gold films and its impact on restoring forces in MEMS devices. Journal of Microelectromechanical Systems 18: 570-576.) proposed standard anelastic solid model for viscoelastic material. In this paper, this model is used to define the elastic modulus relaxation function. Therefore, it is defined as
where γ is the relaxation coefficient. In addition, the E(t) value at t=0 indicates the initial elastic modulus E 0. Introducing the following non-dimensional quantities
Eq. (45) can then be expressed in dimensionless form as
In order to non-dimensionalize the governing equation, the following dimensionless parameters are introduced
where c is the damping coefficient.
The solutions of the simply supported immovable rectangular nanoplates can be assumed as Niyogi (1973Niyogi, A. (1973). Nonlinear bending of rectangular orthotropic plates. International Journal of Solids and Structures 9: 1133-1139.)
where α=mπ and β=nπ. The simply supported immovable boundary conditions of the rectangular nonlinear nanoplate are satisfied with this consideration in Eq. (49). In addition, the u and v consideration satisfy the Eq. (43-a) and Eq.(43-b), simultaneously. As mentioned above, in this paper, it is assumed that the nanoplate is subjected only to the harmonic distributed force, f cosΩt per unit of the surface, in the z direction. The non-dimensional transverse harmonic load amplitude is expanded into the double-Fourier sine series as
where
Inserting Eq. (49) into Eq. (43-c), the residuecan be obtained after some algebraic processes: (with dropping the asterisk notation for brevity)
Using Bubnov-Galerkin approach and setting the integral to zero, the expression of Ë is obtained as Eq. (54)
The above equation can be solved with the fourth-order Runge-Kutta method after some algebraic processes Fu and Zhang (2009Fu, Y. and Zhang, J. (2009). Nonlinear static and dynamic responses of an electrically actuated viscoelastic microbeam. Acta Mechanica Sinica 25: 211-218.). Furthermore, in this paper, the HBM method is applied to solve the above equation Mickens (2010Mickens, R.E. (2010). Truly nonlinear oscillations: harmonic balance, parameter expansions, iteration, and averaging methods, World Scientific). Considering the periodic solution of the first-order approximation as the following form and substituting in Eq.(54), one gets Eq.(56)
Where
By ignoring higher frequency, 3Ω, and applying the steady-state condition the following polynomial equation is obtained
where
Solving the Eq.(58) gives the amplitude of the nanosystem response subjected to harmonic force. The real and positive roots of Eq.(58) are acceptable.
3 Free vibration
Nonlinear system frequencies highly depend on the vibration amplitude. The presence of the past history terms in Eq. (54) obtained from viscoelastic model changes the vibration amplitude over time. Therefore, the system nonlinearity effect changes over time and causes to change the system vibration frequency with time. In order to evaluate the initial excitation value and the viscoelastic relaxation time effects on the system natural frequencies, the short-time Fourier transform (STFT) is performed on the nanosystem model. The nanosystem under consideration is assumed to be made of epoxy with the following mechanical and geometric properties:
STFT spectrum at l0 =0.1 and 𝛾=1: (a-d) Dimensionless frequency respect dimensionless time for V0=75, 50, 10 and 1, respectively.
Fig. 1 displays the STFT spectrum for the nanosystem with l o=0.1 and 𝛾=1 at four different initial excitation values equaling to 75, 50, 10 and 1 (1/s), respectively. The variation of natural frequency of the transverse motion over time spectrum is shown in this figure. Fig.1 (a-c) shows that for the initial excitation values equaling to 75, 50 and 10, the natural frequency decreases as the time increases. Therefore, the viscoelastic nanosystem vibration is non-stationary at these conditions. Moreover, the presence of the nonlinear terms in the vibration equation causes to higher natural frequencies at bigger initial values. However, the Fig (1-d) shows that at initial value equaling 1 (1/s), the viscoelastic model frequency does not change vs. time. This occurs because the nanosystem nonlinearity is weaker at smaller vibration amplitude.
In order to understand the vibration response of the viscoelastic nanoplate, the deflection-time responses of the central point are presented in Fig.2 for two different initial conditions. The dashed and solid lines denote the deflection responses predicted by the Runge- Kutta method for length-scale ratios 0.1 and 0.25, respectively. It can be seen that the vibration frequency displayed by the dashed line is smaller than the solid line.
Vibration response of the center deflection vs. time for the viscoelastic nanoplate at diferente length-scale ratios; (a) X0=1, V0=0 and (b) X0=0, V0=1
4 Dynamic response analysis
The nonlinear dynamic response of the nanosystem is studied in this section with illustrating the frequency- and force-responses obtained based on HBM method. Furthermore the outcomes are validated by the Runge-Kutta method and previous results.
Fig. 3 demonstrates the frequency responses of the viscoelastic nanoplate for the out-of-plane and in-plane motions. The dimensionless relaxation coefficient 𝛾 is set to 5 and amplitude of the dimensionless distributed transverse force f is set to 30. The horizontal axis values, i.e., distributed load frequencies, are normalized with natural frequencies of ù1,1 = 16, obtained via an eigenvalue analysis. The solid and dashed lines are predicted by the HBM method and the dotted symbols are obtained by Runge-kutta method.
Frequency-response curves of viscoelastic nanosystem. a the out-of-plane motion maximum amplitude at midplane ; b, c the in-plane motions maximum amplitude at x=y = 3/4; l0=0.1, f=30 and 𝛾=5
This figure shows that all of the motions have hardening type nonlinearities. Moreover, two saddle node bifurcations are seen in the figure corresponding to Ω =1.50 ù1,1 and Ω =1.19 ù11,1. The first one corresponds to instability beginning and the second one corresponds to stability recapturing. The transverse and longitudinal responses of the nanosystem at x=y=0.5 and x=y=3/4, respectively for Ω = 1.50 ù1,1 are plotted in Fig. 4. It is observed that the nanosystem has a periodic motion. The results show that the in-plane motions, the frequency is much larger than the out-of-plane motion. Moreover, the transverse motion amplitude equals to 0.1 that can be found at lower branch around the first saddle node bifurcations in Fig. (3-a).
Dynamic response of the viscoelastic nanosystem at Ω =1.5 ù1,1; a and b,c time history of the out-of-plane and in-plane motions, respectively
The frequency response of the viscoelastic and elastic models are compared with each other at different applied force amplitudes in Fig.5. The out-of-plane motion response at x=y=0.5 and in-plane motion response at x=y=3/4 are depicted in this figure. The dimensionless relaxation coefficient is set to 𝛾 =5 for viscoelastic model and in elastic model ã is set to zero in Eq.(54) and linear damping with damping “c” is added to the model. The value of the dimensionless damping coefficient is tuned in order to have similar prediction at smaller forcing amplitude c =0.93. The results show that these models predict different response amplitudes at smaller frequency ratios and especially at resonance frequency. As seen in the figure, the maximum amplitude of the elastic model with linear damping is bigger than the viscoelastic model counterpart. More especially, the maximum amplitudes at f =30 for out-of-plane motion are 1.5 and 1.63 for the viscoelastic and elastic models, respectively. This figure shows the importance of using the viscoelastic model at higher applied forces with respect to the elastic model with linear damping.
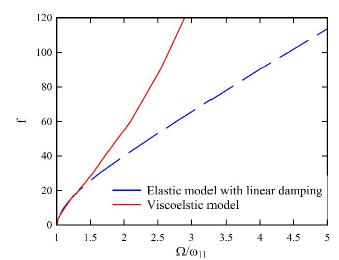
Fig. 6 demonstrates the viscoelasticity effect on the resonance frequency of the viscoelastic nanoplate. In order to depict this figure, the resonance frequency, excitation frequency of the maximum amplitude, corresponds to the frequency response curve of each applied force amplitude that is obtained for elastic model with c=0.93 and viscoelastic models with 𝛾 =5. Then, these resonance frequencies are plotted versus forcing amplitudes at Fig.6. It can be seen that, at the forcing amplitude equaling to 1, both models predict the same results but with increasing the applied force amplitude, the difference between the two models becomes more obvious. More especially, at the same forcing frequency, the viscoelastic model predicts smaller resonance frequency than the elastic model with linear damping. For instance, at f=100, the viscoelastic model resonance occurs at Ω = 2.7 ù1,1 while the elastic one predicts at Ω = 4.4 ù1,1 i.e. with 63% difference. It can be concluded that damping mechanism of the viscoelasticity is amplitude-dependent. In addition, the viscoelasticity reduces the hardening behavior of the nanosystem. Therefore, it is expected that viscoelastic model predicts more reliable dynamic behavior than the elastic model with linear damping.
The effect of the dimensionless relaxation coefficient (𝛾) on the resonance frequency and maximum amplitude of the out-of-plane oscillation, at x=y = 0.5, of the nanosystem is highlighted in Fig. 7(a-b). The forcing amplitude is selected f=30. In Fig. 7 the frequency response is depicted for various dimensionless relaxation coefficients (from 0 to 5); then, the resonance frequency and its corresponding amplitude are plotted in Fig.7. It can be seen that, as the dimensionless relaxation coefficient is increased, the resonance frequency and its corresponding amplitude are decreased to smaller values due to the dissipation of the nanosystem energy. Hence, the nanosystem hardening behavior reduces with increasing the relaxation coefficient.
Frequency response of the viscoelastic, 𝛾=5, and elastic with c=0.93, damping nanoplate for different applied force amplitudes: a the out-of-plane motion maximum amplitude at midplane ; b, c the in-plane motions maximum amplitude at x=y = 3/4, l0=0.1(solid line elastic model with linear damping and dashed line viscoelastic model)
Applied Force amplitude versus the resonance frequency for elastic model with linear damping, c=0.93,and viscoelastic model of the nanosystem
Dimensionless relaxation coefficient effect on resonance frequency and maximum amplitude of the oscillation (at f=30 and l0=0.1)
The frequency response of the viscoelastic nanoplate predicted by means of the CCST and the classical continuum theory are demonstrated in Fig. 8 for the case of f=30, l o=0.25 and 𝛾 =5.This figure highlights more the importance of employing the CCST in comparison with the classical continuum mechanics theory. As seen in the figure, both theories predict the hardening type nonlinear behavior. The peak-amplitude values of the out-of-plane and in-plane motions are larger for the case of the classical continuum theory. Furthermore, it can be seen that the resonance frequency are Ω=23.90 and Ω=24.24 for the case of the classical continuum and CCS theories, respectively. The natural frequency predicted for this nanosystem via CCST theory is larger than classical continuum mechanics one and this is the reason why the resonant region shifts to the larger excitation frequencies. Furthermore, dynamic response of the viscoelastic nanosystem at Ω= 24.24 for the transverse and longitudinal motions are depicted in the framework of the CCST and classical continuum theories in Fig.9. It can be seen that both theories predict periodic motions.
Frequency response of the viscoelastic nanoplate, predicted by means of the classical continuum theory and CCST. a the out-of-plane motion maximum amplitude at midplane; b, c the in-plane motions maximum amplitude at x =y= 3/4, respectively; f = 30, 𝛾= 5 and l0=0.25
The force-response of the viscoelastic nanoplate obtained by means of the classical continuum and CCS theories are depicted in Fig.10. The dimensionless relaxation coefficient, excitation frequency and length-scale parameter are set to 5, 18 and 0.25, respectively. The solid and dashed lines are predicted by the HBM and the dotted symbols are obtained by the Runge-Kutta method. This figure reveals that the CCST and classical continuum theory predict different response paths. Particularly, response amplitude of the CCST increases slowly with the applied force amplitude and no jumps or bifurcations are seen in its response. In addition, the overall amplitude predicted with this theory is much smaller than the classical continuum theory one at bigger applied force. However for the classical continuum theory, as force amplitude is increased, the amplitude of the response increases and then jumps to a higher value. Decreasing the applied force amplitude, because of the nonlinearity that exists in the nanosystem, causes the response amplitude to decrease and then second jump happens to the smaller amplitude response. These characteristics are for all the out-of-plane and in-plane motions of the viscoelastic nanoplate.
Dynamic response of the viscoelastic nanoplate at Ω= 24.24; a-c time history of the out-of-plane and in-plane motions. (Solid and dashed lines correspond to classical continuum theory and CCST results, respectively)
Force response of the viscoelastic nanoplate, 𝛾= 5, predicted by means of classical continuum theory and CCST at Ω=18. a the out-of-plane motion maximum amplitude at midplane; b, c the in-plane motions maximum amplitude at x =y= 3/4, respectively (dotted symbols predicted by Rung-Kutta method)
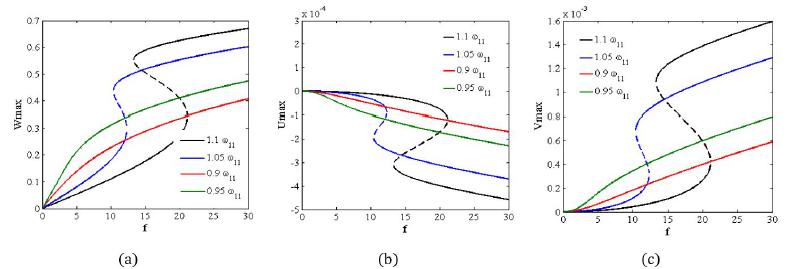
Force response of viscoelastic nanoplate at different frequency ratio; a the out-of-plane motion maximum amplitude at midplane ; b, c the in-plane motions maximum amplitude at x=y = 3/4; l0=0.1, and 𝛾=5
The force response of the mentioned, out-of-plane and in-plane, motions at different normalized frequency and 𝛾 =5 are plotted in Fig. 11. It can be seen that as the applied force amplitude increases, the response amplitude also increases gradually for the Ω/ ù1,1≤1 while no bifurcations and jumps are seen in the response path. However, at the normalized frequencies equaling to 1.1 and 1.05, more than unity, by increasing the applied force amplitude, the response amplitude becomes larger and then shifts to a larger value. This phenomenon, saddle node bifurcation, relates to jumping between stable branches. In addition, as the force amplitude is increased, the response amplitudes for all of these motions increase while the magnitude and the increasing rate of the responses are different.
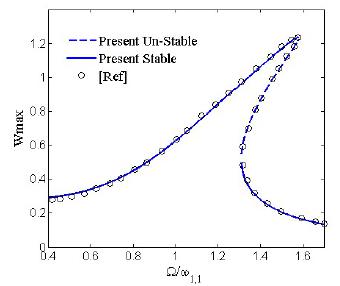
The accuracy of the HBM performed in the present work are also validated by plotting the transverse motion frequency response for an elastic macroplate with linear damping, simplified model with l 0=0, and comparing it with the given frequency response in Amabili (2004Amabili, M. (2004). Nonlinear vibrations of rectangular plates with different boundary conditions: theory and experiments. Computers & structures 82: 2587-2605.) in Fig.12. As the figure shows, there is a good agreement between results. Therefore, the validity of the current simulation and the accuracy of the numerical calculations are partially proved.
The marcoplate transverse motion frequency response: dotted symbol and solid line obtained by present model and Amabili (2004Amabili, M. (2004). Nonlinear vibrations of rectangular plates with different boundary conditions: theory and experiments. Computers & structures 82: 2587-2605.), respectively.
5 Conclusion
This paper analyzed the non-stationary free vibration and nonlinear dynamic behavior of the viscoelastic microplates. For this purpose, a size-dependent model was developed for viscoelastic material based on the CCST. As described, the first version of the couple stress theory suffers from some problems. Hence, its first version was not used widely. In addition, its modification called MCST used some doubtful assumptions. This paper used the recent theory, CCST, which solved the associated problems. The material was supposed to follow the Leaderman integral nonlinear relation. Additionally, in order to capture the geometrical nonlinearity, the von-Karman strain-displacement relation was used. The viscous parts of the size-independent and size-dependent stress tensors are derived by means of the Leaderman integral and their virtual work terms are obtained. The governing equations of motion were derived using the Hamilton's principle in the form of the nonlinear second-order integro-partial differential equations with coupled terms. These size-dependent viscoelastically coupled equations are solved with incorporating the expansion theory and HBM. The short-time Fourier transform were performed to investigate the system free vibration. The effects of the initial excitation values and length scales as well as the viscoelastic parameter on the system vibration are also examined. In addition, frequency and force response curves of the nanosystem subjected to distributive harmonic load were obtained based on the HBM and forth-order Runge-Kutta method.
The STFT analysis showed that the vibration of the nanosystem with viscoelastic model is non-stationary at higher initial excitation values unlike the elastic model. However, the system frequencies do not change with time at smaller initial values. Moreover, the presence of the nonlinear terms in vibration equation causes higher natural frequencies at larger initial values.
The nonlinear analysis showed that out-of-plane and in-plane motions displayed hardening type nonlinearities. Moreover, two saddle node bifurcations are seen in the frequency response of this nanosystem. In addition, the resonance frequency and its corresponding amplitude for all of these motions are increased with increasing the amplitude of the applied force. These reveal that the nanosystem displayed stronger hardening type nonlinearities at larger forcing amplitudes. In addition, it was shown that damping mechanism of the viscoelasticity is amplitude-dependent. Moreover, the viscoelasticity reduces the hardening behavior of the nanosystem. More specifically, the difference between the elastic model with linear damping and viscoelastic model was more obvious at larger amplitude of the applied force. The obtained results showed that, as the dimensionless relaxation coefficient is increased, the resonance frequency and its corresponding amplitude decreased to smaller values due to the dissipation of the nanosystem energy. Hence, the nonlinearities of the nanosystem become weaker. It was observed that, the CCST predicted the resonant frequency at bigger excitation frequencies than the classical continuum theory. Furthermore, the CCST predicted no saddle node bifurcation where the classical continuum theory predicts two nodes. Furthermore, the overall amplitudes predicted by this theory for out-of-plane and in-plane motions were much larger than the classical continuum ones at higher applied forces.
6 Nomenclature
- a,b nanoplate length and width
- E relaxation function
- c damping coefficient
- f Body force
- G modulus of rigidity
- h nanoplate thickness
- K kinetic energy
- t time
- U elastic strain energy
- A,V nanoplate Area and Volume
- W non-conseravtive forces virtual work
- X0, V0 Initial displacement and velocity conditions
- ó Force stress tensors
- 𝜀 permutation tensor
- 𝜅 curvature tensor
- µ Couple-stress tensors
- ω Rotation tensor
- l length-scale parameter
- µ Lame constants
- 𝜒 curvature tensor
- λ Lame constants
- õ Poisson ratio
- 𝛾 relaxation coefficient
- l 0 length-scale ratio
- 𝜌 Density
- Ω External load frequency
- e Elastic
- v Plastic
- vis Viscous forces
- ext External forces
-
Greek symbols
-
Subscript
References
- Amabili, M. (2004). Nonlinear vibrations of rectangular plates with different boundary conditions: theory and experiments. Computers & structures 82: 2587-2605.
- Amabili, M. (2016). Nonlinear vibrations of viscoelastic rectangular plates. Journal of Sound and Vibration 362: 142-156.
- An, F. and Chen, F. (2016). Bifurcations and chaos of the nonlinear viscoelastic plates subjected to subsonic flow and external loads. Chaos, Solitons & Fractals 91: 78-85.
- Asghari, M. (2012). Geometrically nonlinear micro-plate formulation based on the modified couple stress theory. International Journal of Engineering Science 51: 292-309.
- Askari, H., Nia, Z.S., Yildirim, A., Yazdi, M.K. and Khan, Y. (2013). Application of higher order Hamiltonian approach to nonlinear vibrating systems. Journal of Theoretical and Applied Mechanics 51: 287-296.
- Baghelani, M. (2016). Design of a multi-frequency resonator for UHF multiband communication applications. Microsystem Technologies 22: 2543-2548.
- Braun, T., Barwich, V., Ghatkesar, M.K., Bredekamp, A.H., Gerber, C., Hegner, M. and Lang, H.P. (2005). Micromechanical mass sensors for biomolecular detection in a physiological environment. Physical Review E 72: 031907.
- Chen, L.-Q. and Cheng, C.-J. (2005). Instability of nonlinear viscoelastic plates. Applied Mathematics and computation 162: 1453-1463.
- Christensen, R.M. and Freund, L. (1971). Theory of viscoelasticity. Journal of Applied Mechanics 38: 720.
- Cveticanin, L., KalamiYazdi, M., Askari, H. and Saadatnia, Z. (2012). Vibration of a two-mass system with non-integer order nonlinear connection. Mechanics Research Communications 43: 22-28.
- Ebrahimi, F. and Hosseini, S. (2016). Thermal effects on nonlinear vibration behavior of viscoelastic nanosize plates. Journal of Thermal Stresses 39: 606-625.
- Ekinci, K., Huang, X. and Roukes, M. (2004). Ultrasensitive nanoelectromechanical mass detection. Applied Physics Letters 84: 4469-4471.
- Elwenspoek, M. and Jansen, H.V. (2004). Silicon micromachining, Cambridge University Press
- Eringen, A.C. and Edelen, D. (1972). On nonlocal elasticity. International Journal of Engineering Science 10: 233-248.
- Farajpour, A., Shahidi, A., Mohammadi, M. and Mahzoon, M. (2012). Buckling of orthotropic micro/nanoscale plates under linearly varying in-plane load via nonlocal continuum mechanics. Composite Structures 94: 1605-1615.
- Farokhi, H. and Ghayesh, M.H. (2017). Viscoelasticity effects on resonant response of a shear deformable extensible microbeam. Nonlinear Dynamics 87: 391-406.
- Feng, L., Wu, L., Wang, J., Ren, J., Miyoshi, D., Sugimoto, N. and Qu, X. (2012). Detection of a Prognostic Indicator in Early‐Stage Cancer Using Functionalized Graphene‐Based Peptide Sensors. Advanced Materials 24: 125-131.
- Fu, Y. and Zhang, J. (2009). Nonlinear static and dynamic responses of an electrically actuated viscoelastic microbeam. Acta Mechanica Sinica 25: 211-218.
- Ghayesh, M.H., Farokhi, H. and Amabili, M. (2013a). Nonlinear behaviour of electrically actuated MEMS resonators. International Journal of Engineering Science 71: 137-155.
- Ghayesh, M.H., Farokhi, H. and Amabili, M. (2013b). Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Composites Part B: Engineering 50: 318-324.
- Ghorbanpour Arani, A. and Haghparast, E. (2017). Size-dependent vibration of axially moving viscoelastic micro-plates based on sinusoidal shear deformation theory. International Journal of Applied Mechanics 9: 1750026.
- Hadjesfandiari, A.R. and Dargush, G.F. (2011). Couple stress theory for solids. International Journal of Solids and Structures 48: 2496-2510.
- Hadjesfandiari, A.R. and Dargush, G.F. (2013). Fundamental solutions for isotropic size-dependent couple stress elasticity. International Journal of Solids and Structures 50: 1253-1265.
- Hadjesfandiari, A.R., Dargush, G.F. and Hajesfandiari, A. (2013). Consistent skew-symmetric couple stress theory for size-dependent creeping flow. Journal of Non-Newtonian Fluid Mechanics 196: 83-94.
- Hashemi, S.H., Mehrabani, H. and Ahmadi-Savadkoohi, A. (2015). Exact solution for free vibration of coupled double viscoelastic graphene sheets by viscoPasternak medium. Composites Part B: Engineering 78: 377-383.
- Huang, X., Feng, X., Zorman, C., Mehregany, M. and Roukes, M. (2005). VHF, UHF and microwave frequency nanomechanical resonators. New Journal of Physics 7: 247.
- Husain, A., Hone, J., Postma, H.W.C., Huang, X., Drake, T., Barbic, M., Scherer, A. and Roukes, M. (2003). Nanowire-based very-high-frequency electromechanical resonator. Applied Physics Letters 83: 1240-1242.
- Jamalpoor, A., Bahreman, M. and Hosseini, M. (2017). Free transverse vibration analysis of orthotropic multi-viscoelastic microplate system embedded in visco-Pasternak medium via modified strain gradient theory. Journal of Sandwich Structures & Materials 1099636216689384.
- JE., L. (1989). Boundary stabilization of thin plates, SIAM (Philadelphia).
- Jomehzadeh, E., Noori, H. and Saidi, A. (2011). The size-dependent vibration analysis of micro-plates based on a modified couple stress theory. Physica E: Low-dimensional Systems and Nanostructures 43: 877-883.
- Karlièiæ, D., Koziæ, P. and Pavloviæ, R. (2014). Free transverse vibration of nonlocal viscoelastic orthotropic multi-nanoplate system (MNPS) embedded in a viscoelastic medium. Composite Structures 115: 89-99.
- Ke, L.-L., Wang, Y.-S., Yang, J. and Kitipornchai, S. (2012). Free vibration of size-dependent Mindlin microplates based on the modified couple stress theory. Journal of Sound and Vibration 331: 94-106.
- Ke, L., Yang, J., Kitipornchai, S., Bradford, M. and Wang, Y. (2013). Axisymmetric nonlinear free vibration of size-dependent functionally graded annular microplates. Composites Part B: Engineering 53: 207-217.
- Khaniki, H.B. and Hosseini-Hashemi, S. (2017). Dynamic response of biaxially loaded double-layer viscoelastic orthotropic nanoplate system under a moving nanoparticle. International Journal of Engineering Science 115: 51-72.
- Koiter, W. (1964). Couple-stress in the theory of elasticity, North Holland Pub
- Lam, D.C., Yang, F., Chong, A., Wang, J. and Tong, P. (2003). Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids 51: 1477-1508.
- Leaderman, H. (1962). Large longitudinal retarded elastic deformation of rubberlike network polymers. Transactions of the Society of Rheology 6: 361-382.
- Lee, H.-J., Zhang, P. and Bravman, J.C. (2005). Stress relaxation in free-standing aluminum beams. Thin Solid Films 476: 118-124.
- Liu, J., Zhang, Y. and Fan, L. (2017). Nonlocal vibration and biaxial buckling of double-viscoelastic-FGM-nanoplate system with viscoelastic Pasternak medium in between. Physics letters A 381: 1228-1235.
- Lou, J. and He, L. (2015). Closed-form solutions for nonlinear bending and free vibration of functionally graded microplates based on the modified couple stress theory. Composite Structures 131: 810-820.
- Ma, H., Gao, X.-L. and Reddy, J. (2011). A non-classical Mindlin plate model based on a modified couple stress theory. Acta mechanica 220: 217-235.
- Mickens, R.E. (2010). Truly nonlinear oscillations: harmonic balance, parameter expansions, iteration, and averaging methods, World Scientific
- Mindlin, R. and Tiersten, H. (1962). Effects of couple-stresses in linear elasticity. Archive for Rational Mechanics and analysis 11: 415-448.
- Mohammadimehr, M., Navi, B.R. and Arani, A.G. (2015). Free vibration of viscoelastic double-bonded polymeric nanocomposite plates reinforced by FG-SWCNTs using MSGT, sinusoidal shear deformation theory and meshless method. Composite Structures 131: 654-671.
- Murmu, T. and Adhikari, S. (2012). Nonlocal frequency analysis of nanoscale biosensors. Sensors and Actuators A: Physical 173: 41-48.
- Niyogi, A. (1973). Nonlinear bending of rectangular orthotropic plates. International Journal of Solids and Structures 9: 1133-1139.
- Pandey, J., Chu, W., Kim, C., Lee, C. and Ahn, S. (2009). Bio-nano reinforcement of environmentally degradable polymer matrix by cellulose whiskers from grass. Composites Part B: Engineering 40: 676-680.
- Poole, W., Ashby, M. and Fleck, N. (1996). Micro-hardness of annealed and work-hardened copper polycrystals. Scripta Materialia 34: 559-564.
- Pouresmaeeli, S., Ghavanloo, E. and Fazelzadeh, S. (2013). Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Composite Structures 96: 405-410.
- Reddy, J. and Kim, J. (2012). A nonlinear modified couple stress-based third-order theory of functionally graded plates. Composite Structures 94: 1128-1143.
- Smart, J. and Williams, J. (1972). A comparison of single-integral non-linear viscoelasticity theories. Journal of the Mechanics and Physics of Solids 20: 313-324.
- Su, Y., Wei, H., Gao, R., Yang, Z., Zhang, J., Zhong, Z. and Zhang, Y. (2012). Exceptional negative thermal expansion and viscoelastic properties of graphene oxide paper. Carbon 50: 2804-2809.
- Tajaddodianfar, F., Yazdi, M.R.H. and Pishkenari, H.N. (2017). Nonlinear dynamics of MEMS/NEMS resonators: analytical solution by the homotopy analysis method. Microsystem Technologies 23: 1913-1926.
- Tang, Y., Zhang, D., Rui, M., Wang, X. and Zhu, D. (2016). Dynamic stability of axially accelerating viscoelastic plates with longitudinally varying tensions. Applied Mathematics and Mechanics 37: 1647-1668.
- Teh, K.S. and Lin, L. (1999). Time-dependent buckling phenomena of polysilicon micro beams. Microelectronics journal 30: 1169-1172.
- Wang, Y., Li, F.-M. and Wang, Y.-Z. (2015). Nonlinear vibration of double layered viscoelastic nanoplates based on nonlocal theory. Physica E: Low-dimensional Systems and Nanostructures 67: 65-76.
- Xiao, Y., Huang, W., Tsui, C.P., Wang, G., Tang, C.Y. and Zhong, L. (2017). Ultrasonic atomization based fabrication of bio-inspired micro-nano-binary particles for superhydrophobic composite coatings with lotus/petal effect. Composites Part B: Engineering 121: 92-98.
- Yan, X., Brown, W., Li, Y., Papapolymerou, J., Palego, C., Hwang, J. and Vinci, R. (2009). Anelastic stress relaxation in gold films and its impact on restoring forces in MEMS devices. Journal of Microelectromechanical Systems 18: 570-576.
- Yang, F., Chong, A., Lam, D.C.C. and Tong, P. (2002). Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures 39: 2731-2743.
- Yazdi, M. (2016). Approximate solutions to nonlinear oscillations via an improved He's variational approach. Karbala International Journal of Modern Science 2: 289-297.
- Yazdi, M. and Tehrani, P. (2015). The energy balance to nonlinear oscillations via Jacobi collocation method. Alexandria Engineering Journal 54: 99-103.
- Yazdi, M.K. and Tehrani, P.H. (2016). Frequency analysis of nonlinear oscillations via the global error minimization. Nonlinear Engineering 5: 87-92.
- Zhang, Y., Pang, M. and Fan, L. (2016). Analyses of transverse vibrations of axially pretensioned viscoelastic nanobeams with small size and surface effects. Physics letters A 380: 2294-2299.
-
Available Online: August 06, 2018
Publication Dates
-
Publication in this collection
2018
History
-
Received
17 Feb 2018 -
Reviewed
12 July 2018 -
Accepted
30 July 2018