Abstract
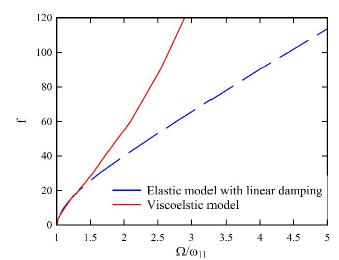
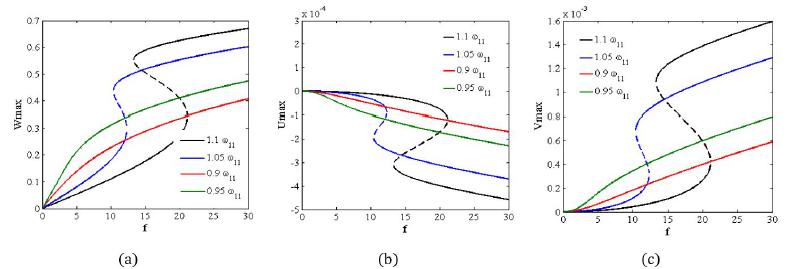
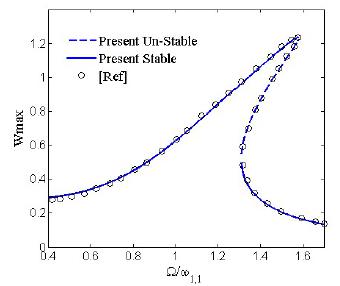
This paper analyses the non-stationary free vibration and nonlinear dynamic behavior of the viscoelastic nano-plates. For this purpose, a size-dependent theory is developed in the framework of the consistent couple stress theory for viscoelastic materials. The previously presented modified couple stress theory was based on some consideration making it partially doubtful to apply. This paper uses the recent findings for the mentioned problem and develops it to analyze the nonlinear dynamic behavior of nano-plates with nonlinear viscoelasticity. The material is supposed to follow the Leaderman integral nonlinear constitutive relation. In order to capture the geometrical nonlinearity, the von-Karman strain displacement relation is used. The viscous parts of the size-independent and size-dependent stress tensors are calculated in the framework of the Leaderman integral and the resultant virtual work terms are obtained. The governing equations of motion are derived using the Hamilton principle in the form of the nonlinear second order integro-partial differential equation with coupled terms. These coupled size-dependent viscoelastic equations are solved using the forth-order Runge-kutta and Harmonic balance method after simplifying by the expansion theory. The short-time Fourier transform is performed to examine the system free vibration. In addition, frequency- and force-responses of the nanosystem subjected to distribute harmonic load are presented. The obtained results show that the viscoelastic model-based vibration is non-stationary unlike the elastic model. Moreover, the damping mechanism of the viscoelasticity is amplitude dependent and the contribution of the viscoelastic damping terms at higher forcing conditions becomes noticeable.
Keywords
nonlinear viscoelastic; consistent couple stress; Harmonic balance method; nonlinear dynamic; nano-plate