Abstract
To great understanding the dynamic crack propagation of rock under in-situ stress and blasting, the static-dynamic loading experimental platform was built. With different confining pressure (0MPa, 2MPa, 4MPa, 6MPa, 8MPa) and different ratios (K) of horizontal-to-vertical pressure (0, 0.25, 0.5, 0.75, 1), nine texts have been carried out in quadrate granite samples. The dynamic strain gauges and high-speed (HS) camera were used to measure strain field and observe crack growth. According to experimental results, the centrosymmetric damage zone is generated around borehole when K=1, the circumference compressive stress is formed by confining pressure, and it reduces the circumference tensile failure by blast loading. The number and size of the broken radius significantly reduce with confining pressure increases. As K decrease from 1 to 0, the tensile stress concentration is obviously around borehole in the vertical direction, and radial cracks grow from the stress concentration zone and develop into boundary under tensile stress wave from blast loading. From the numerical analysis based on Johnson-Holmquist in AUTODYN, crack branching appear near free boundary obviously, meanwhile the radial cracks grow and run through sample by reflected wave at last. Compared to the experimental results, the evolution and final shape of cracks are agree with the experimental results, the central damage area is less than latter because JWL equation neglect the gas loading in numerical calculation.
Keywords
Rock mechanics; dynamic crack propagation; biaxial pre-pressure; blast loading; JH model
1 INTRODUCTION
With the method of drilling and blasting has been widely used in mining and underground engineering. The deep rock located in the high in-situ stress, for example, the vertical stress is approximately 27 MPa when the depth is 1,000 m, and the horizontal part reaches 13.5 MPa ( Brown and Hoek, 1978 Brown, E. T., and Hoek, E. (1978). Trends in relationships between measured in-situ, stresses and depth. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 15(4): 211-215. ). High in-situ stress has a strongly effect on dynamic crack propagation of rock under blast loading ( Zhu et al., 2016 Zhu, J. B., Liao, Z. Y., and Tang, C. A. (2016). Numerical SHPB tests of rocks under combined static and dynamic loading conditions with application to dynamic behavior of rocks under in situ stresses. Rock mechanics and rock engineering 49(10): 3935-3946. ). When the static confining pressure couples dynamic blast loading, the dynamic mechanical behavior of rock becomes more complicated and controlled by many factors, such as the ratio of the horizontal and vertical parts of in-situ stress (K).
In general, the blast loading mainly consists of shock waves and explosion gases, and both of them contribute significantly to dynamic response of rock ( Onederra et al., 2013 Onederra, I. A., Furtney, J. K., Sellers, E., and Iverson, S. (2013). Modelling blast induced damage from a fully coupled explosive charge. International Journal of Rock Mechanics and Mining Sciences 58(58): 73-84. ; Ma and An, 2008 Ma, G. W., and An, X. M. (2008). Numerical simulation of blasting-induced rock fractures. International Journal of Rock Mechanics and Mining Sciences 45(6): 966-975. ). Initially, shock waves with high pressure are produced and propagate to the borehole, and micro fissures are generated by shear band interconnection due to the extremely high pressures of stress wave, which lead to the zone around borehole is pulverized. Then, hoop tensile stress follow by the compressive stress wave and drive the existing flaws developing. The damage area further extends by reflected waves along boundary zone. Finally, radial cracks run through sample because of the subsequent explosion gas flow into cracks ( Rathore and Bhandari, 2007 Rathore, S. S., and Bhandari, S. (2007). Controlled fracture growth by blasting while protecting damages to remaining rock. Rock Mechanics and Rock Engineering 40(3): 317-326. ; Cho and Kaneko, 2004 Cho, S. H., and Kaneko, K. (2004). Influence of the applied pressure waveform on the dynamic fracture processes in rock. International Journal of Rock Mechanics and Mining Sciences 41(5): 771-784. ; Eason, 1963 Eason, G. (1963). Propagation of waves from spherical and cylindrical cavities. Zeitschrift Für Angewandte Mathematik Und Physik Zamp 14(1): 12-23. ; Liu and Katsabanis, 1993 Liu, Q., and Katsabanis, P. D. (1993, July). A theoretical approach to the stress waves around a borehole and their effect on rock crushing. In Proceedings of the Fourth International Symposium on Rock Fragmentation by Blasting-Fragblast-4: 9-16. ; Szuladzinski, 1993 Szuladzinski, G. (1993, July). Response of rock medium to explosive borehole pressure. In Proceedings of the fourth international symposium on rock fragmentation by blasting-Fragblast-4, Vienna, Austria (Vol. 23). ).
In laboratory studies, the modified split Hopkinson pressure bar (SHPB) is widely adopt to study the dynamic properties of rock under static and dynamic loads, and the experimental apparatus and test techniques have been developed ( Christensen et al., 1972 Christensen, R. J., Swanson, S. R., and Brown, W. S. (1972). Split-Hopkinson-bar tests on rock under confining pressure Experimental Mechanics 12(11): 508-513. ). Wu et al. (1998) Wu, Y. K., Hao, H., Zhou, Y. X., and Chong, K. (1998). Propagation characteristics of blast-induced shock waves in a jointed rock mass. Soil Dynamics and Earthquake Engineering 17(6): 407-412. used the accelerometers to examine the propagation characteristics of shock waves from blasting, and found that the amplitude and principal frequency of stress waves are attenuated with distance increases. Li et al. (2008) Li, X., Zhou, Z., Lok, T. S., Hong, L., and Yin, T. (2008). Innovative testing technique of rock subjected to coupled static and dynamic loads. International Journal of Rock Mechanics and Mining Sciences 45(5): 739-748. found the strength of rock under coupling loads was higher than their corresponding individual static or dynamic strengths. The dynamic tensile strength increases with the hydrostatic pressure, and the failure strength mainly depends on the loading rate when the confining pressure reaches a certain value ( Wu et al., 2016 Wu, B., Xia, K., and Guo, Y. (2016, June). Influence of hydrostatic confining pressure on the dynamic tensile failure of rock material. In 50th US Rock Mechanics/Geomechanics Symposium. American Rock Mechanics Association. ). The dynamic compressive strength was determined by a combination of static axial and lateral confining pressures, including the magnitude of the coupled stress and the ratio of their magnitudes ( Zhu et al., 2016 Zhu, J. B., Liao, Z. Y., and Tang, C. A. (2016). Numerical SHPB tests of rocks under combined static and dynamic loading conditions with application to dynamic behavior of rocks under in situ stresses. Rock mechanics and rock engineering 49(10): 3935-3946. ).
Given the above background, laboratory-scale blast experiments were conducted in quadrate granitic samples. The dynamic strain gauges, high-speed (HS)camera and digital image correlation (DIC) technology were adopt to test the dynamic strain and observe dynamic response process under different confining pressures (0 MPa, 2 MPa, 4 MPa, 6 MPa, and 8 MPa) and different ratios (0, 0.25, 0.5, 0.75, 1). In the numerical calculation, the Johnson-Holmquist (JH) constitutive model is selected to study crack propagation processes under static-dynamic loading in AUTODYN. Moreover, the static and SPHB experimental results are used for calibrating the parameters of JH model.
2 EXPERIMENTS
2.1 Rock materials
The granite samples in the experiment were from the Fang Shan area of Beijing, China. Based on the International Society for Rock Mechanics (ISRM) standards, all samples were obtained from the same parent rock, and water drilling was used to avoid the germination of micro cracks. The specimens were ground by a grinding machine to ensure that the parallelism between the top and bottom surface is within 0.1 mm. The molecular constituents of specimen were characterized in the Beijing Center for Physical and Chemical Analysis (Beijing, China), and SiO2 is the dominant mineral and comprises 47.75% of the rock, followed by CaO (8.16%). The parameters of the Fang Shan granite were as follows: density = 2.43 g/cm3, Poisson’s ratio = 0.23, P-wave velocity = 4088 m/s.
The quasi-static properties of granite were tested using the WDW-300 electronic universal testing machine in the Laboratory of Explosion at the Beijing Institute of Technology (Beijing, China). The BX 120-4AA strain gages (sensitive grid size is 4×2 mm) were used to collect deformation during loading. The tensile strength of granite is 6 MPa and compressive strength is 86 MPa. Both the tensile and compressive stress curves drop sharply after stress reach the maximum stress, which indicate the brittle fracture should be responsible for the failure of granite specimens in quasi-static experiment.
SHPB experiment was carried out for the granite with higher strain rate (approximately 100 /s) at China University of Mining and Technology. All bars were steel to match the wave impedance of the rock samples with a diameter of 74 mm. The speed of striker bar was approximately 7 m/s and the strain was recorded by LTT24-Messsystem on 2 MS/s sampling rate. The dynamic compressive strength is 120 MPa and dynamic tensile strength is 8 MPa, the failure strain is 0.007 and 0.0015, respectively.
2.2 Test system and equipment
Previous experiments have studied the dynamic behavior of rock-like materials subjected to blasting. McHugh (1983) McHugh, S. (1983). Crack extension caused by internal gas pressure compared with extension caused by tensile stress. International Journal of Fracture 21(3): 163-176. used Plexiglas cylinder sample with a length of 300 mm and 300 mm in diameter, PETN charges had diameters of 3.2 mm (charge density is 4 g/m); Simha et al. (1984) Simha, K. R. Y., Fourney, W. L., and Dick, R. D. (1984, January). Studies On Explosively Driven Cracks Under Confining In-Situ Stresses. In The 25th US Symposium on Rock Mechanics (USRMS). American Rock Mechanics Association. experimented with Plexiglas sheets (305×305×50 mm), and charge density was 10 g/m; Rathore and Bhandari (2007) Rathore, S. S., and Bhandari, S. (2007). Controlled fracture growth by blasting while protecting damages to remaining rock. Rock Mechanics and Rock Engineering 40(3): 317-326. tested blasts in limestone blocks (550×300×250 mm) at the laboratory scale using the detonating cord with 8.5 g/m. In this experiment, PETN was pressed to a diameter of 4 mm and a length of 50 mm, and had a density of 1.0 g/cm3. Banadaki and Mohanty (2012) Banadaki, M. D., and Mohanty, B. (2012). Numerical simulation of stress wave induced fractures in rock. International Journal of Impact Engineering 40: 16-25. experimented with cubic samples (150×150×150 mm), and the density of PETN cylindrical charges is 1.2~5.3 g/m. A copper tube (0.6 mm thick) was installed in the borehole of each sample to prevent explosion gas from penetrating into fissures.
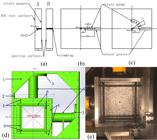
Based on the above research results, the specimen consisted of two parts (A and B), 300 mm square and 50 mm long. The strain sensors pasted on one face of A and another face were used for HS test, meanwhile B was used to remove reflected waves from the strain sensor surface, as shown in Figure 1 . Two models were designed, one focus on the dynamic response of the rock as the biaxial compressive stress increased (K=1), anther study the radial crack propagation under different K. Figure 1 b shows the first model, six target points were located with a spacing of 14 mm, and the nearest sensor was installed 35 mm from center hole. In the second model, six hoop strain gauges pasted along the track of quarter circles with radius of 60 mm, and the central angle between the two sensors was 18°, as seen in Figure 1 c. The center borehole was drilled and had a diameter of 10 mm, the distance between the DIC surface and the bottom surface was 10 mm.
Schematic diagram of the experiment; (a) Two pieces of samples; (b) Strain gauges position in model 1; (c) Strain gauge positions in model 2; (d) Experimental platform; (e) Experiment photograph.
A new experimental instrument is displayed in Figure 1 1-ribbed plate, 2-steel frame, 3-oil cylinder base, 4-side steel plates, 5-hydraulic loading system, and 6-fixed screw. For simulate horizontal and vertical in-situ stress, two hydraulic oil cylinders were applied to make square specimens, the high-pressure oil pipe and pressure gage are used to control the pressure value accurately. Biaxial compressive stress was delivered by hydraulic oil cylinders, which can provide different ratios of biaxial pressure from 0 MPa to 16 MPa. Eight screws were selected to prevent confining pressure unloading during blast loading.
Strain signals were recorded by LTT24-Messsystem with 2 MS/s. High-speed stereo vision was used to quantify the dynamic response under blast loading. Fastcam SA5 high-speed camera, VIC-2D software ver.7, lenses and optical lenses with different focal lengths were selected. The array size was 320×192 (or 256×224), and two 1,000 W halogen lamps were used to provide sufficient light intensity. The speed of the high-speed camera was 100,000 frames/s, the interval time between two images was 10 μs. Photographs of DIC test surface in two models are shown in Figure 2 .
3 EXPERIMENT RESULTS
3.1 Dynamic response of rock (K=1)
All experiments were performed in the Laboratory of Explosion at the Beijing Institute of Technology. Nine tests were completed, tests 1~5 focused on the dynamic response under different confining pressures with constant ratio (K=1), and tests 6~9 aimed to study dynamic crack propagation with different K ( Table 1 ). The electric discharge method inspire the synchronization trigger system.
Parameters of nine test ( is horizontal confining pressure, is vertical confining pressure, ).
The yield strength of rock under blasting is higher than impact loading in SHPB experiment (the rock materials become stronger with strain rates increase), while tensile strength under blasting is similarly with impacting in SHPB test, so take the yield strength from SHPB experiment results as the failure criteria for blasting is suitable. Select the average strain (0.002) on the descending part of tensile stress-strain curve in SHPB experimental results as the fracture strain, and select peak strain (0.0005) on linear part as ultimate elastic strain.
To study the effects of (hoop strain) and (radial strain) on radial cracks, two key points are selected on 30 mm and 90 mm from blast hole. Figure 3 a displays the deformation on 30 mm, the gauge is triggered at 7 μs, reach -0.0075 and rise to 0.009, both of them exceed the fracture threshold stress. The strain sensor on 90 mm is triggered after 25 μs, and the strain peak is lower than the former point. is 0.004 and exceed the tensile strength and radial cracks are mainly caused by hoop tensile stress from combined effect of confining pressure and explosion stress wave ( Figure3 b).
Strain results with K=1. (a) Strain-time curve at 30 mm in test 2; (b) Strain-time curve at 90 mm in test 2; (c) Hoop strain at 30mm in test 1-5; (d) Decrease of strain with confining pressure.
The hoop compressive stress is formed by confining pressure, and it reduces the tensile failure by subsequent blast loading. Figure 3 c presents the hoop strain-time curve collected on 30 mm in tests 1~5 (K=1). The centrosymmetric damage zone is generated around borehole by stress wave, the peak of reduce as the confining pressure increase. The non-linear decrease of hoop strain is found as confining pressure increase ( Figure 3 d).
3.2 Dynamic response under different ratios
Elastic mechanics theory and Kirsch solution is used to describe stress field for a plate assumed to be infinite containing a center circular hole ( Jaeger et al., 2009 Jaeger J C, Cook N G W, Zimmerman R. (2009). Fundamentals of rock mechanics. John Wiley & Sons. ). Figure 4 show the analytical solution of hoop stress under biaxial pre-pressure with different ratios for test 6~9. When K=1, the stress field around center hole is symmetric and hoop compressive stress is about -17 MPa. With K decrease, tensile stress concentration is appeared in vertical direction. As K=0, hoop tensile stress appeared at the top of hole and reaches 8 MPa, and hoop compressive stress in horizontal direction is 24 MPa on hole wall. Initial micro fissures are produced around blast hole by tensile stress in the vertical direction under confining pressure, and then blast loading would drive the cracks run through specimen.
Figure 5 a lists the results of test 6 after blast loading, at 90° reach 0.011 and is higher than other points, and the peak strain of 0° is only 0.002. When K=0.25, decrease to 0.007 at 90°, which is lower than the peak value in test 6. The results show that initial micro fissure caused by the confining pressure would extend further under subsequent blast loading. Similar laws are found in test 8 and test 9, and the strain peaks decrease slowly with K increases. Furthermore, the peak hoop strain in the same location decrease as K increase. In test 9, the strain gage at 90° is failed due to natural defects cause fatigue and damage of specimen ( Figure 5 d).
Hoop strain with different ratios. (a) Test 6 for ; (b) Test 7 for ; (c) Test 8 for ; (d) Test 9 for .
The strain gage technique with a higher sampling rate can capture the deformation of rock by stress waves, and HS camera technique is more easily to observe crack growth due to crack propagation speed is less than stress wave. Notice that the time which is shown in the top right corner is not start at triggering time, and start at the deformation of specimen. The stress wave propagates at a speed of 4088 m/s. Figure 6 displays the evolution of the quarter stress field on the HS test surface during blast lading, crack propagation was recorded with different K. Initial stress wave from borehole propagate during 0~40 μs, and the amplitude gradually decreases with distance increase. When initial stress wave arrive boundary, the reflected stress wave are produced. The speed of crack growth is slower compared with stress waves, and the strain concentration band obviously extends to the boundary at 160 µs.
Dynamic testing results under different ratios. (a) K=0; (b) K=0.25; (c) K=0.5; (d) K=0.75; (e) K=1.
A vertical damage zone can be clearly observed at 20 µs, the strain peak reach 0.012 ( Figure 6 a). With the initial shock waves propagate to the free boundary of specimen at 40 µs, two distinct strain concentration areas are produced at the top of the borehole and in the upper boundary region. In the boundary damage region, the reflected wave is an important role for radial crack growth.
The peak strain in the stress concentration zone decrease with K increase in test 7, and the width of the damage zone gradually decreases under the initial stress wave ( Figure 6 b). The initial narrow damage zone extends and coalesces under reflected wave at 120 μs. This result is in good agreement with test 5. As increased, cracks arose around borehole at 65° and 45°, corresponding to K = 0.5 and K = 0.75, respectively. This result is caused by shear failure under shear stress from initial stress wave. The center symmetric damage zone was generated around the borehole (K=1), the damage band caused by stress concentration, and the reflected tensile stress is not obviously when reached 8 MPa ( Figure 6 e).
Figure 7 displays the experimental results with K is 0 to 1. The vertical cracks were clearly observed at the top of the borehole with K is 0~0.75. Radial cracks generated around boreholes. The width of the crack decrease from 1mm ( Figure 7 a) to 0.1 mm ( Figure 7 d) and controlled by hoop tensile stress, which is caused by confining pressure with different ratios. Under the combined action of the initial wave and reflected tension wave, the zone long the free face was damage. As shown in lower right corner of Figure 7 , the reflected wave has little influence on the middle face for strain gage, the centrosymmetric fracture zone is obviously, and the crushing process was caused by shock waves.
4 NUMERICAL SIMULATIONS
4.1 Geometric modeling
The Johnson-Holmquist model is among the few useful and relatively complex damage models that can be used for investigating the impacting and blasting problems on rock materials. The JH model was originally studied for the mechanism of dynamic response ceramics. Holmquist et al. (2001) Holmquist, Timothy J, D. W. Templeton, and K. D. Bishnoi. (2001). Constitutive modeling of aluminum nitride for large strain, high-strain rate, and high-pressure applications. International Journal of Impact Engineering 25(3): 211-231. suggested a constitutive mode for brittle materials. JH model gradually softens the strength (from intact to failed) as the damage accumulates, and it gradually increases the bulking pressure as the damage accumulates. Based on JH constitutive model, compared the dynamic response under single-hole loading and double-hole loading. Meanwhile, the crack propagation under different uncoupling ratios was researched.
4.1.1 Polynomial EOS for granite
A polynomial state equation is selected to describe the nonlinear compressibility when shock waves transmit into rock materials, the relation between pressure P and compression μ is showed in Figure 8 a. D stand for the damage with a value between 0 and 1, the elastic distortion energy starts to decrease when the pressure exceeds the ultimate strength of the rock ( Ma and An, 2008 Ma, G. W., and An, X. M. (2008). Numerical simulation of blasting-induced rock fractures. International Journal of Rock Mechanics and Mining Sciences 45(6): 966-975. ).
JH model. (a) Relation between P and μ; (b) Normalized equivalent stress under intact and the totally fractured condition; (c) Equivalent plastic strain under intact and the totally fractured condition.
The pressure variable of the Polynomial EOS is expressed as:
where μ is the compression, , represents current density, is reference density, and is an additional pressure increment determined from energy considerations to include the dilatation effect after compression failure.
4.1.2 JH strength model
The strength model as a non-hardening material model is used to study the dynamic response of brittle materials under impact loading. Along with the further development, it is also used to simulate the dynamic fracture process under blasting. The relationship between normalized equivalent stress and normalized pressure under different condition are described ( Figure 8 b) ( Banadaki and Mohanty, 2012 Banadaki, M. D., and Mohanty, B. (2012). Numerical simulation of stress wave induced fractures in rock. International Journal of Impact Engineering 40: 16-25. ). The equivalent stress can be expressed as:
where , , and are the three normal components of the stress tensor, and are the three shear stresses. The intact strength is given as:
The fully fractured strength is given as:
The strength of damaged material is given as:
where A, N, B, M, and C are material constants; are effective stress of the intact material, effective stress of the fully fractured material, current effective stress, pressure, and tensile strength, respectively, which are normalized by the following expressions:
P is the current hydrostatic pressure, T is the maximum tensile hydrostatic pressure, is the effective stress at Hugoniot elastic limit ( ), PHEL is the hydrostatic pressure at the , D is the damage variable, is the effective stress. is the dimensionless strain rate, where is the actual equivalent strain rate and is the reference strain rate, and A, N, and C are the material constants. can be calculated:
where are the three normal strain rates, are the three shear strain rates.
4.1.3 JH failure criterion
The degree of damage is calculated by accumulating plastic strain. At first, the elements are controlled by elastic deformation and no damage appeared ( Figure 8 c). Then the accumulation of plastic strain increases when the equivalent stresses exceed the elastic limit strength, and the permanent deformations of material are generated (0 < D < 1). At last, the equivalent plastic strain becomes equal to fracture strain and the material is damaged completely. The equivalent plastic strain to fracture is calculated as:
where are material constants and and are defined previously. . is -51 GPa. When the plastic deformation happened in the material, the damage accumulates and its value can be obtained from:
where is the increment in the equivalent plastic strain during a calculation cycle.
It is implemented as a damage model in ANSYS AUTODYN hydrocode, which is an advanced explicit code for transient nonlinear dynamics simulation. There are a lot of parameters to consider in JH model, some are easily determined by experiments while others are more difficult to define. In this paper, the static and SPHB experimental results are used for calibrating the parameters of JH model base on the reference literature ( Shi et al. 2015 Shi X, Tao, Z, and Meng Y. (2015). Calculation and verification for Johnson-Holmquist constitutive model parameters of tight sandstone. Chinese Journal of Rock Mechanics and Engineering 34(S2): 3750-3758. ), the parameters as shown in Table 2 . The geometric model is set up in Solidworks, then import it into ANSYS Workbench for meshing and boundary loading. Explicit Dynamics is selected for analyzing the dynamic response in AUTODYN.
As Figure 9 shown, two models were stablished. Six target points were located with a spacing of 14 mm in first design, and six key points were selected along the quarter circles in second model. The quadrate sample is 300 mm in length, and the diameter of PETN cylindrical charge is 4 mm. The JWL EOS is used for calculating blast load, which has been widely used in numerical simulations. The number of rock’s elements is approximately 340,000, and the Euler grids are approximately 20,000. The meshes were enough for the requirement of precision. The velocity of stress wave in rock is approximately equal to P-wave velocity, and the stress wave from confining pressure reached steady state after 70 μs. Meanwhile the shock wave reached stress balanced after 90 μs. Nine tests are completed according to the experiment, tests 1~5 for the first model, and tests 6~9 for the second model.
4.2 Simulation results
4.2.1. Simulation results with K=1
Figure 10 a shows Von Mises stress in test 1 at different times. The central symmetry stress wave originates from borehole, and the pressure on the wall is 300 MPa which exceeds the dynamic strength of rock. Smaller cracks are densely produced in the center damage zone, and visible radial cracks radiate from borehole and propagate to free boundary. The stress wave reduces with the increasing of distance, and the stress below the strength of rock in the damage zone. After 40 μs, the initial stress wave arrive boundary, and then existing cracks further grow under reflected tensile wave, especially the horizontal and vertical cracks run through the specimen at 90 μs. In addition, the radial cracks at 45° are longer than others (except horizontal and vertical cracks).
Simulation results with K=1. (a) Mises stress distribution on test 1. (b) Mises stress distribution on test 5. (c) Crack final shape under different confining pressures.
The results of test 5 are shown as Figure 10 b, the damage pattern between the test 1 and test 5 is indistinctively during incident shock wave loading, because the blast loading is higher and the initial confining pressure has little effect on crack propagation. Moreover, the interaction of confining pressure, initial shock wave and reflected wave are complicated. Figure 10 c presents the finally shape of cracks after blast loading with different confining pressures. The deformation length of radial cracks is almost the same with different K, and the confining pressure has little effect on them. The macroscopic crack branching is appeared near boundary region at horizontal and vertical directions, and become seriously with confining pressure increase. The dynamic expansion process of cracks is complicated under the combined action of reflected stress wave and static pressure.
Figure 11 a describes the stress equilibrium process on 10 mm under the confining pressure. Stress wave come from boundary and arrive the bore hole at 25 μs, and reach the steady state after 70 μs. The compressive stress is generated on 10 mm and the strength increase with confining pressure. For instance, stress is -17 MPa when confining pressure is 8 MPa, and the strength near borehole is approximately double of pre-stress, which is agreed well with theoretical results for elastic deformation. The results also illustrate that the analysis of confining pressure in the explicit solver is accurately when the calculated time is long enough for stress equilibrium.
(a) Hoop stress-time curve on 10 mm under confining pressure loading; (b) Stress on 10 mm; (c) Stress on 35 mm; (d) Stress on 105 mm; (e) Attenuation of stress with distance increase; (f) Attenuation of strain with distance increase.
Figure 11 b~d presents the hoop strain-time curve on 10 mm, 35 mm and 105 mm after blast loading, respectively. The average stress exceeds 90 MPa on 10 mm and the radial cracks appear in crushed zone by tensile failure. Notably, the stress peak with 6 MPa is much larger than others ( Figure 11 b), this results may be caused by distorted element cause the failure. When stress wave arrive 35 mm at 77 μs ( Figure 11 c), the stress peak sharply drop to 25 MPa. A little fracture is produced because the stress wave is lower than dynamic failure strength, and initial radial cracks further grow when the stress concentration is happened on crack tip. Subsequently incident wave meet reflected wave from free boundary at 85 μs, stress peak reaches up to 50 MPa. With the distance increase, the stress is 10 MPa on 105 mm ( Figure 11 d). The reflected tensile wave is approximately 30 MPa, and becomes the major factor for driving the radial crack growing. It's worth noting that the shape of the overlap wave is different under different ratios, for example, the overlap wave appears at 120 μs, 135 μs, and 142 μs correspond to 0 MPa, 8 MPa, and 4 MPa pressures, respectively.
Figure 11 e clearly shows the decreased tendency of stress around borehole with confining pressure increase. The stress near bore hall is maximal and decreases along horizontal direction. The crushing zone is formed by shear failure and tensile failure under shock wave; therefore the stress peaks on 10 mm with different pressures are basically the same. The strength of shock wave reduces as propagation distance increase, and the confining pressure prevents the radial crack from growing. Finally, reflected tensile wave would drive the cracks further developing.
The strain-distance curve is used to analyze the elastic-plastic deformation in the vibration zone (35~105 mm), as see in the Figure 11 f. The non-linear attenuation of strain is found under different pressures, and the plastic deformation reduces with distance increase. The strain is gradually reduced with stress wave propagate, and initial confining pressure has little effect on deformation zone.
4.2.2 Simulation results under different ratios
The stress distribution under confining pressures with different ratios is shown as Figure 12 , four texts consist of 0-8, 2-8, 4-8, 6-8 biaxial pressures are simulated. When is less than , the stress concentration are generated around borehole in vertical and horizontal directions. Meanwhile the boundary is clearly observed in the 45°, the shear stress from pre-pressure combine with the shock wave and drives the existing crack growing after blast loading. With increase, the tension stress turn into compressive stress in vertical direction, and the shear stress gradually reduce. The average stress of pre-stress field decreases with K increases.
To compare the stress concentration around the borehole in different directions, gauge 1 and gauge 2 are selected which locate on 10 mm in horizontal and vertical direction, respectively. Figure 13 shows the stress-time curves on two gauges with different ratios. When MPa, hoop stress ( ) is 0 MPa and -20 MPa correspond to vertical and horizontal direction ( Figure 13 a). After blast loading, the stress peak of gauge 1 reaches 180 MPa and greater than point 1 (150 MPa), and the initial compressive stress reduces the tensile failure from shock wave. The stress of two gauges exceeds the dynamic tensile strength of rock.
Hoop stress on 10 mm. (a) Test 6 for . (b) Test 7 for . (c) Test 8 for . (d) Test 9 for . (e) Attenuation of initial stress under confining pressure on 10 mm.
With increase, the compressive stress of gauge 2 under confining pressure gradually increases and the strength of gauge 1 reaches -20 MPa ( Figure 13 b). The initial stress reduces tensile failure and enhances the compressive stress after dynamic load. When increase from 0 MPa to 6 MPa, the tensile stress peak of gauge 2 is 180 MPa then drop to 160 MPa after blast loading, while the compressive stress peak is -140 MPa and raises up to -190 MPa ( Figure 13 a, d). As shown in Figure 13 e, the stress peak at 90° is higher as K=0, and compressive stress is -20 MPa in the horizontal direction. With K increased, a linear stress attenuation trend is clearly found and the deformation of rock material is elastically under initial pressure. Both of the horizontal and vertical stress reaches -24 MPa when K rose up to 1.
Figure 14 describes the crack propagation under different ratios after blasting, and 10 μs, 50 μs and 90 μs three moments are extracted to exhibit the stress state by initial shock wave, reflected wave and final state respectively. The symmetrical shock wave propagates along radial direction, the zone immediate vicinity of hole is pulverized, and micro cracks are built up in the crushed zone due to the extreme pressure. Under the combined effect of pre-stress and shock wave, micro cracks would further grow by circumferential tensile stress. After initial wave arrive the foundry at 50 μs, both the number and length of radial cracks in the vertical direction are decrease with K increase. The initial compressive stress in vertical direction prevent crack from processing, and the crack propagation velocity is relatively slowly. Then the reflected wave drive the existing cracks further developing, especially in horizontal and vertical direction, and the cracks run though the specimen finally.
Figure 15 shows the shape of cracks with different K, many nondirective micro cracks appeared near borehole, and the crushed radius is almost the same under different confining pressures. The results declared that the crushing zone is largely caused by shock wave and pre-stress has little influence. When K=0, two vertical cracks appear on top of borehole and developed into boundary, and the horizontal cracks stop on 75 mm. As K increase, vertical crack run though sample and the length of horizontal cracks is gradually increased. Especially the horizontal crack length is 125 mm when K=0.75. Notably, the crack branching is seriously on the tip of crack in horizontal direction, which is caused by the combined effect from reflected wave and initial confining pressure.
5 CONCLUSIONS
To study the dynamic crack propagation of rock subjected to couple static confining pressure and dynamic blast loading. HS and strain measurement techniques were used to observe the crack propagation process and to test the dynamic strain under different biaxial confining pressures. With different confining pressure (0MPa, 2MPa, 4MPa, 6MPa, 8MPa) and different ratios (K) of horizontal-to-vertical pressure (0, 0.25, 0.5, 0.75, 1), nine texts have been carried out in quadrate granite samples.
According to experimental results, for the PETN cylindrical charge with a small diameter, cracks in the crushing zone around the borehole were created by shear deformations and tensile stress from blast loading. The centrosymmetric damage zone is generated around borehole when K=1, the circumference compressive stress is formed by confining pressure, and it reduces the circumference tensile failure by blast loading. The number and size of the broken radius significantly reduce with confining pressure increases. As K decrease from 1 to 0, the tensile stress concentration is obviously around borehole in the vertical direction, and radial cracks grow from the stress concentration zone and develop into boundary under tensile stress wave from blast loading. The direction of crack growth was largely controlled by the hoop tensile stress and biaxial pre-pressure ratio.
JH damage constitutive model in the AUTODYN 2D code is successfully applied, and the stress fields and crack shape are agreed well with experimental results. Crack branching appears near the free boundary and becomes obviously as confining pressure increase, meanwhile the radial cracks extend and run through sample by reflected wave. Compared to the experimental results, the damage zone area is less than latter because JWL equation neglects the gas loading in numerical calculation.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No. 51374038).
-
In the article Dynamic crack propagation of granite subjected to biaxial confining pressure and blast loading, doi number: http://dx.doi.org/10.1590/1679-78254463, published in journal Latin American Journal of Solids and Structures, 15(6):e45, page 1:Where it reads:Chenglong HeaJun Yanga*a State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing, China. E-mail: hechenglong@bit.edu.cn, yangj@bit.edu.cn* Corresponding AuthorIt should read:Chenglong Hea*Jun Yangba College of Mechatronics Engineering, North University of China, Taiyuan 030051, China. E-mail: hechenglong@bit.edu.cnb State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing, China. E-mail: yangj@bit.edu.cn* Corresponding Author
References
- Brown, E. T., and Hoek, E. (1978). Trends in relationships between measured in-situ, stresses and depth. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 15(4): 211-215.
- Banadaki, M. D., and Mohanty, B. (2012). Numerical simulation of stress wave induced fractures in rock. International Journal of Impact Engineering 40: 16-25.
- Christensen, R. J., Swanson, S. R., and Brown, W. S. (1972). Split-Hopkinson-bar tests on rock under confining pressure Experimental Mechanics 12(11): 508-513.
- Cho, S. H., and Kaneko, K. (2004). Influence of the applied pressure waveform on the dynamic fracture processes in rock. International Journal of Rock Mechanics and Mining Sciences 41(5): 771-784.
- Eason, G. (1963). Propagation of waves from spherical and cylindrical cavities. Zeitschrift Für Angewandte Mathematik Und Physik Zamp 14(1): 12-23.
- Holmquist, Timothy J, D. W. Templeton, and K. D. Bishnoi. (2001). Constitutive modeling of aluminum nitride for large strain, high-strain rate, and high-pressure applications. International Journal of Impact Engineering 25(3): 211-231.
- Jaeger J C, Cook N G W, Zimmerman R. (2009). Fundamentals of rock mechanics. John Wiley & Sons.
- Liu, Q., and Katsabanis, P. D. (1993, July). A theoretical approach to the stress waves around a borehole and their effect on rock crushing. In Proceedings of the Fourth International Symposium on Rock Fragmentation by Blasting-Fragblast-4: 9-16.
- Li, X., Zhou, Z., Lok, T. S., Hong, L., and Yin, T. (2008). Innovative testing technique of rock subjected to coupled static and dynamic loads. International Journal of Rock Mechanics and Mining Sciences 45(5): 739-748.
- Ma, G. W., and An, X. M. (2008). Numerical simulation of blasting-induced rock fractures. International Journal of Rock Mechanics and Mining Sciences 45(6): 966-975.
- McHugh, S. (1983). Crack extension caused by internal gas pressure compared with extension caused by tensile stress. International Journal of Fracture 21(3): 163-176.
- Onederra, I. A., Furtney, J. K., Sellers, E., and Iverson, S. (2013). Modelling blast induced damage from a fully coupled explosive charge. International Journal of Rock Mechanics and Mining Sciences 58(58): 73-84.
- Rathore, S. S., and Bhandari, S. (2007). Controlled fracture growth by blasting while protecting damages to remaining rock. Rock Mechanics and Rock Engineering 40(3): 317-326.
- Simha, K. R. Y., Fourney, W. L., and Dick, R. D. (1984, January). Studies On Explosively Driven Cracks Under Confining In-Situ Stresses. In The 25th US Symposium on Rock Mechanics (USRMS). American Rock Mechanics Association.
- Shi X, Tao, Z, and Meng Y. (2015). Calculation and verification for Johnson-Holmquist constitutive model parameters of tight sandstone. Chinese Journal of Rock Mechanics and Engineering 34(S2): 3750-3758.
- Szuladzinski, G. (1993, July). Response of rock medium to explosive borehole pressure. In Proceedings of the fourth international symposium on rock fragmentation by blasting-Fragblast-4, Vienna, Austria (Vol. 23).
- Wu, Y. K., Hao, H., Zhou, Y. X., and Chong, K. (1998). Propagation characteristics of blast-induced shock waves in a jointed rock mass. Soil Dynamics and Earthquake Engineering 17(6): 407-412.
- Wu, B., Xia, K., and Guo, Y. (2016, June). Influence of hydrostatic confining pressure on the dynamic tensile failure of rock material. In 50th US Rock Mechanics/Geomechanics Symposium. American Rock Mechanics Association.
- Zhu, J. B., Liao, Z. Y., and Tang, C. A. (2016). Numerical SHPB tests of rocks under combined static and dynamic loading conditions with application to dynamic behavior of rocks under in situ stresses. Rock mechanics and rock engineering 49(10): 3935-3946.
Publication Dates
-
Publication in this collection
02 July 2018 -
Date of issue
2018
History
-
Received
04 Sept 2017 -
Reviewed
08 Jan 2018 -
Accepted
27 Jan 2018