Abstract
Micro-bridge resonator with dielectric elastomer that is sandwiched between two electrodes is studied here with geometric and material nonlinearity. Geometric nonlinearity is introduced with Von-Karman strain-displacement relationship. For material nonlinearity that is modeled rarely in articles, two hyper-elastic models are used here. Governing equation of motion for Neo-Hookean and Yeoh models are derived through Hamilton's principle. These equations show that Neo-Hookean is not a suitable model for this case because of inadequate terms, but the Yeoh one is. Governing equation in Yeoh model is solved by analytical Lindstedt-Poincare method. Time history of micro-beam is presented in different modes and it is shown good agreement with numerical method. It is seen that increasing of mode number leads to increasing of frequency. In addition, the influence of different parameters on nonlinear normalized frequency is illustrated.
Keywords:
micro-beam resonator; free vibration; hyper-elastic; Neo-Hookean; Yeoh
1 INTRODUCTION
Dielectric elastomers (DEs) are referred to dielectric hyper-elastic materials sandwiched between two compliant electrodes. DEs were discovered in the early 1990s (Perline and Kornbluh, 2011). These materials have attracted a great deal of attention recently. Some of their special properties are such as high strains, low cost, simplicity of structure, robustness due to the use of stable and commercially available polymer materials, high energy output (Sou, 2010; Mockensturm et al., 2006Mockensturm, E. M., Goulbourne, N., (2006). Dynamic response of dielectric elastomers. International Journal of Non-Linear Mechanics 41.3: 388-395.; Feng et al., 2014; Carpi et al., 2011Carpi, F., De Rossi, D., Kornbluh, R., Pelrine, R.E., Sommer-Larsen, P. (2011). Dielectric elastomers as electromechanical transducers: Fundamentals, materials, devices, models and applications of an emerging electroactive polymer technology. Elsevier.; Stoyanov et al., 2009Stoyanov, K., H.G., Gerhard, R., (2009). A Co-Axial Dielectric elastomer actuator. Advances in Science and Technology, 61: 81-84. ), so they can be used in different applications such as artificial muscles sensors, actuators, generators, energy harvesting (Perline et al, 1998Perline, R.E., Kornbluh, R.D., Joseph, J.P., (1998). Electrostriction of polymer dielectric with compliant electrodes as a means of actuation. Sensors and Actuators A: Physical, 64.1: 77-85.; Perline et al, 2002Perline, R.E., Kornbluh, R.D., Stanford, P.Q., Oh, S., Eckerle, J., Full, R.J., Rosenthal, M.A., Meijer, K. (2002). Dielectric elasto-mer artificial muscle actuator: toward biomimetic motion. Proceeding of SPIE Electroactive Polymer Actuators and Devices, 126-137.; Lowe et al, 2005Lowe, C., Zhang, X., Kovacs, G., (2005). Dielectric elastomers in actuator technology. Advanced Engineering Materials, 7.5: 361-367.; Feng and Zhang, 2014; Chakravarty, 2014Chakravarty, U. K., (2014). On the resonance frequencies of a membrane of a dielectric elastomer. Mechanics Research Communications 55.1: 72-76.). Because of a shortage of experimental data, there are few mathematical modeling. Some of the experimental articles were presented by Treloar (1944Treloar, L.R.G., (1944). Stress-strain data for vulcanized rubber under various types of deformation. Transaction of Faraday Society, 40: 59-70.), Jones and Treloar (1975Jones, D.F., Treloar, L.R.G., (1975) "The properties of rubber in pure homogeneous strain." Journal of Physics D: Applied Physics. 8.11: 1285-1304.), Martins et al (2006Martins, P. A. L. S., Natal Jorge, R. M., Ferreira, A.J.M., (2006). A comparative study of several material models for prediction of hyperelastic properties: Application to silicon-rubber and soft tissues. Blackwell Publishing Ltd, Strain, 42: 135-147.), Osterlof et al (2015Osterlof, R., Wentzel, H. and Kari, L., (2015). An efficient method for obtaining the hyperelastic properties of filled elas-tomers in finite strain applications. Polymer testing 41.1: 44-54.). These experimental data were fitted by theoretical models by some researchers such as Ogden (1972Ogden, R.W., (1972). Large deformation isotropic elasticity: on the correlation of theory and experiment for incompress-ible rubberlike solids. Proceeding Of The Royal Society A, London 326: 565-584.), Ogden et al (2004Ogden, R.W., Saccomandi, G., Sgura, I. (2004). Fitting hyperelastic models to experimental data. Computational Mechanics, 34.6: 484-502.) to extract the constants in each hyper-elastic models.
DEs and hyper-elastic materials were used in various configurations such as plates, beams, membranes, cylindrical tubes that we review some of these articles shortly.
Verron et al (1999Verron, E., Khayat, R.E., Derdouri, A., Peseux, B., (1999). Dynamic inflation of hyperelastic spherical membrane. Journal of Rheology. 43.5: 1083-1097.) analyzed dynamic inflation of hyper-elastic spherical membranes of a Mooney- Rivlin material. Also they examined the conditions for oscillatory inflation around the static fixed point and found that for a given material, the frequency of oscillation exhibits a maximum at some pressure level, which tends to increase for materials closer to Neo-Hookean behavior. Pimenta and Campello (2003Pimenta, P.M., Campello, E.M.B., (2003). A fully nonlinear multi-parameter rod model incorporating general cross-section in-plane changes and out-of-plane warping. Latin American Journal of Solids and Structures, 1.1: 119-140.) presented a fully nonlinear geometrically exact multi-parameter rod model that incorporates general in-plane cross-sectional changes as well as general out-of-plane cross-sectional warping. They removed restrictions to a rigid cross-section and to a Saint-Venant -like elastic warping and additionally the corresponding weak form was obtained in a more expedient way, rendering always symmetric for hyper-elastic materials. Mason and Maluleke (2007Mason, D.P., Maluleke, G.H. (2007). Non-linear radial oscillations of a transversely isotropic hyperelastic incompressible tube. Journal of Applied Mathematics and applications. 333.1: 365-380) presented a constitutive equation for a transversely isotropic incompressible hyper-elastic material in a covariant form for arbitrary orientation of the anisotropic director. They derived the equation for a transversely isotropic thin-walled cylindrical tube of generalized Mooney-Rivlin material. For a longitudinal transversely isotropic tube the Ermakov-Pinney equation was obtained which was the same as for an isotropic tube. Radial oscillations in a longitudinal transversely isotropic tube were the same as in an isotropic tube because the anisotropic director is orthogonal to the plane of oscillation. Soares and Goncalves (2014Soares, R. M., Goncalves, P. B., (2014). Large-amplitude nonlinear vibration of a Mooney-Rivlin Rectangular membrane. Journal of Sound and Vibration 333.13: 2920-2935.) presented linear and nonlinear vibration response and stability of pre-stretched hyper-elastic annular membrane under harmonic lateral pressure and finite initial deformation. The membrane material is assumed to be homogeneous, isotropic, and incompressible Mooney-Rivlin material. They obtained Neo-Hookean results as a special case and made a comparison of these two models. Gupta and Harursampath (2015Gupta, R., Harursampath, D., (2015). Dielectric elastomers: Asymptotically-correct three-dimensional displacement field. International Journal of Engineering Science 87.2: 1-12.) presented asymptotically accurate dimensional reduction from three to two dimensions and recovery of 3-D displacement field of non-prestretched dielectric hyper-elastic membranes using the Variational Asymptotic Method (VAM) with moderate strains and very small ratio of the membrane thickness to its shortest wavelength of the deformation along the plate reference surface chosen as the small parameters for asymptotic expansion. They unified software package VAMNLM and applicability of their theory was demonstrated through an actuation test case. Pineda et al (2015Pineda, F, Bottausci, F, Icard, B, Malaquin, L, Fouillet, Y. (2015). Using electrofluidic devices as hyper-elastic strain sensors: Experimental and theoretical analysis. Microelectronic Engineering, 144: 27-31.) used from hyper-elastic polymer for the development of soft sensors with large deformation capabilities. They presented the characterization of an electro-fluidic strain sensor. The so-called sensor resist large deformation higher than 200% cycled 150 times. They investigated several device designs to enhance the electrical response of the sensor as a function of its elongation. They discussed the result of cyclic deformation and strain on the sensor. In addition, numerical simulation was done based on Mooney-Rivlin model for hyper-elastic materials. Ritto and Nunes (2015Ritto, T.G, Nunes, L.C.S, (2015). Bayesian model selection of hyperelastic models for simple and pure shear at large deformations. Computer and Structures, 156: 101-109.) identified parameters of some constitutive models for pure and simple shear of an incompressible isotropic hyper-elastic material under large deformation. The constitutive models considered in their analysis are Mooney-Rivlin, Yeoh, Gent, Lopez-Pamies and Ogden with one and two terms. They showed that all models and experimental results are in good agreement but Mooney-Rivlin, Gent and Yeoh models were not able to well describe the available experimental data from simple shear. Rodriguez-Martinez et al (2015Rodriguez-Martinez, J.A, Fernandez-Saez, J, Zaera, R. (2015). The role of constitutive relation in the stability of hyper-elastic membranes subjected to dynamic inflation. International Journal of Engineering Science, 93: 31-45.) investigated mechanical response of hyper-elastic spherical membranes subjected to dynamic inflation. They developed a comprehensive analysis on the role that the constitutive behavior of the material has on the mechanical stability of the membrane. Six different strain energy functions three of the Mooney-Rivlin class and three of the Ogden class have been considered. They showed that essential features of the dynamic response of the spherical shell are closely related to the strain-energy function selected to describe the constitutive behavior of the membrane.
In resonator application there is an important advantage of using dielectric elastomer as material compared to conventional silicon-based one that is tunning actively after fabrication (Feng et al., 2011Feng, C., Jiang, L., Lau, W.M., (2011). Dynamic characteristics of a dielectric elastomer-based microbeam resonator with small vibration amplitude. Journal of Micromechanics and Microengineering. 21.9: 16-23.; Zhang et al., 2005Zhang, G., Gaspar, J., Chu, V., Conde, J.P., (2005). Electrostatically actuated polymer microresonators. Applied Physics Letters. 87.10: 1-3.). In the special case of resonator, also there are few articles that we review some of them.
Zhang et al. (2005Zhang, G., Gaspar, J., Chu, V., Conde, J.P., (2005). Electrostatically actuated polymer microresonators. Applied Physics Letters. 87.10: 1-3.) fabricated a polymeric micro-bridge resonator. They showed that Quality factors are of the order of 100 in vacuum, decreasing with the measurement pressure for values above 1 Torr due to air damping. Li et al (2012Li, T, Qu, S, Yang, W. (2012). Electromechanical and dynamic analyses of tunable dielectric elastomer resonator. International Journal of Solids and Structures. 49: 3754-3761.) focused on dielectric elastomer resonator whose dielectric membrane is subjected to combine loads of tensile forces and voltages. They analyzed stability and natural frequency of the resonator with small-amplitude vibration around the equilibrium state. In case of periodic voltage, the device resonates at multiple frequencies of excitation. Feng et al. (2011Feng, C., Jiang, L., Lau, W.M., (2011). Dynamic characteristics of a dielectric elastomer-based microbeam resonator with small vibration amplitude. Journal of Micromechanics and Microengineering. 21.9: 16-23.) analyzed the dynamic properties of a dielectric elastomer (DE)-based micro-beam resonator with ambient pressure effect by using the squeeze-film theory. They approximated analytical solutions for the quality factor and the resonant frequencies and the results indicated that the ambient pressure has significant effects on the Q-factor and the resonant frequency shift ratio. Also Feng et al. (2014) developed a non-linear vibration equation of a dielectric elastomer (DE)-based micro-beam resonator with the consideration of large amplitude, gas damping and excitation. Their analysis exhibits that active tuning of the resonant frequency of the resonator can be achieved through changing an applied electrical voltage. Also it was observed that increasing amplitude will increase the natural frequency while it will decrease the quality factor of the resonator.
The resonator that we present here will be modeled based on Euler-Bernoulli beam theory with considering geometric and material nonlinearity. Two hyper-elastic models will incorporate material nonlinearity. We show here that models such as Neo-Hookean with insufficient material constants and low order of strain invariants cannot describe the governing equation properly but the other ones such as Yeoh model are so good for dielectric elastomer-based micro-beam resonators.
2 FORMULATION OF THE PROBLEM
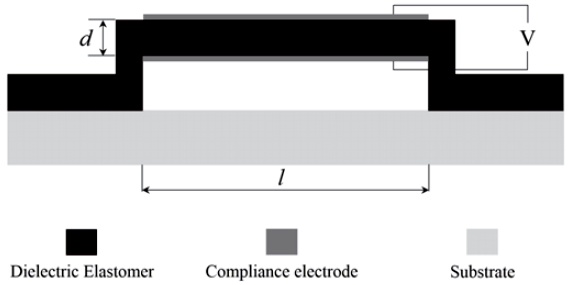
As shown in Figure (1), the so-called elastomer-based micro-beam resonator has uniform thickness d, length L, width b and density ρ. Elastomer is sandwiched between two flexible electrodes and voltage is applied to each side.
Hyper-elastic models are classified into three types of formulation, depending on the approach followed by the authors to develop the strain energy function (Marckmann and Verron, 2006Markmann, G., Verron, E., (2006). Comparision of hyperelastic models for rubber-like materials, Rubber Chemistry and Technology. 79.5: 835-858.):
-
Phenomenological models
-
Fitting material functions using experimental data
-
Physically-based models
We use two hyper-elastic models for deriving the governing equation, Neo-Hookean model from the third type with one constant and Yeoh model from the first type with three constants. In both cases, the geometric nonlinearity of fixed-fixed micro-beam is modelled with Von- Karman formula but material nonlinearity is introduced with related hyper-elastic models. It should be noted that we derive the free vibration equations.
2.1 Neo-Hookean Model
This model that have only one constant is developed from physical motivation and is based on both physics of polymer chains network and statistical methods (Marckmann and Verron, 2006Markmann, G., Verron, E., (2006). Comparision of hyperelastic models for rubber-like materials, Rubber Chemistry and Technology. 79.5: 835-858.):
For deriving the governing equation of motion by Hamilton's principle, we use latter strain energy function to achieve potential energy. Kinetic energy and potential energy are as follows:
Kinetic energy:
Potential energy:
Substituting Eqs. (2) and (3) in Hamilton's principle, we have the following final governing equation of motion:
with boundary conditions w(0) = w(L) =0,  (0) =
(0) =  (L) = 0
(L) = 0
As it is seen, the achieved governing equation using Neo-Hookean hyper-elastic model is the same as a string equation. It is because this model does not have adequate terms for modeling the beam governing equation in this case, so we will not use this model in vibrational behavior study.
2.2 Yeoh Model
Yeoh hyper-elastic model that is a phenomenological type has three constants and is dependent on the first, second and third order of the first strain invariant. Strain energy function of the Yeoh model is as follows:
in which c 1,c 2,c 3 are material constants and I 1 is the first strain invariant:
λi (i = 1, 2, 3) are stretch ratios and square root of the right Cauchy-Green strain tensor (C).
Using Eq. (2) and substituting Eq. (5) into Eq. (3), then applying Hamilton's principle we have following governing equation of motion:
with boundary conditions w(0) = w(L) =0,  (0) =
(0) =  (L) = 0.
(L) = 0.
Latter equation is a beam equation that its geometrical nonlinearity is based on Von-Karman strain-displacement relationship and material nonlinearity is based on Yeoh hyper-elastic model. This equation can be normalized with introducing proper non-dimensional parameters:
So Eq. (7) will be:
and the corresponding non-dimensional boundary conditions are:
In the next part, we solve this strong nonlinear equation by an analytical method and validate it by a numerical method for checking the accuracy of its behavior in different modes. Also, the effect of maximum initial amplitude and aspect ratio on nonlinear frequency will be discussed.
3 SOLUTION METHODOLOGY
Lindstedt-Poincare that is one of the perturbation methods is applied to solve nonlinear equation achieved by Yeoh hyper-elastic model. In accordance with this technique, small perturbation parameter and time transformations are introduced by η = (*t*, respectively. Therefore, Eq. (9) will be: and τ=
and τ=
It should be mentioned that asterisks are removed in this equation for simplicity. Non-dimensional transverse displacement and frequency can be expanded into series forms as:
Substituting Eqs. (12) and (13) into Eq. (11) and arranging them based on different orders of small perturbation, one has the final equations as:
Eqs. (14), (15) and (16) can be reduced to ODE by Galerkin method. First, we express transverse displacements in each equation as the products of two separated functions:
in which Xim(x) is the trial function of the clamped-clamped micro-beam (Peng et al., 2014Peng, J.S., Yang, L., Luo, G.B., Yang, J., (2014). Nonlinear electro-dynamic analysis of micro-actuators: Effect of material nonlinearity. Applied Mathematical Modeling. 38.11: 2781-2790.) and m is the mode number.
Substituting Eq. (17) into Eqs. (14), (15) and (16) and then applying Galerkin method leads to final solutions for these perturbation equations as follows. It should be mentioned that the initial conditions are T(0) = Ã
max,
Ṫ(0) = 0 that Ã
max is the maximum normalized amplitude of deflection so that Ã
max =  .
.
in which g
1 =  (2mπ)8.
(2mπ)8. (2mπ)4 +
(2mπ)4 +  (2mπ)2 and g2 =
(2mπ)2 and g2 =  (2mπ)6 +
(2mπ)6 +  (2mπ)4 -
(2mπ)4 -
Total response of the micro-beam resonator is the sum of all of the above solutions. Therefore, after applying the transformation w* = εη we have:
Removing secular terms in solution procedure leads to nonlinear frequency as:
4 RESULTS AND DISCUSSION
In this section fourth order Runge-Kouta numerical method is applied in order to verify the validity of Lindstedt-Poincare approach. In Runge-Kouta methods, the order of accuracy is increased by using intermediate points in each step interval and the fourth order one is accurate to the fourth-order term of the Taylor expansion. Two versions of the fourth order Runge-Kouta methods are most popularly used, one is based on the Simpson's 1/3 rule and the other version is based on the Simpson's 3/8 rule (Nakamura, 1999) that we used the first one. Deflection of the resonator in versus of normalized length is presented for different modes and times. Also influence of different parameters such as initial maximum amplitude and aspect ratio on non-dimesional nonlinear frequency is studied. Geometric and material (Marckmann and Verron, 2006Markmann, G., Verron, E., (2006). Comparision of hyperelastic models for rubber-like materials, Rubber Chemistry and Technology. 79.5: 835-858.) properties are presented as:
l = 30 (m, d = 0.65 (m, b = 10(m, c 1 = 0.24162Mpa,
c2 = 0.19977Mpa, c 3 = - 0.00541Mpa
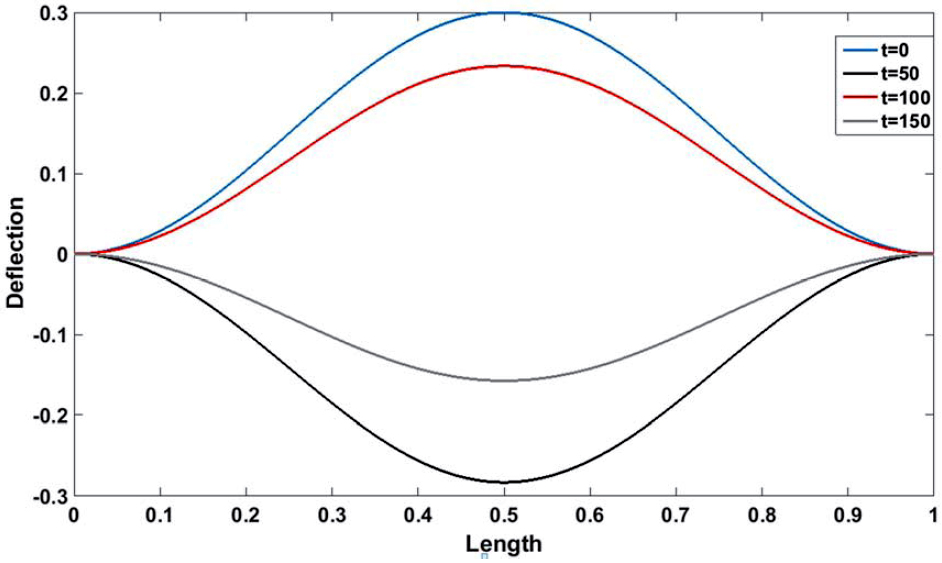
Mode shapes for the three first modes in steady state is shown in Figure (2). Non-dimensional amplitude of initial condition is 0.3 here. It is seen that the ends of resonator are immovable due to related boundary conditions. In addition, Figure (3) shows deflection of first mode in different times. Four assigned normalized times are selected to show the mode shape in different times. As it is seen in this figure, mode shape in the beginning (t=0) reaches maximum amplitude and recede through time.
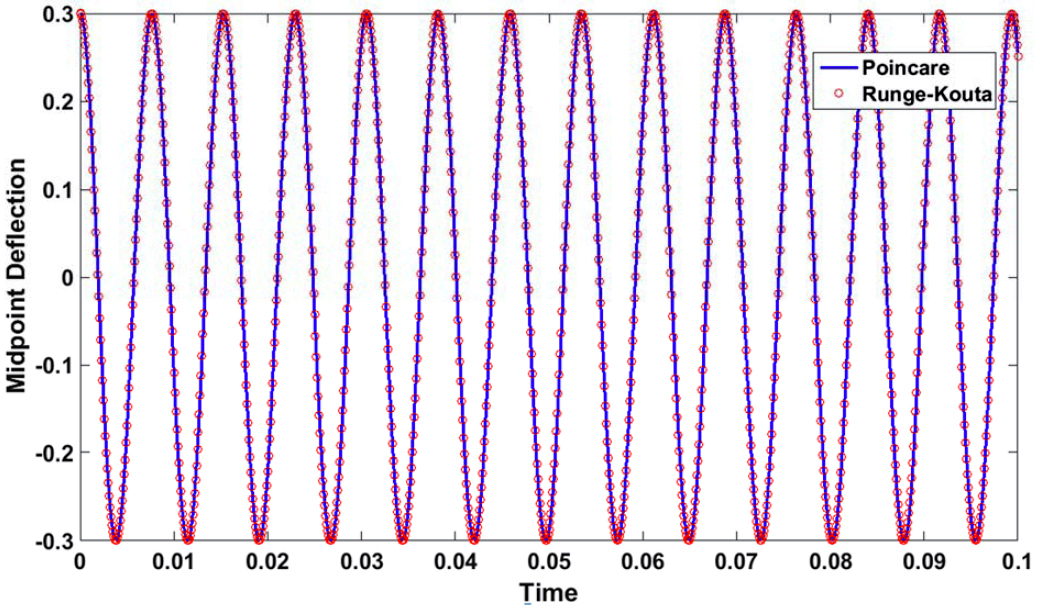
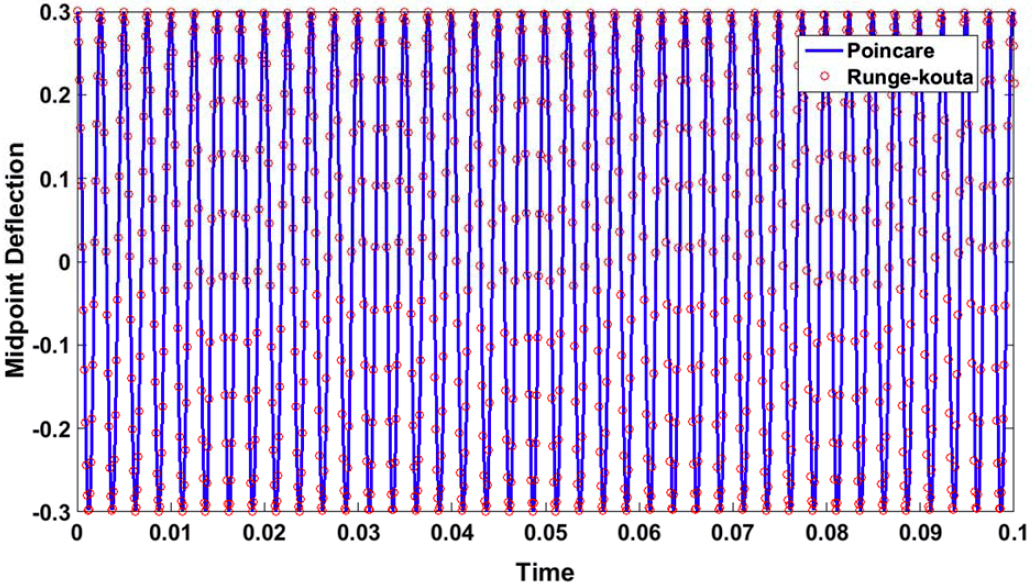
The response time history is depicted for the first mode in Figure (4). As it is seen, the analytical approach is in very good agreement with numerical one. Figures (5) and (6) show an excellent agreement for the third and fifth modes, so it is concluded that third term in series expansion is sufficient to achieve a highly accurate solution of the problem. In addition, increasing mode number of the motion leads to increasing of frequency. To show the accuracy of analytical and numerical method and their closeness we used from Integral Absolute Error (IAE). This technique integrates the error (difference between analytical and numerical solutions) over the time and then we express it by percent. The difference between two methods in Figures (4), (5) and (6) is written in percent in Table (1). It is seen that the difference between Lindstedt-Poincare and Runge-Kouta method is very small in all three modes and validate the excellent agreements in figures. However, the error get a little larger with increasing of the mode number but as it is obvious the quantity of the error percentage is acceptable yet.
In Figure (7) dependency of nonlinear frequency on initial amplitude is depicted. As it is seen, increasing of initial amplitude leads to increasing of nonlinear frequency. Rate of the frequency increasing in higher modes is more than the lower modes so that for the third mode is significant in comparison with the first mode. Dependency of frequency to mode numbers in Figure (7) is in accordance with Figures (4) through (6), because investigating Figures (4), (5) and (6) continuously shows increasing of frequency in effect of increasing mode numbers.
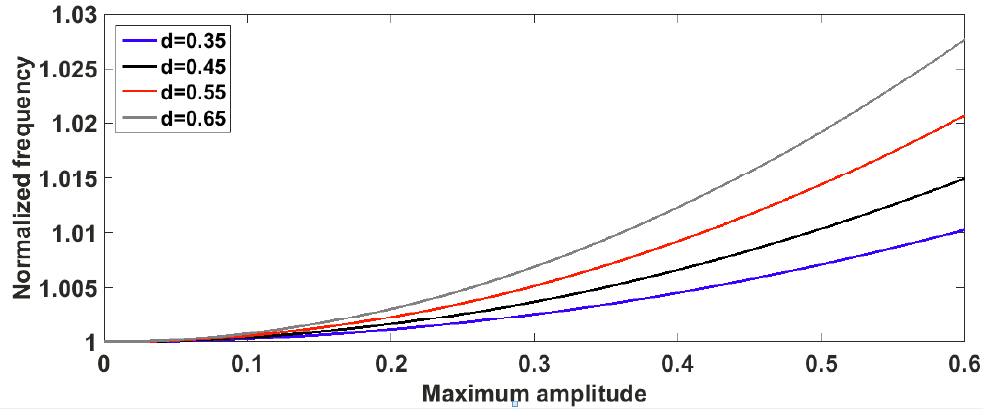
In Figures (8) and (9) normalized frequency curve is shown for the first and third modes under some assigned values of thickness. As it is seen for the first and third mode and all assigned thicknesses, the bigger the maximum amplitude, the larger the normalized frequency. In accordance with Figures (8) and (9), dependency of normalized frequency on maximum amplitude is more for the larger thicknesses in both first and third modes. In addition, comparing these two figures shows that increasing of frequency with maximum amplitude for different thicknesses will be significant for the higher modes.
Influence of aspect ratio in the range of 20-180 for Euler-Bernoulli theory on normalized frequency is illustrated in Figure (10) for three modes. It is shown that in dielectric elastomer-based micro-beam resonator, nonlinear frequency decreases as the beam get thinner. As it is seen in this case, the higher the mode number, the more the influence of aspect ratio.
5 CONCLUSIONS
Dielectric elastomer that is sandwiched between two electrodes is applied here as resonator. Geometric and material nonlinearity are introduced with Von-Karman strain-displacement relationship and hyper- elastic models, respectively. Neo-Hookean model refused because of insufficient parameters. Analytical Lindstedt-Poincare method was used to solve the strong nonlinear equation of Yeoh model and verified by Runge-Kouta numerical method. We plotted mode shapes of micro-beam for steady state and different times. These mode shapes were in accordance with clamped-clamped boundary conditions. Time history of micro-beam was presented in different modes and it is shown good agreement with numerical method. Integral Absolute Error investigated accuracy of analytical validation too. We presented Influence of different parameters such as initial maximum amplitude and aspect ratio on nonlinear normalized frequency. It is shown that mode number has a significant effect on normalized frequency so that the higher the mode number, the more the influence of aspect ratio and initial maximum amplitude. In addition, the normalized frequency increased with maximum amplitude and dependency of normalized frequency on maximum amplitude was more for the larger thicknesses in all modes.
References
- Carpi, F., De Rossi, D., Kornbluh, R., Pelrine, R.E., Sommer-Larsen, P. (2011). Dielectric elastomers as electromechanical transducers: Fundamentals, materials, devices, models and applications of an emerging electroactive polymer technology. Elsevier.
- Chakravarty, U. K., (2014). On the resonance frequencies of a membrane of a dielectric elastomer. Mechanics Research Communications 55.1: 72-76.
- Feng, C., Jiang, L., Lau, W.M., (2011). Dynamic characteristics of a dielectric elastomer-based microbeam resonator with small vibration amplitude. Journal of Micromechanics and Microengineering. 21.9: 16-23.
- Feng, C., Yu, L., Zhang, W., (2006) Dynamic analysis of a dielectric elastomer-based microbeam resonator with large vibration amplitude. International Journal of Nonlinear Mechanics. 41.3: 388-395.
- Feng, C., Yuc, L., Zhang, W., (2006). Dynamic analysis of a dielectricelastomer-based microbeam resonator with large vibration amplitude. International Journal of Non-Linear Mechanics, 41.3: 388-395.
- Gupta, R., Harursampath, D., (2015). Dielectric elastomers: Asymptotically-correct three-dimensional displacement field. International Journal of Engineering Science 87.2: 1-12.
- Jones, D.F., Treloar, L.R.G., (1975) "The properties of rubber in pure homogeneous strain." Journal of Physics D: Applied Physics. 8.11: 1285-1304.
- Li, T, Qu, S, Yang, W. (2012). Electromechanical and dynamic analyses of tunable dielectric elastomer resonator. International Journal of Solids and Structures. 49: 3754-3761.
- Lowe, C., Zhang, X., Kovacs, G., (2005). Dielectric elastomers in actuator technology. Advanced Engineering Materials, 7.5: 361-367.
- Markmann, G., Verron, E., (2006). Comparision of hyperelastic models for rubber-like materials, Rubber Chemistry and Technology. 79.5: 835-858.
- Martins, P. A. L. S., Natal Jorge, R. M., Ferreira, A.J.M., (2006). A comparative study of several material models for prediction of hyperelastic properties: Application to silicon-rubber and soft tissues. Blackwell Publishing Ltd, Strain, 42: 135-147.
- Mason, D.P., Maluleke, G.H. (2007). Non-linear radial oscillations of a transversely isotropic hyperelastic incompressible tube. Journal of Applied Mathematics and applications. 333.1: 365-380
- Mockensturm, E. M., Goulbourne, N., (2006). Dynamic response of dielectric elastomers. International Journal of Non-Linear Mechanics 41.3: 388-395.
- Nakamura, S, (1991). Applied Numerical Methods With Software. Prentice-Hall International (London)
- Ogden, R.W., (1972). Large deformation isotropic elasticity: on the correlation of theory and experiment for incompress-ible rubberlike solids. Proceeding Of The Royal Society A, London 326: 565-584.
- Ogden, R.W., Saccomandi, G., Sgura, I. (2004). Fitting hyperelastic models to experimental data. Computational Mechanics, 34.6: 484-502.
- Osterlof, R., Wentzel, H. and Kari, L., (2015). An efficient method for obtaining the hyperelastic properties of filled elas-tomers in finite strain applications. Polymer testing 41.1: 44-54.
- Peng, J.S., Yang, L., Luo, G.B., Yang, J., (2014). Nonlinear electro-dynamic analysis of micro-actuators: Effect of material nonlinearity. Applied Mathematical Modeling. 38.11: 2781-2790.
- Perline, R.E., Kornbluh, R.D., Joseph, J.P., (1998). Electrostriction of polymer dielectric with compliant electrodes as a means of actuation. Sensors and Actuators A: Physical, 64.1: 77-85.
- Perline, R.E., Kornbluh, R.D., Stanford, P.Q., Oh, S., Eckerle, J., Full, R.J., Rosenthal, M.A., Meijer, K. (2002). Dielectric elasto-mer artificial muscle actuator: toward biomimetic motion. Proceeding of SPIE Electroactive Polymer Actuators and Devices, 126-137.
- Pimenta, P.M., Campello, E.M.B., (2003). A fully nonlinear multi-parameter rod model incorporating general cross-section in-plane changes and out-of-plane warping. Latin American Journal of Solids and Structures, 1.1: 119-140.
- Pineda, F, Bottausci, F, Icard, B, Malaquin, L, Fouillet, Y. (2015). Using electrofluidic devices as hyper-elastic strain sensors: Experimental and theoretical analysis. Microelectronic Engineering, 144: 27-31.
- Ritto, T.G, Nunes, L.C.S, (2015). Bayesian model selection of hyperelastic models for simple and pure shear at large deformations. Computer and Structures, 156: 101-109.
- Rodriguez-Martinez, J.A, Fernandez-Saez, J, Zaera, R. (2015). The role of constitutive relation in the stability of hyper-elastic membranes subjected to dynamic inflation. International Journal of Engineering Science, 93: 31-45.
- Soares, R. M., Goncalves, P. B., (2014). Large-amplitude nonlinear vibration of a Mooney-Rivlin Rectangular membrane. Journal of Sound and Vibration 333.13: 2920-2935.
- Stoyanov, K., H.G., Gerhard, R., (2009). A Co-Axial Dielectric elastomer actuator. Advances in Science and Technology, 61: 81-84.
- Treloar, L.R.G., (1944). Stress-strain data for vulcanized rubber under various types of deformation. Transaction of Faraday Society, 40: 59-70.
- Verron, E., Khayat, R.E., Derdouri, A., Peseux, B., (1999). Dynamic inflation of hyperelastic spherical membrane. Journal of Rheology. 43.5: 1083-1097.
- Zhang, G., Gaspar, J., Chu, V., Conde, J.P., (2005). Electrostatically actuated polymer microresonators. Applied Physics Letters. 87.10: 1-3.
- Zhigang, S., (2010). Theory of dielectric elastomers. Acta Mechanica Solida Sinica, 23.6: 549-578.
Publication Dates
-
Publication in this collection
Oct 2016
History
-
Received
01 Sept 2015 -
Reviewed
02 Feb 2016 -
Accepted
14 Apr 2016