Abstract
In the present study, dynamic pull-in instability of electrostatically-actuated micro-beams is investigated through proposing the nonlinear frequency amplitude relationship. An approximate analytical expression of the fundamental natural frequency is presented by modern asymptotic approach namely Iteration Perturbation Method (IPM). Influences of vibrational amplitude as well as different parameters on dynamic pull-in voltage are investigated. It is demonstrated that two terms in series expansions is sufficient to produce an acceptable solution of the mentioned microstructure. The simulations from numerical methods verify the validity of the analytical procedure.
Iteration Perturbation Method; Frequency – amplitude relationship; Dynamic pull-in voltage; Micro-beam Vibration; Pull-in instability
Application of Iteration Perturbation Method in studying dynamic pull-in instability of micro-beams
Hamid M. SedighiI, * * Author e-mail: h.msedighi@scu.ac.ir, hmsedighi@gmail.com ; Farhang DaneshmandII, III, IV; Amin YaghootianI
IDepartment of Mechanical Engineering, Shahid Chamran University, Ahvaz, Iran
IIDepartment of Mechanical Engineering, McGill. University, 817 Sherbrooke Street West, Montreal, Quebec, Canada H3A 2K6
IIIDepartment of Bioresource Engineering, McGill. University, 21111 Lakeshore Road, Sainte-Anne-de-Bellevue, Quebec, Canada H9X 3V9
IVSchool of Mechanical Engineering, Shiraz University, Shiraz, Iran
ABSTRACT
In the present study, dynamic pull-in instability of electrostatically-actuated micro-beams is investigated through proposing the nonlinear frequency amplitude relationship. An approximate analytical expression of the fundamental natural frequency is presented by modern asymptotic approach namely Iteration Perturbation Method (IPM). Influences of vibrational amplitude as well as different parameters on dynamic pull-in voltage are investigated. It is demonstrated that two terms in series expansions is sufficient to produce an acceptable solution of the mentioned microstructure. The simulations from numerical methods verify the validity of the analytical procedure.
Keywords: Iteration Perturbation Method, Frequency amplitude relationship, Dynamic pull-in voltage, Micro-beam Vibration, Pull-in instability.
1 INTRODUCTION
The application of the micro-scale devices is continuously growing and the microelectromechanical systems (MEMS) have become the interesting area of research in recent years. The application of actuated MEMS includes accelerometers, micro-pumps, micro-resonators and manipulators (Grandinetti et al., 2012). In recent years, several researches have been developed on the nonlinear behavior of MEMS/NEMS devices (Sedighi, 2014; Rahaeifard et al., 2013; Tadi Beni et al., 2012; Abdi et al., 2011; Sedighi et al., 2014; Tadi Beni and Abadyan, 2013; Soroush et al., 2010; Sedighi and Shirazi, 2013; Ansari et al., 2012). In the dynamic analysis of micro-systems, electrostatic forces cause the relationship between the input excitation and the output response to be nonlinear which is performed by applying voltage between the micro-beam and the substrate. The micro-beam deflection increases by increasing the actuation voltage. At a specific voltage namely pull-in voltage instability happens and the micro-structure drops to the substrate.
Rahaeifard et al. (2013) investigated the dynamic behavior of micro-cantilevers under suddenly applied DC voltage based on the modified couple stress theory using numerical and analytical approaches. Stability of a functionally graded (FG) micro-beam, based on modified couple stress theory (MCST), subjected to nonlinear electrostatic pressure and thermal changes have been studied by Zamanzadeh et al. (2013). Sedighi and Shirazi (2013) presented a new asymptotic procedure to predict the nonlinear vibrational behavior of micro-beams pre-deformed by an electric field. The impact of vibrational amplitude on the dynamic pull-in instability and fundamental frequency of actuated microbeams has been investigated by Sedighi (2014) via introducing the second order frequency - amplitude relationship. The nonlinear governing equation of microbeam predeformed by an electric force including the fringing field effect, based on the strain gradient elasticity theory was considered and the predicted results of the strain gradient elasticity theory was compared with the outcomes arise from the classical and modified couple stress theory. Sedighi et al., (2014) investigated the dynamic pull-in instability of vibrating micro-beams undergoing large deflection under electrosatically actuation based on the modified couple stress theory. The modeling and analysis of an optically-actuated, bistable MEMS switches have been studied by Kumar and Rhoads (2012). They investigated the influence of various system and excitation parameters, including the applied axial load and optical actuation profile, on the system's transient response. Sabater and Rhoads (2012) analyzed the control mechanisms of self-excited oscillators, founded upon electromagnetically-actuated microbeams. Their study specifically focused on the characterization of nonlinear behaviors arising in isolated mutually-coupled oscillators. Ramezani (2012) used Hamilton's principle to derive the nonlinear governing equations of motion and boundary conditions of micro scale Timoshenko beam model based on a general form of strain gradient elasticity theory. He demonstrated that both strain gradient and geometric non-linearity effects increase the beam natural frequency. Abdi et al. (2011) employed the modified couple stress theory to model the size effect on the pull-in instability of electrostatic nanocantilevers in the presence of dispersion (Casimir/van der Waals) forces. Ansari et al. (2012) investigated the nonlinear free vibration behavior of microbeams made of functionally graded materials (FGMs) based on the strain gradient elasticity theory and von Karman geometric nonlinearity. Rhoads et al. (2013) presented the highly non-linear dynamic behavior of a new class of parametrically excited, electromagnetically actuated microcantilevers. They studied the frequency response behavior and bifurcation analysis of the micro scale system using perturbation method. Chouvion et al. (2012) reviewed several approaches for calculating semi-infinite support loss in micro-electro-mechanical system resonators undergoing in-plane vibration. Rajabi and Ramezani (2012) presented a micro scale nonlinear beam model based on strain gradient elasticity. They indicated that in a micro-beam having a thickness to length parameter ratio close to unity, the strain gradient effect on increasing the natural frequency is predominant and by increasing the beam thickness, this effect decreases and geometric nonlinearity plays the main role on increasing the natural frequency. The effects of the open crack on the static and dynamic pull-in voltages of an electrostatically actuated fixed-fixed and cantilever micro-beam has investigated by Motallebi et al. (2012). Thermoelastic damping (TED) in a micro-beam resonator with a pair of piezoelectric layers bonded on its upper and lower surfaces have been studied by Vahdat et al. (2012). They demonstrated that thickness of the piezoelectric layers and application of DC voltage can affect the TED ratio and the critical thickness value of the resonator. Daneshmand and Amabili (2012) described a mechanics model of an anisotropic microtubule to predict the coupled frequencies of microtubule-cytoplasm system including the effect of the surrounding cytoplasm. They developed the displacement representation of the first-order shear deformation shell theory for orthotropic materials for modeling the microtubule.
Recently, new asymptotic methods have been increasingly developed in order to solve nonlinear differential equations (Shi-Jun Liao, 2004; Sedighi and Shirazi, 2012; Sedighi et al., 2012a, 2012b). There have been several approaches employed to solve the governing nonlinear differential equations to study the nonlinear vibrations such as Energy Balance Method (Ghadimi et al., 2012), Variational Iteration Method (He, 2007; Sedighi et al., 2012), and Hamiltonian Approach (HA) (He, 2010; Sedighi and Shirazi, 2013), Amplitude - frequency formulation (He, 2008), Max-Min approach (He, 2008), Homotopy Analysis Method (HAM) (Liao, 2003 and 2004), Parameter Expansion Method (Wang and He, 2008; He, 2002), Homotopy Perturbation Method (HPM) (Yazdi, 2013), Iteration Perturbation Method (He, 2001; Sedighi et al., 2013). The Iteration Perturbation Method (IPM), which is developed by Ji-Huan He (2001), provides an effective and efficient tool for solving an extensive range of nonlinear equations.
The present article attempts to indicate the impact of vibrational amplitude on dynamic pull-in instability of actuated micro-beams by introducing the nonlinear frequency - amplitude relationship. In this direction, analytical expressions for vibrational responses of cantilever and clamped-clamped micro actuated beams are presented. The results presented in this paper exhibit that the analytical method is very effective and convenient for nonlinear vibration for which the highly nonlinear governing equations exist. The proposed analytical method demonstrates that two terms in series expansions is sufficient to obtain a highly accurate solution of micro-beam vibration. Finally, the influences of amplitude and significant parameters on the pull-in instability behavior are studied.
2 EQUATION OF MOTION
Consider an actuated micro-beam suspended above a rigid substrate and under electro-statically actuated voltage as shown in Fig. 1. The cantilever and clamped-clamped micro beams have length  , thickness
, thickness  , width
, width  , density
, density  , moment of inertia
, moment of inertia  and a modulus of elasticity
and a modulus of elasticity  . The air initial gap is
. The air initial gap is  and an attractive electrostatic force which originates from voltage
and an attractive electrostatic force which originates from voltage  causes the micro-beam to deform.
causes the micro-beam to deform.
Assume that the beam considered here, be the Euler - Bernoulli beam. By incorporating von Karman nonlinearity, large deflections, large rotations and small strains of the narrow micro-beam are taken into account. The governing equation of motion of micro actuated beam is expressed as follows (Moghimi Zand and Ahmadian, 2009):
Where  represents the axial force. By introducing the following non-dimensional variables
represents the axial force. By introducing the following non-dimensional variables
the non-dimensional nonlinear governing equation of motion can be written as follows:
Assuming  , where
, where  is the first eigenmode of the micro-beam vibration and can be expressed as:
is the first eigenmode of the micro-beam vibration and can be expressed as:
where and
and  are the roots of characteristic equations for the first two eigenmodes of clamped-clamped and cantilever micro beams. It should be pointed out that for cantilever micro-beam vibrations the stretching term as well as the axial load is equal to zero. Applying the Bubnov-Galerkin procedure yields the following non-dimensional nonlinear governing equation of motion:
are the roots of characteristic equations for the first two eigenmodes of clamped-clamped and cantilever micro beams. It should be pointed out that for cantilever micro-beam vibrations the stretching term as well as the axial load is equal to zero. Applying the Bubnov-Galerkin procedure yields the following non-dimensional nonlinear governing equation of motion:
where the parameters  to
to  for clamped-clamped as well as cantilever micro-beam have been described in the Appendix A
Appendix A
.
for clamped-clamped as well as cantilever micro-beam have been described in the Appendix A
Appendix A
.
3 APPROXIMATION BY THE ITERATION PERTURBATION METHOD
The Iteration Perturbation Method proposed by He (2001) is constructed based on perturbation technique coupling with iteration method. This method is valid not only for weakly nonlinear problems but also for strongly nonlinear differential equations. Consider the nonlinear equation (5), in order to obtain an iteration perturbation solution of the governing equation, an artificial parameter  should be introduced as:
should be introduced as:
Equation (6) can be approximated by:
where  is the initial approximate solution. The initial solution can be assumed in the form
is the initial approximate solution. The initial solution can be assumed in the form , where
, where  is the unknown angular frequency and should be determined. Substituting
is the unknown angular frequency and should be determined. Substituting  into equation (6) yields
into equation (6) yields
Equation (8) can be rewritten in the following form
assuming that
Substituting equations (10) and (11) into (9), and equating the coefficients of the same power of  , the following differential equation for
, the following differential equation for  can be obtained
can be obtained
If the term  exists in the right hand side of equation (12), the secular term
exists in the right hand side of equation (12), the secular term  will appear in the final solution. Therefore, the coefficient of this term in (12) should be equal to zero, so we have
will appear in the final solution. Therefore, the coefficient of this term in (12) should be equal to zero, so we have
similarly, the following differential equation for  can be obtained
can be obtained
No secular term in the second equation for  yields:
yields:
thereby, solving equations (11) and (15) with  for fundamental frequency gives the following frequency amplitude relationship for actuated micro-beam vibrations as:
for fundamental frequency gives the following frequency amplitude relationship for actuated micro-beam vibrations as:
Solving Eq. (12) for  gives the following second order approximation for
gives the following second order approximation for  as:
as:
4 RESULTS AND DISCUSSION
To indicate the validity of proposed solution by IPM, the analytical solutions at the side of corresponding numerical results have been plotted. As can be seen in Fig. 2, the second order approximation of  using analytical methods for both clamped-clamped and cantilever micro-beam show good agreement with numerical results from fourth-order Runge-Kutta method. The numerical values of system parameters used for asymptotic analysis are described in Appendix B
Appendix B
.
using analytical methods for both clamped-clamped and cantilever micro-beam show good agreement with numerical results from fourth-order Runge-Kutta method. The numerical values of system parameters used for asymptotic analysis are described in Appendix B
Appendix B
.
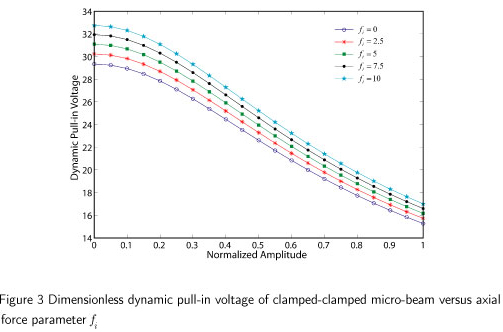
Analytical simulation of the dimensionless dynamic pull-in voltage of clamped-clamped and cantilever micro-beam versus non-dimensional amplitude are depicted in Figs. 3 to 5. The effect of dimensionless axial force parameter  on the dynamic pull-in voltage as a function of initial amplitude is illustrated in Fig. 3. It is obvious that the dynamic pull-in voltage increases by increasing the axial force parameter. It appears from Fig. 3 that the dynamic pull-in voltage decreases when the normalized amplitude increases. Fig. 3 also shows that the effect of normalized amplitude on the dynamic pull-in voltage is more considerable than its effect on the axial force parameter
on the dynamic pull-in voltage as a function of initial amplitude is illustrated in Fig. 3. It is obvious that the dynamic pull-in voltage increases by increasing the axial force parameter. It appears from Fig. 3 that the dynamic pull-in voltage decreases when the normalized amplitude increases. Fig. 3 also shows that the effect of normalized amplitude on the dynamic pull-in voltage is more considerable than its effect on the axial force parameter . Fig. 4 shows the characteristic curves of dynamic pull-in voltage of double clamped micro-beam for various values of dimensionless parameter
. Fig. 4 shows the characteristic curves of dynamic pull-in voltage of double clamped micro-beam for various values of dimensionless parameter  . Fig. 4 indicates that the dynamic pull-in voltage increases as the parameter
. Fig. 4 indicates that the dynamic pull-in voltage increases as the parameter  increases. In addition, the impact of dimensionless parameter
increases. In addition, the impact of dimensionless parameter  is more considerable when the normalized amplitude increases from zero to unity.
is more considerable when the normalized amplitude increases from zero to unity.
The influence of nondimensional parameter  on the dynamic pull-in voltage of cantilever and double clamped actuated micro-beams are depicted in Figs. 5 and 6. The comparison between the values of pull-in voltages reveals that the dynamic pull-in voltage for cantilever micro-beam is less than its value for double clamped one. From Figs. 5 and 6, it is concluded that the increase in the parameter
on the dynamic pull-in voltage of cantilever and double clamped actuated micro-beams are depicted in Figs. 5 and 6. The comparison between the values of pull-in voltages reveals that the dynamic pull-in voltage for cantilever micro-beam is less than its value for double clamped one. From Figs. 5 and 6, it is concluded that the increase in the parameter  causes decrease in the dynamic pull-in voltage. Furthermore, it is clear that the effect of dimensionless parameter
causes decrease in the dynamic pull-in voltage. Furthermore, it is clear that the effect of dimensionless parameter  is more considerable when the normalized amplitude decreases.
is more considerable when the normalized amplitude decreases.
5 CONCLUSIONS
A modern powerful analytical approach called Iteration perturbation method was employed to establish the frequency - amplitude relationship of vibrating actuated micro-beams. The influence of vibrational amplitude on pull-in instability and dynamic pull-in voltage was investigated in this research. The accuracy of the obtained analytical solutions is verified by numerical results. It is indicated that two terms in series expansions is sufficient to produce an acceptable accurate solutions. Finally, the significant effects of non-dimensional parameters on the dynamic pull-in voltage were investigated.
Appendix A
For clamped-clapmed micro beam the defined parameters are:
For cantilever micro beam the defined parameters are:
Appendix B
System parameters used for numerical analysis
- Abdi, J., Koochi, A., Kazemi, A.S., Abadyan, M., (2011). Modeling the effects of size dependence and dispersion forces on the pull-in instability of electrostatic cantilever NEMS using modified couple stress theory, Smart Mater. Struct., 20, 055011, doi:10.1088/0964-1726/20/5/055011.
- Ansari, R.R., Gholami, R.R., Sahmani, SS., (2012). Study of Small Scale Effects on the Nonlinear Vibration Response of Functionally Graded Timoshenko Microbeams Based on the Strain Gradient Theory, J. Comput. Nonlinear Dynam., 7(3), 031009, doi:10.1115/1.4006040.
- Chouvion, B., Mc William, S., Popov, A.A., Fox, C.H.J., (2012). Review and comparison of different support loss models for micro-electro-mechanical systems resonators undergoing in-plane vibration, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 226(1), 283-295.
- Daneshmand, F., Amabili, M., (2012). Coupled oscillations of a protein microtubule immersed in cytoplasm: an orthotropic elastic shell modeling, J Biol Phys, 38, 429 - 448, DOI 10.1007/s10867-012-9263-y.
- Ghadimi, M., Barari, A., Kaliji, H.D., Domairry, G., (2012). Periodic solutions for highly nonlinear oscillation systems, Archives of Civil and Mechanical Engineering, 12(3), 389 - 395.
- Grandinetti, F.J., Soares, A. M. de S., Lamas, W. de Q., Goes, L., C., S., (20112). Notes on vibration control of a micro/macromanipulator mounted on a flexible structure, Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 226(1), 72-82, doi: 10.1177/1464419311424090.
- He, J.H., (2001). Iteration Perturbation Method for Strongly Nonlinear Oscillations, Journal of Vibration and Control, 7, 631-642, DOI: 10.1177/107754630100700501.
- He, J.H., (2002). Modified Lindstedt - Poincare methods for some strongly non-linear oscillations: Part I: expansion of a constant, International Journal of Non-Linear Mechanics, 37(2), 309-314.
- He, J.H., (2007). Variational iteration method-Some recent results and new interpretations, Journal of Computational and Applied Mathematics, 207(1), 3-17.
- He, J.H., (2008). Max-Min approach to nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation, 9, 207-210.
- He, J.H., (2008). An Improved Amplitude-frequency Formulation for Nonlinear Oscillators, International Journal of Nonlinear Sciences and Numerical Simulation, 9(2), 211-212.
- He, J.H., (2010). Hamiltonian approach to nonlinear oscillators, Physics Letters A, 374(23), 2312-2314.
- Kumar, V., Rhoads, J.F., (2012). Modeling and Analysis of an Optically-Actuated, Bistable MEMS Device, J. Comput. Nonlinear Dynam., 7(2), 021007, doi:10.1115/1.4005080.
- Liao, S.J., (2003). An analytic approximate technique for free oscillations of positively damped systems with algebraically decaying amplitude, International Journal of Non-Linear Mechanics, 38(8), 1173-1183.
- Liao, S.J., (2004). An analytic approximate approach for free oscillations of self-excited systems, International Journal of Non-Linear Mechanics, 39(2), 271-280.
- Motallebi, A., Fathalilou, M., Rezazadeh, G., (2012). Effect of the open crack on the pull-in instability of an electrostatically actuated micro-beam, Acta Mechanica Solida Sinica, 25(6), 627-637.
- Moghimi Zand, M. Ahmadian, M.T., (2009). Application of homotopy analysis method in studying dynamic pull-in instability of Microsystems. Mechanics Research Communications, 36, 851 - 858.
- Ramezani, S., (2012). A micro scale geometrically non-linear Timoshenko beam model based on strain gradient elasticity theory, International Journal of Non-Linear Mechanics, 47(8), 863-873.
- Rahaeifard, M., Ahmadian, M.T., Firoozbakhsh, K., (2013). Size-dependent dynamic behavior of microcantilevers under suddenly applied DC voltage, Proc IMechE Part C: J Mechanical Engineering Science, in press, DOI: 10.1177/0954406213490376.
- Rajabi, F., Ramezani, S., (2013). A nonlinear microbeam model based on strain gradient elasticity theory, Acta Mechanica Solida Sinica, 26(1), 21-34.
- Rhoads, J.F., Kumar, V., Shaw, S.W., Turner, K.L., (2013). The non-linear dynamics of electromagnetically actuated microbeam resonators with purely parametric excitations, International Journal of Non-Linear Mechanics, 55, 79-89.
- Sabater, A.B., Rhoads, J.F., (2012). On the Dynamics of Two Mutually-Coupled, Electromagnetically-Actuated Microbeam Oscillators., J. Comput. Nonlinear Dynam., 7(3), 031011, doi:10.1115/1.4005999.
- Sedighi, H.M., Shirazi, K.H., (2012). A new approach to analytical solution of cantilever beam vibration with nonlinear boundary condition. Journal of Computational and Nonlinear Dynamics, 7(3), doi:10.1115/1.4005924.
- Sedighi, H.M., Shirazi, K.H., Zare, J., (2012). Novel Equivalent Function for Deadzone Nonlinearity: Applied to Analytical Solution of Beam Vibration Using He's Parameter Expanding Method. Latin American Journal of Solids and Structures, 9, 443 - 451.
- Sedighi, H.M., Shirazi, K.H., (2013). Asymptotic approach for nonlinear vibrating beams with saturation type boundary condition, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 227(11) 2479 - 2486, DOI: 10.1177/0954406213475561.
- Sedighi, H.M., Shirazi, K.H., (2013). Vibrations of micro-beams actuated by an electric field via Parameter Expansion Method, Acta Astronautica, 85, 19-24.
- Sedighi, H.M., Shirazi, K.H., Attarzadeh, M.A., (2013). A study on the quintic nonlinear beam vibrations using asymptotic approximate approaches, Acta Astronautica, 91, 245-250, doi:10.1016/j.actaastro.2013.06.018.
- Sedighi, H.M., (2014). Size-dependent dynamic pull-in instability of vibrating electrically actuated microbeams based on the strain gradient elasticity theory, Acta Astronautica, 95, 111-123. http://dx.doi.org/10.1016/j.actaastro.2013.10.020
- Sedighi, H.M., Changizian, M., Noghrehabadi, A., (2014). Dynamic pull-in instability of geometrically nonlinear actuated micro-beams based on the modified couple stress theory, Latin American Journal of Solids and Structures, 11, 810-825.
- Soroush, R., Koochi, A., Kazemi, A.S., Noghrehabadi, A., Haddadpour, H., Abadyan, M., (2010). Investigating the effect of Casimir and van der Waals attractions on the electrostatic pull-in instability of nano-actuators, Phys. Scr., 82, 045801, doi:10.1088/0031-8949/82/04/045801.
- Tadi Beni, Y., Abadyan, M., (2013). Use of strain gradient theory for modeling the size-dependent pull-in of rotational nano-mirror in the presence of molecular force, Int. J. Mod. Phys. B 27, DOI: 10.1142/S0217979213500835.
- Tadi Beni, Y., Koochi, A., Kazemi, A.S., Abadyan, M., (2012). Modeling the influence of surface effect and molecular force on pull-in voltage of rotational nano - micro mirror using 2-DOF model, Canadian Journal of Physics, 90(10), 963-974, 10.1139/p2012-092.
- Vahdat, A.S., Rezazadeh, G., Ahmadi, G., (2012). Thermoelastic damping in a micro-beam resonator tunable with piezoelectric layers, Acta Mechanica Solida Sinica, 25(1), 73-81.
- Wang, S.Q., He, J.H., (2008). Nonlinear oscillator with discontinuity by parameter-expansion method, Chaos, Solitons & Fractals, 35(4), 688-691.
- Yazdi, A.A, (2013). Homotopy Perturbation Method for Nonlinear Vibration Analysis of Functionally Graded Plate, Journal of Vibration and Acoustics, doi: 10.1115/1.4023252.
- Zamanzadeh, M., Rezazadeh, G., Jafarsadeghi-poornaki, I., Shabani, R., (2013). Static and dynamic stability modeling of a capacitive FGM micro-beam in presence of temperature changes, Applied Mathematical Modelling, 37(10 - 11), 6964-6978.
Appendix A
Appendix B
Publication Dates
-
Publication in this collection
13 Mar 2014 -
Date of issue
Dec 2014