Abstract
Composite shells, which are being widely used in engineering applications, are often under thermal loads. Thermal loads usually bring thermal stresses in the structure which can significantly affect its static and dynamic behaviors. One of the possible solutions for this matter is embedding Shape Memory Alloy (SMA) wires into the structure. In the present study, thermal buckling and free vibration of laminated composite cylindrical shells reinforced by SMA wires are analyzed. Brinson model is implemented to predict the thermo-mechanical behavior of SMA wires. The natural frequencies and buckling temperatures of the structure are obtained by employing Generalized Differential Quadrature (GDQ) method. GDQ is a powerful numerical approach which can solve partial differential equations. A comparative study is carried out to show the accuracy and efficiency of the applied numerical method for both free vibration and buckling analysis of composite shells in thermal environment. A parametric study is also provided to indicate the effects of like SMA volume fraction, dependency of material properties on temperature, lay-up orientation, and pre-strain of SMA wires on the natural frequency and buckling of Shape Memory Alloy Hybrid Composite (SMAHC) cylindrical shells. Results represent the fact that SMAs can play a significant role in thermal vibration of composite shells. The second goal of present work is optimization of SMAHC cylindrical shells in order to maximize the fundamental frequency parameter at a certain temperature. To this end, an eight-layer composite shell with four SMA-reinforced layers is considered for optimization. The primary optimization variables are the values of SMA angles in the four layers. Since the optimization process is complicated and time consuming, Genetic Algorithm (GA) is performed to obtain the orientations of SMA layers to maximize the first natural frequency of structure. The optimization results show that using an optimum stacking sequence for SMAHC shells can increase the fundamental frequency of the structure by a considerable amount.
Keywords
Shape memory alloys; Composite shells; Free vibration; Thermal buckling; Optimization; Genetic algorithm
| Nomenclature | ||||
| Extensional stiffness coefficient | Total martensite volume fractions | |||
| Extension-bending coupling coefficient | Stress induced martensite volume fraction | |||
| Bending stiffness coefficient | Initial stress induced martensite volume fraction | |||
| Young modulus in 1 direction | Temperature induced martensite volume fraction | |||
| Young modulus in 2 direction | Initial temperature induced martensite volume fraction | |||
| Shear modulus of composite | Recovery stress obtained through SMA activation | |||
| Young modulus of SMA fiber | Strain of SMA fibers | |||
| Young modulus of matrix | Moment resultant | |||
| Reference temperature | Force resultant | |||
| Poisson ratio | Reduced stiffness matrix | |||
| Thermal expansion coefficient in 1 direction | Cylinder co-ordinates in direction | |||
| Thermal expansion coefficient in 2 direction | Stress in direction | |||
| Length of the cylindrical shell | Stress in direction | |||
| Radius of the cylindrical shell | Shear stress in - direction | |||
| Total thickness of the cylindrical shell | Stain in x direction | |||
| volume fraction of the SMA fiber | Strain in direction | |||
| Pre-strain of SMA fibers | Shear strain in -Ɵ direction | |||
| Austenite Young modulus | Displacement in direction | |||
| Martensite Young modulus | v | Displacement in direction | ||
| Thermo-elastic parameter of SMA fiber | Displacement in direction | |||
| Martensite finish temperature | Total density of SMA/Graphite/Epoxy composite shell | |||
| Martensite start temperature | Shear force in direction | |||
| Austenite start temperature | Shear force in direction | |||
| Austenite finish temperature | αx | Thermal expansion coefficient in direction | ||
| Stress influence coefficient | αƟ | Thermal expansion coefficient in direction | ||
| Stress influence coefficient | Force resultant of SMA fibers | |||
| Poisson ratio of SMA fibers | Force resultant of temperature | |||
| Initial stress of SMA fibers | Moment resultant of SMA fibers | |||
| Maximum residual strain of SMA fibers | Moment resultant of temperature | |||
| Thermal expansion coefficient of SMA fibers | weighting coefficients | |||
| Shear modulus of SMA fiber | ||||
1. INTRODUCTION
SMAs are a class of new smart materials that have been receiving increased attention due to their two unique thermo-mechanical characteristics, Shape Memory Effect (SME) and Pseudo-Elasticity (PE). SME refers to the material ability to recover cold-forged permanent large strains (up to 10%) upon a mild increase in material temperature. These permanent strains can also be recovered by loading in opposite direction of inelastic strain which is called ferro-elasticity. At high temperatures, SMAs behave pseudo-elasticity and can recover large strains during mechanical loading-unloading patterns. This property of SMAs produces a hysteretic loop that is responsible of energy-dissipation. The unique properties of SMAs lie in the phase transition between martensite and austenite. Setting SMA components in the form of wires into composite laminates can control the static and dynamic structural response. That is why some researchers have been motivated to analyze thermo-mechanical behavior of smart structures with SMA components, experimentally or/and numerically. Birman (1997) Birman, V., (1997). Stability of functionally graded shape memory alloy sandwich panels. Journal of Smart Material Structure 6: 278–286. studied the stability loss phenomenon in a simply-supported rectangular plates embedded with SMA fibers subjected to uni-axial loading. As concluded, non-uniform distribution of fibers through the width is more influential than the conventional uniform fiber dispersion. To examine the influence of SMA fibers on the stability characteristics of SMAHC plates, a series of experimental studies were carried out by Thompson and Loughlan (2001) Thompson, S.P., Loughlan, J., (2001). Enhancing the post-buckling response of composite panel structure utilizing shape memory alloy actuators - a smart structural concept. . Journal of Composite Structures 51: 21–36. and Loughlan et al. (2002) Loughlan, J., Thompson, S.P., Smith, H., (2002). Buckling control using embedded shape memory actuators and the utilization of smart technology in future aerospace platforms. Journal of Composite Structures 58: 319–347. . Results of these studies accept the high influence of SMA fibers on the buckling delay and alleviation of post-buckling deflections of SMAHC plates. Roh et al. (2004) Roh J.H., Oh I.K., Yang S.M., Han J.H., Lee I., (2004). Thermal post-buckling analysis of shape memory alloy hybrid composite shell panels. Smart materials and structures 13: 1337-1344. analyzed thermal post-buckling of SMA composite shell panels by using the finite element method formulated on the basis of the layer-wise theory and Brinson model. They showed that embedding SMA wires in the composite shell panel could prevent the snapping phenomenon that is one of the unstable post-buckling behaviors. Using Galerkin approximate, harmonic balance method and Brinson model, Yongsheng and Shuangshuang (2007) Yongsheng, R., Shuangshuang, S., (2007). Large amplitude flexural vibration of the orthotropic composite plate embedded with shape memory alloy fibers. Chinese Journal of Aeronautics 20:415-424. examined large amplitude flexural vibration of the orthotropic composite plate with embedded SMA wires. Kuo et al. (2009) Kuo, S.Y., Shiau, L.C., Chen, K.H., (2009). Buckling analysis of shape memory alloy reinforced composite laminates. Journal of Composite Structures 90:188-195. employed experimental data from the SMA curves and investigated buckling of SMA reinforced composite laminates using finite element method. Li et al (2010) Li, S.R., Yu, W.S., Batra, R.C., (2010). Free vibration of thermally pre/post-buckled circular thin plates embedded with shape memory alloy fibers. Journal of Thermal Stresses 33:79–96. analyzed free vibration of thermally per/post-buckled circular thin plates with embedded SMA fibers based on Brinson model and by using shooting method. Mirzaeifar et al (2011) Mirzaeifar, R., Shakeri, M., DesRoches, R., Yavari, A., (2011). A semi-analytic analysis of shape memory alloy thick-walled cylinders under internal pressure. Journal of Arch Appl Mech 81: 1093–1116. presented a semi analytical analysis of thick-walled SMA cylinder under internal pressure. Free vibration analysis of buckled SMA reinforced cross-ply and angle-ply plates was performed by Shiau et al. (2011) Shiau, L.C., Kuo, S.Y., Chang, S.Y., (2011). Free vibration of buckled SMA reinforced composite laminates. . Journal of Composite Structures 93: 2678–2684. . They investigated the effects of SMAs on the vibrational behavior of structure by varying the SMA fiber spacing. Using FEM and Brinson model, Khalili et al. (2013) Khalili, S.M.R., Botshekanan Dehkordi, M., Carrera, E., Shariya, M., (2013). Non-linear dynamic analysis of a sandwich beam with pseudoelastic SMA hybrid composite faces based on higher order finite element theory. . Journal of Composite Structures 96:243–255. analyzed geometrically non-linear dynamic response of flexible sandwich beams with pseudo-elastic SMAHC face sheets. Asadi et al. (2013a) Asadi, H., Bodaghi, M., Shakeri, M., Aghdam, M.M., (2013a). On the free vibration of thermally pre/post-buckled shear deformable SMA hybrid composite beams. . Journal of Aerospace Science and Technology 31:73–86. examined the nonlinear free vibration of SMA composite beams in thermally pre/post-buckled domains based on first-order shear deformation theory and Brinson model. Also Asadi et al. (2013b) Asadi, H., Bodaghi, M., Shakeri, M., Aghdam, M.M., (2013b). An analytical approach for nonlinear vibration and thermal stability of shape memory alloy hybrid laminated composite beams. European Journal of Mechanics A/Solids 42:454-468. presented an exact closed-form solution for buckling temperature, post-buckling deformation and temperature-deformation equilibrium path of symmetric and asymmetric simply supported SMAHC beams under uniform temperature rise. Recently, Thermal bifurcation behavior of cross-ply laminated composite cylindrical shells embedded with SMA fibers was analyzed by Asadi et al. (2015) Asadi H., Kiani Y., Aghdam M.M., Shakeri M., (2015). Enhanced thermal buckling of laminated composite cylindrical shells with shape memory alloy. Journal of composite materials 50(2): 1-14. . Properties of the constituents were assumed to be temperature-dependent. Donnell’s kinematic assumptions accompanied with the von-Karman type of geometrical non-linearity were used to derive the governing equations of the shell. Also, one-dimensional constitutive law of Brinson was implemented to predict the behavior of SMA fibers through the heating process. Forouzesh and Jafari (2015) Forouzesh, F., Jafari, A. A., (2015). Radial vibration analysis of pseudoelastic shape memory alloy thin cylindrical shells by the differential quadrature method. Journal of Thin-Walled Structures, 93:158–168. investigated the radial vibrations of SMAHC cylindrical shells under harmonic internal pressure based on Donnell-type classical shell theory. They used Boyd–Lagoudas model to simulate the non-linear thermo-mechanical behavior of SMA fibers and implemented GDQ method and Newmark approach for the analysis. Nonlinear free vibration of thermally buckled SMAHC sandwich plate was examined by Samadpour et al. (2015) Samadpour, M., Sadighi, M., Shakeri, M., Zamani, H., (2015). Vibration analysis of thermally buckled SMA hybrid composite sandwich plate. Journal of Composite Structures 119:251–263. based on shear deformation plate theories. They showed that SMA fibers can significantly affect the natural frequency and post-buckling deflection of sandwich plates. Using the mixed LW (layer-wise)/ESL (equivalent single layer) models, Botshekanan Botshekanan Dehkordi et al. (2016) Botshekanan Dehkordi, M., Khalili, S.M.R., Carrera E., (2016). Non-linear transient dynamic analysis of sandwich plate with composite face-sheets embedded with shape memory alloy wires and flexible core- based on the mixed LW (layer-wise)/ESL (equivalent single layer) models. Composites Part B 87: 59-74. studied nonlinear dynamic analysis of sandwich plate with flexible core and SMAHC face sheets. Brinson model was implemented to predict the thermo-mechanical behavior of SMA fibers. The effect of volume fraction and location of SMAs, the thickness of face sheets, plate aspect ratio, and boundary conditions on dynamic of structure were examined. Recently, Parhi and Singh (2016) Parhi, A., Singh, B.N., (2016). Nonlinear Free Vibration Analysis of Shape Memory Alloy Embedded Laminated Composite Shell Panel. Journal of Mechanics of Advanced Materials and Structures 24: 713-724. presented nonlinear free vibration analysis of SMAHC spherical and cylindrical composite shell panels. The governing equations were derived based on higher-order shear deformation plate theory and using nonlinear von- Karman strain displacement relations, and were solved by applying nine-nodded isoperimetric element. The influence of pre-strain of SMAs, volume fraction of SMAs, temperature, and curvature on the linear and non-linear frequency of structure were discussed in details.
As can be found from the literature survey, although worthwhile researches have been dedicated to analyze composite structures reinforced by SMA wires, a few works have been devoted to study optimization of SMAHC structures. Optimization of SMAHC plates with cross-ply lay-up subjected to low-velocity impact was performed by Birman et al. (1996) Birman, V., Chandrashekhara, K., Sain, S., (1996). An approach to optimization of shape memory alloy hybrid composite plates subjected to low-velocity impact. Journal of Composites Part B 439-446. . The variations of volume fractions of SMA fibers in each direction subject to a constraint on the total volume fraction of the SMAs were considered for the optimization problem. It was shown that using optimum SMA in the plate significantly reduces deflections and stresses. Recently, Kamarian and Shakeri (2017) Kamarian, S., Shakeri, M., (2017). Thermal buckling analysis and stacking sequence optimization of rectangular and skew shape memory alloy hybrid composite plates. Composites Part B : Engineering, 116: 137-152. optimized SMAHC skew plates with respect to thermal buckling. They used a meta heuristic algorithm called Firefly Algorithm (FA) for stacking sequence optimization of the plate in order to maximize the critical buckling temperature. It was found that optimization of orientation of SMA wires can improve the buckling temperature of composite structures by a considerable amount.
To the best of the authors' knowledge, there is no published work on the optimization of cylindrical shells with SMA wires. Thus, in the present work, analysis and optimization of SMAHC cylindrical shells are presented. In the first part of results, free vibration and buckling analysis of cylindrical shells under thermal environments are studied. The effect of some parameters like volume fraction of SMAs, pre-strain of SMAs, and temperature-dependency of materials on the behavior of structure are examined. GDQ method, which is an efficient numerical method for problems with partial differential equations, is employed to discretize the governing equations and solve the Eigen value problems in order to obtain the natural frequencies and critical buckling temperatures. Then, in the second part of present work, stacking sequence optimization of cylindrical shells reinforced by SMA wires is presented in order to have the maximum natural frequency of structure at a certain temperature. To this end, since the problem cannot be computed analytically and the process takes too much time, GA is employed to predict the best solutions. GA is one of the most approved heuristic methods for optimization problems and has been successfully applied in for various objective functions in composite structures, such as buckling loads, weight, fundamental frequencies, deflection, etc. ( Wu et al. (2012) Wu, Z., Weaver, P.M., Raju, G., Kim, B.C., (2012). Buckling analysis and optimisation of variable angle tow composite plates. Journal of Thin-Walled Structures 60:163–172. , Sliseris and Rocens (2013) Sliseris, J., Rocens, K., (2013). Optimal design of composite plates with discrete variable stiffness. Journal of Composite Structures 98:15–23. , Le-Manh, and Lee (2014) Le-Manh, T., Lee, J., (2014). Stacking sequence optimization for maximum strengths of laminated composite plates using genetic algorithm and isogeometric analysis. Journal of Composite Structures 116:357–363. , An et al (2015) An, H., Chen, S., Huang, H., (2015). Laminate stacking sequence optimization with strength constraints using two-level approximations and adaptive genetic algorithm. Journal of Struct Multidisc Optim 51:903–918. , Xu et al. (2015) Xu, C., Lin, S., Yang, Y., (2015). Optimal design of viscoelastic damping structures using layerwise finite element analysis and multi-objective genetic algorithm. Journal of Computers and Structures 157:1–8. , Vosoughi et al. (2016) Vosoughi, A.R., Dehghani Forkhorji, H., Roohbakhsh, H., (2016). Maximum fundamental frequency of thick laminated composite plates by a hybrid optimization method. Journal of Composites Part B 86:254-260. , Mashrouteh et al. (2017) Mashrouteh, H., Rahnamayan, S., Esmailzadeh, E., (2017). Optimal Vibration Control and Innovization for Rectangular Plate. Journal of IEEE 549-556. , Ou and Mak (2017) Ou, D., Mak, C.M., (2017). Optimization of natural frequencies of a plate structure by modifying boundary conditions. Journal of the Acoustical Society of America 142: 56-62. ).
2. Equilibrium equations
Here, the recovery stress of SMA wires is calculated based on the simplified form of the Brinson model ( Brinson and Huang, 1996 Brinson, L. C., Huang, M. S., (1996). Simplifications and Comparisons of Shape Memory Alloy Constitutive Models. Journal of Intelligent Material Systems and structures 7: 108-114. ) in which the martensite volume fraction ξ is separated into the stress-induced ξs and the temperature-induced components ξT as equations (1 and 2 )).
where ξ denotes the maximum residual strain and the Young’s modulus is expressed based on the Reuss model as ( Auricchio and Sacco, 1997 Auricchio, F., Sacco, E., (1997). A one-dimensional model for superelastic shape memory alloys with different elastic properties between austenite and martensite. International Journal of Non Linear Mechanics 32:1101-I 114. )
In equation (3) , EA and EM represents Young’s modulus of the SMA in the pure austenite and the pure martensite phases, respectively. According to ( Brinson, 1993 Brinson, L.C., (1993). One-dimensional constitutive behavior of shape memory alloys: thermo-mechanical derivation with non-constant material functions and redefined martensite internal variable. Journal of Intelligent Material Systems and Structures 4: 229-242. ), the martensite fractions during heating stage when T>As and CA (T-Af)<σ<CA(T-As) can be calculated as equation (4)
in which a subscript ‘0’ indicates the initial state of a parameter and the constant CA is the slope of the curve of the critical stress for reverse phase transformation. Since the martensite fraction depends on the stress and temperature, transformation kinetics must be coupled with equation (4) to formulate a complete governing equation for SMAs. The elastic properties of an SMA/graphite/epoxy layer are found in Appendix. Appendix E 11 = E S ( ξ ) V S + E m ( 1 − V S ) ; E 22 = E m [ ( 1 − V S ) + V S 1 − V S ( 1 − E m E S ( ξ ) ) ] G 12 = G m [ ( 1 − V S ) + V S 1 − V S ( 1 − G m G S ( ξ ) ) ] ; G S ( ξ ) = E S ( ξ ) 2 ( 1 + ν 12 S ) α 1 = V S α S E S ( ξ ) + ( 1 − V S ) α m E m E 11 ; α 2 = E m E 22 [ α m ( 1 − V S ) + α m V S − V S ( α m − α S ) 1 − V S ( 1 − E m E S ( ξ ) ) ] ν 12 = ν 12 S V S + ν 12 m ( 1 − V S ) ; ρ = ρ S V S + ρ m ( 1 − V S ) where the subscripts ‘m’ and ‘s’ mean the composite matrix and SMA fiber, respectively. Also, parameters E, G, í, á, ñ and Vs are Young modulus, shear modulus, Poisson ratio, thermal expansion coefficient, material density and volume fraction of SMA fibers, respectively ( N T , M T ) = ∑ k = 1 n ∫ h k − 1 h k ( Q ¯ α ¯ ) Δ T ( 1, z ) d z ; α ¯ = [ T ] T . [ α x α θ 0 ] ( N r , M r ) = ∑ k = 1 n ∫ h k − 1 h k ( Q ¯ r ) V S ( 1, z ) d z ; Q ¯ r = [ T ] . [ σ r 0 0 ] [ Q ¯ ] = [ T ] [ Q ] [ T ] T ; [ T ] = [ cos 2 ϕ sin 2 ϕ − sin 2 ϕ sin 2 ϕ cos 2 ϕ sin 2 ϕ sin ϕ cos ϕ − sin ϕ cos ϕ cos 2 ϕ − sin 2 ϕ ] Q = [ Q 11 Q 12 0 Q 12 Q 22 0 0 0 Q 66 ] ; Q 11 = E 11 / ( 1 − ν 12 ν 21 ) , Q 22 = E 22 / ( 1 − ν 12 ν 21 ) , Q 16 = G 12 , Q 66 = G 12
Consider a composite cylindrical shell as shown in Figure 1 . The strains in terms of the mid-surface displacement components (u, ν, w) are defined as equation (5)
Where ex, eƟ, exƟ are the components of axial, circumferential and shear strain, respectively. Considering as the temperature rise from reference temperature T0 to an arbitrary temperature T, the constitutive law for the SMAHC cylindrical shell subjected to thermal loading becomes
where óx, óƟ and óxƟ are the components of axial, circumferential and shear, stress, respectively. In equation (6) , is the transformed form of recovery stress (ór) generated by the temperature-induced reverse phase transformation of the pre-strained SMA fibers from detwinned martensite to austenite (see Appendix Appendix E 11 = E S ( ξ ) V S + E m ( 1 − V S ) ; E 22 = E m [ ( 1 − V S ) + V S 1 − V S ( 1 − E m E S ( ξ ) ) ] G 12 = G m [ ( 1 − V S ) + V S 1 − V S ( 1 − G m G S ( ξ ) ) ] ; G S ( ξ ) = E S ( ξ ) 2 ( 1 + ν 12 S ) α 1 = V S α S E S ( ξ ) + ( 1 − V S ) α m E m E 11 ; α 2 = E m E 22 [ α m ( 1 − V S ) + α m V S − V S ( α m − α S ) 1 − V S ( 1 − E m E S ( ξ ) ) ] ν 12 = ν 12 S V S + ν 12 m ( 1 − V S ) ; ρ = ρ S V S + ρ m ( 1 − V S ) where the subscripts ‘m’ and ‘s’ mean the composite matrix and SMA fiber, respectively. Also, parameters E, G, í, á, ñ and Vs are Young modulus, shear modulus, Poisson ratio, thermal expansion coefficient, material density and volume fraction of SMA fibers, respectively ( N T , M T ) = ∑ k = 1 n ∫ h k − 1 h k ( Q ¯ α ¯ ) Δ T ( 1, z ) d z ; α ¯ = [ T ] T . [ α x α θ 0 ] ( N r , M r ) = ∑ k = 1 n ∫ h k − 1 h k ( Q ¯ r ) V S ( 1, z ) d z ; Q ¯ r = [ T ] . [ σ r 0 0 ] [ Q ¯ ] = [ T ] [ Q ] [ T ] T ; [ T ] = [ cos 2 ϕ sin 2 ϕ − sin 2 ϕ sin 2 ϕ cos 2 ϕ sin 2 ϕ sin ϕ cos ϕ − sin ϕ cos ϕ cos 2 ϕ − sin 2 ϕ ] Q = [ Q 11 Q 12 0 Q 12 Q 22 0 0 0 Q 66 ] ; Q 11 = E 11 / ( 1 − ν 12 ν 21 ) , Q 22 = E 22 / ( 1 − ν 12 ν 21 ) , Q 16 = G 12 , Q 66 = G 12 ). Based on classical shell theory, equations of motion can be obtained as equations (7) ( Shu and Du, 1997 Shu, C., Du, H., (1997). Free vibration analysis of laminated composite cylindrical shells by DQM. Journal of Composites Part B 28B:267-274. , Reddy 2004 Reddy, J.N., (2004). Mechanics of laminated composite plates and shells Theory and analysis, CRC Press LLC (Boca Raton). , Sheng and Wang, 2007 Sheng, G.G., Wang, X., (2007). Thermal Vibration, Buckling and Dynamic Stability of Functionally Graded Cylindrical Shells Embedded in an Elastic Medium. Journal of Reinforced Plastics and Composites 27:117-134. )
in which, the stress resultants are defined as equations (8)
Where NT, MT, Nr and Mr represent thermal force resultant, thermal moment resultant, in-plane force and bending moment resultants induced by the SMA fibers respectively defined in Appendix. Furthermore, Qx and QƟ denote shear forces in x and Ɵ direction respectively and defined as equation (9)
3. GDQ Method
GDQ approach is used to solve the governing equation of the SMAHC shell. In the purposed method, the nth order of a continuous function f(x, z) with respect to x at a given point xi can be approximated as a linear sum of weighting values at all of the discrete points in the domain of x , i.e. ( Shu, 2000 Shu, C., (2000). Differential quadrature and its application in engineering, Berlin: Springer. ):
In equation (10)N is the number of sampling points, and cijn is the xi dependent weight coefficients. In order to determine the weighting coefficients, the Lagrange interpolation basic functions are used as test functions, and explicit formulation for computing these weighting coefficients can be obtained as equations (11 and 12 )) ( Shu, 2000 Shu, C., (2000). Differential quadrature and its application in engineering, Berlin: Springer. ):
where
for the first-order derivative (n=1), and for higher-order derivative, one can use the equations (13 and 14 )) iteratively ( Shu, 2000 Shu, C., (2000). Differential quadrature and its application in engineering, Berlin: Springer. ):
A simple and natural choice of the grid distribution is the uniform grid spacing rule. However, it was found that non-uniform grid spacing yields results with better accuracy. Hence, in this work, the Chebyshev-Gauss-Labatto quadrature points are used ( equations (15) ), that is ( Shu, 2000 Shu, C., (2000). Differential quadrature and its application in engineering, Berlin: Springer. ),
More details about GDQ method can be found in Shu, (2000) Shu, C., (2000). Differential quadrature and its application in engineering, Berlin: Springer. , Shu and Richards (1992) Shu, C., Richards, B.E., (1992). Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stockes equations. International Journal For Numerical Methods In Fluids 15:791-798. .
4. Genetic algorithm
GA is a particular class of evolutionary algorithms that use techniques inspired by evolutionary biology such an inheritance, mutation, selection, and cross over (also called recombination). The basic genetic algorithm is as follows ( Sivanandam and Deepa, 2008 Sivanandam, S.N., Deepa, S.N., (2008). Introduction to Genetic Algorithms, Springer Berlin Heidelberg New York. ):
[start] Genetic random population of n chromosomes (suitable solutions for the problem)
[Fitness] Evaluate the fitness f(x) of each chromosome x in the population.
[New population] Create a new population by repeating following steps until the new population is complete.
[selection] select two parent chromosomes from a population according to their fitness. The better fitness, the bigger chance to get selected.
[crossover] with a crossover probability, cross over the parents to form new offspring (children). If no crossover was performed, offspring is the exact copy of parents.
[Mutation] with a mutation probability, mutate new offspring at each locus (position in chromosome)
[Accepting] Place new offspring in the new population.
[Replace] Use new generated population for a further sum of the algorithm.
[Test] if the end condition is satisfied, stops, and returns the best solution in current population.
[Loop] Go to step2 for fitness evaluation.
The flowchart of the proposed algorithm is shown in Figure 2 . More details about the algorithms are found in Haftka and Gurdal (1992) Haftka, R.T., Gurdal, Z., (1992) Elements of structural optimization, Springer Science+Business Media BV (Dordrecht). , Gurdal et al. (1999) Gurdal, Z., Haftka, R.T., Hajela, P., (1999). Design and optimization of laminated composite materials, John Wiley Sons (New York). , etc.
5. RESULTS
5.1. Verification
To verify the proficiency of GDQ method, two numerical examples are carried out for comparison. As the first example, accuracy of the method is investigated in evaluating fundamental natural frequency parameter of the composite shell (without SMA) for clamped-simply supported boundary conditions. The material parameters of each layer are given as: . The numerical results for the laminated cylindrical shells are given by the dimensionless frequency parameter ë. This parameter is given by . As noticed from Table 1 , good agreement exists between the results of this method and those calculated using Discrete Singular Convolution (DSC) method by Civalek (2007) Civalek, O., (2007). Numerical analysis of free vibrations of laminated composite conical and cylindrical shells: Discrete singular convolution (DSC) approach. Journal of Computational and Applied Mathematics 205:251–271. . It should be noted that only 13 nodes were implemented for GDQ method which shows its efficiency for free vibration analysis of composite structures. For further verification of the results, the critical buckling temperatures of composite cylindrical shells are compared with the existing data in literature. The comparisons are made for two different stacking sequences and different values for . Table 2 reveals that the present GDQ results agree well with those obtained by Shen (2008) Shen, H.S., (2008). Thermal Post-buckling Behavior of Anisotropic Laminated Cylindrical Shells with Temperature-Dependent Properties. Journal of AIAA 46:185-193. and the difference between the results is negligible. It is mentioned that Shen used a singular perturbation technique to determine the buckling temperature of structure. According those mentioned for verification of the results, one can conclude that the GDQ method is accurate enough to handle free vibration of composite cylindrical shells in thermal environments.
First natural frequency parameter of the composite shell (without SMA) for clamped-simply supported boundary conditions
5.2. Free vibration
In this section, numerical results on free vibration of the SMAHC shell are presented. It is assumed that the cylindrical shell is made of NiTi / graphite/epoxy. Material properties of NiTi fibers and graphite-epoxy are considered to be temperature-dependent presented in Tables 3 and 4 , respectively. Brinson model is employed to estimate thermo-mechanical behavior of SMAs. The influence of temperature dependency of materials, volume fraction and pre-strain of SMAs, and stacking sequence of layers on vibrational behavior of composite shells in pre-buckling region are examined.
The material properties of graphite-epoxy ( Asadi et al., 2013a Asadi, H., Bodaghi, M., Shakeri, M., Aghdam, M.M., (2013a). On the free vibration of thermally pre/post-buckled shear deformable SMA hybrid composite beams. . Journal of Aerospace Science and Technology 31:73–86. , Rasid et al., 2011 Rasid, Z.A., Zahari, R., Ayob, A., Majid, D.L., Rafie, A.S.M., (2011). Thermal post-buckling of shape memory alloy composite plates under non-uniform temperature distribution. International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering 5:1649-1654. )
5.2.1. Recover stress
Figure 3 illustrates the effect of temperature on the recovery stress of SMA fibers (which is constrained to maintain the deformation). It is seen from this figure that large internal stresses are produced when the transformation to austenite occurs. It is worth noting that SMA recovery stress is tensile while the temperature raise leads to the compressive thermal stress in the structure as it can be found from Equation.(8) . Therefore, SMA recovery stress can reduce the thermal stress and improve the performance of the structure. The influences of temperature on the axial and circumferential forces produced in the structure are shown in Figure 4 . This figure shows that the tensile SMA recovery stresses induced in the structure can contribute to delay the critical buckling temperature.
Variations of axial and circumferential forces generated by SMA fibers in the structure versus temperature
5.2.2. Temperature dependency of materials
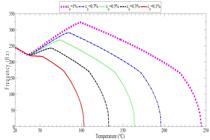
Here, the effect of temperature dependency of material properties on free vibration of SMAHC cylindrical shells is demonstrated. Variations of the fundamental frequency with respect to temperature in the pre-buckled domains are depicted in Figure. 5 . In this figure, TD denotes that the material properties are temperature dependent and TID represents the assumption of constant material properties. As one can observe from Figure 5 , in the absence of SMA fibers, temperature dependency of material properties does not have any significant effects on the free vibration of composite shells while the difference between the natural frequencies becomes more significant for shells with embedded SMA fibers at high temperatures. It means the influence of temperature dependency is considerable in evaluating free vibration of SMAHC structures. It can be also found that TD material properties contribute to higher natural frequency and critical buckling temperature. Therefore, to attain more accurate results, only TD case is addressed in the following.
Influences of temperature and volume fraction of SMA fibers on the fundamental frequency of composite shells lay-up in pre-buckled regions for simply supported boundary conditions
5.2.3. Volume fraction and pre-strain of SMA fibers
Variations of fundamental frequency parameter of composite shells with respect to SMA volume fraction and pre-strain are depicted in Figures 5 and 6 . The numerical results provided in Figure 5 describe that an increase in volume fraction of SMA fibers results in an increase in critical buckling temperature of the structure. It should be mentioned that the temperature at which the natural frequencies reach to zero is buckling temperature. However, the results state a different scenario regarding the vibrational behavior of structure. It is seen that the fundamental frequency of structure is not necessarily increased with the increase of SMA fiber volume fraction. This is because of the fact that though more SMA fiber volume fraction leads to more stiffness in the structure, the weight of structure is also increased. Therefore, at low temperatures, SMA fibers have a destructive effect on the free vibration behavior of structure.
Variations of the fundamental frequency of simply supported shell in pre-buckled regions versus temperature for different values of pre-strain
Now, influence of pre-strain of SMA fibers on the natural frequency of composite shell is illustrated. Various values of pre-strain of SMA fibers are given and free vibrations are demonstrated in Figure 6 . This figure represents that different values of pre-strain do not have any significant effects on the vibrational behavior of SMAHC shell when T<Af but for temperatures more than Af, with the increase of pre-strain value, both natural frequencies and critical buckling temperature increase. This is due to the fact that the weight of structure is not changed but the stiffness is increased when T>Af. Numerical comparison specifies that by increasing the pre-strain of SMAs from 0.1% to 1%, the buckling temperature can improve up to 140% (from 102 to 245).
5.2.4. Stacking sequence of layers
The effect of stacking sequence of layers on the variations of fundamental frequency of SMAHC laminate shell is investigated in Figure 7 by considering various lay-up configurations. It is obviously found that the stacking sequence of layers play an important role in vibrational behavior of the SMAHC structures. As can be observed from Figure 7 , an unsuitable lay-up may lead to destructive influence of SMA fibers on free vibration of structures. As an example, for composite shells, by increasing the SMA volume fraction, the fundamental frequency parameter decreases. On the other hand, one can see that by using a suitable lay-up like , adding SMA fibers improve vibrational characteristics of structure. Thus, it can be concluded that by stacking sequence optimization of SMAHC cylindrical shells, it is possible to maximize the natural frequency of structure at a certain temperature.
Effect of lay-up orientation on the free vibration and thermal buckling behavior of simply supported shell
5.3. Optimization of SMAHC cylindrical shell
The main objective of optimization in the present work is to find the best lay-up orientation for SMA-reinforced layers so that to maximize the fundamental frequency parameter in a certain temperature for a constant amount of SMA volume fraction. As an example, an eight-layer shell is considered with the lay-up orientation . Here, the thicknesses of layers are the same. The constrained optimization problem is defined as:
It is also assumed that fiber orientations of SMA layers take integer values (e.g. 0 0 C, 10, …, 900). If the analytical solution is applied for the optimization problem, the process becomes so complicated and time consuming. In other words, the formed discrete space contains more than design choices to be searched to reach the optimum point. Also, if it is supposed that the process of one search takes 0.25 second in average, the optimization process takes more than 900 hours. Therefore, in the present work, GA is employed for increasing the speed of optimization. Scattered case for crossover, rank case for fitness scaling, stochastic uniform case for selection, and constraint dependent case for mutation are employed. Also, 5% of the population size has been chosen for elitism. Table 5 shows the parameters of GA used to find the optimal solution. GA is applied for 10 times and for the best one, it reaches to values of after about 30 generations. A comparison between the optimum lay-up orientation and two other cases is made in Figure 8 . This figure depicts that stacking sequence optimization can improve the vibrational behavior of SMAHC structures by a considerable amount. It is worth noting that the process of optimization in GA lasted about 15 minutes. It means GA can significantly decrease the running time.
CONCLUSIONS
In this paper, two goals were followed. First, thermal vibration of SMAHC cylindrical shells in pre-buckling region was analyzed. The numerical results were presented based on classical shell theory which is valid only for thin shells. To obtain the natural frequencies, GDQ method was implemented to solve the governing equations. The influences of SMA volume fraction, lay-up orientation, pre-strain of SMA fibers, and temperature-dependency of material on the natural frequency and buckling of structure were examined. The numerical results showed that at low-temperature region, SMAs have a destructive role for natural behavior of structure, but they can significantly improve the vibrational behavior and thermal buckling when the temperatures are high. It was also concluded that, at low temperatures, the variations of pre-strain of SMAs cannot considerably change the vibrational characteristics of the composite structures. Another important conclusion is that the orientation of SMAs in the layers plays an effective role in vibrations of SMAHC shells under thermal environments and can sharply vary the fundamental frequency of the structure. Therefore, an optimization problem was presented to find best stacking sequence for layers with embedded SMAs in order to have the maximum fundamental frequency at a certain temperature. To this end, GA as a heuristic algorithm was employed. It is worth noting that, like other meta heuristic algorithms, GA does not necessarily guarantee the best global optimal solution. However, it at least suggests one of the best answers for optimization problem in short time.
Appendix
where the subscripts ‘m’ and ‘s’ mean the composite matrix and SMA fiber, respectively. Also, parameters E, G, í, á, ñ and Vs are Young modulus, shear modulus, Poisson ratio, thermal expansion coefficient, material density and volume fraction of SMA fibers, respectively
References
- An, H., Chen, S., Huang, H., (2015). Laminate stacking sequence optimization with strength constraints using two-level approximations and adaptive genetic algorithm. Journal of Struct Multidisc Optim 51:903–918.
- Asadi H., Kiani Y., Aghdam M.M., Shakeri M., (2015). Enhanced thermal buckling of laminated composite cylindrical shells with shape memory alloy. Journal of composite materials 50(2): 1-14.
- Asadi, H., Bodaghi, M., Shakeri, M., Aghdam, M.M., (2013a). On the free vibration of thermally pre/post-buckled shear deformable SMA hybrid composite beams. . Journal of Aerospace Science and Technology 31:73–86.
- Asadi, H., Bodaghi, M., Shakeri, M., Aghdam, M.M., (2013b). An analytical approach for nonlinear vibration and thermal stability of shape memory alloy hybrid laminated composite beams. European Journal of Mechanics A/Solids 42:454-468.
- Auricchio, F., Sacco, E., (1997). A one-dimensional model for superelastic shape memory alloys with different elastic properties between austenite and martensite. International Journal of Non Linear Mechanics 32:1101-I 114.
- Birman, V., (1997). Stability of functionally graded shape memory alloy sandwich panels. Journal of Smart Material Structure 6: 278–286.
- Birman, V., Chandrashekhara, K., Sain, S., (1996). An approach to optimization of shape memory alloy hybrid composite plates subjected to low-velocity impact. Journal of Composites Part B 439-446.
- Botshekanan Dehkordi, M., Khalili, S.M.R., Carrera E., (2016). Non-linear transient dynamic analysis of sandwich plate with composite face-sheets embedded with shape memory alloy wires and flexible core- based on the mixed LW (layer-wise)/ESL (equivalent single layer) models. Composites Part B 87: 59-74.
- Brinson, L. C., Huang, M. S., (1996). Simplifications and Comparisons of Shape Memory Alloy Constitutive Models. Journal of Intelligent Material Systems and structures 7: 108-114.
- Brinson, L.C., (1993). One-dimensional constitutive behavior of shape memory alloys: thermo-mechanical derivation with non-constant material functions and redefined martensite internal variable. Journal of Intelligent Material Systems and Structures 4: 229-242.
- Civalek, O., (2007). Numerical analysis of free vibrations of laminated composite conical and cylindrical shells: Discrete singular convolution (DSC) approach. Journal of Computational and Applied Mathematics 205:251–271.
- Forouzesh, F., Jafari, A. A., (2015). Radial vibration analysis of pseudoelastic shape memory alloy thin cylindrical shells by the differential quadrature method. Journal of Thin-Walled Structures, 93:158–168.
- Gurdal, Z., Haftka, R.T., Hajela, P., (1999). Design and optimization of laminated composite materials, John Wiley Sons (New York).
- Haftka, R.T., Gurdal, Z., (1992) Elements of structural optimization, Springer Science+Business Media BV (Dordrecht).
- Kamarian, S., Shakeri, M., (2017). Thermal buckling analysis and stacking sequence optimization of rectangular and skew shape memory alloy hybrid composite plates. Composites Part B : Engineering, 116: 137-152.
- Khalili, S.M.R., Botshekanan Dehkordi, M., Carrera, E., Shariya, M., (2013). Non-linear dynamic analysis of a sandwich beam with pseudoelastic SMA hybrid composite faces based on higher order finite element theory. . Journal of Composite Structures 96:243–255.
- Kuo, S.Y., Shiau, L.C., Chen, K.H., (2009). Buckling analysis of shape memory alloy reinforced composite laminates. Journal of Composite Structures 90:188-195.
- Le-Manh, T., Lee, J., (2014). Stacking sequence optimization for maximum strengths of laminated composite plates using genetic algorithm and isogeometric analysis. Journal of Composite Structures 116:357–363.
- Li, S.R., Yu, W.S., Batra, R.C., (2010). Free vibration of thermally pre/post-buckled circular thin plates embedded with shape memory alloy fibers. Journal of Thermal Stresses 33:79–96.
- Loughlan, J., Thompson, S.P., Smith, H., (2002). Buckling control using embedded shape memory actuators and the utilization of smart technology in future aerospace platforms. Journal of Composite Structures 58: 319–347.
- Mashrouteh, H., Rahnamayan, S., Esmailzadeh, E., (2017). Optimal Vibration Control and Innovization for Rectangular Plate. Journal of IEEE 549-556.
- Mirzaeifar, R., Shakeri, M., DesRoches, R., Yavari, A., (2011). A semi-analytic analysis of shape memory alloy thick-walled cylinders under internal pressure. Journal of Arch Appl Mech 81: 1093–1116.
- Ou, D., Mak, C.M., (2017). Optimization of natural frequencies of a plate structure by modifying boundary conditions. Journal of the Acoustical Society of America 142: 56-62.
- Parhi, A., Singh, B.N., (2016). Nonlinear Free Vibration Analysis of Shape Memory Alloy Embedded Laminated Composite Shell Panel. Journal of Mechanics of Advanced Materials and Structures 24: 713-724.
- Rasid, Z.A., Zahari, R., Ayob, A., Majid, D.L., Rafie, A.S.M., (2011). Thermal post-buckling of shape memory alloy composite plates under non-uniform temperature distribution. International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering 5:1649-1654.
- Reddy, J.N., (2004). Mechanics of laminated composite plates and shells Theory and analysis, CRC Press LLC (Boca Raton).
- Roh J.H., Oh I.K., Yang S.M., Han J.H., Lee I., (2004). Thermal post-buckling analysis of shape memory alloy hybrid composite shell panels. Smart materials and structures 13: 1337-1344.
- Samadpour, M., Sadighi, M., Shakeri, M., Zamani, H., (2015). Vibration analysis of thermally buckled SMA hybrid composite sandwich plate. Journal of Composite Structures 119:251–263.
- Shen, H.S., (2008). Thermal Post-buckling Behavior of Anisotropic Laminated Cylindrical Shells with Temperature-Dependent Properties. Journal of AIAA 46:185-193.
- Sheng, G.G., Wang, X., (2007). Thermal Vibration, Buckling and Dynamic Stability of Functionally Graded Cylindrical Shells Embedded in an Elastic Medium. Journal of Reinforced Plastics and Composites 27:117-134.
- Shiau, L.C., Kuo, S.Y., Chang, S.Y., (2011). Free vibration of buckled SMA reinforced composite laminates. . Journal of Composite Structures 93: 2678–2684.
- Shu, C., (2000). Differential quadrature and its application in engineering, Berlin: Springer.
- Shu, C., Du, H., (1997). Free vibration analysis of laminated composite cylindrical shells by DQM. Journal of Composites Part B 28B:267-274.
- Shu, C., Richards, B.E., (1992). Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stockes equations. International Journal For Numerical Methods In Fluids 15:791-798.
- Sivanandam, S.N., Deepa, S.N., (2008). Introduction to Genetic Algorithms, Springer Berlin Heidelberg New York.
- Sliseris, J., Rocens, K., (2013). Optimal design of composite plates with discrete variable stiffness. Journal of Composite Structures 98:15–23.
- Thompson, S.P., Loughlan, J., (2001). Enhancing the post-buckling response of composite panel structure utilizing shape memory alloy actuators - a smart structural concept. . Journal of Composite Structures 51: 21–36.
- Vosoughi, A.R., Dehghani Forkhorji, H., Roohbakhsh, H., (2016). Maximum fundamental frequency of thick laminated composite plates by a hybrid optimization method. Journal of Composites Part B 86:254-260.
- Wu, Z., Weaver, P.M., Raju, G., Kim, B.C., (2012). Buckling analysis and optimisation of variable angle tow composite plates. Journal of Thin-Walled Structures 60:163–172.
- Xu, C., Lin, S., Yang, Y., (2015). Optimal design of viscoelastic damping structures using layerwise finite element analysis and multi-objective genetic algorithm. Journal of Computers and Structures 157:1–8.
- Yongsheng, R., Shuangshuang, S., (2007). Large amplitude flexural vibration of the orthotropic composite plate embedded with shape memory alloy fibers. Chinese Journal of Aeronautics 20:415-424.
Publication Dates
-
Publication in this collection
2018
History
-
Received
07 May 2016 -
Reviewed
05 Sept 2017 -
Accepted
28 Sept 2017