Abstract
This work addresses an accurate and detailed axial static load dependence linearly elastic free vibration analysis of cylindrical helical springs based on the theory of spatially curved bars and the transfer matrix method. For a continuous system, governing equations comprise coupled vibration modes namely transverse vibrations in two orthogonal planes, torsional and axial vibrations. The axial and shear deformation effects together with the rotatory inertia effects are all considered based on the first order shear deformation theory and their effects on the frequencies are investigated. The effects of the initial stress resultants on the frequencies are also studied. After buckling, forward-shifting phenomenon of higher frequencies is noticeably demonstrated. It is also revealed that a free/forced vibration analysis with an axial static load should not be performed individually without checking buckling loads.
Keywords:
Axial static force; helical spring; free vibration; transfer matrix; buckling load; Timoshenko beam; spatially curved bar
1 INTRODUCTION
Although, in practical applications, the springs are installed in their housing by applying initial static axial loads, the vibration of helical springs subjected to a static axial load have been paid less attention in the literature because of the difficulty and complexity in the problem. Haringx (1949Haringx J. A. (1949). On highly compressible helical springs and rubber rods, and their application for vibration-free mountings. Philips Research Reports 4: 49-80.) performed analytically the earliest study on the current issue by using a rod-model approximation. He studied both buckling and free vibration behavior of cylindrical helical springs with circular sections. As is well known, those formulas give acceptable results for small helix pitch angles. Wittrick (1966Wittrick W.H. (1966). On elastic wave propagation in helical spring. Int. J Mech. Sci. 8(1):25-47) investigated the wave propagation in semi-infinite springs and obtained approximate solutions by taking into account the rotatory inertia and shear deformation effects. Farshad (1980Farshad M. (1980). Wave propagation in prestressed curved rods. J. Eng. Mech. Div. 106: 395-408.) studied wave propagation in prestressed curved rods. By using vector approach and the transfer matrix method, Pearson (1982Pearson D. (1982). The transfer matrix method for the vibration of compressed helical springs. J Mech. Eng. Sci. 24:163-171.) presented originally the linearized disturbance equation set based on the spatial bar theory to consider the vibration of helical springs with a static axial load. Employing Wittrick's (1966)Wittrick W.H. (1966). On elastic wave propagation in helical spring. Int. J Mech. Sci. 8(1):25-47 differential equations Mottershead (1982Mottershead J.E. (1982). The large displacements and dynamic stability of springs using helical finite elements. Int. J Mech. Sci. 24(9):547-558) extended the theory to large displacements through Lagrange-Green strain equations and derived consistent geometric stiffness matrices.
Unlüsoy (1983Ünlüsoy Y.S. (1983). Modelling helical springs for the dynamic behavior. Middle East Technical University (METU) Journal of Applied Researches 3(9): 45-57 (In Turkish).) and Yalçın (1984Yalçın V. (1984). Finite element mobility analysis of helical coil springs, MS Thesis, The Graduate School of Natural and Applied Sciences, METU, Turkey.) studied the free vibration of helical springs subjected to an axial static load by employing the finite element procedure. In their study the helix axis was modelled as a composition of a number of straight beam elements. Haktanır and Kıral (1992Haktanır V. and Kıral E. (1992). Computation of free vibration frequencies of helical springs subjected to axial load. Journal of Engineering Faculty of Isparta of Akdeniz University 6: 201-218.) worked on the free vibration of helical springs subjected to a static axial force with the help of the stiffness matrix formulation and straight beam elements.
Tabarrok and Xiong (1992Tabarrok B. and Xiong Y. (1992). A spatially curved and twisted rod element for buckling analysis. Int. J Solids Struc. 29 (23):3011-3023.) derived the governing equations for the buckling of spatial rods by considering perturbations about the critical state. Xiong and Tabarrok (1992)Xiong Y. and Tabarrok B. (1992). A finite element model for the vibration of spatial rods under various applied loads. International Journal of Mechanical Sciences 34 (1): 41-51. summarized a comprehensive energy formulation for the vibration analysis of spatially curved and twisted rods under various applied loads. In addition to the initial axial force, this formulation took into account the initial moments and shear forces as well as initial deformations. Based on this formulation, a spatially curved and twisted rod finite element was developed and used for several examples.
Becker and Cleghorn (1992Becker L.E. and Cleghorn W.L. (1992). On the buckling of helical compression springs. Int. J Mech. Sci. 34(4):275-282) developed a set of dynamic, partial differential equations in canonical form for helical compression springs for just axial static force, and they solved them for fixed ends and circular cross-section by the transfer matrix method. Chassie et al. (1997Chassie G.G, Becker L.E, Cleghorn W.L. (1997). On the buckling of helical springs under combined compression and torsion. Int. J Mech. Sci. 39(6):697-704) extended the work by Becker and Cleghorn (1992)Becker L.E. and Cleghorn W.L. (1992). On the buckling of helical compression springs. Int. J Mech. Sci. 34(4):275-282 for the buckling of compression springs to include the additional effect of torsion about the axis of the spring. Chassie et al. (1997)Chassie G.G, Becker L.E, Cleghorn W.L. (1997). On the buckling of helical springs under combined compression and torsion. Int. J Mech. Sci. 39(6):697-704 showed that both Mottershead's (1982Mottershead J.E. (1982). The large displacements and dynamic stability of springs using helical finite elements. Int. J Mech. Sci. 24(9):547-558) and Pearson's (1982Pearson D. (1982). The transfer matrix method for the vibration of compressed helical springs. J Mech. Eng. Sci. 24:163-171.) buckling equations do not reduce correctly to the well-known equations for simple rods. The results obtained in the Chassie et al.'s work (1997)Chassie G.G, Becker L.E, Cleghorn W.L. (1997). On the buckling of helical springs under combined compression and torsion. Int. J Mech. Sci. 39(6):697-704 also showed a good agreement with those from Tabarrok and Xiong (1992Tabarrok B. and Xiong Y. (1992). A spatially curved and twisted rod element for buckling analysis. Int. J Solids Struc. 29 (23):3011-3023.) and Haringx's (1949Haringx J. A. (1949). On highly compressible helical springs and rubber rods, and their application for vibration-free mountings. Philips Research Reports 4: 49-80.) theory. They stated that the governing equations derived were in fact a special case of the earlier and more comprehensive analysis of curved and twisted rods under load. Becker et al (2002)Becker L.E., Chassie G.G., Cleghorn W.L. (2002). On the natural frequencies of helical compression springs. International Journal of Mechanical Sciences 44(4): 825-841. broadened their previous works on the buckling analysis for the free vibration analysis of a helical spring subjected to a static axial compressive load by incorporating inertial terms into previous buckling equations. They examined the free vibration analysis numerically based on the transfer matrix method. As they stated this study represents primarily the first detailed examination of the fundamental natural frequencies of helical springs, under static axial load with clamped ends, since the pioneering work by Haringx (1949)Haringx J. A. (1949). On highly compressible helical springs and rubber rods, and their application for vibration-free mountings. Philips Research Reports 4: 49-80..
Frikha et al. (2011Frikha A., Treyssède F., Cartraud P. (2011). Effect of axial load on the propagation of elastic waves in helical beams. Wave Motion 48 : 83-92.) proposed a physical analysis of the effect of axial load on the propagation of elastic waves in helical beams. The general equations proposed in References (Xiong and Tabarrok, 1992Xiong Y. and Tabarrok B. (1992). A finite element model for the vibration of spatial rods under various applied loads. International Journal of Mechanical Sciences 34 (1): 41-51.; Becker and Cleghorn, 1992Becker L.E. and Cleghorn W.L. (1992). On the buckling of helical compression springs. Int. J Mech. Sci. 34(4):275-282; Chassie et al., 1997Chassie G.G, Becker L.E, Cleghorn W.L. (1997). On the buckling of helical springs under combined compression and torsion. Int. J Mech. Sci. 39(6):697-704), which govern the small perturbations of a helical beam subjected to a static axial load, were employed. An eigen-system was obtained through a Fourier transform along the axis of spring with circular section. Frikha et al. (2011)Frikha A., Treyssède F., Cartraud P. (2011). Effect of axial load on the propagation of elastic waves in helical beams. Wave Motion 48 : 83-92. presented dispersion curves of both loaded and unloaded springs for different parameters such as helix angle, helix index, Poisson coefficient, and axial strain. For high, medium and low-frequency ranges they highlighted the effect of load on wave propagation. A branch identification of dispersion curves was performed for both propagating and non-propagating modes. The effect of loading was found to be significant on the four propagating modes in a low-frequency range. The dispersion curve of the flexural mode oscillating in the normal direction shifted to higher frequencies under tensile loads and vice-versa for compressive loads.
Yıldırım (2012Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033.) established governing equations of the helical springs with a static axial load based on the Özbek's work (1966Özbek T. (1966). On the general buckling theory of elastic curved rods, Ph.D. Thesis (in Turkish), Istanbul Technical University, Faculty of Civil Eng. Turkey.). Using the linearized disturbance dynamic equations derived systematically in Yıldırım's study (2012), a few functional works were conducted (Yıldırım, 2009aYıldırım V. (2009a). Numerical buckling analysis of cylindrical helical coil springs in a dynamic manner, Int. J Eng. Appl. Sci. 1 (1), 20-32.; İbrikçi et al. 2010Ibrikçi T, Saçma S, Yıldırım V, Koca T. (2010). Application of artificial neural networks in the prediction of critical buckling loads of helical compression springs. Stroj. Vestn. 56(6):409-417.). In (Yıldırım, 2009aYıldırım V. (2009a). Numerical buckling analysis of cylindrical helical coil springs in a dynamic manner, Int. J Eng. Appl. Sci. 1 (1), 20-32.), the numerical buckling analysis of such springs was performed based on the dynamical approach. Ibrikçi et al. (2010Ibrikçi T, Saçma S, Yıldırım V, Koca T. (2010). Application of artificial neural networks in the prediction of critical buckling loads of helical compression springs. Stroj. Vestn. 56(6):409-417.) proposed the use of artificial neural networks (ANN) to predict perfectly the critical buckling loads of cylindrical isotropic and homogeneous helical spring with fixed ends and with circular sections, and also having large pitch angles. Then almost perfect weight values were obtained to predict the non-dimensional buckling loads. The theory in Yıldırım's study (2012) was extended to the free vibration of composite cylindrical helical springs under compression by Kacar and Yıldırım (2011Kacar İ. and Yıldırım V. (2011). Natural frequencies of composite cylindrical helical springs under compression. Vibration Problems ICOVP 2011. The 10th International Conference on Vibration Problems, Springer Proceedings in Physics, Editors: Náprstek, J., Horáček, J., Okrouhlík, M., Marvalová, B.,Verhulst, F., Sawicki, J.T. (Eds.) 119-124., 2016Kacar İ. and Yıldırım V. (2016) Free Vibration/Buckling Analyses of Non-Cylindrical Initially Compressed Helical Composite Springs. Mechanics Based Design of Structures and Machines DOI: 10.1080/15397734.2015.1066687
https://doi.org/10.1080/15397734.2015.10...
). In Kacar and Yıldırım's study (2016)Kacar İ. and Yıldırım V. (2016) Free Vibration/Buckling Analyses of Non-Cylindrical Initially Compressed Helical Composite Springs. Mechanics Based Design of Structures and Machines DOI: 10.1080/15397734.2015.1066687
https://doi.org/10.1080/15397734.2015.10...
the stiffness matrix method was used for the solution procedure. For a helical element with constant static axial load, the element stiffness matrix which has six degrees of freedom at each node was obtained with the help of the complementary functions method (Haktanır, 1995Haktanır, V. (1995). The Complementary Functions Method for the Element Stiffness Matrix of Arbitrary Spatial Bars of Helicoidal Axes. Journal International Journal for Numerical Methods in Engineering 38 (6): 1031-1056). Kacar and Yıldırım (2016)Kacar İ. and Yıldırım V. (2016) Free Vibration/Buckling Analyses of Non-Cylindrical Initially Compressed Helical Composite Springs. Mechanics Based Design of Structures and Machines DOI: 10.1080/15397734.2015.1066687
https://doi.org/10.1080/15397734.2015.10...
presented natural frequencies and buckling loads of barrel, hyperboloidal and conical unidirectional composite helical springs with circular and rectangular sections.
Kobelev (2014Kobelev V. (2014). Effect of static axial compression on the natural frequencies of helical springs. Multidiscipline Modeling in Materials and Structures 10 (3): 379 - 398. http://dx.doi.org/10.1108/MMMS-12-2013-0078
http://dx.doi.org/10.1108/MMMS-12-2013-0...
) studied the load dependence of transverse vibrations for helical springs by developing equations, which were represented by two coupled second order differential equations. Kobelev's (2014)Kobelev V. (2014). Effect of static axial compression on the natural frequencies of helical springs. Multidiscipline Modeling in Materials and Structures 10 (3): 379 - 398. http://dx.doi.org/10.1108/MMMS-12-2013-0078
http://dx.doi.org/10.1108/MMMS-12-2013-0...
method was based on the concept of an equivalent column. He derived the explicit formulas for the fundamental natural frequency of the transverse vibrations of the spring depends on the variable length of the spring. The reduction of frequency with the load was demonstrated by Kobelev (2014)Kobelev V. (2014). Effect of static axial compression on the natural frequencies of helical springs. Multidiscipline Modeling in Materials and Structures 10 (3): 379 - 398. http://dx.doi.org/10.1108/MMMS-12-2013-0078
http://dx.doi.org/10.1108/MMMS-12-2013-0...
. In this study, similar to the Reference (Yıldırım, 2009aYıldırım V. (2009a). Numerical buckling analysis of cylindrical helical coil springs in a dynamic manner, Int. J Eng. Appl. Sci. 1 (1), 20-32.), it was shown that when the frequency nullifies the spring buckling occurs. It was also shown that the first vibration modes of helical springs correspond to low-frequency motions and they are strongly affected by the presence of applied axial loads.
In the present work, an accurate free vibration frequencies of isotropic and homogeneous cylindrical helical springs with circular section are conducted numerically in a detailed manner with the help of the equations offered by Yıldırım (2012Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033.). The transfer matrix method is employed for the numerical analysis. The exact numerical overall transfer matrix is obtained by an effective numerical algorithm developed previously for the springs without initial loads (Yıldırım, 1996Yıldırım V. (1996). Investigation of parameters affecting free vibration frequency of helical springs. International Journal for Numerical Methods in Engineering 39: 99-114.). Validity of this algorithm for even the springs with initial static loads is demonstrated. To determine the geometrical configuration of the spring subjected to a static axial force, an analytical expression taking into account for the whole effect of the stress resultants such as axial and shearing forces, bending and torsional moments is used (Yıldırım, 2012Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033., 2016Yıldırım V. (2016). Exact determination of the global tip deflection of both close-coiled and open-coiled cylindrical helical compression springs having arbitrary doubly-symmetric cross-sections. Int. J. Mech. Sciences, 115-116: 280-298.). The present natural frequencies obtained by the method described above are then compared with the available literature. A good harmony is observed with related benchmark studies. The effects of shear/axial deformations and stress resultants on the natural frequencies are investigated. The present work also takes attention to the relationship between buckling loads and natural frequencies. Forward-shifting of frequencies in higher modes is made obvious. It is revealed that both free and forced vibration analyses with an axial static load should be performed after carrying out corresponding buckling analysis to achieve rational results.
2 GOVERNING EQUATIONS OF A SPATIAL BAR SUBJECTED TO STATIC AXIAL LOADS
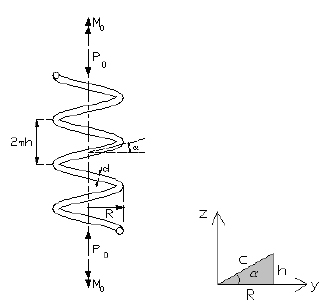
Consider a curved spatial bar having the curvilinear position coordinate s, and let t be the time. Let T* (s,t) =(T* t,T* n,T* b ) be the internal force vector, let M* (s,t) =(M* t,M* n,M* b ) be the internal moment vector. Where T* t is the axial force; T* n and T* b are shearing forces; M* t is the torsional moment; M* n and M* b re the bending moments, respectively. Let Ω* (s,t) =( Ω* t, Ω* n, Ω* b ) be the rotation vector, and U* (s,t) =(U* t,U* n,U* b ) be the displacement vector in Frenet coordinates (t,n,b) (Figure 1). Initial internal static force and moment vectors are denoted by To (s) and Mo (s) respectively. The external distributed force and moment vectors are illustrated by p(s,t) and m(s,t), respectively.
Yıldırım (2012Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033.) derived systematically and consistently the following governing equations in a vector form for a spatial bar to study the static, buckling and vibration problems in the framework of spatial Timoshenko beam theory.
where
In the above, the undeformed cross-sectional area is denoted by A, the moments of inertia with respect to the normal and binormal axes are denoted by In and Ib respectively. Jb is the torsional moment of inertia, G is the shear modulus and E is the Young's modulus. Kn and Kb represent the Timoshenko's k-factors. For doubly symmetric cross sections, Timoshenko's k-factors are equal to each other, Kn = Kb In equations (2)Ct is the axial rigidity, Cn and Cb are shearing rigidities, Dt is the torsional rigidity, Dn and Db are bending rigidities. For the unit length, the inertia force and moments in Equation (1) are defined as
Here, μ is the mass per unit length of the rod, kt, kn, kb are the radii of gyration with respect to the (t, n, b) axes, respectively.
where ρ is the density of the rod material.
3 NON-DIMENSIONAL FREE VIBRATION EQUATIONS OF A CYLINDRICAL HELICAL SPRING SUB JECTED TO A STATIC AXIAL FORCE
Let α be the helix pitch angle, θ be the angular coordinate, and R=(D/2) be the radius of the cylinder. Frenet-Serret relations for cylindrical helical springs are given by (Yıldırım, 1999Yıldırım V. (1999). An efficient numerical method for predicting the natural frequencies of cylindrical helical springs. International Journal of Mechanical Sciences 41/8: 919-939.a)
where the curvature and tortuosity are as follows
and
The free axial length of the helix is defined by
In equation (8), the total number of active turns is denoted by n. Frenet components of the equivalent force-couple system at any section of the spring wire due to the initial static axial force and moment vectors will be in the following form of (Figure 2)
In order to study the free vibration analysis, the following harmonic solution may be assumed for equations (1)
without external loads, p(s,t)=0 and m(s,t)=0. Where ω (rad/s) is the circular frequency. Substituting equation (10) into equation (1), employing Frenet-Serret relations given in equation (5), considering ds = cdθ for helical elements, and then using equation (9), a set of twelve linear differential scalar equations in Frenet trihedral, which govern the free vibration of a cylindrical helical springs subjected to a static axial load, are achieved as follows (Yıldırım, 2012Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033.).
These linear equations given above have constant coefficients and valid for isotropic and homogeneous cylindrical helical springs with uniform sections having double symmetry axes. The free vibration equations presented by Becker et al. (2002Becker L.E., Chassie G.G., Cleghorn W.L. (2002). On the natural frequencies of helical compression springs. International Journal of Mechanical Sciences 44(4): 825-841.) coincide with the equations presented above in the absence of the first terms of Equations (11j), (11k) and (11l). The first terms of Equations (11j), (11k) and (11l) represent the shear deformation effects of the static axial load (Yıldırım, 2012Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033.). Equations (11) may be expressed in a matrix notation as
where the state vector is given by
and D(θ, ω, Po, Mo ) is the dynamic differential matrix. In the present study Equations (11) are put in a non-dimensional form by using the followings
and
Taking Mo = 0 and using Equations (14) and (15), elements of the dimensionless differential matrix to be used in the present study for the free vibration analysis of the spring under a static axial force can be attained.
4 DETERMINATION OF THE GLOBAL TIP DEFLECTION OF THE SPRING UNDER A STATIC FORCE
In a true free vibration formulation of helical springs it is necessary to implement the true deflected configuration of the spring due to the applied static axial force. Otherwise the numerical free vibration studies cannot give satisfactory results according to the specifications of the helix. So a general formulation of the static deflection under an axial force is required for both static and dynamic analyses. It may be noted that this is also achieved by a numerical analysis.
Even today the helical spring formulas derived in 1960s still continue to be used in the spring design. These formulas are used in special conditions/sections and do not consider the whole simultaneous effect of the stress resultants such as axial and shearing forces, bending and torsional moments on the deformations. So they cannot called global. The popular deflection formula for closed coiled springs, α ≤ 10º proposed by Wahl (1963Wahl A.M. (1963). Mechanical Springs, Second Edition, McGraw-Hill, New York.) is given by
This formula may be used for open coiled helices, α ≤ 10º by introducing an additional factor of cosα as follows
Both Equations (16) and (17) account for just the effect of the torsional moment on the tip deflection. However, it is obvious from Equation (9) that when even a single static axial force acts on the center of the helix then the four different types stress resultants such as an axial force, a shearing force, a bending moment and a torsional moment appear at the center of the cross-section of the helix wire. One may readily reach the consequence that there must be contributions of all the remaining stress resultants omitted in the literature on the global tip deflection of the spring.
Under a static axial force, for the determination of the vertical tip deflection of cylindrical helical compression springs with any closed section having double symmetry axes the following equation is proposed by Yıldırım (2012Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033., 2016Yıldırım V. (2016). Exact determination of the global tip deflection of both close-coiled and open-coiled cylindrical helical compression springs having arbitrary doubly-symmetric cross-sections. Int. J. Mech. Sciences, 115-116: 280-298.) and Haktanır (1994Haktanır V. (1994). Analytical expression of the parameters effecting the spring stiffness of helical springs of arbitrary shaped subjected to compression force. 6. International Symposium, Design and Manufacture of Machines, METU, Ankara, September 21-23, 473-482.).
Definitions of the cross sectional rigidities in Equation (18) are given in Equation (2). In the above equation, first term represents the effect of the shearing force, the second term is the effect of the axial force, the third term corresponds to the effect of bending moment and finally the last term is the effect of the torsional moment. Equation (18) implies that even for springs having very small angles there is a contribution of each stress resultants on the total deflection.
While Equation (18), which was obtained based on the Castigliano's first theorem (Haktanır, 1994Haktanır V. (1994). Analytical expression of the parameters effecting the spring stiffness of helical springs of arbitrary shaped subjected to compression force. 6. International Symposium, Design and Manufacture of Machines, METU, Ankara, September 21-23, 473-482.) , is valid for helical springs having doubly symmetric cross-sections such as solid circle, square, rectangle, ellipse, and hollow circle etc., both Equations (16) and (17) are valid for just solid circular cross sections having the following properties.
From the last term of Equation (18), Equation (17) is effortlessly obtained as follows
It is very clear that Equation (16) is a special case of Equation (17) with cosα=1 For closed-coiled springs, the effects of both the shearing force and torsional moment become leading whereas the effects of both the axial force and bending moment gain a gradually increasing impact on open coiled springs. Wahl (1963Wahl A.M. (1963). Mechanical Springs, Second Edition, McGraw-Hill, New York.) also offered the following formula to consider both the shearing force and torsional moment effects on the axial tip deflection.
This equation is also achieved by Equation (18) with C = D/d = 2R/d, cosα=1 and sinα = 0
when Kb = 1 Wahl's (1963Wahl A.M. (1963). Mechanical Springs, Second Edition, McGraw-Hill, New York.) corrected formula concurs with the present closed coil formulas in which α = 0 After a quick inspection for 0 ≤ α ≤ 40º it may be revealed that the maximum effect of the axial force is around 1% and of shearing force is around 6%. For large helix angles, while the effect of the torsional moment on the tip deflection decreases to around 65%, the effect of the bending moment increases to around 35%. Consequently, the computation truly of the tip deflection of the spring under static axial load is one of the crucial step of the vibration analysis of such springs. It may be noted that those effects gain considerably importance for especially non-circular cross-sections.
In the following sections of the present study, equations given in (16-18) are all examined to get a strong idea about the free vibration response of cylindrical helical springs with solid circle sections.
5 NUMERICAL DETERMINATION OF THE OVERALL TRANSFER MATRIX CONSISTING OF A SINGLE HELICAL ELEMENT
As stated above, in the present study, the equations solved numerically based on the transfer matrix method with an effective numerical algorithm previously offered by the author (Yıldırım, 1996Yıldırım V. (1996). Investigation of parameters affecting free vibration frequency of helical springs. International Journal for Numerical Methods in Engineering 39: 99-114.). This algorithm allows to model the whole continuous system by a single helical element without confronting any numerical difficulty and any numerical instability even if the effect of the static axial load is considered. Since it corresponds to the analytical series solution of the governing equation, the numerical results are assumed to be exact. In this section the transfer matrix method and the numerical algorithm for the determination of the element transfer matrix will be described briefly below.
In the transfer matrix method, the solution to Equation (12) is given by Pestel and Leckie (1963Pestel E.C. and Leckie F.A. (1963). Matrix Methods in Elastomechanics, NewYork, McGraw-Hill.) as follows
where S(0) is the state vector at section θ = 0and F(θ ) is the overall transfer matrix. Solution of Equation (23) is applicable for the helix having either varying or constant cross-sections. The transfer matrix also satisfies the following differential equation in all cases.
with the initial conditions
where I is the unit matrix. Numerical computation of the overall transfer matrix is a crucial step in the transfer matrix method. If it is obtained in an accurate manner, then the results should be acceptable as accurate. The analytical solution of the overall transfer matrix in (25) for constant cross-sections is (Pestel and Leckie, 1963Pestel E.C. and Leckie F.A. (1963). Matrix Methods in Elastomechanics, NewYork, McGraw-Hill.).
This solution is generally preferred in the literature due to its simplicity (Pearson, 1982Pearson D. (1982). The transfer matrix method for the vibration of compressed helical springs. J Mech. Eng. Sci. 24:163-171.; Becker et al., 2002Becker L.E., Chassie G.G., Cleghorn W.L. (2002). On the natural frequencies of helical compression springs. International Journal of Mechanical Sciences 44(4): 825-841.). However, it is not possible numerically to take enough terms in the exact solution of Equation (26). So this leads to consider lots of helical elements to form the whole helix axis. In this case the element transfer matrix is computed for each division. A proper successive multiplication of the element transfer matrices renders the overall transfer matrix (Pestel and Leckie, 1963Pestel E.C. and Leckie F.A. (1963). Matrix Methods in Elastomechanics, NewYork, McGraw-Hill.).
Usually, when applying this series solution it should be necessary to take some numerical preventative measures for especially springs having large helix angles and large active turns. One of this precaution is the application of the Cayley-Hamilton theorem to the series solution (26). Based on the theorem, Equation (26) may be put in the form of
where Φk(θ) are functions of scalar infinite series in θ. Utilization of each term of the series Φk(θ) of Equation (27) corresponds to twelve terms in (26). The number of terms taken from the infinite series Φk(θ) determines the accuracy of the solution. In the present study, 1000 terms are taken in each Φk(θ) series of Equation (27) for each θ = π to calculate the overall transfer matrix. This number of terms corresponds to the 12000 terms in Equation (27). The number of terms can be increased without any trouble to increase the accuracy of solution in the numerical algorithm previously developed by the author (Yıldırım, 1996Yıldırım V. (1996). Investigation of parameters affecting free vibration frequency of helical springs. International Journal for Numerical Methods in Engineering 39: 99-114.). Letting m be the total number of terms to be taken in Equation (27), each Φ series may be put in the following form of
where each element Tk ( i ) in Φ series may be computed from the previous element Tk ( i - 1).
where
and for k ≤ 0 for any i, Tk ( i ) becomes zero. The coefficients of the characteristic determinant of the differential matrix, |D - λI| are denoted by pi. The first terms of Tk ( i ) are defined as follows
When the coefficients qk of the characteristic polynomial given by the following equation are available, Tk ( i ) terms are calculated recursively and then the transfer matrix is obtained in an accurate manner.
As it is well known, every square matrix satisfies its characteristic equation as shown below
The numerical algorithm in (Yıldırım, 1996Yıldırım V. (1996). Investigation of parameters affecting free vibration frequency of helical springs. International Journal for Numerical Methods in Engineering 39: 99-114.) is valid for a square matrix D having the following property
It may be proved simply that the differential transfer matrix formed by Equation (11) satisfies this condition for even cylindrical helical springs with a static axial load. Let us change the order of elements of the state vector as follows
In this case the differential matrix may be subdivided into four parts as in the following form of
where
and
In this situation, the coefficients of the odd powers of the differential matrix, Dy in its characteristic polynomial becomes zero. Due to the fundamental features of the transfer matrix, it is stated that the matrices D and Dy are similar, and so they and their powers have the same trace and determinants. This reveals that the numerical algorithm devised for effectively computation of the helical element transfer matrix in the absence of the static axial force may continue to be used for successfully estimation of the helical element transfer matrix with a static axial load.
For a given axial static load and by using the corresponding helix geometry, after computation of F , the frequency equation can be obtained from the boundary conditions given at both ends (θ = 0 and θ = 2(n) using Equation (23). For instance, the eigen value equation for fixed-free ends ((=0, U=0) is reduced to the following
As seen from Equation (39), the order of determinant is only six for the spring supported at both ends. As described, the transfer matrix method offers an exact solution with minimal computation memory requirement for dynamic problems if the overall transfer matrix is calculated numerically in an accurate manner. In this study, the free vibration frequencies are obtained by the method of searching determinant. Accordingly, numerical values are attributed to the natural frequency and the corresponding determinant is computed. The values making the determinant zero are assumed to be the natural frequencies of the helix. All numerical computations were performed using the double-precision arithmetic.
6 VERIFICATION OF THE RESULTS WITH/WITHOUT A STATIC AXIAL FORCE
To check the accuracy of the present results a benchmark spring which is not subjected to any static axial force is first considered. The material and geometrical properties together with boundary conditions of the spring are as follows: Lo/D=3.6, δ/Lo=0, n=7.6, C=D/d=10, d=1mm, ρ =7900kg/m 3 , υ = 0.3, G=79.269 GPa, α 0 = 8.5744º, Kn=Kb=1.1, Fixed-Fixed ends. The results are presented in Table (1). From Table (1) it is observed that the natural frequencies obtained by the transfer matrix method show a good harmony. The minor differences between the present study and Reference (Yıldırım, 1999Yıldırım V. (1999). An efficient numerical method for predicting the natural frequencies of cylindrical helical springs. International Journal of Mechanical Sciences 41/8: 919-939.a) probably steam from the number of terms considered in the numerical computation of the overall transfer matrix.
Natural frequencies (in rad/s) for the benchmark spring (TMM: Transfer matrix method, FEM: Finite element method, EXP: Experimental).
The widely held formula for the fundamental frequency in axial mode, faxial (in Hz), in the literature (Haringx, 1949Haringx J. A. (1949). On highly compressible helical springs and rubber rods, and their application for vibration-free mountings. Philips Research Reports 4: 49-80.) is given by
In the second example a cylindrical helical spring under an axial static load compressed to half of its free axial length is considered. Material and geometric properties of the spring having clamped supports at two ends are: Lo/D=5, δ/Lo=0.5, n=30, C=10, d=1mm, ρ = 7900 kg/m 3 , υ = 0.3 G=79.269 GPa. Those properties correspond to α 0 = 3.036789 (in degrees), α =1.517861 (in degrees), faxial = 118.80Hz (ωaxial = 746.44rad/s) by considering equations L0/D = nπtanα 0 and L/D = nπtanα (where δ = L 0 -L). In this example, since the helix pitch angle is very small (<<5o ), the effects of the axial force and bending moment on the tip deflection may be negligible. However, the shearing effect should be considered.
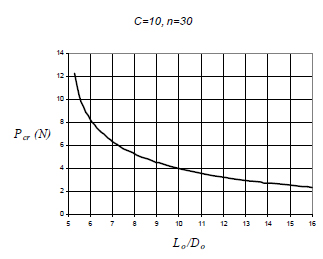
The corresponding axial static load to the prescribed deflection is to be found as Po=8.2532 Newton by using Equation (18). This value was found as 8.242 by Becker et al. (2002Becker L.E., Chassie G.G., Cleghorn W.L. (2002). On the natural frequencies of helical compression springs. International Journal of Mechanical Sciences 44(4): 825-841.). Now, Let's check whether the applied axial force, P 0, is equal to critical buckling load, Pcr , by using Figure (3). As shown from this figure Pcr > 12N for this example. This verifies that the first frequency will be found is certainly to be the fundamental frequency of the spring loaded by a static axial load.
Critical buckling loads obtained in a static manner (Yıldırım, 2009bYıldırım V. (2009b). Report: Buckling and Free Vibration Problems of Helical Compression Springs with Pre-Load: A Software Program and Design Charts. Ankara: Tübitak (The Scientific and Technological Research Council of Turkey).).
For the sake of the comparison, by using Equations (16) and (18), the first 16 natural dimensionless frequencies of the spring considered are presented in Table (2) in a comparative manner with benchmark results. Since the helix pitch angle is small, the additional terms considered in the present study will be gained an importance. As shown from Table (2) those terms affect just symmetric and asymmetric bending modes. As expected, for small helix angles, the analytical theory may give acceptable results. Again a good accordance between Becker et al's (2002Becker L.E., Chassie G.G., Cleghorn W.L. (2002). On the natural frequencies of helical compression springs. International Journal of Mechanical Sciences 44(4): 825-841.) and present results is observed. It may be noted that Becker et al. (2002)Becker L.E., Chassie G.G., Cleghorn W.L. (2002). On the natural frequencies of helical compression springs. International Journal of Mechanical Sciences 44(4): 825-841. computed those frequencies by employing Equation (17).
The first 16 natural dimensionless frequencies (f/faxia l ) for a cylindrical helical spring under a static axial load compressed to half of its free axial length.
By using Equation (18) which considers the whole effect of the resultant force on the tip deflection of the spring, the present first 16 natural frequencies for a cylindrical helical spring considered are tabulated in Table (3) based on the Timoshenko and Bernoulli-Euler hypotheses. As shown from the table, the differences between two theories become visible for P 0 ≠ 0.
The present first 16 natural frequencies for a cylindrical helical spring based on the Timoshenko and Bernoulli-Euler hypotheses by using Equation (18).
For this example, effects of the axial and shear deformations on the first 16 natural dimensionless frequencies are also studied and presented in Table (4). In Bernoulli-Euler results of Becker et al (2002Becker L.E., Chassie G.G., Cleghorn W.L. (2002). On the natural frequencies of helical compression springs. International Journal of Mechanical Sciences 44(4): 825-841.), rotational inertia effects are also neglected together with axial and shear deformation effects. As is well known, those effects will become more clear for small spring indices, C<10 and some types of cross sections such as rectangular shapes.
Effects of the axial and shear deformations on the first 16 natural dimensionless frequencies (Po=8.242 N).
7 NUMERICAL EXAMPLE FOR BUCKLING AND FREE VIBRATION WITH A STATIC AXIAL FORCE
As it is well known, the critical buckling loads may also be determined in a dynamic manner (Yıldırım, 2012Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033.; Kobelev, 2014Kobelev V. (2014). Effect of static axial compression on the natural frequencies of helical springs. Multidiscipline Modeling in Materials and Structures 10 (3): 379 - 398. http://dx.doi.org/10.1108/MMMS-12-2013-0078
http://dx.doi.org/10.1108/MMMS-12-2013-0...
). In this method, for a given static axial load, from P
0 to Pcr
at which the fundamental frequency of the spring becomes zero, the fundamental frequencies of the spring are searched.
The effect of especially bending moment on the tip deflection increases with increasing helix pitch angle. Increasing the helix pitch angle results in an increase in Lo/D ratios while the number of active turns remain constant. To see the effect of bending moment on both the critical buckling load and the free vibration frequencies of a compressed spring, here a cylindrical helical spring having the same properties of the spring in the previous example, except n=5 and Lo/D=10, is studied. Those properties are in contact with α 0 = 32.4816366o and faxial = 712.8014 Hz (ωaxial =4478.663 rad/s).
By using Equation (18), it is almost impossible to distinguish directly of the initial force which corresponds to a given δ/L 0 ratio. This may be done by numerically as shown in Table (5).
Percent effects of the each stress resultants on the relative compression for some applied axial forces.
From the Table (5), for δ = 10cm, it is stated that while the percent contribution of the bending moment on the total tip deflection is about 24%, this value is about 76% for the torsional moment.
For this example present free vibration frequencies and critical buckling load which are both obtained by using Equation (18) are presented in Table (6). The critical buckling load corresponds Pcr =21.283 (N) at which the fundamental frequency is ω 1 =1.31086 (Hz), critical helix pitch angle is αcr = 29.287 (o), and the relative compression is δ/L 0 0.11897.
Free vibration frequencies and critical buckling load which are both obtained by using Equation (18).
From the Table (6) it is shown that after determining the critical buckling load, the fundamental frequency is lost and replaced by the lowest second frequency. This means that buckling occurred. For the spring with a static axial force, natural frequencies higher than the first are all shifted forward. The numerical free vibration analysis continues to produce natural frequencies for the post buckling case.
As stated above, Equation (17), consider the deflection due to just torsional moment for large helix angles. Using this equation, the present free vibration frequencies and critical buckling load are also computed and presented in Table (7). In this case natural frequencies are found smaller than frequencies given in Table (6). From table (7), it is again observed the forward-shifting phenomenon of the frequencies in higher modes.
Free vibration frequencies and critical buckling load which are both obtained by using Equation (17).
As it is well known, the common equation numbered by (16) consider the deflection due to the just torsional moment for small helix angles. Finally, to see the effect of Equation (16), Let's consider Table (8). In this situation, natural frequencies have the numerical values between Table (6) and Table (7).
Free vibration frequencies and critical buckling load which are both obtained by using Equation (16).
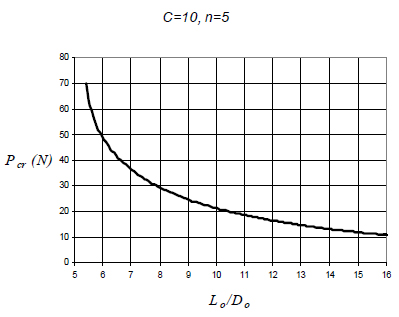
Figure (5) shows the critical buckling loads obtained in a static manner for this example. The numerical values of the critical buckling loads calculated by both static and dynamic manners are exhibited in Table (9) in a concise way. From this table, it may be concluded that critical buckling loads obtained by using Equation (18) gives the higher values. This means that critical buckling loads found by Equations (16) and (17) fell in a safe region in design for this example.
Critical buckling loads obtained in a static manner for C=10 and n=5 (Yıldırım, 2009bYıldırım V. (2009b). Report: Buckling and Free Vibration Problems of Helical Compression Springs with Pre-Load: A Software Program and Design Charts. Ankara: Tübitak (The Scientific and Technological Research Council of Turkey).).
8 CONCLUSIONS AND DISCUSSIONS
Vibration analysis of the springs under axial static loads requires a precise study to understand the real behavior of the springs. To accomplish such an accurate analysis first the most comprehensive differential equations which comprise some additional terms for taking into account for the axial and shear deformation terms on the buckling and vibration were used, second the exact total tip deformation for a spring subjected to an axial force is calculated by using a global analytical formula considering the whole effect of the resultant forces on the tip deflection, third the overall exact transfer matrix is numerically calculated by using an effective numerical algorithm. As a result, those choices render an accurate numerical free vibration analysis of cylindrical helical springs under a static axial force based on the transfer matrix method.
The vibration modes correspond to low-frequency motions are strongly affected by the presence of applied static axial loads as Kobelev stated (2014Kobelev V. (2014). Effect of static axial compression on the natural frequencies of helical springs. Multidiscipline Modeling in Materials and Structures 10 (3): 379 - 398. http://dx.doi.org/10.1108/MMMS-12-2013-0078
http://dx.doi.org/10.1108/MMMS-12-2013-0...
). In the present study the forward-shifting phenomenon of the natural frequencies in higher modes are observed after buckling. That is with a small increment of the value of the applied static load, one may get the next natural frequency after buckling occurs. Before determining the natural frequencies subjected to a certain static axial force, the axial force considered should be tested for the critical buckling load. The author offers that a free and/or forced vibration analysis with an axial static load should not be performed individually without checking buckling loads.
Acknowledgements
The material covered in this paper is based upon work was supported by the research grant 106M307 from Technical Research Council of Turkey (TUBITAK).
References
- Becker L.E. and Cleghorn W.L. (1992). On the buckling of helical compression springs. Int. J Mech. Sci. 34(4):275-282
- Becker L.E., Chassie G.G., Cleghorn W.L. (2002). On the natural frequencies of helical compression springs. International Journal of Mechanical Sciences 44(4): 825-841.
- Busool W. and Eisenberger M. (2002). Free Vibration of Helicoidal Beams of Arbitrary Shape and Variable Cross Section. J. Vib. Acoust. 124(3), 397-409.
- Chassie G.G, Becker L.E, Cleghorn W.L. (1997). On the buckling of helical springs under combined compression and torsion. Int. J Mech. Sci. 39(6):697-704
- Farshad M. (1980). Wave propagation in prestressed curved rods. J. Eng. Mech. Div. 106: 395-408.
- Frikha A., Treyssède F., Cartraud P. (2011). Effect of axial load on the propagation of elastic waves in helical beams. Wave Motion 48 : 83-92.
- Girgin K., Olgun O., Darılmaz K., and Omurtag M.H. (2006). Dynamic analysis of cylindrical and conical helices by mixed FEM, Journal of Turkish Chamber of Civil Engineering (İMO Teknik Dergi) 4003-4023 (in Turkish)
- Haktanır V. (1994). Analytical expression of the parameters effecting the spring stiffness of helical springs of arbitrary shaped subjected to compression force. 6. International Symposium, Design and Manufacture of Machines, METU, Ankara, September 21-23, 473-482.
- Haktanır V. and Kıral E. (1992). Computation of free vibration frequencies of helical springs subjected to axial load. Journal of Engineering Faculty of Isparta of Akdeniz University 6: 201-218.
- Haktanır, V. (1995). The Complementary Functions Method for the Element Stiffness Matrix of Arbitrary Spatial Bars of Helicoidal Axes. Journal International Journal for Numerical Methods in Engineering 38 (6): 1031-1056
- Haringx J. A. (1949). On highly compressible helical springs and rubber rods, and their application for vibration-free mountings. Philips Research Reports 4: 49-80.
- Ibrikçi T, Saçma S, Yıldırım V, Koca T. (2010). Application of artificial neural networks in the prediction of critical buckling loads of helical compression springs. Stroj. Vestn. 56(6):409-417.
- Kacar İ. and Yıldırım V. (2011). Natural frequencies of composite cylindrical helical springs under compression. Vibration Problems ICOVP 2011. The 10th International Conference on Vibration Problems, Springer Proceedings in Physics, Editors: Náprstek, J., Horáček, J., Okrouhlík, M., Marvalová, B.,Verhulst, F., Sawicki, J.T. (Eds.) 119-124.
- Kacar İ. and Yıldırım V. (2016) Free Vibration/Buckling Analyses of Non-Cylindrical Initially Compressed Helical Composite Springs. Mechanics Based Design of Structures and Machines DOI: 10.1080/15397734.2015.1066687
» https://doi.org/10.1080/15397734.2015.1066687 - Kobelev V. (2014). Effect of static axial compression on the natural frequencies of helical springs. Multidiscipline Modeling in Materials and Structures 10 (3): 379 - 398. http://dx.doi.org/10.1108/MMMS-12-2013-0078
» http://dx.doi.org/10.1108/MMMS-12-2013-0078 - Lee J. (2007). Free vibration analysis of non-cylindrical helical springs by the pseudospectral method. Journal of Sound and Vibration 305 (3): 543-551.
- Mottershead J.E. (1982). The large displacements and dynamic stability of springs using helical finite elements. Int. J Mech. Sci. 24(9):547-558
- Mottershead J.E. (1980). Finite elements for dynamical analysis of helical rods, International Journal of Mechanical Sci. 22: 267-283.
- Özbek T. (1966). On the general buckling theory of elastic curved rods, Ph.D. Thesis (in Turkish), Istanbul Technical University, Faculty of Civil Eng. Turkey.
- Pearson D. (1982). The transfer matrix method for the vibration of compressed helical springs. J Mech. Eng. Sci. 24:163-171.
- Pestel E.C. and Leckie F.A. (1963). Matrix Methods in Elastomechanics, NewYork, McGraw-Hill.
- Tabarrok B. and Xiong Y. (1992). A spatially curved and twisted rod element for buckling analysis. Int. J Solids Struc. 29 (23):3011-3023.
- Ünlüsoy Y.S. (1983). Modelling helical springs for the dynamic behavior. Middle East Technical University (METU) Journal of Applied Researches 3(9): 45-57 (In Turkish).
- Wahl A.M. (1963). Mechanical Springs, Second Edition, McGraw-Hill, New York.
- Wittrick W.H. (1966). On elastic wave propagation in helical spring. Int. J Mech. Sci. 8(1):25-47
- Xiong Y. and Tabarrok B. (1992). A finite element model for the vibration of spatial rods under various applied loads. International Journal of Mechanical Sciences 34 (1): 41-51.
- Yalçın V. (1984). Finite element mobility analysis of helical coil springs, MS Thesis, The Graduate School of Natural and Applied Sciences, METU, Turkey.
- Yıldırım V. (1996). Investigation of parameters affecting free vibration frequency of helical springs. International Journal for Numerical Methods in Engineering 39: 99-114.
- Yıldırım V. (1999). An efficient numerical method for predicting the natural frequencies of cylindrical helical springs. International Journal of Mechanical Sciences 41/8: 919-939.
- Yıldırım V. (2009a). Numerical buckling analysis of cylindrical helical coil springs in a dynamic manner, Int. J Eng. Appl. Sci. 1 (1), 20-32.
- Yıldırım V. (2009b). Report: Buckling and Free Vibration Problems of Helical Compression Springs with Pre-Load: A Software Program and Design Charts. Ankara: Tübitak (The Scientific and Technological Research Council of Turkey).
- Yıldırım V. (2012). On the linearized disturbance dynamic equations for buckling and free vibration of cylindrical helical coil springs under combined compression and torsion. Meccanica 47: 1015-1033.
- Yıldırım V. (2016). Exact determination of the global tip deflection of both close-coiled and open-coiled cylindrical helical compression springs having arbitrary doubly-symmetric cross-sections. Int. J. Mech. Sciences, 115-116: 280-298.
- Yu A. M., Yang C.J., Nie G.H. (2010). Analytical formulation and evaluation for free vibration of naturally curved and twisted beams Journal of Sound and Vibration 329: 1376-1389
Publication Dates
-
Publication in this collection
Dec 2016
History
-
Received
29 May 2016 -
Accepted
18 Aug 2016