Abstract
The paper deals with the effect of stress state on the dynamic damage behavior of ductile materials. The rate- and temperature-dependent continuum damage model has been enhanced to take into account the influence of the stress triaxiality and the Lode parameter on damage condition and on rate equations of damage strains. Different branches of these criteria depending on the current stress state are considered based on different damage and failure processes on the micro-level. To get more insight in the dynamic damage and fracture processes micro-mechanical behavior of void-containing representative volume elements have been analyzed numerically. These three-dimensional numerical simulations based on different dynamic loading conditions take into account a wide range of stress states in tension, shear and compression domains. Based on the numerical results general trends of dynamic damage and failure behavior can be shown and stress-state-dependent equations for damage criteria and for the formation of damage strains can be proposed.
Keywords
Ductile damage; stress state dependence; micro-mechanical numerical simulations; dynamic loading
1 Introduction
During the last decades the use of high quality ductile metals like high strength steels, advanced high strength steels and various improved aluminum alloys in complex engineering structures has been remarkably increased especially caused by demands on economic, environmental and material strength requirements. Therefore, accurate and realistic modeling of rate-dependent and rate-independent inelastic deformation and failure behavior of these materials is essential for the numerical simulation of quasi-static and dynamic loading processes of structures. In addition, high strain rate deformation processes such as impact problems, dynamic shear banding or high speed machining have to be analyzed in many industrial applications. This leads to an increasing request on accurate, robust and efficient material models to be able to realistically simulate the mechanical response of engineering structures under dynamic loading conditions. Thus, constitutive approaches taking into account large strains, high strain rates and thermal softening as well as stress-state-dependent damage and fracture criteria have to be developed to realistically predict the failure mechanisms observed in experiments and in various engineering applications.
Different models for analyzing the occurrence of damage and failure in metals under general loading conditions have been proposed to predict heterogeneous material behavior and failure. Motivated by experimental observations phenomenological approaches have been developed using internal damage variables whose growth is described by evolution laws. General frameworks of internal variable theories of high strain rate deformation processes in metals based on rate-dependent continuum mechanics have been published, for example, by Bruhns and Diehl (1989Bruhns, O.T., Diehl, H., 1989. An internal variable theory of inelastic behaviour at high rates of strain. Archive of Mechanics 41, 427-460.); Voyiadjis et al. (2003Voyiadjis, G.Z., Abu Al-Rub, R., Palazotto, R.K., 2003. Non-local coupling of viscoplasticity and anisotropic viscodamage for impact problems using the gradient theory. Archives of Mechanics 55, 39-89.); Brünig (2006Brünig, M., 2006. Continuum framework for rate-dependent behavior of anisotropic damaged ductile metals. Acta Mechanica 186, 37-53.); Brünig and Gerke (2011)Brünig, M., Gerke, S., 2011. Simulation of damage evolution in ductile metals undergoing dynamic loading conditions. International Journal of Plasticity 27, 1598-1617.. These models are able to predict the evolution of damage in high strain rate processes but the calibration of material properties and their stress state dependence seems to be difficult. However, accurate and efficient constitutive approaches for stress-state-dependent formation of damage are needed as a basis for theories of ductile fracture.
The main mechanisms leading to damage and fracture in metals are nucleation, growth and coalescence of micro-defects as well as formation of macro-cracks. In this context, analysis of behavior of individual micro-defects can be seen as a straight-forward approach for modeling and simulation of ductile failure processes. Thus, features on the scale of the micro-defects have to be included in studies in order to simulate damage and fracture behavior in an accurate manner. For example, numerical results of unit-cell analyses can be used to develop damage evolution equations in continuum models as well as to identify corresponding micro-mechanically motivated material parameters (Brünig et al. (2013Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65., 2014Brünig, M., Gerke, S., Hagenbrock, V., 2014. Stress-state-dependence of damage strain rate tensors caused by growth and coalescence of microdefects. International Journal of Plasticity 63, 49-63., 2018bBrünig, M., Hagenbrock, V., Gerke, S., 2018b. Macroscopic damage laws based on analysis of microscopic unit cells. ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 98, 181-194.)). Therefore, combination of analyses on both the micro- and the macro-level has widely enriched the understanding of damage and failure processes in ductile metals.
Detailed information on stress state dependence of the microscopic mechanisms can be obtained by systematic finite element analyses with micro-defect containing unit-cells loaded by different macroscopic stress states (Barsoum and Faleskog (2011Barsoum, I., Faleskog, J., 2011. Micromechanical analysis on the influence of the Lode parameter on void growth and coalescence. International Journal of Solids and Structures 48, 925-938.); Brünig et al. (2013Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65., 2014Brünig, M., Gerke, S., Hagenbrock, V., 2014. Stress-state-dependence of damage strain rate tensors caused by growth and coalescence of microdefects. International Journal of Plasticity 63, 49-63., 2018bBrünig, M., Hagenbrock, V., Gerke, S., 2018b. Macroscopic damage laws based on analysis of microscopic unit cells. ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 98, 181-194.); Gao and Kim (2006Gao, X., Kim, J., 2006. Modeling of ductile fracture: Significance of void coalescence. International Journal of Solids and Structures 43, 6277-6293.); Gao et al. (2005Gao, X., Wang, T., Kim, J., 2005. On ductile fracture initiation toughness: Effects of void volume fraction, void shape and void distribution. International Journal of Solids and Structures 42, 5097-5117., 2010Gao, X., Zhang, G., Roe, C., 2010. A study on the effect of the stress state on ductile fracture. International Journal of Damage Mechanics 19, 75-94.); Kim et al. (2003)Kim, J., Gao, X., Srivatsan, T., 2003. Modeling of crack growth in ductile solids: a three-dimensional analysis. International Journal of Solids and Structures 40, 7357-7374.; Nielsen et al. (2012Nielsen, K., Dahl, J., Tvergaard, V., 2012. Collapse and coalescence of spherical voids subject to intense shearing: studies in full 3D. International Journal of Fracture 177, 97-108.); Scheyvaerts et al. (2011Scheyvaerts, F., Onck, P., Tekoğlu, C., Pardoen, T., 2011. The growth and coalescence of ellipsoidal voids in plane strain under combined shear and tension. Journal of the Mechanics and Physics of Solids 59, 373-397.); Zhang et al. (2001Zhang, K., Bai, J., Francois, D., 2001. Numerical analysis of the influence of the Lode parameter on void growth. International Journal of Solids and Structures 38, 5847-5856.)). Their quasi-static numerical studies have shown that the stress state remarkably affects the macroscopic deformation of the representative volume elements, the growth of the micro-defects and the amount of the fracture strain. Even if these numerical calculations are restricted to materials with periodic microstructure they can be seen as an important tool in gaining better understanding of the processes on the micro-level of damage and failure in ductile metals.
Although many papers dealing with quasi-static loading of void containing volume elements exist only minor attention has been drawn on growth of micro-defects under dynamic loading conditions. For example, Carroll and Holt (1972Carroll, M., Holt, A., 1972. Static and dynamic pore-collapse relations for ductile porous materials. Journal of Applied Physics 43, 1626-1636.) studied the dynamic void collapse in an ideally plastic material using a hollow sphere model and Johnson (1981Johnson, J., 1981. Dynamic fracture and spallation in ductile solids. Journal of Applied Physics 52, 2812-2825.) extended this approach considering rate-dependent materials under dynamic hydrostatic tension. Furthermore, Ortiz and Molinari (1992Ortiz, M., Molinari, A., 1992. Effect of strain hardening and rate sensitivity on the dynamic growth of a void in a plastic material. Journal of Applied Mechanics 59, 48-53.) examined the dynamic growth of a single void in an unbounded solid under rapidly varying remote hydrostatic tension loading. They studied the effects of inertia, strain hardening and rate sensitivity on the short and long time behavior of the porous material under dynamic loading conditions as well as the influence of ramp loading. At the early stage of the deformation process the growth of the single pore was affected by strain hardening and strain rate sensitivity whereas inertia dominated the long term part of void growth. Benson (1993Benson, D., 1993. An analysis of void distribution effects on the dynamic growth and coalescence of voids in ductile metals. Journal of the Mechanics and Physics of Solids 41, 1285-1308.) investigated the effect of void distribution on dynamic failure of copper and 4340 steel. Numerical studies with a representative volume element with discrete set of randomly distributed voids loaded by a tension wave showed that the peak transmitted stress was insensitive to the magnitude of the tension wave but dependent on void distribution. The dynamic behavior of porous materials under hydrostatic tension and compression as well as axisymmetric loading conditions has been analyzed by Molinari and Mercier (2001)Molinari, A., Mercier, S., 2001. Micromechanic modelling of porous materials under dynamic loading. Journal of the Mechanics and Physics of Solids 49, 1497-1516. to take into account the effect of the stress triaxiality. They proposed a rate-dependent material model for void-containing solids based on averaging methods and homogeneous kinematic boundary conditions. In addition, Wu et al. (2003aWu, X., Ramesh, K., Wright, T., 2003a. The dynamic growth of a single void in a viscoplastic material under transient hydrostatic loading. Journal of the Mechanics and Physics of Solids 51, 1-26.,bWu, X., Ramesh, K., Wright, T., 2003b. The effects of thermal softening and heat conduction on the dynamic growth of voids. International Journal of Solids and Structures 40, 4461-4478.) investigated the dynamic growth of a single void in an elastic-viscoplastic material under transient hydrostatic loading conditions with focus on inertia, thermal and rate-dependent effects. They found out that the influence of inertia was small in the early stages of void growth but strongly depended on the initial size of the pore and on the loading rate. The process of coalescence of voids in ductile materials subjected to dynamic loading has been examined numerically by Jaques et al. (2012Jaques, N., Mercier, S., Molinari, A., 2012. Void coalescence in a porous solid under dynamic loading conditions. International Journal of Fracture 173, 203-213.). Their finite element simulations showed that inertia led to stabilizing effects and slowed down the coalescence process. This stabilizing influence of inertia is enhanced by higher stress triaxialities, larger initial sizes of the voids and higher loading rates.
The numerical analyses discussed above have clearly shown that the mechanisms of damage and failure processes on the micro-level under dynamic loading conditions are different to those observed under quasi-static loading. These results may give important aspects for rate-dependent constitutive damage approaches. Therefore, the stress-state-dependent continuum damage model proposed by Brünig et al. (2013Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65., 2018bBrünig, M., Hagenbrock, V., Gerke, S., 2018b. Macroscopic damage laws based on analysis of microscopic unit cells. ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 98, 181-194.) will be reconsidered and modified in the present paper and assessed to ensure its suitability for dynamic problems.
2 Fundamental governing equations
The anisotropic continuum damage model proposed by Brünig (2003Brünig, M., 2003. An anisotropic ductile damage model based on irreversible thermodynamics. International Journal of Plasticity 19, 1679-1713.,2004Brünig, M., 2004. An anisotropic continuum damage model: Theory and numerical analyses. Latin American Journal of Solids and Structures 1, 185-219., 2006Brünig, M., 2006. Continuum framework for rate-dependent behavior of anisotropic damaged ductile metals. Acta Mechanica 186, 37-53.); Brünig and Gerke (2011)Brünig, M., Gerke, S., 2011. Simulation of damage evolution in ductile metals undergoing dynamic loading conditions. International Journal of Plasticity 27, 1598-1617. is used to predict the rate-dependent inelastic deformation behavior as well as the evolution of ductile damage and failure in aluminum alloys caused by dynamic loading. Phenomenological modeling of macroscopic damage and failure behavior corresponding to different mechanisms acting on the micro-level caused by various stress states is based on combination of microscopic and macroscopic investigations. They take into account results of numerical simulations on the micro-level analyzing deformation and failure behavior of micro-void-containing unit-cells (Brünig et al. (2013Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65., 2014Brünig, M., Gerke, S., Hagenbrock, V., 2014. Stress-state-dependence of damage strain rate tensors caused by growth and coalescence of microdefects. International Journal of Plasticity 63, 49-63., 2018bBrünig, M., Hagenbrock, V., Gerke, S., 2018b. Macroscopic damage laws based on analysis of microscopic unit cells. ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 98, 181-194.)) as well as results of various experiments with carefully designed specimens under different loading conditions (Brünig et al. (2008)Brünig, M., Chyra, O., Albrecht, D., Driemeier, L., Alves, M., 2008. A ductile damage criterion at various stress triaxialities. International Journal of Plasticity 24, 1731-1755.; Driemeier et al. (2010Driemeier, L., Brünig, M., Micheli, G., Alves, M., 2010. Experiments on stress-triaxiality dependence of material behavior of aluminum alloys. Mechanics of Materials 42, 207-217.); Brünig et al. (2015Brünig, M., Brenner, D., Gerke, S., 2015. Stress state dependence of ductile damage and fracture behavior: Experiments and numerical simulations. Engineering Fracture Mechanics 141, 152-169., 2016Brünig, M., Gerke, S., Schmidt, M., 2016. Biaxial experiments and phenomenological modeling of stress-state-dependent ductile damage and fracture. International Journal of Fracture 200, 63-76.)). This phenomenological approach is briefly summarized and discussed in the present paper.
The continuum model is based on the introduction of damaged and corresponding fictitious undamaged configurations. Considering undamaged configurations the temperature- dependent elastic law for the effective stress tensor of an undamaged material sample is given. In addition, rate-dependent plastic behavior is described using a yield criterion and a flow rule. Furthermore, considering the damaged configurations, the dynamic elastic law for the stress tensor of a damaged material sample also depending on current state of damage is proposed. In addition, rate-dependent damage behavior is governed by a damage criterion and a damage rule both depending on stress triaxiality and the Lode parameter.
Considering the undamaged configurations, the temperature-dependent elastic behavior of the undamaged ductile matrix material is modeled by an isotropic hyper-elastic law leading to the effective Kirchhoff stress tensor
where and are the constant shear and bulk modulus, denotes the coefficient of thermal expansion, represents the elastic part of the logarithmic strain tensor and and mean the current and the reference temperature, respectively. In addition, plastic behavior is characterized by the Drucker-Prager-type yield condition
with the first and second deviatoric stress invariants and and the hydrostatic stress coefficient . The equivalent stress measure
depends on the current equivalent plastic strain measure, , its rate, , and on the current temperature. Following Brünig and Gerke (2011Brünig, M., Gerke, S., 2011. Simulation of damage evolution in ductile metals undergoing dynamic loading conditions. International Journal of Plasticity 27, 1598-1617.), a multiplicative decomposition of the function (3) is taken into account where is the quasi-static yield stress and and are functions of the respective scalar variables and .
Furthermore, the isochoric effective plastic strain rate
is taken to model the evolution of plastic deformations in an accurate manner. In Eq. (4) means a non-negative scalar factor, denotes the normalized deviatoric effective stress tensor and represents the equivalent plastic strain rate characterizing the amount of plastic strain.
Considering the damaged configurations of the continuum approach, constitutive equations for the anisotropically damaged material sample undergoing dynamic loading conditions are formulated. Since formation of damage leads to deterioration of elastic material properties the elastic law takes into account both the elastic and the damage strain tensors, and . Thus, the Kirchhoff stress tensor can be written in the form
where the additional material parameters describe the deteriorating effects of the macroscopic elastic material properties caused by different damage and failure mechanisms acting on the micro-level. In addition, onset and continuation of damage is characterized by the damage criterion
where and represent the first and second deviatoric invariants of the Kirchhoff stress tensor (5) and the rate- and temperature-dependent equivalent damage stress measure
denotes the material toughness to micro-defect propagation depending on the equivalent damage strain measure characterizing the amount of increase in damage and its rate where, again, a multiplicative decomposition is assumed to adequately describe the different effects. In Eq. (7) represents the quasi-static equivalent damage stress and is a function of the scalar variable . The stress-state-dependent parameters and in Eq. (6), which will be identified by results of numerical simulations on the micro-scale for different dynamic loading processes discussed in the present paper, are damage mode parameters corresponding to the different damage mechanisms acting on the micro-level: shear modes for negative stress triaxialities, void-growth-dominated modes for high positive stress triaxialities and mixed modes (simultaneous growth of voids and formation of micro-shear-cracks) for lower positive stress triaxialities. Dependence on the stress state is here formulated in terms of the stress intensity (von Mises equivalent stress), of the stress triaxiality
defined as the ratio of the mean stress and the von Mises equivalent stress as well as of the Lode parameter
written in terms of the principal Kirchhoff stress components , and .
Furthermore, irreversible deformations caused by damage can be determined by the damage strain rate tensor
where the normalized stress related deviatoric tensors and with
have been used and denotes the stress tensor work-conjugate to the damage strain rate tensor (10) (see Brünig (2003Brünig, M., 2003. An anisotropic ductile damage model based on irreversible thermodynamics. International Journal of Plasticity 19, 1679-1713.) for further details). The parameters , and in Eq. (10) are kinematic parameters denoting the portion of volumetric and isochoric damage-based deformations also corresponding to different damage and failure mechanisms on the micro-level. These stress-state-dependent parameters will also be identified by results of numerical simulations on the micro-scale presented below.
3 Numerical simulations on the micro-scale
Dynamic numerical calculations on the micro-level considering a representative volume element (RVE) of ductile metals containing a micro-void have been performed with the commercial finite element software LS-Dyna. The investigated material is an aluminum alloy of series 2017 and its behavior is modeled by the LS-Dyna material model 12. Thus, the constitutive parameters mass density , shear modulus , bulk modulus , plastic hardening modulus and microscopic yield stress have been chosen to adequately characterize the material behavior.
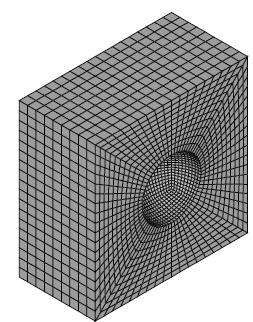
The numerical studies performed by Benson (1993Benson, D., 1993. An analysis of void distribution effects on the dynamic growth and coalescence of voids in ductile metals. Journal of the Mechanics and Physics of Solids 41, 1285-1308.) have shown that the range of the peak transmitted stress was not affected by the number of voids in the representative volume element for both copper and 4340 steel. The mean values were comparable to the values predicted for unit-cells with a single pore with the same void volume fraction. Therefore, in the present dynamic analysis only the effect of a single void on the macroscopic deformation and damage behavior is considered. Figure 1 shows the finite element mesh of one half of the RVE containing 21,384 standard under-integrated LS-Dyna brick elements. The mesh size is rather homogeneous without mesh refinement near the voids since in explicit finite element analysis the smallest element edge determines the time step size.
In contrast to quasi-static analysis on the micro-scale (Brünig et al. (2013Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65.,2014Brünig, M., Gerke, S., Hagenbrock, V., 2014. Stress-state-dependence of damage strain rate tensors caused by growth and coalescence of microdefects. International Journal of Plasticity 63, 49-63., 2018bBrünig, M., Hagenbrock, V., Gerke, S., 2018b. Macroscopic damage laws based on analysis of microscopic unit cells. ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 98, 181-194.)) for microscopic numerical simulations under dynamic loading conditions the physical size of the investigated RVE is of significant importance because material inertia, wave propagation and reflection of waves affect the numerical results. Therefore, the micro-pore structure of the material studied by Becker et al. (1988Becker, R., Needleman, A., Richmond, O., Tvergaard, V., 1988. Void growth and failure in notched bars. Journal of the Mechanics and Physics of Solids 36, 317-351.) has been chosen as reference initially damaged material. Thus, the RVE with initial porosity of is a cube with the initial side length including an initially spherical void.
For numerical analysis of the inelastic deformation behavior of RVEs under various multiaxial dynamic loadings the choice of appropriate boundary conditions is a challenging task since a straight forward approach from static simulations is not possible. Benson (1993Benson, D., 1993. An analysis of void distribution effects on the dynamic growth and coalescence of voids in ductile metals. Journal of the Mechanics and Physics of Solids 41, 1285-1308.) proposed for two-dimensional studies under one-dimensional tension loading the enlargement of the RVE with homogeneous material in loading direction to facilitate an interference-free launching of the applied tension pulse because the applied load is reflected at free surfaces, especially at voids. In his studies, zero displacements are taken into account perpendicular to the unloaded surfaces. Preliminary numerical calculations by Gerke et al. (2014Gerke, S., Kuhnt, K., Brünig, M., 2014. Micro-mechanical numerical analysis of ductile damage under dynamic loading conditions. In: E. Oñate, J. Oliver, A. Huerta (Eds.), Proc. 11th World Congress on Computational Mechanics (WCCM XI), CIMNE Barcelona, 1187-1198.) have shown that this approach could be extended to three-dimensional studies under tension loading. However, generalization of this proceeding to further three-dimensional loading conditions was not possible. Embedding the RVE in all three directions into homogeneous material leads to restriction of inelastic deformations in zones close to the void and softening of the surrounding material results into interferences at material boundaries. Therefore, this approach was not followed up and a new access has to be developed.
Extensive numerical studies of various possible boundary conditions of RVEs with one single void performed by Gerke et al. (2014Gerke, S., Kuhnt, K., Brünig, M., 2014. Micro-mechanical numerical analysis of ductile damage under dynamic loading conditions. In: E. Oñate, J. Oliver, A. Huerta (Eds.), Proc. 11th World Congress on Computational Mechanics (WCCM XI), CIMNE Barcelona, 1187-1198.) have given the following indications: Zero displacements perpendicular to the loading surface may reflect the situation inside of a bigger material sample most appropriatly, but do not allow the application of loading in this direction. Coupled displacements perpendicular to the loading surface guarantee that no gaps between neighboring unit-cells arise, but restrict the deformation during wave propagation and result into not required stress states. Flow-out boundary conditions avoid reflections at the boundaries of the RVE, but consequently the stress intensity within the RVE drops remarkably during the numerical simulation and only smaller deformations are reached which do not reflect the situation in a bigger material sample. Furthermore, for analysis of stress-state-dependent dynamic damage and failure behavior it has to be discussed if the stress pulse is applied on one side of the RVE or simultaneously on both opposite sides. Whereas the application on one side seems to be more appropriate reflecting the real situation, the application on both sides has the advantage that the RVE deforms symmetrically and that the macro-stress-state and, consequently, the stress triaxiality as well as the Lode parameter of the RVE are defined definitely which is an important aspect for identification of stress-state-dependent functions developed in the present paper.
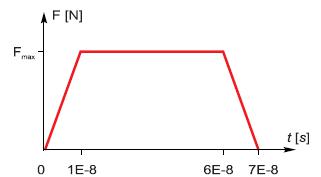
Based on these numerical studies the boundary and loading conditions shown in Fig. 2 are taken to be most appropriate for the objective of the present analysis and have been applied in this paper. In particular, the displacements of the nodes located on each side are not coupled allowing non-continuous displacements of neighboring unit-cells whereas no flow-out boundary conditions are applied. The pulse indicated in Fig. 3 is applied as tension or compression loading simultaneously on opposite sides of the RVE whereas the shape of the pulse is similar to the one occurring in Split-Hopkinson-Pressure-Bar (SHPB) experiments (Brünig and Gerke (2011Brünig, M., Gerke, S., 2011. Simulation of damage evolution in ductile metals undergoing dynamic loading conditions. International Journal of Plasticity 27, 1598-1617.)). The sum of the absolute values of the applied maximum loads is which facilitates a reproducible comparison between different load cases.
The scope of all numerical calculations discussed below is to keep the stress triaxiality coefficient and the Lode parameter nearly constant during the entire loading history of the unit-cell to be able to accurately analyze their effect on damage and failure behavior of ductile metals under dynamic loading conditions. Therefore, for given parameters and and the macroscopic maximum principal stress component , Eqs. (8, 9)))) lead to the other principal stress components (Brünig et al. (2013Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65.)):
with
and
It is worthy to note that only the boundary conditions shown in Fig. 2 lead to almost constant stress triaxialities and Lode parameters during the dynamic loading process allowing analysis of the stress-state-dependent damage behavior of the RVE.
Various loading conditions with principal macroscopic stresses acting on the outer bounds of the representative volume elements are taken into account to be able to cover the wide range of the stress triaxiality coefficients (Eq. (8)) = -1, -2/3, -1/3, 0, 1/3, 1 and 3 as well as of the Lode parameters (Eq. (9)) = -1, 0 and 1.
The effect of stress state on damage during dynamic loading can be demonstrated by the deformation of the micro-defects. Fig. 4 shows the ratios of the principal stress components (first line, bold underlined letters) and the normalized ratios of the deformed semi-axes of the void (second line) as well as the initial (contours) and deformed (blue) shapes of one eighth of the initially spherical voids. As indicated in Brünig et al. (2013Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65.) for numerical simulations under static loading conditions the numerical results of dynamic simulations (Fig. 4) confirm that the effect of the Lode parameter on void deformation is marginal for high stress triaxialities (). The initially spherical voids nearly remain spherical during these loading processes but their sizes remarkably increase. This clearly indicates that also under dynamic loading conditions isotropic void growth is the main microscopic damage mechanism in the high stress triaxiality regime and anisotropy induced by damage does not play a significant role. On the other hand, based on the results of the dynamic unit-cell calculations an increase of the influence of the Lode parameter on micro-defect deformation is observed with decreasing stress triaxiality 1/3. In particular, for the negative Lode parameter = -1 the evolution of prolate elliptical pores with one elongated principal direction is observed whereas for the positive Lode parameter = 1 the formation of oblate elliptical voids with two elongated principal directions is numerically predicted. Therefore, the Lode parameter has remarkable effect on the dynamic damage behavior in the low or slightly negative stress triaxiality regime. Furthermore, it is worthy to note that for the high negative stress triaxiality = -1 the sizes of the voids decrease. This indicates that no further damage occurs and verifies the existence of a cut-off value of stress triaxiality proposed by Bao and Wierzbicki (2005Bao, Y., Wierzbicki, T., 2005. On the cut-off value of negative triaxiality for fracture. Engineering Fracture Mechanics 72, 1049-1069.); Kweon (2012Kweon, S., 2012. Damage at negative triaxiality. European Journal of Mechanics A/Solids 31, 203-212.); Brünig et al. (2018a)Brünig, M., Gerke, S., Schmidt, M., 2018a. Damage and failure at negative stress triaxialities: Experiments, modeling and numerical simulations. International Journal of Plasticity 102, 70-82. for the investigated ductile material under dynamic loading conditions. It is worthy to note that the stress-state-dependent deformation modes of the initially spherical voids predicted by dynamic numerical simulations only slightly differ from the ones presented by Brünig et al. (2013)Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65. for static analysis.
In order to quantify the state of damage in the dynamically loaded RVE macroscopic damage strain components are analyzed. In particular, the current volume of the unit-cell is approximated by a cuboid with side lengths , and
where the respective lengths are calculated from the initial side lengths and the averaged node displacements of the corner nodes of the finite element mesh.
The shape of the void is approximated by an ellipsoid with principal semi-axes , and where the directions of the semi-axes coincide with the axes of the principal coordinate system leading to the current volume of the void
Here, the respective length of the semi-axes is calculated from the initial radius of the void and the corresponding node displacements. With these definitions the current void volume fraction
is calculated. The evolution of the void volume fraction during the loading process for different stress triaxialities and Lode parameters is shown in Fig. 5. It can be clearly seen that this scalar parameter is nearly insensitive to the Lode parameter whereas larger increase in the porosity with time is observed for higher stress triaxialities. This observation corresponds to the results shown in Fig. 4 where void growth is predicted for high stress triaxialities while nearly isochoric void deformation is characteristic for zero stress triaxiality.
Progress of principal damage strain components vs. time for different stress triaxialities and Lode parameters
Furthermore, with the principal stretches
of the initially spherical void the principal components of the damage strain tensor
are directly extracted.
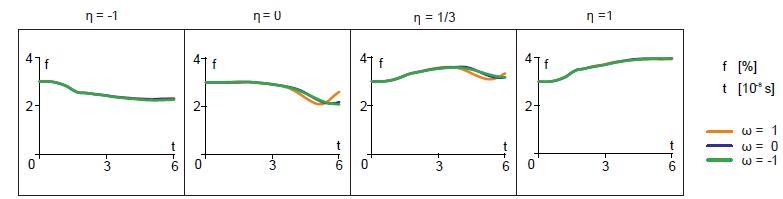
The evolution of respective components of the damage strain tensor during the loading process for different stress triaxialities and Lode parameters is shown in Fig. 6. In particular, for the stress triaxiality remarkable influence of the Lode parameter on the damage strain components can be seen concerning the amount and the sign of these parameters. This corresponds to formation of different ellipsoidal voids shown in Fig. 4. This influence can also be seen for the small positive stress triaxiality but the damage strain components are smaller and the effect of the Lode parameter is less marked. For the higher stress triaxiality smaller damage strain components are numerically predicted and only small influence of the Lode parameter on the respective damage strain components can be seen in Fig. 6. And for the negative stress triaxiality nearly all damage strain components are negative indicating that the initial void is compressed and no further damage occurs.
4 Damage equations and identification of associated parameters
The numerical results based on dynamic unit-cell-model analyses shown in Figs. 4-6 represent the development of anisotropic damage behavior in ductile materials undergoing different proportional dynamic loading conditions. These numerical results are used to propose stress-state-dependent dynamic damage equations and to identify corresponding constitutive parameters. Stress state dependence is here characterized by the stress triaxiality and the Lode parameter .
In particular, for the dynamic damage criterion (6) the damage mode parameter is taken to be
and the parameter is proposed to be the non-negative function
with
and
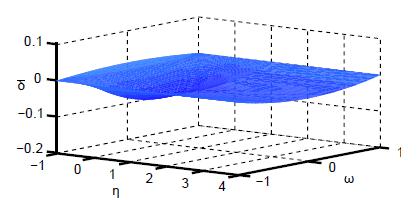
In addition, the parameters , and in the damage rule (10) are also determined from the results of the dynamic unit-cell calculations. For example, the parameter is given by the stress-state-dependent relation
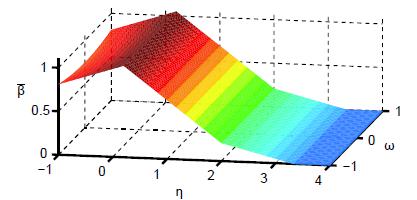
which is shown in Fig. 7. The parameter corresponding to the volumetric part of the damage strain rates caused by isotropic growth of micro-defects is high for high stress triaxialities, decreases with decreasing hydrostatic stress and is zero for negative stress triaxialities. Additional dependence on the Lode parameter has not been detected by the numerical calculations on the micro-level. The parameter is expressed in the form
with the Lode-parameter-dependent part
which is illustrated in Fig. 8. The parameter corresponding to the anisotropic isochoric part of the damage strain rates caused by formation of micro-shear-cracks is large for small stress triaxialities, decreases with increasing hydrostatic stress and is zero for high stress triaxialities. An additional dependence on the Lode parameter has been revealed by the numerical calculations on the micro-scale for small amounts of stress triaxialities.
Three-dimensional representation of strain rate parameter vs. stress triaxiality and Lode parameter
Three-dimensional representation of strain rate parameter vs. stress triaxiality and Lode parameter
Three-dimensional representation of strain rate parameter vs. stress triaxiality and Lode parameter
Furthermore, the parameter is expressed in the form
which is shown in Fig. 9. This parameter also corresponding to the anisotropic isochoric part of the dynamic strain rate tensor only exists for small stress triaxialities and mainly depends on the Lode parameter.
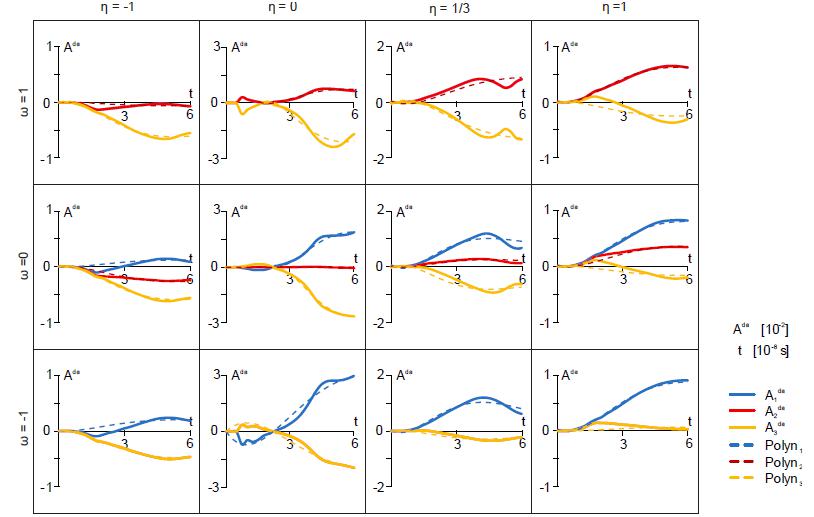
Moreover, the damage strain rate parameters , and resulting from static (see Brünig et al. (2013Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65.)) and dynamic unit-cell calculations depending on the stress triaxialities and for different Lode parameters are shown in Fig. 10. It can be seen that there are only marginal differences in and whereas larger differences are shown for for . It is worthy to note that for negative stress triaxialities negative values for the parameter are identified based on the results of the unit-cell analysis. These negative values correspond to compression of the initial void. However, if initial porosity is marginal this compression behavior will also be marginal and, therefore, for seems to be realistic.
Damage strain rate parameters , und resulting from static and dynamic unit-cell calculations (marks) and numerical approximation (lines) at different stress triaxialities
Based on the stress-state-dependent parameters discussed above numerical simulation of deformation and damage behavior of dynamically loaded homogeneous representative volume elements using the proposed continuum damage model shows good agreement with the numerical results obtained from void-containing unit-cell calculations, see Fig. 11. For all investigated stress states the continuum damage model accurately predicts the anisotropic damage behavior for dynamically loaded ductile metal samples.
5 Conclusions
The main objective of this paper was to investigate the effect of dynamic loading conditions on damage behavior of ductile metals. For this purpose, series of numerical calculations on the micro-level considering void-containing representative volume elements under different three-dimensional dynamic loading scenarios have been performed. They enabled insight in the complex stress-state- and rate-dependent damage and failure processes on the micro-scale and their effect on the macroscopic behavior of ductile material samples. The numerical results have been used to discuss general mechanisms of dynamic damage for different stress states and to propose equations for phenomenological damage criteria corresponding to different processes on the micro-level. The results have also been used to develop rate-dependent evolution equations for macroscopic damage strains corresponding to anisotropic formation of micro-defects and to identify stress-state-dependent parameters of the dynamic continuum model. The accuracy of the proposed model has been demonstrated by comparison of numerical results based on the macroscopic continuum model with data obtained by unit-cell calculations for different stress-state-dependent dynamic loading conditions. It has been shown that for dynamic loading scenarios the parameters in the damage rule characterizing the dependence on the stress state are similar to those modeling static behavior.
Acknowledgement
Financial support from the Deutsche Forschungsgemeinschaft DFG (German Research Foundation, BR1793/12-2) is greatfully acknowledged.
References
- Bao, Y., Wierzbicki, T., 2005. On the cut-off value of negative triaxiality for fracture. Engineering Fracture Mechanics 72, 1049-1069.
- Barsoum, I., Faleskog, J., 2011. Micromechanical analysis on the influence of the Lode parameter on void growth and coalescence. International Journal of Solids and Structures 48, 925-938.
- Becker, R., Needleman, A., Richmond, O., Tvergaard, V., 1988. Void growth and failure in notched bars. Journal of the Mechanics and Physics of Solids 36, 317-351.
- Benson, D., 1993. An analysis of void distribution effects on the dynamic growth and coalescence of voids in ductile metals. Journal of the Mechanics and Physics of Solids 41, 1285-1308.
- Bruhns, O.T., Diehl, H., 1989. An internal variable theory of inelastic behaviour at high rates of strain. Archive of Mechanics 41, 427-460.
- Brünig, M., 2003. An anisotropic ductile damage model based on irreversible thermodynamics. International Journal of Plasticity 19, 1679-1713.
- Brünig, M., 2004. An anisotropic continuum damage model: Theory and numerical analyses. Latin American Journal of Solids and Structures 1, 185-219.
- Brünig, M., 2006. Continuum framework for rate-dependent behavior of anisotropic damaged ductile metals. Acta Mechanica 186, 37-53.
- Brünig, M., Brenner, D., Gerke, S., 2015. Stress state dependence of ductile damage and fracture behavior: Experiments and numerical simulations. Engineering Fracture Mechanics 141, 152-169.
- Brünig, M., Chyra, O., Albrecht, D., Driemeier, L., Alves, M., 2008. A ductile damage criterion at various stress triaxialities. International Journal of Plasticity 24, 1731-1755.
- Brünig, M., Gerke, S., 2011. Simulation of damage evolution in ductile metals undergoing dynamic loading conditions. International Journal of Plasticity 27, 1598-1617.
- Brünig, M., Gerke, S., Hagenbrock, V., 2013. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. International Journal of Plasticity 50, 49-65.
- Brünig, M., Gerke, S., Hagenbrock, V., 2014. Stress-state-dependence of damage strain rate tensors caused by growth and coalescence of microdefects. International Journal of Plasticity 63, 49-63.
- Brünig, M., Gerke, S., Schmidt, M., 2016. Biaxial experiments and phenomenological modeling of stress-state-dependent ductile damage and fracture. International Journal of Fracture 200, 63-76.
- Brünig, M., Gerke, S., Schmidt, M., 2018a. Damage and failure at negative stress triaxialities: Experiments, modeling and numerical simulations. International Journal of Plasticity 102, 70-82.
- Brünig, M., Hagenbrock, V., Gerke, S., 2018b. Macroscopic damage laws based on analysis of microscopic unit cells. ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 98, 181-194.
- Carroll, M., Holt, A., 1972. Static and dynamic pore-collapse relations for ductile porous materials. Journal of Applied Physics 43, 1626-1636.
- Driemeier, L., Brünig, M., Micheli, G., Alves, M., 2010. Experiments on stress-triaxiality dependence of material behavior of aluminum alloys. Mechanics of Materials 42, 207-217.
- Gao, X., Kim, J., 2006. Modeling of ductile fracture: Significance of void coalescence. International Journal of Solids and Structures 43, 6277-6293.
- Gao, X., Wang, T., Kim, J., 2005. On ductile fracture initiation toughness: Effects of void volume fraction, void shape and void distribution. International Journal of Solids and Structures 42, 5097-5117.
- Gao, X., Zhang, G., Roe, C., 2010. A study on the effect of the stress state on ductile fracture. International Journal of Damage Mechanics 19, 75-94.
- Gerke, S., Kuhnt, K., Brünig, M., 2014. Micro-mechanical numerical analysis of ductile damage under dynamic loading conditions. In: E. Oñate, J. Oliver, A. Huerta (Eds.), Proc. 11th World Congress on Computational Mechanics (WCCM XI), CIMNE Barcelona, 1187-1198.
- Jaques, N., Mercier, S., Molinari, A., 2012. Void coalescence in a porous solid under dynamic loading conditions. International Journal of Fracture 173, 203-213.
- Johnson, J., 1981. Dynamic fracture and spallation in ductile solids. Journal of Applied Physics 52, 2812-2825.
- Kim, J., Gao, X., Srivatsan, T., 2003. Modeling of crack growth in ductile solids: a three-dimensional analysis. International Journal of Solids and Structures 40, 7357-7374.
- Kweon, S., 2012. Damage at negative triaxiality. European Journal of Mechanics A/Solids 31, 203-212.
- Molinari, A., Mercier, S., 2001. Micromechanic modelling of porous materials under dynamic loading. Journal of the Mechanics and Physics of Solids 49, 1497-1516.
- Nielsen, K., Dahl, J., Tvergaard, V., 2012. Collapse and coalescence of spherical voids subject to intense shearing: studies in full 3D. International Journal of Fracture 177, 97-108.
- Ortiz, M., Molinari, A., 1992. Effect of strain hardening and rate sensitivity on the dynamic growth of a void in a plastic material. Journal of Applied Mechanics 59, 48-53.
- Scheyvaerts, F., Onck, P., Tekoğlu, C., Pardoen, T., 2011. The growth and coalescence of ellipsoidal voids in plane strain under combined shear and tension. Journal of the Mechanics and Physics of Solids 59, 373-397.
- Voyiadjis, G.Z., Abu Al-Rub, R., Palazotto, R.K., 2003. Non-local coupling of viscoplasticity and anisotropic viscodamage for impact problems using the gradient theory. Archives of Mechanics 55, 39-89.
- Wu, X., Ramesh, K., Wright, T., 2003a. The dynamic growth of a single void in a viscoplastic material under transient hydrostatic loading. Journal of the Mechanics and Physics of Solids 51, 1-26.
- Wu, X., Ramesh, K., Wright, T., 2003b. The effects of thermal softening and heat conduction on the dynamic growth of voids. International Journal of Solids and Structures 40, 4461-4478.
- Zhang, K., Bai, J., Francois, D., 2001. Numerical analysis of the influence of the Lode parameter on void growth. International Journal of Solids and Structures 38, 5847-5856.
-
Available Online: May 25, 2018
Publication Dates
-
Publication in this collection
2018
History
-
Received
01 Mar 2018 -
Reviewed
11 Mar 2018 -
Accepted
31 Mar 2018