Abstract
Micro-buckling of unidirectional fiber-reinforced composites is investigated in this paper by means of an explicit representation of a geometrically imperfect fiber within the context of kinematical and material non-linear behavior. Two types of fiber imperfections are considered: a helicoidal shape, identified as 3D imperfection; and a sinusoidal plane shape (2D imperfection). Both imperfection models are characterized by a maximum misalignment angle of the fiber with respect to the ideal or perfect configuration, as is usually considered in this field. A total of 816 cases were computed in terms of imperfection type (either 2D or 3D), fiber volume fraction, fiber arrangement (square or hexagonal array), orientation for 2D models, matrix yield stress, and misalignment angle. Two load cases, with constrained and unconstrained transverse strain, were considered. Assuming periodic boundary conditions, homogenization was carried out to obtain macroscopic stresses. Numerical results are compared with an analytical model available in the literature. The results show a high imperfection-sensitivity for small misalignment angles; on the other hand, the type of imperfection and the fiber arrangement do not have a large influence on the results. In addition, it was found that this problem is governed by fiber volume fraction and matrix yield stress only for small imperfections, whereas for large misalignment angles, a change in fiber volume fraction produces small changes in micro-buckling stress.
Keywords:
Composites; micromechanics; fiber misalignment; micro-buckling
1 INTRODUCTION
In the context of fiber-reinforced composite materials, the term fiber micro-buckling refers to the buckling of fibers involving transverse displacements under compression in the direction of the fiber. By analogy with a structural behavior, micro-buckling is frequently modeled as the buckling of a column which is laterally supported on an elastic matrix. This problem has attracted a number of researchers, starting from the pioneer work of Rosen (1965)Rosen, B. W. (1965). Fiber composite materials. American Society for Metals, Metals Park, Ohio, 37.. There are two general ways in which such instability can occur: either due to elastic buckling of the fiber involving deformations of the matrix (a problem which is usually called micro-buckling), or by plastic deformations (called kinking), as reported by Budiansky and Fleck (1993)Budiansky, B., and Fleck, N. A. (1993). Compressive failure of fibre composites. Journal of the Mechanics and Physics of Solids, 41(1): 183-211.. Comparison between both modes has been made by Sun and Tsai (2001)Sun, C. T., and Tsai, J. L. (2001). Comparison of microbuckling model and kink band model in predicting compressive strength of composites. In Proceedings of the 13th International Conference on Composite Materials, Beijing, China. among others: both are seen to be different problems and involve different assumptions; however, these authors concluded that the loads (stress fields) found at buckling or kinking are not very different.
Micro-buckling may occur in mainly two modes: in a periodic (or "in-phase") mode there are periodic deformations of the fibers and shear of the matrix but no significant transverse deformation occurs. Micro-buckling can also occur in a non-periodic (or "out-of-phase") mode, in which shear is negligible and buckling is dominated by transverse deformations, much in the form of a beam on an elastic foundation. Both cases were discussed by Rosen (1965)Rosen, B. W. (1965). Fiber composite materials. American Society for Metals, Metals Park, Ohio, 37. and were reviewed in the classical text by Jones (1975)Jones R.M., Mechanics of Composite Materials, Hemisphere, New York, 1975.. Regarding stability of the post-critical path, Maewal (1981)Maewal, A. (1981). Postbuckling behavior of a periodically laminated medium in compression. International Journal of Solids and Structures, 17(3): 335-344. anticipated a stable post-buckling behavior for the in-phase problem. On the other hand, Yurgartis and Sternstein (1994)Yurgartis, S. W., and Sternstein, S. S. (1994). Experiments to reveal the role of matrix properties and composite microstructure in longitudinal compression strength. ASTM Special Technical Publication, 1185: 193-193. performed tests that showed the detrimental influence of fiber misalignment on the micro-buckling process, a behavior that is typical of unstable postbuckling.
Tomblin et al. (1997)Tomblin, J. S., Barbero, E. J., and Godoy, L. A. (1997). Imperfection sensitivity of fiber microbuckling in elastic-nonlinear polymer-matrix composites. International Journal of Solids and Structures, 34(13): 1667-1679. investigated imperfection-sensitivity of fiber micro-buckling as a consequence of fiber misalignment under compression in the direction of the fiber within the framework of the general theory of elastic stability. Material nonlinearity was introduced in the shear constitutive equations by means of a hyperbolic relation, and the adopted RVE focused on in-phase modes. This led to the identification of an unstable symmetric bifurcation behavior for a RVE, in which a 2/3 power law was found to characterize the imperfection-sensitivity caused by fiber misalignment. Such deterministic theoretical results indicated the nature of the expected unstable behavior and were followed by probabilistic studies by Tomblin and Barbero (1997)Tomblin, J. S., and Barbero, E. J. (1997). Statistical microbuckling propagation model for compressive strength prediction of fiber-reinforced composites. In Composite Materials: Testing and Design, Thirteenth Volume. ASTM International. and Barbero (1998)Barbero, E. J. (1998). Prediction of compression strength of unidirectional polymer matrix composites. Journal of Composite Materials, 32(5): 483-502..
The importance of stacking sequence on micro-buckling was highlighted by Drapier et al. (1996)Drapier, S., Gardin, C., Grandidier, J. C., and Potier-Ferry, M. (1996). Structure effect and microbuckling. Composites Science and Technology, 56(7): 861-867.with reference to bending tests which were performed to identify limit states under compression. Rather than considering a UC, these authors took into account a two-dimensional model of a homogenized laminated composite. For the same periodic configuration of fiber misalignment (under an in-phase mode), a nonlinear Finite Element model of a unidirectional carbon-fiber and epoxy-matrix composite was used (Drapier et al., 1998Drapier, S., Grandidier, J. C., and Potier-Ferry, M. (1998). A non-linear numerical approach to the analysis of microbuckling. Composites Science and Technology, 58(5): 785-790.). The results under compression with misalignment showed significant loss of stress carrying capacity, exhibiting high imperfection-sensitivity. This was the first numerical study to quantify the effect of geometric imperfections on micro-buckling.
Consideration of waviness in other composites, such as biaxial and triaxial textile composites, was recently addressed by Mallikarachchi et al. (2013)Mallikarachchi, H. M. Y. C. and Pellegrino, S. (2013). Failure criterion for two-ply plain-weave CFRP laminates. Journal of Composite Materials 47(11), 1357-1375., Kueh (2013Kueh, A. B. H. (2013). Buckling of sandwich columns reinforced by triaxial weave fabric composite skin-sheets. International Journal of Mechanical Sciences 66, 45-54., 2014Kueh, A. B. H. (2014). Size-influenced mechanical isotropy of singly-plied triaxially woven fabric composites. Composites Part A: Applied Science and Manufacturing 57, 76-87.), and Rasin et al. (2016)Rasin, N., Kueh, A. B., Mahat, M. N., and Yassin, A. Y. M. (2016). Stability of triaxially woven fabric composites employing geometrically nonlinear plate model with volume segmentation ABD constitution. Journal of Composite Materials, 50(19) 2719-2735..
All models reported in the literature were based on a two-dimensional idealization of fiber waviness, where as in reality the fiber may adopt a 3D helicoidal shape rather than a 2D sinusoidal one. Nevertheless, the 2D idealization is often used to calculate imperfection sensitivity of fiber micro-buckling because it is mathematically tractable. Therefore, a pressing question is whether or not a 2D approximation is sufficiently accurate with respect to a 3D one, and thus the motivation for this workin which a more detailed model and refined results are discussed.
2 MODEL
2.1 Framework of Analysis
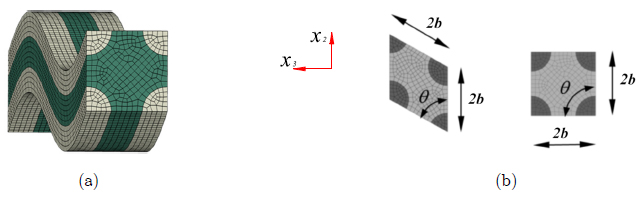
At a unit cell level, a composite is modeled in this work by means of computational micro-mechanics (see, for example, Zohdi and Wriggers, 2008Zohdi, T. I., and Wriggers, P. (2008). An Introduction to Computational Micromechanics.Springer);in which there are macro and micro scales. This methodology has been employed to model a wide range of heterogeneous materials, such as particle-reinforced composites (Li and Wongsto, 2004Li, S., and Wongsto, A. (2004). Unit cells for micromechanical analyses of particle-reinforced composites. Mechanics of Materials, 36(7): 543-572.); and fiber-reinforced composites (Car et al., 2002Car, E., Zalamea, F., Oller, S., Miquel, J., and Oñate, E. (2002). Numerical simulation of fiber reinforced composite materials-two procedures. International Journal of Solids and Structures, 39(7): 1967-1986.). Matrix and fiber are modeled as two separate materials at the micro scale; whereas a single homogenous material (which is assumed to have an equivalent behavior to the heterogeneous fiber-matrix material) is taken into account at the macro scale. In a periodic heterogeneous material, this UC is employed to reconstruct the composite material by means of a repetitive pattern, as shown in Figure 1.
In computational micro-mechanics, a UC is considered with given boundary conditions and under a specific load configuration. With the solution of the stress field at the UC level, usually known as microscopic stresses, a post-process follows to evaluate the stress field in an equivalent homogeneous material, usually known as macroscopic stresses. This process at the micro level is carried out in this work using a Finite Element approximation. The model employed in this work is discussed in this section, including UC geometry, boundary conditions, and constitutive materials. The stability analysis is performed by means of the general purpose Finite Element code ABAQUS (2009)Abaqus v. 6.7, (2009). Dassault Systèmes, Providence, RI, USA..
2.2 Unit Cell Geometry
A UC shown in Figure 2a was used in this work to represent the microstructure in the periodic composite together with the geometric deviations with respect to an ideal or perfect configuration. The UC is constructed by means of the scan of a transverse section (see Figure 2b) by introducing displacements without rotation along the curve that defines the fiber along the imperfect location (imperfection lines, shown in Figure 3).Finite Element models were investigated by assuming hexagonal (designated as Hx) and square (Sq) fiber arrangements, which are shown in Figure 2b. This allows representation of a three-dimensional periodic microstructure, leading to a geometry that can be easily meshed.
For a given fiber radius Rf, the dimensions of the UC were calculated based on fiber volume fraction Vf
and the ratio between fiber length Lf and diameter Df, i.e. β= Lf/Df. Since a first order computational micromechanics technique is employed in this work, absolute UC dimension values, such as fiber radius Rf, would not affect results. Higher order homogenization theories would be necessary to take into account such absolute UC dimensions, as explained by van Dijk (2016)vanDijk, N. P. (2016). Formulation and implementation of stress-driven and/or strain-driven computational homogenization for finite strain. International Journal for Numerical Methods in Engineering, 107: 1009-1028. doi: 10.1002/nme.5198.
https://doi.org/10.1002/nme.5198...
among others. The angle θ is equal to 60º in Hx, and 90º in the Sq configuration (see Figure 2). The value of b in Figure 2 is given by
2.3 Fiber Imperfections
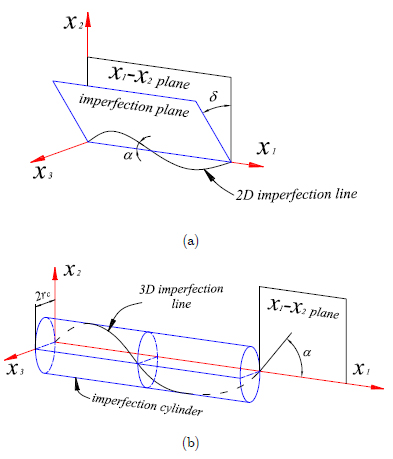
Two types of imperfections with respect to a straight fiber were considered in this work: (i) Three-dimensional (3D) deviations, with the fiber having a helicoidal shape; (ii) Two-dimensional (2D) deviations following a sinusoidal shape. In their initial positions, the fibers are assumed to be in phase. As shown in Figure 3, the 3D imperfection is contained in a cylinder whereas the 2D imperfection lies in a plane.
With reference to Figure 3, perfect alignment would be given by a fiber placed in the direction of axis x1 ; a 2D imperfection has been illustrated in the plane containing axis x1 and has a given angle δ measured with respect to the plane x1 -x2 ; in other words, δ defines the orientation of the plane where the 2D imperfection develops. Following the usual definitions in the micro-buckling field, both imperfections have a maximum angle of misalignment (α) of the fiber with respect to axis x1 .
The difference between angles δ and α should be emphasized. The orientation of the plane which contains the imperfect fiber in the 2D model is δ; whereas α is the maximum angle of the fiber with respect to axis x1 . Thus, angle δ has relevance in a 2D model, but α is a relevant parameter in both 2D and 3D models.
The Cartesian equations of the 2D imperfection line are given by
The equations for a 3D imperfection line are
where rc is the radius of the cylinder which contains the helicoid. This value may be obtained from the expression
2.4 Periodic Boundary Conditions
Periodic boundary conditions (PBC) were used to represent a periodic microstructure. PBC are described at large in the literature on computational micro-mechanics, such as Li and Wongsto (2004)Li, S., and Wongsto, A. (2004). Unit cells for micromechanical analyses of particle-reinforced composites. Mechanics of Materials, 36(7): 543-572., Sharma et al. (2014),among others; they were also used by Kueh and Pellegrino (2007)Kueh, A. B. H. and Pellegrino, S. (2007) ABD matrix of single-ply triaxial weave fabric composites. 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, 23-26 April 2007, Honolulu, Hawaii, AIAA-2007-2161. and by Mallikarachchi et al. (2011)Mallikarachchi, H. M. Y. C. and Pellegrino, S. (2011). Quasi-static folding and deployment of ultrathin composite tape-spring hinges. Journal of Spacecraft and Rockets 48(1), 187-198. by means of 1D beam elements for 2D structures.
To model the micro-structure in a periodic material it is possible to employ the concept of periodicity vectors (Oller et al., 2005Oller, S., Miquel Canet, J., and Zalamea, F. (2005). Composite material behavior using a homogenization double scale method. Journal of Engineering Mechanics, 131(1): 65-79.; Car et al., 2002Car, E., Zalamea, F., Oller, S., Miquel, J., and Oñate, E. (2002). Numerical simulation of fiber reinforced composite materials-two procedures. International Journal of Solids and Structures, 39(7): 1967-1986.). Following the nomenclature adopted in Zahr-Viñuela and Pérez-Castellanos (2011)Zahr-Viñuela, J., and Pérez-Castellanos, J. (2011). Elastic constants and isotropy considerations for particulate metal-matrix composites. A multi-particle, cell-based approach. Composites Part A: Applied Science and Manufacturing, 42(5): 521-533., two points in a microstructure are identified as "corresponding points" if the position of one of them may be obtained as the position of the other one plus a linear combination of the periodicity vectors using integer coefficients. To illustrate the concept, periodicity vectors P1 and P2 are shown in Figure 4. The points in pairs:(C0; C1), (C0; C2) and (C0; C3) are corresponding points.
Three vectors of periodicity, shown in Figure 5, were used in this work.
where i, j, k are unit vectors in the coordinate directions x1 , x2 , and x3 .
The boundary conditions are relations involving the forces and displacements at the boundary of the cell (Li and Wongsto, 2004Li, S., and Wongsto, A. (2004). Unit cells for micromechanical analyses of particle-reinforced composites. Mechanics of Materials, 36(7): 543-572.). If the traction at a boundary point and its corresponding point are t+ and t- respectively, then the following condition should be satisfied at all boundary pairs of points
Assuming that the displacements at a boundary point are written as u+ and at its corresponding point as u-, then the condition
applies at all boundary points, where ε0 is the macroscopic strain tensor; and P is a periodicity vector (or a linear combination of them) which satisfies the condition
where X+ and X- are the coordinates of each node of the considered couple, for which the displacements are u+ and u-.
For a UC modeled by Finite Elements, it is only necessary to specify the conditions (7) for the displacements at the boundary. The conditions (6) for the boundary tractions are automatically satisfied because a displacement-based variational Finite Element formulation is employed, as explained by Li and Wongsto (2004)Li, S., and Wongsto, A. (2004). Unit cells for micromechanical analyses of particle-reinforced composites. Mechanics of Materials, 36(7): 543-572..
There are several ways to implement the conditions (7) in practice, including Lagrange multipliers or a penalty formulation. In this work, periodicity was implemented by means of multipoint linear constraints (using the *EQUATION command in ABAQUS). Basically, following(7), the scalar equation
(for i=1, 2, 3) holds, where Ui j are the displacement components in direction i of the additional node j that has been included as a control node. Three control nodes have been selected in this work, and a boundary condition is assigned to them in terms of the components of the macroscopic strain tensor which is to be imposed on the UC:
To avoid problems with units, equations (9) and (10) are assumed to include a unit coefficient to homogenize units. Equations (7) are thus implemented by use of equation (9) and boundary conditions (10).
Some further details need to be considered. When implemented using multipoint linear constraints in a program like ABAQUS, the first degree-of-freedom involved in equation (9) is eliminated as an unknown from the problem and cannot be further employed in new restrictions or in other boundary conditions. For this reason, the equations that are included in the programming should be selected to achieve an effective enforcement of all necessary relationship at the UC boundary. Following this procedure it is possible to select the conditions to be employed and avoid problems with missing degrees-of-freedom.
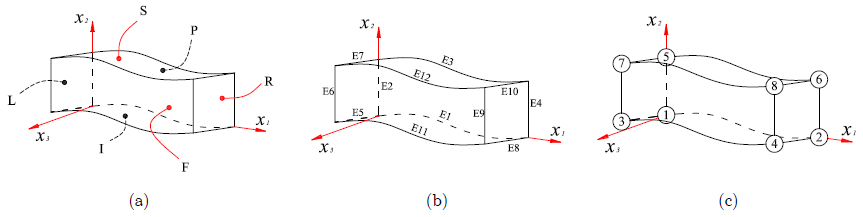
Boundary faces, edge lines, and vertices, are identified in Figure 6.
All equations to be implemented have the form of equation (9), but for each pair of nodes itis necessary to specify the associated vector P. As an example, consider a couple of faces, such as R and L in Figure 6, and corresponding nodes on each face. Equation (9) establishes the condition for this pair of nodes, and for any other pair of corresponding nodes on faces R and L with vector of periodicity P1:
A summary of the P vectors to be used with each pair of nodes on faces, edges, and vertices is given in Tables 1 to 3 for the first and second degree of freedom (DOF) in equation (11). This procedure allows implementation of any macroscopic strain.
2.5 Load Cases
Under compression in direction x1 , a single lamina can freely deform in the transverse directions. However, if it is used as part of a laminate, then it cannot deform transversely in the same way because other laminae produce an effect of transverse constraint. The question arises regarding how this may influence the micro-buckling of a fiber which is part of a laminate? To distinguish between possible situations, two loading cases are considered in this work: one with constrained transverse strain and another one without such constraint. Notice that the first case is not fully representative of the strain state of a lamina in a laminate, but it may be seen as a limiting condition.
Both loading cases are deformations without macroscopic distortions, i.e. the macroscopic strain tensor has zero off-diagonal components and a compressive component 11. In one case (which is identified as case A) the transverse strain components are not specified, so that the UC can expand in the transverse directions while being under 11 compression. In the other load case (identified as case B) the transverse strain components are zero, with the consequence that no lateral expansion occurs under axial compression.
Implementation of load cases A and B described above is done through boundary conditions, eq. (10), applied on displacements at control nodes since they are directly related to macro strain components. In load case B, all displacements are specified; this means that all macroscopic strain components ε0 ij are imposed. For load case A, boundary conditions related to ε0 11 diagonal component and zero off-diagonal components are imposed; whereas the displacements of control nodes related to transverse strains ε0 22 and ε0 33 are kept as degree of freedoms in the model, and they can be obtained from the numerical solution of the UC.
2.6 Fiber and Matrix Materials
In order to investigate imperfection sensitivity, this model includes two sources of non-linearity: The epoxy matrix is modeled as a non-linear material, whereas the strain-displacement relations are geometrically non-linear. The nonlinear equilibrium paths are followed using the Riks algorithm in ABAQUS (2009)Abaqus v. 6.7, (2009). Dassault Systèmes, Providence, RI, USA..
To illustrate the micro-buckling behavior, a composite made of glass fibers and epoxy matrix was considered having Rf = 3.5 x10-6 m. Both constituent materials were assumed to be isotropic: the fiber was modeled as linear elastic with modulus Ef = 84 GPa, and Poisson's ratio νf = 0.22, whereas the matrix was modeled as an elasto-perfectly plastic material with Em= 4 GPa and νm = 0.38. Two yield stresses for the matrix material were considered with values given by σy = 48.26 MPa and σy =100 MPa. An associative flow rule was used together with von Mises yield surface.
2.7 Post-Processing and Finite Element Mesh
The macroscopic Cauchy stress tensor, σk ij , is computed, as in many other works, as
where σk ij is the ij component of the microscopic Cauchy stress tensor at Gauss point k in the Finite Element mesh that covers the UC; Vk is the integration weight (in terms of volume associated with the Gauss point k) for a mesh with N Gauss points and, V is the current volume of the UC.
Approximately 30,000 elements (C3D8 in the ABAQUS library, a solid 8-node linear brick) were used in the Finite Element mesh. This element does not have volumetric locking when used in plasticity problems. Meshes with 200,000 elements were also used in some configurations to test convergence. The maximum stress changed less than 0.7% respect to values reported in the following Section.
3 RESULTS AND DISCUSSION
Under load condition A, 384 cases were solved for this work, where as 432 cases were computed for load condition B. The cases cover changes in the variables of interest, which include the type of imperfection (either 2D or 3D); orientation angle δ of the 2D imperfection; configuration of fiber arrangement; matrix yield stress σy; fiber volume fraction Vf , and misalignment angle α. Cases with Vf = 10%, 30%, 50% and 70% were investigated, together with values of angle α between 0.01º and 20º and β = Lf/Df between 12.5 and 200 to have a wide perspective of the phenomenon covering results reported in experimental tests; as a reference value, Jochum and Grandidier (2004)Jochum, C., and Grandidier, J. C. (2004). Microbuckling elastic modelling approach of a single carbon fibre embedded in an epoxy matrix. Composites science and technology, 64(16): 2441-2449. measured values of β between 20 and 50 with misalignment angles up to 10º.
To facilitate the presentation of results, each case was identified with a group number ranging from 1 to 24, a letter to identify the load case, the misalignment angle, and the yield stress of the matrix. Group numbers are given for a Vf value, a type of imperfection, a specific fiber arrangement, and an angle δ (in cases of 2D imperfection). The codification is shown on Tables 4 to 7. For example, Group 4 includes cases with Vf = 70%, Sq arrangement, 2D imperfection, and δ= 0.
3.1 Equilibrum Paths
Equilibrium paths are shown in Figure 7 for selected cases of Groups 4A and 4B (Vf = 70%, 2D imperfection, square fiber array, δ = 0) and σy = 48.26 MPa, whereas values of misalignment angles are given in each case. Notice that because only compressive behavior is of interest for micro-buckling, negative values of strain and stress are reported. For small deviation angles, the equilibrium path is fairly linear and reaches a maximum value at a bifurcation load; then the path drops in the post-buckling path. For large deviation angles, the equilibrium path exhibits nonlinearity until a maximum is reached; this is a limit point in the nomenclature of the theory of elastic stability (see, for example, Godoy, 2000Godoy, L. A. (2000). Theory of Elastic Stability: Analysis and Sensitivity. CRC Press. Boca Raton FL.); then, the path drops in an unstable behavior.
Equilibrium paths for selected cases of Group 4 as a function of misalignment angle α. Results for σy = 48.26 MPa. (a): Unconstrained load case A; (b): Constrained load case B.
A comparison of load cases A and B shows that the slope is slightly higher in cases B, because the transverse strain has been constrained.
Equilibrium paths for various misalignment angles α, for Groups 4A and 4B and σy = 48.26 MPa, are plotted in Figure 8. The scale has been modified with respect to Figure 7 to highlight details of the curves.
Details of equilibrium paths for selected cases of Group 4 as a function of misalignment angle. Results for σy = 48.26 MPa. (a): Unconstrained load case A; (b): Constrained load case B.
For configurations with moderate imperfections α there are local maximum points in the equilibrium paths. But for large values of α the maximum vanishes, with the consequence that the stress increases with a compressive strain without crossing a singularity in the path; micro-buckling does not occur in such cases and the problem is governed by large displacements. This behavior of having a limiting angle α for which the maximum ceases to exist, occurs in most groups studied and is typical of shell buckling problems (Godoy, 2000Godoy, L. A. (2000). Theory of Elastic Stability: Analysis and Sensitivity. CRC Press. Boca Raton FL.).
Values of the maximum loads (a limit point in the equilibrium path) in each case are shown in Tables 4 to 7. In groups for which a value is missing means that a maximum in the path was not found, i.e. micro-buckling did not occur. For all cases in Tables 4 to 7 a value of β = 50 was assumed. Such value was selected based on results of experimental tests reported in the literature. Moreover, to illustrate the influence of β, cases with β between 12.5 and 200 were solved for Groups 1, 7, 13, and 19 (3D imperfection and Hx fiber array), load case B, α = 0.01º and σy = 48.26 MPa. Results of maximum stresses are shown in Figure 9 and they show a small change in limit stress for high β values.
Limit stresses as a function of ratio β = Lf/Df. Results for constrained load case B, σy = 48.26 MPa, 3D imperfection, Hx array (Groups 1, 7, 13, and 19).
Equilibrium paths for groups 19A and 19B (Vf = 10%, 3D imperfection, hexagonal fiber arrangement Hx, and σy = 48.26 MPa) are plotted in Figure 10, for cases with α = 0.01º, 2.5º, and 20º.
Equilibrium paths for selected cases from Group 11 for different misalignment angles α. Results for σy = 48.26 MPa. (a): Unconstrained load case A; (b): Constrained load case B.
In the almost-perfect case, α = 0.01º, a line is shown with the initial slope. There is a change in slope during the loading process of the UC which is caused by plasticity in the matrix. This change in slope occurs at a strain σ11 = -0.012, and is more evident in load case A than in case B. Similar behavior was found for the other cases with Vf = 10%, but the slope change caused by plasticity is not clearly observed in higher volume fractions because the matrix has less incidence in the stiffness of the UC.
3.2 Parametric Studies
Parametric studies have been performed by taking into account the limit stresses in Tables 4 to 7, and results are presented (as in many stability problems) in terms of a knock-down factor η, i.e. the critical stress for a given α divided by the stress for αzero. Because of space restrictions, not all values from Tables 4 to 7 can be plotted.
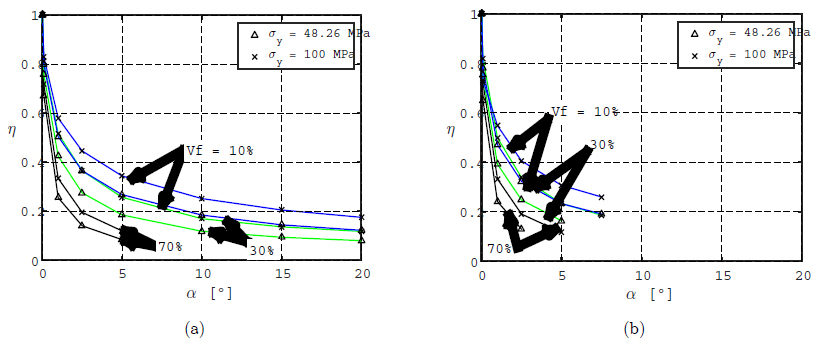
The knock-down factor η has been plotted as a function of misalignment α for unconstrained load cases A, and constrained cases B, in Figure 11, for 3D imperfections with Sq and Hx fiber arrangement, and several values of misalignment α. The results indicate that the fiber arrangement does not have an incidence on the results. A similar graph for 2D imperfections could also be plotted from values of Tables 4 to 7, and similar results are found.
Influence of fiber arrangement, considering square (Sq) and hexagonal (Hx). For 3D imperfections knock-down factors η are given for Groups 1, 2, 7, 8, 13, 14, 19, and 20, with σy = 48.26 MPa. (a): Unconstrained load cases A; (b): Constrained load cases B.
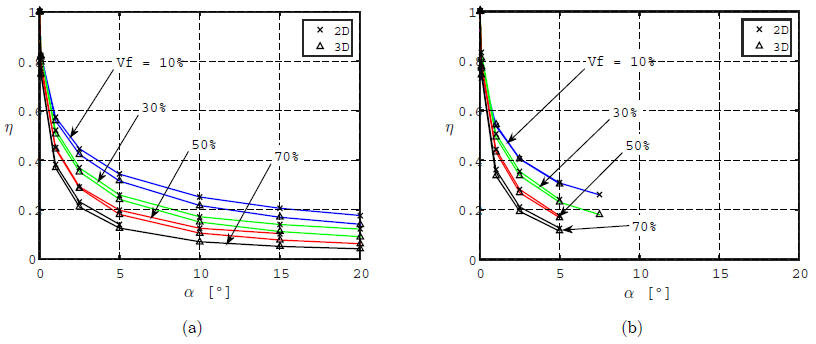
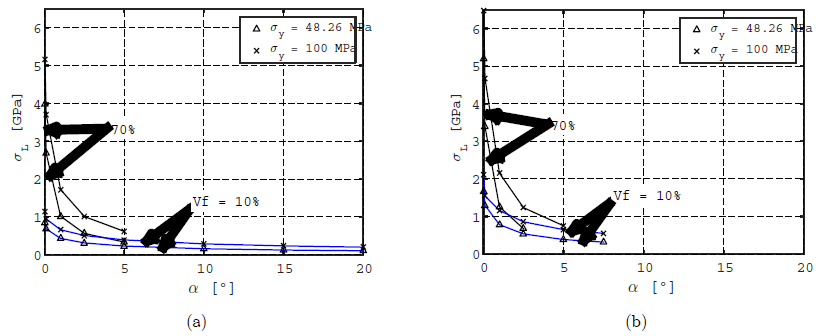
The incidence of Vf for various misalignment angles is shown in Figure 12, for a given type of imperfection and fiber arrangement (3D and Hx array), and yield stress σy = 48.26 MPa. The results show high imperfection-sensitivity to small amplitude imperfections: as an example, for α = 1º, the knock-down factor falls to less than 50% in all cases. This sensitivity increases with increasing Vf . Similar behavior was obtained for 2D imperfections and for Sq configurations and σy = 100 MPa.
Micro-buckling sensitivity. Knock-down factor for Groups 1, 7, 13 and 19 (3D imperfection, Hx array, and σy = 48.26 MPa). (a): Unconstrained load cases A; (b): Constrained load cases B.
The influence of the type of imperfection (2D or 3D) has been investigated for groups 1, 3, 7, 9, 13, 15, 19, and 21, considering an hexagonal fiber configuration (Hx) and σy = 100 MPa. The knock-down factors are shown in Figure 13, and it is clear that the curves with different types of imperfection become almost identical. The conclusion is that the type of assumed imperfection (either 2D or 3D) does not have a significant influence on the knock-down factor.
Influence of imperfection type: two-dimensional (2D) and three-dimensional (3D). Knock-down factors for Groups 1, 3, 7, 9, 13, 15, 19 and 21 (Hx array and σy = 100 MPa). (a): Unconstrained load cases A; (b): Constrained load cases B.
The influence of angle α (the orientation of the 2D imperfection plane), for Groups 3, 5, 9, 11, 15, 17, 21, and 23, for both load configurations A and B and for the same fiber arrangement (Hx) and σy = 100 MPa has been plotted in Figure 14. The results indicate that δ does not have an influence on the limit stress. The same behavior was found for square fiber arrangement (Sq) and σy = 48.26 MPa.
Influence of angle δ (orientation of 2D imperfection plane). Knock-down factors for cases 3, 5, 9, 11, 15, 17, 21 and 23 (2D imperfection, σy = 100 MPa, and Hx array) for δ = 0º and 30º, as shown in legend. (a): Unconstrained load cases A; (b): Constrained load cases B.
Cases with higher matrix yield stress produced higher limit stresses. In Figure 15 results for cases 4 and 22 (2D imperfection, Sq array, δ = 0, and σy = 48.26 MPa) are shown and the same trend was found in all cases considered in this work. The influence of matrix yield stress on knock-down factor is shown in Figure 16 for cases 4, 16, and 21, with 2D imperfection, Sq fiber arrangement, and δ = 0. The results show an increase in knock-down factor but the problem is still highly sensitive to imperfection.
Influence of matrix strength on limit stress for cases 4 and 22 (2D imperfection and Sq array). (a): Unconstrained load cases A; (b): Constrained load cases B.
Influence of matrix strength on knock-down factors for cases 4, 16, and 22 (2D imperfection and Sq array). (a): Unconstrained load cases A; (b): Constrained load cases B.
3.3 Comparison with a Simplified Model
Comparison of the present Finite Element results with a simplified model presented by Barbero (1998)Barbero, E. J. (1998). Prediction of compression strength of unidirectional polymer matrix composites. Journal of Composite Materials, 32(5): 483-502. is performed in this section. The analytical equation (eq. 4.93 in Barbero, 2010Barbero, E. J. (2010). Introduction to composite materials design.CRC Press. Boca Raton FL.) is given by
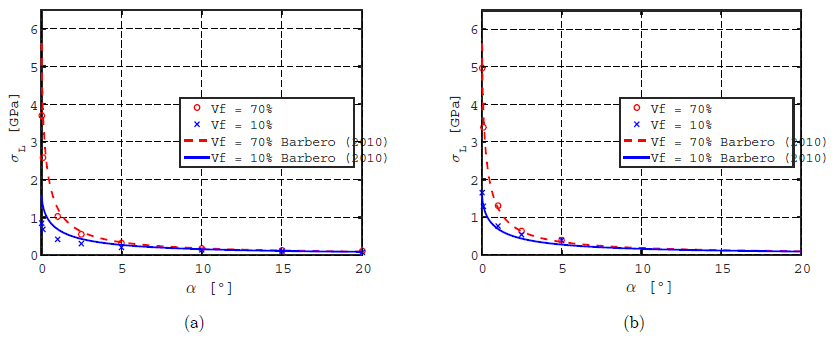
This analytical equation approximates the limit stress σ(α) of a unidirectional composite under compressive load, without taking into account transverse effects. The composite properties required in this model are the in-plane shear strength F6 and the in-plane shear modulus G12 . Such results are compared in Figure 17 for groups 1 and 19 (3D configuration, Hx array, and σy = 48.26 MPa). For this numerical example and based on the assumed von Mises yield criterion for the matrix parameters, a value F6 = 27.86 MPa was adopted in concordance with σy = 48.26 MPa. The elastic modulus G12 was obtained using the Periodic Microstructure Model (PMM), equation (4.39) in Barbero (2010)Barbero, E. J. (2010). Introduction to composite materials design.CRC Press. Boca Raton FL..
Comparison with analytical results. Sensitivity curves for Groups 11 and 1 (3D imperfection, σy = 48.26 MPa, and Hx array) and analytical equation (Barbero, 2010Barbero, E. J. (2010). Introduction to composite materials design.CRC Press. Boca Raton FL.). (a): Unconstrained load cases A; (b): Constrained load cases B.
The results of the present Finite Element and the approximate analytical model are in very good agreement. Constrained cases A yield lower limit stresses. Similar trends are obtained for all cases considered.
As a reference, the limit stress for both load cases considered has been normalized in Table 8 with respect to bifurcation loads obtained from the model due to Rosen (1965)Rosen, B. W. (1965). Fiber composite materials. American Society for Metals, Metals Park, Ohio, 37..
Limit stresses normalized with respect to bifurcation loads due to Rosen (1965)Rosen, B. W. (1965). Fiber composite materials. American Society for Metals, Metals Park, Ohio, 37.. Results for α = 0.01º.
Only results of cases from Group 1, 7, 13, and 19 (3D imperfection and Hx array) for α = 0.01º are considered, and it is found that unconstrained cases A have lower values than constrained cases B. Such discrepancies between simplified model due to Rosen and the present one could be caused by different assumptions in stress states for the fiber and matrix, consideration of fiber misalignment and matrix plasticity, among other reasons. Similar trends were found with Sq array or 2D imperfection.
Finally, Figure 17 and 15 show that there is a loss in fiber reinforcing contribution for large misalignment angles. Also, for such misalignment angles, a change in the matrix yield stress produces limit stresses that are comparable and even higher than those generated by changing Vf . As an example, case 22A in Table 4 (10% of fiber volume fraction, 2D imperfection, σy = 48.26 MPa, and Sq array) with α = 5º has a limit stress of 0.228 GPa. If Vf is increased up to 70% (case 4A from Table 4 is recovered), then a value of 0.335 GPa is obtained. If case 22A with α = 5º in Table 4 is considered again and the matrix yield stress is changed from 48.26 MPa to 100 MPa, recovering case 22A from Table 5, a value of 0.391 GPa is obtained. Similar results were found for all cases considered here. Finally, the results seem to show that, for large misalignment angles, the matrix yield strength have a more important role than fiber volume fraction on limit stress.
4 CONCLUSIONS
The micro-buckling of unidirectional fiber-reinforced composites has been investigated in this research by means of a computational micromechanics simulation in which misalignment imperfections were geometrically represented. Results were obtained by means of a Finite Element discretization of the periodic Unit Cell domain, using the general purpose package ABAQUS, and assuming non-linear kinematic and material behavior.
Based on the results, it is possible to conclude that there is a high imperfection-sensitivity in the critical stress of fiber micro-buckling. This is in agreement with earlier results by Drapier et al. (1998)Drapier, S., Grandidier, J. C., and Potier-Ferry, M. (1998). A non-linear numerical approach to the analysis of microbuckling. Composites Science and Technology, 58(5): 785-790. for a unidirectional carbon fiber/epoxy resin material for a fixed imperfection wavelength. A sharp drop is seen to occur for very small angles less than α = 1º, which is consistent with the 2/3 power law identified by Tomblin et al. (1997)Tomblin, J. S., Barbero, E. J., and Godoy, L. A. (1997). Imperfection sensitivity of fiber microbuckling in elastic-nonlinear polymer-matrix composites. International Journal of Solids and Structures, 34(13): 1667-1679.. For higher values of imperfection amplitude, the asymptotic model of Tomblin et al. (1997)Tomblin, J. S., Barbero, E. J., and Godoy, L. A. (1997). Imperfection sensitivity of fiber microbuckling in elastic-nonlinear polymer-matrix composites. International Journal of Solids and Structures, 34(13): 1667-1679. is only an approximation, and more refined values are shown in this work, for example in Tables 4 to 7.
The type of imperfection (either 2D or 3D), the fiber configuration (hexagonal or square), and angle of the plane of 2D imperfection (orientation of 2D imperfection) do not have a great influence on the limit stresses due to micro-buckling. For small values of misalignment, the problem is mainly influenced by fiber volume fraction and matrix yield stress.
For large imperfection amplitude, as given by large misalignment angle, there is a significant loss in the reinforcing effect that is contributed by the fiber. Also, for such imperfection level, increasing the matrix yield stress produces comparable or even higher limit stresses than those produced by fiber volume fraction changes. In other words, micro-buckling seem to be dominated by fiber volume fraction for small misalignment angles, whereas, for large fiber angles it shows as a property dominated by matrix yield stress. A sequel of this conclusion is that increasing fiber volume fraction is not an effective way to increase micro-buckling capacity unless a misalignment control is introduced during the fabrication process.
This work has been restricted to an analysis at the micro level, and no attempt has been made to couple micro and macro levels; this is seen as a topic for further research. The research reported aims to highlight which micromechanics variables play the most important influences on the micro-buckling phenomenon, which is a necessary ingredient before proceeding to multi-scale coupling.
References
- Abaqus v. 6.7, (2009). Dassault Systèmes, Providence, RI, USA.
- Barbero, E. J. (1998). Prediction of compression strength of unidirectional polymer matrix composites. Journal of Composite Materials, 32(5): 483-502.
- Barbero, E. J. (2010). Introduction to composite materials design.CRC Press. Boca Raton FL.
- Budiansky, B., and Fleck, N. A. (1993). Compressive failure of fibre composites. Journal of the Mechanics and Physics of Solids, 41(1): 183-211.
- Car, E., Zalamea, F., Oller, S., Miquel, J., and Oñate, E. (2002). Numerical simulation of fiber reinforced composite materials-two procedures. International Journal of Solids and Structures, 39(7): 1967-1986.
- Drapier, S., Gardin, C., Grandidier, J. C., and Potier-Ferry, M. (1996). Structure effect and microbuckling. Composites Science and Technology, 56(7): 861-867.
- Drapier, S., Grandidier, J. C., and Potier-Ferry, M. (1998). A non-linear numerical approach to the analysis of microbuckling. Composites Science and Technology, 58(5): 785-790.
- Godoy, L. A. (2000). Theory of Elastic Stability: Analysis and Sensitivity. CRC Press. Boca Raton FL.
- Goudarzi, R. H., and Khedmati, M. R. (2015). An experimental investigation of static load capacity of AL-GFRP adhesively bonded single lap and double butt lap joints. Latin American Journal of Solids and Structures, 12(8): 1583-1594.
- Jochum, C., and Grandidier, J. C. (2004). Microbuckling elastic modelling approach of a single carbon fibre embedded in an epoxy matrix. Composites science and technology, 64(16): 2441-2449.
- Jones R.M., Mechanics of Composite Materials, Hemisphere, New York, 1975.
- Kueh, A. B. H. (2013). Buckling of sandwich columns reinforced by triaxial weave fabric composite skin-sheets. International Journal of Mechanical Sciences 66, 45-54.
- Kueh, A. B. H. (2014). Size-influenced mechanical isotropy of singly-plied triaxially woven fabric composites. Composites Part A: Applied Science and Manufacturing 57, 76-87.
- Kueh, A. B. H. and Pellegrino, S. (2007) ABD matrix of single-ply triaxial weave fabric composites. 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, 23-26 April 2007, Honolulu, Hawaii, AIAA-2007-2161.
- Li, S., and Wongsto, A. (2004). Unit cells for micromechanical analyses of particle-reinforced composites. Mechanics of Materials, 36(7): 543-572.
- Maewal, A. (1981). Postbuckling behavior of a periodically laminated medium in compression. International Journal of Solids and Structures, 17(3): 335-344.
- Mallikarachchi, H. M. Y. C. and Pellegrino, S. (2011). Quasi-static folding and deployment of ultrathin composite tape-spring hinges. Journal of Spacecraft and Rockets 48(1), 187-198.
- Mallikarachchi, H. M. Y. C. and Pellegrino, S. (2013). Failure criterion for two-ply plain-weave CFRP laminates. Journal of Composite Materials 47(11), 1357-1375.
- Oller, S., Miquel Canet, J., and Zalamea, F. (2005). Composite material behavior using a homogenization double scale method. Journal of Engineering Mechanics, 131(1): 65-79.
- Rasin, N., Kueh, A. B., Mahat, M. N., and Yassin, A. Y. M. (2016). Stability of triaxially woven fabric composites employing geometrically nonlinear plate model with volume segmentation ABD constitution. Journal of Composite Materials, 50(19) 2719-2735.
- Rosen, B. W. (1965). Fiber composite materials. American Society for Metals, Metals Park, Ohio, 37.
- Sun, C. T., and Tsai, J. L. (2001). Comparison of microbuckling model and kink band model in predicting compressive strength of composites. In Proceedings of the 13th International Conference on Composite Materials, Beijing, China.
- Tomblin, J. S., and Barbero, E. J. (1997). Statistical microbuckling propagation model for compressive strength prediction of fiber-reinforced composites. In Composite Materials: Testing and Design, Thirteenth Volume. ASTM International.
- Tomblin, J. S., Barbero, E. J., and Godoy, L. A. (1997). Imperfection sensitivity of fiber microbuckling in elastic-nonlinear polymer-matrix composites. International Journal of Solids and Structures, 34(13): 1667-1679.
- Van Den Einde, L., Zhao, L., and Seible, F. (2003). Use of FRP composites in civil structural applications. Construction and Building Materials, 17(6): 389-403.
- vanDijk, N. P. (2016). Formulation and implementation of stress-driven and/or strain-driven computational homogenization for finite strain. International Journal for Numerical Methods in Engineering, 107: 1009-1028. doi: 10.1002/nme.5198.
» https://doi.org/10.1002/nme.5198 - Yurgartis, S. W., and Sternstein, S. S. (1994). Experiments to reveal the role of matrix properties and composite microstructure in longitudinal compression strength. ASTM Special Technical Publication, 1185: 193-193.
- Zahr-Viñuela, J., and Pérez-Castellanos, J. (2011). Elastic constants and isotropy considerations for particulate metal-matrix composites. A multi-particle, cell-based approach. Composites Part A: Applied Science and Manufacturing, 42(5): 521-533.
- Zohdi, T. I., and Wriggers, P. (2008). An Introduction to Computational Micromechanics.Springer
Publication Dates
-
Publication in this collection
Dec 2016
History
-
Received
19 Feb 2016 -
Reviewed
22 Sept 2016 -
Accepted
11 Oct 2016