Abstract
In order to study the critical ricochet velocity and critical penetration velocity of tungsten alloy rod obliquely penetrating a finite-thickness metal plate, experiment and numerical calculation of tungsten alloy rod impacting on homogeneous armor steel plate with a thickness of 30mm at an angle of 60° were carried out. Compared the experimental and numerical results with the results using models, it is found that, the results of the ricochet models proposed by Tate, Rosenberg and Steven B for semi-infinite thick plate are quite different from those of experiment and numerical calculation, so they can not be applied to the ricochet situation of finite-thickness plate. The critical penetration velocity model proposed by De Marre and Zhao are in good agreement with the numerical and experimental results, which can predict critical penetration velocity of tungsten alloy rod obliquely penetrating a finite-thickness metal plate with large impact angle. The penetration depth of the projectile under the critical ricochet velocity is about 1/3 of the thickness of the target plate, and the angle between the ejection trajectory of the fragments produced by projectile and target plate and projectile penetration trajectory is exactly 90° in the first penetration stage.
Keywords:
tungsten alloy rod; oblique penetration; finite-thickness metal plate; critical ricochet velocity; critical penetration velocity
1 INTRODUCTION
Owing to the limitation of launching conditions, the influence of flight aerodynamic characteristics and the upgrade of armor protection structure, the projectile usually has certain angle of attack when it impacts the target plate, that is, the projectile penetrates the target obliquely (Goldsmith, 1999Goldsmith, W. (1999). Non-ideal projectile impact on targets. International Journal of Impact Engineering 22:95-395.). When the projectile impacts the target obliquely, the velocity direction, the axis of projectile and the normal direction of the target plate have an intersection angle. Compared with the normal penetration (the velocity direction, the axis of projectile and the normal direction of the target are on the same line), the oblique penetration is more complex. The resistance of the target plate to the projectile is asymmetric, which leads to ballistic deflection and even fracture of projectile in the penetration process (Lee et al., 2002Lee, W., Lee, H., Shin, H. (2002). Ricochet of a tungsten heavy alloy long-rod projectile from deformable steel plates. Journal of Physics D Applied Physics 35:2676.; Børvik et al., 2011Børvik, T., Olovsson, L., Dey, S., et al. (2011). Normal and oblique impact of small arms bullets on AA6082-T4 aluminium protective plates. International Journal of Impact Engineering 38:577-589.; Tiwari et al., 2018Tiwari, G., Iqbal, M. A., Gupta, P. K. (2018). Impact Response of Thin Aluminium Plate with Varying Projectile Obliquity and Span Diameter. Iranian Journal of Science & Technology Transactions of Mechanical Engineering 1-10.; Lidén et al., 2011Lidén, E., Andersson, O., Lundberg, B. (2011). Deformation and fracture of a long-rod projectile induced by an oblique moving plate: Experimental tests. International Journal of Impact Engineering 38):989-1000., 2012). Therefore, the oblique penetration of tungsten alloy rod into finite-thickness metal plate has always been an important subject in the field of armor piercing. At present, the research on oblique penetration of tungsten alloy rod mainly focuses on the factors affecting oblique penetration of projectile, such as impact velocity, oblique angle of target plate, material and geometry of projectile and target plate, and the critical ricochet velocity and critical penetration velocity of projectile etc. At the same time, many scholars try to study the oblique penetration process, ricochet situation, critical penetration velocity and residual velocity of projectile by establishing kinematics equation and mechanics equation of oblique penetration of projectile into target plate. Jonas and Zukas (1978) used X-ray photography experiment and simulation method to study the jumping phenomenon of long rod projectile. It is considered that the ricochet process is that at the moment of impact, a plastic hinge is formed between the projectile and the target, and the rod deflects to the outside of the target along the contact point. Chao et al. (2015) studied oblique penetration trajectory of projectiles with different head shapes and composite materials to medium and thick steel targets, and obtained the variation law of deflection moment of projectiles during oblique penetration. Tate (1979Tate, A. (1979). A simple estimate of the minimum target obliquity required for the ricochet of a high speed long rod projectile. Journal of Physics D Applied Physics 12:1825-1829.) described ricochet of projectile with a simplified two-dimensional hydrodynamic model, assuming that the projectile is a rigid body. When the overall moment of the projectile caused by the impact force on the projectile head is greater than a certain value, the projectile rotates and then jumps, but the geometry and material properties of the target plate are not considered. Rosenberg et al. (2009Rosenberg, Z., Ashuach, Y., Yeshurun, Y., et al. (2009). On the main mechanisms for defeating AP projectiles, long rods and shaped charge jets. International Journal of Impact Engineering 36:588-596.) proposed a new formula considering the effect of target plate strength and projectile bending. Dong et al. (2014Dong, Y. C., Du, Z. H., Liu, R. Z ., et al. (2014). Research on ricochet of tungsten alloy long rod impacting thin steel target with high-velocity. Journal of Ballistics 26:73-77.) used numerical simulation and the characteristics of Tate model to modify his model by adding the thickness of target plate parameter, so as to realize the prediction of the ricochet angle of thin steel target plate .
At present, the research on oblique penetration of tungsten alloy rod, especially theoretical research, is to simplify the projectile into rigid body or elastomer with small deformation. But in fact, the high-strength projectile often breaks up during oblique penetration of high-strength steel target plate. Lankford et al. (1996Lankford J, Anderson C E, Royal S A, et al. (1996). Penetration erosion phenomenology. International Journal of Impact Engineering, 18:565-578.) systematically described the erosion phenomenon of tungsten alloy rod penetrating armor plate. According to his description, under extremely high impact pressure, plastic flow occurs in the head of the rod to form a “mushroom head”, the subsequent shear localization results in local instability and fracture at the “mushroom head”. According to the simulation of penetration process of tungsten alloy rod projectile into armor steel made by Meng et al. (2015Meng W, Mingchuan Y, Guang R, et al. (2015). Failure Model and Numerical Simulation of the Tungsten Alloy Long Rod when Piercing into Armor Target. Rare Metal Materials and Engineering, 44: 2170-2174), in the process of penetration, the “mushroom head” of tungsten alloy rod keeps forming and falling off, and the rod is corroded and gradually shortened. The “mushroom head” of the projectile rod deforms violently like plastic flow. Deformation localization mainly occurs at the edges or front end of the “mushroom head”.
In this paper, numerical simulation and armor penetration experiment were used to study the penetration process, the critical ricochet velocity, the critical penetration velocity, erosion and fragmentation of tungsten alloy rod into high-strength and finite-thickness homogeneous armor steel target plate.
2 THEORETICAL CALCULATION
During our study, the impact velocity direction of projectile coincides with the axis of projectile, and has an angle of 60° with the normal direction of target plate. The sketch diagram of impact condition of projectile and target plate is shown in Figure 1. The projectile is tungsten alloy tungsten alloy rod with a diameter of 11mm and a length of 90mm and the target plate is made of homogeneous armor steel with a size of 200mm×200mm×30mm. The following situations may occur when a tungsten alloy rod impacting a finite-thickness metal target plate with a certain large oblique angle, ricochet, critical ricochet, embedded, critical penetration and penetration, as shown in Figure 1. The critical ricochet velocity and the critical penetration velocity are the focuses of many studies. When the impact velocity is less than the critical ricochet velocity, the projectile will ricochet, which seriously reduces the penetration damage ability of the projectile. Similarly, only when the impact velocity of the projectile is greater than the critical penetration velocity can the projectile penetrate the target plate and damage the target objects behind the target plate.
2.1 Critical ricochet velocity
2.1.1 Tate model
Tate (1979Tate, A. (1979). A simple estimate of the minimum target obliquity required for the ricochet of a high speed long rod projectile. Journal of Physics D Applied Physics 12:1825-1829.) described ricochet condition with a simplified two-dimensional hydrodynamic model
Where denotes oblique angle (the angle between the velocity direction of projectile and the normal direction of target plate), denote density of projectile and target plate respectively, v is impact velocity, Yp is yield strength of projectile, L, D denote the length and diameter of the projectile respectively. When the impact angle of the projectile is fixed (60°), formula (1) can be rewritten as follows.
Formula (2) shows that when the impact velocity of a projectile is less than a certain value, the projectile will ricochet. When a tungsten alloy tungsten alloy rod with a diameter of 11 mm and a length of 90 mm impacts a 30 mm thick homogeneous armor steel plate at an angle of 60°, the yield strength Yp of the tungsten alloy projectile is 1506 MPa, its density is 17800 kg/m3, and the density of the homogeneous armor steel is 7830 kg/m3. The critical ricochet velocity obtained by substituting these parameters into formula (2) is 33.9989m/s.
2.1.2 Rosenberg model
Considering the effects of target strength and projectile bending, Rosenberg et al. (1989Rosenberg, Z., Yeshurun, Y., Mayseless, M. et al. (1989). On the ricochet of long rod projectiles. Proceeding of the 11th International Symposium on Ballistics (Belgium).) proposed the following ricochet formula.
Where Rt denotes the resistance of target plate, u is penetration velocity of projectile.
When the impact angle of the projectile is 60°, formula (3) can be rewritten as follows.
Since the penetration velocity u is greater than 0, formula (4) is further simplified approximately.
Rosenberg simulated the impact of tungsten alloy rod projectiles on steel targets with different strength, and obtained the relationship between Rt and target material strength as follows (Rosenberg and Dekel, 1994).
Where is the elastic modulus of the target plate, and Y t is yield strength of target plate (900MPa for homogeneous armor steel), therefore R t =4.93Y t=4.437GPa. The density of tungsten alloy projectile is 17800kg/m3. The critical ricochet velocity obtained by substituting these parameters into formula (2) is 288.2549m/s.
2.1.3 Steven B model
Segletes (2006Segletes, S.B . (2006). A model for rod ricochet. International Journal of Impact Engineering 32:1403-1439.) assumed that the rod projectile formed a plastic hinge when it collided with the target plate. Based on this assumption, the ricochet condition of the projectile was proposed as follows.
Using this formula, the critical ricochet velocity of projectile can be calculated to be 310.0711m/s or 450.9596m/s.
2.2 Critical penetration velocity
2.2.1 De Marre model
De Marre assumed that the flat-nosed cylindrical projectile would not deform during the process of penetrating the target plate, and that the failure mode of the target plate was adiabatic shear (Huang and Zu, 2007Huang, Z., Zu, X. (2007). Terminal effects, Science Press.). The kinetic energy of the projectile was completely consumed in the adiabatic shear band formed by the thrust part of the target plate. The classical De Marre critical penetration velocity formula was obtained.
Where K is the composite coefficient of armor piercing, which is related to the properties of target plate and projectile material, projectile structure and other factors. For ordinary armor-piercing projectiles, K ranges from 6200 to 73300. When estimating, K usually takes 67650. D, T, M indicate the diameter of projectile, the thickness of target plate and the mass of projectile, respectively. denotes oblique angle. When a projectile with a diameter of 11mm and a mass of 109g impacts a homogeneous armor steel target with a thickness of 30mm at an angle of 60°. The critical penetration velocity of projectile can be calculated to be 1195.46m/s using this model.
2.2.2 RI model
Recht and Ipson (1963Recht, R. F., Ipson, T. W. (1963). Ballistic Perforation Dynamics. Journal of Applied Mechanics 30:384.) believed that the kinetic energy of projectile in the process of penetrating the target plate was converted to the residual kinetic energy of projectile, the kinetic energy of plug, the energy of projectile lost by plastic collision between projectile and target Efn , and the work done by projectile to push the plug out W p . According to the conservation of energy, the following equation was obtained.
Where denotes the residual velocity of projectile. The velocity of the plug is the same as the residual velocity of the projectile. M and m denote the mass of the projectile and plug, respectively.The critical penetration velocity can be expressed as follows.
The W p in the formula is determined by the performance of the target plate, such as strength, thickness, hardening, strain rate sensitivity and failure strain. The W p is usually hard to be calculated. Woodward and Cimpoeru (1998Woodward, R. L., Cimpoeru, S. J. (1998). A study of the perforation of aluminium laminate targets. International Journal of Impact Engineering 21:117-131.) proposed a simplified model. He assumed that the thickness and diameter of the plug are H and and respectively, and constant shear stress τ acts on the lateral area of the cylinder (πH). He also suggested that τ=Y t /, where Y t is yield strength of target plate. The critical penetration velocity of the projectile is obtained as follows.
Assuming that the thickness of the plug is equal to the initial thickness of the target plate, and the diameter of the plug is equal to the diameter of the projectile. L eff is the equivalent length of the projectile, equals to the mass of the projectile divided by the cross-sectional area of the projectile. denotes the density of the projectile. When a projectile with a diameter of 11mm and a mass of 109g impacts a homogeneous armor steel target with a thickness of 30mm at an angle of 60°, the thickness T can be rewritten as T/cos60°. L eff equals 109g/=0.064mm. The critical penetration velocity obtained by substituting these parameters into formula (12) is 1088.83m/s.
2.2.3 Zhao model
Zhao (1989Zhao, G. (1989). Simplified model for oblique penetration of long-rod into plates of finite thickness. Acta Armamentarii 4:1-8.) fully considered the influence of target plate strength on the critical penetration velocity, and considered the breakage and erosion of projectile in the process of penetration, proposed a formula for calculating the critical penetration velocity of rod type kinetic energy projectile on homogeneous armor steel plate, which is as follows.
Where , . M, D, T denote the mass, diameter of projectile and the thickness of target plate respectively. denotes oblique angle. Y t is yield strength of target plate. The expression for calculating K 1 from a large number of experiments is as follows.
Where
Where K d is the correction factor of projectile diameter. When the diameter of projectile is 11mm, 1.093 is chosen. The exponent of C m in expression is variable. When , The exponent of Cm equals 1/3; When , The exponent of Cm equals 1/4 ~1/5. According to the research in this paper, Cm=81893.3133, 1/5 was chosen for the exponent of Cm. The critical penetration velocity obtained by substituting these parameters into formula (13) is 1204.29 m/s.
3 EXPERIMENT
In this paper, the tungsten alloy rod with a diameter of 11mm and a length of 90mm was used to impact 30mm thick homogeneous armor steel plate at an angle of 60°. A 25mm caliber ballistic gun was used to launch the projectile as shown in Figure 2, impacting a homogeneous armor steel target with a thickness of 30mm at an angle of 60°. The velocity of the projectile was measured before it hits the target using on-off velocity measurement. The high speed photography was used to supervise the flight attitude of the projectile.
The impact velocities and results of the projectile obtained from the experiment are shown in Table 1. The flying projectile recorded by high-speed photography is shown in Figure 3. The profiles of craters formed by projectile impact are shown in Figure 4.
From the experimental results and crater morphology, it can be seen that the critical penetration velocity of the projectile to a homogeneous armor steel target with a thickness of 30mm at an angle of 60° is between 1207.5m/s and 1225.0m/s. The empirical formulas proposed by Zhao and De Marre can also calculate the ultimate penetration velocity of projectiles well. While the result calculated by RI model is quite different from the experimental result. The main reason is that the RI model does not consider the fragmentation of projectile during penetration. The critical ricochet velocity of the projectile in the experiment is between 1113.8m/s and 1179.5. The ricochet models found by Tate, Rosenberg and Steven B for semi-infinite thick target have large errors with experimental results, and can not be applied to the ricochet situation of finite thick target. Therefore, the critical ricochet velocity of tungsten alloy rod obliquely penetrating a homogeneous armor plate of finite-thickness will be further discussed by numerical calculation and mechanics analysis.
3 NUMERICAL CALCULATION
3.1 Numerical model
Using AUTODYN-3D, a half model of projectile and target was established as shown in Figure 5. The tungsten alloy projectile was simulated by using smooth particle hydrodynamic model. The distance between adjacent particles is 0.2 mm. Lagrangian mesh is used to describe homogeneous armor steel target. The mesh at the center of the target was refined. The mesh size increases gradually from the center to the edge of the target plate. The mesh size at the center of the target plate is 0.5mm×0.5mm×0.5mm. The velocity direction of projectile coincides with the axis of projectile and has an angle of 60 ° with the normal direction of target plate.
In order to effectively simulate the ablation and fragmentation of projectile, Johnson-Cook strength model (Senthil et al., 2018Senthil, K, Iqbal, M. A., Arindam, B. (2018). Ballistic resistance of 2024 aluminium plates against hemispherical, sphere and blunt nose projectiles. Thin-Walled Structures 126: 94-105) was selected and maximum principal stress failure and random failure criteria were introduced. The Johnson-Cook strength model was validated by modified Taylor impact test and numerical simulation. It is proved that the Johnson-Cook strength model can effectively simulate the dynamic deformation and failure behavior of tungsten alloy (Rohr et al., 2008Rohr I, Nahme H, Thoma K, et al. (2008). Material characterisation and constitutive modelling of a tungsten-sintered alloy for a wide range of strain rates. International Journal of Impact Engineering 35:811-819.). The constitutive relation of target plate was also expressed by Johnson-Cook strength model. The Johnson-Cook strength model is expressed as follows
Where denotes equivalent stress. A is the yield strength of material at reference strain rate and temperature. Coefficients B, C and m represent strain hardening coefficient, strain rate sensitivity coefficient and temperature softening coefficient, respectively. Exponent n denotes strain hardening exponent. is the user-defined reference strain rate, which is usually set to 1.
Where ,and indicate absolute temperature, ambient temperature and melting temperature of material, respectively.
The main parameters of Johnson-Cook strength model for tungsten alloy and homogeneous armor steel (Verreault, 2015Verreault, J. (2015). Analytical and numerical description of the PELE fragmentation upon impact with thin target plates. International Journal of Impact Engineering 76:196-206.; Couque et al., 2007Couque, H, Nicolas, G., Altmayer, C. (2007). Relation between shear banding and penetration characteristics of conventional tungsten alloys. International Journal of Impact Engineering 34:412-423.; Luo et al., 2016Luo, R., Huang, D., Yang, M., et al. (2016). Penetrating performance and “self-sharpening” behavior of fine-grained tungsten heavy alloy rod penetrators. Materials Science & Engineering A 675:262-270.; Song and Ning, 2011Song, W. D., Ning, J. G. (2011). Dynamic mechanical characterization and optimization of particle-reinforced W-Ni-Fe composites. Science China 54:1651-1658.;) are shown in Table 2.
The fragments have obvious statistical characteristics of probability, because the fragments are random when the projectile is broken, but the structure and material of the projectile are uniform and the material properties are unique in numerical simulation. Therefore, in order to simulate the random characteristics of the projectile fragmentation, the stochastic failure model based on Mott’s theory was introduced to the failure criterion of tensile principal stress in numerical simulation. In this model, Mott simplifies a cylindrical shell into a two-dimensional ring according to its radial cross-section (Mott, 1947), and assumes that the probability of fracture occurring on an unbroken shell of unit length along the circumferential direction when the strain changes from to .
Where p is the probability of fracture. D andare material characteristic parameters respectively, which related to loading strain rate. The probability of fracture increases exponentially with strain increasing. It is assumed that when the strain is, the probability of unbroken of the shell is 1-p,in that way, when the strain increases by, the probability that the shell will fracture is as follows,
After solving the integral, it is possible to get the probability p of fracture before a certain point of the shell reaches plastic strain.
Mott considers that the average fracture strain exists in the material.
The standard deviation of the average fracture strain is as follows,
3.2 Numerical results
In order to explore the critical ricochet conditions, the critical penetration velocity, the breakage of the projectile and the crater morphology of the target during penetration, the impact velocities of the projectile were set to 1000m/s, 1100m/s, 1200m/s and 1300m/s respectively. When the impact velocity of the projectile is 1000m/s, the projectile ricochets completely, the head of the projectile is broken, but the whole projectile does not break. The the projectile flying and the final crater formed on the target plate is shown in Figure 6. The ratio of crater depth h to the thickness of target plate T is equal to 0.294. The crater interface curve can be divided into two sections. l 1 is the trajectory of projectile jumping, l 2 is the trajectory of projectile penetration. The length ratio of l 1 and l 2 is about 0.549, and the angle between l 1 and l 2 is about 135°. When the impact velocity of the projectile is 1100 m/s, the projectile jumps completely, the whole projectile is broken and deformed, and the backside of the target bulges, as shown in Figure 7. The ratio of crater depth h to the thickness of target plate T is 0.549 . The length ratio of l 1 and l 2 is about 0.634, and the angle between l 1 and l 2 is about 120°.
When the impact velocity of the projectile is 1200m/s, the simulation results show that the head of the projectile is broken and the remaining projectile is embedded in the target plate as shown in Figure 8, but the integrity of the remaining projectile is obviously better than that of the remaining projectile when the impact velocity is 1100m/s. The ratio of penetration depth h to the thickness of target plate T is equal to 0.919, and there is obvious bulge on the back of the target plate, which indicates that the projectile is about to penetrate the target plate. When the penetration is completed, the trajectory l 1 of fragments produced by the head of projectile and target plate is changed greatly, and the angle between the extended line of l 1 and the extended line l 2 of projectile penetration trajectory is about 40°. When the impact velocity of the projectile is 1300m/s, the simulation results show that the projectile penetrates the target plate and the residual projectile bends greatly as shown in Figure 9. From the crater morphology, the trajectory of the projectile has changed greatly. When the penetration depth reaches to about 55 percent of the target plate, the projectile deflects greatly. The upper part of the crater is horn-shaped and the lower part is a through-hole.
From the simulation results, when the tungsten alloy tungsten alloy rod with diameter of 11m and length of 90mm impacts a homogeneous armor steel target plate with a thickness of 30mm at an angle of 60°. When the impact velocity is 1000m/s and 1100m/s, the projectile ricochets. When the impact velocity is 1200m/s, the projectile is embedded in the target. When the impact velocity is 1300m/s, the projectile penetrates the target plate. In the ricochet phase, with the increase of impact velocity, the degree of fragmentation and penetration depth of projectile increase gradually. The length ratio of ejection trajectory of fragments produced by projectile and target plate to penetration trajectory of projectile decreases gradually, and the angle between them decreases gradually. When the impact velocity is 1100 m/s, the projectile ricochets and the residual projectile deforms seriously. When the impact velocity is 1200 m/s, the residual projectile is embedded in the target. The ratio of penetration depth h to the thickness of target plate T is about 0.919, but the integrity of the remaining body is obviously better than that of the remaining projectile when the impact velocity is 1100 m/s. It can be inferred that the critical penetration velocity of projectile is about 1200m/s (slightly greater than 1200m/s), and the critical critical velocity is between 1000m/s and 1100m/s. In order to further determine the critical ricochet velocity range, the impact of projectile on 60°/30mm homogeneous armor steel target at 110m/s velocity was simulated, and the results shown in Figure 10. The projectile is all broken and thrown out, and there is an obvious bulge behind the target plate. The ratio of ejection trajectory of fragments produced by projectile and target plate to penetration trajectory of projectile continues to decrease (about 0.486), and the angle between them also continues to decrease (about 100°). It can be inferred that the critical ricochet velocity of projectile is about 1150 m/s. From the experiments, the critical ricochet velocity of the projectile is between 1113.8m/s and 1179.5 and the critical penetration velocity is between 1207.5m/s and 1225.0m/s. The numerical results are in good agreement with the experimental results.
5 DISCUSSION
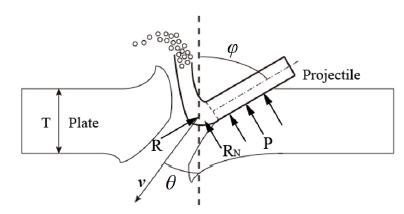
In the process of oblique impact of tungsten alloy tungsten alloy rod on homogeneous armor steel, the interaction between projectile and target plate is complicated due to the continuous breakage of projectile body, the continuous penetration and destruction of target plate, and the continuous ejection of fragments produced by projectile body. When analyzing the penetration process of projectile, some simplified and reasonable assumptions should be made. The forces of the projectile at the initial stage of penetration are shown in Figure 11. In the initial stage of penetration, the projectile head is subjected to the action of front resistance R and lateral force P. The resultant force of frontal resistance and lateral force produces a turning moment ω, which makes the projectile rotate around its own center of mass. The projectile obtains angular velocity around the center of mass, and the projectile trajectory deviates. When the projectile rotates to a certain angle, the projectile trajectory will deviate from the target plate and ricochet. When the velocity of the projectile is very low, the projectile may ricochet directly without penetrating the target plate. When the velocity of the projectile is slightly higher but still less than the critical critical velocity, the projectile will ricochet after penetrated part of the target plate.
When the projectile penetrates the target plate, the target plate is squeezed by the invading projectile and moves at high speed to the free surface in front of the projectile on both sides. Hole enlargement, fracture and fragmentation of the target plate occur at the same time. Meanwhile, the fragments of the fragmented target plate are thrown out along the axial direction of the projectile. This stage is also called the first stage of penetration. At this time, new penetration interface is formed between projectile and target plate. In this process, the lower surface of the projectile head is always in direct contact with the target plate, while the upper surface is in contact with the debris produced by target plate. In the axial direction, the resistance of the target plate to the projectile is symmetrical positive resistance R. In the lateral direction, the projectile is also subjected to the lateral resistance R N given by a target plate due to the difference of the media on both sides of the projectile head. In addition, with the penetration of the projectile, the action range of the lateral force P gradually expands. The forces acting on the projectile during penetration are shown in Figure 12. When the projectile penetrates a certain depth, it enters the second penetration stage. There is a straight hole left on the target during the second penetration stage.
From the numerical results, the angle between the ejection trajectory of fragments produced by projectile and target plate to penetration trajectory of projectile in the first penetration stage decreases gradually with the increase of impact velocity. The same rule can be obtained from the experimental results. The angles obtained from the experimental results are shown in Figure 13. It can be seen from the variation law of the angle that the condition of critical ricochet of projectile is that the angle is exactly 90°. From the experimental results, the ratio of penetration depth to the thickness of target plate increases with the increase of impact velocity in the first penetration stage . But it does not increase continually. When the impact velocity exceeds 1225 m/s, the ratio tends to be stable as shown in Figure 14. Throughout the whole variation curve, the ratio is about 1/3, so it can be inferred that the penetration depth of the first penetration stage should reach 1/3 of the thickness of the target plate if the projectile wants to insert or penetrate the target plate. Combining with the penetration depth of the projectile in the simulation results when the projectiles ricochet, it can be concluded that the penetration depth of the projectile under the critical ricochet velocity is about 1/3 of the thickness of the target plate.
5 CONCLUSION
In this paper, numerical calculation and experimental study on oblique penetration of tungsten alloy rod kinetic energy projectile with diameter of 11mm and length of 90mm into homogeneous armor steel plate of with thickness of 30mm at an impact angle of 60° are carried out. The critical ricochet velocity of the projectile was calculated by using the ricochet models established by Tate, Rosenberg and Steven B. The critical penetration velocity of the projectile was calculated by using the critical penetration velocity models established by De Marre, Recht and Zhao. Comparing the results of model calculation, numerical calculation and experimental results, the following conclusions are obtained.
The critical ricochet velocity of the projectile obtained by numerical calculation is basically the same as that obtained by experiment. The calculation results using the ricochet models established by Tate, Rosenberg and Steven B are quite different from those of the experiment.
The calculation results using the critical penetration velocity models established by De Marre and Zhao are in good agreement with the numerical results and the experimental results. Whereas the calculation result using the critical penetration velocity model established by Recht is slightly smaller than the experimental result.
Through experiment and numerical simulation, the critical ricochet condition of projectile is obtained. In the first penetration stage, the angle between the ejection trajectory of the fragments produced by projectile and target plate and projectile penetration trajectory is exactly 90°and the penetration depth of the projectile under the critical ricochet velocity is about 1/3 of the thickness of the target plate.
-
Nomenclature
- oblique angle
- v impact velocity
- u penetration velocity of projectile
- density of projectile
- Y p yield strength of projectile
- L length of projectile
- D diameter of projectile
- M mass of projectile
- residual velocity of projectile. The velocity of the plug
- K d correction factor of projectile diameter
- T thickness of target plate
- density of target plate
- R t denotes the resistance of target plate
- elastic modulus of the target plate
- Y t yield strength of target plate
- K composite coefficient of armor piercing
- E fn energy of projectile lost by plastic collision between projectile and target
- W p work done by projectile to push the plug out
- L ef equivalent length of the projectile
- m mass of plug
- H thickness of plug
- diameter of plug
- shear stress acts on the lateral area of the plug
- critical penetration velocity
- parameters in Zhao model
References
- Goldsmith, W. (1999). Non-ideal projectile impact on targets. International Journal of Impact Engineering 22:95-395.
- Lee, W., Lee, H., Shin, H. (2002). Ricochet of a tungsten heavy alloy long-rod projectile from deformable steel plates. Journal of Physics D Applied Physics 35:2676.
- Børvik, T., Olovsson, L., Dey, S., et al. (2011). Normal and oblique impact of small arms bullets on AA6082-T4 aluminium protective plates. International Journal of Impact Engineering 38:577-589.
- Tiwari, G., Iqbal, M. A., Gupta, P. K. (2018). Impact Response of Thin Aluminium Plate with Varying Projectile Obliquity and Span Diameter. Iranian Journal of Science & Technology Transactions of Mechanical Engineering 1-10.
- Lidén, E., Andersson, O., Lundberg, B. (2011). Deformation and fracture of a long-rod projectile induced by an oblique moving plate: Experimental tests. International Journal of Impact Engineering 38):989-1000.
- Lidén, E., Mousavi, S., Helte, A., et al. (2012). Deformation and fracture of a long-rod projectile induced by an oblique moving plate: Numerical simulations. International Journal of Impact Engineering 40:35-45.
- Jonas G H, Zukas J A . (1978). Mechanics of penetration: Analysis and experiment. International Journal of Engineering Science 16:879-903.
- Chao G E, Yong-Xiang D, Zhi-Chao L U, et al. (2015). Ballistic Deflection on Oblique Penetration of Projectiles with Different Noses. Acta Armamentarii 36:255-262.
- Tate, A. (1979). A simple estimate of the minimum target obliquity required for the ricochet of a high speed long rod projectile. Journal of Physics D Applied Physics 12:1825-1829.
- Rosenberg, Z., Ashuach, Y., Yeshurun, Y., et al. (2009). On the main mechanisms for defeating AP projectiles, long rods and shaped charge jets. International Journal of Impact Engineering 36:588-596.
- Dong, Y. C., Du, Z. H., Liu, R. Z ., et al. (2014). Research on ricochet of tungsten alloy long rod impacting thin steel target with high-velocity. Journal of Ballistics 26:73-77.
- Lankford J, Anderson C E, Royal S A, et al. (1996). Penetration erosion phenomenology. International Journal of Impact Engineering, 18:565-578.
- Meng W, Mingchuan Y, Guang R, et al. (2015). Failure Model and Numerical Simulation of the Tungsten Alloy Long Rod when Piercing into Armor Target. Rare Metal Materials and Engineering, 44: 2170-2174
- Rosenberg, Z., Yeshurun, Y., Mayseless, M. et al. (1989). On the ricochet of long rod projectiles. Proceeding of the 11th International Symposium on Ballistics (Belgium).
- Rosenberg, Z., Dekel, E. (1994). A critical examination of the modified Bernoulli equation using two-dimensional simulations of long rod penetrators. International Journal of Impact Engineering 15:711-720.
- Segletes, S.B . (2006). A model for rod ricochet. International Journal of Impact Engineering 32:1403-1439.
- Huang, Z., Zu, X. (2007). Terminal effects, Science Press.
- Recht, R. F., Ipson, T. W. (1963). Ballistic Perforation Dynamics. Journal of Applied Mechanics 30:384.
- Woodward, R. L., Cimpoeru, S. J. (1998). A study of the perforation of aluminium laminate targets. International Journal of Impact Engineering 21:117-131.
- Zhao, G. (1989). Simplified model for oblique penetration of long-rod into plates of finite thickness. Acta Armamentarii 4:1-8.
- Senthil, K, Iqbal, M. A., Arindam, B. (2018). Ballistic resistance of 2024 aluminium plates against hemispherical, sphere and blunt nose projectiles. Thin-Walled Structures 126: 94-105
- Rohr I, Nahme H, Thoma K, et al. (2008). Material characterisation and constitutive modelling of a tungsten-sintered alloy for a wide range of strain rates. International Journal of Impact Engineering 35:811-819.
- Verreault, J. (2015). Analytical and numerical description of the PELE fragmentation upon impact with thin target plates. International Journal of Impact Engineering 76:196-206.
- Couque, H, Nicolas, G., Altmayer, C. (2007). Relation between shear banding and penetration characteristics of conventional tungsten alloys. International Journal of Impact Engineering 34:412-423.
- Luo, R., Huang, D., Yang, M., et al. (2016). Penetrating performance and “self-sharpening” behavior of fine-grained tungsten heavy alloy rod penetrators. Materials Science & Engineering A 675:262-270.
- Song, W. D., Ning, J. G. (2011). Dynamic mechanical characterization and optimization of particle-reinforced W-Ni-Fe composites. Science China 54:1651-1658.
- Mott N F. (1947). Fragmentation of Shell Cases. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 189:300-308.
Edited by
Publication Dates
-
Publication in this collection
04 Nov 2019 -
Date of issue
2019
History
-
Received
08 July 2019 -
Reviewed
08 Oct 2019 -
Accepted
08 Oct 2019 -
Accepted
08 Oct 2019