Abstract
In this paper, a new numerical technique, the differential quadrature method (DQM) has been developed for dynamic analysis of the nanobeams in the polar coordinate system. DQ approximation of the required partial derivatives is given by a weighted linear sum of the function values at all grid points. A semicircular arch with small-scale effects is investigated by the nonlocal continuum theory with simply supported boundary conditions. The governing equations for Euler-Bernoulli nonlocal beam models are derived. The expressions of the bending displacement are presented analytically. The convergence properties and the accuracy of the DQM for bending of curved nanobeams are investigated through a number of numerical computations. It can be observed that use of DQM, which is independent of domain discretization to be efficient.
DQM; curved nanobeam; moving particle load
Application of nonlocal elasticity and DQM to dynamic analysis of curved nanobeams
Hassan KananipourI,* * Author email: h.kananipour@usc.ac.ir ; Mehdi AhmadiII; Hossein ChavoshiI
IDepartment of Civil Engineering, University of Science and Culture, Tehran, Iran. P.O. Box: 13145-871
IIDepartment of Civil and Environmental Engineering, College of Engineering, Shiraz University, Shiraz, Fars 7134851156, Iran. Email: mehdi_ahmadi@shiraz.ac.ir
ABSTRACT
In this paper, a new numerical technique, the differential quadrature method (DQM) has been developed for dynamic analysis of the nanobeams in the polar coordinate system. DQ approximation of the required partial derivatives is given by a weighted linear sum of the function values at all grid points. A semicircular arch with small-scale effects is investigated by the nonlocal continuum theory with simply supported boundary conditions. The governing equations for Euler-Bernoulli nonlocal beam models are derived. The expressions of the bending displacement are presented analytically. The convergence properties and the accuracy of the DQM for bending of curved nanobeams are investigated through a number of numerical computations. It can be observed that use of DQM, which is independent of domain discretization to be efficient.
Keywords: DQM, curved nanobeam, moving particle load.
1 INTRODUCTION
DQM is a proper method in solving mathematic and engineering equations straightly. This method estimates a partial derivative of a variable function with respect to a coordinate at a grid point as a weighted linear sum of the function values at all grid points along that coordinate direction. DQ method was introduced for the first time by Bellman and Casti (1971), and was applied in solving partial differential equations by Bellman et al. (1972). The mentioned method is an efficient one in partial derivative estimations as well as in solving differential equations (Bellman and Adomin 1985, Bellman and Roth 1986). DQ method application in solving dynamic equations is fairly hard to cope with due to the simultaneous existence of boundary and initial conditions. Wu and Liu (2000) utilized DQM with generalized boundary condition to solve the sixth-order differential equations related to a ring deformation excited by a static load. Recently, dynamic analysis of curved beams are mentioned for various boundary conditions by Nikkhoo et al. (2012).
2 GOVERNING EQUATIONS
The beam is assumed as a plane circular arch of constant cross section and an incompressible centerline. It is essential to utilize the polar coordinates with the origin at the center of the arch, and denotes by r the radius of the arch, φ the variable angle, s the arch length equal to φr and ds the variations along the arch equal to rdφ. One element is taken out of the arch and the element equilibrium conditions in the tangential and normal direction as well as the moment conditions are written. Neglecting the effect of shear, element rotation and infinitely small quantities of higher orders, the following equation would be obtained (Fryba 1999).
where u(φ,t) represents tangential displacement, pn(φ,t) normal load per unit length of arch, pt(φ,t) tangential load per unit length of arch, pm(φ,t) bending load per unit length of arch, E is the Young's modulus and I is moment of inertia at the beam sections and µ constant mass per unit length of arch. Taking the solution of this non-homogeneous equation, though possible, would be very time-consuming and laborious. Therefore, the approximate estimations as numerical methods are required to be employed.
3 DIFFERENTIAL QUADRATURE METHOD
Differential Quadrature (DQ) is capable of calculating derivative orders of the field variable up to N-1 order in the case of N grid points. DQ equations based on polynomial or Fourier series expansion are computable; in this paper, DQ based on polynomials, which provides fine compatibility in analyzing high-order differential equations, is employed. The value derived for the function w(x) in the ith grid point is calculated via summing weighting-linear function values in the other nodes (Eq. (2)). Besides, nth order derivative (n = 2, 3, ..., N-1) in the ith grid point can be calculated in the same way (Eq. (3))
where N is the number of grid points in the x-direction,  and
and  are the weighting coefficient associated with the first and nth-order derivative, respectively, and w(xk) are field variables at the point xk(k = 1, 2, ..., N).
are the weighting coefficient associated with the first and nth-order derivative, respectively, and w(xk) are field variables at the point xk(k = 1, 2, ..., N).
Weighting coefficients for the first and nth-order derivatives are obtained from the following recurrence equations
where R(x) and R(1)(x) are defined as
x1, x2, xN are coordinates of the grid points that might be selected as desired. Obviously, weighting coefficients of the second and higher-order derivatives is computable via weighting coefficients of the first-order derivative (Eqs. (4-6)).
4 RESULTS AND DISCUSSION
The curved nanobeam was assumed as a semicircular arch with the opening angle of the arch Φ = n radian. Eq. (1) would be solved via DQM for a simply supported curved nanobeam. Chebyshev grid point distribution model is chosen as the grid point distribution model along the domain since it corresponds well with the interpolation of polynomials


In order to apply boundary and initial conditions separately, the Generalized Differential Quadrature Method was utilized since it provides acceptable convergence in obtaining analysis results of high-order differential equations (Wang et al. 2005).
According to the nonlocal continuum theory (Eringen 1972), the stress at a reference point depends on strain at all points in the body. The nonlocal constitutive equations can be simplified to where σij, Cijkl and εkl are the nonlocal elasticity stress tensor, fourth order local stress tensor and strain tensor, respectively. The parameter e0 is estimated nonlocal elasticity constant suitable to each material, and a is the internal characteristic length (e.g. the C-C bond length, lattice parameter and granular size). e0a is nonlocal parameter or distinctive length that means the scale coefficient which denotes the small-scale effect on the mechanical characteristics. Choice of the value of a parameter e0 is crucial to calibrate the nonlocal model with experimental results. In the limit when e0a goes to zero, nonlocal elasticity will be reduced to the classical local mode. Generally, for the analysis of carbon nanobeams, the nonlocal scale coefficients e0a are taken in the range 0-2 nm. Still contemporary research is going on to find the exact values of nonlocal parameters for various nanolevel structural problems. Furthermore, ∇2 is the Laplacian operator and is given by ∇2 = (∂2/∂x2 + ∂2/∂y2).
The results are normalized. The tangential displacements, radial displacements and bending moments of the numerical solutions for the curved nanobeam under a moving load are divided by the tangential displacement, radial displacement and bending moment of the analytical solution same prismatic circular arch, subjected to a concentrated unit force, P, at the middle of the nanobeam, respectively (Tsumura 1956).
The results of the mentioned beam and nanobeam dynamic analysis solved via DQM are indicated in Table 1 for 11, 15, and 19 nodes along φ and in t domain. The dynamic amplification factors for the normalized maximum bending moments (DAF1), maximum radial displacements (DAF2) and maximum tangential displacements (DAF3) are assumed.
According to Figure 1, maximum radial displacement and bending moment of the curved beam with simple boundary conditions decrease as the load moves at higher speeds. The structure deformations were investigated logarithmically in the time range during the load moves over the beam.
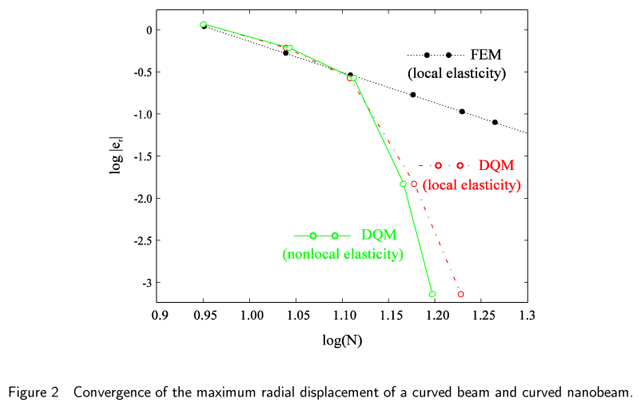
In Figure. 2, the DQM convergence rate in local and nonlocal elasticity has been compared to the finite element method (FEM) in local elasticity. The rate of convergence for the DQM increased when the number of grid points increases. The FEM convergence is constant by increasing the number of elements.
5 CONCLUSIONS
Considering the mentioned issues and the curved nanobeam dynamic analysis excited by a moving load, it would be concluded that:
1- The numerical examples revealed DQM provides acceptable convergence in solving high-order differential equations compared to other numerical methods. DQ method was assessed in the dynamic in-plane deflection analysis model of curved nanobeams with different boundary conditions, and it was illustrated that this numerical method is adequately efficient in these problems.
2- In DQM, convergence rate augments quadratically as the number of grid points increases and almost complete convergence would be achieved by assuming 20 grid points in the whole domain. However, when the number of grid points exceeds a certain limit, DQM leads to an ill-conditioned problem. In the FEM, convergence rate is constant.
3- Initial conditions and boundary conditions of the displacement field derivative were applied simultaneously in the start/end grid points of the domain. It was revealed that DQM provides suitable compatibility with applying initial conditions, rigid boundary conditions, slopes and bending moments.
4- DQ method is of relative superiority compared to the other numerical methods given its independence from domain discretization in the structural problems with particular geometry.
Received in 16 Apr 2013
In revised form 30 Jul 2013
- Bellman, R. and Casti, J. (1971) Differential quadrature and long-term integration. J. Math. Anal. Appl. 34: 235-238.
- Bellman, R., Kashef, B.G. and Casti, J. (1972). Differential quadrature: a technique for the rapid solution of nonlinear partial differential equations. J. Comput. Phys. 10: 40-52.
- Bellman, R. and Adomian, G. (1985). Partial differential equations. D Reidel Publishing, Dordrecht, Netherlands.
- Bellman, R. and Roth, R.S. (1986). Methods in approximation. D Reidel Publishing, Dordrecht, Netherlands.
- Eringen, A.C. (1972). Nonlocal polar elastic continua. Int. J. Eng.Sci., 10, 1-16.
- Fryba, L. (1999). Vibration of Solids and Structures under Moving Loads. Thomas Telford. London.
- Nikkhoo, A., Kananipour, H., Chavoshi, H. and Zarfam R.(2012). Application of differential quadrature method to investigate dynamics of a curved beam structure acted upon by a moving concentrated load. India J. Sci. Technol. 5: 3085-3089.
- Tsumura, T. (1956), Strength Design Data Book, Shokabo Publishing Co., Ltd., Tokyo.
- Wang, X., Liu, F., Wang, X. and Gan L. (2005). New approaches in application of differential quadrature method to fourth-order differential equations. Commun. Numer. Meth. Eng. 21: 61-71.
- Wu, T.Y. and Liu, G.R. (2000). Application of generalized differential quadrature rule to sixth-order differential equations. Commun. Numer. Meth. Eng 16: 777-784.
Publication Dates
-
Publication in this collection
03 Feb 2014 -
Date of issue
Oct 2014
History
-
Received
16 Apr 2013 -
Accepted
30 July 2013