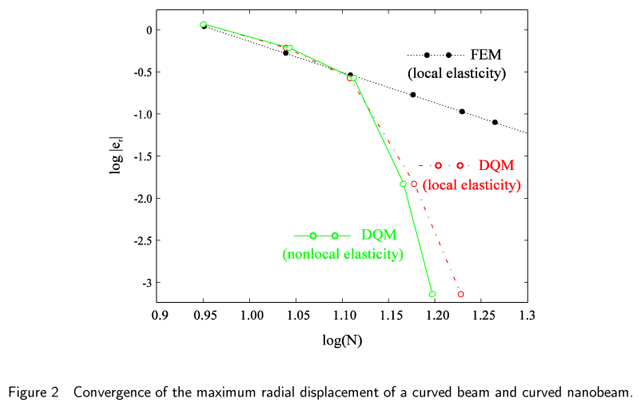
In this paper, a new numerical technique, the differential quadrature method (DQM) has been developed for dynamic analysis of the nanobeams in the polar coordinate system. DQ approximation of the required partial derivatives is given by a weighted linear sum of the function values at all grid points. A semicircular arch with small-scale effects is investigated by the nonlocal continuum theory with simply supported boundary conditions. The governing equations for Euler-Bernoulli nonlocal beam models are derived. The expressions of the bending displacement are presented analytically. The convergence properties and the accuracy of the DQM for bending of curved nanobeams are investigated through a number of numerical computations. It can be observed that use of DQM, which is independent of domain discretization to be efficient.
DQM; curved nanobeam; moving particle load