Abstract
Resonance is a phenomenon of utmost importance in railways engineering, leading to vast damages both in track and vehicles. A short-span bridge has been modeled by means of a finite elements method model, calibrated and validated with real data, to study resonance vibrations induced by the passage of trains. Furthermore, the influence of vehicle speed and track damping on the vibrations registered on the rail, the sleeper and the bridge has been assessed. Different track and vehicle pathologies have been proposed and their effect on the resonance of the bridge has been evaluated.
Keywords:
railways vibrations; resonance; corrugation; squat; wheelflat
1 INTRODUCTION
Resonance is a well known phenomenon which occurs when the loading frequencies coincide with the natural frequencies of the bridges or the trains, and it is able to induce severe damages in a structure, in extreme cases, to its collapse. For this reason, many investigations have recently been focused on characterizing such an important phenomenon. The main aim of these studies is, firstly, to take measures in order to avoid the excitation of the eigenfrequencies of the system and, secondly, to minimize the effect of resonance when it occurs.
As stated by (Xia et al., 2006Xia, H., Zhang, N., & Guo, W. W. (2006). Analysis of resonance mechanism and conditions of train-bridge system. Journal of Sound and Vibration, 297(3):810-822.), the resonance of train-bridge systems is influenced by many factors, such as the periodically loading on the bridge induced by the moving load series formed by the wheel-axle weights of the train vehicles, the harmonic forces caused by irregularities, and the periodical actions on the moving vehicles of long bridges with identical spans and their deflections.
Within this context, train-structure interaction models have been implemented so as to deepen on vehicle and bridge responses. As an example, (Wang et al., 2010Wang, Y., Wei, Q., Shi, J., & Long, X. (2010). Resonance characteristics of two-span continuous beam under moving high speed trains. Latin American Journal of Solids and Structures, 7(2): 185-199.) simulated a two-span continuous beam and obtained the two critical velocities causing the resonance response. By means of numerical models, (Lu et al., 2012Lu, Y., Mao, L., & Woodward, P. (2012). Frequency characteristics of railway bridge response to moving trains with consideration of train mass. Engineering Structures, 42: 9-22.) studied the influence of the bridge-to-carriage length ratio and (Yang & Lin, 2005Yang, Y. B., & Lin, C. W. (2005). Vehicle-bridge interaction dynamics and potential applications. Journal of sound and vibration, 284(1): 205-226.) demonstrated that the primary frequencies in the bridge response might be caused by the driving frequencies, which are related to the time the train spent crossing the bridge, and the dominant frequencies, caused by the repeated loads.
According to (Mao & Lu, 2011Mao, L., & Lu, Y. (2011). Critical speed and resonance criteria of railway bridge response to moving trains. Journal of Bridge Engineering, 18(2): 131-141.) the bridge response under a moving train is quite complicated since the excitation does not only involve characteristics from a moving load but also repeated load pulses from consecutive axles, bogies and carriages. Furthermore, authors as (Yau, 2001Yau, J. D. (2001). Resonance of continuous bridges due to high speed trains. Journal of Marine Science and Technology, 9(1):14-20.) and (Kwark et al., 2004Kwark, J. W., Choi, E. S., Kim, Y. J., Kim, B. S., & Kim, S. I. (2004). Dynamic behavior of two-span continuous concrete bridges under moving high-speed train. Computers & structures, 82(4): 463-474.) studied the resonance of continuous bridges due to moving trains.
Since models based on finite elements method have been found to be a useful tool to reproduce the behavior of the track and the structure ((Ju & Lin, 2003Ju, S. H., & Lin, H. T. (2003). Resonance characteristics of high-speed trains passing simply supported bridges. Journal of sound and vibration, 267(5): 1127-1141.)), in the present investigation a three-dimensional FEM model has been developed so as to study the phenomenon of resonance in a short-span railway bridge.
2 METHODOLOGY
To study the resonance vibrations caused by a train running along a short-span railway bridge, a finite elements model has been developed, being its main characteristics presented in first term. Then, the gathering campaign carried out in a real stretch of track used to calibrate the model will be described, and the proper behavior of the model, according to the data measured in the real track, will be proven.
Subsequently, the flexural modes of vibration of the bridge will be calculated and the influence of vehicle speed in different elements of the vehicle-track-structure system will be assessed. Moreover, different scenarios of track damping will be assessed. Finally, several pathologies available in many railway systems will be presented, studying their influence on the generation of vibrations and interaction with the resonant phenomenon.
2.1 Finite Elements Model
The structure-track-vehicle system has been simulated by means of a finite elements model, developed with the commercial software ANSYS LS-DYNA V14. It has been divided into two submodels: the structure-track model and the vehicle model. In the present section, both submodels will be presented, as well as the interaction between them.
First of all, the geometry of structure-track submodel has been implemented, reproducing a real stretch placed near Xativa (Spain). The track built over the bridge, is provided with UIC 45 rails, wooden sleepers and a ballast layer. Further details on the real track will be presented below.
The dynamic response of the submodel is calculated by relating the internal forces of the system to the external forces. This relationship can be written by means of the equation of motion:
Being [M] is the global mass matrix, [C] the damping matrix, [K] the stiffness matrix and {u}, α(t)} represents the time-dependent external forces vector. and {ü} the vectors of displacement, speed and acceleration respectively. {F
and {ü} the vectors of displacement, speed and acceleration respectively. {F
Following (Real et al., 2014), the damping matrix [C] can be expressed as:
Where α and β are the so-called Rayleigh coefficients.
Regarding the external forces, they are given by the vehicle submodel detailed below. Thus, displacements, velocities and accelerations can be calculated for each node of the model solving (Eq. 1).
The frequency range studied with the model varies between 2 and 100 Hz. In addition, the frequency range limits determine the model dimensions and also the model elements size as explained in (Real et al., 2014).
It must be pointed that material behavior is assumed to be linear elastic. This hypothesis is assumed because it has been previously checked that the dynamic wave produced by the moving train does not induce large strains in the soil in this case. Consequently, the displacements are limited to the elastic range in the stress-strain diagram as studied by (Real et al., 2014). 8-node hexahedral elements have been selected to model the mesh.
Regarding the vehicle sub model, it has been modeled considering a three-mass system, accounting the wheel, bogie and the carbody masses. The masses are linked by springs and dampers in parallel which simulate the primary and secondary suspensions, as shown in Figure 1:
In the three-mass system which represents the vehicle, the wheel-rail interaction is modeled as a node-to-beam contact allowing for sliding and loss of contact, using the Penalty algorithm. The contact elements provide an elastic support between the rail and the wheel simulating the hertzian contact.
Vehicle submodel has also been solved by the equation of motion. To solve the non-linear equations of the problem, full Newton-Raphson method has been used, while Newmark implicit time integration method has been used to solve the transient dynamic equilibrium equations.
2.2 Calibration of the Model
Although many characteristics of the track elements were known at the moment of developing it, some others - as ballast, soil stiffness and the damping coefficient of the track - were still unknown. In order to provide the model the ability to accurately reproduce the behavior of the real track, a gathering campaign was performed to: (1) estimate the unknown parameters of the track and (2) assess the performance of the model.
To these aims, Sequoia Fast Tracer accelerometers were placed at different points of a ballasted track built over a 5m long bridge. The main characteristics of the elements available in the track are detailed in the following Table:
Mechanical parameters of the elements. * denotes that the parameter is, at first term, unknown.
Meanwhile, the characteristics of the vehicle, an Alstom S-592, are detailed below
Following (Griffin, 1996Griffin, M. J. (1996). Handbook of human vibration. Academic press, USA.), the most relevant frequency range from the point of view of negative effects on humans is comprised between 2 and 80Hz. Thus, the data recorded in the data gathering campaign was treated so as to fit in the range of 2 to 100 Hz. To do so, a high-pass filter with a cut-off frequency of 2Hz has been applied to the register, as well as a low pass filter has been set to 100Hz.
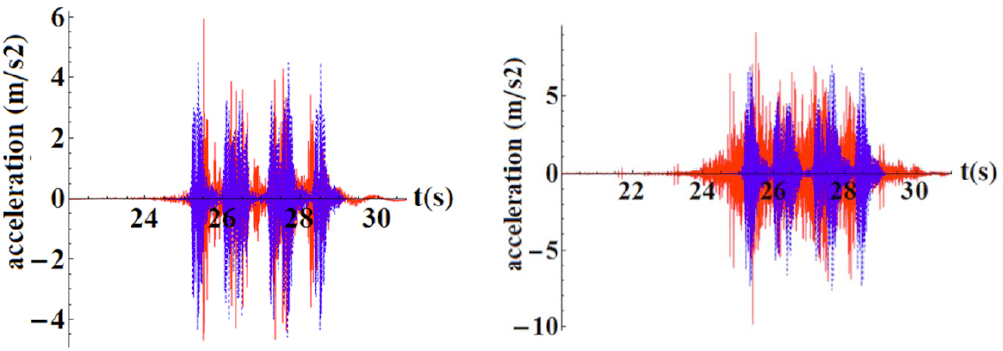
Once registers are treated, results from the model have been compared with them, leading to the Figures shown below. It must be pointed that both calibration and validation were carried out in the mid-span of the bridge, being the calibration performed at a sleeper and the validation in the rail.
Comparison between registered data (red) and calculated accelerations (blue). Calibration (left) at a sleeper and validation (right) at the rail.
3 MODAL ANALYSIS
The natural frequencies of the bridge have been calculated by means of a modal analysis, carried out with the finite elements model. For the modal analysis, materials have been assumed to present a linear-elastic behavior, damping has been neglected and the external actions have been disregarded. Consequently, the dynamic equation presented in (Eq. 1) is reduced to (Eq. 3):
In the linear system considered, free vibration is determined by harmonic functions as shown in Eq. 4.
In which ϕi represents the eigenvector associated with the mode shape of the i-th natural frequency (ωi).
Combining the previous equations, the modal analysis is performed solving (Eq. 5):
(Eq. 5) can be solved for n values of the natural circular frequencies of the system ωi and eigenvectors {ϕ}. Natural frequencies fi are then calculated as shown (Eq. 6).
In single-track bridges, the main natural frequencies that may induce the resonance of the bridge are those related to the flexural shape modes since, due to the geometric and loading symmetry, torsional modes are not excited. Some authors as (Museros, 2002Museros, P., Romero, M. L., Poy, A., & Alarcón, E. (2002). Advances in the analysis of short span railway bridges for high-speed lines. Computers & structures, 80(27): 2121-2132.) claim that the first flexural mode is the most influential in the dynamic behavior of a bridge. In the present study, the firsts 20 natural frequencies (Table 3) are calculated by means of the FE model.
4 INFLUENCE OF VEHICLE SPEED AND TRACK DAMPING
Once the model has been validated, its correct behavior has been proven and the natural modes of vibration of the structures are known, the study of two of the most influential parameters on resonance phenomenon will be assessed. Thus, in the present section, the influence of vehicle speed and track damping on accelerations will be assessed.
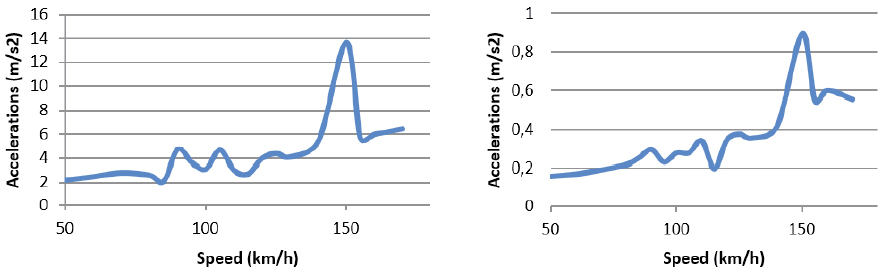
In the next figure, the accelerations measured at the mid-span of the bridge in different elements of the track: the concrete slab, the sleepers and the rail are presented for different vehicle speeds, ranging from 50 to 170 km/h:
From the figure, it can be seen how the same trend is followed in all the elements. Furthermore, in every case, the maximum peak is found at a vehicle speed close to 90km/h. Considering a distance between axles of the same bogie of 2.5m, the frequency associated with this speed can be estimated as:
Being f the frequency (Hz), V vehicle speed (km/h) and d the distance (m). Thus, the frequency associated to the passage of the axles at 90km/h is 10Hz, which is very close to the first flexural mode of the bridge. It is clear from this analysis that maintenance problems of both track and vehicle, situations of passengers discomfort or even lack of security would be derived from the excitation of the first flexural mode of vibration.
On the other hand, it can be seen that, for every speed, the deeper the point where accelerations are calculated, the higher the attenuation of vibrations.
Analogously, accelerations in the unsprung and sprung masses of the vehicle have been calculated, being the results presented in the following figure:
It can be seen from the figure that similar behavior has been obtained for both unsprung and sprung masses. As expected, accelerations at the sprung masses are significantly lower than in the unsprung masses. Moreover, it can be deduced that the higher the vehicle speed, the higher the accelerations calculated in the vehicle and, furthermore, an operational speed close to 150km/h should be avoided for the vehicle maintenance issue and for the sake of passengers comfort.
The influence of track damping on resonance vibrations has also been assessed in the current study. As exposed in section 2, track damping has been introduced by means of the coefficients of Rayleigh. Following (Real et al., 2014), coefficient α may be disregarded, while β coefficient was set to 0.00007 in the calibration process. Thus, damping influence has been studied in terms of this parameter.
To this aim, seven different damping values have been considered, being the results presented in the next figure:
The maximum value for accelerations calculated in the rail, the sleeper and in the slab is shown for the damping of the original case. Following (Gupta & Ahuja, 2014Gupta, A., & Ahuja, A. S. (2014). Dynamic Analysis of Railway Bridges under High Speed Trains. Universal Journal of Mechanical Engineering, 2(6): 199-204.), the damping of the bridge has a great influence on the amplitude of the response; in the present case, resonance phenomenon for a speed of 90km/h occurs for a β equal to 0.00007. Thus, at this point, a maximum in the calculated accelerations is reached. Far from this point, high damping values lead to small acceleration responses, while small damping values conduce to the opposite behavior.
From this analysis, solutions focused on reducing the effect of resonance in the studied bridge may be proposed for the real track. Thus, knowing the usual speed at which vehicles travel through the stretch, an optimum damping may be provided to the track so as to avoid the maintenance costs derived from the huge vibrations which take place because of resonance phenomenon.
5 INFLUENCE OF PATHOLOGIES
In the previous sections, the supposition that both train and track were in perfect conditions was considered. However, the appearance of damages in one or both of them is usual in real tracks. For this reason, at the present section, the influence of different types of wheel and rail defects on the response of the studied track will be assessed. Following the procedure carried out by (Sheng et al., 2004Sheng, X., Jones, C. J. C., & Thompson, D. J. (2004). A theoretical model for ground vibration from trains generated by vertical track irregularities. Journal of sound and vibration, 272(3): 937-965.), the considered defects have been introduced into the model by means of an equivalent rail profile, as detailed below for each considered case.
The pathologies chosen for their study have been rail corrugation, squat and a wheel flat. Rail corrugation is a defect available in many tracks, and it was described and classified by (Grassie & Kalousek, 1993Grassie, S. L., & Kalousek, J. (1993). Rail corrugation: characteristics, causes and treatments. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 207(1): 57-68.). Furthermore, authors as (Biang et al., 2014) studied the influence of the amplitude and the wavelength of the defect on the vibrations generated on a track. In the present investigation, corrugation has been modeled as a sinusoidal wave, defined by its wavelength and its amplitude. In this sense, an amplitude of 0.5mm has been set, and two wavelengths (0.25m and 0.5m) have been analyzed.
Squats are localized defects, related to the rolling contact fatigue produced in the wheel-rail contact, and they are associated to a loss of material. The genesis of this phenomenon was studied by authors as (Pal et al., 2012Pal, S., Valente, C., Daniel, W., & Farjoo, M. (2012). Metallurgical and physical understanding of rail squat initiation and propagation. Wear, 284:30-42.) and (Simon et al., 2013Simon, S., Saulot, A., Dayot, C., Quost, X., & Berthier, Y. (2013). Tribological characterization of rail squat defects. Wear, 297(1): 926-942.). In the current work, following (Simon et al., 2013), the squat has been modeled as a gap, whose depth is 1mm and its length 50mm.
Wheelflats are localized defects available at wheels, being its formation produced as a consequence of the blockage of the wheel when the vehicle is moving. Authors like (Ahlström & Karlsson, 1999Ahlström, J., & Karlsson, B. (1999). Microstructural evaluation and interpretation of the mechanically and thermally affected zone under railway wheel flats. Wear, 232(1): 1-14.) and (Makino et al., 2002Makino, T., Yamamoto, M., & Fujimura, T. (2002). Effect of material on spalling properties of railroad wheels. Wear, 253(1):284-290.) studied this type of wheels pathology. In the current study, the equivalent rail profile for the wheelflat has been obtained taking into account the trocoid curve that the wheel center describes as the wheel rolls. It must be considered that this approach is only valid for studying vertical dynamics. Moreover, wheelflat can be defined by its length which, in this study, has been set to 80mm.
Thus, the studied cases are summed up in the following table:
For each case, results have been calculated in a point placed at the mid-span of the bridge, over three different elements of the track: (1) the rail, (2) a sleeper, and (3) the slab. Then, for each case, element and vehicle speed, an accelerogram as the one shown in (Figure 7) has been obtained.
(Figure 7) shows the comparison between the accelerations generated in the rail by a train running at 60km/h in a healthy track (blue) and in case A (red). From this figure, the increment on vibrations produced by the presence of this pathology is clearly noticed.
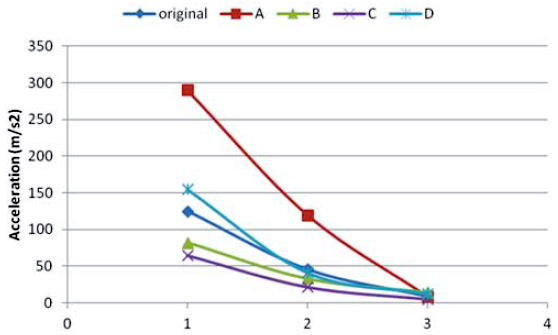
The maximum value of acceleration in each situation has been calculated. Thus, Fig. 8 shows the maximum accelerations induced by a train running at 60 km/h for cases A to D, while in Fig. 9 the considered vehicle sped is 90km/h.
At Fig. 8, the maximum accelerations due to train passage through the stretch have been presented for all the studied cases and for the reference case. In first term, it can be seen how vibrations are attenuated while the wave is propagated through the track; furthermore, the existence of defects significantly increase the vibrational response of the track, especially at the rail.
Punctual defects, as the squat and the wheelflat, generate more vibrations than continuous ones, since they induce forces in the rail-wheel contact presenting high amplitudes in a short and reduced lapse of time, being the squat the most harmful pathology.
Regarding the continuous defects, the influence of the excitation frequency on the generation of vibrations is clearly seen when comparing cases A and B: being unaltered the rest of parameters, accelerations are higher for the case A, since wavelength is lower than in case B. Then, from (equation 7), the excitation frequency is lower in case A, leading to the conclusion that the higher the excitation frequency the higher the calculated accelerations.
In an analogous manner than above, the maximum accelerations calculated in the three considered elements of the track are now plotted for a vehicle speed of 90km/h in the next figure. It must be taken into account that, accelerations for case A - shown in red at Fig. 9 - have been divided by 10 for the sake of the readability of the figure.
Fig. 9 shows results quite different from those obtained for the prior vehicle speed. First of all, it must be taken into account that at 90km/h, the passage of the axles of the train excites the first mode of vibration of the bridge, leading to the appearance of resonant conditions.
According to the figure, resonance phenomenon is, in some cases, enhanced by the effect of the defects, such as in case A while in other cases, as in case B, resonance vibrations are mitigated by the effect of the pathologies. This difference of behavior in the interaction between defects and resonance vibrations may be explained by the fact that they are out of phase. Thus, depending on the frequency associated to each defect, the addition of both waves will present one or other behavior.
As has been previously noticed, under resonance conditions there are some divergences on the results. For some defects, the accelerations mitigate the resonance conditions. For instance, when the rail corrugation has a wavelength of 0.5 meters, the calculated accelerations are lower than in the original case, as shown in next figure.
However, there are other situations where the accelerations are increased over the resonance conditions. When the rail corrugation has a wavelength of 0.25m the amplitude of the accelerations in the slab arises to 87m/s2, as it is seen in Figure 11.
These huge accelerations are induced by the rail corrugation, which amplifies the resonance conditions. If the slab displacements are compared for both previous cases (Figure 12) it is seen that the slab presents an oscillation once the train of loads has passed over the mid-span for the case of the enhancement of resonance vibrations.
6 CONCLUSIONS
A FEM model has been implemented in order to reproduce the vibrational behavior of a track subjected to resonance conditions. In order to assure the reliability of the model, a gathering campaign was carried out on a real track.
From the model, the effect of vehicle speed, track damping and several pathologies placed both on the rail and in the wheel on vibrations has been studied, concluding:
-
Vehicle speed presents a non-linear influence on the accelerations registered both in the track and vehicle
-
The maximum value of accelerations occurs at a speed of 90km/h, matching with the speed at which the passage of adjacent axles excite the first flexural mode of the bridge
-
The maximum accelerations are reached for a β equal to 0.00007. Far from this value, the higher the damping of the track, the lower the vibrations.
-
Under no resonance conditions, the presence of irregularities in the rail-wheel contact induces an increase of vibrations.
-
Punctual irregularities lead to bigger vibrations than continuous defects. Furthermore, the higher the excitation frequency, the higher the accelerations obtained.
-
Defects in the vehicle and in the track may increase or mitigate the amplitude of resonance.
References
- Ahlström, J., & Karlsson, B. (1999). Microstructural evaluation and interpretation of the mechanically and thermally affected zone under railway wheel flats. Wear, 232(1): 1-14.
- Bian, X. C., Chao, C., Jin, W. F., & Chen, Y. M. (2011). A 2.5 D finite element approach for predicting ground vibrations generated by vertical track irregularities. Journal of Zhejiang University SCIENCE A, 12(12): 885-894.
- Comendador, R., Real, T., Zamorano, C., Real Herráiz, J. I., & Hernández, C. (2014). Computational considerations of 3-D finite element method models of railway vibration prediction in ballasted tracks. Journal of Vibroengineering, 16(4): 1709-1722.
- Grassie, S. L., & Kalousek, J. (1993). Rail corrugation: characteristics, causes and treatments. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 207(1): 57-68.
- Griffin, M. J. (1996). Handbook of human vibration. Academic press, USA.
- Gupta, A., & Ahuja, A. S. (2014). Dynamic Analysis of Railway Bridges under High Speed Trains. Universal Journal of Mechanical Engineering, 2(6): 199-204.
- Ju, S. H., & Lin, H. T. (2003). Resonance characteristics of high-speed trains passing simply supported bridges. Journal of sound and vibration, 267(5): 1127-1141.
- Kwark, J. W., Choi, E. S., Kim, Y. J., Kim, B. S., & Kim, S. I. (2004). Dynamic behavior of two-span continuous concrete bridges under moving high-speed train. Computers & structures, 82(4): 463-474.
- Lu, Y., Mao, L., & Woodward, P. (2012). Frequency characteristics of railway bridge response to moving trains with consideration of train mass. Engineering Structures, 42: 9-22.
- Makino, T., Yamamoto, M., & Fujimura, T. (2002). Effect of material on spalling properties of railroad wheels. Wear, 253(1):284-290.
- Mao, L., & Lu, Y. (2011). Critical speed and resonance criteria of railway bridge response to moving trains. Journal of Bridge Engineering, 18(2): 131-141.
- Museros, P., Romero, M. L., Poy, A., & Alarcón, E. (2002). Advances in the analysis of short span railway bridges for high-speed lines. Computers & structures, 80(27): 2121-2132.
- Pal, S., Valente, C., Daniel, W., & Farjoo, M. (2012). Metallurgical and physical understanding of rail squat initiation and propagation. Wear, 284:30-42.
- Sheng, X., Jones, C. J. C., & Thompson, D. J. (2004). A theoretical model for ground vibration from trains generated by vertical track irregularities. Journal of sound and vibration, 272(3): 937-965.
- Simon, S., Saulot, A., Dayot, C., Quost, X., & Berthier, Y. (2013). Tribological characterization of rail squat defects. Wear, 297(1): 926-942.
- Wang, Y., Wei, Q., Shi, J., & Long, X. (2010). Resonance characteristics of two-span continuous beam under moving high speed trains. Latin American Journal of Solids and Structures, 7(2): 185-199.
- Xia, H., Zhang, N., & Guo, W. W. (2006). Analysis of resonance mechanism and conditions of train-bridge system. Journal of Sound and Vibration, 297(3):810-822.
- Yang, Y. B., & Lin, C. W. (2005). Vehicle-bridge interaction dynamics and potential applications. Journal of sound and vibration, 284(1): 205-226.
- Yau, J. D. (2001). Resonance of continuous bridges due to high speed trains. Journal of Marine Science and Technology, 9(1):14-20.
Publication Dates
-
Publication in this collection
July 2016
History
-
Received
07 Jan 2016 -
Reviewed
26 Feb 2016 -
Accepted
29 Feb 2016