Abstract
The structure-soil-structure interaction (SSSI) between high-rise buildings is numerically investigated. ANSYS has been further developed for calculation in the frequency domain, in which hysteretic damping can be considered for both the soil and structure. This study is presented in two subsequent papers. In the first part, i.e., this paper, the variations in the story shear force, interstory drift angle, displacement, velocity and acceleration of the superstructure, the sway of the foundation, and the axial and shearing forces of the pile are presented. The major influencing factors are the excitation frequency of a harmonic wave or the frequency components of a seismic wave, shaking direction of an exciting wave and direction of the structure arrangement. Under harmonic waves, the interaction mainly occurs when the excitation frequency is 1-5 Hz. Under seismic waves, when the shaking direction of an exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure, the influence on the superstructure is greatest.
Keywords:
structure-soil-structure interaction; seismic interaction; adjacent structure; clustering structure; building cluster;
Introduction
The conventional seismic design or evaluation of structures considers local site effects; the effects of the soil-structure interaction (SSI) have also recently been considered in design texts, i.e., only the concerned structure is taken into account[1[1] Kausel E. Early history of soil-structure interaction[J]. Soil Dynamics and Earthquake Engineering, 2010,30(9):822-832.]. While these approximations are reasonable in most cases, they are questionable in urban areas, where high-rise buildings, which are similar in height and design, are built in close proximity to each other. If there are other structures located in the neighborhood of the considered structure, during earthquake events, the radiation energy would be emitted from a vibrating structure to other structures through the soil. This action will influence the dynamic characteristics and earthquake response among the closely spaced structures, which is referred to as the structure-soil-structure interaction (SSSI). For buildings located in dense urban environments that are composed of city blocks, the assumption that buildings are isolated from each other is invalid and can produce erroneous results. There are plants of previous studies that have verified the importance of the SSSI[2[2] Lou M, Wang H, Chen X, et al. Structure-soil-structure interaction: Literature review[J]. Soil Dynamics and Earthquake Engineering, 2011,31(12):1724-1731.]. Therefore, consideration of the interaction among soil, foundations, and structures requires a more holistic approach. However, the effects of the coupling of adjacent structures, i.e., the SSSI, are not well quantified because the investigation of the SSSI effects is practically more challenging than that of the SSI. In addition to the subsoil properties, consideration of the relationship among the dynamic properties of adjacent structures, the geometric setup, and the natural uncertainty of the ground motions need to be considered. The study of the SSSI has importance in accurately predicting the seismic responses of structures and has become a popular topic in earthquake engineering research.
Assuming elastic wave propagation, the SSSI occurs as a result of the diffraction of an incident wave field due to a structure's foundation generating a secondary wave field, which affects (an) adjacent structure(s). An SSSI analysis requires knowledge of two interaction mechanisms, including the SSI and dynamic cross interaction (DCI). While the SSI deals with the interaction between individual structures and their underlying soil, the DCI is concerned with the through-the-soil interaction between adjacent structures within a structure cluster. The SSSI is one of the branches of the SSI, and as a natural protraction, research techniques, including analytical[3[3] Luco J E, Contesse L. Dynamic structure-soil-structure interaction[J]. Bulletin of the Seismological Society of America, 1973,63(4):1289-1303.
[4] Lee T H, Wesley D A. Soil-structure interaction of nuclear reactor structures considering through-soil coupling between adjacent structures[J]. Nuclear Engineering and Design, 1973,24(3):374-387.
[5] Lee T H, Wesley D A. Influence of through-soil coupling between adjacent structures on seismic response of nuclear reactors: Proceedings 2nd International Conference on Structural Mechanics in Reactor Technology, Berlin, Germany, 1973[C].
[6] Wong H L, Trifunac M D. Two-dimensional, antiplane, building-soil-building interaction for two or more buildings and for incident plane SH waves[J]. Bulletin of the Seismological Society of America, 1975,65(6):1863-1885.
[7] Kobori T, Kusakabe K. Dynamic cross-interaction between two embedded structure: Proceedings of the 5th Japan Earthquake Engineering Symposium, Toky, Japan, 1978[C].
[8] Warburton G B, Richardson J D, Webster J J. Harmonic responses of masses on an elastic half space[J]. Journal of Engineering for Industry, ASME, 1972,194(2):193-200.
[9] Warburton G B, Richardson J D, Webster J J. Forced vibrations of two masses on an elastic half space[J]. Journal of Applied Mechanics-Transactions, ASME, 1971,38(1):148-156.-10[10] Richardson J D. Forced vibrations of rigid bodies on a semi-infinite elastic medium[D]. Nottinghamshire, England: University of NottinghamDepartment of Mechanical Engineering, 1969.], numerical[11[11] Bybordiani M, Arici Y. Structure‐soil‐structure interaction of adjacent buildings subjected to seismic loading[J]. Earthquake Engineering & Structural Dynamics, 2019,48(7):731-748.
[12] Liang J, Han B, Todorovska M I, et al. 2D dynamic structure-soil-structure interaction for twin buildings in layered half-space II: Incident SV-waves[J]. Soil Dynamics and Earthquake Engineering, 2018,113:356-390.
[13] Santana A, Aznarez J J, Padron L A, et al. A BEM-FEM model for the dynamic analysis of building structures founded on viscoelastic or poroelastic soils[J]. Bulletin of Earthquake Engineering, 2016,14(1):115-138.
[14] Rahgozar M A. Accounting for soil nonlinearity in three-dimensional seismic structure-soil-structure-interaction analyses of adjacent tall buildings structures[J]. International Journal of Civil Engineering, 2015,13(3B):213-225.-15[15] Fariborz N, Ali R. Nonlinear dynamic response of tall buildings considering structure-soil-structure effects[J]. The Structural Design of Tall and Special Buildings, 2013,22(14):1075-1082.] and experimental[16[16] Ngo V, Kim J, Chang S, et al. Effect of Height Ratio and Mass Ratio on Structure-Soil-Structure Interaction of Two Structures Using Centrifugal Experiment[J]. Applied Sciences, 2019,9(3):526.
[17] Barrios G, Nanayakkara V, De Alwis P, et al. Effects of Slenderness and Fundamental Frequency on the Dynamic Response of Adjacent Structures[J]. International Journal of Structural Stability and Dynamics, 2019,19(09):1950105.
[18] Kirkwood P, Dashti S. A Centrifuge Study of Seismic Structure-Soil-Structure Interaction on Liquefiable Ground and Implications for Design in Dense Urban Areas[J]. Earthquake Spectra, 2018,34(3):1113-1134.
[19] Li P, Liu S, Lu Z, et al. Numerical analysis of a shaking table test on dynamic structure-soil-structure interaction under earthquake excitations[J]. The Structural Design of Tall and Special Buildings, 2017,26(15):e1382.-20[20] Aldaikh H, Alexander N A, Ibraim E, et al. Shake table testing of the dynamic interaction between two and three adjacent buildings (SSSI)[J]. Soil Dynamics and Earthquake Engineering, 2016,89:219-232.] methods, that are implemented to investigate the SSSI are similar to those employed in SSI analyses[2[2] Lou M, Wang H, Chen X, et al. Structure-soil-structure interaction: Literature review[J]. Soil Dynamics and Earthquake Engineering, 2011,31(12):1724-1731.]. A real or complete SSI analysis must take into account the possible consideration of interactions with adjacent structures. The SSSI is an interdisciplinary field of endeavor that lies at the intersection of soil and structural mechanics, soil and structural dynamics, earthquake engineering, geophysics and geomechanics, material science, computational and numerical methods, and other diverse technical disciplines.
Similar to the study of the SSI[1[1] Kausel E. Early history of soil-structure interaction[J]. Soil Dynamics and Earthquake Engineering, 2010,30(9):822-832.], the study of the SSSI is aroused from mechanical vibration[8[8] Warburton G B, Richardson J D, Webster J J. Harmonic responses of masses on an elastic half space[J]. Journal of Engineering for Industry, ASME, 1972,194(2):193-200.
[9] Warburton G B, Richardson J D, Webster J J. Forced vibrations of two masses on an elastic half space[J]. Journal of Applied Mechanics-Transactions, ASME, 1971,38(1):148-156.-10[10] Richardson J D. Forced vibrations of rigid bodies on a semi-infinite elastic medium[D]. Nottinghamshire, England: University of NottinghamDepartment of Mechanical Engineering, 1969.]. The first known study was performed by Warburton et al.[8[8] Warburton G B, Richardson J D, Webster J J. Harmonic responses of masses on an elastic half space[J]. Journal of Engineering for Industry, ASME, 1972,194(2):193-200.
[9] Warburton G B, Richardson J D, Webster J J. Forced vibrations of two masses on an elastic half space[J]. Journal of Applied Mechanics-Transactions, ASME, 1971,38(1):148-156.-10[10] Richardson J D. Forced vibrations of rigid bodies on a semi-infinite elastic medium[D]. Nottinghamshire, England: University of NottinghamDepartment of Mechanical Engineering, 1969.], and the following 1970s was the initial phase of the SSSI study[3[3] Luco J E, Contesse L. Dynamic structure-soil-structure interaction[J]. Bulletin of the Seismological Society of America, 1973,63(4):1289-1303.
[4] Lee T H, Wesley D A. Soil-structure interaction of nuclear reactor structures considering through-soil coupling between adjacent structures[J]. Nuclear Engineering and Design, 1973,24(3):374-387.
[5] Lee T H, Wesley D A. Influence of through-soil coupling between adjacent structures on seismic response of nuclear reactors: Proceedings 2nd International Conference on Structural Mechanics in Reactor Technology, Berlin, Germany, 1973[C].
[6] Wong H L, Trifunac M D. Two-dimensional, antiplane, building-soil-building interaction for two or more buildings and for incident plane SH waves[J]. Bulletin of the Seismological Society of America, 1975,65(6):1863-1885.-7[7] Kobori T, Kusakabe K. Dynamic cross-interaction between two embedded structure: Proceedings of the 5th Japan Earthquake Engineering Symposium, Toky, Japan, 1978[C].]. The rapid progress of SSSI studies in subsequent decades has been stimulated by the needs of nuclear power plants (NPPs), which always consist of a reactor building adjacent to a turbine building and control building[21[21] Nakagawa S, Kuno M, Naito Y, et al. Forced vibration tests and simulation analyses of a nuclear reactor reactor building[J]. Nuclear Engineering and Design, 1998,179(2):145-156.
[22] Kitada Y, Hirotani T, Iguchi M. Models test on dynamic structure-structure interaction of nuclear power plant buildings[J]. Nuclear Engineering and Design, 1999,192(2/3):205-216.-23[23] Xu J, Costantino C, Hofmayer C, et al. Seismic response prediction of NUPEC's field model tests of NPP structures with adjacent building effect: 2004 ASME/JSME Pressure Vessels and Piping Conference, San Diego, California, USA, 2004[C].]. In recent years, apart from its continuation in NPPs[24[24] Roy C, Bolourchi S, Eggers D. Significance of structure-soil-structure interaction for closely spaced structures[J]. Nuclear Engineering and Design, 2015,295:680-687.
[25] Yue D, Ghiocel D M, Fuyama H, et al. Structure-soil-structure interaction effects for two heavy npp buildings with large-size embedded foundations: 22nd Conference on Structural Mechanics in Reactor Technology, San Francisco, California, USA, 2013[C].
[26] Clouteau D, Broc D, Devesa G, et al. Calculation methods of Structure-Soil-Structure Interaction (3SI) for embedded buildings: Application to NUPEC tests[J]. Soil Dynamics and Earthquake Engineering, 2012,32(1):129-142.-27[27] Anderson L M, PhD S C, Amin J. Effect of Structure, Soil, and Ground Motion Parameters on Structure-Soil-Structure Interaction of Large Scale Nuclear Structures: Structures congress, Las Vegas, NV(US), 2011[C].], studies related to the SSSI have focused more on structure clusters in urban areas. Population growth and the limited available urban space in large cities, such as New York, Istanbul, and Shanghai, inevitably result in the closer spatial proximity (only a few meters or even a few decimeters) of structures, which has even caused the occurrence of seismic pounding of adjacent structures[28[28] Ghandil M, Aldaikh H. Damage-based seismic planar pounding analysis of adjacent symmetric buildings considering inelastic structure-soil-structure interaction[J]. Earthquake Engineering & Structural Dynamics, 2017,46(7):1141-1159.,29[29] Li P, Liu S, Lu Z. Studies on Pounding Response Considering Structure-Soil-Structure Interaction under Seismic Loads[J]. Sustainability, 2017,9(12):2219.]. Thus, the seismic interaction of adjacent structures in city blocks that contain clusters of closely spaced structures through the underlying soil is inevitable.
The SSSI that occurs in urban areas can be subdivided into the interaction between underground structures (such as tunnels[30[30] He C, Zhou S, Di H, et al. Effect of Dynamic Interaction of Two Neighboring Tunnels on Vibrations from Underground Railways in the Saturated Soil[J]. KSCE Journal of Civil Engineering, 2019,23(11):4651-4661.]), between an underground structure and a surface structure (such as between a subway station and high-rise building[31[31] Guo J, Chen J, Bobet A. Influence of a subway station on the inter-story drift ratio of adjacent surface structures[J]. Tunnelling and Underground Space Technology, 2013,35:8-19.
[32] Wang H, Lou M, Chen X, et al. Structure-soil-structure interaction between underground structure and ground structure[J]. Soil Dynamics and Earthquake Engineering, 2013,54(11):31-38.-33[33] Wang H, Lou M, Zhang R. Influence of presence of adjacent surface structure on seismic response of underground structure[J]. Soil Dynamics and Earthquake Engineering, 2017,100(09):131-143.] or between a tunnel and frame[34[34] Abate G, Massimino M R. Parametric analysis of the seismic response of coupled tunnel-soil-aboveground building systems by numerical modelling[J]. Bulletin of Earthquake Engineering, 2017,15(1):443-467.
[35] Abate G, Massimino M R. Numerical modelling of the seismic response of a tunnel-soil-aboveground building system in Catania (Italy)[J]. Bulletin of Earthquake Engineering, 2017,15(1):469-491.-36[36] Abate G, Corsico S, Massimino M R. FEM Modelling of the Seismic Behavior of a Tunnel-soil-Aboveground Building System: A Case History in Catania (Italy): 6th Italian Conference of Researchers in Geotechnical Engineering, Bologna, Italy, 2016[C]. Elsevier Ltd, 2016.]), between surface structures[37[37] Ghandil M, Behnamfar F, Vafaeian M. Dynamic responses of structure-soil-structure systems with an extension of the equivalent linear soil modeling[J]. Soil Dynamics and Earthquake Engineering, 2016,80(1):149-162.
[38] Alamo G M, Padron L A, Aznarez J J, et al. Structure-soil-structure interaction effects on the dynamic response of piled structures under obliquely incident seismic shear waves[J]. Soil Dynamics and Earthquake Engineering, 2015,78(11):142-153.
[39] Aldaikh H, Alexander N A, Ibraim E, et al. Two dimensional numerical and experimental models for the study of structure-soil-structure interaction involving three buildings[J]. Computers & Structures, 2015,150(4):79-91.-40[40] Alexander N A, Ibraim E, Aldaikh H. A simple discrete model for interaction of adjacent buildings during earthquakes[J]. Computers & Structures, 2013,124(SI):1-10.], and between structures of other types (such as between liquid-storage tanks[41[41] Mykoniou K, Butenweg C, Holtschoppen B, et al. Seismic response analysis of adjacent liquid-storage tanks[J]. Earthquake Engineering & Structural Dynamics, 2016,45(11):1779-1796.], or between a duct and bridge pier[42[42] Moshirabadi S, Soltani M, Maekawa K. Seismic interaction of underground RC ducts and neighboring bridge piers in liquefiable soil foundation[J]. Acta Geotechnica, 2015,10(6):761-780.]). In addition to these interactions among a small number of structures, some researchers have proceeded one step further to analyze the influence of large groups of buildings and site effects due to the subsoil configuration on the seismic response of the overall system by theoretical, numerical and experimental methods[43[43] Schwan L, Boutin C, Padrón L A, et al. Site-city interaction: theoretical, numerical and experimental crossed-analysis[J]. Geophysical Journal International, 2016,205(2):1006-1031.
[44] Kumar N, Narayan J P. Quantification of site-city interaction effects on the response of structure under double resonance condition[J]. GEOPHYSICAL JOURNAL INTERNATIONAL, 2018,212(1):422-441.
[45] Lu X, Tian Y, Wang G, et al. A numerical coupling scheme for nonlinear time history analysis of buildings on a regional scale considering site-city interaction effects[J]. EARTHQUAKE ENGINEERING & STRUCTURAL DYNAMICS, 2018,47(13):2708-2725.-46[46] Kumar N, Narayan J P. Effects of site-city interaction and polarization of the incident S-wave on the transfer function and fundamental frequency of structures[J]. NATURAL HAZARDS, 2019,97(2):747-774.]. A comprehensive review of the SSSI problem is discussed in the work by Lou et al.[2[2] Lou M, Wang H, Chen X, et al. Structure-soil-structure interaction: Literature review[J]. Soil Dynamics and Earthquake Engineering, 2011,31(12):1724-1731.]. Thus, only a brief overview of the newest findings about the seismic interaction of high-rise buildings, which is more relevant to this paper, is presented in the following section.
Alexander et al.[40[40] Alexander N A, Ibraim E, Aldaikh H. A simple discrete model for interaction of adjacent buildings during earthquakes[J]. Computers & Structures, 2013,124(SI):1-10.], Aldaikh et al.[20[20] Aldaikh H, Alexander N A, Ibraim E, et al. Shake table testing of the dynamic interaction between two and three adjacent buildings (SSSI)[J]. Soil Dynamics and Earthquake Engineering, 2016,89:219-232.,39[39] Aldaikh H, Alexander N A, Ibraim E, et al. Two dimensional numerical and experimental models for the study of structure-soil-structure interaction involving three buildings[J]. Computers & Structures, 2015,150(4):79-91.,47[47] Aldaikh H, Alexander N A, Ibraim E, et al. Evaluation of Rocking and Coupling Rotational Linear Stiffness Coefficients of Adjacent Foundations[J]. INTERNATIONAL JOURNAL OF GEOMECHANICS, 2018,18(040171311).], and Vicencio et al.[48[48] Vicencio F, Alexander N A. Higher mode seismic structure-soil-structure interaction between adjacent building during earthquakes[J]. Engineering Structures, 2018,174:322-337.
[49] Vicencio F, Alexander N A. Dynamic Structure-Soil-Structure Interaction in unsymmetrical plan buildings due to seismic excitation[J]. Soil Dynamics and Earthquake Engineering, 2019,127:105817.-50[50] Vicencio F, Alexander N A. Dynamic interaction between adjacent buildings through nonlinear soil during earthquakes[J]. Soil Dynamics and Earthquake Engineering, 2018,108:130-141.] employed discrete models, in which the soil is simplified as a spring, to investigate a series of SSSI problems. Alexander et al.[40[40] Alexander N A, Ibraim E, Aldaikh H. A simple discrete model for interaction of adjacent buildings during earthquakes[J]. Computers & Structures, 2013,124(SI):1-10.] introduced a rotational spring to address the two-dimensional through-soil coupling between two adjacent footings, encapsulating both the effects of the foundation soil interaction and DCI. The spring properties were determined by equating energies from the low-order discrete and its corresponding high-order finite element systems for infinitesimal footing rotations when one of the footings was subjected to a rocking moment applied statically. The model was extended by Aldaikh et al.[20[20] Aldaikh H, Alexander N A, Ibraim E, et al. Shake table testing of the dynamic interaction between two and three adjacent buildings (SSSI)[J]. Soil Dynamics and Earthquake Engineering, 2016,89:219-232.,39[39] Aldaikh H, Alexander N A, Ibraim E, et al. Two dimensional numerical and experimental models for the study of structure-soil-structure interaction involving three buildings[J]. Computers & Structures, 2015,150(4):79-91.,47[47] Aldaikh H, Alexander N A, Ibraim E, et al. Evaluation of Rocking and Coupling Rotational Linear Stiffness Coefficients of Adjacent Foundations[J]. INTERNATIONAL JOURNAL OF GEOMECHANICS, 2018,18(040171311).] and Vicencio et al.[48[48] Vicencio F, Alexander N A. Higher mode seismic structure-soil-structure interaction between adjacent building during earthquakes[J]. Engineering Structures, 2018,174:322-337.
[49] Vicencio F, Alexander N A. Dynamic Structure-Soil-Structure Interaction in unsymmetrical plan buildings due to seismic excitation[J]. Soil Dynamics and Earthquake Engineering, 2019,127:105817.-50[50] Vicencio F, Alexander N A. Dynamic interaction between adjacent buildings through nonlinear soil during earthquakes[J]. Soil Dynamics and Earthquake Engineering, 2018,108:130-141.] to cases involving three footings and soil nonlinearity, respectively. However, these models suffer from some limitations. For example, the models presented by Alexander et al.[40[40] Alexander N A, Ibraim E, Aldaikh H. A simple discrete model for interaction of adjacent buildings during earthquakes[J]. Computers & Structures, 2013,124(SI):1-10.] are restricted to 2D analyses. Lu et al.[51[51] Lu Y, Li B, Xiong F, et al. Simple discrete models for dynamic structure-soil-structure interaction analysis[J]. Engineering Structures, 2020,206:110188.] also utilized discrete models. Alamo et al.[38[38] Alamo G M, Padron L A, Aznarez J J, et al. Structure-soil-structure interaction effects on the dynamic response of piled structures under obliquely incident seismic shear waves[J]. Soil Dynamics and Earthquake Engineering, 2015,78(11):142-153.] addressed the influence of the SSSI on shear forces, lateral spectral deformations, etc., via a boundary element-finite element method model and obtained an important result: the SSSI affects groups of structures with similar dynamic characteristics. Santana et al.[13[13] Santana A, Aznarez J J, Padron L A, et al. A BEM-FEM model for the dynamic analysis of building structures founded on viscoelastic or poroelastic soils[J]. Bulletin of Earthquake Engineering, 2016,14(1):115-138.] also employed the boundary element-finite element method to explore the SSSI, whereas Bybordiani et al.[11[11] Bybordiani M, Arici Y. Structure‐soil‐structure interaction of adjacent buildings subjected to seismic loading[J]. Earthquake Engineering & Structural Dynamics, 2019,48(7):731-748.] and Rahgozar[14[14] Rahgozar M A. Accounting for soil nonlinearity in three-dimensional seismic structure-soil-structure-interaction analyses of adjacent tall buildings structures[J]. International Journal of Civil Engineering, 2015,13(3B):213-225.] applied the finite element method. Liang et al.[12[12] Liang J, Han B, Todorovska M I, et al. 2D dynamic structure-soil-structure interaction for twin buildings in layered half-space II: Incident SV-waves[J]. Soil Dynamics and Earthquake Engineering, 2018,113:356-390.,52[52] Liang J, Han B, Todorovska M I, et al. 2D dynamic structure-soil-structure interaction for twin buildings in layered half-space I: Incident SH-waves[J]. Soil Dynamics and Earthquake Engineering, 2017,102:172-194.] utilized an indirect boundary element method to analyze an SSSI system that was excited by an SH-wave or SV-wave. They used a model of two identical shear walls supported by rigid foundations embedded in a soft layer over elastic bedrock and pointed out that the SSSI effects are enhanced by soil layering and are more pronounced for shallower layers and stiffer bedrock. For inclined wave incidence, the SSSI effects occur for larger separation distances than for vertical incidence. Trombetta et al.[53[53] Trombetta N W, Mason H B, Hutchinson T C, et al. Nonlinear Soil-Foundation-Structure and Structure-Soil-Structure Interaction: Centrifuge Test Observations[J]. 2014,140(5):4013051-4013057.,54[54] Trombetta N W, Benjamin Mason H, Hutchinson T C, et al. Nonlinear soil-foundation-structure and structure-soil-structure interaction: Engineering demands[J]. Journal of Structural Engineering, 2015,141(7):4014177.] successfully conducted centrifuge tests to investigate the SSSI effects between a higher structure and a nonlinear frame structure using multi-earthquakes as input motions. They exposed changes in the overturning moment, base shear, structural drift, settlement and residual rotation due to the SSSI effect. Then, they[55[55] Tombari A, Zentner I, Cacciola P. Sensitivity of the stochastic response of structures coupled with vibrating barriers[J]. Probabilistic Engineering Mechanics, 2016,44:183-193.
[56] Tombari A, Garcia Espinosa M, Alexander N A, et al. Vibration control of a cluster of buildings through the Vibrating Barrier[J]. Mechanical Systems and Signal Processing, 2018,101:219-236.-57[57] Cacciola P, Tombari A. Vibrating barrier: a novel device for the passive control of structures under ground motion[J]. PROCEEDINGS OF THE ROYAL SOCIETY A-MATHEMATICAL PHYSICAL AND ENGINEERING SCIENCES, 2015,471(201500752179).] developed a novel device - a vibrating barrier - to reduce the vibrations of adjacent structures. Ngo et al.[16[16] Ngo V, Kim J, Chang S, et al. Effect of Height Ratio and Mass Ratio on Structure-Soil-Structure Interaction of Two Structures Using Centrifugal Experiment[J]. Applied Sciences, 2019,9(3):526.,58[58] Ngo V, Kim J, Lee C. Influence of structure-soil-structure interaction on foundation behavior for two adjacent structures: Geo-centrifuge experiment[J]. GEOMECHANICS AND ENGINEERING, 2019,19(5):407-420.] conducted geotechnical centrifuge tests to investigate the SSSI effects on silica sand, while Hayden et al.[59[59] Hayden C P, Zupan J D, Bray J D, et al. Centrifuge Tests of Adjacent Mat-Supported Buildings Affected by Liquefaction[J]. JOURNAL OF GEOTECHNICAL AND GEOENVIRONMENTAL ENGINEERING, 2015,141(040141183).] and Kirkwood et al.[18[18] Kirkwood P, Dashti S. A Centrifuge Study of Seismic Structure-Soil-Structure Interaction on Liquefiable Ground and Implications for Design in Dense Urban Areas[J]. Earthquake Spectra, 2018,34(3):1113-1134.,60[60] Kirkwood P, Dashti S. Influence of prefabricated vertical drains on the seismic performance of similar neighbouring structures founded on liquefiable deposits[J]. GEOTECHNIQUE, 2019,69(11):971-985.] also conducted geotechnical centrifuge tests to investigate the SSSI effects on liquefiable deposits. Barrios et al.[17[17] Barrios G, Nanayakkara V, De Alwis P, et al. Effects of Slenderness and Fundamental Frequency on the Dynamic Response of Adjacent Structures[J]. International Journal of Structural Stability and Dynamics, 2019,19(09):1950105.] and Li et al.[19[19] Li P, Liu S, Lu Z, et al. Numerical analysis of a shaking table test on dynamic structure-soil-structure interaction under earthquake excitations[J]. The Structural Design of Tall and Special Buildings, 2017,26(15):e1382.] used shaking table tests to examine the SSSI. Gueguen et al.[61[61] Gueguen P, Colombi A. Experimental and numerical evidence of the clustering effect of structures on their response during an earthquake: A case study of three identical towers in the City of Grenoble, France[J]. Bulletin of the Seismological Society of America, 2016,106(6):2855-2864.] applied instrumental records and feild reports to analyze the SSSI after an earthquake. They analyzed three identical stand-alone buildings located in Grenoble, France after an earthquake. A local survey based on the protocol used for macroseismic intensity analysis was conducted among the inhabitants of the three towers. The survey revealed the SSSI between the buildings, resulting in different levels of perception of seismic loading by inhabitants. Fariborz et al. investigated the nonlinear dynamic responses of two adjacent 15-story and 30-story buildings. Naserkhaki et al.[62[62] Naserkhaki S, Pourmohammad H. SSI and SSSI effects in seismic analysis of twin buildings: discrete model concept[J]. Journal of Civil Engineering and Management, 2012,18(6):890-898.] numerically demonstrated that a massive structure can have detrimental SSSI effects on a lighter structure. Ghandil et al.[37[37] Ghandil M, Behnamfar F, Vafaeian M. Dynamic responses of structure-soil-structure systems with an extension of the equivalent linear soil modeling[J]. Soil Dynamics and Earthquake Engineering, 2016,80(1):149-162.] evaluated the SSSI in three different buildings, considering the elastoplastic frame hinges in the structure and two soil profiles with a reduction in the soil shear modulus in areas close to the foundation. Generally, analytical methods are seldom adopted due to rigorous mathematical restrictions, while prototype observations are also rarely conducted because (1) it is impossible to know when an earthquake will affect an instrumented structure, and (2) it is difficult to differentiate the SSSI effect from other complex phenomena. With the rapid development of computers and testing techniques, the main method in SSSI studies is the numerical method, including the finite element method, the boundary element method, the combination of both methods, and others, and the experimental method, including the shaking table test and centrifuge test.
The SSSI effects under earthquake excitations are quite complex and remain unknown. This study only provides a glimpse of the SSSI via a series of detailed finite element models on the dynamic structure-soil-structure interaction of piled high-rise buildings under earthquake excitations and provides some references for engineering designs. This study is presented in two subsequent papers. The first paper is this paper. In the next section, the problem is stated, and the parameters and properties are defined. The calculation method and model are then briefly outlined. Afterwards, to evaluate the effect of the SSSI on the seismic response of high-rise buildings, the variations in the story shear force, interstory drift angle, displacement, velocity and acceleration of the superstructure, the sway of the foundation, and the axial and shearing forces of the pile are taken into account, and the assessment of the calculated effects are compared with the case of standalone structures. In the following paper[63[63] Wang H, Zhang R. Dynamic structure-soil-structure interaction of piled high-rise buildings II: Influence of key parameter[J]. 2020.], a parametric study is conducted to evaluate the influence of each key parameter, including the separation distance between two structures; the damping ratio, thickness and shear wave velocity of the soil; the length of the pile; the damping ratio, style, material stiffness, mass and story number of the superstructure; and the position and number of the structure, of a dynamic system on the SSSI effect.
Problem definition
The system under investigation is composed of one or more common multistory frame structures, which are founded on fixed-head pile groups embedded in a homogeneous soil layer and three-dimensionally distributed. Considering that this study is general, the structure and soil are derived from a representative example and then simplified.
Fig.1 shows a two-dimensional representation of the three-dimensional model in this study. The mechanical and geometrical properties of the frame structure are defined by the following parameters: the story height is ; the story number is ; the cross-section of the frame column is ; the cross-section of the frame beam is ; the cross-section of the foundation beam is ; the diameter of the pile is ; the length of the pile is ; the thickness of the floor slab is ; the thickness of the base plate is ; the concrete modulus is ; the mass density of the concrete is ; the Poisson’s ratio of the concrete is ; and the damping ratio is . The fundamental frequencies of the 10-story frame structure on a rigid base are along the lateral axis and along the longitudinal axis, which corresponds to the natural periods of and .
On the other hand, as a generalized exploration of the SSSI instead of an analysis for a specific case, the soil is assumed to be single, consecutive, homogeneous and isotropous to avoid too many influencing factors. The most important parameters for defining the soil dynamic behavior are listed as follows: the mass density is ; the shear wave velocity is ; the bedrock depth is and the soil thickness is ; the damping ratio is ; and the Poisson’s ratio is . The bedrock is assumed to be rigid, and the seismic wave enters the soil from the interface between the bedrock and the soil.
The seismic inputs include harmonic waves, whose amplitudes are equal to 1 and whose frequency ranges from 0 to ; 25 ground motion records from outcrops, whose epicentral distances are from several kilometers to more than one thousand kilometers; and 3 artificial seismic waves with different exceedance probabilities for bedrock. The time histories of the acceleration and their spectra are shown in Fig.2 and Fig.3.
Analyses of the dynamic behaviors of several SSSI systems under vertically incident S waves from rigid bedrock are performed. As shown in Fig.4, the structures are abreast, the direction of the structure arrangement is parallel to the longitudinal or lateral axis of the structure, and the shaking direction is parallel or perpendicular to the direction of the structure arrangement. The configuration in which the direction of the structure arrangement is parallel to the longitudinal axis of the structure and the shaking direction is parallel to the direction of the structure arrangement is termed CON.1. The configuration in which the direction of the structure arrangement is parallel to the lateral axis of the structure and the shaking direction is parallel to the direction of the structure arrangement is termed CON.2. The configuration in which the direction of the structure arrangement is parallel to the longitudinal axis of the structure and the shaking direction is perpendicular to the direction of the structure arrangement is termed CON.3. The configuration in which the direction of the structure arrangement is parallel to the lateral axis of the structure and the shaking direction is perpendicular to the direction of the structure arrangement is termed CON.4. The separation distance between two adjacent structures is , which is only sufficient for three people to walk side by side and is common in downtown areas with a high density of population and buildings. Additional separation distances are considered in the second paper. Similar to many existing studies[20[20] Aldaikh H, Alexander N A, Ibraim E, et al. Shake table testing of the dynamic interaction between two and three adjacent buildings (SSSI)[J]. Soil Dynamics and Earthquake Engineering, 2016,89:219-232., 33[33] Wang H, Lou M, Zhang R. Influence of presence of adjacent surface structure on seismic response of underground structure[J]. Soil Dynamics and Earthquake Engineering, 2017,100(09):131-143., 37[37] Ghandil M, Behnamfar F, Vafaeian M. Dynamic responses of structure-soil-structure systems with an extension of the equivalent linear soil modeling[J]. Soil Dynamics and Earthquake Engineering, 2016,80(1):149-162.], the dimensionless distance , which is defined as where is the width of a structure along the lateral axis, is applied for comparison. Here, . The dynamic responses of the structures in group are compared with that of the single-structure-soil system to determine whether the SSSI effects between two or more high-rise buildings are important.
Finite element model
Past studies have shown that finite element analyses by various finite element analysis software programs provide reliable and accurate results[11[11] Bybordiani M, Arici Y. Structure‐soil‐structure interaction of adjacent buildings subjected to seismic loading[J]. Earthquake Engineering & Structural Dynamics, 2019,48(7):731-748.,32[32] Wang H, Lou M, Chen X, et al. Structure-soil-structure interaction between underground structure and ground structure[J]. Soil Dynamics and Earthquake Engineering, 2013,54(11):31-38.,33[33] Wang H, Lou M, Zhang R. Influence of presence of adjacent surface structure on seismic response of underground structure[J]. Soil Dynamics and Earthquake Engineering, 2017,100(09):131-143.,56[56] Tombari A, Garcia Espinosa M, Alexander N A, et al. Vibration control of a cluster of buildings through the Vibrating Barrier[J]. Mechanical Systems and Signal Processing, 2018,101:219-236.]. A commercial software product for finite element analysis, ANSYS, has been further developed and enhanced for calculation in the frequency domain, in which hysteretic damping can be considered for both the soil and the structures by defining a complex soil shear modulus and a complex structural stiffness . The time domain result under a seismic wave is obtained by fast Fourier transform from the frequency domain result.
In this way, the ability to observe the nonlinear behavior of the system is lost. Obviously, nonlinear behavior, which has attracted a substantial amount of attention now[50[50] Vicencio F, Alexander N A. Dynamic interaction between adjacent buildings through nonlinear soil during earthquakes[J]. Soil Dynamics and Earthquake Engineering, 2018,108:130-141.,54[54] Trombetta N W, Benjamin Mason H, Hutchinson T C, et al. Nonlinear soil-foundation-structure and structure-soil-structure interaction: Engineering demands[J]. Journal of Structural Engineering, 2015,141(7):4014177.], is an important characteristic of the SSI[1[1] Kausel E. Early history of soil-structure interaction[J]. Soil Dynamics and Earthquake Engineering, 2010,30(9):822-832.]. However, nonlinear analysis of the SSSI system with numerous degrees of freedom is computationally costly and time-consuming and sensitive to changes in constitutive model parameters[47[47] Aldaikh H, Alexander N A, Ibraim E, et al. Evaluation of Rocking and Coupling Rotational Linear Stiffness Coefficients of Adjacent Foundations[J]. INTERNATIONAL JOURNAL OF GEOMECHANICS, 2018,18(040171311).]. More importantly, analysis in the frequency domain, which is only appropriate for linear behavior, can employ hysteretic damping, which is more reasonable for soils and structures in seismic analysis[64[64] Clough R W, Penzien J. Dynamics of Structures[M]. Berkeley, USA: Computers & Structures, 2003.]. Analysis in the time domain, which can be appropriate for nonlinear behavior, can only employ viscous damping, such as Rayleigh damping, which will introduce nonnegligible error when the foundational frequency of a system is substantially less than the dominant frequency of the seismic input[65[65] Lou M, Dong Y, Zhang R. Several Problems on Refined Local Modeling for Seismic Response Analysis of Immersed Tunnel[J]. Chinese Journal of Geotechnical Engineering, 2016,38(9):1-11.]. In this way, the essence of the SSSI may be hidden. Although new methods of model damping exist[66[66] Chopra A K, McKenna F. Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation[J]. Earthquake Engineering & Structural Dynamics, 2016,45(2):193-211.
[67] Spears R E, Jensen S R. Approach for selection of Rayleigh damping parameters used for time history analysis[J]. Journal of Pressure Vessel Technology, 2012,134(6):61801-61807.-68[68] Yang D B, Zhang Y G, Wu J Z. Computation of Rayleigh damping coefficients inseismic time-history analysis of spatial structures[J]. Journal of the International Association for Shell and Spatial Structures, 2010,51(2):125-135.], the frequency dependency of viscous damping is an unalterable property. In addition, many studies have shown the strong frequency dependency of the SSSI. Thus, as an initial exploration, linear analysis, which is still utilized for the SSSI by many researchers[11[11] Bybordiani M, Arici Y. Structure‐soil‐structure interaction of adjacent buildings subjected to seismic loading[J]. Earthquake Engineering & Structural Dynamics, 2019,48(7):731-748.,12[12] Liang J, Han B, Todorovska M I, et al. 2D dynamic structure-soil-structure interaction for twin buildings in layered half-space II: Incident SV-waves[J]. Soil Dynamics and Earthquake Engineering, 2018,113:356-390.,49[49] Vicencio F, Alexander N A. Dynamic Structure-Soil-Structure Interaction in unsymmetrical plan buildings due to seismic excitation[J]. Soil Dynamics and Earthquake Engineering, 2019,127:105817.,51[51] Lu Y, Li B, Xiong F, et al. Simple discrete models for dynamic structure-soil-structure interaction analysis[J]. Engineering Structures, 2020,206:110188.], is introduced in this paper to study the universal law and obtain a deeper recognition of the SSSI. This is a meaningful basis for further study of the SSSI with nonlinear behavior.
Relative arrangement of the structures and shaking direction of the exciting wave. a) CON.1. b) CON.2. c) CON.3. d) CON.4.
The soil, which is considered as a linear, viscous-elastic medium, is modeled by solid elements (SOLID45). Fully bonded contact conditions are assumed between the soil and piles. The beams and columns of the structures are modeled as Bernoulli beams via beam elements (beam188), and the floor slabs and walls are modeled by shell elements (shell63). The piles, whose heads can be fixedly connected to the base plate of the frame structure, are modeled as vertical Bernoulli beams via pipe elements (pipe16). One of the three-dimensional finite element models is shown in Fig.5. The maximum number of elements is 188,704, and the maximum number of degrees of freedom is 569,562. Fixed constraints are applied at the bottom of the soil to simulate the rigid bedrock where seismic waves come from. As shown in Fig.6, in view of the radiation damping of the semi-infinite space and based on numerical trials, the scope of soil is set to be sufficiently large, extending a length of from the structure scope along the shaking direction of the exciting wave, and the vertical degrees of freedom of the nodes at the boundary are constrained. In view of the transmission of energy, the inadequacy of the finite element size can cause numerical damping. The finite element size is set to be sufficiently small, limited to , where is the minimum premeditated wavelength. Here, is the maximum premeditated frequency of the seismic wave.
Numerical results and analysis
The influence of the SSSI on the dynamic response of high-rise buildings is addressed in this section. To explicitly show the SSSI effect, the influence of the SSSI is illustrated with the influence coefficient , which is defined as , where is the dynamic response, the steady-state response amplitude under a harmonic wave or the seismic response amplitude under a seismic wave, of a high-rise building of the single-structure-soil system and is that of a high-rise building of the multistructure-soil system.
1.1 Story shear force
Fig.7 shows the influence coefficients of the story shear force at each story under seismic waves. Unless otherwise stated, the figure legends of the latter figures, which show the influence coefficient of the dynamic response under seismic waves, are similar to those in Fig.7 and are omitted for brevity.
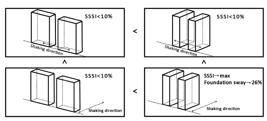
A seismic wave has an influence on the SSSI, and the influence coefficient varies for different seismic waves. This influence is closely associated with the Fourier spectrum of the seismic wave. When the SSSI system, as shown in Fig.4d (CON.4: the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement, and the direction of the structure arrangement is parallel to the lateral axis of the structure), is excited by seismic wave C08-050, the maximum influence coefficient of the story shear force is (almost all of the influence coefficients exceed ). However, except that, the influence coefficients of the story shear force are within , and more than of the influence coefficients are within .
The influence of the SSSI varies from one configuration to another. The direction of the structure arrangement and the shaking direction of the exciting wave both influence the SSSI. When the shaking direction of the exciting wave is parallel to the direction of the structure arrangement (CON.1 and CON.2), the influence coefficients of the story shear force are almost negative or just slightly greater than zero. In these two configurations, regardless of whether the direction of the structure arrangement is parallel to the lateral axis (CON.2) or longitudinal axis (CON.1) of the structure, the influence coefficients of the story shear force are basically equivalent and almost within . When the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement (CON.3 and CON.4), the influence coefficients of the story shear force can be positive or negative depending on the Fourier spectrum of the seismic wave and the ratio of the number of positive influence coefficients to the number of negative influence coefficients is approximately . In these two configurations, the variation range of the influence coefficients of the story shear force for the direction of the structure arrangement parallel to the lateral axis of the structure (CON.4) are approximately double that for the direction of the structure arrangement parallel to the longitudinal axis of the structure (CON.3), which are almost within . Thus, when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.4), the influence of the SSSI on the story shear force is the greatest. However, for each exciting seismic wave, it is difficult to determine when the SSSI has a greater influence before calculation.
For different stories, the SSSI has the comparatively same influence on the story shear force with the same seismic wave. This finding can be explained by Fig.8, which shows the story shear force at each story of the single-structure-soil system and the influence coefficients of the SSSI under harmonic waves. Obviously, the curves of the influence coefficients for different stories are almost equivalent.
For harmonic waves, the influence coefficients, which depend on the excitation frequency, fluctuate around zero with the excitation frequency, and the influence of the SSSI on the story shear force can be positive or negative. When the excitation frequency is lower than , the influence coefficients are almost zero, which means that the SSSI has minimal influence on the story shear force. Around each order of natural frequency of the superstructure, the story shear forces are affected prominently by the SSSI, and the influence coefficient curves show peaks. When the shaking direction of the exciting wave is parallel to the direction of the structure arrangement (CON.1 and CON.2), the peaks of the influence coefficient curves are negative. When the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement (CON.3 and CON.4), the peaks of the influence coefficient curves are first positive and then negative. The peaks of the influence coefficient curves for the direction of the structure arrangement parallel to the lateral axis of the structure (CON.2 and CON.4), whose maximum absolute values can be and , respectively, are slightly higher than those for the direction of the structure arrangement parallel to the longitudinal axis of the structure (CON.1 and CON.3). In general, the absolute values of the influence coefficients that correspond to low-frequency excitation () are greater than the absolute values of the influence coefficients that correspond to high-frequency excitation (). However, the absolute values of the influence coefficients that correspond to high-frequency excitation are not negligible when the shaking direction of the exciting wave is parallel to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.2). This is mainly because the dynamic response that corresponds to high-frequency excitation is too small, and a slight difference will create a large impact. Although the influence is not negligible here, the dynamic response is small enough, and thus, for a seismic wave with different frequency components, it will not cause a remarkable interaction.
Story shear force at each story of a single-structure-soil system and influence coefficients of the SSSI under harmonic waves.
1.2 Interstory drift angle
Fig.9 shows the influence coefficients of the interstory drift angle, which excludes the component due to the whole bending of the building, at each story under seismic waves. As expected, the influence of the SSSI on the interstory drift angle is consistent with that on the story shear force.
For different seismic waves, when the SSSI system, as shown in Fig.4d (CON.4: the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement, and the direction of the structure arrangement is parallel to the lateral axis of the structure), is excited by seismic wave C08-050, the maximum influence coefficient of the interstory drift angle is (almost all of the influence coefficients exceed ). However, except that, the influence coefficients of interstory drift angle are within , and more than of the influence coefficients are within .
For structure arrangements and seismic waves with different directions, when the shaking direction of the exciting wave is parallel to the direction of the structure arrangement (CON.1 and CON.2), the influence coefficients of the interstory drift angle are almost negative or just slightly larger than zero. In these two configurations, regardless of whether the direction of the structure shaking and structure arrangement is parallel to the lateral axis (CON.2) or longitudinal axis (CON.1) of the structure, the influence coefficients of the interstory drift angle are equivalent and almost within . When the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement (CON.3 and CON.4), the influence coefficients of the interstory drift angle can be positive or negative depending on the Fourier spectrum of the seismic wave, and the ratio of the number of positive influence coefficients to the number of negative influence coefficients is approximately . In these two configurations, the variation range of the influence coefficients of the interstory drift angle for the direction of the structure arrangement parallel to the lateral axis of the structure (CON.4) are approximately double that for the direction of the structure arrangement parallel to the longitudinal axis of the structure (CON.2), which are within . Thus, when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.4), the influence of the SSSI on the interstory drift angle is a maximum. However, for each exciting seismic wave, it is difficult to determine when the SSSI has a greater influence before calculation.
For different stories, the SSSI has almost the same influence on the interstory drift angle with the same seismic wave. This finding can also be explained by the influence coefficients of the SSSI under harmonic waves. Similar to the story shear force, for different stories, the curves of the influence coefficients of the interstory drift angle under harmonic waves are almost the same. Given space limitations, the curves of the influence coefficients of the interstory drift angle under harmonic waves are omitted because they are almost the same as that of the story shear force. Naturally, under harmonic waves, the influence of the SSSI on the interstory drift angle is basically the same as that on the story shear force.
1.3 Foundation sway
Tab.1 shows the influence coefficients of foundation sway under seismic waves. The influence of the SSSI on the foundation sway shows a slight difference form that on the story shear force and interstory drift angle. When the shaking direction of the exciting wave is parallel to the direction of the structure arrangement (CON.1 and CON.2), the foundation sway decreases, and the influence coefficients of the foundation sway are all negative, which can be as low as . When the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement (CON.3 and CON.4), except for that of CON.3 excited by seismic wave CPE-045, the foundation sway increases, and the influence coefficients of the foundation sway are all positive; the maximum value is . For all seismic waves, when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.4), the influence on the foundation sway is greatest in all four configurations.
1.4 Displacement, velocity and acceleration
When a system is excited by a harmonic wave, the amplitude of the relative acceleration is a product of the amplitude of the velocity and exciting frequency, while the amplitude of the velocity is a product of the amplitude of the displacement and exciting frequency. The phase difference between the relative acceleration and the velocity and the phase difference between the velocity and the displacement is . Thus, the curves of the influence coefficients of the displacement, velocity and relative acceleration should be exactly the same under harmonic waves, while the curve of the influence coefficient of the absolute acceleration should exhibit a slight difference from the former three. That is, the influence of the SSSI on the displacement, velocity and relative acceleration is the same under a harmonic wave. This can be verified by Fig.10, which shows the displacement, velocity, relative and absolute accelerations at the top floor of the single-structure-soil system and the influence coefficient of the SSSI under harmonic waves.
Obviously, the absolute values of the influence coefficients that correspond to low-frequency excitation () are greater than the absolute value of the influence coefficients that correspond to high-frequency excitation (), which are approximately zero. This is different from the interaction between an underground structure and an adjacent high-rise building[32[32] Wang H, Lou M, Chen X, et al. Structure-soil-structure interaction between underground structure and ground structure[J]. Soil Dynamics and Earthquake Engineering, 2013,54(11):31-38.,33[33] Wang H, Lou M, Zhang R. Influence of presence of adjacent surface structure on seismic response of underground structure[J]. Soil Dynamics and Earthquake Engineering, 2017,100(09):131-143.], in which the system of the interaction under a high-frequency wave is often greater than that under a low-frequency wave. There are peaks at approximately on the influence coefficient curves of the displacement, velocity and relative acceleration respectively. This is mainly because the displacement, velocity and relative acceleration around are too small, and a slight difference will produce a large impact. The peak on the influence coefficient curve of the absolute acceleration vanishes naturally because the absolute acceleration around is not close to zero as the displacement, velocity and relative acceleration. Although the influence coefficient around is not negligible, the displacement, velocity and relative acceleration are small enough, and thus, for a seismic wave with different frequency components, it will not a cause remarkable interaction.
Displacement, velocity, relative acceleration and absolute acceleration at the top floor of the single-structure-soil system (thin line) and influence coefficients of the SSSI (thick lines) under harmonic waves (CON.4). a) Displacement. b) Velocity. c) Relative acceleration. d) Absolute acceleration.
Fig.11, Fig.12 and Fig.13 show the influence coefficients of the displacement, velocity and acceleration, respectively, at each floor under seismic waves.
Generally, for the same floor in the same configuration, the influence of the SSSI on the displacement, velocity and acceleration is basically the same under seismic waves but is not exactly the same as that under harmonic waves. The reason for the small difference is the difference in the harmonic response spectra of the displacement, velocity and acceleration.
In accordance with the story shear force and interstory drift, when the SSSI system, as shown in Fig.4d (CON.4: the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement, and the direction of the structure arrangement is parallel to the lateral axis of the structure), is excited by seismic wave C08-050, the maximum influence coefficient of the displacement, velocity and acceleration is (almost all of the influence coefficients exceed ). However, except that, the influence coefficients of the displacement, velocity and acceleration are almost within and more than , , and of the influence coefficients of the displacement, velocity and acceleration, respectively, are within .
Unlike the story shear force and interstory drift angle, for different floors, the influence of the SSSI on the displacement, velocity or acceleration is different under the same seismic wave. When the shaking direction of the exciting wave is parallel to the direction of the structure arrangement (CON.1 and CON.2), the influence coefficients of the displacement, velocity and acceleration are not always negative as the story shear force and interstory drift angle. The influence coefficients of the upper floors are comparatively smaller and almost negative, while those of the lower floors are comparatively larger and almost positive. In these two configurations, for the displacement, velocity and acceleration, regardless of whether the direction of the structure arrangement is parallel to the lateral axis (CON.2) or longitudinal axis (CON.1) of the structure, the influence coefficients are similar and almost within . When the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement (CON.3 and CON.4), the influence coefficients of displacement, velocity and acceleration can be positive or negative depending on the Fourier spectrum of the seismic wave as the story shear force and interstory drift angle, and the ratio of the number of positive influence coefficients to the number of negative influence coefficients is approximately for the displacement, for the velocity and for the acceleration. In these two configurations, the variation range of the influence coefficients of the displacement, velocity and acceleration for the direction of the structure arrangement parallel to the lateral axis of the structure (CON.4) are greater than, as story shear force and interstory drift angle, but not double that for the direction of the structure arrangement parallel to the longitudinal axis of the structure (CON.3), which are almost within . Thus, when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.4), the influence of the SSSI on the displacement, velocity and acceleration is a maximum. However, for each exciting seismic wave, it is difficult to determine when the SSSI has a greater influence before calculation.
1.5 Axial force of the piles
In previous work on the SSSI, the authors usually focused on the dynamic response of the superstructure and seldom investigated the influence of the SSSI on the dynamic response of the foundation. One reason for this is that an extremely simplified model with a shallow foundation has been widely utilized in numerous works. However, a deep foundation is commonly utilized in modern structures. In the following section, the influence of the SSSI on the dynamic response of a pile foundation is explored. The arrangement of the pile is shown in Fig.14. Numbers 1-6 and letters A-Q denote the position of the pile.
Arrangement of the pile. a) The direction of the structure arrangement is parallel to the longitudinal axis of the structure. b) The direction of the structure arrangement is parallel to the lateral axis of the structure.
As everyone knows, without considering the raft, the base overturning moment of the superstructure balances the axial force at the top of piles, and the total axial force at the top of all piles is always close to zero. Meanwhile, the rigidity of the superstructure is immense compared with that of the soil and foundation. For a symmetrical structure, the axial force at the top of each pile in the same line, which is perpendicular to the shaking direction of the exciting wave, is nearly the same. Thus, in the following section, the influence of the SSSI on the total axial force at the top of the piles in each line, which is perpendicular to the shaking direction of the exciting wave, is examined.
Fig.15 shows the influence coefficients of the total axial force at the top of the piles in each line, which is perpendicular to the shaking direction of the exciting wave, under seismic waves. Considering that the total axial force at the top of the piles in line I (Fig.14), which is at the middle of the structure, is close to zero and easily affected by a small perturbation; its influence coefficient is omitted here.
Influence coefficients of the total axial force at the top of the piles in each line, which is perpendicular to the shaking direction of the exciting wave, under seismic waves.
In accordance with the superstructure, the influence of the SSSI on the total axial force at the top of the piles in each line is affected by the seismic wave, the shaking direction of the exciting wave and the direction of the structure arrangement. A more important influence factor is the line (position of the pile).
When the shaking direction of the exciting wave is parallel to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the longitudinal axis of the structure (CON.1), the influence on the lines in the middle zone of the structure (line E - line H and line J - line M) is greatest, and the influence coefficients, whose maximum is , are almost positive. The influence on the lines near the adjacent structure (line N - line Q) is second greatest, and the influence coefficients, whose maximum is , are almost positive as well. The influence on the lines far from the adjacent structure (line A - line D) is lowest, and the influence coefficients, whose maximum can be , are almost negative.
When the shaking direction of the exciting wave is parallel to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.2), the influence on the lines in the middle zone of the structure (line 3 - line 4) is lowest, and the influence coefficients, which are , are all negative. The influence on the lines near the adjacent structure (line 5 - line 6) is greater, and the influence coefficients, which are , are almost positive. The influence on the lines far from the adjacent structure (line 1 - line 2) is also greater, and the influence coefficients, which are , are almost negative. All of the influence coefficients in this configuration are within .
When the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the longitudinal axis of the structure (CON.3), the influence on each line is very low, and the influence coefficients are within .
When the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.4), the influence on the lines in the middle zone of the structure (line E - line H and line J - line M) is comparatively greater, and the influence coefficients, whose maximum can be , are almost positive. The influence on the lines at the border zone of the structure (line A - line D and line N - line Q) is comparatively lower, and the influence coefficients, whose maximum can be , are almost negative.
In general, the influence of the SSSI on the total axial force at the top of the piles in each line is greater when the shaking direction of the exciting wave is parallel to the longitudinal axis of the structure (CON.1 and CON.4). In these two configurations, the influence on the lines in the middle zone of the structure is greater than that at the border zone of the structure. As the axial force of the former is much less than that of the latter, the readers may infer that a slight perturbation produces a large impact. This conjecture can be indicate to be incorrect since the axial force of the lines around the middle of the structure is also much less than that at the border zone of the structure and the influence on the former is still less than that on the latter when the shaking direction of the exciting wave is parallel to the lateral axis of the structure (CON.2 and CON.3). Meanwhile, checking the axial force in all four configurations, the influence coefficient does not increase with the decrease in the axial force. It is indeed that the SSSI leads to a nonnegligible variation in the total axial force at the top of the piles in each line.
1.6 Shearing force of the piles
Tab.2 shows the influence coefficients of the total shearing force at the top of all the piles under seismic waves.
When the direction of the structure arrangement is parallel to the longitudinal axis of the structure (CON.1 and CON.3), the influence coefficients of the total shearing force at the top of all piles, which are if the shaking direction of the exciting wave is parallel to the direction of the structure arrangement (CON.1) and if the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement (CON.3), are almost positive or just slightly smaller than zero. When the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.2 and CON.4), the influence coefficients of the total shearing force at the top of all piles, which are if the shaking direction of the exciting wave is parallel to the direction of the structure arrangement (CON.2) and if the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement (CON.4), are almost negative or just slightly larger than zero.
In general, the influence of the SSSI on the total shearing force at the top of all the piles is greatest when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.4), while it is slightest when the shaking direction of the exciting wave is parallel to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the longitudinal axis of the structure (CON.1), which can be disregarded.
The total shearing force at the top of all the piles varies under different seismic waves, the shaking direction of the exciting wave and the direction of the structure arrangement, but its influence coefficients are within . In the following section, similar to the axial force, the influence of the SSSI on the total shearing force at the top of piles in each line is investigated, which shows a notable difference.
Influence coefficients of the total shearing force at the top of all the piles under seismic waves (unit: %).
Fig.16 shows the influence coefficients of the total shearing force at the top of the piles in each line, which is perpendicular to the shaking direction of the exciting wave, under seismic waves.
When the shaking direction of the exciting wave is parallel to the direction of the structure arrangement (CON.1 and CON.2), the influence on the line adjacent to the adjacent structure (line Q for CON.1 and line 6 for CON.2) is the greatest. The shearing force increases sharply, and the influence coefficients are for CON.1 and for CON.2. The influence on the line far from the adjacent structure (line A for CON.1 and line 1 for CON.2) is the second greatest. The shearing force decreases remarkably, and the influence coefficients are for CON.1 and for CON.2. The influence on each line between line A and line Q for CON.1 and between line 1 and line 6 for CON.2 is comparatively limited, and the influence coefficients, which are for CON.1 and for CON.2, are almost within . In general, with different seismic waves, the greater the increase in the total shearing force at the top of the piles in line Q for CON.1 and line 6 for CON.2, the larger the decrease in the total shearing forces at the top of the piles in line A for CON.1 and line 1 for CON.2, while the total shearing forces at the top of piles in each line between line A and line Q for CON.1 and between line 1 and line 6 for CON.2 vary mildly.
When the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement (CON.3 and CON.4), the influence on the lines just at the outer edge of the structure (line 1/6 for CON.3 and line A/Q for CON.4) is the greatest. The shearing force decreases, and the influence coefficients are for CON.3 and for CON.4. The influence on each line between line 1 and line 6 for CON.3 and between line A and line Q for CON.4 is comparatively limited, and the influence coefficients, which are for CON.3 and for CON.4, are within .
In general, the influence of the SSSI on the total shearing force at the top of the piles in each line is lowest when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the longitudinal axis of the structure (CON.3). For all four configurations, the influence of the SSSI on the total shearing force at the top of the piles in the lines just at the outer edge of the structure is great and should be given more attention, while the influence on the other lines is comparatively limited.
Influence coefficients of the total shearing force at the top of the piles in each line, which is perpendicular to the shaking direction of the exciting wave, under seismic waves.
Summary, comparison and analysis
Compared with the interaction between a high-rise building and an underground structure, the influence of a high-rise building on an adjacent high-rise building and that of an underground structure on an adjacent high-rise building have the same magnitude, which is less than the influence of a high-rise building on an adjacent underground structure.
The major influencing factors of the interaction between two high-rise buildings are the excitation frequency of a harmonic wave or the frequency components of the seismic wave, the shaking direction of the exciting wave and the direction of the structure arrangement, which are the same as the major influencing factors of the interaction between a high-rise building and an underground structure[32[32] Wang H, Lou M, Chen X, et al. Structure-soil-structure interaction between underground structure and ground structure[J]. Soil Dynamics and Earthquake Engineering, 2013,54(11):31-38., 33[33] Wang H, Lou M, Zhang R. Influence of presence of adjacent surface structure on seismic response of underground structure[J]. Soil Dynamics and Earthquake Engineering, 2017,100(09):131-143.]. The influence of the SSSI on the axial force or shearing force at the top of a pile is also greatly affected by the position of the pile. The influence of the SSSI on the story shear force and interstory drift angle is almost the same, while that on the displacement, velocity and acceleration is basically the same. The former and the latter are not affected and slightly affected, respectively, by the story position.
The excitation frequency of a harmonic wave influences the SSSI, and the interaction mainly occurs when the excitation frequency is . However, this finding does not mean that the interaction between two high-rise buildings is greater under a seismic wave with abundant components of . Because the influence coefficients that correspond to some frequency components are positive, while those of others are negative, the positive influence and negative influence are canceled by each other. In addition, in accordance with the interaction between a high-rise building and an underground structure, when the excitation frequency is lower than , the influence coefficients are close to zero. However, the interaction between two high-rise buildings is greater under a low-frequency wave (), while the interaction between a high-rise building and an underground structure is greater under a high-frequency wave ().
Likewise, the seismic wave influences the SSSI, and the influence is closely associated with the Fourier spectrum of the seismic wave. However, summarizing the regularity and correlation between the influence and the Fourier spectrum is difficult since the interaction between two structures is very sensitive to the excitation frequency and the influence coefficient varies without regularity under different seismic waves. When the focus is each exciting seismic wave, before calculation, it is difficult to determine when the influence of the SSSI on the dynamic response (except foundation sway) is greater.
The direction of the structure arrangement, which is parallel to the longitudinal axis or lateral axis of the structure, has some influence on the SSSI, which is mainly reflected in the axial force of the piles. For the superstructure, the influence of the SSSI on the dynamic response for the direction of the structure arrangement parallel to the lateral axis of the structure is greater than that for the direction of the structure arrangement parallel to the longitudinal axis of the structure.
The shaking direction of the exciting wave, which is parallel or perpendicular to the direction of the structure arrangement, is the most important influencing factor of the interaction between two high-rise buildings. With different shaking directions of the exciting wave, completely different interactions occur. For the superstructure, the influence of the SSSI on the dynamic response for the shaking direction of the exciting wave perpendicular to the direction of the structure arrangement is greater than that for the shaking direction of the exciting wave parallel to the direction of the structure arrangement.
1.7 Influence on the superstructure
Similar to the interaction between a high-rise building and an underground structure[32[32] Wang H, Lou M, Chen X, et al. Structure-soil-structure interaction between underground structure and ground structure[J]. Soil Dynamics and Earthquake Engineering, 2013,54(11):31-38., 33[33] Wang H, Lou M, Zhang R. Influence of presence of adjacent surface structure on seismic response of underground structure[J]. Soil Dynamics and Earthquake Engineering, 2017,100(09):131-143.], under harmonic waves, the interaction between two high-rise buildings is prominent at some frequencies, and the maximum absolute values of the influence coefficients can be several dozen percent. However, under seismic waves, the interaction is limited, and the influence coefficients are almost within . This is because a seismic wave includes different frequency components, and the influence coefficients that correspond to some frequency components are positive, while other frequency components are negative. Thus, the positive influence and the negative influence cancel each other, and the interaction under seismic waves is limited.
For all seismic waves, when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.4), the influence of the SSSI on the dynamic response (story shear force, interstory drift angle, foundation sway, displacement, velocity and acceleration) of the superstructure is the greatest. However, this greatest influence is not a truly great impact from the viewpoint of engineering applications. In this configuration, the influence on the story shear force, interstory drift angle, displacement, velocity and acceleration (foundation sway not included here) is almost within , while the greatest influence is when this SSSI system is excited by seismic wave C08-050. Here, seismic wave C08-050 is not special or very different from the other seismic waves. The influence under seismic wave C08-050 is slightly larger than that under the other seismic waves because the energy of the seismic wave is higher at the frequency around which the influence coefficient is comparatively larger, while the energy of the seismic wave is lower at the frequency around which the influence coefficient is comparatively smaller. In this configuration, more attention should be paid to the influence on foundation sway, which is , since it is greater than the influence on the other aforementioned dynamic responses. Another reason is that, for a high-rise building, the increase in the foundation sway will cause deterioration of the effect and the stability of the structure.
In the other three configurations (CON.1, CON.2 and CON.3), although the separation distance between two structures is as low as one-tenth of the width of the structure (), the influence of the SSSI on the dynamic response of the superstructure is very limited, and the influence coefficients are almost within .
1.8 Influence on the foundation
As mentioned in section 5.1, under seismic waves, the influence of the SSSI on the dynamic response of the superstructure is limited, but that on the foundation is prominent.
The influence of the SSSI on the total axial or shearing force at the top of the piles in each line is the smallest in the four configurations and can be disregarded in an engineering project when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the longitudinal axis of the structure (CON.3).
In the other three configurations, the influence of the SSSI on the total axial or shearing force at the top of the piles in each line is conspicuous and much greater than that on the dynamic response of the superstructure. When the shaking direction of the exciting wave is parallel to the longitudinal axis of the structure (CON.1 and CON.4), in general, the influence of the SSSI on the total axial force at the top of the piles in each line of the middle zone of the structure is greater than that in the border zone of the structure, while that on the total shearing force at the top of the piles in each line just at the outer edge of the structure is greater than that in the other zone of the structure. When the shaking direction of the exciting wave is parallel to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure (CON.2), the influence of the SSSI on the total axial or shearing force at the top of the piles in each line just at the outer edge of the structure is comparatively greater.
Conclusion
A three-dimensional numerical procedure for the dynamic analysis of pile-supported multistory frame structure is presented in this work to solve the problem of through-soil interaction between two high-rise buildings. Commercial software (ANSYS), which is based on the finite element method, has been further developed and enhanced for calculation in the frequency domain, in which hysteretic damping has been considered for both the soil and structure, and linear assumptions have been put forward for rigorous three-dimensional modeling. The time domain results under seismic waves are conducted through a fast Fourier transform from the frequency domain results. In this way, the SSSI phenomena are implicitly included in the model. The variations in the story shear force, interstory drift angle, displacement, velocity and acceleration of the superstructure, sway of the foundation, and axial and shearing forces of the pile under harmonic waves and under real or artificial seismic waves are presented to assess the influence of the SSSI phenomena on the structural seismic response of a high-rise building subject to a vertically incident S wave. The main objective is to determine the influence level of the SSSI effect on each kind of dynamic response of the structure and study the influence of the excitation frequency of a harmonic wave or the frequency components of the seismic wave, the shaking direction of the exciting wave and the direction of the structure arrangement on the SSSI effect. The conclusions from this paper can be summarized as follows:
-
1) The influence of a high-rise building on an adjacent high-rise building is less than that on an adjacent underground structure.
-
2) The major influencing factors of the interaction between two high-rise buildings are the excitation frequency of a harmonic wave or the frequency components of a seismic wave, the shaking direction of the exciting wave and the direction of the structure arrangement. Another major influencing factor of a pile is the position of the pile.
-
3) Under harmonic waves, the interaction mainly occurs when the excitation frequency is and is prominent at some frequencies; the maximum absolute values of the influence coefficients can be several dozen percent. However, under seismic waves, the interaction is limited, and the influence coefficients are almost within . More attention should be paid to the influence on foundation sway, which can be up to .
-
4) For the superstructure, the influence of the SSSI on the dynamic response for the direction of the structure arrangement parallel to the lateral axis of the structure is greater than that for the direction of the structure arrangement parallel to the longitudinal axis of the structure, and the influence of the SSSI on the dynamic response for the shaking direction of the exciting wave perpendicular to the direction of the structure arrangement is greater than that for the shaking direction of the exciting wave parallel to the direction of the structure arrangement.
-
5) For all seismic waves, overall, when the shaking direction of the exciting wave is perpendicular to the direction of the structure arrangement and the direction of the structure arrangement is parallel to the lateral axis of the structure, the influence of the SSSI on the dynamic response (story shear force, interstory drift angle, foundation sway, displacement, velocity and acceleration) of the superstructure is a maximum.
Acknowledgment
The authors would like to gratefully acknowledge the support from National Natural Science Foundation of China under Grant No. 51608462 and 51408609, from the Fundamental Research Funds for the Central Universities under Grant No. 18CX02081A and from Shandong Provincial Natural Science Foundation under Grant No. ZR2019MEE099.
References
-
[1]Kausel E. Early history of soil-structure interaction[J]. Soil Dynamics and Earthquake Engineering, 2010,30(9):822-832.
-
[2]Lou M, Wang H, Chen X, et al. Structure-soil-structure interaction: Literature review[J]. Soil Dynamics and Earthquake Engineering, 2011,31(12):1724-1731.
-
[3]Luco J E, Contesse L. Dynamic structure-soil-structure interaction[J]. Bulletin of the Seismological Society of America, 1973,63(4):1289-1303.
-
[4]Lee T H, Wesley D A. Soil-structure interaction of nuclear reactor structures considering through-soil coupling between adjacent structures[J]. Nuclear Engineering and Design, 1973,24(3):374-387.
-
[5]Lee T H, Wesley D A. Influence of through-soil coupling between adjacent structures on seismic response of nuclear reactors: Proceedings 2nd International Conference on Structural Mechanics in Reactor Technology, Berlin, Germany, 1973[C].
-
[6]Wong H L, Trifunac M D. Two-dimensional, antiplane, building-soil-building interaction for two or more buildings and for incident plane SH waves[J]. Bulletin of the Seismological Society of America, 1975,65(6):1863-1885.
-
[7]Kobori T, Kusakabe K. Dynamic cross-interaction between two embedded structure: Proceedings of the 5th Japan Earthquake Engineering Symposium, Toky, Japan, 1978[C].
-
[8]Warburton G B, Richardson J D, Webster J J. Harmonic responses of masses on an elastic half space[J]. Journal of Engineering for Industry, ASME, 1972,194(2):193-200.
-
[9]Warburton G B, Richardson J D, Webster J J. Forced vibrations of two masses on an elastic half space[J]. Journal of Applied Mechanics-Transactions, ASME, 1971,38(1):148-156.
-
[10]Richardson J D. Forced vibrations of rigid bodies on a semi-infinite elastic medium[D]. Nottinghamshire, England: University of NottinghamDepartment of Mechanical Engineering, 1969.
-
[11]Bybordiani M, Arici Y. Structure‐soil‐structure interaction of adjacent buildings subjected to seismic loading[J]. Earthquake Engineering & Structural Dynamics, 2019,48(7):731-748.
-
[12]Liang J, Han B, Todorovska M I, et al. 2D dynamic structure-soil-structure interaction for twin buildings in layered half-space II: Incident SV-waves[J]. Soil Dynamics and Earthquake Engineering, 2018,113:356-390.
-
[13]Santana A, Aznarez J J, Padron L A, et al. A BEM-FEM model for the dynamic analysis of building structures founded on viscoelastic or poroelastic soils[J]. Bulletin of Earthquake Engineering, 2016,14(1):115-138.
-
[14]Rahgozar M A. Accounting for soil nonlinearity in three-dimensional seismic structure-soil-structure-interaction analyses of adjacent tall buildings structures[J]. International Journal of Civil Engineering, 2015,13(3B):213-225.
-
[15]Fariborz N, Ali R. Nonlinear dynamic response of tall buildings considering structure-soil-structure effects[J]. The Structural Design of Tall and Special Buildings, 2013,22(14):1075-1082.
-
[16]Ngo V, Kim J, Chang S, et al. Effect of Height Ratio and Mass Ratio on Structure-Soil-Structure Interaction of Two Structures Using Centrifugal Experiment[J]. Applied Sciences, 2019,9(3):526.
-
[17]Barrios G, Nanayakkara V, De Alwis P, et al. Effects of Slenderness and Fundamental Frequency on the Dynamic Response of Adjacent Structures[J]. International Journal of Structural Stability and Dynamics, 2019,19(09):1950105.
-
[18]Kirkwood P, Dashti S. A Centrifuge Study of Seismic Structure-Soil-Structure Interaction on Liquefiable Ground and Implications for Design in Dense Urban Areas[J]. Earthquake Spectra, 2018,34(3):1113-1134.
-
[19]Li P, Liu S, Lu Z, et al. Numerical analysis of a shaking table test on dynamic structure-soil-structure interaction under earthquake excitations[J]. The Structural Design of Tall and Special Buildings, 2017,26(15):e1382.
-
[20]Aldaikh H, Alexander N A, Ibraim E, et al. Shake table testing of the dynamic interaction between two and three adjacent buildings (SSSI)[J]. Soil Dynamics and Earthquake Engineering, 2016,89:219-232.
-
[21]Nakagawa S, Kuno M, Naito Y, et al. Forced vibration tests and simulation analyses of a nuclear reactor reactor building[J]. Nuclear Engineering and Design, 1998,179(2):145-156.
-
[22]Kitada Y, Hirotani T, Iguchi M. Models test on dynamic structure-structure interaction of nuclear power plant buildings[J]. Nuclear Engineering and Design, 1999,192(2/3):205-216.
-
[23]Xu J, Costantino C, Hofmayer C, et al. Seismic response prediction of NUPEC's field model tests of NPP structures with adjacent building effect: 2004 ASME/JSME Pressure Vessels and Piping Conference, San Diego, California, USA, 2004[C].
-
[24]Roy C, Bolourchi S, Eggers D. Significance of structure-soil-structure interaction for closely spaced structures[J]. Nuclear Engineering and Design, 2015,295:680-687.
-
[25]Yue D, Ghiocel D M, Fuyama H, et al. Structure-soil-structure interaction effects for two heavy npp buildings with large-size embedded foundations: 22nd Conference on Structural Mechanics in Reactor Technology, San Francisco, California, USA, 2013[C].
-
[26]Clouteau D, Broc D, Devesa G, et al. Calculation methods of Structure-Soil-Structure Interaction (3SI) for embedded buildings: Application to NUPEC tests[J]. Soil Dynamics and Earthquake Engineering, 2012,32(1):129-142.
-
[27]Anderson L M, PhD S C, Amin J. Effect of Structure, Soil, and Ground Motion Parameters on Structure-Soil-Structure Interaction of Large Scale Nuclear Structures: Structures congress, Las Vegas, NV(US), 2011[C].
-
[28]Ghandil M, Aldaikh H. Damage-based seismic planar pounding analysis of adjacent symmetric buildings considering inelastic structure-soil-structure interaction[J]. Earthquake Engineering & Structural Dynamics, 2017,46(7):1141-1159.
-
[29]Li P, Liu S, Lu Z. Studies on Pounding Response Considering Structure-Soil-Structure Interaction under Seismic Loads[J]. Sustainability, 2017,9(12):2219.
-
[30]He C, Zhou S, Di H, et al. Effect of Dynamic Interaction of Two Neighboring Tunnels on Vibrations from Underground Railways in the Saturated Soil[J]. KSCE Journal of Civil Engineering, 2019,23(11):4651-4661.
-
[31]Guo J, Chen J, Bobet A. Influence of a subway station on the inter-story drift ratio of adjacent surface structures[J]. Tunnelling and Underground Space Technology, 2013,35:8-19.
-
[32]Wang H, Lou M, Chen X, et al. Structure-soil-structure interaction between underground structure and ground structure[J]. Soil Dynamics and Earthquake Engineering, 2013,54(11):31-38.
-
[33]Wang H, Lou M, Zhang R. Influence of presence of adjacent surface structure on seismic response of underground structure[J]. Soil Dynamics and Earthquake Engineering, 2017,100(09):131-143.
-
[34]Abate G, Massimino M R. Parametric analysis of the seismic response of coupled tunnel-soil-aboveground building systems by numerical modelling[J]. Bulletin of Earthquake Engineering, 2017,15(1):443-467.
-
[35]Abate G, Massimino M R. Numerical modelling of the seismic response of a tunnel-soil-aboveground building system in Catania (Italy)[J]. Bulletin of Earthquake Engineering, 2017,15(1):469-491.
-
[36]Abate G, Corsico S, Massimino M R. FEM Modelling of the Seismic Behavior of a Tunnel-soil-Aboveground Building System: A Case History in Catania (Italy): 6th Italian Conference of Researchers in Geotechnical Engineering, Bologna, Italy, 2016[C]. Elsevier Ltd, 2016.
-
[37]Ghandil M, Behnamfar F, Vafaeian M. Dynamic responses of structure-soil-structure systems with an extension of the equivalent linear soil modeling[J]. Soil Dynamics and Earthquake Engineering, 2016,80(1):149-162.
-
[38]Alamo G M, Padron L A, Aznarez J J, et al. Structure-soil-structure interaction effects on the dynamic response of piled structures under obliquely incident seismic shear waves[J]. Soil Dynamics and Earthquake Engineering, 2015,78(11):142-153.
-
[39]Aldaikh H, Alexander N A, Ibraim E, et al. Two dimensional numerical and experimental models for the study of structure-soil-structure interaction involving three buildings[J]. Computers & Structures, 2015,150(4):79-91.
-
[40]Alexander N A, Ibraim E, Aldaikh H. A simple discrete model for interaction of adjacent buildings during earthquakes[J]. Computers & Structures, 2013,124(SI):1-10.
-
[41]Mykoniou K, Butenweg C, Holtschoppen B, et al. Seismic response analysis of adjacent liquid-storage tanks[J]. Earthquake Engineering & Structural Dynamics, 2016,45(11):1779-1796.
-
[42]Moshirabadi S, Soltani M, Maekawa K. Seismic interaction of underground RC ducts and neighboring bridge piers in liquefiable soil foundation[J]. Acta Geotechnica, 2015,10(6):761-780.
-
[43]Schwan L, Boutin C, Padrón L A, et al. Site-city interaction: theoretical, numerical and experimental crossed-analysis[J]. Geophysical Journal International, 2016,205(2):1006-1031.
-
[44]Kumar N, Narayan J P. Quantification of site-city interaction effects on the response of structure under double resonance condition[J]. GEOPHYSICAL JOURNAL INTERNATIONAL, 2018,212(1):422-441.
-
[45]Lu X, Tian Y, Wang G, et al. A numerical coupling scheme for nonlinear time history analysis of buildings on a regional scale considering site-city interaction effects[J]. EARTHQUAKE ENGINEERING & STRUCTURAL DYNAMICS, 2018,47(13):2708-2725.
-
[46]Kumar N, Narayan J P. Effects of site-city interaction and polarization of the incident S-wave on the transfer function and fundamental frequency of structures[J]. NATURAL HAZARDS, 2019,97(2):747-774.
-
[47]Aldaikh H, Alexander N A, Ibraim E, et al. Evaluation of Rocking and Coupling Rotational Linear Stiffness Coefficients of Adjacent Foundations[J]. INTERNATIONAL JOURNAL OF GEOMECHANICS, 2018,18(040171311).
-
[48]Vicencio F, Alexander N A. Higher mode seismic structure-soil-structure interaction between adjacent building during earthquakes[J]. Engineering Structures, 2018,174:322-337.
-
[49]Vicencio F, Alexander N A. Dynamic Structure-Soil-Structure Interaction in unsymmetrical plan buildings due to seismic excitation[J]. Soil Dynamics and Earthquake Engineering, 2019,127:105817.
-
[50]Vicencio F, Alexander N A. Dynamic interaction between adjacent buildings through nonlinear soil during earthquakes[J]. Soil Dynamics and Earthquake Engineering, 2018,108:130-141.
-
[51]Lu Y, Li B, Xiong F, et al. Simple discrete models for dynamic structure-soil-structure interaction analysis[J]. Engineering Structures, 2020,206:110188.
-
[52]Liang J, Han B, Todorovska M I, et al. 2D dynamic structure-soil-structure interaction for twin buildings in layered half-space I: Incident SH-waves[J]. Soil Dynamics and Earthquake Engineering, 2017,102:172-194.
-
[53]Trombetta N W, Mason H B, Hutchinson T C, et al. Nonlinear Soil-Foundation-Structure and Structure-Soil-Structure Interaction: Centrifuge Test Observations[J]. 2014,140(5):4013051-4013057.
-
[54]Trombetta N W, Benjamin Mason H, Hutchinson T C, et al. Nonlinear soil-foundation-structure and structure-soil-structure interaction: Engineering demands[J]. Journal of Structural Engineering, 2015,141(7):4014177.
-
[55]Tombari A, Zentner I, Cacciola P. Sensitivity of the stochastic response of structures coupled with vibrating barriers[J]. Probabilistic Engineering Mechanics, 2016,44:183-193.
-
[56]Tombari A, Garcia Espinosa M, Alexander N A, et al. Vibration control of a cluster of buildings through the Vibrating Barrier[J]. Mechanical Systems and Signal Processing, 2018,101:219-236.
-
[57]Cacciola P, Tombari A. Vibrating barrier: a novel device for the passive control of structures under ground motion[J]. PROCEEDINGS OF THE ROYAL SOCIETY A-MATHEMATICAL PHYSICAL AND ENGINEERING SCIENCES, 2015,471(201500752179).
-
[58]Ngo V, Kim J, Lee C. Influence of structure-soil-structure interaction on foundation behavior for two adjacent structures: Geo-centrifuge experiment[J]. GEOMECHANICS AND ENGINEERING, 2019,19(5):407-420.
-
[59]Hayden C P, Zupan J D, Bray J D, et al. Centrifuge Tests of Adjacent Mat-Supported Buildings Affected by Liquefaction[J]. JOURNAL OF GEOTECHNICAL AND GEOENVIRONMENTAL ENGINEERING, 2015,141(040141183).
-
[60]Kirkwood P, Dashti S. Influence of prefabricated vertical drains on the seismic performance of similar neighbouring structures founded on liquefiable deposits[J]. GEOTECHNIQUE, 2019,69(11):971-985.
-
[61]Gueguen P, Colombi A. Experimental and numerical evidence of the clustering effect of structures on their response during an earthquake: A case study of three identical towers in the City of Grenoble, France[J]. Bulletin of the Seismological Society of America, 2016,106(6):2855-2864.
-
[62]Naserkhaki S, Pourmohammad H. SSI and SSSI effects in seismic analysis of twin buildings: discrete model concept[J]. Journal of Civil Engineering and Management, 2012,18(6):890-898.
-
[63]Wang H, Zhang R. Dynamic structure-soil-structure interaction of piled high-rise buildings II: Influence of key parameter[J]. 2020.
-
[64]Clough R W, Penzien J. Dynamics of Structures[M]. Berkeley, USA: Computers & Structures, 2003.
-
[65]Lou M, Dong Y, Zhang R. Several Problems on Refined Local Modeling for Seismic Response Analysis of Immersed Tunnel[J]. Chinese Journal of Geotechnical Engineering, 2016,38(9):1-11.
-
[66]Chopra A K, McKenna F. Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation[J]. Earthquake Engineering & Structural Dynamics, 2016,45(2):193-211.
-
[67]Spears R E, Jensen S R. Approach for selection of Rayleigh damping parameters used for time history analysis[J]. Journal of Pressure Vessel Technology, 2012,134(6):61801-61807.
-
[68]Yang D B, Zhang Y G, Wu J Z. Computation of Rayleigh damping coefficients inseismic time-history analysis of spatial structures[J]. Journal of the International Association for Shell and Spatial Structures, 2010,51(2):125-135.
Edited by
Editor:
Publication Dates
-
Publication in this collection
23 Apr 2021 -
Date of issue
2021
History
-
Received
06 Aug 2020 -
Reviewed
19 Jan 2021 -
Accepted
10 Feb 2021 -
Published
17 Feb 2021