Abstract
A spiral case with its steel spiral case (SSC) being embedded in reinforced concrete under a pressurized condition is called a preloaded filling spiral case structure (PFSCS) in a hydropower plant. As a steel-concrete composite structure, a PFSCS is designed to work reliably. The non-uniform gap and contact nonlinearity between the SSC and the surrounding mass concrete have a great effect on the bearing mechanism of the composite structure. However, the description of the gap and contact nonlinearity in a PFSCS is a tough work. With the aim of efficiently describing the evolution process of the non-uniform gap and contact nonlinearity, we performed an experimental investigation and proposed a novel numerical simulation technique for structural finite element analyses (FEA) of PFSCSs. In the technique, the gap and contact nonlinearity as well as the construction process and operation process of a PFSCS are taken into account. A friction-contact model is used to simulate the sliding of the SSC against the concrete. A plasticity damage model is employed to describe the concrete. The development of the gap, contact status between the steel liner and the surrounding concrete, stresses of the steel liner and the steel bars, as well as the concrete cracking time and crack pattern, are presented in this work. The FEA results agree well with the experimental results. The agreement provides evidence that the applicability and competence of the proposed technique are valid and satisfactory.
Keywords
numerical simulation technique; preloaded filling spiral case structure; contact nonlinearity; finite element analyses; steel-concrete composite structure; hydropower plant
1 INTRODUCTION
Hydropower is considered a renewable energy source and accounts for 6.9% of world energy production (Global B P 2017Global B P (2017). BP statistical review of world energy. bp.com/statisticalreview.). With the positive contributions to climate mitigation, hydropower has attracted more attention of researchers. Numerous hydroelectric facilities have been constructed at a furious pace in recent years (Wang et al. 2016Wang, Y., Shi, C.Z., Wu, H.G., Zhang, Q.L., and Su, K. (2016). Flat-bottomed design philosophy of Y-typed bifurcations in hydropower stations. Structural Engineering and Mechanics, 57(6), 1085-1105.). Against this background, the engineering technology with regard to hydropower plant (HP) has been greatly developed and improved.
In a HP, a water passage providing a circular water intake for a turbine is generally called a spiral case structure (SCS) (Zhang and Wu 2012Zhang, Q.L., and Wu, H.G. (2012). Effect of compressible membrane's nonlinear stress-strain behavior on spiral case structure. Structural Engineering and Mechanics, 42(1), 73-93., 2013Zhang, Q.L., and Wu, H.G. (2013). Using softened contact relationship describing compressible membrane in FEA of spiral case structure. Archives of Civil and Mechanical Engineering, 13(4), 506-517.). Usually, a SCS is a composite structure of a steel spiral case (SSC) and surrounding mass concrete (SMC) in a medium or high head HP (Zhang and Wu 2017Zhang, Q.L., and Wu, H.G. (2017). Embedment of steel spiral cases in concrete: China's experience. Renewable and Sustainable Energy Reviews, 72, 1271-1281.). It also refers to a steel-lined SCS. Figure 1 illustrates an uncovering SSC under construction in a practical engineering. The SMC will be placed around the SSC later on.
Since the steel-lined SCS is a composite structure, the composite method of the SSC and the SMC determines its structural performance (Spacone and El-Tawil 2004Spacone, E., and El-Tawil, S. (2004). Nonlinear analysis of steel-concrete composite structures: State of the art. Journal of Structural Engineering, 130(2), 159-168.). The composite method refers to the embedment condition of the SSC. A SCS with its SSC being embedded in concrete under a pressurized condition is called a preloaded filling spiral case structure (PFSCS) (Zhang and Wu 2017Zhang, Q.L., and Wu, H.G. (2017). Embedment of steel spiral cases in concrete: China's experience. Renewable and Sustainable Energy Reviews, 72, 1271-1281.). During the construction period of PFSCSs, the SSC is full of water and pressurized to a temporary internal water pressure (IWP) while the SMC is placed. Before pressurization, the openings of the SSC should be closed off with a test barrel and test head (EM 1110-2-3001, 1995EM 1110-2-3001 (1995). Planning and Design of Hydroelectric Power Plant Structures. Department of the Army, Washington, DC.). After the concrete has been placed for several days and reached a certain strength, the temporary IWP should be unloaded with the test barrel and test head removed. The pressure relief gives rise to the shrinkage of the SSC. Hence, an initial gap between the SSC and the SMC appears. During the operation period, the SSC is filled with water again and pressurized to the design IWP. The SSC begins to extend outwardly and be in contact with the SMC.
The gap between the SSC and the SMC plays a key role in affecting the structural performance of PFSCSs. If the gap remains open, the IWP is only resisted by the SSC. If the gap is in the closed state, the IWP is resisted by the SSC as well as the SMC. Considering the fact that the tensile strength of concrete is generally limited (Park and Paulay 1975Park, R., and Paulay, T. (1975). Reinforced Concrete Structures. John Wiley & Sons, New York, NY, USA.), the IWP-resisting percentage of the SMC should be small. Based on this understanding, the gap is a key issue in the structural analyses of PFSCSs.
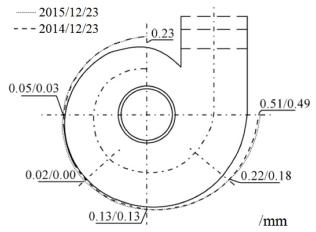
It has been argued that the initial gap between the SSC and the SMC is completely closed during the operation period of PFSCSs in traditional numerical methods. In other words, when the IWP increases to the temporary IWP, the whole SSC is assumed to be in completely contact with the SMC accompanied by a full closing of the in-between gap (Aronson et al. 1985Aronson, A.Y., Bazhenov, V.A., Gotsulyak, E.A., Gulyaev, V.I., and Ogloblya, A.I. (1985). Nonlinear deformation of shells of the volute chambers of hydraulic turbines in an elastic medium. Strength of Materials, 17(4), 555-560.; Zhang and Zhang 2009Zhang, C.H., and Zhang, Y.L. (2009). Nonlinear dynamic analysis of the Three Gorge Project powerhouse excited by pressure fluctuation. Journal of Zhejiang University-Science A, 10(9), 1231-1240.). The contact behavior in the steel-concrete composite structure is ignored (Wu et al. 2003Wu, H.G., Ma, S.D. and Bai, J.M. (2003). 2-D nonlinear analysis for the spiral case of Three Gorges Power Station. Journal of Hydraulic Engineering, 34(5), 57-61.). However, some field monitoring data has called into question the assumption. The monitoring data (Figure 2) of the Three Gorge HP showed that the gap was not completely closed during the operation period. The monitoring data of the Ertan HP showed that only part of the in-between gap was closed when the water pressure was equal to the temporary IWP (Zhang and Wu 2017Zhang, Q.L., and Wu, H.G. (2017). Embedment of steel spiral cases in concrete: China's experience. Renewable and Sustainable Energy Reviews, 72, 1271-1281.). The loading-unloading-loading of the water pressure on the SSC results in the opening/closing phenomenon of the gap, which involves a nonlinear process and is not entirely determined by the temporary IWP. This view gives us a better understanding of the gap in PFSCSs and makes it more difficult to describe the evolution process of the gap in structural FEA.
The field monitoring data of the gap between the SSC and the SMC in No.3 unit of the Three Gorge HP.
In addition, several numerical investigations indicate that the contact nonlinear behavior between the SSC and the SMC affects the bearing mechanism of the PFSCS to a great extent (Wu et al. 2012Wu, H.G., Shen, Y., Jiang, K.C. and Shi J. (2012). Structural analysis of the embedded spiral case in the three gorges hydropower station. Practice Periodical on Structural Design & Construction, 17(2), 41-47.; Guo et al. 2015aGuo, T., Zhang, L.X. and Li, S.J. (2015a). Research on three-dimensional simulation algorithm of preloaded filling spiral case with non-uniform gap. Journal of Hydraulic Engineering, 46(12), 1434-1443.; Zhang and Wu 2016Zhang, Q.L. and Wu, H.G. (2016). Sliding behaviour of steel liners on surrounding concrete in c-cross-sections of spiral case structures. Structural Engineering International, 26(4), 333-340.). The nonlinear gap-opening/closing phenomenon increases the complexity of the contact behavior (Su et al. 2017Su, K., Yang, Z.J., Zhang, W., Wu, H.L., Zhang, Q.L., and Wu, H.G. (2017). Bearing mechanism of composite structure with reinforced concrete and steel liner: An application in penstock. Engineering Structures, 141(2017), 344-355.). Consequently, the description of bearing mechanism of PFSCSs is a tough work in comparison with that of a general steel-concrete composite structure.
With the aim of efficiently describing the evolution process of the non-uniform gap and contact nonlinearity in a PFSCS, an experimental investigation was performed and a novel numerical simulation technique (NST) was proposed for structural finite element analyses (FEA) of PFSCSs in this work. To validate the technique, as it should be, detailed comparisons between FEA results and experimental data were carried out on a PFSCS.
2 Experimental investigation
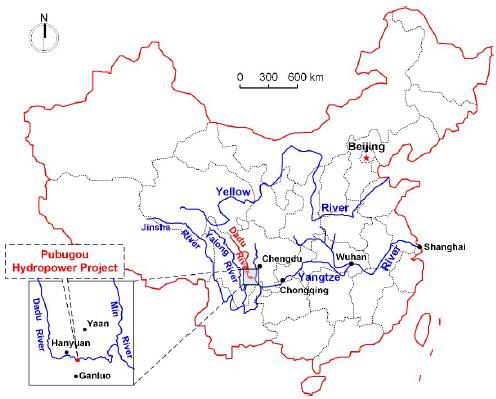
The Pubugou hydropower station, with a production capacity of 14.58 billion kWh a year and an effective storage of 5.177 billion m3, is located on the border between Hanyuan County and Ganluo County, Sichuan Province, China (Figure 3). As a landmark project of China’s Western Development, the Pubugou hydropower station is designed to ensure the leading role of electric power generation and the supplementary role of flood controlling and sediment retaining (Figure 4).
2.1 Experimental model
To research the bearing mechanism of PFSCSs in the whole life cycle, an experimental investigation was conducted based on the Pubugou hydropower station. The experimental model contains a standard block with a width (upstream-downstream dimension) of 3.2 m, a length (left-right dimension) of 3.3 m and a height (vertical dimension) of 2.19 m.
The SSC is composed of welded steel plates (Figure 5). The thickness of the steel plate is 30~75 mm. After the assembly of the SSC, the reinforcements were arranged around the circumferential and longitudinal direction of the steel liner. The reinforcement layout of the PFSCS is presented in Figure 6. The diameter of the reinforcement bars used in the model is 6 mm. The strength and elongation of the steel and reinforcement bars were obtained through a mechanical properties test (ISO 6892-1, 2016ISO 6892-1 (2016). Metallic materials -- Tensile testing -- Part 1: Method of test at room temperature). The test result shows that the strength of the steel material is 358MPa, and the elongation is 30%.
The SSC was full of water and pressurized to a temporary IWP (1.4 MPa) while the SMC was placed. Field-pouring process of the SMC is presented in Figure 7. The concrete was poured in three stages. In each stage, approximately one-third of the SMC was placed. This pouring technique is called laminated placement. The concrete was cured for 28 days with the temperature range of 10°C to 15°C. The material mechanical properties of the concrete were tested. The test was conducted with reference to Chinese Codes (GB/T50080-2016GB/T50080-2016 (2016). Standard for test method of performance on ordinary fresh concrete, Ministry of Housing and Urban-Rural Development of the People’s Repulic of China, Beijing, China.; GB/T50081-2016GB/T50081-2016 (2016). Standard for test method of mechanical properties on ordinary concrete, Ministry of Housing and Urban-Rural Development of the People’s Repulic of China, Beijing, China.). The age of the concrete specimens is 28 days. The tensile strength of the concrete was obtained from a Brazilian test. The test result shows that the tensile modulus of the concrete is 33.7GPa, the tensile strength of the concrete is 1.95 MPa and the compressive strength is 27 MPa.
View of the complete PFSCS model is shown in Figure 8. Mechanical parameters of the materials are shown in Table 1.
After the concrete had been placed for at least 28 days, the water in the SSC was released. The consequent pressure relief gave rise to the shrinkage of the SSC. An initial gap between the SSC and the SMC appeared. Then the construction process of the PFSCS model was finished. The model was prepared for experiments to observe the evolution process of the gap and contact behavior in the PFSCS during the operation period.
2.2 Strain gages and displacement sensors
Strain gages and displacement sensors were employed at several cross-sections and points in the experimental model. Cross-sections 1#~9# are distributed along the direction of water flow, as shown in Figure 9(a). In each cross-section, the typical points to be tested are located around the circumference of the spiral case, as shown in Figure 9(b). In addition, crack width test of concrete was conducted when the concrete was severely strained and cracked, as shown in Figure 10. The crack width of the concrete was tested with a crack width measuring instrument. The measuring instruments are shown in Fig. 10(b).
Distribution of cross-sections and points to be tested: (a) cross-sections, (b) points in each cross-section.
2.3 Experimental procedure
A considerable amount of research indicates that the strain and the stress in the concrete of a SCS are mainly caused by the water pressure in the SSC (Kalkani 1995Kalkani, E.C. (1995). Expected displacements and stresses in the encasing concrete of a Francis turbine scroll case. Computers and Structures, 55(4), 735-739.; Cui and Su 2007Cui, J.H. and Su, H.D. (2007). 3-D FEM emulation computation on surrounding concrete of steel spiral case keeping internal pressure during construction. Computational Mechanics, 286-286.; Tian et al. 2008Tian, Z.Q., Zhang, Y.L., Ma, Z.Y. and Chen, J. (2008). Effect of concrete cracks on dynamic characteristics of powerhouse for giant- scale hydro station. Transactions of Tianjin University, 14(4), 307-312.). Structural weight, equipment load and live load play a minor role in affecting the responses of the concrete. In the light of this, the main load applied on the PFSCS model is the IWP. Additionally, the gravitation is taken into account in this study.
Experiments were conducted to observe the development process of the non-uniform gap, the concrete crack pattern and the stresses of the structure under three water pressure conditions including temporary IWP condition (1.4MPa), design IWP condition (2.45MPa) and overload IWP condition (3.85MPa). The IWP was gradually applied on the inner face of the SSC.
The experimental procedure during the operation period of a PFSCS is as follows: (1) closing off the opening by using a test barrel and test head, gradually pressuring the SSC to the temporary IWP; (2) gradually pressuring the SSC to the design IWP; (3) gradually pressuring the SSC to the overload IWP. In each step, responses of the PFSCS model were recorded by the strain gages and displacement sensors.
3 Numerical analysis
3.1 Description of NST
The finite element method is usually considered to be a feasible analysis method for various kinds of structures. NST for the structural FEA of PFSCSs has aroused a renewed interest for scholars. A significant number of researchers attempt to find an available technique to describe the evolution of the gap and contact behavior in PFSCSs. Mazzucco et al. (2012Mazzucco, G., Salomoni, V.A., and Majorana, C.E. (2012). Three-dimensional contact-damage coupled modelling of FRP reinforcements-simulation of delamination and long-term processes. Computers & Structures, 110(2012), 15-31.) have developed an available contact algorithm to reconstruct the adhesion properties of composite structures. Xu et al. (2013Xu, X.Y., Ma, Z.Y. and Zhang, H.Z. (2013). Simulation algorithm for spiral case structure in hydropower station. Water Science and Engineering, 6(2), 230-240.) conducted several numerical investigations into the gap in PFSCSs. They presented the early-closing and delayed-closing of the gap. Fu et al. (2014Fu, D., Wu, H.G. and Hu, L. (2014). Gap closing and contact transferring mechanism in preloading filling spiral case of hydropower station. Journal of Huazhong University of Science & Technology, 42(7), 27-32.) performed a numerical simulation of a PFSCS to investigate the closing characteristic of the gap. Guo et al. (2015bGuo, T., Zhang, L.X. and Wu, L. (2015b). Advance in research and application of preload filling spiral case structure in hydroelectric power plant. Journal of Kunming University of Science and Technology (Natural Science Edition), 40(3), 70-78.) proposed an improved simulation method for the construction process of a PFSCS. The contact model was used for the interface of different materials. Their studies show that the gap between the SSC and the SMC is not completely closed in the PFSCS.
However, the abovementioned NST still needs to be improved in two aspects. First, the nodes on the SSC may penetrate the internal surface of the SMC when the SSC shrinks discontinuously. The penetration is obviously contrary to the reality. Second, the reliability of the NST in describing the mechanical property of a PFSCS was not verified effectively. Thus, further improvements are needed to be done in the structural FEA of PFSCSs.
3.1.1 Novel NST
In this section, a novel NST for the structural FEA of PFSCSs is proposed. In the NST, the gap and contact nonlinearity as well as the construction process and operation process in a PFSCS are taken into consideration.
The construction and operation of a PFSCS involve installation and sealing of a SSC, temporary water-filling, concrete placement, pressure relief and re-pressurization. To simulate the complete procedure of a PFSCS, a complete finite element (FE) model should be established. The FE model includes solid elements representing concrete, shell elements representing SSC, connector elements and contact elements. Nodes on the interface between the SSC and the SMC are set to be separated nodes initially. The entire simulation process of the novel NST for PFSCSs is as follows (Figure 11):
-
(1) Temporary pressurization on SSC: this process involves installation of the SSC on the concrete pedestal, water-filling in the SSC and pressuring to the temporary IWP.
-
(2) Laminated placement of SMC: this process involves concrete placement by activating the concrete elements, joining the separated nodes on the interface between the SSC and the SMC by activating the connector elements.
-
(3) IWP relief: this process involves regaining the separated nodes by killing the connector elements, and unloading the temporary IWP. The initial gap between the SSC and the SMC appears in this process.
-
(4) Re-pressurization on SSC: this process involves activating the contact elements between the SSC and the SMC, pressuring the SSC to the design IWP or overload IWP gradually.
The novel NST emphasizes the accurate simulation of the gap and contact nonlinearity as well as the complete simulation procedure. It is an automatic simulation technique and consists in the combination of the connector element (Systèmes 2013Systèmes, D. (2013). Abaqus analysis user’s manual. Simulia Corp. Providence, RI, USA.) and the contact model.
The procedure for the using of the element type (connector element or contact element) is illustrated as follows:
-
1) In experimental model, the SSC is employed on the concrete pedestal. The SSC is unwatered initially and then pressured to the temporary IWP. Then it expands outward. The expansion leads to the movement of the outer surface of the SSC. Subsequently, the concrete is placed on the outer surface of the SSC. At this time, the inner surface of the concrete and the outer surface of the SSC are coincident. In FE model, the inner surface of the concrete and the outer surface of the SSC are coincident at the beginning. Nodes on the inner surface of the concrete and the outer surface of the SSC are separated nodes (It is because there is a small-sliding contact between them). When the SSC is filled with water and pressured to the temporary IWP, the SSC begins to expand outward. But at this time, the inner surface of the concrete is still in its initial location because the separated nodes. That means the inner surface of the concrete and the outer surface of the SSC are not coincident, which obviously does not match the experiment. So the connector elements with the JOIN connection type are used in this stage to makes the position of the inner surface of the concrete equal to that of the outer surface of the SSC.
-
2) In experimental model, the SSC should be unwatered after the concrete has been placed. With the temporary IWP released, the SSC begins to shrink and separate from the internal face of the concrete. This means that the inner surface of the concrete and the outer surface of the SSC may not be coincident any more. So, in the FE model, nodes on the inner surface of the concrete and the outer surface of the SSC should go back to be the separated nodes. At this time, the connector elements will be killed.
-
3) In experimental model, an initial gap between the SSC and the SMC exists in the PFSCS model after the construction process is finished. When the SSC is filled with water again during the operation period, the contact behavior between the SSC and the SMC affects the bearing mechanism of the PFSCS. So, in the FE model, the contact elements should be activated at this time.
The connector element is used to connect two nodes in case of penetration between the node and the surface node on the contact element. The contact model is employed to describe the contact nonlinearity. In the circumstances, we can control the separation and merging of two nodes by the connector element and simulate contact behavior by the contact element.
3.1.2 Connector element
A connection between two nodes can be defined by connector elements in the finite element code Abauqs (Systèmes 2013Systèmes, D. (2013). Abaqus analysis user’s manual. Simulia Corp. Providence, RI, USA.). Several connection types are available for the connector elements. The connection type can control the degrees of freedom of the nodes. For instance, a connector element with JOIN connection type can be used to merge degrees of freedom of two nodes. That means the connection type JOIN makes the position of node b equal to that of node a (Figure 12). If the two nodes are not in the same position initially, the relative position of them remains constant. The connector element code is CONN3D2.
The constraint force acts in three local directions. At node a it can be defined as follows:
where in two-dimensional analysis.
3.1.3 Contact model
The Abaqus/Standard provides a capability to model small-sliding interaction between two neighboring bodies in two and three dimensions. In the two bodies, one surface is considered as the master surface while the other one is considered as the slave surface. In two dimensions, the required mathematical condition is expressed as
where is the overclosure; represents the unit normal; stands for coordinates vector of a slave point; stands for a master line vector. stands for the tangent vector.
Similarly, in three dimensions the required mathematical condition is expressed as
To enforce the contact constraint and for the Newton iterations, the variations and are needed. is the relative slippage between the slave node and master surface. The variations and are expressed as
where
3.2 Theoretical validation of the novel NST
In this section we consider an example of a cylindrical pipe embedded in concrete to validate the applicability of the novel NST with regard to the formation of the initial gap. Numerical analysis and theoretical calculation are conducted respectively. The technique’s reliability is verified theoretically by the comparison between the numerical results and the theoretical solutions.
3.2.1 A simplified example
As illustrated in Figure 13, we consider a 30-mm-thick cylindrical steel pipe of 2m in radius, embedded in 3-m-thick concrete. The material parameters are presented in Table 2. The temporary IWP is 2.0 MPa.
It is assumed that the method of embedment of the cylindrical pipe is analogous to that of PFSCSs. Connector elements and contact elements are used in the model. The entire simulation process consists mainly of temporary pressurization, placement of concrete and IWP relief. Gravitation is ignored in this simplified example. The main focus is on the formation of the initial gap.
3.2.2 FEA result
Figure 14 shows the deformation and contact status of the steel pipe in the entire simulation process. In the stage of temporary pressurization, the steel pipe was employed on the concrete pedestal and pressurized to the temporary pressure of 2.0 MPa. It was deformed outwardly. In the circumstances, the concrete was placed against the steel pipe while the connector elements were activated. The contact status between the pipe and concrete was closed with sticking. In the stage of IWP relief, the water pressure was unloaded while the connector elements were killed. The steel pipe began to shrink. The shrinking caused a 1.291-mm-wide uniform gap.
3.2.3 Theoretical solution
Figure 15 presents the sketch of an ideal cylindrical steel pipe and a micro element in polar coordinate system. To verify the above FEA results, theoretical solutions are derived with elastic mechanics method and comparisons between them are conducted.
In the light of the elastic mechanics method, equations for stress analysis problems of symmetrical structures in polar coordinate system are as follows:
Equations for each displacement component are given by:
The above equations are subjected to the follow boundary conditions
Substituting Equation (16) into Equations (12)-(13) and (15) results in:
Therefore, the displacement component is obtained by substituting Equation (17) into Equation (14):
Then, substituting the values of the variables into Equation (18) gives:
So, the FEA result is accurate and available compared with the theoretical value. The error is only about 0.2%. The performance of the proposed novel NST is validated in the simplified example.
3.3 FEA
3.3.1 Concrete damage plasticity model
The stresses of concrete are expressed as follows:
where represents plastic strain; represents plastic strain rate; represents temperature; represents field variable; subscripts t and c represent tensile condition and compressive condition, respectively.
The concrete damage can be described by two variables, and (Mazars and Pijaudier-Cabot 1989Mazars, J. and Pijaudier-Cabot, G. (1989). Continuum damage theory-application to concrete. Journal of Engineering Mechanics, 115(2), 345-365.), which are represented as:
where is the damage factor of the material.
The damage can cause a decline of the strength of the concrete (Lubliner et al. 1989Lubliner, J., Oliver, J., Oller, S. and Onate, E. (1989). A plastic-damage model for concrete. International Journal of solids and structures, 25(3), 299-326.; Grassl and Jirásek 2006Grassl, P. and Jirásek, M. (2006). Damage-plastic model for concrete failure. International journal of solids and structures, 43(22-23), 7166-7196.; Cicekli et al. 2007Cicekli, U., Voyiadjis, G.Z., and Al-Rub, R.K.A. (2007). A plasticity and anisotropic damage model for plain concrete. International Journal of plasticity, 23(10-11), 1874-1900.). The mechanical properties under uniaxial tensile and compressive loading are defined as (Figure 16):
Behavior of concrete under (a) uniaxial tensile loading and (b) uniaxial compressive loading.
3.3.2 Modeling of steel and reinforcements
The steel structures in a PFSCS, such as the SSC and stay ring, usually work in elastic state (EM1110-2-3001, 1995EM 1110-2-3001 (1995). Planning and Design of Hydroelectric Power Plant Structures. Department of the Army, Washington, DC.). For this reason, the mechanical behavior of the steel structures is described by the linear elastic and perfectly plastic model in this work. This model is commonly employed for metal plasticity material. The stress-strain relationship is described as follows:
The concrete reinforcements are simulated by bar elements with an embedded discrete model. The bar element is a 2-node element, namely T3D2. It is assumed that the element T3D2 is embedded in the concrete without slippage (Demir et al. 2016Demir, A., Caglar, N., Ozturk, H. and Sumer, Y. (2016). Nonlinear finite element study on the improvement of shear capacity in reinforced concrete T-Section beams by an alternative diagonal shear reinforcement. Engineering Structures, 120, 158-165.).
3.3.3 Numerical analysis
A FE model (Figure 17) was established based on the experimental model of the PFSCS. The size of the model is 3.2 m in width, 3.3 m in length, and 2.19 m in height. The FE model contains 85242 elements and 83274 nodes. The Abaqus software was used in this work. The concrete is meshed by C3D8 solid elements (Systèmes 2013Systèmes, D. (2013). Abaqus analysis user’s manual. Simulia Corp. Providence, RI, USA.). The stay ring and the SSC are simulated by S4 shell elements. The steel bars are simulated by T3D2 truss elements. The CONN3D2 connector elements are used to define connections between nodes on the SSC and the internal face of the concrete. The orders of shape functions of these elements used in this study are linear (Systèmes 2013). The exterior circular surface of the SSC is in contact with the internal surface of the concrete by the employment of contact elements.
Nonlinear contact was assumed between the SSC and the SMC. Considering the potential sliding behavior, the friction property was introduced into the contact model. The friction coefficient was defined as 0.25 in line with the original design data. Abaqus/Standard uses Newton's method as a numerical technique for solving the nonlinear equilibrium equations.
The material parameters have been presented in Table 1. For the concrete, the Young’s modulus, Ec, is 33.7 GPa and the Poisson’s ratio is 0.167. For the steel, the Young’s modulus is 208 GPa and the Poisson’s ratio is 0.31.
The bottom face of the model is fixed while the side face of the model is free. As the main load of the model, the IWP was applied on the inner face of the SSC. The loading process was consistent with the experimental investigation.
The construction process and operation process of the PFSCS were simulated with the novel NST. The entire simulation process of the novel NST has been described in Chapter 3.1 (Figure 11). The loading process during the operation period of the PFSCS is as follows: (1) gradually pressuring the SSC to the temporary IWP (0~1.4 MPa); (2) gradually pressuring the SSC to the design IWP (1.4~2.45 MPa); (3) gradually pressuring the SSC to the overload IWP (2.45~3.85 MPa).
4 Comparisons between experimental and FEA results
4.1 Gap and contact status
Before the SSC is filled with water again, an initial gap caused by the temporary IWP relief exists between the SSC and the SMC. Figure 18(a) shows the distribution of selected cross-sections along the SSC. The cross-sections include cross-sections 1#, 3#, 5#, 7# and 9#. The detailed distribution of the gap at each cross-section is illustrated in Figure 18(b) ~ (f).
Blue represents the experimental data while black represents the FEA results. It can be found from Figure 18(b) ~ (f) that the FEA results are consistent with the experimental data. For example, the maximum value of the gap at cross-section 1# in FEA results is 4.02 while that in experimental data is 3.68. The difference between the two values is about 9%.
The trends of the gap distributions at all cross-sections are similar. The initial gap is not uniformly distributed along the circumferential direction of the SSC. The initial gap in the waist and top area of the SSC reaches the maximum while that in the bottom area reaches the minimum. The cause of the non-uniformity is the asymmetry of the pressurized SSC. The asymmetry causes unbalanced forces under the IWP. The unbalanced forces give rise to the torsion of the SSC. As a result, the initial gap is not uniformly distributed along the circumferential direction of the SSC.
The development of the gap is a dynamic process. That is to say, the gap is not only non-uniformly distributed in multi-dimensional space, but also changes with time. The pressure relief causes shrinkage of the SSC, resulting in the initial gap. The reloading of the IWP makes the gap narrow.
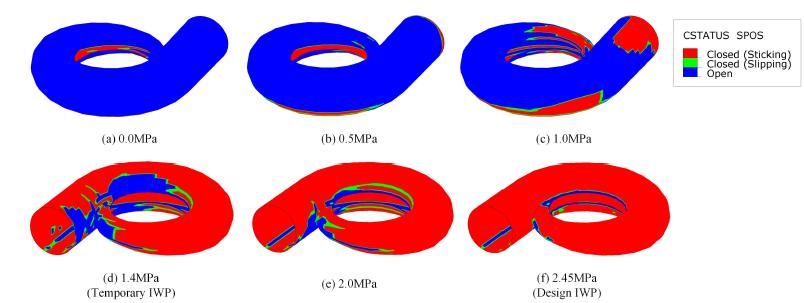
Figure 19 shows the closing process of the gap with the increase of the IWP applied to the SSC. Blue indicates that the gap is not closed while red and yellow indicate that the gap is closed. As shown in Figure 19(c), when the IWP increases to 71% of the temporary IWP, part of the SSC comes into contact with the SMC. That means a little part of the gap is closed before the water pressure reaches the temporary IWP (1.4MPa). This phenomenon is called early closure of gaps in PFSCSs. When the IWP increases to the temporary IWP (1.4 MPa), most of the gap is closed while a small part of the gap is still not closed (as shown in Figure 19(d)). This phenomenon is called delayed closure of gaps in PFSCSs. When the IWP increases to the design IWP (2.45 MPa), almost all the interfaces between the SSC and SMC are in contact (as shown in Figure 19(f)). The in-between gap is almost completely closed.
The abovementioned results indicate that the closing time of the gap is not exactly the time when the temporary IWP is reached, and the gap may not be completely closed when the temporary IWP is reached. The early closing and delayed closing phenomena are obvious. The radial outward expansion of the SSC caused by the water pressure is one of the reasons. But it is not the most important one. On account of the asymmetry of PFSCSs, imbalance torque caused by the IWP is an important factor affecting the closing time of the gap.
4.2 Stresses of steel materials
With the increase of the water pressure, the stresses of the steel materials change greatly. The steel materials involve the SSC and the steel bars. Figure 20 shows the comparisons of the max experimental and numerical results of steel stresses in cross-sections 1#, 3#, 5# and 7#. The cross-sections have been plotted in Figure 9.
Comparisons between the max experimental and numerical results of steel stresses of (a) SSC and (b) steel bars in Cross-section 1#, 3#, 5# and 7#.
As shown in Figure 20, the points in the diagram represent the experimental data and the lines represent the FEA results. The FEA results are found to be consistent with the experimental data. The mean absolute error is less than 5%.
The experimental and FEA results present a positive correlation between the steel stresses of the SSC and water pressure (Figure 20(a)). Two distinct inflection points can be found on the curves in Figure 20(a). The first inflection point occurs when the IWP is 1.4 MPa, which causes a change in the slope of the curves. This change can be explained by the gap between the SSC and the SMC. Because of the existence of the gap, the pressure is solely resisted by the SSC before the SSC comes into contact with the SMC. After the SSC is contact with the SMC, the pressure is resisted by the SSC as well as the SMC. The second inflection point occurs when the IWP is about 3.25MPa. At this point the concrete cracks begin to appear. The cracked concrete has no ability to withstand tensile stresses, which can be observed in Figure 21. Before the concrete cracks, the water pressure is supported by the concrete and the steel materials. After the concrete cracks, however, the water pressure is only supported by the steel materials in the cracked area. Thus, the stresses of the steel materials begin to accelerate.
For the steel bars, the FEA results agree well with the experimental results (Figure 20(b)). The stresses of the steel bars increase with the water pressure. As the concrete cracks, the pressure is transferred into the steel bars and the stresses of the steel bars begin to accelerate. Cracking of concrete leads to the inflection point.
4.3 Displacements of generator pedestal
Figure 22 shows the comparisons of the experimental and numerical calculated displacements of the generator pedestal and stay ring. Locations of the generator pedestal and stay ring are presented in Figure 11. The result shows that the displacements are consistent with experimental data. The mean absolute error is less than 2%.
The vertical displacements of the generator pedestal and the stay ring are mainly positive and increase with the water pressure. The water pressure causes the tension of the fixed guide vanes. Then the transmission of tension results in the uplift of the stay ring and the generator pedestal. The displacements of the generator pedestal and the top of the stay ring are greater than the bottom of the stay ring. When the water pressure reaches 1.4 MPa, the vertical displacements begin to increase. When the water pressure reaches about 3.25 MPa, the vertical displacements begin to increase rapidly. It can be seen that two distinct inflection points exist on the curves. The regularity is consistent with the abovementioned results in Section 4.2.
4.4 Cracks and damage values of concrete
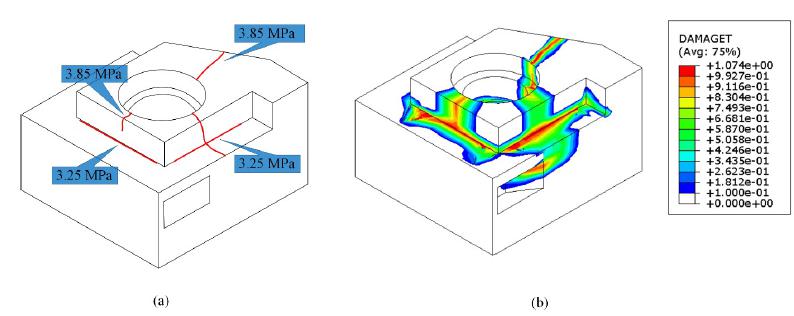
Figure 23 illustrates the major cracks and damage values of the reinforced concrete under the water pressure. Figure 23(a) represents the experimental results while Figure 23(b) represents the FEA results. In experimental investigation, the cracks were measured with crack width measuring instruments. In numerical analysis, the damage was simulated with a damaged plasticity model in Abaqus/Standard. Figure 23(a) gives the location and formation time of the cracks. Figure 23(b) presents the damage values of the concrete under the overload IWP.
From Figure 23 we can find that the damage values are consistent with the experimental cracks in the concrete. A few cracks begin to appear when the water pressure reaches 3.25 MPa. One of them is a radial crack, which appears at cross-section 3# and extends gradually from the inside to the outside of the generator support. Another one is a horizontal crack, which occurs at the intersection of the outer generator pedestal and the turbine floor. When the water pressure reaches 3.85 MPa, the number of cracks increases. New cracks appear in the inlet area of the SSC and the outside of the structure. The damage process and damage region in FEA results are similar to those in the experiments. The comparisons between the experimental and FEA results show that the novel NST is available for FEA of PFSCSs.
5 Conclusions
In this work, an experimental investigation and a numerical analysis have been carried out to research the non-uniform gap and contact nonlinearity between the SSC and the SMC in PFSCSs. A novel NST is proposed to accurately and conveniently describe the non-uniform gap and contact nonlinearity in PFSCSs.
In the technique, the non-uniform gap and contact nonlinearity as well as the complete simulation procedure of PFSCSs is taken into account. It overcomes the limitation of traditional technique neglecting the gap and contact behavior. In addition, the NST is an automatic simulation technique, in which the penetration of the nodes into the internal surface of the concrete can be avoided. The FEA results agree well with the experimental results. The agreement provides evidence that the applicability and competence of the proposed technique are valid and satisfactory.
The FEA with the novel NST reveals the early closing and delayed closing phenomena of the non-uniform gap and contact nonlinearity in PFSCSs. The closing time of the gap is not exactly the time when the water pressure is just equal to the temporary IWP, and the gap may not be completely closed when the water pressure reaches the temporary IWP. The phenomena significantly affect the structural performance of PFSCSs. The asymmetry of PFSCSs and the change of the boundary conditions caused by the removing of sealing devices are the key factors in affecting the closing time of the gap.
Acknowledgments
This paper was based on a study carried out by the authors at the State Key Laboratory of Water Resources and Hydropower Engineering Science and Changjiang River Scientific Research Institute. The authors are grateful to the National Natural Science Foundation of China (51679175, 51679013, 51609020, and 51409194) and the Basic Scientific Research Operating Expenses of Central-level Public Academies and Institutes (Changjiang River Scientific Research Institute CKSF2017067/GC).
References
- Aronson, A.Y., Bazhenov, V.A., Gotsulyak, E.A., Gulyaev, V.I., and Ogloblya, A.I. (1985). Nonlinear deformation of shells of the volute chambers of hydraulic turbines in an elastic medium. Strength of Materials, 17(4), 555-560.
- Cui, J.H. and Su, H.D. (2007). 3-D FEM emulation computation on surrounding concrete of steel spiral case keeping internal pressure during construction. Computational Mechanics, 286-286.
- Cicekli, U., Voyiadjis, G.Z., and Al-Rub, R.K.A. (2007). A plasticity and anisotropic damage model for plain concrete. International Journal of plasticity, 23(10-11), 1874-1900.
- Demir, A., Caglar, N., Ozturk, H. and Sumer, Y. (2016). Nonlinear finite element study on the improvement of shear capacity in reinforced concrete T-Section beams by an alternative diagonal shear reinforcement. Engineering Structures, 120, 158-165.
- EM 1110-2-3001 (1995). Planning and Design of Hydroelectric Power Plant Structures. Department of the Army, Washington, DC.
- Fu, D., Wu, H.G. and Hu, L. (2014). Gap closing and contact transferring mechanism in preloading filling spiral case of hydropower station. Journal of Huazhong University of Science & Technology, 42(7), 27-32.
- Grassl, P. and Jirásek, M. (2006). Damage-plastic model for concrete failure. International journal of solids and structures, 43(22-23), 7166-7196.
- Guo, T., Zhang, L.X. and Li, S.J. (2015a). Research on three-dimensional simulation algorithm of preloaded filling spiral case with non-uniform gap. Journal of Hydraulic Engineering, 46(12), 1434-1443.
- Guo, T., Zhang, L.X. and Wu, L. (2015b). Advance in research and application of preload filling spiral case structure in hydroelectric power plant. Journal of Kunming University of Science and Technology (Natural Science Edition), 40(3), 70-78.
- GB/T50080-2016 (2016). Standard for test method of performance on ordinary fresh concrete, Ministry of Housing and Urban-Rural Development of the People’s Repulic of China, Beijing, China.
- GB/T50081-2016 (2016). Standard for test method of mechanical properties on ordinary concrete, Ministry of Housing and Urban-Rural Development of the People’s Repulic of China, Beijing, China.
- Global B P (2017). BP statistical review of world energy. bp.com/statisticalreview.
- ISO 6892-1 (2016). Metallic materials -- Tensile testing -- Part 1: Method of test at room temperature
- Kalkani, E.C. (1995). Expected displacements and stresses in the encasing concrete of a Francis turbine scroll case. Computers and Structures, 55(4), 735-739.
- Lubliner, J., Oliver, J., Oller, S. and Onate, E. (1989). A plastic-damage model for concrete. International Journal of solids and structures, 25(3), 299-326.
- Mazars, J. and Pijaudier-Cabot, G. (1989). Continuum damage theory-application to concrete. Journal of Engineering Mechanics, 115(2), 345-365.
- Mazzucco, G., Salomoni, V.A., and Majorana, C.E. (2012). Three-dimensional contact-damage coupled modelling of FRP reinforcements-simulation of delamination and long-term processes. Computers & Structures, 110(2012), 15-31.
- Park, R., and Paulay, T. (1975). Reinforced Concrete Structures. John Wiley & Sons, New York, NY, USA.
- Spacone, E., and El-Tawil, S. (2004). Nonlinear analysis of steel-concrete composite structures: State of the art. Journal of Structural Engineering, 130(2), 159-168.
- Systèmes, D. (2013). Abaqus analysis user’s manual. Simulia Corp. Providence, RI, USA.
- Su, K., Yang, Z.J., Zhang, W., Wu, H.L., Zhang, Q.L., and Wu, H.G. (2017). Bearing mechanism of composite structure with reinforced concrete and steel liner: An application in penstock. Engineering Structures, 141(2017), 344-355.
- Tian, Z.Q., Zhang, Y.L., Ma, Z.Y. and Chen, J. (2008). Effect of concrete cracks on dynamic characteristics of powerhouse for giant- scale hydro station. Transactions of Tianjin University, 14(4), 307-312.
- Wu, H.G., Ma, S.D. and Bai, J.M. (2003). 2-D nonlinear analysis for the spiral case of Three Gorges Power Station. Journal of Hydraulic Engineering, 34(5), 57-61.
- Wu, H.G., Shen, Y., Jiang, K.C. and Shi J. (2012). Structural analysis of the embedded spiral case in the three gorges hydropower station. Practice Periodical on Structural Design & Construction, 17(2), 41-47.
- Wang, Y., Shi, C.Z., Wu, H.G., Zhang, Q.L., and Su, K. (2016). Flat-bottomed design philosophy of Y-typed bifurcations in hydropower stations. Structural Engineering and Mechanics, 57(6), 1085-1105.
- Xu, X.Y., Ma, Z.Y. and Zhang, H.Z. (2013). Simulation algorithm for spiral case structure in hydropower station. Water Science and Engineering, 6(2), 230-240.
- Zhang, C.H., and Zhang, Y.L. (2009). Nonlinear dynamic analysis of the Three Gorge Project powerhouse excited by pressure fluctuation. Journal of Zhejiang University-Science A, 10(9), 1231-1240.
- Zhang, Q.L., and Wu, H.G. (2012). Effect of compressible membrane's nonlinear stress-strain behavior on spiral case structure. Structural Engineering and Mechanics, 42(1), 73-93.
- Zhang, Q.L., and Wu, H.G. (2013). Using softened contact relationship describing compressible membrane in FEA of spiral case structure. Archives of Civil and Mechanical Engineering, 13(4), 506-517.
- Zhang, Q.L. and Wu, H.G. (2016). Sliding behaviour of steel liners on surrounding concrete in c-cross-sections of spiral case structures. Structural Engineering International, 26(4), 333-340.
- Zhang, Q.L., and Wu, H.G. (2017). Embedment of steel spiral cases in concrete: China's experience. Renewable and Sustainable Energy Reviews, 72, 1271-1281.
-
Available Online: July 17, 2018
Publication Dates
-
Publication in this collection
2018
History
-
Received
27 Apr 2018 -
Reviewed
15 June 2018 -
Accepted
16 July 2018