Abstract
In the present study, an analytical closed form solution for free vibration response of hybrid composite plate reinforced with shape memory alloy (SMA) fibers is derived. Recovery stresses generated during martensitic phase transformation are obtained based on one- dimensional Brinson's model. The mechanical properties of plate are assumed to be temperature dependent. Based on the first-order shear deformation theory (FSDT) the governing equations are obtained via Hamilton's principle. Ritz method is used to obtain the fundamental natural frequency of the plate for different temperatures. A detailed parametric analysis shows the strong influence of the volume fraction, pre-strain, orientation and location of SMA fibers as well as the aspect ratio of the plate on the fundamental natural frequency and the onset of the thermal buckling.
Keywords:
Laminated composite plate; First-order shear deformation theory; shape memory alloy fibers; free vibration
1 INTRODUCTION
The demand for the so-called smart materials which are sensitive to the environmental fluctuation is continuously increasing. Nitinol shape memory alloy, used in the current study, has two unique properties: shape memory effect (SME) and super elasticity. The former means returning back to the predetermined shapes upon heating. The latter is related to the large amount of inelastic deformation which can be recovering after unloading (Aguiar and Savi, 2013). Composites are being increasingly used in aerospace, marine and civil due to the advantages they offer. In order to avoid the resonant behavior, free vibration of the laminated structures should be analysed (Reddy et al., 2013).
Despite the continuous advances in composites with embedded SMA fibers, there are still many unsolved challenges in the field of free vibration. (Birman, 1997) compared the effect of composite and SMA stiffeners on the stability of composite cylindrical shells and rectangular plates which are subjected to compressive loads. It is shown that composite stiffeners are more efficient in cylindrical shells, whereas SMA stiffeners are preferable in plates or long shallow shells. (Lau, 2002) investigated the vibration characteristic of SMA composite beam considering different boundary conditions using Finite Element Method. They have demonstrated that increasing temperature in the composite beam with SMA fibers results in increasing the natural frequency and damping ratios of smart composite beams. (Park et al., 2006) investigated the effect of SMA on vibrational behavior of thermally buckled composite plate. The results depicted that SMA fibres have significant influence on increasing the critical buckling temperature. (Zhang et al., 2006) explored the vibrational characteristics of a laminated composite plate containing unidirectional fine SMA wires and laminated composite plates with embedded woven SMA layer experimentally and theoretically. They showed the influence of both SMA arrangement and temperature on the vibrational characteristics. (Kuo et al., 2009) used the Finite Element Method to study the buckling of laminated composite plate embedded with SMA fibers. According to their findings, the concentration of these fibers on the middle of plate improves buckling load. (Asadi et al., 2013-2014)proposed an analytical solution for free vibration and thermal stability of SMA hybrid composite beam. They found that increase of temperature can postpone the critical thermal buckling temperature of plate. (Malekzadeh et al., 2014) studied the effect of some geometrical and physical parameters on the response of free vibration of rectangular laminated composite embedded with SMA fibers. (Asadi et al., 2014) developed an analytical solution to obtain the post buckling behavior of geometrically imperfect composite plates embedded with SMA fibers. They illustrated that the SMA hybrid laminated plate is barely sensitive to the initial imperfections.
Studies on the free vibration of hybrid composites embedded with SMA fibers are mostly based on the approximated data derived from the experimental curves of an SMA. In this paper, obtaining the natural frequency of laminated composite plate embedded with SMA fibers is based on the Brinson's model for the SMA fibers and employing the Ritz method. In the present study, free vibration of laminated composite plate with shape memory alloy fibers is examined using the Ritz method. The influence of some geometrical and material properties on the free vibration response of the plate is investigated. The first-order shear deformation theory of plate is used to provide more accurate solution in comparison with classic theory of plate. The (Brinson, 1993) model is used to simulate the behavior of the SMA fibers.
2 GOVERNING EQUATIONS
2.1 Constitutive Modeling of Shape Memory Alloy Fibers
Several models which predict the behavior of SMA fibers are provided in literature. In the present study the simplified Brinson model which is a one dimensional model is used. According to this model, the total martensitic fraction is expressed as
Where ζ, ζs and ζT are used to describe total martensitic fraction, stress-induced martensitic fraction, and temperature induced martensitic fraction (Auricchio and Sacco, 1997). Young modulus of SMA fibers is defined as
EA and EM are the modulus of SMAs in the pure austenite and the pure martensitic fraction, respectively (Auricchio et al., 1997). The recovery stress can be calculated using the equation (3) (Brinson, 1996).
where ε, σ, Θ, ΔT, and εL are strain, stress, thermos-elastic tensor, temperature difference with respect to the reference temperature, and maximum residual strain of the SMA fibers, respectively. Calculation of the martensitic fractions during the heating stage constrained with T > As and CA(T-Af) < σ < CA(T - As)can be written as follows:
where the constant CA is the gradient of the curve of critical stress for the reverse phase transformation, and the initial state is expressed by 'O'. CA and Af are austenitic start temperature and austenitic finish temperature, respectively. Equations 3 and 4 must be solved simultaneously in each temperature to obtain the recovery stress and martensitic fraction (Brinson, 1993).
The recovery stress versus temperature has been reproduced by Brinson's model for various pre-strains. It is illustrated in figure 1. The slope of the curve reaches its largest amount in the phase transformation temperature of SMA fibers. It is depicted in figure 1 that increase of pre-strain will increase the recovery strain accordingly.
2.2 Constitutive Equations
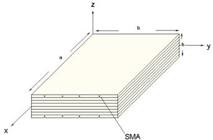
The length, width, and thickness of the hybrid composite plate are presented with a, b, and h, respectively. Laminated composite plate is reinforced with SMA fibers which are aligned with fibers of composite medium.
The multi-cell mechanics approach is employed to find the effective thermos-mechanical properties of hybrid plate (Chamis, 1983). Thermos-elastic properties are as follows
where subscript 'm' denotes matrix of composite and 's' represents SMA fibers. Furthermore, volume fraction of SMA fibers, Young modulus, shear modulus, Poisson ratio, thermal expansion coefficient in principal coordinate of the plate are represented as Vs,E,G, ν and α, respectively.
In the present study, FSDT is applied, and the displacement field is defined by
in which uo,vo and wo are displacements in the middle surface with assigning zero to z. Furthermore, Φx and Φy corresponds to the rotation of transverse normal of middle surface about y and x axes (Liew et al., 2004). Linear strains based on the displacements field shown in equation (6) are as follows
Considering ΔT as temperature change from reference temperature T0, constitutive law for hybrid composite can be written as follows (Asadi et al., 2014).
where parameters Mr,MT,Nr,NT, θk and σr are moment resultant induced by stress recovery, thermal moment resultant, resultant force induced by recovery stress, thermal resultant force, fiber orientation of kth layer and generated recovery stress, respectively.Aij,Bij,Dij and Qij are extensional, coupling, bending stiffness matrices and transformed reduced stiffness matrix of lamina in the principal coordinate of the plate, respectively. The components of these matrices are specified in equations (9) and (10).
Strain energy (U), kinetic energy (K) and work which is done by external forces (W) yields to the following equations (Reddy, 1997).
Where  denotes the resultant force obtained by applying the SMA fibers and uniform thermal loading. By substituting these equations into the Hamilton's principle (
denotes the resultant force obtained by applying the SMA fibers and uniform thermal loading. By substituting these equations into the Hamilton's principle ( (δU + δV - δK)dt = 0), equations of motion (12) can be derived.
(δU + δV - δK)dt = 0), equations of motion (12) can be derived.
The plate is assumed to be immovable simply supported in each edges.
3 RESULTS
The fundamental natural frequency of smart hybrid composite is computed by Ritz method. The plate is simply supported in each four edges. The harmonic series described in equation (14) are assumed in order to satisfy the essential boundary conditions of the plate
Applying the assumed functions in the energy functions and taking derivative with respect to the coefficients, the mass and stiffness matrices are formed. Then the eigenvalue problem can be solved to obtain the natural frequencies of the hybrid smart plate.
3.1 Comparative Study
To verify the results of proposed method, some comparative studies have been done. The obtained natural frequency of the composite plate is compared with results in (Asadi et al, 2014, Reddy, 1984, Senthilnathan, 1987, Whitney et al., 1970, Kant et al, 2001, Srikanth et al, 2003 and Shariyat, 2007). In the first experiment, a rectangular composite plate with simply supported boundary condition at four edges is considered. The stacking sequence is set to[0/ 90/ 90/ 0]. The properties and dimensions are given by

In Table 2,the result of dimensionless fundamental natural frequency parameter  is compared with (Reddy, 1984, Senthilnathan, 1987, Whitney et al., 1970, Kant et al, 2001 andSrikanth et al, 2003). The results is approximated by using the first 4 terms of equation (14).
is compared with (Reddy, 1984, Senthilnathan, 1987, Whitney et al., 1970, Kant et al, 2001 andSrikanth et al, 2003). The results is approximated by using the first 4 terms of equation (14).
Next, the obtained results for plate under thermal loading is compared with natural frequency of (Asadi et al, 2014), (Srikanth et al, 2003), and (Shariyat, 2007). Material properties are given in table 2. Table 3 compares the critical buckling temperature of eight-layered composite plate. Srikanth (2003) proposed a nonlinear method, while (Shariyat, 2007) used Hermitian finite element strategy, and results in (Asadi, 2014) are based on Galerkin procedure.
Since the model seems accurate in comparison with results of literature, the composite plate with shape memory alloy fibres is studied in the next part.
3.1 Parametric Studies
In this section the effect of various material and geometry parameters on the first natural frequency of a composite plate embedded with shape memory alloy fibers is studied. The material and geometrical properties are described in table 4 and 5, and the plate's dimensions are 0.1(m) x 0.1(m) x 0.002(m). The default values for stacking sequence of laminated composite plate and volume fraction of SMA fibers are [0/ 90/90/0/0/90/90/0] and 0.15, respectively. SMA fibers are aligned with Graphite fibers in the top and bottom most layer of laminated composite plate. The first dimensionless natural frequency is calculated as  .
.
where EA, EM,Mf, Ms,CM and αs areYoung modulus in austenite phase, Young modulus in martensite phase, martensitic start temperature, martensitic finish temperature, transformation constant, , thermal expansion coefficient of SMA.
3.1.1 Effect of Pre-Strain on the First Dimensionless Frequency
The effect of pre-strain on the first dimensionless frequency is depicted in figure 3. It can be concluded that the increase of pre-strain will leads to increase of natural frequency and critical temperature of thermal buckling. At the beginning of the curves, the frequency is less than that of a plate without SMA. Since SMA fibers are denser in comparison to the composite plate, they increase the mass. Then, the generated recovery stress increases the frequency. After completion of martensitic transformation phase of the SMA fibers, the increase of temperature results in decrease of stiffness which in turn leads to decrease of frequency.
Dimensionless fundamental natural frequency of plate for different pre-strains to SMA fibers versus Temperature.
Table 6 specifies the fundamental natural frequency (Hz) of laminated composite plate embedded with SMA fibers.
3.1.2 Effect of the Volume Fraction of SMA Fibers on Natural Frequency
As figure 4 demonstrates, from the reference temperature (20ºC) to 57ºC the frequency decreases and it is less than the frequency of the plate without SMA fibers. As it is shown, increasing the volume fraction of SMA fibers results in decrease of the frequency until 57ºC. On the other hand, generated recovery stress during phase transformation increases the natural frequency and critical temperature of thermal buckling after 57ºC.
Dimensionless fundamental natural frequency of plate for different volume fraction of SMA fibers versus Temperature.
3.1.3 Effect of Geometrical Properties of Plate
The fundamental natural frequency is computed for different length to width (a/b) ratios. Figure 5 shows the first dimensionless natural frequency versus temperature for both the plate with and without SMA fibers. Increase of length to width ratio for a constant length increases the rigidity of the plate, since the plate becomes like a beam with four supported edges, which in turn results in increase of the natural frequency. On the other hand, since SMA fibers are aligned with the length of the plate, with a constant volume fraction of the SMA fibers and decrease of cross section al area, the amount of SMA fibers decreases. Thus, the recovery stress becomes less than the required amount for increase of natural frequency. As the green curve illustrates, for a/b=2.5 the SMA fibers do not improve the natural frequency, instead, because of increase of them ass of the plate, they decrease the natural frequency.
Dimensionless fundamental natural frequency of plate for different aspect ratios of plate versus Temperature. Solid lines represent curves of composite plate with SMA fibers, while the dashed lines depict the behavior of composite plate without SMA fibers.
3.1.4 Effect of Changing the SMA Fibers' Location Through Thickness of the Plate
Changing the layers which contains SMA fibers might change the critical buckling temperature and the natural frequency. In order to avoid the influence of other parameters on the results, the plate is considered as an eight-layered composite plate with stacking sequence of [45]4s. Figure 6 depicts the effect of inserting SMA fibers in different layers on natural frequency and critical thermal buckling temperature. Inserting SMA fibers in top and bottom most layers results in more increase in the critical thermal buckling temperature and natural frequency of plate for temperaturas higher than 270ºC. On the other hand, putting them in other layers leads to more increase of natural frequency until 270ºC. This demonstrates that based on the application needs one of the two suggested options can be used.
Dimensionless fundamental natural frequency of plate for embedding SMA fibers in different layers of plate versus Temperature.
3.1.4 Effect of Changing the SMA Fibers Orientation
The stacking sequence is considered as[θ/ 90/ 45/ 0/ 0/ 45/ 90/ θ] where θ can be changed from 0 to 90 degrees, and the volume fraction of SMA fibers is 0.1 in the top and bottom most layers. In figure 7, the orientation of SMA fibers and graphite fibers is changed simultaneously. No specific pattern can be resulted with changing 0 and natural frequency of the plate for simultaneous change of orientation of SMA fibers and graphite fibers since they both affect the frequency of the plate. The reason of changing them simultaneously is that the resulting abrasion caused by the non-aligned SMA and graphite fibers will decrease the strength of the plate thus the SMA and graphite fibers should be aligned.
Dimensionless fundamental natural frequency of plate for orientation of SMA fibers versus Temperature.
4 CONCLUSIONS
In this paper, linear free vibration of hybrid laminated composite plates embedded with SMA fibers is studied. The one-dimensional Brinson's model is used for simulating the behavior of SMA fibers and the recovery stress generated in martensitic phase transformation. By employing first-order shear deformation theory and Hamilton's principle, governing equations are obtained. In addition, employing Ritz method leads to extracting the fundamental natural frequency of plate. Moreover, the influence of SMA fibers' volume fraction, pre-strain, orientation, embedding in different layers, and change of aspect ratio of plates are investigated. From the conducted experiments, the following main results can be drawn.
-
Inserting the SMA fibers increases the mass of the plate. However, there is no recovery stress in the temperatures below the martensitic phase transformation temperature to increase the stiffness and natural frequency of the plate. This in turn, decreases the natural frequency of the plate. On the other hand, in the temperatures above the martensitic phase transformation, inserting the SMA fibers in the plate increases critical thermal buckling temperature and natural frequency of the plate noticeably.
-
Increasing the pre-strain and volume fraction of SMA fibers will result in more increase of critical thermal buckling temperature and natural frequencies after the martensitic phase transformation temperature.
-
As the length to width ratio of the plate increases, the effect of SMA fibers decreases. SMA fibers are aligned with the length of the plate. Hence, for constant length, decrease of plate width will decrease its cross section. Thus, for a constant volume fraction of SMA fibers, the rectangular plate has less SMA fibers than the square plate with the same length. Having less SMA fiber will result in less stress recovery and less increase in critical thermal buckling and natural frequency of the plate.
REFERENCES
- Aguiar, R.A.A., Savi, M.A., Pacheco, P.M.C.L., (2013). Experimental investigation of vibration reduction using shape memory alloys. Journal of Intelligent Material Systems and Structures. 24(2): 274-61.
- Asadi, H., Bodaghi, M., Shakeri, M., Aghdam, M.M. (2013). An analytical approach for nonlinear vibration and ther- mal stability of shape memory alloy hybrid laminated composite beams. European Journal of Mechanics. 42: 454-68. Asadi, H.,
- Asadi, H., Bodaghi, M., Shakeri, M., Aghdam, M.M. (2014). Nonlinear dynamics of SMA-fiber-reinforced composite beams subjected to a primary/secondary-resonance excitation. Acta Mechanica. 226: 437-455.
- Asadi, H., Kiani, Y., Shakeri, M., Eslami, M.R. (2014). Exact solution for nonlinear thermal stability of hybrid lami- nated composite Timoshenko beams reinforced with SMA fibers. Composite Structures. 108: 811-22.
- Asadi, H., Eynbeygi, M., Wang, Q. (2014). Nonlinear thermal stability of geometrically imperfect shape memory alloy hybrid laminated composite plates. Smart Materials and Structures. 23: 1-13.
- Auricchio, F., Sacco, E (1997). A one-dimensional model for superelastic shape memory alloys with different elastic properties between austenite and martensite. International Journal of Non-Linear Mechanics. 32: 1101-14.
- Birman, V., (1997). Theory and comparison of the effect of composite and shape memory alloy stiffeners on stability of composite shells and plates. International Journal of Mechanical Sciences. 39: 1139-49.
- Bodaghi, M., Shakeri, M., Aghdam, M.M. (2013). On the free vibration of thermally pre/post-buckled shear deformable SMA hybrid composite beams. Aerospace Science and Technology. 31: 73-86.
- Brinson, L.C. (1993). One-dimensional constitutive behavior of shape memory alloys: thermomechanical derivation with non-constant material functions and redefined martensite internal variable. Journal of Intelligent Material Systems and Structures. 7: 229-42.
- Brinson, L.C., Huang, M.S. (1996). Simplifications and comparisons of shape memory alloy constitutive models. Journal of Intelligent Material. 7: 108-14.
- Chamis, C.C. (1983). Simplified composite micromechanics equation for hygral, thermal and mechanical properties. NASATM-83320.
- Duan, B., Tawfik, M., Goek, S., Ro, J., Mei, C. (2000). Analysis and control of large thermal deflection of composite plates using shape memory alloy. SPIE's 7th International Symposium on Smart Structures and Materials, Newport Beach, CA, USA. 3991: 358-65.
- Kant, T., Swaminathan, K. (2001). Analytical solutions for free vibration of laminated composite and sandwich plates based on a higher-order refined theory. Composite Structures. 53: 73-85.
- Kuo, S.Y., Shiau, L.C., Chen, K.H. (2009). Buckling analysis of shape memory reinforced composite laminates. Com- posite Structures. 90: 188-95.
- Lau, K.T., (2002). Vibration characteristics of SMA composite beams with different boundary conditions. Materials and Design. 23: 741-49.
- Liew, K.M., Yang, J., Kitipornchai, S. (2004). Thermal post-buckling of laminated plates comprising functionally graded materials with temperature-dependent properties. Journal of Applied Mechanics. 71(6): 839-50.
- Malekzadeh, K., Mozafari, A., Ashenai Ghasemi, F. (2014). Free vibration response of a multilayer smart hybrid composite plate with embedded SMA wires. Latin American Journal of Solids and Structures. 11: 279-98.
- Park, J.S., Kim, J.H., Moon, S.H., (2004). Vibration of thermally post-buckeld composite plates embedded with shape memory alloy fibers. Composite Structures. 63: 179-88.
- Reddy, J.N. (1984). A simple higher order theory for laminated composite plates. ASME Journal of Applied Mechanics. 51(4): 745-52.
- Reddy, J.N. (1997). Mechanics of laminated composite plates and shells theory and analysis. 2nd Edition. CRC PRESS.
- Reddy, B.S., Reddy, M.R.S., Reddy, V.N., (2013). Vibration analysis of laminated composite plates using design of experiments approach. International Journal of Engineering. 2: 40-49.
- Senthilnathan, N.R., Lim, K.H., Lee, K.H., Chow, S.T. (1987). Buckling of shear deformable plates. AIAA journal. 25: 1268_71.
- Shariyat, M. (2007). Thermal buckling analysis of rectangular composite plates with temperature-dependent properties based on a layer wise theory. Thin-walled Structures. 45: 439-52.
- Srikanth, G., Kumar, A. (2003). Post buckling response and failure of symmetric laminates under uniform temperature rise. Composite Structures. 59: 109-18.
- Whitney, J.M. and Pagano, N.J. (1970). Shear deformation in heterogeneous anisotropic plates. ASME Journal of Applied Mechanics. 37: 1031-36.
- Zhang, R., Ni, Q.Q., Masuda, A., Yamamura, T., (2006). Vibration characteristics of laminated composite plates with embedded shape memory alloys. Composite Structures. 74(4): 389:98.
-
Erratum
In the article Free Vibration of Laminated Composite Plate with Shape Memory Alloy Fibers, published in volume 13, number 2, 2016:In the part of authors:M. DaneshpazhoohcShould read:M. Danesh PazhoohcThe affiliation of all three authors:Amirkabir University of technology (Tehran Polytechnic)Should read:AmirKabir University of Technology (Tehran Polytechnic)In the first line of the last paragraph of the page 322:In Table 2, the result of first dimensionless fundamental natural frequency parameter...Should read:In Table 2, the result of dimensionless fundamental natural frequency parameter...In the third line of the first paragraph of the page 323:Strikanth (2003)Should read:Srikanth (2003)In the Table 2 of the page 323:(Strikanth et al,2003)Should read:(Srikanth et al,2003)In the header of the forth column in the Table 3 of the page 323:Strikanth (2003)Should read:Srikanth (2003)
Publication Dates
-
Publication in this collection
Feb 2016
History
-
Received
27 May 2015 -
Reviewed
08 Nov 2015 -
Accepted
08 Nov 2015

 Free Vibration of Laminated Composite Plate with Shape Memory Alloy Fibers
Free Vibration of Laminated Composite Plate with Shape Memory Alloy Fibers




















 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail









