Abstract
The floor pan is an important component that connects the front and rear segments of the automotive underbody structure. Global stiffness and NVH characteristics of BIW are highly dependent to shape, thickness and mass of the body panels and could be evaluated by modal characteristics of these panels. The feeling of solidness and comfort of passengers in an automotive is also dependent to the modal behavior of the underbody components as well as the floor pan. On the other hand, it is desired to reduce the total mass of the floor pan, in order to have a lighter vehicle with better fuel economy and emission standards. In this paper, the effect of geometrical parameters on natural frequency and total mass of the floor pan of a conventional B-Segment automotive body is investigated using finite element simulation. The finite element model is verified using an experimental test on the floor pan. Taguchi L 16 orthogonal array is used to design the numerical experiments. Subsequently, S/N ratio analysis is performed to evaluate the effect of each design variable on the output functions. The panel's thickness is determined to have the most contribution in affecting the natural frequency and weight using Analysis of Variance (ANOVA). The best combination of geometrical variables which leads to the trade-off results is then figured out by a new multi-criteria decision making (MCDM) method developed in this study. Accuracy of this method is verified by comparing the trade-off results with TOPSIS, as a conventional MCDM method.
Keywords:
Floor pan; modal; natural frequency; Taguchi; MCDCM; SVCB
1 INTRODUCTION
Statistics has reported a growing rate of automotive manufacturing in the last two decades Kline (2016)Steve Kline, J. (March 2016). Automotive Production Growth Strong. Plastics Technology.. Furthermore, growth in global automotive production is likely to remain at around 4% per year in the future years and the production is expected to exceed 100 million vehicles by 2017 Economic Outlook (2014)The global automotive market. (2014). Economic Outlook, 1210, 1-20.. This breathtaking volume of production requires an extremely high level of industrial and management technology to remain in the highly competitive market of automotive manufacturing. This is not possible unless they employ efficient design and manufacturing techniques. Today, Computer-Aided Engineering (CAE) is known as a necessary technique which helps the engineers to remarkably save time and money in the design and manufacturing process. In the recent years, a wide range of studies have been carried out to develop Finite Element (FE) analyses as alternatives of the experimental conventional procedures of automotive design such as (Noise, Vibration and Harshness) NVH Sobieski et al (2001)Sobieszczanski-Sobieski, Jaroslaw, Srinivas Kodiyalam, R.Y. Yang. (2001). Optimization of car body under constraints of noise, vibration and harshness (NVH) and crash. Structural and Multidisciplinary Optimization, 22 (4), 295-306., safety Shin et al (2012)Shin, Jaeho, Neng Yue and Costin D.Untaroiu. (2012). A finite element model of the foot and ankle for automotive impact applications. Annals of Biomedical Engineering, 40 (12), 2519-31. and strength Palmonella et al (2005)Palmonella, Matteo, Michael l. Friswell, John E. and Arthur W, Lees. (2005). Finite element models of spot welds in structural dynamics: review and updating. Computers & Structures, 83 (8), 648-61..
Stiffness is a crucial attribute in design process of every road vehicle. Previous studies have been carried out to investigate the effects of automotive body stiffness on vehicle dynamic characteristics. These investigations have demonstrated that the overall response of the vehicle is improved with a stiffer body due to stiffer connection between front and rear components Krishnan (2011)Krishnan, H. (2011). Establishing correlation between torsional and lateral stiffness parameters of BIW and vehicle handling performance. SAR International Journal of Passenger Cars, 4, 22-31.. The stiffer a road vehicle's body, the better ride, handling and NVH performance is obtained Chaturved et al (2010)B. Chaturved, D. Rana and M. Ravindran. (2010). Correlation of vehicle dynamics & NVH performance with body static & dynamic stiffness through CAE and experimental analysis. SAE World Congress and Exhibition, 1-8.. The overall stiffness of a road vehicle depends on the local stiffness of the constituent parts Chaturved et al (2010)B. Chaturved, D. Rana and M. Ravindran. (2010). Correlation of vehicle dynamics & NVH performance with body static & dynamic stiffness through CAE and experimental analysis. SAE World Congress and Exhibition, 1-8.. Hence, the target of stiffening a vehicle's body is automatically cascaded to a set of new targets: stiffening the constituent parts of the Body in White (BIW). The overall stiffness of BIW is remarkably affected by the floor panel. This is why the stiffness of this part of automotive body is specially focused by researchers in the last two decades Mohan Kumar et al (2015)Mohan Kumar, G.R., Maruthi, B.H., Chandru B.T. Manoranjan,S.N. (2015). Vibration analysis of automotive car floor using FEM and FFT analyzer. International Journal for Technological Research in Engineering, 2 (11), 2891-96.. A conventional approach to judge about stiffness of the floor panel is vibration analysis Mignery (2016)Mignery, L. A. (n.d.). Quiet steel body panel design with DAMP- A custom preprocessor utilizing MSC-PATRAN/NASTRAN. Retrieved from https://web.mscsoftware.com/support/library/conf/auto00/p03700.pdf
https://web.mscsoftware.com/support/libr...
. Due to the direct relation between the natural frequencies and stiffness, the higher the natural frequency, the stiffer structure of the panel is expected.
Geometric parameters of the floor pan affect the natural frequency and subsequently, the stiffness of this component Suh et al (2007)Suh,E. Weck,O. Kim,Y. Chang,D. (2007). Flexible platform component design under uncertainty. Journal of Intelligent Manufacturing, 18, 115-26.. It is important for automotive design engineers to find information about the effect of each geometrical variable of the floor pan on the natural frequency. Parametric study of the floor pan's vibration is important from two points of view: 1- Sensitivity of the natural frequencies with respect to each of the geometrical variables; 2- To obtain a set of geometrical variables leading to the highest natural frequencies.
On the other hand, weight reduction is an important task in automotive engineering which usually has conflict with stiffening the structure. Therefore, a compromised solution is required to have a road vehicle with light weight and high stiffness simultaneously. Finding the best combination of geometrical design variables leading to the highest natural frequencies and subsequently the stiffest design of the floor pan, is a time-consuming and tiresome process using traditional trial and error methods of design, due to the large number of possible combinations of the design variables. Hence, it is more efficient and more scientific to employ one of the engineering optimization methods in this situation. As a widely used technique in engineering optimization, Taguchi method developed by Taguchi et al (1987)Taguchi G., Konishi S. (1987). Taguchi methods, orthogonal arrays and linear graphs, tools for quality. Ammerican Supplier Institute, 8-35. has been proved to be a handy and efficient approach in engineering analyses to optimize the performance characteristics within the combination of design parameters. Taguchi technique is also a conductive asset for finding the best parameter design leading to high quality and robust systems. It provides an integrated approach that is simple and efficient to find the best design considering quality, performance and computational cost. Several applications of this method in the engineering optimization problems including aerospace Mathan Kumar (2016)N. Mathan Kumar, S.S.. (2016). Aerospace application on Al 2618 with reinforced - Si3N4, AIN and ZrB2 in-situ composites. Journal of Alloys and Compounds, 672, 238-50., mechanical engineering Parvin Kumar et al (2016)Parvin Kumar, Singh D. Patel S.B. Parsad. (2016). Optimization of process parameters during vibratory welding technique usin Taguchi's analysis. Perspectives in Science, Accepted Manuscript. and automotive engineering P. Senthil Kumar (2013)P. Senthil Kumar, R. Kalidas, K. Sivakumar, E. Hariharan, B. Gautham, R. Ethiraj. (2013). Application of Taguchi method for optimizating passenger- friendly vehicle suspension system. International Journal of Latest Trends in Engineering and Technology, 2 (1). could be found in the literature.
Sun et al (2015)Guangyong Sun, Jiang Fang, Xuanyi Tian, Guangyo Li, Qing Li. (2015). Discrete robust optimization algorithm based on Taguchi method for structural crashworthiness design. Expert Systems with Applications, 42, 4482-92. used Taguchi method to explore how to maximize the crashworthiness of the hybrid steel-aluminum tailor welded structures involving uncertainties. The optimal results showed that Taguchi method is successful not only to reduce the peak force, but also to improve the absorbed energy of impact. Furthermore, the robustness of these two indicators was also significantly enhanced. P. Senthil Kumar et al (2013)P. Senthil Kumar, R. Kalidas, K. Sivakumar, E. Hariharan, B. Gautham, R. Ethiraj. (2013). Application of Taguchi method for optimizating passenger- friendly vehicle suspension system. International Journal of Latest Trends in Engineering and Technology, 2 (1)., used Taguchi method for optimizing a vehicle's suspension system. They presented an optimum concept to design a passenger- friendly vehicle suspension system. Using Analysis of Variance (ANOVA) sensitivity analysis, they also found that the stiffness of absorber and seat spring are the most significant parameters which affect the seat displacement. Wang Mingqi et al (1997)Wang,M. Guodong, J. (1997). The application of Taguchi method to the stiffness improvement of a double- decker structure. International Journal of Materials and Product Technology (4-6). used Taguchi method to maximize the stiffness of a full structure double-decker finite element model. As a result of this study, they improved the torsional stiffness by 20% and the bending stiffness by 23.3%. This study verified that the Taguchi method is effective in improving the stiffness of a vehicle. But a full road vehicle is made up by more than 300 distinct components which each part's stiffness is influenced by several geometrical and mechanical parameters. Therefore, it is a cumbersome, time consuming and costly process to optimize the stiffness of all of these components separately. A good approach is to identify the key components which have the most contribution in the global stiffness of the vehicle. One of these key components is the car's floor pan Mohan Kumar et al (2015)Mohan Kumar G R, Dr. Maruthi B H, Chandru B T, Manoranjan S N. (2015). Vibration analysis of automotive car floor using FEM and FFT analyzer. International Journal for Technological Research in Engineering, 2 (11), 2891-96..
In this paper, floor pan of a B-segment automotive is selected as a key part which plays an important role in total stiffness of a full body vehicle. A geometrical set of parameters is considered as design variables which affect the natural frequency and subsequently the stiffness of the structure. It is desired to find the best combination of these design variables leading to the highest natural frequency and the lowest weight of the floor pan. This is never possible for more than one conflicting objectives such as stiffness and weight to have the best values simultaneously. For this purpose, a hybrid method of Taguchi and a new Multi Criteria Decision Making (MCDM) method is developed and used to find the best compromising solution of this case. In the first step, model of the floor pan of a B-segment automotive is developed. A verification of the model and simulation method, as an effective method used in this paper to perform a set of experiments, is carried out using an experimental test on the real floor pan. Then, Taguchi method is employed to design a set of experiments with four geometrical parameters and four levels for each parameter. Design of experiment (DOE) is performed using Taguchi's L 16 orthogonal array. Signal to Noise (S/N) ratio analysis is then carried out; and as a result of this analysis, variations of the output functions with respect to the design variables are determined. ANOVA is then carried out to find the contribution percentage of each control factor in the output functions. In the next step, an MCDM method is needed to choose a trade-off design among 16 design vectors. A new MCDM method is developed in this paper which is able to find the best combination of design variables leading to optimum values of the weighted objective functions. This method is based on summing percentages of variations in the objective functions comparing to the initial solution. Finally, these results are compared to the results found by a conventional MCDM method.
2 EXPERIMENTAL MODAL ANALYSIS
In this section, details of the modal experiment on the prototype of the research case are reported. The research case is the floor pan of NP01 (Natural platform project), a B-segment automotive product family which is under development in Automotive department of Iran University of Science and Technology. The aim of this experiment is to validate the results of the FE modeling and simulation (Section 3) with the real values.
2.1 Experiment Specimen
A prototype of the floor pan is produced and submitted to modal experimental test as shown in Figure 1. The fabrication method is stamping by soft tools, drawing operation and trimming is carried out by laser cut. The experiment details are explained as follows.
2.2 Impact Testing
A roving hammer test is the most common type of modal analysis test. An accelerometer is fixed at a Single Degree of Freedom (DOF), and the structure is subjected to impacts at as many DOFs as desired to define the mode shapes of the structure. Using a two channel Fast Fourier Transform (FFT) analyzer, Frequency Response Functions (FRFs) are computed between each impact DOF and the fixed response DOF. A suitable grid is usually marked on the structure to define the impact points.
It is generally impossible to impulse a structure in all three directions at all points, so three-dimensional (3-D) motion cannot be measured at all points. When 3-D motion at all points is desired, a roving tri-axial accelerometer may be used and the structure is excited at a fixed DOF with the hammer. However, tri-axial accelerometers are usually more massive. Since the tri-axial accelerometer must be simultaneously sampled together with the force data, a four-channel FFT analyzer is required. Note, however, that the roving accelerometer presents a different mass-load to the structure at each response site. This can lead to inconsistencies in the data that makes more difficult to find an accurate curve fit.
Because the impulse signal exists for such a short period, it is important to capture all of it in the sampling window of the FFT analyzer. To ensure that the entire signal is captured, the analyzer must be able to capture the impulse and the response signals prior to the occurrence of the impulse. The analyzer must begin sampling data before the trigger point occurs. This is called a pre-trigger delay.
It is important that the impact hammer provides a pulse that is well matched to the frequency span of the analysis. This is accomplished by fitting a striking tip of appropriate stiffness to the hammer's force gauge. A soft tip produces a broad pulse time-history with a narrow spectrum. A hard tip increases the force spectrum bandwidth by applying a narrow pulse. The spectrum of the force pulse has a lobed structure and all tests are done using the spectral content of the first lobe. Because the biggest portion of excitation energy is created in the first lobe and the frequency spectra which is excited in this lobe is in the order of several hundred Hz. So, it is not required to consider the next lobes. Trial measurements are made to select a tip that provides a force spectrum that falls off no more than 25 dB from the direct-current (DC) point to the selected analysis bandwidth.
In this research, the charge type hammer has been used to excite the frame. To cover frequency ranges of interest, a rubber tip has been utilized. Excitation point has been selected so that the maximum mode shapes could be obtained (It must not be on the nodal points of any mode of interest). In order to reduce the noises in the measurements, each of the stage results have been obtained by averaging 10 measurements of the same kind.
2.3 Test Equipments
Equipment used during the modal test is listed as below:
Multi-channel data acquisition system, Difa Measuring System, Type ScadasII
Impact Hammer (charge type), Type 8202, B&K
Force Transducer, 208B03, PCB
Tri- directional accelerometers, type 356 A11, PCB
Thermometer, CEWAL CO; Type 11/98-L
Hygrometer, TFA CO.
LMS CADA-X (The post-processing software for the experimental test)/ FMON (Fourier monitor module of LMS CADA-X).
LMS CADA-X/ Modal Analysis (The modal analysis module of LMS CADA-X)
2.4 Test Conditions
As an overall rule to find the natural frequencies of a system, it is required that the stiffness of suspension be about 10 times higher than the first natural frequency of the system. This matter is checked before any experiment in the modal laboratory Ewins (1984)Ewins, D. J. (1984). Modal testing: theory and practice (Vol. 15). Letchworth: Research studies press.. The frame was suspended using cables having the elasticity suitable enough for the natural mode extraction as depicted in Figure 1. In order to get first 4 natural frequencies of the panel, 48 points were marked on it for accelerometers installation locations. A schematic image of the points where accelerometers are mounted is shown in Figure 2. A geometrical model of the system was created using six coordinates required for each node. Each node corresponds to a point on the panel. The tri-directional accelerometers were attached to these points.
2.5 Obtaining Modal Parameters
Most experimental modal analysis relies on modal parameter estimation (curve-fitting) technique to obtain modal parameters from the FRFs. Curve fitting is a process of matching a mathematical expression to a set of experimental points by minimizing the squared error between the analytical function and the measured data. Multiple-degrees-of-freedom (MDOF), global, and multi-reference methods can estimate modal parameters for two or more modes at a time Ewins (1984)Ewins, D. J. (1984). Modal testing: theory and practice (Vol. 15). Letchworth: Research studies press..
Here, the most general purpose parameter estimation technique called Time Domain MDOF Analysis has been used LMS theory and background (2000)LMS theory and background (2000), LMS International 2000.. It provides a complete and accurate modal model from single input multiple output frequency response functions. It uses global estimators; this means that it analyzes all the data records simultaneously in order to estimate the structure's characteristics. With this approach, a unique estimation of the pole values (natural frequencies) has been obtained.
3 FINITE ELEMENT ANALYSIS
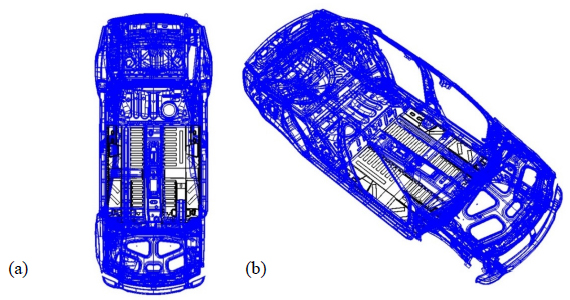
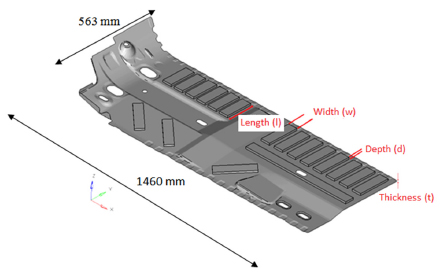
Position of the floor pan in the BIW is shown in Figure 3. Furthermore, the geometrical shape and overall dimensions of the floor pan are shown in Figure 4. Geometrical details of the basic model of the floor pan are presented in Table 1.
Position of the left and right floor pans (symmetric) in the wireframe preview of BIW of NP01 project. (a) Top view (b) Isometric view.
Steel is considered as the constituting material of the panel with mechanical properties of ρ = 7800kg/m3, E = 210GPa and v =0.3 Sun et al (2015)Guangyong,S. Jiang,F. Xuanyi,T. Guangyo,L. Qing,L. (2015). Discrete robust optimization algorithm based on Taguchi method for structural crashworthiness design. Expert Systems with Applications, 42, 4482-92.. The boundary edges of the model are supposed to be free. Due to the low aspect of thickness to the other dimensions, the complex 3D model is replaced by 2D shell elements. As a result of a mesh independence investigation, the model is divided by 6309 elements including 5966 quadratic and 343 triangular elements (about 5%). In the basic model, thickness of the panel is considered to be 0.65mm by benchmarking in the concept design phase.
A modal analysis is performed to obtain the main natural frequencies and corresponding mode shapes. The first four natural frequencies of the floor pan's basic model are reported in Table 2.
First four natural frequencies of the floor pan's basic model of NP01 project found by FEM and Experiment.
3.1 Experimental Results and Validation of the FE Model
First four natural frequencies of the floor panel found by the experiment are listed in Table 2. A comparison with the FEM results shows the maximum and average difference of 4.2% and 2.67% respectively. A good accordance between the frequency results is observed. But this comparison is not enough to make sure about consistency of the mode shapes found by experiment and FEM. Hence, the MAC criterion is used to compare the first four mode shapes. The MAC has been used in the literature as a Mode Shape Correlation Constant to quantify the accuracy of identified mode shapes Pastor et al (2012)Pastor, M., Binda, M., & Harčarik, T. (2012). Modal assurance criterion. Procedia Engineering, 48, 543-548.. For complex modes of vibration the MAC value is found by:
Table 3 shows the CrossMAC matrix calculating the MAC between the test model and the FEM model. The values close to 1 show a good accordance between the mode shapes and the values close to one state that there is almost no accordance between the corresponding mode shapes. As it is obvious in the Table, the diagonal values are close to one and demonstrate the good accuracy of the simulation method.
Therefore, the finite element model and simulation method are accurate along with a reasonable difference.
4 PARAMETRIC STUDY
4.1 Design of Experiment by Taguchi Method
In this section, four geometrical parameters are considered as the design variables affecting two output functions: first natural frequency and total mass of the floor pan. These design variables are show in Figure 4. Based on design and production restrictions, the upper and lower bound for variations of the design variables are supposed as follows:
where t is the thickness of the panel and w, l and d are the width, length and depth of the panel's embosses. The higher the number of levels, the lower effects of nonlinearity error in the parametric study becomes Ranjit et al (2001)Ranjit, K. (2001). Roy. Design of experiments using the Taguchi approach. John Willey & Sons Inc., New York.. However, four levels of variations are considered for each variable based on time and financial resources including t (0.65, 0.8, 0.9, and 1.2), w (20, 30, 40, and 48), l (80, 103, 143, and 173), and d (2, 5, 10, and 15). Values of the four variables corresponding to each level are summarized in Table 4.
The total number of possible combinations of these variables according to number of levels and variables is equal to 256. In Taguchi method two main parameters are needed to be specified. First is control factor or the vector of design variables; another is the noise factor that denotes all factors that cause variation. Taguchi proposed orthogonal arrays to acquire the attribute data and to analyze the performance measure of the data to decide the optimal process parameters Senthil Kumar [14]. In this study, L 16 orthogonal array is employed. This array is suitable for the cases with four design variables and four levels for each design variable Ranjit et al (2001)Ranjit, K. (2001). Roy. Design of experiments using the Taguchi approach. John Willey & Sons Inc., New York.. The total number of experiments is 16 and the corresponding configuration of the experiments is shown in Table 5 (S/N ratio in this table is described in the next section).
Modal results and S/N ratio analysis of the set of experiments proposed by Taguchi L 16 orthogonal array.
4.2 S/N ratio analysis
S/N ratio is an index which describes the signals to noise ratio in the Taguchi method. Signal and noise refer to mean (desirable) and standard deviation (undesirable) values of the output respectively. In reality, the target functions will be never fixed in a desired value. Hence, there are always fluctuations around the desired (mean) value which depend on external factors such as human errors and temperature effects; these uncontrollable factors are named as noise factors. The S/N ratio characteristics are classified into three categories based on the final decision on the performance:
Case 1: "Smaller is the better"
This case is valid when minimizing the output function is desired.
Case 2: "Nominal is the best"
This case is valid when the nominal or target value and variation about that value are minimized.
Case 3: "Larger is the better"
This case is valid when maximizing the output function is desired.
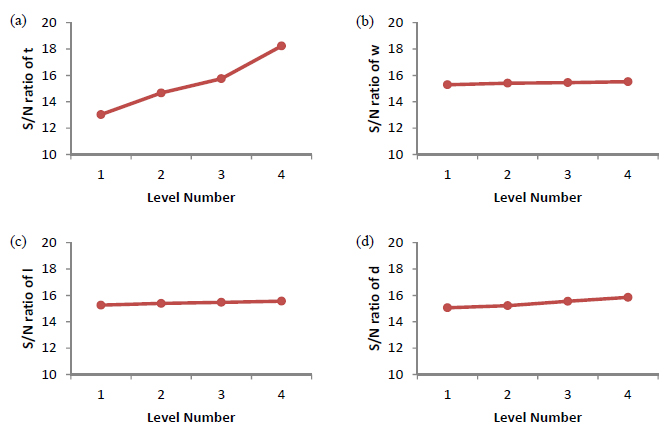
In the above equations, N represents the number of repetition of each experiment and y denotes the objective function. In the present study, the natural frequency of the floor pan is desired to make maximized and the total mass of the panel is supposed to make minimized. Therefore, the third case is suitable for maximizing frequency and the first case is desired to minimize the total mass of the panel. S/N ratio analysis results are presented in Table 5. Moreover, the graphical figures corresponding to S/N ratios of the first and second natural frequency and total mass with respect to the four design variables are depicted in Figures 5-7. Clearly, higher S/N ratios have led to the higher natural frequencies and higher weights. A big conflict is observed between the objective functions. First, let's consider three separate cases:
Signal to noise ratio graphs of the first natural frequency with respect to the four design variables in four different levels is shown in four sub-figures respectively.
Signal to noise ratio graphs of the second natural frequency with respect to the four design variables in four different levels is shown in four sub-figures respectively.
Signal to noise ratio graphs of the total mass with respect to the four design variables in four different levels is shown in four sub-figures respectively.
Case I: If the first natural frequency is considered as a single objective function in this study, among the 16 cases of experiment, the last case has better results due to the higher natural frequency and S/N ratio. Table 6 shows the S/N ratio corresponding to each design variable in different levels. Based on this table and Figure 5 as well, the highest value of S/N ratio among all of the design variables is related to the fourth level. Therefore, the best combination of the design variables leading to the highest value of first natural frequency is predicted to be A 4 B 4 C 4 D 4. According to Figure 5, thickness (t) with the sharpest slope is the most significant factor which affects the natural frequency. Secondly, the depth (d) is more important than the two other variables. The other fact observed in this figure is that variations of depth (d) will not have any significant effects on the natural frequency after the third level of depth.
S/N ratio response of the first natural frequency in different levels of control parameters.
Case II: If the second natural frequency is considered as a single objective function, among the 16 cases of experiment, the last case has better results due to the higher natural frequency and S/N ratio. Table 7 shows the S/N ratio corresponding to each design variable in different levels. S/N ratio analysis respect to different design variables, suggests a design which shows better results even compared to the 16th design of Taguchi. Based on Table 7 and Figure 6 as well, the highest value of S/N ratio respect to thickness, width and depth of the embossments is related to the fourth level. Furthermore, the highest S/N ratio respect to length of the embossments is related to the third level. Therefore, the best combination of the design variables leading to the highest value of second natural frequency is predicted to be A 4 B 4 C 3 D 4. This design combination could not be found among the 16 design vectors proposed by Taguchi. According to Figure 6, thickness (t) with the sharpest slope is the most significant factor which affects the natural frequency. Secondly, the depth (d) is more important than the two other variables.
S/N ratio response of the second natural frequency in different levels of control parameters.
Case III: If the total mass of the panel is considered as a single objective function in this study, among the 16 cases of experiment, the first case (base model) has better results due to the lower mass and S/N ratio based on the results shown in Table 8. On the contrary, the last case has led to the worst results. According to Figure 7 and Table 8, S/N ratio analysis shows that thickness (t) and depth (d) are the most effecting parameters on the mass of the panel. But this effect is in the opposite way compared to the natural frequency; meaning that due to the mass growth, it is not desired to increase the thickness and depth of the emboss.
According to this conclusion, a big conflict is apparent between the first and second natural frequency and the total mass of the floor pan. In this situation, a good solution is using MCDM methods to find the best combination of the design variables leading to the trade-off values of the objective functions. An MCDM investigation is carried out in Section 5.
4.3 Analysis of Variance (ANOVA)
As verification for the S/N ratio results, ANOVA is performed to determine the effect of different design parameters on the output variables. Furthermore, contribution percentage of each control factor is determined from the results of this analysis. As seen, there is a statistical tool called an F test to see which design parameters has a significant effect on the quality characteristic. Usually, when F > 4, it means that the change of the design parameter has a significant effect on the quality characteristic Khalkhali. A, Noraei. H et al (2016)Khalkhali, A., Noraie, H., & Sarmadi, M. (2016). Sensitivity analysis and optimization of hot-stamping process of automotive components using analysis of variance and Taguchi technique. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 0954408916633491.. The higher the F-test result, the more contribution percentage in affecting the quality characteristics is expected. The results of this analysis are provided in Tables 9-11 for the first natural frequency, second natural frequency and mass respectively. As it is anticipated from Section 4.2 (S/N ratio analysis), the panel's thickness is the most effective parameter on the first and second natural frequency and mass with F-test values of 11.2, 11.03 and 142.14 respectively. Comparing to the first natural frequency, the total mass is more sensitive to the variations of the panel's thickness according to the F-test results. After that, the depth of emboss (d) has the highest response of F-test equal to 0.83, 0.99 and 0.09 for the first natural frequency, second natural frequency and mass respectively. This conclusion is completely approving the results found by the S/N ratio analysis. Additionally, the length of emboss (l) is the least important parameter in affecting the output value in this study.
Analysis of variance (ANOVA) of the first natural frequency with respect to different factors.
Analysis of variance (ANOVA) of the second natural frequency with respect to different factors.
4.4 Numerical Validation
Combination of A 1 B 1 C 1 D 1 will be confirmed as the lowest mass case if we compare the mass of 16 different cases demonstrated in Table 5. On the contrary, the best combination of design variables leading to the highest value of the first and second natural frequencies could not be found in the 16 design cases of Taguchi DOE. To make sure about the results of S/N ratio analysis and this fact that the highest first and second natural frequencies of the floor pan are related to these combination of design variables (t=1.2, w=48, l=173, h=15) and (t=1.2, w=48, l=143, h=15) respectively, a numerical simulation is performed in this section. The geometrical configuration, mass and the first and second natural frequencies corresponding to these cases are declared in Table 12. Finally, it is figured out that the first natural frequency in the A 4 B 4 C 4 D 4 case is higher than the all 16 cases which were simulated before. Similarly the second natural frequency in the A 4 B 4 C 3 D 4 case is higher than the other cases. Hence, as expected, the elected combinations of design variables proposed by Taguchi method and S/N ratio analysis are the optimum designs of the floor pan considering the first natural frequency and the second natural frequency separately as the single objective functions.
5 MULTI-CRITERIA DECISION MAKING
In this section, a new method is developed to find the trade-off design considering three objective functions, including the first natural frequency, the second natural frequency and the total mass. These quantities are selected to be optimized based on target cascading plan of the platform project to reduce the mass and improve the NVH characteristics of the panel. First, using Taguchi L 16 array a sixteen-sized set of experiments is defined as previously explained in Section 4. Now, a multi-criteria decision making (MCDM) method is needed to choose the trade-off design, among the present cases. Different strategies may be employed by engineers in MCDM problems based on the importance priorities that they previously designated to different attributes. Three different strategies are declared in Table 13 in case of choosing a trade-off design for the floor pan of a B-segment automotive body. The first strategy (St1) is used when there is no difference in importance of weight and stiffness attributes of the vehicle. The second and third strategies (St2 and St3) are used when stiffening or mass reduction is two times more important than the other respectively. A weight-sensitive MCDM method is needed to cope with such a problem which the objectives have different weight factors. Two different weight-sensitive MCDM methods are introduced and employed to choose the trade-off design with different strategies.
Strategy definition and corresponding weight factors. (W 1, W 2, W 3 are the weight coefficients corresponding to first and second natural frequencies and mass respectively).
5.1 Sum of Variations Compared to the Base Design (SVCB)
In this section, a new easy to use and general method is developed and used to choose the trade-off design in three different cases of design strategies. In this method, a base design is considered and it is desired to improve the objectives as much as possible compared to the base design. Despite of many conventional MCDM methods such as The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) Khalkhali et al (2014)Khalkhali, A. Khakshournia, Sh. Narimanzadeh, N. (2014). A hybrid method of FEM, modified NSGAII and TOPSIS for structural optimization of sandwich panels with corrugated core. Journal of Sandwich Structures and Materials. and Nearest to Ideal Point (NIP) Khalkhali. A, Khakshournia. Sh et al (2016)Khalkhali,A. Khakshournia,S. Saberi,P. (2016). Optimal design of functionally graded PmPV/CNT nanocomposite cylindrical tube for purpose of torque transmission. Journal of Central South University, 23 (2), 362-9. no distance calculation and data projection is needed in this method.
In the first step, non-dimensional variation of each objective function is calculated:
where, fi,j is the i-th objective function of the j-th case and fi,b is the i-th objective function of the base case.
Subsequently, the weighted sum of non-dimensional variations of the objective functions is obtained as follows:
where, NNI is the Non-dimensional Net Improvement in the objective functions of the j-th case compared to the base case, n is the number of objective functions, wi is the weight of i-th objective function, m is the number of design alternatives (cases) and k applies the effect of minimizing or maximizing the i-th objective function to the Equation 6, which is found using the following relation:
This method which is named as "Sum of Variations Compared to the Base Design (SVCB)" is set up to solve the current MCDM problem and is applicable to all of the weighted MCDM problems where a base design is supposed to be improved.
5.2 The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)
TOPSIS is a conventional method used in this study to validate operation of the new developed MCDM method (SVCB). The objective of TOPSIS is to determine the best compromise solution based on the distance from the positive, (S+ ), and negative, (S- ), ideal solutions according to the weights appointed for every criterion. The best solution is the closest one to the positive ideal solution and the farthest one from the negative ideal solution. This method is widely used in both engineering and non-engineering MCDM problems. The governing equations and the procedure of this method are present in the prior works Khalkhali et al (2014)Abolfazl Khalkhali, Sharif Khakshournia, Nader Narimanzadeh. (2014). A hybrid method of FEM, modified NSGAII and TOPSIS for structural optimization of sandwich panels with corrugated core. Journal of Sandwich Structures and Materials..
5.3 Results and Discussion
SVCB sorting of the Taguchi 16 cases is demonstrated in Table 14. Considering St1 or St2 as the current strategy, the fifteenth case is elected. Comparing the results of St1 with the base case, 119% improvement in the first natural frequency, 97% improvement in the second natural frequency and 106% deteriorating in the mass is observed. Totally, a non-dimensional net improvement (NNI) of 110% is observed in the three objective functions. An analogous conclusion is derived considering St2 as the current strategy. But NNI in this case is 327% due to the higher effect of natural frequency enhancements. If mass reduction is an important attribute in the automotive design, the third strategy St3 is suitable to be employed.
In this situation, the fourth case is proposed as the optimum design by SVCB. Comparing the corresponding objectives with the base case, 51% and 40% improvements are observed in the first and second natural frequencies respectively, whereas a 32% unfavorable enhancement in the floor pan's mass is also observed. Totally, the value of NNI is 58.6% compared to the base design.
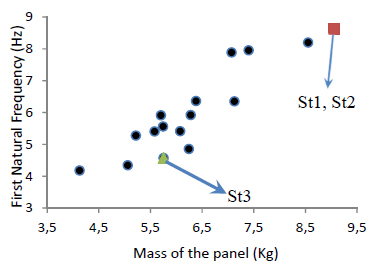
The output domain for different pairs of objective functions is shown in Figures 8-10. The trade-off design points proposed by SVCB corresponding to different strategies are shown in these figures. As a result, a direct relation is observed between each arbitrary pair of the objective functions. As it is obvious in these figures, the selected points for St1 and St2 are the same. Although it is desired to reduce the weight, the heaviest design is proposed as trade-off point for St1 and St2. Because improvement in the first and second natural frequencies of the panel dominates deterioration of the mass. As the importance of weight is increased in St3, the trade-off point is reduced in weight down to a compromised value as expected. Figure 11 shows the four first natural frequencies of the trade-off designs introduced by SVCB based on different strategies and the base case. The corresponding frequencies are also reported in this figure.
The output domain, First natural frequency with respect to second natural frequency of the panel.
Comparison of first four natural mode shapes of (a) the base case and the trade-off design introduced by SVCB method based on different strategies: (b) Case 15 by St1 and St2 and (c) Case 4 by St3.
The TOPSIS ranking of all cases with three different strategies are also shown in Table 14. A very good accordance between the results found by SVCB and TOPSIS is clearly observed. Therefore, the present method (SVCB) is trustable and has the following advantages over TOPSIS:
1-SVCB has a simpler and shorter procedure compared to TOPSIS
We face to a more complicated procedure in TOPSIS compared to SVCB. The first step in both methods is similar. Calculation of the non-dimensional variation for each alternative in SVCB and according to Khalkhali et al (2014)Khalkhali, A. Khakshournia, Sh. Narimanzadeh, N. (2014). A hybrid method of FEM, modified NSGAII and TOPSIS for structural optimization of sandwich panels with corrugated core. Journal of Sandwich Structures and Materials., calculation of the normalized rating S
+ and S- must be calculated and then, two distances (the distance from best and worst virtual designs) are found using square root of sum of squares. But the next step in SVCB is much shorter and simpler; NNI is calculated using summation of a limited number of products. for each alternative in TOPSIS. However, this procedure is shorter and simpler in SVCB; because a division (SVCB) takes shorter time compared to a division along with calculation of square root of sum of squares (TOPSIS). The next steps are different in the two methods. In TOPSIS, first two parameters
for each alternative in TOPSIS. However, this procedure is shorter and simpler in SVCB; because a division (SVCB) takes shorter time compared to a division along with calculation of square root of sum of squares (TOPSIS). The next steps are different in the two methods. In TOPSIS, first two parameters
2-In SVCB, it is possible to make a clear comparison between the trade-off design and the base case, based on negative or positive values of NNI.
In TOPSIS, no base case is defined. Instead, a virtual best and a virtual worst point are considered. Therefore, in TOPSIS the best alternative is the design which has the minimum relative closeness to the virtual best point. This gives no sense about being the results better or worse compared to a base case. In SVCB, the negative, zero or positive value of NNI clearly gives information about being worse, equal or better than the base case.
It should be noted that requiring a base design is not a limitation for SVCB. If a base case is not available, an arbitrary design case could be chosen as the base case among all of the present cases. In this situation, the trade-off design corresponds to the highest positive value of NNI.
6 CONCLUSIONS
A finite element model of the floor pan of a B-segment automotive body is provided in this study. Validation of this model is performed with a comparison between the results found by simulation and experiment of modal analysis of the floor pan. The average difference of 2.67% showed the good accuracy of the numerical simulation. As a parametric study, a set of experiments is designed using L 16 orthogonal array of Taguchi method to reduce the time and cost of the experiments. Four geometrical parameters of the floor pan are considered as control factors including the thickness of panel and the depth, width and length of the panel's emboss as depicted in Figure 4. Four levels are considered for each of the parameters in the parametric study. The 16 experiments proposed by Taguchi are performed using numerical simulation to find the corresponding natural frequencies and weights. S/N ratio analysis is then performed to figure out the effect of each control factor on the final outputs (the first natural frequency and total mass of the floor pan). As a result of S/N ratio analysis, the best combination of design variables leading to the single objective optimum design of the floor pan, considering one of the objectives and ignoring the other is obtained. Analysis of variances (ANOVA) is then carried out to determine the contribution percentage of different control factors on the objective functions. The thickness of panel is found to be the most effective parameter on the both objectives simultaneously. Then, an MCDM method was developed to consider the effects of first natural frequency, second natural frequency and mass at the same time. Three strategies were introduced based on the importance of different parameters deciding according to the automotive design attributes. Considering these three strategies, trade-off ranking was reported using the new developed MCDM method (SVCB) and the conventional method (TOPSIS). A very good accordance was observed between the rankings found by two methods. Using this newly developed MCDM model, NNI of the trade-off design associated with St1 and St2 was reported to be 110% showing a good improvement in total behavior of the floor pan.
References
- Abolfazl Khalkhali, Sharif Khakshournia, Nader Narimanzadeh. (2014). A hybrid method of FEM, modified NSGAII and TOPSIS for structural optimization of sandwich panels with corrugated core. Journal of Sandwich Structures and Materials.
- Abolfazl Khalkhali, Sharif Khakshournia, Parvaneh Saberi. (2016). Optimal design of functionally graded PmPV/CNT nanocomposite cylindrical tube for purpose of torque transmission. Journal of Central South University, 23 (2), 362-9.
- B. Chaturved, D. Rana and M. Ravindran. (2010). Correlation of vehicle dynamics & NVH performance with body static & dynamic stiffness through CAE and experimental analysis. SAE World Congress and Exhibition, 1-8.
- Eun Suk Suh, Olivier de Weck, Yong Kim, David Chang. (2007). Flexible platform component design under uncertainty. Journal of Intelligent Manufacturing, 18, 115-26.
- Ewins, D. J. (1984). Modal testing: theory and practice (Vol. 15). Letchworth: Research studies press.
- Guangyong Sun, Jiang Fang, Xuanyi Tian, Guangyo Li, Qing Li. (2015). Discrete robust optimization algorithm based on Taguchi method for structural crashworthiness design. Expert Systems with Applications, 42, 4482-92.
- Guangyong,S. Jiang,F. Xuanyi,T. Guangyo,L. Qing,L. (2015). Discrete robust optimization algorithm based on Taguchi method for structural crashworthiness design. Expert Systems with Applications, 42, 4482-92.
- Hari Krishnan. (2011). Establishing correlation between torsional and lateral stiffness parameters of BIW and vehicle handling performance. SAR International Journal of Passenger Cars, 4, 22-31.
- Khalkhali, A., Noraie, H., & Sarmadi, M. (2016). Sensitivity analysis and optimization of hot-stamping process of automotive components using analysis of variance and Taguchi technique. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 0954408916633491.
- Khalkhali,A. Khakshournia,S. Saberi,P. (2016). Optimal design of functionally graded PmPV/CNT nanocomposite cylindrical tube for purpose of torque transmission. Journal of Central South University, 23 (2), 362-9.
- Khalkhali, A. Khakshournia, Sh. Narimanzadeh, N. (2014). A hybrid method of FEM, modified NSGAII and TOPSIS for structural optimization of sandwich panels with corrugated core. Journal of Sandwich Structures and Materials.
- Krishnan, H. (2011). Establishing correlation between torsional and lateral stiffness parameters of BIW and vehicle handling performance. SAR International Journal of Passenger Cars, 4, 22-31.
- Kumar, P. Singh, D. Patel, S.B. Parsad. (2016). Optimization of process parameters during vibratory welding technique usin Taguchi's analysis. Perspectives in Science, Accepted Manuscript.
- LMS theory and background (2000), LMS International 2000.
- Mathan Kumar, N. S. (2016). Aerospace application on Al 2618 with reinforced - Si3N4, AIN and ZrB2 in-situ composites. Journal of Alloys and Compounds, 672, 238-50.
- Mignery, L. A. (n.d.). Quiet steel body panel design with DAMP- A custom preprocessor utilizing MSC-PATRAN/NASTRAN. Retrieved from https://web.mscsoftware.com/support/library/conf/auto00/p03700.pdf
» https://web.mscsoftware.com/support/library/conf/auto00/p03700.pdf - Mohan Kumar G R, Dr. Maruthi B H, Chandru B T, Manoranjan S N. (2015). Vibration analysis of automotive car floor using FEM and FFT analyzer. International Journal for Technological Research in Engineering, 2 (11), 2891-96.
- Mohan Kumar, G.R., Maruthi, B.H., Chandru B.T. Manoranjan,S.N. (2015). Vibration analysis of automotive car floor using FEM and FFT analyzer. International Journal for Technological Research in Engineering, 2 (11), 2891-96.
- N. Mathan Kumar, S.S.. (2016). Aerospace application on Al 2618 with reinforced - Si3N4, AIN and ZrB2 in-situ composites. Journal of Alloys and Compounds, 672, 238-50.
- P. Senthil Kumar, R. Kalidas, K. Sivakumar, E. Hariharan, B. Gautham, R. Ethiraj. (2013). Application of Taguchi method for optimizating passenger- friendly vehicle suspension system. International Journal of Latest Trends in Engineering and Technology, 2 (1).
- Palmonella, Matteo, Michael l. Friswell, John E. and Arthur W, Lees. (2005). Finite element models of spot welds in structural dynamics: review and updating. Computers & Structures, 83 (8), 648-61.
- Parvin Kumar, Singh D. Patel S.B. Parsad. (2016). Optimization of process parameters during vibratory welding technique usin Taguchi's analysis. Perspectives in Science, Accepted Manuscript.
- Pastor, M., Binda, M., & Harčarik, T. (2012). Modal assurance criterion. Procedia Engineering, 48, 543-548.
- Ranjit, K. (2001). Roy. Design of experiments using the Taguchi approach. John Willey & Sons Inc., New York.
- Shin, Jaeho, Neng Yue and Costin D.Untaroiu. (2012). A finite element model of the foot and ankle for automotive impact applications. Annals of Biomedical Engineering, 40 (12), 2519-31.
- Sobieszczansk,S. Jaroslaw, Srinivas,K.Yang, R. (2001). Optimization of car body under constraints of noise, vibration and harshness (NVH) and crash. Structural and Multidisciplinary Optimization, 22 (4), 295-306.
- Sobieszczanski-Sobieski, Jaroslaw, Srinivas Kodiyalam, R.Y. Yang. (2001). Optimization of car body under constraints of noise, vibration and harshness (NVH) and crash. Structural and Multidisciplinary Optimization, 22 (4), 295-306.
- Steve Kline, J. (March 2016). Automotive Production Growth Strong. Plastics Technology.
- Steve Kline, J. (March 2016). Automotive Production Growth Strong. Plastics Technology.
- Steven Tebby, Ahmad Barari and Ebrahim Esmailzadeh. (2012). Analysis and optimization of automotive's structure's bending stiffness using beam elements. ASME, 14th International Conference on Advanced Vehicle Technologies , 6, 12-15.
- Suh,E. Weck,O. Kim,Y. Chang,D. (2007). Flexible platform component design under uncertainty. Journal of Intelligent Manufacturing, 18, 115-26.
- Taguchi G., Konishi S. (1987). Taguchi methods, orthogonal arrays and linear graphs, tools for quality. Ammerican Supplier Institute, 8-35.
- The global automotive market. (2014). Economic Outlook, 1210, 1-20.
- Wang Mingqi, Jin Guodong. (1997). The application of Taguchi method to the stiffness improvement of a double- decker structure. International Journal of Materials and Product Technology (4-6).
- Wang,M. Guodong, J. (1997). The application of Taguchi method to the stiffness improvement of a double- decker structure. International Journal of Materials and Product Technology (4-6).
Publication Dates
-
Publication in this collection
Dec 2016
History
-
Received
26 June 2016 -
Reviewed
10 Sept 2016 -
Accepted
06 Oct 2016