Abstract
The mathematical model for wave motion in a fractured porous solid is solved for the propagation of harmonic plane wave along a general direction in 3-D space. The solution is obtained in the form of Christoffel equations, which are solved further to define the complex velocities and polarisations of five attenuated wavesin the medium. Four of these waves are longitudinal waves and the one is transverse wave. For any of these five attenuated waves, a general inhomogeneous propagation is considered with a complex specification of slowness vector involving a finite non-dimensional inhomogeneity parameter. The phase velocities and attenuation coefficients are calculated for the inhomogeneous propagation of each of the five attenuated waves in the medium. A numerical example is studies to analyse the effect of wave frequency, saturating pore-fluid, volume fraction of fractures and inhomogeneity parameter on the phase velocity and attenuation. The phenomenon of reflection is studied to calculate the partitionof wave-induced energy incident at the plane boundary of the fractured porous solid. The effect of wave frequency, volume fraction of fractures, saturating pore-fluid and inhomogeneity parameter on the energy partition are studied in the numerical example.
fractured porous solid; immiscible fluids; propagation; attenuation; reflection coefficients
Reflection of attenuated waves at the surface of a fractured porous solid saturated with two immiscible viscous fluids
M. KumarI, * * Author e-mail: manjit.msc@gmail.com ; M. KumariII
IDept. of Mathematics, Govt. National College Sirsa, India-125 055
IIDept. of Mathematics, M. P. College for Women Mandi Dabwali, India-125 104
ABSTRACT
The mathematical model for wave motion in a fractured porous solid is solved for the propagation of harmonic plane wave along a general direction in 3-D space. The solution is obtained in the form of Christoffel equations, which are solved further to define the complex velocities and polarisations of five attenuated wavesin the medium. Four of these waves are longitudinal waves and the one is transverse wave. For any of these five attenuated waves, a general inhomogeneous propagation is considered with a complex specification of slowness vector involving a finite non-dimensional inhomogeneity parameter. The phase velocities and attenuation coefficients are calculated for the inhomogeneous propagation of each of the five attenuated waves in the medium. A numerical example is studies to analyse the effect of wave frequency, saturating pore-fluid, volume fraction of fractures and inhomogeneity parameter on the phase velocity and attenuation. The phenomenon of reflection is studied to calculate the partitionof wave-induced energy incident at the plane boundary of the fractured porous solid. The effect of wave frequency, volume fraction of fractures, saturating pore-fluid and inhomogeneity parameter on the energy partition are studied in the numerical example.
Keywords: fractured porous solid, immiscible fluids, propagation, attenuation, reflection coefficients
1 INTRODUCTION
Fractures play a significant role in hydrology and in many oil and gas reservoirs. In recent years, fractured reservoirs attracted more attention in the research of exploration and production geophysics. The direct prediction of fracture is difficult due to the complexity of the fracture development system. Generally, seismic wave propagation through the Earth (or reservoir rocks) is strongly affected by the presence of fractures and micro-pores. The type and state of the fluid (liquid or gas) can make a large difference in the response of seismic waves, when these fractures are filled with fluids (oil, gas, water, CO2, etc.). The studies of elastic wave propagation and related phenomena in fractured porous medium are of great interest in various fields, namely hydrology, nuclear waste industry, petroleum engineering, mining engineering, seismology and exploration of subsurface resources.
The dynamical equations formulated by Biot (1956, 1962a, b) are, generally, used to derive mathematical models for wave propagation studies in poroelastic media. Biot established the fundamental theory for wave propagation in fluid-saturated porous media. It is still well-accepted and forms the basis for wave propagation studies in porous media. This theory successfully predicted the existence of the second compressional wave (the slow compressional wave), which had been observed in the laboratory (Plona 1980; Berryman 1980). Deresiewicz & Skalak (1963) applied the Neumann's uniqueness theorem to poroelasticity and derived the boundary conditions, further which are used to define the boundary value problems for particle dynamics in saturated porous materials.
In general, fractured reservoirs are more complex due to the presence of fractures and pores. Generally, we consider reservoirs containing fractures that are embedded in a porous background. Several treatments of the porous media with fractures have been developed in recent years, which are much closer to real fractured rocks. In addition to matrix porosity and permeability, fracture porosity and fracture permeability also need to be included. As available in the literature, the early models were based on the single porosity or continuum concept. In this approach, a fractured porous medium was grossly treated as an equivalent continuum with a single fluid constituent. A major departure from the single porosity approach was first made by Barenblatt et al. (1960) and Warren & Root (1963). They proposed a phenomenological double porosity model to investigate fluid transport in hydrocarbon reservoirs. They modelled flow through rigid fractured porous media as a complex of two interacting flow regions: one representing the fracture network and the other the porous blocks. The fracture network was characterized by high permeability and low storage, and the porous blocks were characterized by low permeability and high storage. The two flow regions were in turn coupled through a leakage term controlling the transfer of fluid mass between the pores and fractures. An extension of Barenblatt's model to deformable fractured porous media was later given by Duguid & Lee (1977). Aifantis (1977, 1979, 1980) used the theory of mixtures and proposed a coupled double-porosity model for deformable fractured porous media. Alternatives to Aifantis' formulation were given by Wilson and Aifantis (1982), Khaled et al. (1984), Valliappan & Khalili- Naghadeh (1990), Khalili-Naghadeh & Valliappan (1991), Auriault & Boutin (1993) and Bai et al. (1993), among others. Aifantis and his co-workers (Wilson & Aifantis 1982; Beskos & Aifantis 1986; Khaled et al. 1984) published interesting and important series of papers on saturated fractured porous media. It is noted that the final set of governing equations is a direct generalization of Biot's consolidation theory. Wilson & Aifantis (1984) studied the propagation of waves in a saturated fractured porous medium and showed the existence of an extra compressional wave (which appears due to the presence of fractures in the medium), in addition to those encountered in Biot's theory. However, Aifantis model was incomplete, in the sense that it related pore and fracture volume changes only to the overall volume change of the fractured porous medium. More specifically, it ignored the cross-coupling effects between the volume change of the pores and fractures within the system. This deficiency was eliminated in the formulations proposed by Khalili & Valliappan (1996), Tuncay & Corapcioglu (1996), Wang & Berryman (1996), Khalili et al. (1999), and Loret & Rizzi (1999). Khalili (2003) highlighted the significance of the cross-coupling effects on the pore and fracture fluid pressure response of double-porosity media. Then the credit for comprehensive discussion on wave propagation in fractured porous media saturated with two immiscible viscous fluids goes to Tuncay & Corapcioglu (1996a, b). They derived a general set of coupled partial differential equations to describe the wave propagation through an fractured porous medium permitted by two immiscible viscous fluids. In the absence of volume fractions of the fractures, the constitutive relations reduce to those obtained by Tuncay & Corapciaglu (1997) in the theory of porous media without fractures. Tuncay & Corapcioglu (1996b) studied the propagation of body waves in a fractured porous medium containing two immiscible fluids. They showed that there may exists four compressional waves and one rotational wave. Berryman & Wang (2000) extended Biot's theory of poroelasticity to incorporate the concept of fractures or cracks in the medium, in addition to the generalization to double porosity modelling done in their previous work (Berryman & Wang 1995).
Recently, Arora & Tomer (2010) have considered the reflection and refraction of plane harmonic waves at the boundaries of fractured porous media saturated by two immiscible fluids. In this study, pore-fluids were assumed non-viscous so as to avoid the involvement of attenuation. For the same reason, the incidence was restricted to pre-critical angles. Unfortunately, this is in contrast to the realistic flow mechanics in crustal rocks where the equilibration of fluid pressure produces a great deal of seismic attenuation (Sams et al., 1997). Moreover, the displacements of constituent particles in fractured porous aggregate were subjected to an unintended restriction, which implies that dilatational contribution to the displacement in different constituents comes from different but only one of the four longitudinal waves. However, Sharma & Kumar (2011) and Kumar & Saini (2012) ignored all these restrictions. Sharma & Saini (2012) studied the wave propagation in porous solid containing liquid filled bound pores and two-phase fluid in connected pores. Kumar & Sharma (2013) studied the reflection and transmission of attenuated waves at the boundary between two dissimilar poroelastic solids saturated with two immiscible viscous fluids.
This study considers the propagation of attenuated waves in fractured porous solids saturated with two immiscible viscous fluids. The equation of motion from Tuncay & Corapcioglu (1996a) are solved for propagation of harmonic plane waves. The solution is obtained in the form of Christoffel equations, which provide the complex velocities and polarisations of four attenuated waves in the medium. A particular specification of complex slowness vector is considered to define a general inhomogeneous propagation of attenuated waves. Reflection is studied for the incidence of an inhomogeneous wave at the free plane boundary of the fractured porous medium. An energy matrix is calculated, which defines the shares of five reflected waves in the incident energy. This matrix also identifies the energy due to the interaction between various inhomogeneous waves in the medium. This is required to ensure the conservation of incident energy at the boundary. The effect of wave frequency, volume fraction of fractures, saturating pore-fluid and inhomogeneity parameter on the energy partition are studied in the numerical example. For convenience, the two immiscible pore-fluids are identified as gas and liquid.
2 FRACTURED POROUS SOLID
2.1 Fundamental equations
In the theory of Tuncay & Corapcioglu (1996a), the presence of fractures in the porous medium is assumed to have two part one can be identified as fractured and other can be non-fractured part. The pores in the non-fractured (fractured) part of the porous medium are referred as primary (secondary) pores. The secondary pores are assumed to be saturated by the wetting fluid, whereas the primary pores are assumed to be saturated by the wetting and non-wetting fluids. Therefore, there are four phases in the system i.e. solid phase, wetting fluid phase in secondary pores, wetting and non-wetting fluid phases in the primary pores. Following Tuncay & Corapcioglu (1996a), under the assumption of no mass exchange between the porous blocks and fractures, the equations of motion for the low-frequency vibrations of constituent particles in isotropic fractured porous solid, in the absence of body forces, are given by
where the subscripts 0, 1, 2, and f identify the four phases of the fractured porous solid, i.e. solid phase, non-wetting phase, wetting phase in the primary pores, and wetting fluid phase in the fractures, respectively. The 's are used to define stresses and
's are used to define stresses and  's are partial densities. The
's are partial densities. The  and
and  denote the components of displacements of solid, non-wetting fluid, wetting fluid particles in the primary pores, and wetting fluid particles in the fractures, respectively. The indices can take values 1, 2 and 3. A repeated index implies summation. Dot over a variable implies partial derivative with time and comma before an index implies partial space differentiation. Darcy's law relates viscous dissipation to the motion of wetting particles in the secondary pores, wetting and non-wetting fluid particles in the primary pores relative to the pore-walls. The dissipation coefficients for wetting fluid (
denote the components of displacements of solid, non-wetting fluid, wetting fluid particles in the primary pores, and wetting fluid particles in the fractures, respectively. The indices can take values 1, 2 and 3. A repeated index implies summation. Dot over a variable implies partial derivative with time and comma before an index implies partial space differentiation. Darcy's law relates viscous dissipation to the motion of wetting particles in the secondary pores, wetting and non-wetting fluid particles in the primary pores relative to the pore-walls. The dissipation coefficients for wetting fluid ( ), non-wetting fluid (
), non-wetting fluid ( ), in primary pores and wetting fluid (
), in primary pores and wetting fluid ( ) in secondary pores are defined as follows.
) in secondary pores are defined as follows.
where  and
and  define the viscosity and the relative permeability of fluid phase k.
define the viscosity and the relative permeability of fluid phase k.  denotes the intrinsic permeability of the fractures (non-fractured porous medium). The constitutive relations for four phases system are defined as follows.
denotes the intrinsic permeability of the fractures (non-fractured porous medium). The constitutive relations for four phases system are defined as follows.
where  is Kronecker symbol.
is Kronecker symbol.  is the shear modulus of solid matrix. The elastic constants used in the above equations are given in Appendix
Appendix
.
is the shear modulus of solid matrix. The elastic constants used in the above equations are given in Appendix
Appendix
.
In terms of the displacement components, the equations of motion are expressed as follows.
2.2 Plane wave propagation
To seek the harmonic solution of system of equations (4), for the propagation of plane waves, the displacement components are written as follows.
where  is angular frequency and
is angular frequency and  is slowness vector
is slowness vector  . The vectors
. The vectors  and
and  and
and  define, respectively, the polarizations for the motions of the solid, non-wetting fluid and wetting fluid particles in primary pores, and wetting fluid particles in secondary pores in the composite medium. Substituting (5) in (4) yields a system of twelve equations, given by
define, respectively, the polarizations for the motions of the solid, non-wetting fluid and wetting fluid particles in primary pores, and wetting fluid particles in secondary pores in the composite medium. Substituting (5) in (4) yields a system of twelve equations, given by
where  denotes the transpose of
denotes the transpose of  . The equations (7), (8) and (9) of this system are solved into three relations, given by
. The equations (7), (8) and (9) of this system are solved into three relations, given by
which relate the polarisations (or displacements) of particles of solid, non-wetting and wetting fluid phases in the primary pores, and wetting fluid in secondary pores in the composite medium. Using these relations in (6) yields a system of three equations, given by
which are the Christoffel equations for the propagation of harmonic plane waves in the fractured porous medium saturated by two immiscible fluids. The coefficients used in various relations are defined as follows.
2.3 Five attenuated waves
In terms of velocity V, the slowness is defined as  such that
such that  and
and  . The dual (complex) vector
. The dual (complex) vector  represents the directions of propagation and attenuation of a wave in the fractured porous medium. In terms of
represents the directions of propagation and attenuation of a wave in the fractured porous medium. In terms of  and V, the Christoffel equations (13) are expressed as
and V, the Christoffel equations (13) are expressed as
The non-trivial solution for Christoffel equations is ensured by vanishing the determinant ( ) of the matrix
) of the matrix  . This condition translates into two equations as follows.
. This condition translates into two equations as follows.
The first one (i.e.  ) implies that
) implies that
Four roots of this complex biquadratic equation define the complex velocities  of four attenuating waves in the dissipative porous medium. In this case the polarization vector
of four attenuating waves in the dissipative porous medium. In this case the polarization vector , corresponding to equation (14), is calculated to be parallel to
, corresponding to equation (14), is calculated to be parallel to  and hence the four waves identified with velocities
and hence the four waves identified with velocities  and
and  are longitudinal waves.
are longitudinal waves.
Another equation (i.e.  ) yields
) yields
which implies a wave with complex velocity  . The corresponding polarization vector
. The corresponding polarization vector  , is represented through a singular matrix
, is represented through a singular matrix  . So, the polarization vector may be parallel to a column (or, row) vector of this symmetric matrix. This defines the direction of polarisation in a plane, which is normal to the propagation vector
. So, the polarization vector may be parallel to a column (or, row) vector of this symmetric matrix. This defines the direction of polarisation in a plane, which is normal to the propagation vector  . This implies that the attenuated wave with velocity
. This implies that the attenuated wave with velocity  is a transverse wave.
is a transverse wave.
The polarisation vector  defines the polarisation of solid particles in the fractured porous medium. Polarisations of the non-wetting, wetting fluid particles in primary pores and wetting fluid particles in secondary pores are calculated from the relations (10), (11) and (12), respectively. For convenience in discussion, the four longitudinal waves with velocity order
defines the polarisation of solid particles in the fractured porous medium. Polarisations of the non-wetting, wetting fluid particles in primary pores and wetting fluid particles in secondary pores are calculated from the relations (10), (11) and (12), respectively. For convenience in discussion, the four longitudinal waves with velocity order  are named as
are named as  waves, respectively. The lone transverse wave is identified as S wave.
waves, respectively. The lone transverse wave is identified as S wave.
3 INHOMOGENEOUS PLANE WAVES
The general plane waves propagating in a dissipative medium are inhomogeneous waves (Borcherdt 1982). The propagation of an attenuated wave is defined with complex slowness vector. The real and imaginary parts of complex slowness vector are termed as propagation vector and attenuation vector, respectively. In general, the inhomogeneity of an attenuating wave is represented through the difference in the directions of its propagation vector and attenuation vector. In other words, an angle between equi-amplitude plane and equi-phase plane of an attenuating plane wave represent its inhomogeneous character. However, some restrictions may be needed on the choice of this inhomogeneity angle. The invalid values of the inhomogeneity angle are termed as forbidden directions, which were discovered first in the pioneering works of Krebes & Le (1994) and Carcione & Cavallini (1995). As an alternative to this conventional representation, Sharma (2008) used a finite non-dimensional parameter to define inhomogeneous waves in anisotropic media. In terms of this inhomogeneity parameter ( ), the complex slowness vector p of an attenuated wave is written as follows.
), the complex slowness vector p of an attenuated wave is written as follows.
where the propagation direction  and an orthogonal unit vector
and an orthogonal unit vector  identifies the propagation-attenuation plane. The total attenuation is a vector sum of two orthogonal vectors. The first one,
identifies the propagation-attenuation plane. The total attenuation is a vector sum of two orthogonal vectors. The first one,  defines the attenuation along the direction of propagation. Hence, it represents the homogeneous wave and its contribution
defines the attenuation along the direction of propagation. Hence, it represents the homogeneous wave and its contribution  to total attenuation is termed as homogeneous attenuation. The other part
to total attenuation is termed as homogeneous attenuation. The other part  in (17) then represents the contribution of inhomogeneous propagation of wave to total attenuation
in (17) then represents the contribution of inhomogeneous propagation of wave to total attenuation  For
For  , the attenuated wave is considered to be propagating as homogeneous wave. This implies that inhomogeneous propagation of the attenuated wave is represented through the deviation of
, the attenuated wave is considered to be propagating as homogeneous wave. This implies that inhomogeneous propagation of the attenuated wave is represented through the deviation of  from zero. Hence, the magnitude of inhomogeneity parameter
from zero. Hence, the magnitude of inhomogeneity parameter  is considered as the strength of the inhomogeneous wave. For known values of propagation direction
is considered as the strength of the inhomogeneous wave. For known values of propagation direction  , orthogonal direction
, orthogonal direction  and inhomogeneity parameter
and inhomogeneity parameter  we need to determine the attenuation coefficient
we need to determine the attenuation coefficient  and the phase velocity c . It may be noted that the sign of
and the phase velocity c . It may be noted that the sign of  does not affect the values of
does not affect the values of  and c. Using the relations p=N/V and
and c. Using the relations p=N/V and  in (17), we get
in (17), we get
The quality factor of attenuation (i.e. Q) for a wave is defined as
The equations (15) and (16) do not involve N. That means, for a chosen medium, the value of  is independent of N. It may be noted that a change in
is independent of N. It may be noted that a change in  can affect
can affect  only through N. This implies that for any value of
only through N. This implies that for any value of  (in other words, N), the
(in other words, N), the  will be same. Then, from the first equality in (19), this implies a constant
will be same. Then, from the first equality in (19), this implies a constant  for each attenuated wave in the medium. Then the effect of wave inhomogeneity (i.e.
for each attenuated wave in the medium. Then the effect of wave inhomogeneity (i.e. ) on attenuation may be observed in an attenuation coefficient given by
) on attenuation may be observed in an attenuation coefficient given by
For the homogeneous propagation (i.e.  ) of an attenuated wave, the above defined relations reduce to
) of an attenuated wave, the above defined relations reduce to
The other extreme value of  (=1) implies
(=1) implies  and then slowness vector
and then slowness vector  defines a wave with attenuation direction orthogonal to its propagation direction, i.e. evanescent wave.
defines a wave with attenuation direction orthogonal to its propagation direction, i.e. evanescent wave.
4 REFLECTION AT PLANE BOUNDARY
The present study aims to analyse the propagation and attenuation of five reflected waves arising from the incidence of an inhomogeneous wave at the free plane surface of a fractured porous solid saturated with two immiscible fluids (non-wetting and wetting).
4.1 Definition of the problem
Consider a rectangular coordinate system  to represent a three-dimensional space. The half-space
to represent a three-dimensional space. The half-space  is occupied by a saturated fractured porous solid with its depth increasing along the
is occupied by a saturated fractured porous solid with its depth increasing along the  -direction. The plane
-direction. The plane  is the surface of this medium. The medium being isotropic, the propagation and attenuation of waves are considered in a plane and this plane is assumed to be a coordinate (i.e.
is the surface of this medium. The medium being isotropic, the propagation and attenuation of waves are considered in a plane and this plane is assumed to be a coordinate (i.e.  ) plane. In this plane, a wave travels towards the surface and become incident at a point on the surface making an angle
) plane. In this plane, a wave travels towards the surface and become incident at a point on the surface making an angle  with the
with the  -axis. Then the propagation direction
-axis. Then the propagation direction  and its orthogonal direction
and its orthogonal direction  identify the
identify the  plane as the propagation-attenuation plane. The incident wave can be any of the five attenuated waves in the fractured porous medium. For an arbitrarily chosen value of inhomogeneity parameter
plane as the propagation-attenuation plane. The incident wave can be any of the five attenuated waves in the fractured porous medium. For an arbitrarily chosen value of inhomogeneity parameter  , the values of
, the values of  and c for this incident wave are calculated from (18). Using all these values, the slowness vector is calculated for the incident wave as
and c for this incident wave are calculated from (18). Using all these values, the slowness vector is calculated for the incident wave as  such that
such that  , where
, where  denotes the complex velocity of the incident wave. Being a square-root of a complex quantity, the value for
denotes the complex velocity of the incident wave. Being a square-root of a complex quantity, the value for  is chosen such that
is chosen such that  In the present geometry of the medium, this restriction ensures the propagation of incident wave towards the surface
In the present geometry of the medium, this restriction ensures the propagation of incident wave towards the surface . The incident wave results in five waves
. The incident wave results in five waves  reflected back into the porous medium. Snell's law implies that horizontal slowness of each of the reflected wave will be same as that of incident wave, i.e.
reflected back into the porous medium. Snell's law implies that horizontal slowness of each of the reflected wave will be same as that of incident wave, i.e.  . Then the slowness vectors for the reflected waves are written as
. Then the slowness vectors for the reflected waves are written as  The decay of a reflected wave along positive
The decay of a reflected wave along positive  -direction is ensured with the positive value for imaginary part of corresponding
-direction is ensured with the positive value for imaginary part of corresponding .
.
4.2 Displacements
The displacement of solid particles in the fractured porous medium due to the presence of an incident wave and five reflected waves is expressed as follows.
where  are the excitation factors for reflected waves relative to incident wave. The complex vector
are the excitation factors for reflected waves relative to incident wave. The complex vector  defines the polarisation and phase shift of the motion of solid particles for incident wave (k=0) and reflected waves (k=1,2,3,4,5). The corresponding displacements of the non-wetting, wetting fluid particles in primary pores and wetting fluid particles in secondary pores can be calculated from the relations (10), (11) and (12) using the wave-specific values of the matrices A, B and C, respectively.
defines the polarisation and phase shift of the motion of solid particles for incident wave (k=0) and reflected waves (k=1,2,3,4,5). The corresponding displacements of the non-wetting, wetting fluid particles in primary pores and wetting fluid particles in secondary pores can be calculated from the relations (10), (11) and (12) using the wave-specific values of the matrices A, B and C, respectively.
4.3 Boundary conditions
Surface of the fractured porous solid is considered to be free of stresses. Hence, at every point on the surface of material, the resultant energy must vanish. This is achieved through the equation
The index n (or, t) is used to denote the component normal (or, tangential) to the surface. The repetition of index n in this section does not imply summation. The boundary conditions at the surface are obtained from the physical conditions there, subjected to the energy constraint defined in (23). So, at the stress-free surface of fractured porous medium, the aggregate stress from the solid phase (i.e.,  ), non-wetting phase
), non-wetting phase  , wetting phase
, wetting phase  in the primary pores, and
in the primary pores, and  wetting fluid phase in secondary pores together should vanish. For sealed surface pores, there will be no fluid discharge (i.e.
wetting fluid phase in secondary pores together should vanish. For sealed surface pores, there will be no fluid discharge (i.e.  at the surface. Hence, the appropriate boundary conditions to be satisfied at the stress-free surface
at the surface. Hence, the appropriate boundary conditions to be satisfied at the stress-free surface  are given by
are given by
The equations (3) relate the stress components in different phases to the displacements of particles. The above boundary conditions are satisfied through a system of five linear inhomogeneous equations in  and
and  . This system of equations is given by,
. This system of equations is given by,
where the coefficients  , (i=1,2,3,4,5; j=0,1,2,3,4,5), are expressed as follows.
, (i=1,2,3,4,5; j=0,1,2,3,4,5), are expressed as follows.
The matrices used in the above expressions are defined as
where the superscript ´(j)´ on matrices A, B and C means the matrices are evaluated for slowness vector p of the corresponding wave represented with a value of j (=0,1,2,3,4,5).
4.4 Energy ratios
Distribution of incident energy among different reflected waves is considered across a surface element of unit area at the plane  . Following Achenbach (1973), the scalar product of surface traction and particle velocity per unit area, denoted by
. Following Achenbach (1973), the scalar product of surface traction and particle velocity per unit area, denoted by  , represents the rate at which the energy is communicated per unit area of the surface. The time average of
, represents the rate at which the energy is communicated per unit area of the surface. The time average of  over a period, denoted by
over a period, denoted by , represents the average energy transmission per unit surface area per unit time. For a surface with normal along the
, represents the average energy transmission per unit surface area per unit time. For a surface with normal along the  -direction, the average energy flux is represented through the components
-direction, the average energy flux is represented through the components  given by
given by
The incidence of a general inhomogeneous wave involves the concept of interaction energy (Borcherdt 1982; Krebes 1983) or the interference energy (Ainslie & Burns 1995) between the dissimilar pairs of incident and reflected waves in the medium. To explain the distribution of incident energy at the free surface of a dissipative fractured porous medium, a matrix is defined with its elements given by
where bar over an entity implies its complex conjugate. The elements of matrix F are defined as follows.
Solving the system of equations (24), by Gauss elimination method, provides the values for excitation factors ( ), which are required to calculate the matrix (26) for
), which are required to calculate the matrix (26) for  . This energy matrix explains the energy partition at the boundary
. This energy matrix explains the energy partition at the boundary  of the porous solid. The sum of all the non-diagonal entries of this energy matrix calculates the share of interaction energy in the medium. The diagonal entries
of the porous solid. The sum of all the non-diagonal entries of this energy matrix calculates the share of interaction energy in the medium. The diagonal entries  and
and  of this matrix denote the energy shares of reflected
of this matrix denote the energy shares of reflected  and S waves in the incident energy. The energy due to the interaction of incident wave with the five reflected waves is given by
and S waves in the incident energy. The energy due to the interaction of incident wave with the five reflected waves is given by  . The energy due to the interaction among the five reflected waves is given by
. The energy due to the interaction among the five reflected waves is given by  . Then the conservation of energy at the free-surface is ensured through the relation
. Then the conservation of energy at the free-surface is ensured through the relation
5 NUMERICAL RESULTS AND DISCUSSION
5.1 Numerical example
In order to investigate the dependence of velocities, amplitude ratios and energy ratios on the various material parameters, a numerical study was conducted in MATLAB for an illustrative example. A fractured sandstone (rock) saturated with air and water is chosen for the numerical model of fractured porous medium (Tuncay & Corapcioglu 1996). The solid grains of the rock with bulk modulus  shear modulus
shear modulus  and density
and density  form a porous frame of porosity
form a porous frame of porosity  The primary pore space (i.e., non-fractured part) is filled with the gas of bulk modulus
The primary pore space (i.e., non-fractured part) is filled with the gas of bulk modulus  density
density  relativity permeability
relativity permeability  and viscosity
and viscosity  mixed in water of bulk modulus
mixed in water of bulk modulus 
 relativity permeability
relativity permeability  and viscosity
and viscosity  . The secondary pore space (i.e., fractured part) is filled with the water having same density and viscosity as water in primary pore. The bulk modulus
. The secondary pore space (i.e., fractured part) is filled with the water having same density and viscosity as water in primary pore. The bulk modulus  and
and  of fractured and non-fractured medium, respectively. Intrinsic permeability
of fractured and non-fractured medium, respectively. Intrinsic permeability  and
and  of fractured and non-fractured medium, respectively. A dimensionless material parameter F = 0.8. The value of
of fractured and non-fractured medium, respectively. A dimensionless material parameter F = 0.8. The value of  is used to represent capillary pressure. The secondary pore space (i.e., fractured part) is filled with the water having same density and viscosity as water in primary pore. For computation purposes, Low-frequency propagation is ensured with
is used to represent capillary pressure. The secondary pore space (i.e., fractured part) is filled with the water having same density and viscosity as water in primary pore. For computation purposes, Low-frequency propagation is ensured with  .
.
5.2 Velocity and attenuation
The numerical values of various parameters given above are used to calculate the complex velocities of the five attenuated (i.e.  ) waves in the fractured porous medium. Phase velocities
) waves in the fractured porous medium. Phase velocities  and attenuation coefficients
and attenuation coefficients  are computed for inhomogeneous propagation of these waves. Effect of various parameters on
are computed for inhomogeneous propagation of these waves. Effect of various parameters on  and
and  are exhibited in Fig. 1-Fig. 4
are exhibited in Fig. 1-Fig. 4
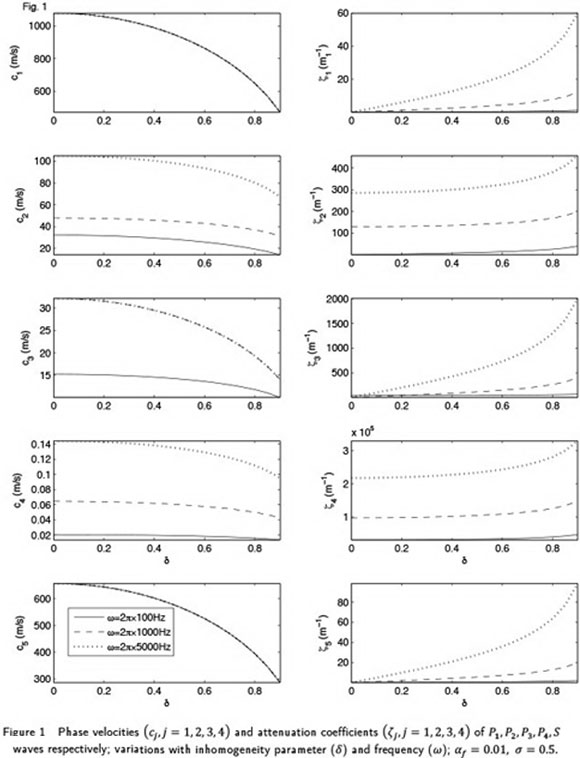
Effect of frequency
The variations of phase velocities and attenuation coefficients of the  and S waves with
and S waves with  are exhibited in Fig. 1 for three different frequencies,
are exhibited in Fig. 1 for three different frequencies,  Values chosen for other parameters are
Values chosen for other parameters are  It is quite evident that with the increase of inhomogeneity of an attenuated wave of given frequency, its phase velocity decreases but attenuation increases. The velocity of three (
It is quite evident that with the increase of inhomogeneity of an attenuated wave of given frequency, its phase velocity decreases but attenuation increases. The velocity of three ( ) waves may reduce up to one-half with the change in propagation from homogeneous to evanescent. The increase of frequency may not have much effect on the velocity of (
) waves may reduce up to one-half with the change in propagation from homogeneous to evanescent. The increase of frequency may not have much effect on the velocity of ( ) waves. However, the three slower longitudinal (i.e.
) waves. However, the three slower longitudinal (i.e.  ) waves propagate faster at higher frequency. At low-frequency, the velocity of (
) waves propagate faster at higher frequency. At low-frequency, the velocity of ( ) waves may not decrease much with the increase of inhomogeneity strength. For each of the five waves in porous medium, an increase of frequency (and/or inhomogeneity) increases its attenuation. However, the effect of inhomogeneity on attenuation may be mild at low frequencies. The general observations are that slower the propagation higher is the attenuation and homogeneous waves may travel faster but cannot represent the wave motion with larger attenuation.
) waves may not decrease much with the increase of inhomogeneity strength. For each of the five waves in porous medium, an increase of frequency (and/or inhomogeneity) increases its attenuation. However, the effect of inhomogeneity on attenuation may be mild at low frequencies. The general observations are that slower the propagation higher is the attenuation and homogeneous waves may travel faster but cannot represent the wave motion with larger attenuation.
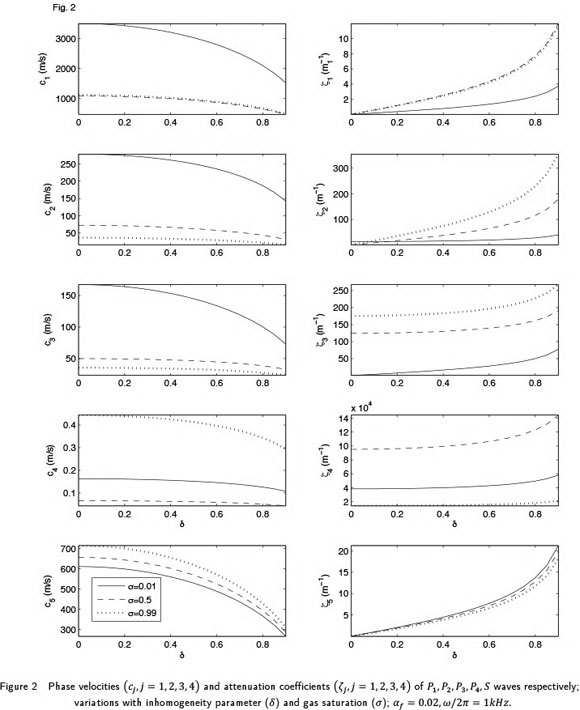
Effect of gas share in pores
The variations of phase velocities and attenuation coefficients of the five (i.e.  ) waves with
) waves with  are presented in Fig. 2, for three different values
are presented in Fig. 2, for three different values  of gas saturation. Values chosen for other parameters are
of gas saturation. Values chosen for other parameters are  A smaller gas share in pores means more liquid in pores and vice-verse. The limiting values of
A smaller gas share in pores means more liquid in pores and vice-verse. The limiting values of  (i.e., 0, 1) are avoided for representing the non-realistic situations of no gas/all liquid and all gas/no liquid. The increase of gas share increases the velocity of S wave whereas three longitudinal waves (i.e.
(i.e., 0, 1) are avoided for representing the non-realistic situations of no gas/all liquid and all gas/no liquid. The increase of gas share increases the velocity of S wave whereas three longitudinal waves (i.e.  ) travel faster when the pore space is filled only with liquid. However, the slowest travel of longitudinal waves may be expected when pore space is equally shared by the two fluids. It is quite evident that the variations of the velocity of a wave with gas share in the pores appear nearly opposite to the variations in its attenuation coefficient.
) travel faster when the pore space is filled only with liquid. However, the slowest travel of longitudinal waves may be expected when pore space is equally shared by the two fluids. It is quite evident that the variations of the velocity of a wave with gas share in the pores appear nearly opposite to the variations in its attenuation coefficient.
Effect of volume fraction of fractures
For three different values of volume fraction of fractures  , the variations of phase velocities and attenuation coefficients of the
, the variations of phase velocities and attenuation coefficients of the  and S waves with
and S waves with  are as shown in Fig. 3. Except
are as shown in Fig. 3. Except  and
and  , the values of other parameters are unchanged. Clearly, the velocity of the three longitudinal waves (i.e.
, the values of other parameters are unchanged. Clearly, the velocity of the three longitudinal waves (i.e.  ) increases with the increase of volume fraction of fractures whereas velocity of fast longitudinal wave (i.e.
) increases with the increase of volume fraction of fractures whereas velocity of fast longitudinal wave (i.e.  ) decreases with the increase of volume fraction of fractures. However, the volume fraction of fractures shows no effect on the velocity and attenuation of faster shear wave (i.e. S). It is quite evident that the variations of the attenuation coefficient of a longitudinal wave with volume fraction of fractures appear nearly opposite to the variations in its velocity.
) decreases with the increase of volume fraction of fractures. However, the volume fraction of fractures shows no effect on the velocity and attenuation of faster shear wave (i.e. S). It is quite evident that the variations of the attenuation coefficient of a longitudinal wave with volume fraction of fractures appear nearly opposite to the variations in its velocity.
Effect of inhomogeneity parameter
The variations of phase velocities and attenuation coefficients of the  and S waves with
and S waves with  are exhibited in Fig. 4 for three different values of
are exhibited in Fig. 4 for three different values of  . Values chosen for other parameters are unchanged except
. Values chosen for other parameters are unchanged except  and
and  . Increase of gas share seems to have a quiet significant effect of the velocities and attenuation coefficients of all the longitudinal waves (i.e.,
. Increase of gas share seems to have a quiet significant effect of the velocities and attenuation coefficients of all the longitudinal waves (i.e.,  ). However, effect of gas share is observed very little on the velocity and attenuation coefficient of lone shear wave.
). However, effect of gas share is observed very little on the velocity and attenuation coefficient of lone shear wave.
5.3 Reflection coefficients
The energy matrix defined in subsection 4.4 is calculated for a given value of incident angle  varying from
varying from  to
to  . For the present study, the incidence is considered of only two main waves, i.e.
. For the present study, the incidence is considered of only two main waves, i.e.  and S. The low-frequency propagation is considered with circular frequency of 5kHz. The energy shares
and S. The low-frequency propagation is considered with circular frequency of 5kHz. The energy shares  and
and  are computed and conservation of incident energy is ensured for each incidence. The
are computed and conservation of incident energy is ensured for each incidence. The  and
and  denote the reflection coefficients for the reflected
denote the reflection coefficients for the reflected  and S waves, respectively. The variations of energy shares of reflected waves and interaction energies
and S waves, respectively. The variations of energy shares of reflected waves and interaction energies  ,
,  ) with incident angle are shown in figures 5 to 8 (for incident
) with incident angle are shown in figures 5 to 8 (for incident  wave) and in figures 9 to 12 (for incident S wave). The detailed discussion on figures is as follows.
wave) and in figures 9 to 12 (for incident S wave). The detailed discussion on figures is as follows.
The Fig. 5 exhibits the energy variations for three values (i.e. 0, 0.3, 0.5) of inhomogeneity parameter  . Values chosen for other parameters are
. Values chosen for other parameters are 
 It is noted that homogeneous propagation means almost no interaction of waves. In general, the presence of wave inhomogeneity strengthens the reflected waves with extra energy coming from the interaction (interference) of inhomogeneous waves present in the medium. It is quite evident that the energy shares of two slower longitudinal
It is noted that homogeneous propagation means almost no interaction of waves. In general, the presence of wave inhomogeneity strengthens the reflected waves with extra energy coming from the interaction (interference) of inhomogeneous waves present in the medium. It is quite evident that the energy shares of two slower longitudinal  waves are negligible. Further, the reflected
waves are negligible. Further, the reflected  waves get more stronger with the increase of inhomogeneity strength of incident wave. Near the normal incidence, for any
waves get more stronger with the increase of inhomogeneity strength of incident wave. Near the normal incidence, for any  reflected
reflected  waves have larger energy shares. On the other hand, at grazing incidence, for any
waves have larger energy shares. On the other hand, at grazing incidence, for any  only reflected S wave has a significant energy share. Negative sign of interaction energy implies the travel of energy towards the interface.
only reflected S wave has a significant energy share. Negative sign of interaction energy implies the travel of energy towards the interface.
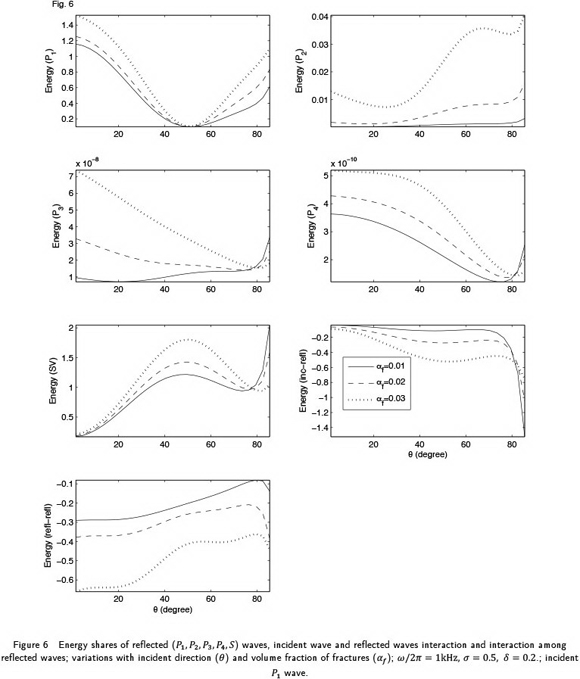
The Fig. 6 exhibits the energy variations for three values (i.e., 0.01, 0.02, 0.03) of volume fraction of fractures (i.e.  ). Values chosen for other parameters are
). Values chosen for other parameters are 
 . It is quite evident that the reflected
. It is quite evident that the reflected  waves get more stronger with the increase of volume fraction of fractures. Near the normal incidence, for any
waves get more stronger with the increase of volume fraction of fractures. Near the normal incidence, for any  , reflected
, reflected  waves have larger energy shares. On the other hand, at grazing incidence, for any
waves have larger energy shares. On the other hand, at grazing incidence, for any  , only reflected S wave has a significant energy share. From the energy shares of reflected waves, it is crystal clear that existence of the two slower longitudinal (i.e.
, only reflected S wave has a significant energy share. From the energy shares of reflected waves, it is crystal clear that existence of the two slower longitudinal (i.e.  and
and  ) waves is namesake. A significant effect of volume fraction change is noticed on the interaction energies (
) waves is namesake. A significant effect of volume fraction change is noticed on the interaction energies ( ).
).
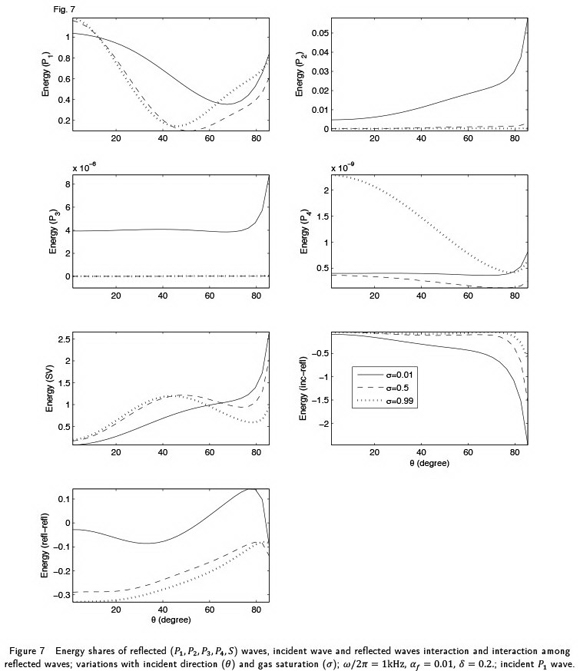
The Fig. 7 exhibits the energy variations for three different values (i.e., 0.01, 0.5, 0.99) of gas saturation (i.e.,  ). Values chosen for other parameters are
). Values chosen for other parameters are 
 . From the plots, it is quite evident that the significant energy shares of
. From the plots, it is quite evident that the significant energy shares of  wave, particularly for
wave, particularly for  It was also noticed that
It was also noticed that  and
and  waves are weakest when pore space is shared equally by two fluids. This implies that little gas share of gas in pores is more important for the existence of slower P waves then all gas or all liquid in pores. For the incidence below
waves are weakest when pore space is shared equally by two fluids. This implies that little gas share of gas in pores is more important for the existence of slower P waves then all gas or all liquid in pores. For the incidence below  , the reflected
, the reflected  wave strengthens with the increase of gas share in pores and beyond
wave strengthens with the increase of gas share in pores and beyond  , the reflected
, the reflected  wave weaken with the increase of gas share in pores, up to the incidence
wave weaken with the increase of gas share in pores, up to the incidence  . Further, it is noticed that for the incidence below
. Further, it is noticed that for the incidence below  , the reflected S wave strengthens with the increase of gas share in pores and beyond
, the reflected S wave strengthens with the increase of gas share in pores and beyond  , the reflected S wave weaken a lot with the increase of gas share in pores. A significant effect of saturating pore-fluid is noticed on the variations of interaction energies (i.e.,
, the reflected S wave weaken a lot with the increase of gas share in pores. A significant effect of saturating pore-fluid is noticed on the variations of interaction energies (i.e.,  ).
).
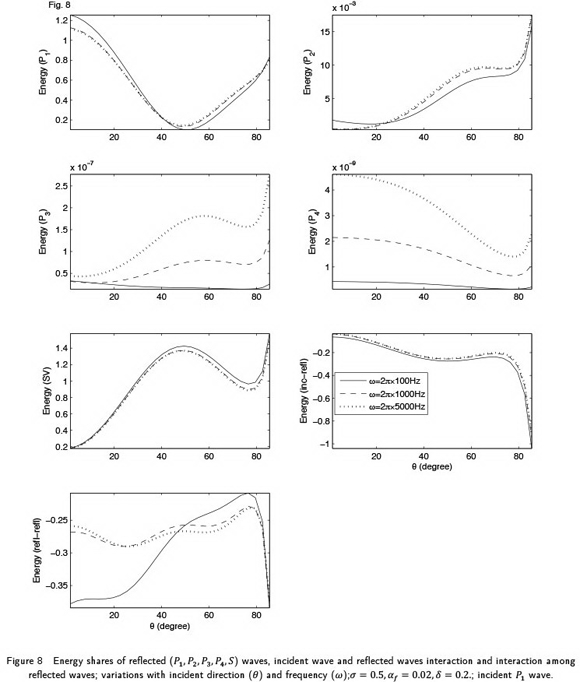
The variations of the energy shares with the incident direction are shown in Fig. 8, for three different frequencies i.e.,  Values chosen for other parameters are
Values chosen for other parameters are  From the plots, it is noticed that a little effect of frequency change is observed on the energy shares of reflected
From the plots, it is noticed that a little effect of frequency change is observed on the energy shares of reflected  and S waves. The effect of frequency is observed mainly for reflected
and S waves. The effect of frequency is observed mainly for reflected  waves and interaction energy (
waves and interaction energy ( ).
).
For the incidence of the S wave, energy partition at the surface is presented in Fig. 9 for three values (i.e., 0, 0.1, 0.2) of inhomogeneity parameter  . Values chosen for other parameters are
. Values chosen for other parameters are 
 The zero value of
The zero value of  denotes the incidence of homogenous wave and a critical angle for reflected
denotes the incidence of homogenous wave and a critical angle for reflected  wave is around
wave is around  . Except near this critical incidence, more inhomogeneity of incident wave results in stronger reflected waves as well as excessive interaction. The energy shares are much larger near the grazing incidence. The reflection coefficients of
. Except near this critical incidence, more inhomogeneity of incident wave results in stronger reflected waves as well as excessive interaction. The energy shares are much larger near the grazing incidence. The reflection coefficients of  and
and  waves are negligible. Further, it is quite evident that beyond critical incidence inhomogeneous propagation of waves is occurred for
waves are negligible. Further, it is quite evident that beyond critical incidence inhomogeneous propagation of waves is occurred for  .
.
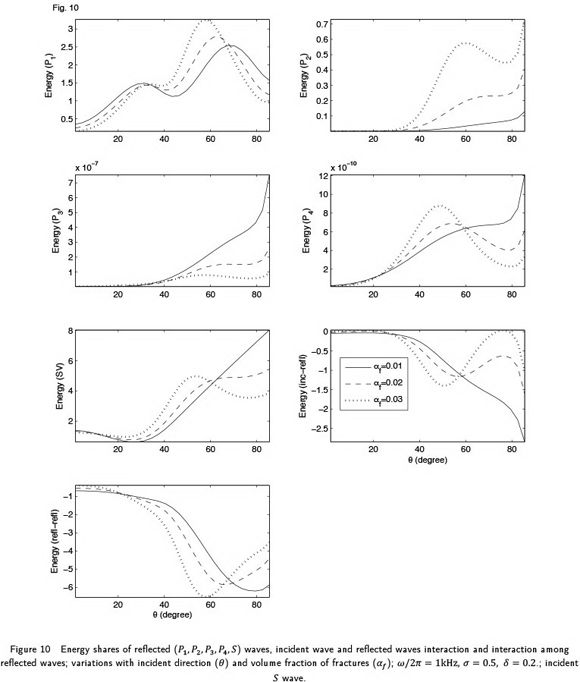
Fig. 10 exhibits the variations of the energy shares with the incident direction for three different values (i.e., 0.01, 0.02, 0.03) of volume fraction of fractures (i.e.,  ). Values chosen for other parameters are
). Values chosen for other parameters are 
 . From the plots, it is noticed that the energy shares of all the the reflected waves, except
. From the plots, it is noticed that the energy shares of all the the reflected waves, except  wave are decreases with the increase of volume fraction of fractures, near the grazing incidence. It is quite evident that beyond
wave are decreases with the increase of volume fraction of fractures, near the grazing incidence. It is quite evident that beyond  , for any
, for any  , the reflected
, the reflected  wave have significant energy shares. Therefore, out of slower P waves, only
wave have significant energy shares. Therefore, out of slower P waves, only  wave is significant. For the incidence below
wave is significant. For the incidence below  , the energy shares of reflected
, the energy shares of reflected  wave decreases with the increase of
wave decreases with the increase of  and after that it start increasing with the increase of
and after that it start increasing with the increase of  . Then, beyond
. Then, beyond  , it again decreases with the increase of
, it again decreases with the increase of  . A noticeable effect of volume fraction of fractures is observed on the energy shares of all the reflected waves and interaction energies.
. A noticeable effect of volume fraction of fractures is observed on the energy shares of all the reflected waves and interaction energies.
Fig. 11 exhibits the variations of the energy shares with the incident direction for three different values (i.e., 0.01, 0.5, 0.99) of gas saturation (i.e.,  ). Values chosen for other parameters are
). Values chosen for other parameters are 
 . It is quite evident that near grazing incidence, for any value of
. It is quite evident that near grazing incidence, for any value of  , the energy shares of reflected S wave dominates over other reflected waves. A significant energy shares of reflected
, the energy shares of reflected S wave dominates over other reflected waves. A significant energy shares of reflected  wave is observed, particularly for
wave is observed, particularly for  . A noticeable effect of gas shares is observed on the energy shares of all the reflected waves and interaction energies.
. A noticeable effect of gas shares is observed on the energy shares of all the reflected waves and interaction energies.
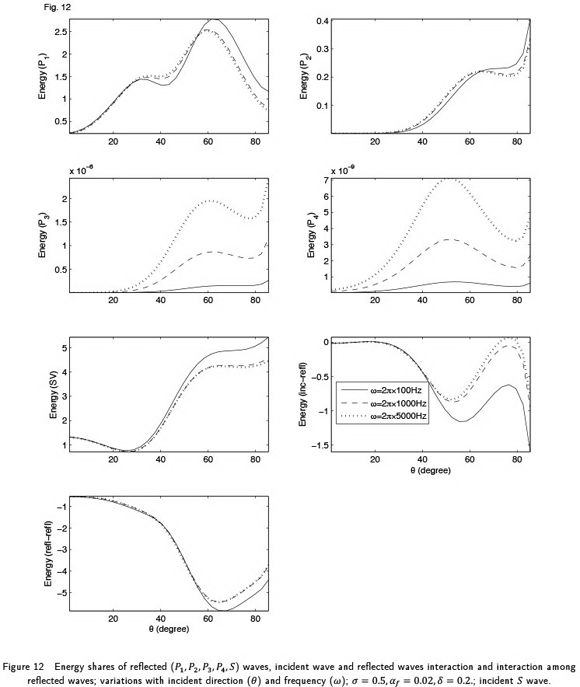
The variations of the energy shares with the incident direction are shown in Fig. 12, for three different frequencies i.e.,  Values chosen for other parameters are
Values chosen for other parameters are  Similar to the case on incident
Similar to the case on incident  wave in Fig. 8, a little effect of frequency change is observed on the energy shares of reflected
wave in Fig. 8, a little effect of frequency change is observed on the energy shares of reflected  and S waves. The effect of frequency is observed mainly for reflected
and S waves. The effect of frequency is observed mainly for reflected  waves and interaction energy (
waves and interaction energy ( ).
).
6 CONCLUDING REMARKS
The work presented studies the inhomogeneous propagation of five attenuated (four dilatational and one shear) waves in a fractured porous solid. The fractured porous medium is dissipative due to the presence of viscous fluids in primary pores as well as secondary pores. The five attenuated waves in this dissipative medium are identified with complex velocities, which are resolved to calculate their phase velocities and attenuation coefficients for the general inhomogeneous propagation defined through a finite non-dimensional parameter. The variable gas share in pores enables to represent the pore saturation from almost all liquid to all gas. Reflection phenomenon is studied for incidence of only two main waves, that is  and S. The changes in reflection energy coefficients are analyzed for a particular numerical model with variations in gas share in pores, frequency, volume fraction of fractures and inhomogeneity of incident wave. Some interesting observations from the numerical example may be important and hence are explained as follows.
and S. The changes in reflection energy coefficients are analyzed for a particular numerical model with variations in gas share in pores, frequency, volume fraction of fractures and inhomogeneity of incident wave. Some interesting observations from the numerical example may be important and hence are explained as follows.
-
The phase velocities of all the waves may reduces to half with the change in propagation from homogeneous to evanescent. Attenuation increases with frequency as well as inhomogeneity. That means, the homogeneous waves may travel faster but cannot represent the wave motion with a larger attenuation. Moreover, a slower wave attenuates more in dissipative medium.
-
Any change in frequency may not affect the phase velocity of two faster (
 , S) waves.
, S) waves. -
The increase of gas share increases the phase velocity of S wave whereas longitudinal waves except one
 travel faster when the pore space is filled only with liquid.
travel faster when the pore space is filled only with liquid. -
The increase of volume fraction of fractures (i.e.
 ) decreases the phase velocity of faster
) decreases the phase velocity of faster  wave whereas phase velocity of other slower longitudinal waves increases with the increase of
wave whereas phase velocity of other slower longitudinal waves increases with the increase of  However, the effect of
However, the effect of  is not observed on the phase velocity and attenuation of S wave.
is not observed on the phase velocity and attenuation of S wave. -
The variations of the phase velocity of a longitudinal wave with, frequency as well as volume fraction of fractures appear nearly opposite to the variations in its attenuation coefficient.
-
The variations of the phase velocity of a wave with inhomogeneity appear nearly opposite to the variations in its attenuation coefficient. Moreover, the attenuation of two main waves is attributed more to the inhomogeneous propagation than the presence or increase of gas share in pores.
-
For the considered numerical model, critical angle is observed only for reflected
 wave resulting from the incidence of the S wave, particularly for
wave resulting from the incidence of the S wave, particularly for  .
. -
For the incidence of
 waves, out of slower P waves, only
waves, out of slower P waves, only  wave is significant. However, slower
wave is significant. However, slower  and
and  waves are just negligible.
waves are just negligible. -
An increase of volume fraction of fractures may strengthen the reflected
 wave from the near-normal incidence of
wave from the near-normal incidence of  wave. However, for incidence near-grazing, an increase of volume fraction of fractures may strengthen the reflected
wave. However, for incidence near-grazing, an increase of volume fraction of fractures may strengthen the reflected  and
and  waves whereas reflected
waves whereas reflected  and S waves may weaken.
and S waves may weaken. -
At the normal incidence of S wave, the change of volume fraction of fractures may have negligible effect on the energy shares of all reflected waves except
 wave. While at the grazing incidence of S wave, an increase of volume fraction of fractures may weaken the reflected
wave. While at the grazing incidence of S wave, an increase of volume fraction of fractures may weaken the reflected  and S waves whereas reflected
and S waves whereas reflected  wave may strengthen.
wave may strengthen. -
The effect of inhomogeneity, volume fraction of fractures, frequency and gas shares in pores on energy partition is observed for all the reflected waves.
-
Conservation of the incident energy is obtained for the presence of interaction energies due to the interference of incident wave and reflected waves. This certifies the correctness of all the analytic derivations which form the complete procedure.
Appendix
where
where  and
and  denote the bulk modulus of non-wetting fluid phase, wetting fluid phase, solid grains, fractured porous medium and non-fractured porous medium, respectively.
denote the bulk modulus of non-wetting fluid phase, wetting fluid phase, solid grains, fractured porous medium and non-fractured porous medium, respectively.  is the volume fraction of phase i.
is the volume fraction of phase i.  is the fraction of non-wetting fluid saturation in the composite medium. F is a material parameter associated with the change in volume fraction of fractures
is the fraction of non-wetting fluid saturation in the composite medium. F is a material parameter associated with the change in volume fraction of fractures  is equivalent bulk modulus for macroscopic capillary pressure (Garg & Nayfeh 1986).
is equivalent bulk modulus for macroscopic capillary pressure (Garg & Nayfeh 1986).
- Achenbach, J. D., 1973. Wave Propagation in Elastic Solids. 1st Edition, North-Holland Publishing, Amsterdam.
- Aifantis, E. C., 1977. Introducing a multiporous medium. Development in Mechanics 8, 209-211.
- Aifantis, E. C., 1979. On the response of fractured rocks. Development in Mechanics 8, 249-253.
- Aifantis, E. C., 1980. On the problem of diffusion in solids. Acta Mechanica 37, 265-296.
- Ainslie, M. A., and Burns, P. W., 1995. Energy-conserving reflection and transmission coefficients for a solid-solid boundary. Journal of the Acoustical Society of America 98, 2836-2840.
- Arora, A., Tomar, S. K., 2010. Seismic reflection from an interface between an elastic solid and a fractured porous medium with partial saturation. Transport in Porous Media 85(2), 375-396.
- Auriault, J. L., Boutin, C., 1993. Deformable porous media with double porosity. Transport in Porous Media 10, 153-159.
- Bai, M., Elsworth, D., Roegiers, J. C., 1993. Modelling of naturally fractured reservoirs using deformation dependant flow mechanism. International Journal of Rock Mechanics and Mining Sciences and Geomechanics 30(7), 1185-1191.
- Barenblatt, G. I., Zheltov, I. P., Kochina, I. N., 1960. Basic concepts in the theory of seepage of homogeneous liquids in fractured rocks (strata). Prikladnaya Matematika i Mekhanika 24(5), 1286-1303.
- Berryman, J. G., 1980. Confirmation of Biot's theory. Applied Physics Letters 37(4), 382-384.
- Berryman, J.G., Wang, H.F., 1995. The elastic coefficients of double-porous models for fluid transport in jointed rock. Journal of Geophysical Research: Solid Earth 100, 24611-24627.
- Berryman, J.G., Wang, H.F., 2000. Elastic wave propagation and attenuation in a double-porosity dual-permeability media. International Journal of Rock Mechanics and Mining Science 37, 63-78.
- Beskos, D.E., Aifantis, E.C., 1986. On the theory of consolidation with double porosity-II. International Journal of Engineering Science 24, 1697-1716.
- Biot, M. A., 1956. Theory of propagation of elastic waves in a fluid saturated porous solid, I. Low-frequency range, II. Higher frequency range. Journal of the Acoustical Society of America 28(2), 168-191.
- Biot, M. A., 1962. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics 33, 1482-1498.
- Biot, M. A., 1962. Generalized theory of acoustic propagation in porous dissipative media. Journal of the Acoustical Society of America 34(5), 1254-1264.
- Borcherdt, R.D., 1982. Reflection-refraction of general P and type-I S waves in elastic and anelastic solids. Geophysical Journal of Royal Astronomical Society 70, 621-638.
- Carcione, J. M., Cavallini, F., 1995. Forbidden directions for inhomogeneous pure shear waves in dissipative anisotropic media. Geophysics 60, 522-530.
- Deresiewicz, H., Skalak, R., 1963. On uniqueness in dynamic poroelasticity. Bulletin of the Seismological Society of America 53, 783-789.
- Duguid, J. O., Lee, P.C.Y., 1977. Flow in fractured porous media. Water Resources Research 13(3), 558-566.
- Krebes, E. S., 1983. The viscoelastic reflection/ transmission problem: two special cases. Bulletin of Seismological Society of America 73, 1673-1683.
- Krebes, E. S., Le, L. H. T., 1994. Inhomogeneous plane waves and cylindrical waves in anisotropic anelastic media. Journal of Geophysical Research 99, 23899-23919.
- Khaled, M. Y., Beskos, D. E., Aifantis, E. C., 1984. On the theory of consolidation with double porosity-III. A finite element formulation. International Journal for Numerical and Analytical Methods in Geomechanics 8, 101-123.
- Khalili, N., 2003. Coupling effects in double porosity media with deformable matrix. Geophysical Research Letters 30(22), 2153. doi:10.1029/2003GL018544.
- Khalili, N., Valliappan, S., 1996. Unified theory of flow and deformation in double porous media. European Journal of Mechanics A/Solids 15(2), 321-336.
- Khalili-Naghadeh, N., Valliappan, S., 1991. Flow through fractured porous media with deformable matrix: Implicit formulation. Water Resources Research 27(7), 1703-1709.
- Khalili, N., Valliappan, S., Wan, C. F., 1999. Consolidation of fractured clays. Geotechnique, 49(1), 75-89.
- Kumar, M., Saini, R., 2012. Reflection and refraction of attenuated waves at boundary of elastic solid and porous solid saturated with two immiscible viscous fluids. Applied Mathematics and Mechanics 33(6), 2012, 797-816.
- Kumar, M., Sharma, M. D., 2013. Reflection and transmission of attenuated waves at the boundary between two dissimilar poroelastic solids saturated with two immiscible viscous fluids. Geophysical Prospecting 61(5), 1035-1055.
- Loret, B., Rizzi, E., 1999. Strain localization in fluid saturated anisotropic elastic-plastic porous media with double porosity. Journal of the Mechanics and Physics of Solids 47, 503-530.
- Plona, T. J., 1980. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Applied Physics Letters 36(4), 259-261.
- Sams, M.S., Neep, J.P., Worthington, M.H., King, M. S., 1997. The measurements of velocity dispersion and frequency-dependent intrinsic attenuation in sedimentary rocks. Geophysics 62, 1456-1464.
- Sharma, M. D., 2008. Propagation of inhomogeneous plane waves in viscoelastic anisotropic media. Acta Mechanica 200, 145-154.
- Sharma, M. D., Kumar, M., 2011. Reflection of attenuated waves at the surface of a porous solid saturated with two immiscible viscous fluids. Geophysical Journal International 184, 371-384.
- Sharma, M. D., Saini, R., 2012. Wave propagation in porous solid containing liquid filled bound pores and two-phase fluid in connected pores. European Journal of Mechanics A/Solids 36, 53-65.
- Tuncay, K., Corapcioglu, M.Y., 1996a. Wave propagation in fractured porous media. Transport in Porous Media 23, 237-258.
- Tuncay, K., Corapcioglu, M.Y., 1996b. Body waves in fractured porous media saturated by two immiscible newtonian fluids. Transport in Porous Media 23, 259-273.
- Tuncay, K., Corapcioglu, M.Y., 1997. Wave propagation in poroelastic media saturated by two fluids. Journal of Applied Mechanics 64, 313-319.
- Valliappan, S., Khalili-Naghadeh, N., 1990. Flow through fractured porous media with deformable matrix. International Journal of Numerical Method in Engineering Science 29, 1079-1094.
- Wang, H. F., Berryman, J. G., 1996. On constitutive equations and effective stress principles for deformable, double-porosity media. Water Resources Research 32(12), 3621-3622.
- Warren, J. B., Root, P. J., 1963. The behaviour of naturally fractured reservoirs. Society of Petroleum Engineers Journal 3, 245-255.
- Wilson, R. K., Aifantis, E. C., 1982. On the theory of consolidation with double porosity-II. International Journal of Engineering Science 20(9), 1009-1035.
- Wilson, R. K., Aifantis, E. C., 1984. A double porosity model for acoustic wave propagation in fractured-porous rock. International Journal of Engineering Science 22, 1209-1217.
Appendix
Publication Dates
-
Publication in this collection
13 Mar 2014 -
Date of issue
Dec 2014